Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Minerals such as zircon are routinely used by geochronologists to confidently provide the U-Pb and Pb-Pb ages which underpin the conventional multi-millions-of-years’ time scale. These dating methods and the underlying assumptions are reviewed. It is then documented from the conventional literature that both U and Pb isotopes naturally mass fractionate due to the nuclear-field shift effect and differential mass diffusion. Furthermore, the beams used in the instruments to sample tiny volumes of such minerals for their mass spectrometer isotopic analyses also cause isotopic mass fractionation, especially of Pb isotopes. Much effort has thus been expended in the conventional geochronology community to quantify the amounts of fractionation the various beams induce so that appropriate uncertainties can be stipulated for the obtained U-Pb and Pb-Pb dates. However, all such efforts involve the use of standards of “known” ages determined by U-Pb, Pb-Pb and /or other radiometric methods such as K-Ar or Ar-Ar. This is circular reasoning, especially compounded by the decay constants of all the other parent isotopes used for dating the standards having been calibrated against the 238U decay constant. Yet the uncertainties are still significant and are compounded further by the uncertainties in the measured 238U and 235U decay rates, the crucial 238U/235U ratio, the amount and composition of inherited, initial and/or common Pb, and the possibility of both U and Pb mobility after minerals and the rocks containing them were formed. Thus, the resultant U-Pb and Pb-Pb ages obtained are subjective and only provide systematic relative ages, even though geochronologists take numerous precautions to make the U-Pb and Pb-Pb methods still have a strong aura of validity. Yet all these uncertainties are overshadowed by the underlying unprovable assumptions on which the radioisotope dating methods are based, especially the assumption of time-invariant decay rates, built on the foundation of an assumed deep time history. Instead, the evidence for grossly accelerated radioisotope decay during a past cataclysmic event such as the Genesis Flood has been well established. Therefore, those absolute ages cannot be used to dismiss the history of the earth and its approximately 6,000-year chronology provided in God’s infallible Word.
Keywords: radioisotope dating, half-lives, 238U, 235U, 206Pb, 207Pb, uranium-lead dating, 238U/235U, lead-lead dating, Pb-Pb isochrons, zircons, diffusion, TIMS, SIMS, LA-ICP-MS, isotope mass fractionation, standards, uncertainties, assumptions, circular reasoning, accelerated radioisotope decay
Introduction
Radioisotope dating of minerals, rocks and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Many in both the scientific community and the general public around the world thus remain convinced of the earth’s claimed great antiquity.
The decay of 238U and 235U to 206Pb and 207Pb, respectively, forms the basis for one of the oldest methods of geochronology (Dickin 2005; Faure and Mensing 2005). While the earliest studies focused on uraninite (an uncommon mineral in igneous rocks), there has been intensive and continuous effort over the past five decades to utilize U-Pb dating of more-commonly occurring trace minerals. Zircon (ZrSiO4) in particular has been the focus of thousands of geochronological studies, because of its ubiquity in felsic igneous rocks and its claimed extreme resistance to isotopic resetting (Begemann et al. 2001).
However, accurate radioisotopic age determinations require that the decay constants or half-lives of the respective parent radionuclides be accurately known and constant in time. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is still not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with direct half-life determinations are, in most cases, still at the 1% level, which is still significantly better than any radioisotope method for determining the ages of rock formations. However, even uncertainties of only 1% in the half-lives lead to very significant discrepancies in the derived radioisotope ages. The recognition of an urgent need to improve the situation is not new (for example, Renne, Karner, and Ludwig 1998; Min et al. 2000). It continues to be mentioned, at one time or another, by every group active in geo-or cosmochronology (Boehnke and Harrison 2014; Schmitz 2012).
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further in-roads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was the issue of how reliable the determinations of the radioisotope decay rates are, which are so crucial for calibrating these dating “clocks.” However, in a recent series of papers, Snelling (2014a, b, 2015a, b, 2016, 2017a) reviewed how the half-lives of the parent radioisotopes used in long-age geological dating have been determined and collated all the determinations of them reported in the literature to discuss the accuracy of their currently accepted values. He documented the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes 87Rb, 176Lu, 187Re, 147Sm, 40K, 238U, and 235U which are used as the basis for the Rb-Sr, Lu-Hf, Re-Os, Sm-Nd, K-Ar, Ar-Ar, U-Pb, and Pb-Pb long-age dating methods respectively. He showed that there is still some uncertainty in what the values for these measures of the 87Rb, 176Lu, 40K, and 235U decay rates should be, in contrast to the apparent agreement on the 187Re, 147Sm, and 238U decay rates. This uncertainty is especially prominent in determinations of the176Lu decay rate by physical direct counting experiments. Furthermore, the determined values of the 87Rb decay rate differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rates of isotopes such as 87Rb, 176Lu, 187Re, and 147Sm used for deep time dating that makes precise measurements of their decay rates so difficult. Thus, it could be argued that direct measurements of their decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology employed by the secular community in their rock dating methods.
Ultimately, the 87Rb, 176Lu, 187Re, 147Sm, and 40K decay half-lives have all been calibrated against the U-Pb radioisotope systems. This is the case even for the 147Sm decay half-life whose accepted value has not changed since it was calibrated against the U-Pb dating of two meteorites in the 1970s, in spite of the fact that more recent thorough physical direct counting experiments suggest a higher value. However, confidence in U-Pb radioisotope dating as the “gold standard” is very questionable, as there are now known measured variations in the 238U/235U ratio that is critical to that method (Brennecka and Wadhwa 2012; Goldmann et al. 2015; Hiess et al 2012; Tissot and Dauphas 2015), as well as uncertainties as to the 238U and 235U decay rate values (Mattinson 2010; Schön, Winkler, and Kutschera 2004; Schoene et al. 2006; Snelling 2017a; Villa et al. 2016). It is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life measurements because these are difficult measurements to make. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks and minerals, and the question still remains as to whether the half-life values for each long-lived parent radioisotope are independently determined.
Nevertheless, accurate radioisotope age determinations not only depend on accurate determinations of the decay constants or half-lives of the respective parent radioisotopes, but on the reliability of the other two assumptions these supposed absolute dating methods rely on. Those are the starting conditions and no contamination of closed systems. Both of these assumptions are unprovable. Yet they can supposedly be circumvented somewhat via the isochron technique, because it is claimed to be independent of the starting conditions and sensitive to revealing any contamination, which is still significantly better than any of the model radioisotope age methods for determining the ages of rock formations. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. That this is common practice is illustrated with numerous examples cited from the literature throughout the textbooks by Faure and Mensing (2005) and Dickin (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is arbitrary and therefore is not good science, because it is merely assumed the “aberrant” values are due to contamination rather than that being proven to be so. Indeed, in order to discard such outliers in any data set, one must establish a reason for discarding those data points which cannot be reasonably questioned.
Undoubtedly the U-Pb and Pb-Pb radioisotope dating methods are now the cornerstone in current geochronology studies. Thus, it is imperative every aspect of the methodology used in these methods be carefully examined to investigate whether the age results obtained by them are really as accurate and absolute as portrayed in the geological literature. Therefore, it is highly significant that Amelin et al. (2009) listed the potential problems which cause possible inaccuracies in obtaining reliable U-Pb and Pb-Pb ages. These are:
- Presence of non-radiogenic Pb of unknown isotopic composition;
- Deviations from closed system evolution (loss of Pb, gain or loss of U);
- Misidentification of the processes that start or reset the isotopic clocks;
- Analytical problems (fractionation, instrument specific, etc.) and blank subtraction;
- Fractionation of radiogenic Pb isotopes induced by leaching of alpha recoil tracks;
- Variations in the 238U/235U ratio;
- Uncertainties in the half-lives of 238U and 235U; and
- Deviations of the 234U/238U ratio from secular equilibrium.
Of these eight potential problems, Amelin et al. (2009) admitted that the first five are important and common, whereas the last three they considered insignificant or unlikely. But recent research has even found that these last three problems are more critical than they estimated, not least the variations in the 238U/235U ratio (Goldmann et al. 2015; Tissot and Dauphas 2015), and the uncertainties in the half lives of 238U and 235U (Boehnke and Harrison 2014; Snelling 2017a).
But what of the other five of the eight problems listed by Amelin at al. (2009)? Snelling (2017b) has closely examined the first of them, the problem of the presence of non-radiogenic Pb of unknown isotopic composition, that is, common, initial or primordial Pb. It was demonstrated that by being unable to be sure of the starting isotopic composition of the U-Pb system in a rock or mineral from that measured today, it is simply not possible to be so sure that the determined U-Pb age is absolute. Then Snelling (2018) investigated the evidence of deviations from close system evolution of U-Pb systems, as well as misidentification of the processes that start or reset the isotopic clocks. Indeed, the mobility of both Pb and U at all observational scales underscores that the U-Pb system in rocks and minerals is never closed. Thus, this foundational dating method is rendered unreliable due to the inherent uncertainties of the ever-present, difficult-to-measure mobilities of the U and Pb atoms.
So, it is now the last of these potential problems listed by Amelin et al. (2009) on which we need to focus, namely, the fractionation of U and Pb isotopes within minerals, and particularly during the use of the necessary analytical instruments But before that, there is a need to go over some important background informational issues germane to this subject.
Uranium and Lead Geochemistry
Uranium is element 92 (Z = 92) and a member of the actinide series in which the 5f orbitals are progressively filled with electrons. It occurs naturally in the tetravalent oxidation state U4+ with an ionic radius of 1.05 Å. But under oxidizing conditions forms the uranyl ion (UO22+) in which U has a valence of 6+. The uranyl ion forms compounds that are soluble in water, so U is a mobile element under oxidizing conditions. In contrast to U, Pb (Z = 82) is in period 6 and is a group 14 post-transitional metal. It is insoluble in water but is a chalcophile element because it reacts with sulfur. It forms Pb2+ and Pb4+ ions with ionic radii of 1.32 Å and 0.91 Å respectively, so Pb ions cannot substitute for U ions in minerals.
In the course of partial melting of the rocks in the earth’s mantle U is concentrated in the liquid (melt) phase and thus becomes incorporated into the more silica-rich products. Thus, the progressive geochemical differentiation of the earth’s upper mantle has enriched the rocks of the earth’s continental crust in U compared to those of the upper mantle. At an average of 1.3 ppm U is the 51st most abundant element in the earth’s crust, whereas Pb is regarded as quite a common element in the earth’s crust with an average of 11 ppm (Rudnick and Gao 2005). The concentrations of U and Pb increase from basaltic rocks (0.5 ppm U and 4 ppm Pb) to granites (5 ppm U and 23 ppm Pb) (Faure and Mensing 2005). The concentrations of U in the common rock-forming silicate minerals are uniformly low, on the order of a few ppm or less. Instead, U occurs primarily in certain accessory minerals in which it is either a major constituent or replaces other elements. These minerals include uraninite, zircon, baddeleyite, monazite, apatite, and sphene (titanite).
All six naturally occurring U isotopes are unstable and decay. Of these, 238U is the dominantly abundant isotope in natural U. It and 235U, the next most abundant isotope, are the starting radioisotopes in two decay chains or series (figs. 1 and 2), with 234U one of the early steps in the 238U decay chain. There are also several other trace U isotopes. 239U is formed indirectly when 238U undergoes spontaneous fission as neutrons released by 238U are captured by other 238U atoms. 237U is formed when 238U captures a neutron but emits two more, which then decays to 237Np (neptunium). And then 233U is formed in the decay chain of that 237Np. 233U is also made from 232Th by neutron bombardment, usually in a nuclear reactor.
On the other hand, Pb has four stable isotopes, three of which (206Pb, 207Pb and 208Pb) are the end members of decay chains (238U, 235U and 232Th respectively). Only stable 204Pb has no radioactive precursor from which it is derived, and thus it is often called common Pb. Thus, the isotopic concentration of Pb in a natural rock sample depends on how much U and Th are also present. Thus, for example, the relative amount of 208Pb can range from 52.4% in normal samples to 90% in thorium ores. Similarly, the ratios of 206Pb and 207Pb to 204Pb increase in different samples, since the former two are supplemented by radioactive decay of U and the latter is not. For this reason, the atomic weight of lead is given to only one decimal place. Both 214Pb and 210Pb are short-lived intermediates in the 238U decay chain (fig. 1), while 211Pb and 212Pb are short-lived intermediates in the 235U and 232Th decay chains respectively (fig. 2). Lastly, very minute traces of 209Pb are also present from the cluster decay of 223Ra, one of the daughter products of natural 235U (fig. 2). Hence, natural Pb consists of not only the four stable isotopes, but also minute traces of another five short-lived radioisotopes.
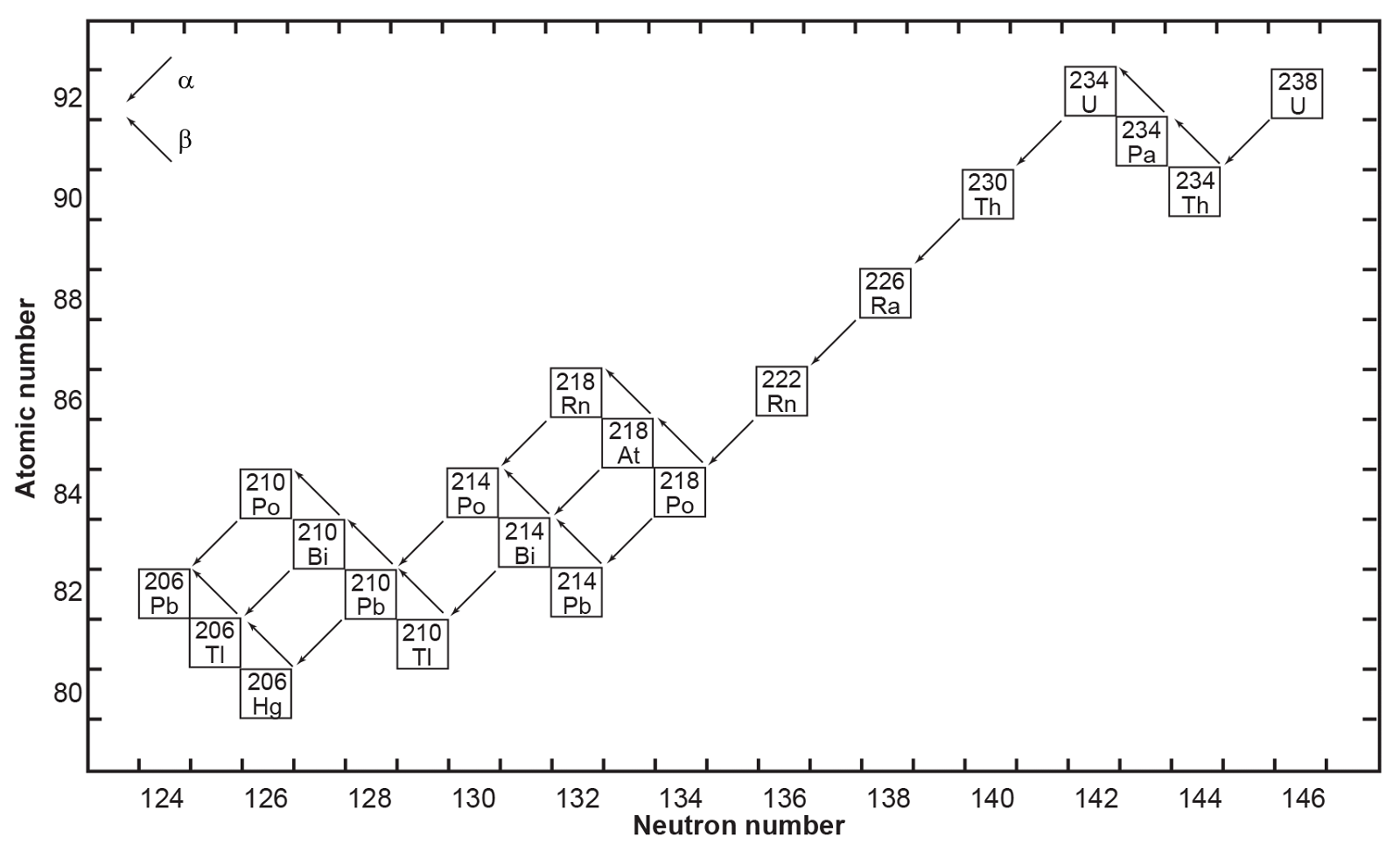
Fig. 1. The decay chain of 238U resulting from the successive emission of α-particles and β-particles from intermediate isotopes as indicated (after Faure and Mensing 2005). The final decay product is stable 206Pb.
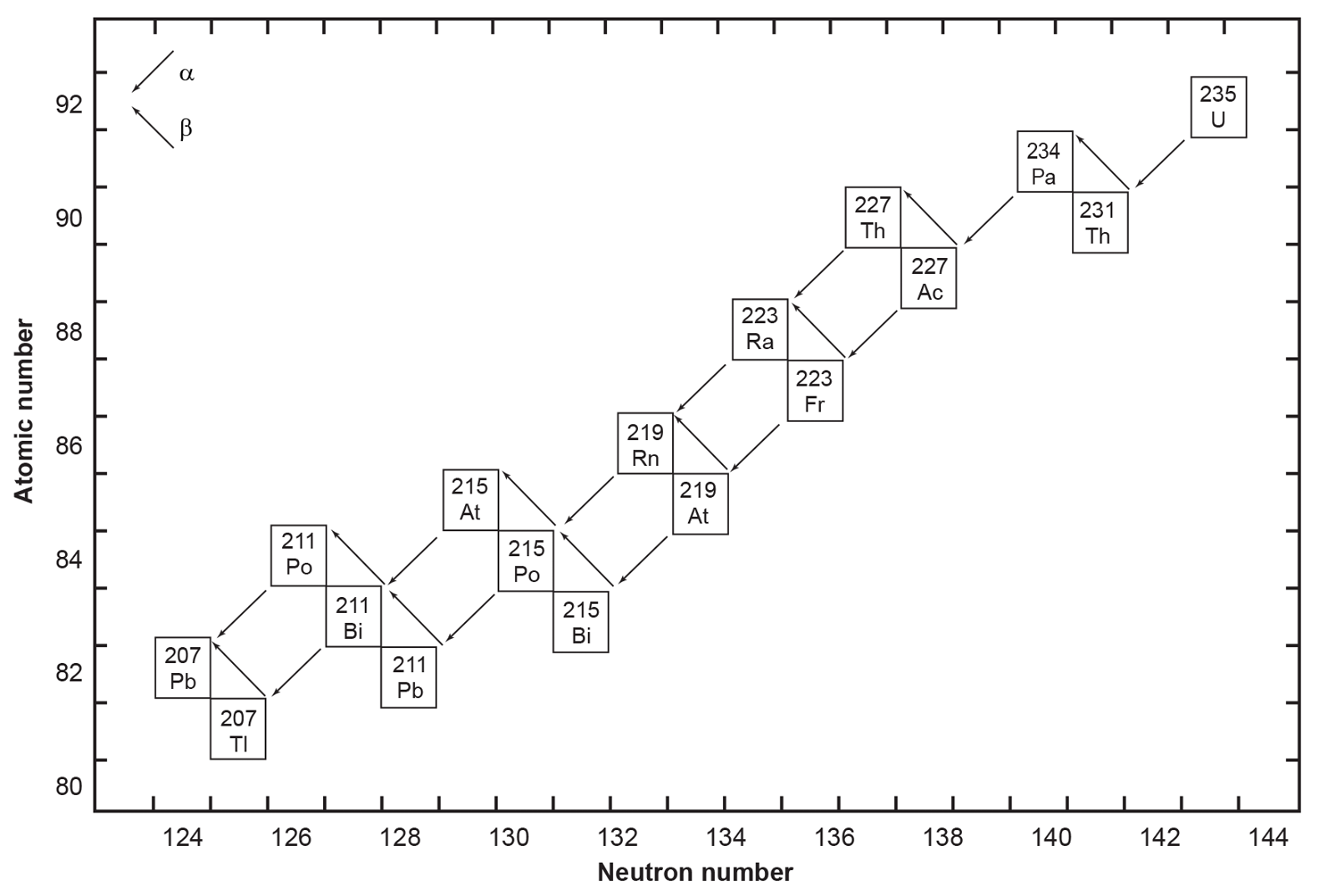
Fig. 2. The decay chain of 235U resulting from the successive emission of α-particles and β-particles from intermediate isotopes as indicated (after Faure and Mensing 2005). The final decay product is stable 207Pb.
Primordial Pb, which comprises the isotopes 204Pb, 206Pb, 207Pb, and 208Pb, has been defined as the Pb isotopic composition of troilite (FeS) in the Canyon Diablo iron meteorite (Chen and Wasserburg 1983; Tatsumoto, Knight, and Allègre 1973). It is postulated to have been mostly created as a result of repetitive rapid and slow neutron capture processes occurring in stars. Thus, it should be noted that this is not an absolute value, but merely an artifact of the reigning popular model for the naturalistic formation of the universe and its component stars and planetary systems.
238U and 235U Decay
The decay of the uranium isotopes 238U and 235U to the stable lead isotopes 206Pb and 207Pb respectively is the basis for the several most important methods of radioisotope dating. These not only derive from the transformation of 238U and 235U to 206Pb and 207Pb respectively, but also derive from the time-dependent “evolution” of common lead 204Pb from the decay of the intermediate daughters of 238U and 235U, and from the resulting isotopic composition of the accumulating daughter He (helium). Age determinations of rocks based on the decay of U and resulting accumulation of Pb and He were first attempted in the early years of the 20th century by Rutherford (1906) and Boltwood (1907). Subsequently, Holmes (1913) used chemical U-Pb and U-He dates to propose the first geological timescale based on radioisotope dating in his book on the age of the earth.
The invention of the first mass spectrometer by Thomson (1911) was followed by the work of Dempster (1918) and Ashton (1919), who designed the mass spectrographs which they used in subsequent years to discover the naturally occurring isotopes of most of the elements in the periodic table and to measure their masses and abundances. The design of mass spectrographs was further improved in the 1930s, but it was the mass spectrometers based on a design by Nier (1940) that made possible the measurement and interpretation of variations in the isotopic composition of certain elements in natural materials such as minerals and rocks. Modern mass spectrometers follow his design and achieve a high level of accuracy and reliability of operation which enable isotope ratios to be measured for radioisotope dating, such as that based on the isotopic composition of Pb due to the decay of U to Pb, but also on the isotope ratios of common Pb. As a result of continuing refinement of the analytical procedures and of the sophistication of the instrumentation, the U-Pb and Pb-Pb methods of radioisotope dating are now regarded as the most precise and accurate geochronometers for determining the ages of terrestrial and extra-terrestrial minerals and rocks.
Uranium has three naturally occurring isotopes, 238U, 235U and 234U, all of which are radioactive. 238U and 235U are the principal U isotopes that each parent a chain of radioactive daughters ending in stable isotopes of Pb. The decay of 238U gives rise to what is called the uranium series, which includes 234U as one of the intermediate daughters and ends in stable 206Pb (fig. 1). The decay of 238U to 206Pb can be summarized by the equation
238U ⟶ 206Pb + 84He + 6β- + Q (1)
where Q = 47.4 MeV per atom or 0.71 calories per gram per year (Wetherill 1966). Each atom of 238U that decays produces one atom of 206Pb by emission of eight α-particles and six β-particles. The parameter Q represents the sum of the decay energies of the entire series in units of millions of electron volts and calories of heat produced per gram per year. Several intermediate daughters in this series (fig. 1) undergo branched decay involving the emission of either an α-particle or a β-particle. The chain therefore splits into separate branches but 206Pb is the stable end product of all possible decay paths.
The decay of 235U gives rise to what is called the actinium series (fig. 2), which ends with stable 207Pb after emission of seven α-particles and four β-particles, as summarized by the equation
238U ⟶ 207Pb + 74He + 4β- + Q (2)
where Q = 45.2 MeV per atom or 4.3 calories per gram per year (Wetherill 1966). This series also branches as shown in fig. 2. In spite of there being 33 isotopes of 12 elements formed as intermediate daughters in these two decay series (not counting 4He), none is a member of more than one series. In other words, each decay chain always leads through its unique set of intermediate isotopes to the formation of a specific stable Pb isotope. The decay of 238U always produces 206Pb, and 235U always produces 207Pb.The half-lives of 238U and 235U are very much longer than those of their respective intermediate daughter isotopes. Therefore, these decay series satisfy the prerequisite condition for the establishment of secular equilibrium, provided none of the intermediate daughters escaped from the U-bearing mineral or were added from external sources (Faure and Mensing 2005). When secular equilibrium exists in a U-bearing mineral because it is a closed system, the decay rates of the intermediate daughters are equal to those of their respective parents, and thus the production rate of the stable daughter at the end of the decay chain is equal to the decay rate of its parent at the head of that chain. Therefore, the decay of 238U and 235U in minerals in which secular equilibrium has established itself can be treated as though it occurred directly to the respective 206Pb and 207Pb isotopes. As a result, the growth of these radiogenic Pb isotopes can be described by means of equations (1) and (2), which are similar to the equations used to represent the decay of 87Rb to 87Sr and 147Sm to 143Nd.
The U-Pb Dating Methods
The accumulation of stable daughter atoms from the decay of parent atoms over time is expressed by the equation known as the law of radioactivity, namely
D* = N (eλt – 1) (3)
where D* is the number of measured stable radiogenic daughter atoms, N is the number of measured parent atoms remaining, λ is the decay constant (decay rate), and t is the time since decay of the parent atoms began (Faure and Mensing 2005). [It should be noted, incidentally, that equation (3) automatically forces D* = 0 at t = 0 in the subsequent equations derived from it, which in effect assumes no stable daughter radiogenic atoms in the mineral or rock when it formed, an assumption known to be always violated!]. In any case, since D* and N can be measured in a mineral, then if λ is known the equation can be solved for t, which is thus declared to be the age of the mineral. Thus the accumulation of stable radiogenic 206Pb and 207Pb by decay of their respective parents 238U and 235U in a mineral is governed by equations derivable from equation (3) as follows
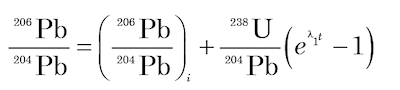 (4)
(4)
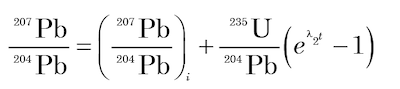 (5)
(5)
where λ1 and λ2 are the decay constants of 238U and 235U respectively; 238U/204Pb and 235U/204Pb are ratios of these isotopes calculated from the measured concentrations of U and Pb in the mineral; and the subscript i refers to the initial values of the 206Pb/204Pb and 207Pb/204Pb ratios.
To date U-bearing minerals by the U-Pb methods, the concentrations of U and Pb are measured by an appropriate analytical technique (usually isotope dilution), and the isotopic composition of Pb is determined by using a solid-source mass spectrometer, an ion-probe mass spectrometer, or an ICP mass spectrometer. The U-Pb dates are calculated by means of equations (4) and (5) being solved for t using assumed values of the initial isotope ratios of Pb (for example, Ludwig 1993) as follows
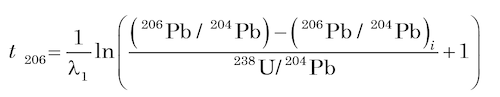 (6)
(6)
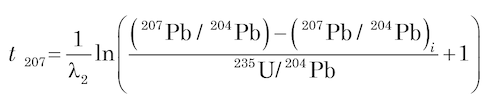 (7)
(7)
These are known as 206Pb and 207Pb model ages respectively. They are independent of each other, but will be concordant (that is, agree with each other) if the mineral samples satisfy the conditions for dating (Faure and Mensing 2005):
- The mineral has remained closed to U and Pb, and all the intermediate daughters throughout its history;
- Correct values are used for the initial Pb isotope ratios;
- The decay constants of 238U and 235U are known accurately;
- The isotopic composition of U is normal and has not been modified by isotope fractionation or by occurrence of a natural chain reaction based on induced fission of 235U; and
- All analytical results are accurate and free of systematic errors.
The assumption that the samples being dated remained closed to U, Pb, and all intermediate daughters throughout their history “is satisfied only in rare cases because U is a mobile element in oxidizing environments and therefore tends to be lost during chemical weathering” (Faure and Mensing 2005, 219, emphasis theirs). In addition, the emission of α-particles causes radiation damage to the crystal structures of the U-hosting minerals, which facilitates the loss of Pb and the other intermediate daughters in both decay chains. Consequently, U-Pb dates for rocks and minerals are rarely concordant, so procedures have been devised to overcome that problem.
The choice of the initial Pb isotope ratios would seem to only be a problem for dating rocks and minerals that have low U/Pb ratios and additionally are young. The numerical values of the initial Pb isotope ratios do not appear to significantly affect the calculated U-Pb ages of Precambrian rocks and minerals having high U/Pb ratios because their present Pb isotope ratios in most cases reach large values.
The decay constants and half-lives of 238U and 235U were fixed by the International Union of Geological Sciences (IUGS) Subcommission of Geochronology in 1975 (Steiger and Jäger 1977). At the same time a value of 137.88 was adopted for the 238U/235U ratio. Since then these values have been used in almost all U-Pb age calculations so as to avoid any potential confusion by the use of different values. It has been continually claimed that the numerical values of the 238U and 235U decay constants and half-lives are probably more accurately known that those of other long-lived radionuclides because of their importance in the nuclear industry. Therefore, refractory U-bearing minerals such as zircon (ZrSiO4) that often yield concordant U-Pb ages have been used to refine (that is, adjust) the decay constants of other radionuclides used in geochronology (Begemann et al. 2001; Snelling 2014a, b, 2015a, b, 2016).
In should be mentioned here that decay rates are not just measured and expressed by the parameter known as the decay constant (λ), but also by the parameter called the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, whereas the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:
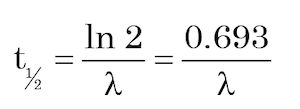 (8)
(8)
Additionally, the issue of the abundances of the U isotopes and thus the adopted value of the 238U/235U ratio deserves further comment here. Real differences in the isotopic composition of terrestrial and extra-terrestrial U have been reported. For example, uranium deposits of Precambrian age at Oklo in Gabon, Africa were found to be significantly depleted in 235U because the 235U appears to have been consumed by neutron-induced fission when these high-grade uranium deposits apparently became natural fission reactors at 1.8 Byr ago (Cowan 1976; Kuroda 1982; Lancelot, Vitrac, and Allègre 1975). The abundance of 235U in the ore mined at Oklo was as low as 0.3%, compared to 0.725% in normal U. Thus, the 238U/235U ratio is as high in the Oklo U ore as 333.33 compared to the normal 137.88. However, natural fission reactors appear to be rare. Therefore, until recently (Brennecka and Wadhwa 2012; Goldmann et al. 2015; Hiess et al 2012; Tissot and Dauphas 2015) there has been no compelling evidence to the contrary, so age determinations of terrestrial and lunar rocks and minerals, and of meteorites and their minerals, by the U-Pb method have been, and continue to be, based on a value of 137.88 for the present-day 238U/235U ratio.
It is claimed that the effect of Pb loss on U-Pb dates can be minimized by calculating a date based on the 207Pb/206Pb ratio which is supposed to be insensitive to recent Pb loss provided that the Pb which was lost from the mineral had the same isotopic composition as the Pb which remained, that is, there has been no isotopic fractionation. The relationship between the 207Pb/206Pb ratio and time results from the difference in the half-lives of 238U and 235U. The desired equation is obtained by combining equations (4) and (5) above:
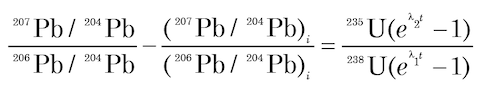 (9)
(9)
This equation has several interesting properties (Faure and Mensing 2005, 219–220):
- It involves the 235U/238U ratio which at 1/137.88 is regarded as a constant for all U of normal isotopic composition on and in the earth, the Moon, Mars, and meteorites at the present time.
- The equation does not require knowledge of the concentrations of U and Pb and involves only isotope ratios of Pb.
- The left hand side of equation (9) is equal to the 207Pb/206Pb ratio of radiogenic Pb:
where the asterisk * identifies the radiogenic isotopes.
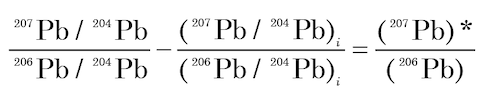 (10)
(10)
- Equation (9) cannot be solved for t by algebraic means because it is transcendental, but it can be solved by iteration and by interpolation in a table.
A difficulty arises in the solution of equation (9) when t = 0, because it yields the indeterminate result 0/0. (Faure and Mensing 2005, 220). It is claimed thus that this difficulty is overcome by means of l’Hôpital’s rule, which requires that the differentiated functions in the ratio are differentiable over the entire open interval in question, that is, over millions to billions of years (Faure and Mensing 2005, 220). However, it appears questionable whether this is a proper application of l’Hôpital’s rule. This is because the decay rates of 235U and 238U are not equal, and therefore the quantities of 235U and 238U are functions of time and thus the 235U/238U ratio must be a function of time. Hence the right side of equation (9) is not in a form amenable to l’Hôpital’s rule, that is, there are four functions of time involved in the open interval 0 < t < ta, where t = the elapsed time since the “clock” was reset. However, it appears harmless to only apply this rule to the value of (207Pb/206Pb)* at time t = 0 (the instant of clock reset) and this yields
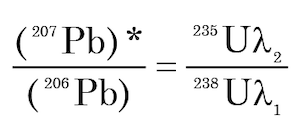 (11)
(11)
Equation (11) indicates that the (207Pb/206Pb)* which forms by the decay of 235U and 238U at the present time is equal to the rates of decay of these two U isotopes at the present time. Substituting into equation (11) the relevant values for the 235U/238U ratio, and the decay constants λ1 and λ2 yields a value at the present time (t = 0) for (207Pb/206Pb)* of 0.04604.
Incidentally, it could be argued that equation (9) from which this value for t = 0 is obtained is based on equations (4) and (5) that both use t = 0 as the beginning point for the age determination not the end point. Thus, the construction of the functional dependence of the radiogenic 207Pb/206Pb* ratio should begin at t = 0 when 207Pb/206Pb* would equal zero [based on equation (3) when t = 0] and then go forward in time. This seems to be an inconsistent application of mathematics, both in the application of l’Hôpital’s rule and the identification of t = 0 as the instant of clock reset and at the same time as the current value of the 207Pb/206Pb* ratio defined in equation (11). It would also seem that method is predicting what the radiogenic Pb isotope ratio will be in the future, not the past.
The numerical values of (eλ1t–1) and (eλ2t–1) are listed in Table 1 and yield the (207Pb/206Pb)* ratios for increasing values of t ranging from t = 0 to t = 4.6 Byr. [Incidentally, if one solves equations (4) and (5) for the U isotope concentrations at t = 0 one obtains an infinite concentration for those isotopes at t = 0!] This table can be used to solve equation (9) for t by linear interpolation based on the (207Pb/206Pb)* ratio calculated from equation (10). Conversely, by determining the (207Pb/206Pb)* ratio in a mineral from measurements of its Pb isotope ratios, the age (t) of the mineral can be calculated by linear interpolation between the (207Pb/206Pb)* ratio values in table 1. This is known as the 207Pb-206Pb model age.
| t, ×109y | eƛ1t–1 | eƛ2t–1 | 207Pb*/206Pb |
|---|---|---|---|
| 0 | 0.0000 | 0.0000 | 0.04604 |
| 0.2 | 0.0315 | 0.2177 | 0.05012 |
| 0.4 | 0.0640 | 0.4828 | 0.05471 |
| 0.6 | 0.0975 | 0.8056 | 0.05992 |
| 0.8 | 0.1321 | 1.1987 | 0.06581 |
| 1.0 | 0.1678 | 1.6774 | 0.07250 |
| 1.2 | 0.2046 | 2.2603 | 0.08012 |
| 1.4 | 0.2426 | 2.9701 | 0.08879 |
| 1.6 | 0.2817 | 3.8344 | 0.09872 |
| 1.8 | 0.3221 | 4.8869 | 0.11004 |
| 2.0 | 0.3638 | 6.1685 | 0.12298 |
| 2.2 | 0.4067 | 7.7292 | 0.13783 |
| 2.4 | 0.4511 | 9.6296 | 0.15482 |
| 2.6 | 0.4968 | 11.9437 | 0.17436 |
| 2.8 | 0.5440 | 14.7617 | 0.19680 |
| 3.0 | 0.5926 | 18.1931 | 0.22266 |
| 3.2 | 0.6428 | 22.3716 | 0.25241 |
| 3.4 | 0.6946 | 27.4597 | 0.28672 |
| 3.6 | 0.7480 | 33.6556 | 0.32634 |
| 3.8 | 0.8030 | 41.2004 | 0.37212 |
| 4.0 | 0.8599 | 50.3878 | 0.42498 |
| 4.2 | 0.9185 | 61.5752 | 0.48623 |
| 4.4 | 0.9789 | 75.1984 | 0.55714 |
| 4.6 | 1.0413 | 91.7873 | 0.63930 |
Although U occurs in a large number of minerals, only a few are suitable for dating by the U-Pb methods. To be useful for dating, a mineral must be retentive with respect to U, Pb and the intermediate daughters, and it should be widely distributed in a variety of rocks. The minerals that satisfy these conditions include zircon, baddeleyite, monazite, apatite, and sphene (titanite). All of these minerals contain trace amounts of U but low concentrations of Pb, giving them high U/Pb ratios favorable for dating. For example, concentrations of U in zircons range from a few hundred to a few thousand parts per million and average 1350 ppm (Faure and Mensing 2005). The presence of U in zircon is due to the isomorphous substitution within the zircon crystal lattice of U4+ (ionic radius 1.05 Å) for Zr4+ (0.87 Å), though this substitution is limited by the differences in their ionic radii. However, whereas U4+ is admitted into zircon crystals, Pb2+ is excluded because of its large ionic radius (1.32 Å) and its low charge (2+). Therefore, zircons are supposed to contain very little Pb at their time of formation and have high U/Pb ratios. This appears to enhance their sensitivity as a geochronometer, so zircons have for several decades become increasingly used for dating via the U-Pb methods.
Pb-Pb Isochron Dating
Equations (4) and (5) above describe the accumulation of the radiogenic 206Pb and 207Pb from 238U and 235U respectively. The same equations can be used with multiple samples to plot independent isochrons in which 238U/204Pb and 235U/204Pb are plotted against 206Pb/204Pb and 207Pb/204Pb respectively. The slopes of the resultant 238U-206Pb and 235U-207Pb isochrons yield dates that are concordant only when the samples remained closed to Pb diffusion and had identical initial Pb isotopic ratios. However, in most cases, U-Pb isochrons based on whole-rock samples have not been successful, primarily because rocks that are exposed to chemical weathering lose a significant fraction of U. Thus, the U-Pb isochron method of dating igneous and metamorphic rocks composed of silicate minerals does not work in most cases because of the variable losses of U by chemical weathering, which occurs not only at the earth’s surface, but also in the subsurface where rocks are in contact with oxygenated groundwater.
On the other hand, igneous and metamorphic rocks that have lost U by recent chemical weathering may also have lost Pb. However, the isotopic ratios of the remaining Pb may not have changed if the isotopes of Pb were not fractionated. In other words, the isotope ratios of Pb in the weathered rocks are not changed if the Pb that was lost had the same isotope composition as the Pb that was present before the loss occurred. Consequently, it is maintained that a date can be calculated based on the slope of the Pb-Pb isochron obtained from samples of even weathered rocks.
The equation for Pb-Pb isochrons is derived from combining equations (4) and (5) above to yield equation (10) above, which expresses the ratio of radiogenic 207Pb to 206Pb and then yields equation (9) above:
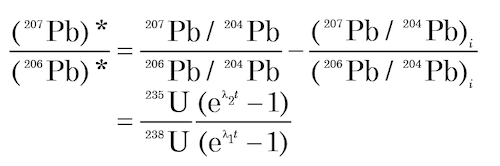
This is the equation for a straight line in coordinates of 206Pb/204Pb (x) and 207Pb/204Pb (y) whose slope m is
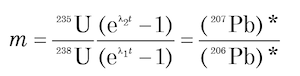 (12)
(12)
Age determinations by this Pb-Pb isochron method depend on the assumptions that all the samples that define the isochron
- had the same initial Pb isotope ratios;
- formed at the same time; and
- remained closed to U and Pb until the recent past (defined as when the present land surface was exposed, which is typically in the last 10–70 million years of the conventional timescale), when they were exposed to chemical weathering
In addition, the 238U/204Pb and 235U/204Pb ratios of the samples must have sufficient range to allow Pb having different isotope ratios to form within them. The slope of Pb-Pb isochrons can be used for dating by solving equation (12) for t by interpolating within table 1. Alternately, equation (12) can be solved by iteration on a computer to any desired level of precision. The Pb-Pb isochron method has been used very widely for dating igneous and metamorphic rocks, especially those of Precambrian age, as well as meteorites. The method is claimed to yield the time elapsed since the isotopic homogenization of Pb and subsequent closure of rocks to U and its intermediate daughters. However, it is exceedingly doubtful that minerals and rocks remained closed through millions of years to the migration of the chemically inert daughter radon gas which today is well known to diffuse out of minerals and rocks!
The several assumptions involved in the various U-Pb and Pb-Pb model and isochron dating methods have a somewhat tenuous validity, because they are based on an unknown and unconfirmed uniformitarian evolutionary past history. Yet in spite of that, all these methods depend on the decay constants or half-lives of 238U and 235U being known accurately. Furthermore, the isotopic composition of U has to have been normal and must not have been modified by isotope fractionation, by different decay rates in the past, or by occurrence of a natural chain reaction based on induced fission of 235U, that is, the 238U/235U ratio has to be known and must have remained constant at that value.
Defining Errors and Uncertainties
Before investigating further how the geochronology community handles the determination of, and correction for, isotopic mass fractionation, it is necessary to define a few terms and discuss how they are used. These are the terms “error” and “uncertainty,” “accuracy” and “precision.” They are used frequently in all discussions on the methodology of U-Pb geochronology, as the dating results from the various analytical equipment are reported and contrasted. The goal of the geochronology community is understandably to reduce errors and uncertainties to produce better accuracy and precision. The fact is that after a decade or more of intense intentional effort little progress has been made. The sources of error are still not “tamed” and “uncertainties” adequately reduced is testimony to the severe problems that still plague this U-Pb dating method.
Schoene et al. (2013) described the use of the terms “accuracy,” “precision,” “error,” and “uncertainty” in U-Pb geochronology, and differentiating between these terms and defining them is very useful for discussing data measurement and reporting protocols. Potts (2012) utilized the International Vocabulary of Metrology guidelines and defined “measurement error” as a “measured quantity value minus a reference quantity value.” This definition depends on the accuracy of the reference quantity value and automatically introduces bias into the whole process because the reference value also must be previously measured with its own measurement error. Potts (2012) also defined the “measurement uncertainty” as a “non-negative parameter characterizing the dispersion of the quantity values being attributed to a measurand [defined as the quantity intended to be measured], based on the information used.” Thus, an error is a single value (for example, 0.1) and is not known unless a reference value exists to compare against. In contrast, an uncertainty is a range (for example, 99.9 ± 0.1) that is expected to contain the true value with a given probability, often referred to as a confidence interval.
Measurement error can be random (unpredictably offset from the measurand value) or systematic (consistently or predictably offset from a reference value) (Potts 2012). Once quantified, a systematic error is referred to as a bias. Each type of error has an uncertainty associated with it. These uncertainties are commonly referred to as systematic or random in reference to the error to which they relate. The uncertainty related to random error is reflected in the measurement precision (“closeness of agreement between indications or measured quantity values obtained by replicate measurements on the same or similar objects under specified conditions” (Potts 2012) and can be reduced by increasing the number of measurements. However, it could be argued that measurement precision has nothing to do with the number of measurements made but rather reflects the sensitivity of the measuring apparatus used. In a sense precision is a function of current instrument technology.
The obtained standard deviation of the mean (historically referred to as “standard error”) represents the confidence in the determined average value (Potts 2012) but does not reduce the actual scatter in the data (that is, the standard deviation of the population remains the same). The uncertainty related to a systematic error reflects how well that bias can be quantified when determined under differing conditions, that is, how reproducibly it can be measured; it cannot be further reduced simply by acquiring more measurements. The use of the term “error” should be reserved exclusively for its defined purpose—to refer to the offset of the measurement from a mean or expected value. But it can be argued that this is not always the case. In fact, the best way to think of error in a given measurement is to assess the possible deviation of a series of measurements from the mean. This makes the measurement error stand alone and not be dependent on some “expected value.” Thus, when referring to a confidence interval, the term “uncertainty” should always be used.
Of course, the expected value is fundamentally a theoretical value deduced from application of current theories and/or laws of science and it may or may not be accurate. Thus, the purpose of the measurements is to confirm or deny the predictions/expectations of theory. In this context of U-Pb radioisotope dating of rocks and minerals the expected value is very much determined by theory, that is, where the rocks fit within the presumed geologic record and its timescale based on evolutionary assumptions. Yet any number of other factors, such as the initial composition, inheritance when subsequently formed, contamination after formation, and accelerated nuclear decay during a past catastrophic geologic event, could all differently influence the expected value and hence the uncertainty in what the true age might be. Thus, it would probably behoove the geochronology community to stop thinking of measurements in terms of the ages they represent. The measurement of a given quantity such as Pb isotope ratios in a material in the present is totally independent of the age of that material. Age comes into the picture as a model, or actually an hypothesis, which uses those measurements to make a prediction of what the age might be, an age which can never be verified because it is a past unobserved and unrepeatable event.
Although it is common practice for geochemists to express uncertainties using σ, strictly this should be reserved only for statistics relating to a total population (the population standard deviation). Since geochemists only ever take a representative sample of a population (rather than analyzing an entire granite pluton or, in this example, every zircon within it), the correct statistical term is s (the sample standard deviation). However, both terms explicitly refer to the “standard deviation,” while the reported uncertainties derive from the standard error of the mean of isotope ratios, combined often with a statistical analog of a standard deviation (the excess variance parameter as described). These are ultimately combined with several other systematic uncertainties—for example, from TIMS measurements of reference materials and from the isotopic purity and particle-counting experiments that determine decay constants. Indeed, particle counting experiments are usually dominated by the random/statistical errors of the measurement, especially in situations involving very low count rates such as is the situation for long lived radioisotopes such as U and Th. The result is neither a standard deviation nor a standard error, but an uncertainty which describes the dispersion of the resulting normal distribution.
So, now that we have gone over some important background informational issues, we now turn to the last of the potential problems listed by Amelin et al. (2009) on which we need to focus, namely, the fractionation of U and Pb isotopes. First, we will discuss the evidence of isotope fractionation in minerals, before we turn to the problem of isotope fractionation during analyses using the various available instrumental procedures.
Isotope Fractionation Within Minerals
Bigeleisen (1996) predicted that uranium isotopes fractionate as a result of nuclear-field shift. Differences in size and shape of the nuclei of individual isotopes should lead to slightly different bonding environments for each isotope, based on the nuclear charge and mass distributions which depend on the nuclear shell structure. The magnitude of this effect correlates with the nuclear volume of each isotope rather than strictly with mass and is therefore referred to as the nuclear volume effect or, alternatively, the nuclear field shift. Nuclei of isotopes forming a bond repel each other when fully ionized (which is not likely), since the nuclei are both positively charged, but the distance between the nuclei of a chemical bond is dependent on the size and charge distribution of those nuclei. They cannot approach each other close enough for the nuclear force to play any part in their interaction. Yet 235U with an odd number of neutrons, and a smaller number of neutrons, has a smaller nucleus relative to nuclei with an even number of neutrons, such as those of 238U. This results in different bond strengths, with 238U preferentially incorporated into the more condensed solid phase. Schauble (2007) confirmed the theoretical calculations and suggested that the nuclear-field shift results in 238U/235U ratios that vary as a function of uranium oxidation state, with the highest 238U/235U ratio in more reduced species. The oxidation of U4+ to U6+ involves 5f electrons, and their removal actually increases the electronic charge density at the nucleus, leading to a preference of light U isotopes in the oxidized species (Brennecka 2011). Consequently, the effects of mass-dependent and volume dependent fractionation on the 238U/235U ratio are in opposite directions, leaving the dominant volume-dependent fractionation as the observable effect. Apparently what Bigeleisen (1996) meant is the electron cloud shifts due to the orientation of the nucleus and thus changes the geometric configuration of the isotope. Moreover, a subsequent ab initio relativistic molecular orbital study for the 238U-235U pairs showed that the nature of ligands surrounding uranium atoms effects isotope fractionation caused by nuclear-shift (Abe et al. 2008, 2010). Thus, the mass difference of the various uranium isotopes would be the dominant cause for fractionation if those isotopes are in elemental form.
Chen, Siebel, and Satir (2002) analyzed two homogeneous zircons to study U and Pb behaviour during stepwise HF acid leaching. From the Phalaborwa (South Africa) zircon, ~11% of the radiogenic Pb and ~7% of the U were extracted into solution at the first leaching step and a reverse discordance was obtained. After extraction of ~27.0% of the total radiogenic Pb budget and ~24.5% of the U, the zircon residue gave concordant ages. It contained ~75.8% of the total radiogenic 206Pb budget, ~76.4% of the total radiogenic 207Pb budget, and ~68.0% of the total radiogenic 208Pb budget, indicating different mobilities of these Pb isotopes. The 208Pb*/206Pb* ratios of the solutions and the residue decreased systematically from ~1.10 to ~0.60. This pattern seemed to demonstrate that domains with different Th/U ratios were successively sampled during acid attack. Thus, the highly reverse discordant age observed in the solution of the first leaching step had to originate from the fractionation between U and Pb*, and between radiogenic Pb isotopes, consistent with the observations of Mattinson (2000) and Davis and Krogh (2000). These observations indicate the high mobility of Pb* probably resulted from radiation damage. Moreover, the fractionation between 207Pb* and 206Pb* in the first leaching step(s), which had been observed by Mattinson (2000) and Davis and Krogh (2000), implies that discordant domains of zircons have to be completely removed in the leaching steps to avoid artificially high 207Pb*/206Pb* ratios in the residues.
In contrast to the Phalaborwa zircon, only ~1% of the total radiogenic Pb budget was extracted in leaching steps from each of three Kuehl Lake (Ontario, Canada) zircon fragments (Chen, Siebel, and Satir 2002). Thus, evaluation of data from these leaching studies showed that the extractability of Pb is positively correlated with the total radiogenic Pb budgets in zircons and subsequently with U contents and ages of zircons, indicating the important role of radiation damage. This correlation is consistent with the fact that old zircons with high U contents are much more susceptible to Pb loss than younger ones with low U contents. Therefore, Chen, Siebel, and Satir (2002) concluded that careful application of the acid-leaching method is an important prerequisite to achieve concordant ages as demonstrated in previous studies (Mattinson 1994) and in the Phalaborwa zircon of their study. However, the 207Pb*/206Pb* ratios in the residues of the fragments of both the Phalaborwa and Ontario zircons were systematically higher than the unleached fragments. Although it cannot be completely excluded that the high 207Pb*/206Pb* ratios of all three Ontario zircon residues were caused by a systematic bias of the correction for the common Pb contribution, the phenomenon of artificial Pb fractionation causing artificially high 207Pb*/206Pb* ratios during the acid leaching has already been reported (Corfu 2000). Keeping this in mind, they suggested that cautions should also be taken in interpretation of all geochronological data, not only of the early leaching steps (Mattinson 1997) but also of the later steps and the residues.
Since uranium is the heaviest naturally occurring element and isotope fractionation between 235U and 238U is not normally considered significant given the small ~1% difference in mass, it is therefore usual to assume that the 238U/235U ratio is constant in the terrestrial environment and equal to 137.88. However, Stirling et al. (2007) developed experimental protocols for the precise measurement of 235U/238U by multiple-collector ICP-MS (MC-ICP-MS) and analyzed a suite of low-temperature samples formed in a wide range of marine and continental near-surface terrestrial environments. Using a high-purity 233U–236U double spike to internally monitor the large (percent-level) but essentially constant instrumental mass fractionation effects that are inherent to plasma source mass spectrometry, they were able to resolve variations in 235U/238U at the 0.4ε level (2σ; 1 epsilon = 1 part in 10,000) on samples comprising 50 ng of 238U. Furthermore, the natural variability in ε235U shown by the analyzed samples was ~13ε and exceeded the analytical reproducibility by more than an order of magnitude. Compositions that are both isotopically heavier and lighter than the terrestrial standard (the “normal” value), by 4 and 9 ε units respectively, were observed. In their dataset, the greatest variability in ε235U is displayed by speleothems precipitated from groundwaters. Additionally, the 235U/238U ratio appeared to broadly correlate with the 234U/238U ratio in samples showing the most extreme isotopic compositions.
Stirling et al. (2007) explored possible mechanisms to account for this fractionation of 235U from 238U in the context of abiotic fractionation processes. Specifically, sequential leaching experiments of U-rich minerals indicate that mineral weathering is a possible mechanism by which 235U can be fractionated from 238U in groundwaters and incorporated into speleothems. They thus maintained that the observed variability in 235U/238U indicates that uranium isotopes may offer the potential to monitor new reaction pathways, such as those activated during the redox transition between the U(IV) and U(VI) oxidation states. Their experiments involving the redox transition of U(VI) to U(IV) in the presence of zero-valent zinc did not produce a resolvable shift in 235U/238U towards anomalous values, although they suggested that fractionation need not occur if the reaction is governed by a fast kinetic process.
Stirling et al. (2007) concluded that isotopic fractionation of 238U from 235U has broad implications for low-temperature geochemistry. In contrast to the lighter stable isotope systems, which can be readily fractionated in a wide range of environmental and geological environments, uranium’s heavy atomic mass may limit the range of processes by which it can be fractionated. Thus, Stirling et al. (2007) suggested that U may potentially offer new insight into the processes at work during low temperature biotic, abiotic, and redox processing. For example, U is linked with elements such as Fe during redox processing and coupled measurements of 235U/238U and Fe isotopic composition may provide useful information on oxidation-reduction mechanisms. However, they warned that these observations have a direct impact on the U-series and U–Th–Pb chronometers, when applied in paleoclimate research to samples formed in low-temperature environments, as these chronometers currently assume an invariant 238U/235U equal to 137.88. Yet they asserted that these limitations can, in large part, be overcome by the utilizing a 236U–233U double spike with a well-characterized 236U/233U for the purpose of monitoring the instrumental mass fractionation factor, in place of the “natural” 238U/235U ratio, and by careful consideration of the standards adopted for calibration procedures.
Weyer et al. (2008) similarly reported variations of the 238U/235U isotope ratio in natural samples (basalts, granites, seawater, corals, black shales, suboxic sediments, ferromanganese crusts/nodules and banded iron formations) of ~1.3‰, exceeding by far the analytical precision of their method (≈ 0.06‰, 2SD) (fig. 3). U isotopes were analyzed with MC-ICP-MS using a mixed 236U–233U isotopic tracer (double spike) hoping to correct for isotope fractionation during sample purification and instrumental mass bias.
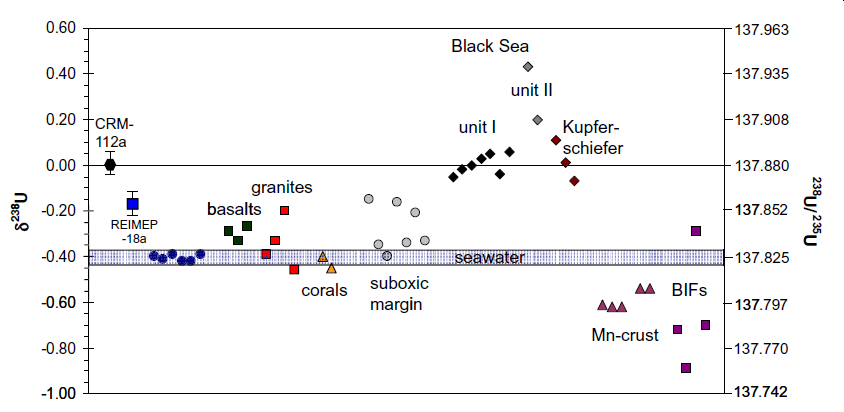
Fig. 3. Summary of all delta δ for all samples investigated by Weyer et al. (2008). The dark blue dots within the seawater field represent δ238U of individual seawater samples. Significant U isotope fractionation appears to occur between seawater and the black shales (Black Sea, unit-I, unit-II and Kupferschiefer) which all display heavy U isotope compositions, and between seawater and ferromanganese crusts/nodules and banded iron formations (BIFs) which all display low δ238U. The low δU of most of the BIFs may also reflect low δ238U of the seawater at the time of their formation.
Weyer et al. (2008) found that the largest isotope variations are between oxidized and reduced depositional environments, with the most significant U isotope fractionation occurring during U reduction in anoxic/euxinic environments. This was indicated by large δ238U of black shales relative to seawater (up to +0.84‰). A much smaller but resolvable fractionation (also toward heavier isotope compositions) appears to occur during U removal in suboxic environments. In oxic environments, they found that U isotopes are fractionated toward lower δ238U during incorporation into ferromanganese crusts (Δ238Useawater–Mn-crust ≈ 0.13‰ to −0.21‰). The lightest U isotope compositions are seen in three banded iron formations (BIFs) (−0.70‰ to −0.89‰) which they thought may reflect particularly strong fractionation of light U isotopes to the BIFs or differences in the U isotope budget of Archean oceans, or Archean weathering conditions, compared to today.
Weyer et al. (2008) concluded that these findings demonstrate that U isotope fractionation occurs in nature and imply that U isotope fractionation occurs in both oxic (manganese crusts) and suboxic to euxinic environments with opposite directions. The magnitude and direction of U isotope fractionation during U reduction is in agreement with theoretical calculations of volume-dependent fractionation (Schauble 2006). They are of opposite direction to expectations from classic mass-dependent fractionation or from recently observed kinetic U isotope fractionation during microbial reduction (Rademacher et al. 2006). Thus, in the first case, Weyer et al. (2008) hypothesized that this fractionation results from adsorption of U to ferromanganese oxides, as is the case for Mo and possibly Tl isotopes. In the second case, reduction of soluble UVI to insoluble UIV probably results in fractionation toward heavy U isotope compositions relative to seawater.
This discovery that the 238U/235U ratio varies in nature also implies that the U isotope variations in U-bearing minerals that are used for U–Pb dating would be of sufficient magnitude to affect the precision of U–Pb dating. Indeed, the total observed range in U isotope compositions as documented by Weyer et al. (2008) would produce variations in 207Pb/206Pb ages of young U-bearing minerals of up to 3 Ma, and up to 2 Ma for minerals that are supposedly 3 billion years old. Subsequent investigators have measured more variations in the 238U/235U ratio that is critical to U-Pb dating method (Brennecka and Wadhwa 2012; Goldmann et al. 2015; Hiess et al. 2012; Tissot and Dauphas 2015), revealing that the same mineral in different rocks can have very different 238U/235U ratios. The implications of this have been discussed by Snelling (2017a).
McLean (2014) has pointed out that although a number of straight-line regression algorithms are used by the geochemistry and geochronology communities (for example, York 1968), none treat the general case of data with correlated uncertainties in two or more dimensions. Indeed, isotopic fractionation is often modeled by linear functions in log-ratio space, such as the Rayleigh and exponential laws. Thus, McLean (2014) applied the maximum likelihood method to straight-line regression through data in any number of dimensions to calculate a vector-valued slope and intercept as well as the covariance matrix that describes their uncertainties and uncertainty correlations. He then applied this algorithm to Pb data measured by TIMS with a silica gel activator and showed that progressive fractionation during an analysis is well fit by a linear trend in a three-dimensional log-ratio space. He found that while the log-ratios of even mass number Pb isotopes followed the slope predicted by mass-dependent fractionation with a Rayleigh or exponential law within calculated uncertainties, the log-ratio containing the odd mass number isotope 207Pb diverged significantly, exhibiting mass-independent fractionation. Furthermore, the straight-line regression algorithm is appropriate for fractionation lines that form linear trends in log-ratio space, but not for isochrons or mixing lines, which are predicted to be linear only when plotted as isotope or compositional ratios.
Hayes (2017) has asserted that an overlooked key flaw in the radioisotope dating methodology is the reasonable assumption that the Pb isotope ratios are influenced only by radioactive decay of U and Th into Pb. However, that assumption does not take into account differential mass diffusion—the tendency of different atoms to diffuse through materials at different rates, which is another form of isotope fractionation. Thus, 206Pb atoms can diffuse (or leak) more readily than 207Pb and 208Pb atoms, simply because 206Pb atoms are smaller, though not by much. The experimentally measured nuclear charge radii are 5.4902, 5.4943, and 5.5012 fermis (1 fermi = 1 × 10-15 m) for 206Pb, 207Pb, and 208Pb, respectively (Angeli and Marinova 2013), the differences are only about 0.2%. Hayes (2017) claimed that this differential diffusion of 206Pb, 207Pb, and 208Pb may contribute to a linear distribution of the 207Pb/206Pb and 208Pb/206Pb ratios, as in an isochron. Any such linear bias that might occur from this isotope diffusion or fractionation effect would then have to be corrected in applying the isochron radiometric dating methodology to the isotopic ratios.
Snelling (2018) has already presented Hayes’ analysis in great detail, which demonstrated that obtaining an isochron-like linear plot is virtually guaranteed based on this differential isotope diffusion or fractionation effect alone! Hayes (2017) established that almost all rock and mineral samples which are affected by differential diffusion or fractionation of isotopes will have some non-linearity in the distribution of their isotopic ratios. That distribution can then be related back to the bias from this differential diffusion or fractionation effect independent of the purely linear distribution caused by radioactive decay. Unless that is done, Hayes (2017) demonstrated that the resultant isochrons will be wrongly estimating the true ages of the rocks and minerals. He emphasized that such differential diffusion or fractionation is an inescapable reality in rocks and minerals, including in the U-Pb system. This is because the parent radioisotopes (238U, 235U, and 232Th) and their daughter products (206Pb, 207Pb, and 208Pb respectively) are not the elements which form the minerals in the rocks being dated (for example, zircon), but are merely trace elements that substitute into, or are trapped inside, the crystal lattices of rock-forming minerals. As such they are held more loosely in the crystal lattices and thus are much more likely to diffuse and thus fractionate than any of the major elements that are more tightly bonded to form the mineral crystals.
Hayes (2017) concluded that the simplest approach to remove these solid-state mass diffusion and fractionation effects would be not to use isotopic ratios in dating samples, an assertion at direct odds with the work done by geochronologists. Furthermore, both of his proposed solutions are subjective and any rigorous statistical analysis sufficient to discriminate a linear from a nonlinear distribution in the isotopic data is generally not possible without a much larger number of samples, as many as thirty, a number rarely achieved in U-Pb dating studies. The only other alternative he proposed is to remove the edges of the mineral grains separated for isotopic analyses before proceeding to the mass spectrometer determinations of their isotopic ratios. This suggestion is based on the premise that the two dominant components of differential diffusion or fractionation occur along the surfaces of rocks and the edges of minerals, and between and along the grain boundaries. By removing the grain boundaries, one effectively removes those two dominant components of the differential isotopic diffusion or fractionation that has occurred. However, it is uncertain that this procedure will actually remove the diffusion from rock surfaces and mineral boundaries, as differential diffusion will occur throughout crystals within rocks and not just at their boundaries. So, even then there is no guarantee that all grain boundaries have been removed and thus the effects of the dominant differential isotopic diffusion or fractionation have been eliminated. Indeed, there is always the possible breaking of the correlation between the U isotopes and the Pb isotopes via loss of radon gases.
Isotope Fractionation Due to Beam-Induced Mass Spectrometer Analyses
Yet another potential problem which causes possible inaccuracies in obtaining reliable U-Pb and Pb-Pb ages listed by Amelin et al. (2009) is “analytical problems (fractionation, instrument-specific, etc.) and blank subtraction,” which they state are “important.” Of these analytical problems they state that “they are widely recognized,” and that “ongoing analytical developments help to reduce them.”
Richards (1981) had warned against systematic errors of measurement caused by isotope fractionation in the mass spectrometer which may generate linear arrays of Pb isotopic ratios. Such “pseudo-isochrons” yield erroneous dates that confuse the geological interpretation of the isotopic data. Yet at the same time it had been also claimed this problem with mass-dependent isotope fractionation could be eliminated by use of a “double spike” (Compston and Oversby 1969; Cumming 1973; Russell 1971, 1975).
Isotope Fractionation Using Thermal Ionization Mass Spectrometers (TIMS)
Thirlwall (2000) developed a method for precise Pb isotopic analyses using a 207Pb–204Pb double spike during thermal ionization mass spectrometry (TIMS). Pb isotope ratios were calculated relative to 206Pb and were normalized in each run to an arbitrary 208Pb/206Pb ratio to permit good estimates of error propagation through the fractionation correction. For almost all Pb isotope analyses published up to that time, this correction assumed that natural samples undergo the same extent of mass fractionation as the isotopic standard. Consequently, reproducibility of Pb isotope ratios was not better than that observed for the isotopic standard, and accuracy was significantly worse.
From his experiments, Thirlwall (2000) reported on numerous sources of uncertainty in common Pb isotope data in the order of their magnitudes. Heading the list was environmental contamination of crushed sample powders prior to leaching for analyses. This could result in 206Pb/204Pb ratios up to 2% lower than the true ratios of the samples and does not only affect low-Pb samples. He found that mass fractionation of 0.08% per atomic mass unit (amu) was the biggest difference between mass fractionation of unknown samples and the mean fractionation of the isotopic standard, based on the preferred 208Pb/206Pb ratios. Then while 204Pb/206Pb normalized to 208Pb/206Pb appeared free from interferences and obeys power- or exponential-law mass fractionation within analytical error, 207Pb/206Pb showed systematic decreases with increase in 208Pb/206Pb at >1250°C that are extremely difficult to explain by isobaric interference and may indicate abnormal mass fractionation behavior.
Thirlwall (2000) also found uncertainty in measurement of the small Pb ion beam. The 204Pb error in conventional Pb isotope analyses gives rise to error trajectories on 207Pb/204Pb and 208Pb/204Pb versus 206Pb/204Pb plots that have significantly shallower gradient than mass fractionation trajectories. In 207Pb–204Pb double spike corrected analyses error trajectories are not identical to simple 204Pb error lines because all ratios are affected through the double spike correction. Furthermore, static data collection introduced significant errors in the double spike procedure if there were small defects in transmission to the Faraday cup collectors of the mass spectrometer. Static data have similar internal precision to multi-dynamic data, but Thirlwall (2000) found that reproducibility of the static isotopic standard used was about two times worse. Inaccuracy in calibrating inter-Faraday-cup efficiencies may thus have generated small errors in other Pb isotope standards routinely used.
Thirlwall (2000) concluded that relative to the fractionation-corrected isotope ratios, measured ratios for unknown samples analyzed were significantly more enriched in the lighter isotopes than were runs of the isotopic standard, indicating that corrections based on average isotopic standard mass fractionation were likely to be in error. Furthermore, acid-leached rock sample chips and acid-leached sample powders generally gave identical Pb isotope ratios within analytical error. However, Thirlwall (2000) expressed concern that re-analyses of samples previously analyzed by several other laboratories showed large differences, up to thirty times the supposed reproducibility of conventional Pb isotope determinations. He surmised that this was probably related both to laboratories using inadequate fractionation corrections and to local environmental contamination of rock powders.
Doucelance and Manhès (2001) focused on precise Pb isotope analysis by TIMS and presented extensive measurements of two commonly used laboratory standards, consisting of chemically pure Pb and of equal-atom mixtures of the four stable Pb isotopes. Their measurements at low temperatures (1050–1175°C) displayed reproducible values and were coherent with the usual mass discrimination laws at the level of precision achievable (± 0.0065‰ per amu) with careful loading conditions in multi-collector mass spectrometers. In contrast, their experiments at higher temperatures showed evolutions of Pb isotopic ratios which did not follow classical mass discrimination laws at the level of precision achieved with multi-collector mass spectrometers in static mode (20 ppm). They observed systematic shifts, the most important deviation with respect to theoretical laws, with a total deviation that can reach values up to 400 ppm, being observed for 207Pb relative to other isotopes. Nevertheless, all three isotope systems show nonlinear isotopic evolution at the 50 ppm level. This confirmed the same observation by Thirlwall (2000). Similarly, Doucelance and Manhès (2001) did not have a physical explanation for this abnormal behaviour. They attributed these isotopic evolutions to the superposition of the classical mass discrimination evolution with a nonlinear effect whose physical origin has not been identified yet. They excluded the contribution of “organic” interferences and of polyatomic ions resulting from the presence of inorganic impurity introduced in the beads. In such cases, the physical phenomenon responsible for the observed deviations would have induced a fractionation of Pb isotopes which is not related to their mass differences.
Amelin, Davis, and Davis (2005) undertook high-precision Pb isotopic analyses of a zircon standard SRM-981, spiked with 202Pb and 205Pb, to further evaluate the anomalous fractionation of 207Pb relative to even mass isotopes in TIMS, as reported by Thirlwall (2000) and Doucelance and Manhès (2001). The analyses were performed using TIMS in static multi-collector mode using three different silica gel formulations—silicic acid, hydrolysis of silicon tetrachloride, and hydrolysis of sodium orthosilicate. Ratios involving the even-mass isotopes (202Pb, 204Pb, 206Pb, and 208Pb) obeyed standard mass-dependent fractionation laws over a wide range of fractionation (208Pb/206Pb between 2.160–2.172). In contrast, isotopic ratios involving odd and even isotopes (for example, 205Pb/206Pb or 207Pb/206Pb), exhibited mass-independent fractionation when normalized to 208Pb/206Pb, and systematically decrease as the sample approaches exhaustion. The relative change of normalized 205Pb/206Pb and 207Pb/206Pb were between 0.02–0.05% for the silicic acid and silicon tetrachloride gels, and up to 0.16% for the sodium orthosilicate gel. The relative deviations of both ratios were strongly correlated, with the slope of correlation lines close to one. Thus, the fractionation between odd isotopes was similar to the mass-dependent fractionation between even isotopes, but the behaviour of even- and odd-mass isotopes was decoupled, that is, the inter-relationship was disconnected. For example, the ratio 206Pb/208Pb, normalized to 205Pb/207Pb, did not vary with sample exhaustion. If the ratio 207Pb/206Pb, most important for high-precision Pb-isotope dating, was normalized to 205Pb/202Pb or 207Pb/204Pb in a double-spike procedure, the 207Pb bias was reduced by 1/3 but not removed completely.
The cause of the mass independent fractionation appeared related to a higher volatility and/or ionization efficiency of Pb atoms with non-zero nuclear spin. Large differences in ionization of even versus odd isotopes have been noted for a number of elements in laser resonance ionization mass spectrometry (for example, Wunderlich et al. 1993). However, it remains unclear how the process by which silica gel enhances ionization is affected by nuclear spin.
Manhès and Göpel (2007) detected “abnormal fractionation” of the 207Pb isotope relatively to the mass dependent fractionation between 204Pb, 206Pb, and 208Pb during long high precision Pb isotope measurements by TIMS of the zircon standard SRM-981 (Doucelance and Manhès 2001; Thirlwall 2000). Zn, Cd, and Pb isotope measurements with TIMS revealed that the odd isotopes (67Zn, 207Pb, 111Cd-113Cd) were affected during extended runs by a mass independent fractionation in addition to the purely mass dependent fractionation shown by the even isotopes, leading to an accumulated depletion of the odd isotopes. TIMS Pb isotopic measurements of the zircon standard SRM-981 spiked with 202Pb and 205Pb (Amelin, Davis, and Davis, 2005) confirmed this effect. Both studies suggested the nuclear spin carried by the odd nuclides as responsible for these mass independent fractionations.
It was suggested that the observed accumulated depletion of odd isotopes relative to the even isotopes resulted from a larger volatility of odd isotopes due to the differences in the shape of the nuclei. For a spherical nucleus, the nuclear quadrupole moment Q will be zero. Prolate ellipsoids have Q> 0, oblate ellipsoids have Q< 0, but more complicated deformations and oscillations are possible. With a doubly closed shell nucleus at Z = 82 and N = 126, and even Z and even N, 208Pb has a spherical nucleus. So the other Pb isotopes consequently have small deformations, if any. 205Pb in its 5/2- ground state has Q= +0.23(4) barns (1 barn = 10-24 cm2) (Anselment et al. 1986). According to Zumbro et al. (1984) the 233U 5/2+ ground state has Q= 3.663(8) barns and the 235U 7/2- ground state has Q= 4.936(6) barns. Note that these values are larger than those seen for the Pb isotopes because uranium can undergo spontaneous fission and shape oscillations result.
This idea resulted from a new interpretation of mass independent isotope fractionation observed in FUN inclusions (referring to Fractionated and Unknown Nuclear effects), which are unusual calcium–aluminum-rich inclusions (CAIs) found in the Allende carbonaceous chondrite meteorite (Fujii, Moynier, and Albarède 2006) implying the nuclear field shift (Bigeleisen 1996). The nuclear field shift effect is suspected in the origin of mass independent fractionation in chemical exchange reactions (Bigeleisen 1996). The aim of their study was to identify the process that induced the mass independent fractionation during the thermal ionization processes. Their experiments with the thermal ionization of Pb and Cd suggest that the palpable difference in volatility between odd and even isotopes is not the dominant process but rather the change in oxidation states of the elements inside the glass beads.
Isotope Fractionation Using Secondary Ion Mass Spectrometers (SIMS)
Wingate and Compston (2000) showed that 206Pb/238U ratios measured in baddeleyite by ion microprobe (SHRIMP II, a SIMS instrument) vary significantly (up to ±10% or more) and systematically with the relative orientation of the baddeleyite crystal structure and the primary ion beam (fig. 4). Though Wingate and Compston (2000) didn’t suggest it, there is the real possibility that this effect they measured of systematically varying 206Pb/238U ratios with relative crystal orientation to the ion beam could be a symptom of different diffusion rates along the crystal axes. They did find that low dispersion between multiple analyses of single crystals demonstrated that it is possible to measure undispersed 206Pb/238U ratios in multi-grain baddeleyite samples if all material is in a single orientation. Owing to the small size of most crystals and their ubiquitous polysynthetic {100} twinning, however, it was extremely difficult to arrange a reasonable number of crystals in identical orientations for analysis. These orientation effects constitute an intractable problem, and place unacceptable limits on the accuracy and precision that can be obtained for 206Pb/238U in baddeleyite by ion microprobe techniques. Comparisons with isotope dilution measurements indicate that any Pb isotope discrimination during analysis of baddeleyite by ion microprobe is negligible, and there is no evidence that Pb isotope ratios vary with crystal orientation, though it is unclear how isotope diffusion gets around different diffusion rates. Although the precision of 207Pb/206Pb ages decreases for younger samples, rocks younger than 1 Ga can be dated precisely if the baddeleyite is enriched sufficiently in U and if enough analyses are performed. Wingate and Compston (2000) speculated that orientation effects in baddeleyite might involve channeling of primary ions into the crystal, emission of secondary ions along preferred directions, and/or differential ionization of secondary species. No orientation-related differences in 206Pb/238U were detected during ion microprobe analyses of zircon or monazite.
Fig. 4. SHIMP analytical results for baddeleyite, illustrating observed orientation effects (after Wingate and Compston 2000). (a) A U-Pb evolution (concordia) diagram showing apparent ages for four different oriented surfaces (shown in the inset) of a single large baddeleyite crystal (PC2 from the Phalaborwa carbonatite, South Africa). (b) Correlated variation in total 208Pb/206Pb with 232Th/238U for the same surfaces measured in (a). (c) Variation of apparent 206Pb/238U age with orientation for (100) surfaces of 47 oriented baddeleyite crystals.
Stern and Amelin (2003) calculated analytical errors for individual spot 206Pb/238U measurements of zircon analyzed using high mass resolution secondary ion mass spectrometry (HR-SIMS, namely, SHRIMP II) and assessed them using natural zircon and synthetic glass standards. Evidence for U/Pb homogeneity of these materials included new thermal ionization mass spectrometry (TIMS) U–Pb analyses of 22 fragments of the same natural zircon from two laboratories, which were identical within error and yielded a weighted mean 206Pb/238U age of 559.0 ± 0.2 Ma. TIMS U–Pb analyses of the synthetic glass standard yielded homogeneous 206Pb/238U = 0.2566. Of course, while Stern and Amelin (2003) do not recognize this, it needs to be stated that this is not simply case of errors in the actual measurements, because the resultant calculated ages are numbers deduced from the standard age model.
Stern and Amelin (2003) distinguished three types of error estimates for individual ion microprobe zircon 206Pb/238U zircon analyses: within-spot (that is, within the ion beam’s analytical spot on the zircon crystal), within-session (internal), and external errors. SHRIMP II ion microprobe experiments conducted upon SRM 610 glass demonstrated that the methods described here of estimating within-spot analytical errors of isotopic (for example, 208Pb+/206Pb+) and elemental (for example, 248[ThO]+/254[UO]+) ratios are reasonably accurate. The within-spot errors were based upon counting statistics for the individual isotopes augmented by any additional scatter encountered during the analysis. By whatever scheme the within-spot errors were calculated, the simple experiment of obtaining MSWD’s near unity for repeat analyses of a homogeneous sample were crucial in demonstrating that these errors are not too large or small. In contrast, it was not possible with the synthetic glass standard to reproduce the 206Pb+/238U[Ox = 0,1,2]+ ratios from spot-to-spot within the limits of the within spot errors, after correcting the data for obvious systematic variations in the discrimination of the Pb and U isotopes. Identical findings were made following replicate 206Pb+/238U[Ox]+ analyses of the natural zircon standard. That is, for both glass and zircon standards, there remained on average about ±1% (1σ) unaccounted variation per 206Pb+/238U[Ox]+ analysis (that is, MSWDs »1). Thus, unlike for 248[ThO]+/254[UO]+, the within-session errors in 206Pb+/238U[Ox]+ were necessarily higher than the within-spot errors.
In contrast to 208Pb+/206Pb+ and 248[ThO]+/254[UO]+, the 206Pb+/238U[Ox]+ ratios in glass and zircon were significantly fractionated relative to accepted values, and it seemed probable that this difference underlies the larger within-session errors for 206Pb+/238U[Ox]+. The usual methods (for example, using 254[UO]+/238U+) to correct for the inherent discrimination are imperfect and sensitive to small differences in analytical conditions between spots. Matrix variations are ruled out, leaving the precise cause(s) of the additional variation in 206Pb+/238U[Ox]+ currently undetermined, and a hindrance to decreasing the uncertainties in spot 206Pb/238U measurements. The minimum within-session error for an individual 206Pb/238U measurement is the standard deviation (dispersion) of the discrimination-corrected 206Pb+/238U[Ox]+ values for a homogeneous reference material (for example, the synthetic glass standard). The external error in 206Pb/238U additionally incorporates the standard deviation of the mean of the discrimination corrected 206Pb+/238U[Ox]+ for a natural zircon standard. The analysis of 206Pb+/270[UO2]+ offers an improvement over measuring 206Pb+/238U+ because variable discrimination is reduced or eliminated with respect to 254[UO]+/238U+ and counting statistics are superior.
Stern et al. (2009) discussed the significance of the problem of the fractionation of 206Pb+/238U+ from natural 206Pb/238U values that occurs during secondary ion mass spectrometry (SIMS) of zircon under negative-oxygen-ion bombardment. The problem has been well-known (Compston, Williams, and Meyer 1984; Hinthorne et al. 1979), and the correction for the inter-element discrimination has consumed much time and attention of practitioners through concurrent analysis of suitable zircon reference materials. For zircon U-Pb analysis using large-geometry SIMS instruments such as the SHRIMP II, the uncertainties in calibrated 206Pb/238U ratios for individual spots are typically about ± 2% at 95% confidence (Black et al. 2004; Ireland and Williams 2003; Stern and Amelin 2003).
In contrast to the approach for 206Pb/238U ratios, it has become common practice to treat the 207Pb+/206Pb+ ratios measured by SIMS as essentially free of analytical bias (Ireland and Williams 2003), which has resulted in the widespread reporting of radiogenic 207Pb*/206Pb* ratios and ages with very small uncertainties, following correction for deadtime and common Pb (Li et al. 2009). These radiogenic 207Pb*/206Pb* ratios were usually assumed to be accurate, which entailed the underlying assumption that the SIMS instrumental mass fractionation for Pb+ isotopes was, for all practical purposes, zero. In other cases, a small fixed value for instrumental mass fractionation was assumed. Stern et al. (2009) showed that analytical bias in 207Pb*/206Pb* ratios may be more significant than assumed, which is a serious concern for high-precision zircon geochronology and correlation of Precambrian events. For such applications, they argued that, along with the requisite reference materials for calibrating 206Pb/238U, a Precambrian zircon reference material should be an integral part of a SIMS zircon analytical regime.
Stern et al. (2009) illustrated the significance of the instrumental mass fractionation for Pb isotope measurements of zircon (fig. 5). The effect of fractionation is expressed in terms of the absolute difference between the date derived from the true 207Pb*/206Pb* ratio and the fractionated 207Pb*/206Pb* ratio, for instrumental mass fractionation values from 1 to 5‰ u-1 (per atomic mass unit). For example, if the measured 207Pb*/206Pb* is fractionated from the true value by 2‰ u-1, a systematic error in the 207Pb*/206Pb* date (relative to the true value) of the order of 3–4 Ma (depending on the absolute age of the zircon) is introduced (fig. 5). For correlating Precambrian events, such a bias in the age (either too young or too old), induced entirely in this example by an error in the 207Pb*/206Pb* ratio, could be unacceptable. Note that here Stern et al. (2009) did not concern themselves with any bias in the 207Pb*/206Pb* dates arising from systematic errors of the decay constants selected. Furthermore, since the dates are derived quantities, it could be argued that comparisons should instead be made for the specific isotopes being measured.
Fig. 5. Age of zircon (Ma) vs. absolute error (bias) in the 207Pb*/206Pb* age (Ma) caused by various levels of instrumental mass fractionation for 207Pb*/206Pb* in ‰ u-1 (after Stern et al. 2009). The dashed line is illustrative of typical 207Pb*/206Pb* age (95% confidence limit) uncertainties that are governed mainly by counting statistics and common Pb correction. The shaded region highlights conditions where the error introduced by instrumental mass fractionation exceeds typical uncertainties.
An important consideration is the actual magnitude of instrumental mass fractionation for the 207Pb*/206Pb* ratios relative to the typical uncertainties based upon counting statistics. The dashed curve in fig. 5 approximates (for purely illustrative purposes) the 95% confidence intervals typical in the literature for composite 207Pb*/206Pb* ages obtained via SIMS, as a function of age. If instrumental mass fractionation is consistently less than 1‰ u-1, it is unlikely to contribute significantly to the overall uncertainties of most 207Pb*/206Pb* datasets. However, an instrumental mass fractionation of 2‰ u-1 or greater could match or even exceed the assigned uncertainties of some 207Pb*/206Pb* datasets (as illustrated by the shaded region in fig. 5), with correspondingly important implications for both the accuracy of the composite 207Pb*/206Pb* ratios and their overall uncertainties.
Stern et al. (2009) commented that as far as they knew at that time the instrumental mass fractionation for Pb+ isotopes in zircon has never been precisely measured, let alone determined as a matter of routine, as it had been for 206Pb+/238U+. Previous instrumental mass fractionation values for Pb isotopes in zircon and other materials such as galena, Pb metal, and Pb-feldspar were either too small to measure or indicated light isotope enrichment by < 1% u-1 (for example, Belshaw et al. 1994; Compston et al. 1986: Hoskin and Wysoczanski 1998: Roddick and van Breemen 1994: Shimizu and Hart 1982b; Stern 1997; Wiedenbeck 1992; Williams 1998). However, due to insufficient precision, it had either been difficult to demonstrate any significant instrumental mass fractionation for 207Pb+/206Pb+ (the critical ratio for dating) directly from zircon, or the reference values were not sufficiently constrained. Wiedenbeck (1992), for example, examined the evidence for zircon Pb isotope fractionation in the SHRIMP I instrument, but was hampered by lack of a suitable zircon reference material. Unfortunately, the instrumental mass fractionation for Pb isotopes determined from analyzing Pb-rich materials may not be directly applicable to zircon owing to matrix effects on isotopic fractionation (Shimizu and Hart 1982b), and other differences relating to sensitivities to spectral interferences and various corrections to the determinations. In addition to the uncertainty of the magnitude of instrumental mass fractionation, it was also unclear whether instrumental mass fractionation is more or less a constant value for zircon analysis by SIMS, or whether it is dependent on the particular instrument type, or the analytical protocol.
Stern et al. (2009) claimed that whatever value for the instrumental mass fractionation, if any, is adopted, its effect is usually insignificant for any single spot measurement, as the analytical uncertainties due to ion counting statistics and correction for common Pb normally overwhelm any instrumental mass fractionation correction. For example, the uncertainty in the measured 207Pb*/206Pb* ratio of a Precambrian zircon would typically be ± 0.5-5% (all uncertainties represent 95% confidence intervals, unless otherwise stated), 5–10 times greater than any likely instrumental mass fractionation correction. However, the practice of combining several individual 207Pb*/206Pb* measurements into a composite 207Pb*/206Pb* ratio with a much smaller uncertainty may mean that the instrumental mass fractionation can no longer be ignored. Composite 207Pb*/206Pb* ratios on Paleoproterozoic and Archaean zircon with analytical uncertainties of ± 1–3‰ (2–5 Ma) are not uncommon (see fig. 5), so it is conceivable that residual bias of the same order could arise from instrumental mass fractionation. Thus Stern et al. (2009) concluded that if the instrumental mass fractionation for zircon 207Pb*/206Pb* is significant or subject to variability between analytical sessions and instruments, then distinguishing differences of a few Ma in the Precambrian becomes tenuous, thereby precluding the application of SIMS to high-precision zircon dating.
Although the overall Pb-isotopic composition of the sputtered zircon and the bulk sample are identical under steady-state conditions (Shimizu and Hart 1982a), Stern et al. (2009) maintained that it is much less important.
Stern et al. (2009) reported their repeated SHRIMP analysis of a 3465.4 Ma zircon reference material (OG1). Their results indicated that the instrumental mass fractionation for 207Pb*/206Pb* in that zircon varied between instruments and between analytical sessions and was sometimes opposite in direction to general expectations based on previously reported instrumental mass fractionation measurements. Their observations raised several concerns regarding the accuracy of ion probe 207Pb*/206Pb* dates and, particularly, the inter-comparison of such dates between laboratories.
Stern et al. (2009) found that the calculated instrumental mass fractionation for 207Pb*/206Pb* in OG1 zircon ranged from +3.6 ± 1.7‰ to –2.4 ± 1.3‰, indicating both enrichment and depletion of the heavy isotope, respectively. However, the largest data set from a single instrument (SHRIMP II at Geoscience Australia [GA]) suggested a discernable and relatively consistent apparent enrichment of 207Pb+ over 206Pb+, in the form of an instrumental mass fractionation value of +0.87 ± 0.49‰. The instrumental mass fractionation values depended on an accurate reference value for 207Pb*/206Pb*, and although they argued that the selected value (corresponding to TIMS analyses of natural zircons that were air-abraded but not subjected to chemical abrasion) was correct, the zircon reference age is not unambiguous. Thus, the question of the sign of the instrumental mass fractionation for Pb+ in zircon could potentially be further evaluated by analyzing OG1 that has been chemically abraded. In any case, they reasoned that the current data were sufficient to demonstrate that if the chosen reference value was too low, the instrumental mass fractionation for the GA SHRIMP II machine would be zero within uncertainties. Therefore, they did not propose that the measured instrumental mass fractionation value for the GA SHRIMP II machine is the preferred value for anything but that instrument, as it is probably the sum of a number of instrument-specific factors.
However, Stern et al. (2009) then argued that the most useful application of a reference material, such as OG1 zircon, lay in the potential to standardize 207Pb*/206Pb* values. Their twenty-six SHRIMP data sets indicated that the dispersal of session-specific OG1 207Pb*/206Pb* values between instruments and between sessions (exemplified by a value of ± 2.6‰ for two standard deviations) significantly exceeded that attributable to within-session uncertainties (typically ± 1.5‰). In general, instrumental drift did not appear to be a major problem within analytical sessions, but there were measurable differences in overall instrument performance between some instruments and some analytical sessions. The causes of such variations remain to be established, but they felt that in their case must reflect some subtleties in analytical conditions.
Stern et al. (2009) concluded that the data for the GA SHRIMP II machine indicated that the utilization of a zircon reference material such as OG1 to monitor instrumental mass fractionation of Pb+ as a routine part of the ion probe U-Pb dating procedure complemented the use of young zircon reference materials to monitor the accuracy of the 204Pb common-Pb correction, in addition to the obvious need to calibrate the U-Pb ratio. Of course, they had to assume there were no significant matrix effects (or isobaric interferences) that caused the instrumental mass fractionation in the zircon reference material and the unknown to differ, although the extent to which this was a valid assumption was unknown but could be evaluated using more than one reference material. Stern et al. (2009) maintained that their experience with the use of Pb isotope reference materials such as galena, Pb metal and Pb feldspar to determine instrumental mass fractionation indicated that the values do not reflect those determined using zircon. Furthermore, non-zircon Pb isotope reference materials presented a number of practical difficulties in terms of conducting concurrent analyses with unknown zircons, including their significantly different mass spectra, the usual physical location of such material on separate mounts, and the need for separate data processing. Thus, they recommended that published zircon 207Pb*/206Pb* ages, particularly those claiming uncertainties of ± 5 Ma or less, incorporate a measurement of, and correction for, instrumental mass fractionation using a zircon reference material, with appropriate error propagation.
White and Ireland (2012) acknowledged that a correlation had previously been noted between extremely high-uranium concentrations in zircon and apparent U/Pb age as measured in ion microprobe analysis. They then presented data from two zircon populations with extremely high-uranium concentrations in an attempt to quantify effects related to the nature of the samples and/or instrumentally induced fractionation (instrument, analytical setup, and/or matrix effect). They found that the high-uranium matrix effect was apparent in zircons from the 180 Ma Tasmanian Dolerite, which typically showed an increase in Pb/U age of around 3% per thousand μg/g of uranium when measured on the SHRIMP RG machine. Indeed, one session on SHRIMP RG showed a correlation with 8% per thousand μg/g of uranium. In contrast, data from the SHRIMP II instrument showed a weak correlation and no correlation was evident in data collected on the SHRIMP I machine. Furthermore, high-uranium zircons from the 98 Ma Mt Dromedary monzonite showed little to no correlation between uranium concentration and U/Pb age. And analyses of even younger (~20–50 Ma) high-uranium zircons showed a correlation between uranium concentration and an increase in apparent age, but this was less pronounced than the results obtained from the older Tasmanian Dolerite zircons.
Thus, White and Ireland (2012) found that zircons with extremely high uranium can show an apparent increase in Pb/U age that is correlated with the U content. This effect is both sample dependent and instrument dependent. Raman spectroscopy of the Tasmanian Dolerite zircons showed that these zircons are metamict. The link between uranium concentration and apparent age thus appeared to be related to the incipient degradation of the zircon matrix structure from radiation damage. The change in the matrix enhances the emission of Pb+ relative to U and U oxide species, and thus these zircons have a higher likelihood of migration of Pb and U enabling Pb loss, U loss, and common Pb ingress. As this effect is associated with matrix and machine parameters, an external correction cannot be made assuming a constant correction value.
White and Ireland (2012) thus recommended that zircons with high-uranium need to be assessed individually and, in some detail, because the magnitude of the correlation between uranium and apparent age is also instrument dependent. As such, there can be no overall correction factor that can be applied externally. It is possible that concurrent analyses of a high-U secondary standard might allow calibration of the effect, but this standard would need to be matched in age and degree of metamictization to the zircons being analyzed. Therefore, White and Ireland (2012) instead proposed that workers be aware of this matrix effect in SHRIMP analyses of zircon and use Raman spectroscopy before or after SHRIMP analyses to ensure that the zircon is crystalline. This is especially the case if SHRIMP results show an increase in apparent age associated with higher uranium. Their findings thus have important consequences for the use of SHRIMP data for zircon geochronology.
Isotope Fractionation Using Inductively Coupled Plasma-Mass Spectrometers (ICP-MS)
Košler and Sylvester (2003) reported that the raw isotopic and elemental ratios measured by ICP-MS are almost never in agreement with the “true” values. In fact, there are three fundamentally different processes that cause this discrepancy. Instrument mass discrimination (bias) is an offset of the measured values relative to the true values which they maintained is constant at least over the period of time of a single analysis. It results from differential transmission of ions of different masses from the ICP-MS interface to the detector. Different processes are thought to contribute to this mass discrimination, including matrix and space-charge effects and differential ion transmission related to particular instrument settings. Differences in the ionization potential of elements contribute to different responses of ICP-MS and can also bias the measured elemental ratios. The other two processes causing differences between measured and “true” isotopic and elemental ratios Košler and Sylvester (2003) referred to as fractionation and defined it as a continuous change of isotopic or elemental ratios with time during the measurement, as is also well known in TIMS analyses. Such fractionation includes both laser-induced depth-dependent fractionation, which affects volatile/refractory element pairs such as Pb/U ratios as the laser drills progressively into the target, and plasma-induced fractionation during laser ablation (LA)-ICP-MS which is thought to result from non-representative sampling of the ablated aerosols supplied to the plasma, particularly due to incomplete atomization and ionization of the larger particles (such as U and Pb isotopes) (Guillong and Günther 2002).
The size distribution of particles produced during laser ablation is considered to be an important parameter affecting elemental fractionation as well as the stability of the signal measured by ICP-MS (Guillong and Günther 2002). It is affected by the fluence (laser energy per sample area) and wavelength of laser radiation, laser pit diameter/depth ratio, composition of sample carrier gas and size-dependent transport efficiency of ablated particles. Nanometer-sized particles are transported with the highest efficiency and are thus mostly atomized and ionized in the plasma, whereas coarse particles (>1.0 μm) are more effectively trapped in the sample carrier tube, on ablation cell interior surfaces, or form a thin deposit (ejecta blanket) on the sample surface. Košler and Sylvester (2003) concluded that the combination of mass discrimination and elemental fractionation and difficulties in separating the two processes represent a serious challenge for U-Th-Pb dating of accessory minerals by LA-ICP-MS.
In order to derive precise and accurate age data, appropriate corrections must be applied to the raw isotopic and elemental ratios (Košler and Sylvester 2003). The correction procedures that are applicable to the LA-ICP-MS dating of zircons, for example, include using an external zircon of known age (which requires the standard’s age to be known accurately and independently), correction mathematically by using empirical equations that describe fractionation (Horn, Rudnick, and McDonough 2000), or by calculating the fractionation-corrected Pb/U ratios as zero ablation time intercepts of the least-squares linear regression lines fitted to the time-resolved isotopic ratio data (Košler et al. 2002). However, the first method requires the instrument and data acquisition parameters to remain constant for both the standard and the unknown sample and that there are no significant matrix effects on the measured Pb/U and Pb isotopic ratios between the standard and the sample. Furthermore, the latter two methods assume the Pb/U ratios measured at the start of ablation are biased only by the mass discrimination (bias) of the ICP-MS instrument and that the laser-induced, volatile/refractory element fractionation is a linear function of time which can be corrected by extrapolating the measured ratios back to the start of ablation. They also assume that for a given laser spot size and laser energy density there is a linear relationship between the depth of the laser pit (the number of laser pulses applied) and the measured Pb/U ratio, and that the analyzed volume of zircon has a homogeneous Pb/U ratio.
After correction for time-dependent fractionation, Pb/U and Pb isotopic ratios are still biased relative to the “true values” due to mass discrimination in the ICP-MS (Košler and Sylvester 2003). There are two fundamentally different approaches for the mass bias correction, which is a form of standardization. The external correction method utilizes a measurement of an external standard of known isotopic composition to correct for mass bias on measured isotopic ratios in the unknown sample, which requires matrix-matched external standards. The internal correction method is matrix-independent as it utilizes measurements of known isotopic ratios (sometimes of another element) in the unknown sample to correct the measured unknown isotopic ratios (of the target element) in the same sample. A variation of this method utilizes a tracer solution of known isotopic composition that is not present in the sample being analyzed which is nebulized to the plasma during the laser ablation and the aspirated solution is used to correct for instrument bias of the Pb/U and Pb/Pb ratios. There are two fractionation laws commonly used for mass bias corrections in ICP-MS—the power and exponential laws (Košler and Sylvester 2003). However, empirical cross-calibration of mass discrimination factors is often required if accurate mass bias corrections of high-precision data are being made.
Klötzli et al. (2009) used a laser ablation-multi-collector-inductively-coupled plasma-mass spectrometer (LA–MC–ICP–MS) system, with careful control of analytical procedures, to test the long-term external reproducibility and accuracy of the ages of Phanerozoic zircons measured over a period of months. The calibrator bracketing for the 206Pb/238U and 207Pb/206Pb ages was ca. 1% (2 RSD) using a single reference zircon for the matrix-matched calibration. When different reference zircons were used for the calibration, suspicious systematic shifts in the obtained ages were observed and thus a reduction in the overall accuracy of the dating method became obvious. Such shifts were within a few percent range of the U-Pb and Pb-Pb ages and seemed to vary independently of zircon age and composition.
Klötzli et al. (2009) therefore conducted a “test of accuracy” experiment reducing instrumental mass bias effects as far as possible by analyzing five different reference zircons mounted on a single mount eight times during the same session. An identical protocol was used for all analyses, with unchanged instrument parameters and with ion beam intensities kept as identically constant as possible. For data reduction, every zircon served consecutively as the reference zircon for calibration, with the others in the batch treated as unknowns. The known reference age and the four calculated ages obtained using the four other RMs for calibration were then compared. Even using such a very strict analytical protocol, shifts in 206Pb/238U, 207Pb/235U, and 207Pb/206Pb ratios were still present. These shifts varied non-systematically and ranged from –4.35% to 3.08% for the investigated age range (1065 Ma to 226 Ma). Assuming the absence of instrumental effects because great efforts were made to suppress them (that is, memory, dead-time correction, non-linearity of ion counters and inter-detector calibration, crystallographic orientation, ablation cell geometry and setup, and gas flows), the observed shifts were most readily attributed to matrix and/or ablation process-related effects. Klötzli et al. (2009) thus proposed that non-spectral matrix effects in the Ar plasma torch of the MC-ICP-MS resulted in non-uniform signal enhancement (or depression?) leading to the observed shifts both in elemental and Pb isotopic ratios. Additionally, the ablated particle size distribution could be an important factor controlling plasma conditions and thus mass bias and fractionation. Until such effects are well understood and controlled, Klötzli et al. (2009) concluded that it would seem that current state-of-the-art methods for LA–ICP–MS zircon U-Pb and 207Pb/206Pb age determinations cannot be meaningfully interpreted at below a ca. 3% to 4% (2 RSD) confidence level and are thus limited to uncertainties of no better than 3% (2σ) of the determined age.
Paton et al. (2010) reiterated that U-(Th)-Pb zircon geochronology by laser ablation ICP-MS is both rapid and relatively inexpensive and has already become an extremely popular and widespread method. However, the single largest constraint on the accuracy and precision of the technique is the correction of downhole elemental fractionation. They noted that patterns of fractionation with hole depth can vary dramatically both between laboratories, and with changes in operating conditions, and there is no a priori reason for them to be linear. In fact, nonlinear patterns of varying complexity have been observed in multiple laboratories. Therefore, several methods have been proposed to minimize the degree of downhole fractionation, typically by rastering or limiting acquisition to relatively short intervals of time, but these compromise minimum target size or the temporal resolution of data. Alternatively, other methods have been developed which attempt to correct for the effects of downhole elemental fractionation. A common feature of all these techniques, however, is that they impose an expected model of elemental fractionation behavior; thus, any variance in actual fractionation response between laboratories, mineral types, or matrix types cannot be easily accommodated.
Paton et al. (2010) investigated an alternate approach that aimed to reverse the problem by first observing the elemental fractionation response and then applying an appropriate (and often unique) model to the data. They thus suggested that as a general approach, users should attempt to develop an appropriate model of downhole fractionation based upon observations of their own data during each analytical session, instead of attempting to fit the data to a preconceived fractionation model. They counseled that this approach has the versatility to treat data from any laboratory, regardless of the expression of downhole fractionation under any given set of analytical conditions. Employing this strategy, they also demonstrated that the use of more complex models of nonlinear elemental fractionation such as exponential curves and smoothed cubic splines can efficiently correct complex downhole fractionation trends, allowing detection of spatial heterogeneities, while simultaneously maintaining data quality. They found that these models are capable of producing high-quality ages, accurate to within 1% of accepted values, and can be used for demanding applications, such as depth profiling, without compromising data quality. Careful attention should be given though to the propagation of analytical uncertainties, particularly in relation to downhole fractionation and instrumental drift correction. Finally, they presented a data reduction module including uncertainty propagation and error correlation for use in U-(Th)-Pb dating with the Iolite software package that implements this methodology. It provides a method that allows the estimation of analytical uncertainties, using only a single reference standard, in a manner that best reflects the actual uncertainties of individual spot analyses, and the means for simpler interlaboratory comparisons and, perhaps most importantly, enables the rapid reduction of large quantities of data with maximum feedback to the user at each stage.
Allen and Campbell (2012) reiterated that it has become apparent over the last ten years that there is a small systematic error in LA–ICP–MS 206Pb/238U dates for zircons. This was first recognized by Black et al. (2004) who demonstrated small differences between Thermal Ionization Mass Spectrometry (TIMS), and SIMS (Secondary Ion Mass Spectrometry including “SHRIMP”) and LA–ICP–MS 206Pb/238U dates. They showed that this difference is greater for LA–ICP–MS than for SIMS and that it correlates with the incompatible trace element content (Sm, Nd, U, etc.) of the zircon. They studied a group of zircon “standards,” or zircons of good quality that are well characterized, called “reference zircons” in accordance with the International Association of Geoanalysts. Because almost all of the zircons examined by Allen and Campbell (2012) fit this category they reserved the term “primary reference” for the zircon used to reduce the age data. They used the term “secondary reference” for a well-characterized zircon that is treated as an unknown to test precision and accuracy in the session or across sessions, and those zircons dated by the reference zircon were simply called “unknowns.”
In the Black et al. (2004) study, which used Temora 1 as the primary reference, they showed that ICP–MS 206Pb/238U ages for standards QGNG were 1–2% too old, AS3 (similar to FC1) was 2–4% too old, Temora 2 overlapped with Temora 1 or was somewhat younger, and that R33 gave ages that were 1–2% too young. On average Temora 1 is more radiogenic than Temora 2 and both have variable U and Th contents. These inaccuracies were well above quoted precision. Although Black et al. (2004) recognized that the likely cause of these differences was a matrix effect they were unable to identify the mechanism or to suggest a solution. Black et al. (2004) identified this systematic difference between LA–ICP–MS and TIMS measurements of 206Pb/238U in these zircon standards, which they correlated with the incompatible trace element contents of the zircons. Klötzli et al. (2009), in research aimed at placing realistic limits on the interlaboratory accuracy of LA–ICP–MS dating, confirmed the importance of the matrix effect by dating five reference zircons by LA–ICP–MS in a round robin single session, using each of the reference zircons in turn as the primary reference to date the others. They showed that the measured 206Pb/238U of the zircons vary by between 1 and 3% from the TIMS age depending on which zircon was used as the primary reference. Their quoted session-to-session reproducibility was about 1% (2 RSD) if the same primary reference was employed, an amount clearly insufficient to embrace the observed inaccuracies. They therefore suggested that the real between laboratory or external precision of LA–ICP–MS 206Pb/238U dating can be no better than the 3% uncertainty observed in their experiment.
Allen and Campbell (2012) maintained that there is no theoretical reason why the 206Pb/238U age discrepancy between LA–ICP–MS and TIMS dating should correlate with the incompatible trace element content of the zircon. The incompatible trace elements in zircon generally correlate with each other including U and Th, which in turn correlate with the alpha dose received by the zircon crystal lattice and, as a consequence, its radiation damage assuming closure with respect to radiation damage (that is, cooling through about 230°C) happened soon after crystallization, and that the zircon has not been thermally disturbed since. Therefore, Allen and Campbell (2012) concluded that most likely source of a matrix effect in LA–ICP–MS zircon dating is a physical difference and not a compositional one, per se; it is the difference between the alpha dose of the reference zircons and the unknowns, which can lead to the measured LA–ICP–MS 206Pb/238U ages of the unknowns being either younger or older than the TIMS age for the same sample depending on whether the reference or unknown zircon received the higher dose. Alpha-dose is defined as the total number of α-decays the zircon has undergone per gram. It is the calculated number of α-particles emitted since zircon crystallization knowing that 238U emits 8 α-particles as it decays to 206Pb, 235U emits 7 as it decays to 207Pb, and 232Th emits 6 as it decays to 208Pb.
Allen and Campbell (2012) tested their hypothesis that structural damage by α-particles is the underlying cause of matrix differences in two ways. First, they showed that there is a strong correlation between the difference in the LA–ICP–MS and TIMS measured 206Pb/238U and the difference in the alpha dose received by unknown and reference zircons. Six reference zircons were dated by LA–ICP–MS in a round robin experiment and the results were confirmed using data from the literature. The LA–ICP–MS ages for the zircons they dated were as much as 5.1% younger than their TIMS age to 2.1% older, depending on whether the unknown or reference received the higher alpha dose. Second, they showed that by annealing both reference and unknown zircons at 850°C for 48 h in air they could eliminate the alpha-dose-induced differences in measured 206Pb/238U. This was achieved by analyzing six reference zircons a minimum of 16 times in two round robin experiments: the first consisting of unannealed zircons and the second of annealed grains. The maximum offset between the LA–ICP–MS and TIMS measured 206Pb/238U for the unannealed zircons was 2.3%, which reduced to 0.5% for the annealed grains, as predicted by within-session precision based on counting statistics.
Allen and Campbell (2012) concluded that a principal source of inaccuracy in 206Pb/238U LA–ICP–MS dating of zircon arises from matrix differences caused by differences in the alpha dose retained by the unknown and reference zircons. Furthermore, by annealing unknown zircons and references at 850°C for 48 h to the same state prior to analysis can eliminate this source of error and probably reduces the 3% external error in the precision for the measurement of 206Pb/238U of zircon by LA–ICP–MS, indicated by Klötzli et al. (2009) based on experiments where the alpha dose of the primary reference standards varied by 80-fold, to better than 1%. But additional analyses of annealed zircons by other laboratories are required to evaluate the true potential of the annealing method.
Marillo-Sialer et al. (2014) also reiterated that many studies now acknowledge the occurrence of systematic discrepancies between U–Pb ages determined in zircons in situ by LA–ICP–MS and the benchmark analytical method ID-TIMS. So, in their study, Marillo-Sialer et al. (2014) presented detailed investigations into the ablation characteristics of zircons that suggest an underlying mechanism responsible for these age biases relative to ID-TIMS. They found that the observed biases in LA–ICP–MS zircon 206Pb/238U ages, relative to the ID-TIMS reference ages, could be entirely explained by the differences in ablation rate between reference and sample zircons. Confocal laser scanning microscopy of laser ablation pits revealed that there are small but significant differences in the amount of material removed by the laser between different zircons. Based on numerous pit depth and LA–ICP–MS 206Pb/238U ratio measurements of a suite of natural zircon reference materials and samples, Marillo-Sialer et al. (2014) demonstrated that a systematic age bias is strongly correlated with the offset in ablation rates between the primary reference material and sample zircons. Both the intrinsic optical properties of the zircon matrix itself and subtle defocusing effects of the laser beam lead to variations in zircon ablation rates which can, on a day-to-day or lab-to-lab basis, give the impression of being almost random in nature, despite an underlying control.
Marillo-Sialer et al. (2014) thus concluded that, although radiation damage plays a major role in defining the optical and mechanical character of zircons, thermal annealing of zircons in itself does not completely eliminate the differences in ablation behaviour between different zircon matrices and thus is of limited value in improving the accuracy of LA–ICP–MS zircon dating. Indeed, they showed that slight variations in laser focus also influenced the ablation behaviour of zircons and may further degrade the accuracy of U–Pb age determinations. They went on to suggest that in future the ability to precisely measure laser penetration depths in a variety of zircons would enable quantification of the LA–ICP–MS 206Pb/238U age bias. Based on this knowledge, they hoped that it would be possible to develop a proxy able to accurately predict differences in ablation rates between zircons and that this could provide a new strategy for improvement of the accuracy of 206Pb/238U age determinations in zircons by LA–ICP–MS.
Steely, Hourigan, and Juel (2014) presented a discrete multi-pulse depth-profiling method for single-collector ICP-MS laser ablation systems that is applicable to any arbitrary geochemical system that seeks to interrogate isotopic variation as a function of sample depth. The fidelity of the method was assessed with a 183-sample U-Pb analysis session of zircons with known age, which resolved determined U-Pb ages at the integration-level (~0.55 μm depth resolution and ~6% 2σ age uncertainty) using bursts of five laser pulses and calculating ratios from total integrated counts. [It should be noted here, parenthetically, that in these U-Pb analysis sessions they weren’t measuring ages but isotope concentrations and ratios from which the ages were calculated based on the conventional age models.] To avoid signal aliasing, isotopic ratios were calculated using total ion counts for each integration, instead of on a cycle-by-cycle basis. This total count approach provided better stability and accuracy than cycle-by-cycle ratios, especially when signal transience is high. Fractionation correction was achieved through iterative smoothing and interpolation by constructing a continuous-function, non-parametric 3D surface from which discrete values for any time and sample depth could be calculated. This method offered a high degree of flexibility and is validated by Reduced χ2 values near unity for both sample- and session-level weighted mean ages. At the sample level (15 integrations), depths were 7–10 μm and average 2σ uncertainty was ~2.5% for 206Pb/238U ages; 95% of samples and ~90% of integrations overlapped with their accepted age at 2σ.
The data reduction software developed by Steely, Hourigan, and Juel (2014) was designed to be flexible. They also discussed the effects of varying method parameters. Total ablation depth was measured using white light interferometry and ranged between 7 and 10 μm. They thus identified several previously unrecognized factors that appeared to contribute to the accuracy and precision of laser ablation U–Pb zircon ages, which were found to vary as a function of the surface topography of ablation pits, the parent radionuclide concentration, measures of crystal lattice disorganization from Raman spectroscopy, and metrics of radiation damage (α-dose). Indeed, a high positive correlation was found to exist between measures of radiation damage (α-dosage), crystal lattice distortion (shifted and broadened ʋ3 Zr–SiO4 spectra peaks) and ablation pit depths. Steely, Hourigan, and Juel (2014) interpreted these results to indicate that laser ablation efficiency is fundamentally controlled by the accumulation of radiation damage in the zircon crystal lattice, although the exact physical process is unknown at present. Consequently, significant damage variation within a reference zircon can potentially translate to excessive variance in fractionation-correction values and will decrease accuracy and precision. Thus, fractionation-correction values derived for a reference material may not be appropriate for unknowns with vastly different crystal structure, because they would either over- or under-correct intervening “unknown” samples if their damage profiles are significantly different. This second issue would be undetectable if the primary and secondary reference materials have similar damage profiles, yet it contributes significantly to age dispersion.
The stated aim of the study by Marillo-Sialer et al. (2016) was to improve our understanding of the current limitations to high-precision U–Pb analysis of zircon by LA–ICP–MS by investigating the underlying causes of variation in ablation behaviour between different zircon matrices. Accurate identification and refinement of the multiple variables affecting the rate of material removal by the laser is a first step towards the adequate correction for the systematic LA–ICP–MS U–Pb age bias observed between zircon matrices and could potentially lead to a significant decrease of measurement uncertainty in LA–ICP–MS age determinations. Multiple factors such as: the degree of accumulated radiation damage; trace element composition; crystal color; and crystallographic orientation were all systematically investigated.
Marillo-Sialer et al. (2016) found that due to the marked decrease in elastic moduli of natural zircon crystals with increasing radiation damage, the accumulation of this damage was the dominant factor controlling the rate of ablation for partially damaged to highly metamict zircon samples. Indeed, differences in the degree of metamictization between natural zircon samples seemed to play a dominant role in defining the observed variation in ablation characteristics for well crystallized to highly metamict matrices, consistent with prior observations by Steely, Hourigan, and Juel (2014). There were slight differences, however, in ablation behaviour between highly crystalline matrices that could not be attributed solely to differences in the degree of accumulated radiation damage. These differences were associated with structural weakening (that is, decrease in elastic moduli and overall lower mechanical resistance) caused by an increasing degree of cation substitution in some of the zircon samples. Indeed, samples with a well-crystallized structure (ʋ3 (SiO4) FWHM [Full-Width Half-Max] ≤5 cm−1) showed differences in ablation rates that were related to the increasing cation substitution into the zircon structure (and associated changes in mechanical properties; for example, decrease in elastic moduli), and to a much lesser extent (almost negligible) to the crystallographic orientation. As a result of this, crystalline zircon samples showed significant variations in ablation rates that were not strictly correlated to their degree of accumulated radiation damage. According to Marillo-Sialer et al. (2016) it followed that, in general, the increase in laser penetration rate is associated with a decrease in the ability of a zircon crystal to withstand the thermo-mechanical stress applied during laser irradiation, which is a consequence of a weakening of interatomic bonds induced by increasing cation substitution and radiation damage.
Marillo-Sialer et al. (2016) also found that effects of crystallographic orientation and of crystal opacity (that is, color) on ablation behaviour were negligible compared to the combined influences of accumulated radiation damage and trace element substitution (which could also affect crystal color) into the zircon structure. Experiments performed on natural and annealed zircon grains using Raman spectroscopy demonstrated that the reduction in ablation rates observed for the thermally treated samples compared to the untreated grains was proportional to the degree of structural reconstitution achieved after annealing. They showed that differences in ablation rate between zircon matrices after annealing at 850°C for 48 h were caused by the incomplete structural reconstitution of samples which were originally moderate to highly metamict. In contrast, equivalent ablation rates were measured between different zircon matrices after thermal treatment at 1000°C for 36 h, regardless of their initial structural state. And thermal annealing of natural zircon at temperatures >1000°C resulted in much more uniform ablation characteristics. This “homogenization” of ablation behaviour between zircon matrices produced a decrease in the laser-induced matrix effects and subsequent improvement in the accuracy of 206Pb/238U ratio determinations by LA–ICP–MS.
Marillo-Sialer et al. (2016) concluded that, taken together, their experiments provided a roadmap for improvements in the accuracy of U-Pb age determinations by LA–ICP–MS. They claimed that their studies confirmed the usefulness of annealing to increase the similarities in ablation behaviour between zircon matrices, and thus decrease the predominant matrix-related bias. Wherever possible, such annealing should be undertaken as a prerequisite to laser ablation U-Pb geochronology. They noted, however, that a significant improvement in U-Pb age determination was observed only after all zircon materials (reference and unknown) have reached a high degree of structural reconstitution due to annealing with ʋ3 (SiO4) FWHM values of 5 cm−1 or lower. They recommended therefore that annealing temperatures of over 950°C should be used in order to avoid incomplete structural reconstitution of metamict to highly metamict zircon samples. If prior annealing is not available, it may be possible to make corrections for differential ablation behaviour due to accumulated radiation damage either by measurement of Raman spectra (only feasible for a limited number of grains representative of magmatic populations) or by calculation of accumulated radiation dose from measured U and Th contents. In the absence of such strategies, matching the primary reference material to the unknowns in terms of accumulated radiation damage would certainly likely increase accuracy to some extent, although not to the levels achievable with thermal annealing. In addition, to better mitigate the laser-induced matrix effects, closer matching of the total content of minor and trace elements between annealed zircon reference materials and samples is likely to be advantageous. Samples with unusual Hf or trace element contents may exhibit unexpected ablation characteristics resulting in the potential for increased matrix-related age inaccuracy.
Ver Hoeve et al. (2018) likewise admitted that among the most significant challenges in maximizing the precision and accuracy of U-Pb zircon geochronology by LA–ICP–MS is minimizing the impact of downhole fractionation, that is, the time-dependent evolution of Pb/U ratios caused mainly by complex differences in the volatility and chemical properties of elements as they are excavated from the ablation site. To produce meaningful dates for unknown materials, downhole fractionation is typically quantified in a reference zircon and a time-based correction factor subsequently employed to yield constant Pb/U in both standard and unknown zircons. This assumes that both the reference and unknown zircon exhibit similar downhole behaviour.
As a test of this assumption, Ver Hoeve et al. (2018) characterized and quantified during LA-ICP-MS analysis for U-Pb geochronology the downhole fractionation trends in three common zircon reference materials (Plešovice, 337 Ma; Temora-2, 417 Ma; 91500; 1065 Ma) and in three low-U (< 300 ppm) zircon samples with coherent U-Pb systematics from mafic intrusions (Laramie, 1436 Ma; Bushveld, 2057 Ma; Stillwater, 2710 Ma). Zircons from each of the analyzed samples yielded non-linear downhole fractionation behaviour by LA–ICP–MS and the results from each sample required application of an exponential downhole correction model based on each of the untreated zircon reference materials. The corrections were applied to each of the “unknowns” and the resulting time-dependent Pb/U ratios and final ages were compared. The effectiveness of pre-treatment protocols was also evaluated by comparing downhole fractionation trends for untreated grains, annealed grains, and grains that were annealed and leached (that is, chemical abrasion, abbreviated as CA). Each of the three zircon reference materials exhibited distinct downhole fractionation and their calculated correction factors had variable influence in correcting each of the unknowns. Application of the fit parameters either over-corrected or under-corrected the Pb/U ratios of the unknowns due to differences in slope for the different downhole rates at a given time. In most cases, annealing zircon prior to LA–ICP–MS analysis lessened the magnitude of U-Pb mass fractionation during laser ablation, whereas chemical abrasion did not significantly change ablation behaviour beyond simply annealing the grains.
Based on the relative effectiveness of the downhole correction that was applied (that is, similarity of the downhole fit between the reference and the unknown), the resulting U-Pb dates of zircon from the Precambrian mafic intrusions varied significantly when compared to the CA-ID (isotope dilution)-TIMS ages established for these samples (fig. 6). [The isotope dilution method is based on the mass spectrometer determination of the isotopic composition of an element in a mixture of a known quantity of “spike” with an unknown quantity of the normal element (see Faure and Mensing 2005, 68–71).] For Laramie zircon (SR336) where Plešovice was used as a reference standard, the downhole fractionation corrections yielded dates that are close to the CA-TIMS age. In contrast, for Bushveld zircon (SA04-13), the 206Pb/238U dates were all significantly younger than the CA-TIMS age. Using Temora-2 as a primary reference material did not produce satisfying downhole corrections for either Laramie zircon (SR336) or Stillwater zircon (ST05-03), and the resultant U-Pb dates showed larger deviations from the CA-TIMS ages compared with the other two reference materials. Comparison of the downhole fractionation corrections of Stillwater zircon (ST05-03) using the three zircon reference materials reveal that using both 91500 and Plešovice do not result in ideal corrections.
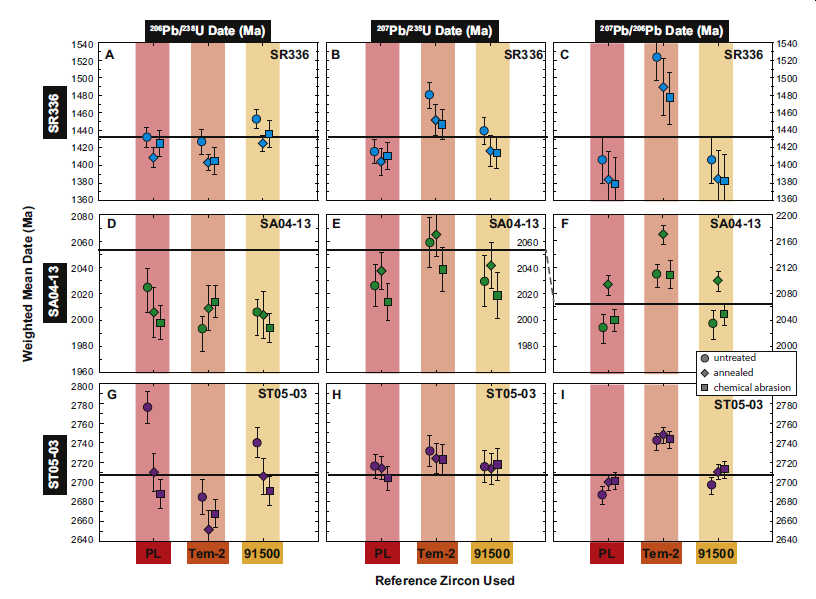
Fig. 6. Summary figure showing the effect of using the three zircon reference materials (Plešovice, Temora-2, 91500) for downhole fractionation corrections on the weighted mean 206Pb/238U, 207Pb/235U, and 207Pb/206Pb dates for the untreated grains from three in-house samples (SR336 Laramie, top row; SA04-13 Bushveld, middle row; ST05-03 Stillwater, bottom row) (after Ver Hoeve et al. 2018). The CA (chemically abraded)-TIMS crystallization age for each sample is noted by a solid line. Age scales are constant across each sample with the exception of panel F due to the larger uncertainties and variation present in the sample. Abbreviations: PL, Plešovice; Tem-2, Temora-2. Uncertainties shown represent 2σ propagated error on each weighted mean.
Ver Hoeve et al. (2018) concluded that the results of their study highlighted the importance of characterizing available reference materials for downhole fractionation by individual laboratories to accurately calibrate unknowns and to ensure that matrix-related biases are minimized. The most robust correction method LA–ICP–MS U-Pb geochronology of zircon would involve quantifying the downhole fractionation behaviour in different reference materials followed by matching the corrections to the unknowns that behaved similarly to the reference material during ablation. The proposed approach would be best suited to producing reliable U-Pb dates by LA–ICP–MS with high analytical precision and accuracy for magmatic zircon for use in constraining igneous crystallization ages, emplacement histories, and crustal magmatic processes. Different pre-treatment protocols were applied by Ver Hoeve et al. (2018) to the reference and “unknown” zircon to assess the relative effects of pre-treatment on ablation characteristics. In most cases, annealing zircon grains prior to LA–ICP–MS analysis decreased the magnitude of U-Pb mass fractionation during laser ablation, although some samples showed negligible effects. Acid leaching of the annealed grains appeared to have little effect on the ablation behavior of the analyzed zircon beyond the effects of annealing.
Discussion
The potential problems which cause possible inaccuracies in obtaining reliable U-Pb and Pb-Pb ages listed by Amelin et al. (2009) when added to one another are overall quite devastating. These potential problems are:
- Presence of non-radiogenic Pb of unknown isotopic composition;
- Deviations from closed system evolution (loss of Pb, gain or loss of U);
- Misidentification of the processes that start or reset the isotopic clocks;
- Analytical problems (fractionation, instrument specific, etc.) and blank subtraction;
- Fractionation of radiogenic Pb isotopes induced by leaching of alpha recoil tracks;
- Variations in the 238U/235U ratio;
- Uncertainties in the half-lives of 238U and 235U; and
- Deviations of the 234U/238U ratio from secular equilibrium.
Of these eight potential problems, Amelin et al. (2009) admitted that the first five are important and common, whereas the last three they considered insignificant or unlikely.
Snelling (2017b) closely examined the first of these, the problem of the presence of non-radiogenic Pb of unknown isotopic composition, that is, common, initial or primordial Pb. It was demonstrated that by being unable to be sure of the starting isotopic composition of the U-Pb system in a rock or mineral from its isotopic composition measured today, it is simply not possible to be so sure that the determined U-Pb age is absolute. Then Snelling (2018) investigated the evidence of deviations from close system evolution of U-Pb systems, as well as misidentification of the processes that start or reset the isotopic clocks. Indeed, the mobility of both Pb and U at all observational scales underscores that the U-Pb system in rocks and minerals is never closed because of the ever-present, difficult-to-measure mobilities of the U and Pb atoms. Furthermore, recent research has even found that these last three problems are more critical than they estimated, not least the variations in the 238U/235U ratio (Goldmann et al. 2015; Tissot and Dauphas 2015), and the uncertainties in the half lives of 238U and 235U (Boehnke and Harrison 2014; Snelling 2017a).
Mass Fractionation
Here we have examined the investigations of instrument-specific mass fractionation during isotopic analyses and of fractionation of both U and Pb isotopes in minerals, problems (4) and (5) above, respectively. In both instances, significant fractionation of both U and Pb isotopes is known to occur. All mass spectrometer system instruments have been documented as causing mass fractionation of isotopes during analytical sessions (problem #4). Whether the sample is targeted by thermal ionization in the TIMS, or secondary ions in the SIMS, or by laser ablation in the LA–ICP–MS instruments, the heat, ion beam and laser all strike and excite the atoms of the various isotopes so they move, which of course is the objective, to move them into the mass spectrometer where powerful magnets accelerate them through a curved path to separate the various isotopes according to their atomic weights so that the detectors can measure their signals to calculate isotopic ratios. However, when these isotopes are excited so that they move out of the samples for the mass spectrometer analyses, whether via thermal ionization, a secondary ion beam or laser ablation, because the isotopes have different atomic weights, they will move different distances within the time frame of the analytical session thus fractionating according to their masses. So, mass fractionation is intrinsic to these analytical techniques and cannot be avoided, and thus trying to quantify the amount of mass fractionation in each instrument during each analytical session is essential if accurate and precise isotopic rations are to be obtained.
Additionally, mass fractionation of U and Pb isotopes occurs within the minerals even before they are subjected to the TIMS, SIMS, or LA–ICP–MS beam analyses (problem #5). This is primarily because in the minerals the daughter Pb isotopes are usually not bonded within their crystal lattices, so those isotopes are not held tightly in place and can be moved. There are two processes believed to be responsible. First, there is diffusion, the ability of atoms held loosely in a mineral to “leak out” of the crystals. Since the atoms vibrate due to the energy of motion of the subatomic particles in them, they will thus move within the crystal lattice, lighter atoms travelling further than heavier atoms. Thus, the different Pb isotopes are fractionated according to their mass differences. Second, when U atoms decay “firing off” α-particles they recoil, that is, just like a rifle when firing a bullet “kicks back” in the opposite direction, each U atom when it decays “kicks back,” dislodging it from where it was held in the host crystal. There are almost one hundred more 238U atoms to every 235U atom, and the few 235U atoms decay a lot more frequently (faster) than all the many more 238U atoms, plus the different U isotopes eject α-particles of different energies. Together these factors will cause the mass fractionation of the resultant Pb isotopes as the end-products of these processes. Thus, mass fractionation of U and Pb isotopes is a significant process already occurring in the host minerals even before they are subjected to the TIMS, SIMS or LA–ICP–MS beam analyses.
The Inherent Assumptions and Circular Reasoning
In a nutshell then, all these problems listed above can be summarized by the three over-arching assumptions that these supposed absolute dating methods rely on, namely:
- One must know the starting conditions;
- One must be sure there has been no contamination of closed systems (that is, no gain or loss of parent and/or daughter isotopes); and
- One must be sure that the decay rates of the parent isotopes has always been the same as the decay rates measured today.
Yet all three assumptions are unprovable, because they require knowledge of the unobserved and unobservable past. Thus, based on isotopic measurements in rocks and minerals today we can never be sure of their isotopic compositions when the minerals and rocks formed, and then during their subsequent history. Furthermore, the copious documented investigations in the present have demonstrated that these assumptions are not even reasonable. For example, Snelling (2000a, 2005c) has extensively reported from the conventional literature, as also documented by Dickin (2005, 136–173) and Faure and Mensing (2005, 363–411) in their textbooks on geochronology, that magmas inherit the isotopic compositions of their sources in the upper mantle and lower crust, so the resulting basalt lavas and granite plutons will always have initial isotopic compositions that reflect those sources respectively. Thus, on ocean islands recently erupted basalt lavas yield Pb-Pb ages of 1–2 billion years, an abundantly repeated observation which has been known for more than 50 years as the Pb isotope paradox and is recognized as due to their starting isotopic compositions reflecting their inheritance of isotopes from their sources.
Much current conventional research has been focused intensely on solving these problems listed above. And as investigated here, a critical problem is that even the various instruments used to measure the isotopic ratios in rocks and minerals cause mass fractionation of U and Pb isotopes. Intense efforts have been made, as reported here, to try and quantify such mass fractionation and thus derive correction factors which could be routinely applied to all U-Pb and Pb-Pb age calculations. While thermal ionization mass spectrometry (TIMS) is regarded as producing the highest precision and accuracy in Pb isotope analyses, some mass fractionation still occurs and needs to be somehow circumvented. The routine ploy is to also use standards of known ages analyzed at the same time on the same instrument for comparison, especially trying to make sure the standard is the same mineral as the unknown being dated. It is thus assumed that the Pb isotopes in the standard will undergo the same amount of mass fractionation as in the unknown of the same mineral in the same instrument analyzed at the same time. While this seems reasonable and would appear then to overcome the mass fractionation error in the resultant U-Pb and Pb-Pb age calculations, it overlooks the obvious critical question, namely, how do we know the true ages of the standards?
The answer to that question of how we know the true ages of the standards underscores the ultimate problem for the U-Pb and Pb-Pb dating methodology. The standards themselves have been independently dated using the same U-Pb and Pb-Pb dating technology, so those analyses have also been subject to the same mass fractionation effects! To overcome that problem, if the standard is a mineral such as zircon, then the rock from which the zircon was extracted has also been dated, or some other mineral within the same rock, using other dating methods such as K-Ar or Ar-Ar. However, the 40K decay constant needed for calculation of the K-Ar and Ar-Ar dates has been determined by calibrating against the U-Pb and/or Pb-Pb dates obtained on the same rocks and/or minerals (Min et al. 2000; Snelling 2016). Furthermore, the much-touted and preferred Ar-Ar dating method requires standards of known ages to be mounted in the same holder as the unknown during irradiation to derive the fluence factor for the age calculation, which again begs the question of how do we know the true ages of the standards? Thus, if the zircon standard’s known U-Pb or Pb-Pb age has been derived by cross-calibration with the K-Ar or Ar-Ar age of another mineral in the same rock, then it’s because the 40K decay constant has been calibrated against the 238U decay constant. Indeed, the decay constants of all the other parent radioisotopes used in radiometric dating have been calibrated against the decay constant of 238U, the determination of which has also involved uncertainties (Snelling 2014a, 2014b, 2015a, 2015b, 2016, 2017a). In other words, there has been circular reasoning and there is no object independent standard by which these agreements have been obtained.
Now it should be acknowledged that much genuine ingenuity has been applied to these problems and extreme care has been taken with both the sample preparations and the instrumental analyses. There can be no question about the integrity of the laboratories, the instruments, and the analysts and technicians. However, the geochronologists cannot escape from the web of assumptions and circular reasoning inherent in their science of U-Pb and Pb-Pb dating methods. There are absolutely no standards for use in determining the ages of unknowns whose known ages have been independently and objectively determined. Trying to overcome the effects on the true ages of mass fractionation of Pb isotopes during all analyses with all instruments cannot be accomplished without resorting to using standards whose known ages have not been independently and objectively determined without circular reasoning. So, the fractionation correction factors that have been determined are only as good as the standards used to determine them, standards whose known ages have not been objectively and independently determined without circular reasoning. And underpinning the circular reasoning they use are the three unprovable assumptions concerning the known starting conditions, no contamination of closed systems and constant radioactive decay rates inherent in all dating methods. Thus, the claimed ages obtained cannot be absolute ages, even within their stated error margins, which after all represent the probability of the true ages being within the stated error ranges that has been determined from all the analytical uncertainties, including the mass fractionation corrections.
The Combined Effects on U-Pb and Pb-Pb Ages
Two further issues need to be considered. First, what are the combined effects of all these listed problems on the resultant U-Pb and Pb-Pb ages? Fig. 5 provides graphical estimates of the absolute error (bias) in the 207Pb*/206Pb* age (Ma) caused by various levels of instrumental mass fractionation (problem #4) for 207Pb*/206Pb* in units of ‰ u-1 using a SIMS instrument (after Stern et al. 2009). The solid lines represent different estimated levels of mass fractionation errors, so that a 1‰ fractionation error generally causes a 2 Ma error to derived dates, whereas a 5‰ fractionation error produces an error of 10 Ma for a 1000 Ma date and about an 8 Ma error for a 4000 Ma date. Furthermore, the dashed line is the typical 207Pb*/206Pb* age uncertainties (at the 95% confidence limit) that are governed mainly by the counting statistics and the common Pb correction (problems #1 and #4), which suggests an error of 4 Ma for a 4000 Ma date, and an error of >12 Ma for a 1000 Ma date (perhaps close to 14 Ma if the dashed line is extrapolated).
It is not clear from this diagram (fig. 5) whether these errors compound with one another. However, if they do, which is most likely, then the 5‰ mass fractionation error which causes a 10 Ma error for a 1000 Ma date added to the counting statistics and common Pb correction error (at the 95% confidence limit uncertainties) of ~14 Ma for a 1000 Ma date results in a potential error of ~24 Ma for a 1000 Ma date (or ~2.5%). Furthermore, it is clear from the diagram that the lower the date is below 1000 Ma, the greater are these errors. That this is the case is likely due to the smaller measurable quantities of the Pb isotopes present in the rock or mineral.
Added to these errors are the unaccounted-for variations in the 238U/235U ratio (problem #6) and the uncertainties in the half-lives of 238U and 235U (problem #7). If the 238U/235U ratio has been measured specifically for the mineral standard (which has not always been the case), then there would be the errors from measurements of the 238U/235U ratio and the half-lives of 238U and 235U. And it would be exceedingly unlikely the 238U/235U ratio has been measured for the unknowns. The 238U/235U ratio has been measured as varying between 137.72 and 137.94 in minerals used for U-Pb and Pb-Pb dating, the most recent measurements of the half-life of 238U have determined a value between 4.433 and 4.4779 Byr, and the most recent measurements of the half-life of 235U have determined a value between 702.47 and 703.63 Myr, although that determination was anchored to the half-life of 238U as 4.467 Byr (Snelling 2017a). Thus, the unaccounted-for variations in the 238U/235U ratio and the uncertainties in the half-lives of 238U and 235U could add another 1–2% error to the calculation of U-Pb and Pb-Pb dates.
Therefore, the combined effects of all these listed problems on the resultant U-Pb and Pb-Pb ages could be as much as 3.5%–4.5% for a 1000 Ma date, or 35–45 Myr. And as already noted, the combined error could be much worse for dates below 1000 Ma. Yet the conventional geochronology community continues to expend much time and effort to reduce the uncertainties and errors that accumulate from these listed problems, almost universally by employing the use of standards that have been exhaustively analyzed and tested with accuracy and precision to provide them with certified “known” ages with very low uncertainties. However, they are “blind” by choice to both the three primary over-arching assumptions that are unprovable and have been demonstrated repeatedly to be unreasonable, and the inescapable circular reasoning involved in certifying these standards with “known” ages. And furthermore, significant variations in the 238U/235U ratio even in the same minerals are still being documented, and the uncertainties in the half-lives of 238U and 235U have still not been objectively eliminated. Thus, the claimed millions-billions of years U-Pb and Pb-Pb ages obtained cannot be absolute ages, but at best only relative ages.
U-Pb and Pb-Pb “Ages” Within the Biblical Time Framework
The earth’s deep time history has only been assumed, not proven. To the contrary, the infallible divine eyewitness account in the Scriptures provides a reliable framework for the earth’s short history of only 6000 or so years marked by the progressive supernatural creation processes during the days of the Creation Week, the supernatural Curse at the Fall, and the cataclysmic total reshaping of the earth in the year-long Flood. Thus, the other issue which needs to be discussed here is how the claimed millions and billions of years ages obtained by the U-Pb and Pb-Pb dating should be considered within the biblical time framework of only 6000 or so years? Since the biblical time framework provides the true ages of the earth’s rocks, all those claimed U-Pb and Pb-Pb ages for rocks and minerals are grossly inflated. How then do we reconcile this enormous disparity? Three considerations provide a definitive reconciliation.
First, we need to recognize that while these claimed millions and billions of years ages obtained by the U-Pb and Pb-Pb dating cannot be absolute ages for the reasons discussed above, the errors and uncertainties due to the listed problems are largely systematic. That is, the same errors and uncertainties occur systematically for all the dates, as is well illustrated in fig. 5. The errors and uncertainties may increase for different ranges of dates, but even the scales of the errors and uncertainties are systematic. Furthermore, even the common Pb corrections are systematic due to magmas being consistently sourced from the various upper mantle and lower crustal isotopic domains (Snelling 2000a, 2005c, 2017b). Similarly, both U and Pb mobility are usually systematic because of the underlying causes (Snelling 2018). Thus, while the conventionally published U-Pb and Pb-Pb dates are not absolute ages, they are still systematic relative ages, usually being in the correct order of decreasing “ages” according to where the various dated rock units are found in the geologic column, both locally and globally. For example, in the Grand Canyon region, the dated rock units found in the Precambrian crystalline basement yield Precambrian ages of a billion years or more, whereas volcanic ash beds and tuffs found up in the Phanerozoic yield progressively younger relative ages according to the layers’ positions in the local and regional geologic columns (Snelling 2005b, 2005c). Therefore, there must have been some systematic process involved that has caused this systematic “younging” of these relative radiometric “ages” up through the geologic column.
Second, is the question of whether physical radioactive decay has been responsible for the claimed millions and billions of years ages, or whether the isotope abundances in the minerals and rocks used to calculate their presumed dates are simply the product of their original geochemistries and/or subsequent geochemical processes. However, the fact is that there is abundant observable evidence in the minerals and rocks that a lot of radioactive decay has physically occurred in the past. Snelling (2005b) investigated volcanic ash beds and tuffs at various levels in the Grand Canyon regional geologic column and found that the zircon grains in those layers had different intensities of fission tracks commensurate with their radiometric ages. Fission tracks are produced by U atoms spontaneously splitting apart (fissioning) into two smaller atoms of similar atomic weight and physically damaging the surrounding host mineral’s crystal lattice leaving trails or tracks that can be made visible. Thus, Snelling (2005b) found that zircon grains in a tuff bed in the Cambrian Tapeats Sandstone had many fission tracks equivalent to a fission track age virtually identical to its relative radiometric age of c.520 Ma, compared to the zircon grains in the Cenozoic Peach Springs Tuff at the top of the regional geologic column having comparatively few fission tracks commensurate with their relative radiometric age of c.20 Ma. Similarly, Snelling (2005a) investigated the biotite flakes in granites of various relative radiometric ages and found in them many overexposed 238U radiohalos surrounding tiny embedded zircon grains. These radiohalos are the result of 238U atoms within the zircons decaying and ejecting α-particles that shoot out of the zircon grains in all directions like little bullets into the surrounding host biotite damaging its crystal lattice and leaving dark trails or tracks. It takes 500 million to 1 billion α-particles to form a well-developed 238U radiohalo, equivalent to about 100 million years’ worth of 238U decay at today’s measured 238U decay rate (Snelling 2000b). Thus, 238U radiohalos are physical evidence that radioactive decay has occurred and a lot of it, at least about 100 million years’ worth of 238U decay at today’s measured 238U decay rate. And while magmas may have inherited their initial isotopic compositions from their mantle and crustal sources (Snelling 2000a, 2005c), the resultant lavas, tuffs and granites still contain physical evidence of abundant radioactive decay having occurred within them after they crystallized and cooled yielding vast systematic radiometric ages relative to each rock unit’s position or level in the geologic record.
Third, Vardiman, Snelling, and Chaffin (2000) proposed that systematic accelerated nuclear decay must have occurred in some past cataclysmic event or events to produce the rocks’ highly inflated radiometric dates within the biblical time frame of earth history. Subsequently, Vardiman, Snelling, and Chaffin (2005) reported on investigations that had revealed several independent lines of evidence that radioisotope decay rates were grossly accelerated during the recent global Flood cataclysm, and perhaps also during the Creation Week. These evidences included discordant radioisotope dates obtained by the different radiometric methods on the same rock units, commensurate fission track and radioisotope ages for the same rock units, Po radiohalos alongside 238U radiohalos in the same biotite grains in granites, He diffusion (leakage) ages for zircons in a Precambrian granodiorite compared to their radioisotope age, and thousands of years radiocarbon ages for coalbeds and diamonds supposedly millions and billions of years old respectively. So, since the grossly accelerated radioisotope decay during those cataclysmic biblical events was systematic, the resultant grossly inflated radioisotope ages are systematic in accordance with the relative timing of the formation of each rock unit during those events. For example, a lava flow erupted during the first month of the Flood year would have subsequently experienced eleven months of grossly accelerated radioisotope decay, whereas a lava erupted in the last month of the Flood year would only have suffered less than a month of the same grossly accelerated radioisotope decay. So the two lavas would have relative ages commensurate with their respective positions or levels within the geologic record left behind during the Flood year.
This then is how the enormous disparity between the claimed millions and billions of years ages of rocks and minerals obtained by the U-Pb and Pb-Pb dating can be definitively reconciled within the biblical time framework of only 6000 or so years. As to the cause of the grossly accelerated radioisotope decay, Vardiman, Snelling, and Chaffin (2000, 2005) provided evidence that it may be due to changes in the strong and weak nuclear forces which bind protons and neutrons within atomic nuclei. But what caused such changes remains unsolved, although supernatural involvement in both the Creation Week and the Flood are stipulated clearly in the Genesis accounts of those events. Thus, the biblical creationist need not be intimidated by the conventional claims of absolute ages of millions and billions of years for the earth’s rocks, as the radioisotope methods used to produce them are riddled with systematic uncertainties that render them only relative, not absolute. Instead, the biblical creationist can remain fully confident and convinced of the integrity and trustworthiness of the God-given biblical account and time framework for the earth’s history, guaranteed by the infallible eyewitness, the Creator Himself.
Conclusions
Minerals such as zircon are routinely used by geochronologists to confidently provide the U-Pb and Pb-Pb ages which underpin the conventional multi-millions-of-years’ time scale. However, it is now well-documented that both U and Pb isotopes naturally mass fractionate due to the nuclear-field effect and differential mass diffusion. Furthermore, the beams used in the instruments to sample tiny volumes of such minerals for their mass spectrometer isotopic analyses also cause isotopic mass fractionation, especially of Pb isotopes. Knowing this problem, much effort has been expended in the conventional geochronology community to try and quantify the amounts of fractionation induced by thermal ionization, by secondary ion beams and by laser ablation so that appropriate uncertainties can be stipulated for the U-Pb and Pb-Pb dates obtained by each instrument. However, all such efforts involve the use of standards deemed to have “known” ages that have been determined by U-Pb, Pb-Pb, and /or other radiometric methods such as K-Ar or Ar-Ar. This is unavoidable circular reasoning, which is especially compounded by the decay constants of all the other parent isotopes used for dating the standards having been calibrated against the 238U decay constant, and methods such as Ar-Ar also using standards of “known” ages during age determinations. Besides, the uncertainties are significant, amounting to as much as 10 Ma for a 1000 Ma date due to a 5‰ mass fractionation, and even higher for younger ages, using a SIMS instrument and based on standards of known ages.
These uncertainties due to the mass fractionation of isotopes are compounded further by similar and larger uncertainties in the measured 238U and 235U decay rates, the crucial 238U/235U ratio, the amount and composition of inherited, initial and/or common Pb, and the possibility of both U and Pb mobility after minerals and the rocks containing them were formed. All these uncertainties are inadequately acknowledged by geochronologists, and instead they take numerous precautions to still give the U-Pb and Pb-Pb methods a strong aura of validity which readily mesmerizes other geologists and the lay public. However, all these uncertainties are overshadowed by the underlying unprovable assumptions on which the radioisotope dating methods are based, known starting conditions, no contamination, and especially the assumption of time-invariant decay rates, built on the foundation of an assumed deep time history. Furthermore, their use of standards with assumed “known” ages to calibrate the uncertainties in samples with unknown ages is fraught with circular reasoning as the same methods are used to determine the “known” ages. The resultant U-Pb and Pb-Pb ages obtained are thus subjective and only provide systematic relative ages. Instead, the evidence for grossly accelerated radioisotope decay during a past cataclysmic event such as the Genesis Flood has been well established, so those absolute ages therefore cannot be used to dismiss the history of the earth and its approximately 6000-year chronology provided in God’s infallible Word.
Acknowledgments
The three reviewers, particularly Dr. Eugene Chaffin and Dr. Vernon Cupps, are acknowledged for their helpful comments and input, though the final content of this paper is solely my responsibility. Our production assistant Laurel Hemmings is also especially thanked for her painstaking work in preparing this paper for publication.
References
Abe, Minori, Tatsuya Suzuki, Yasuhiko Fujii, Masahiko Hada, and Kimihiko Hirao. 2008. “An Ab Initio Molecular Orbital Study of the Nuclear Volume Effects in Uranium Isotope Fractionations.” The Journal of Chemical Physics 129, no. 6 (24 October): 164309-1–164309-7.
Abe, Minori, Tatsuya Suzuki, Yasuhiko Fujii, Masahiko Hada, and Kimihiko Hirao. 2010. “Ligand Effect on Uranium Isotope Fractionations Caused by Nuclear Volume Effects: An Ab Initio Relativistic Molecular Orbital Study.” The Journal of Chemical Physics 133, no. 4 (30 July): 044309-01–044309-05.
Allen, Charlotte M., and Ian H. Campbell. 2012. “Identification and Elimination of a Matrix-Induced Systematic Error in LA–ICP–MS 206Pb/238U Dating of Zircon.” Chemical Geology 332–333 (25 November): 157–165.
Amelin, Y., D. W. Davis, and W. J. Davis. 2005 “Decoupled Fractionation of Even- and Odd-Mass Isotopes of Pb in TIMS.” Geochimica et Cosmochimica Acta 69, no. 10 (January): A215
Amelin, Y., J. Connelly, R. E. Zartman, J. H. Chen, C. Göpel, and L. A. Neymark. 2009. “Modern U-Pb Chronometry of Meteorites: Advancing to Higher Time Resolution Reveals New Problems.” Geochimica et Cosmochimica Acta 73, no. 17 (1 September): 5212–5223.
Angeli, I., and K. P. Marinova. 2013. “Table of Experimental Nuclear Ground State Charge Radii: An Update.” Atomic Data and Nuclear Data Tables 99, no. 1 (January): 69–95.
Anselment, M., W. Faubel, S. Göring, A. Hanser, G. Meisel, H. Rebel, and G. Schatz. 1986. “The Odd-Even Staggering of the Nuclear Charge Radii of Pb isotopes.” Nuclear Physics A 451, no. 3 (31 March): 471–480.
Ashton, F. W. 1919. “A Positive Ray Spectrograph.” Philosophical Magazine 38, no. 228 (series 6): 707–714.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. “Call for an Improved Set of Decay Constants for Geochronological Use.” Geochimica et Cosmochimica Acta 65, no. 1 (1 January): 111–121.
Belshaw, N. S., R. K. O’Nions, D. J. Martel, and K. W. Burton. 1994. “High-Resolution SIMS Analysis of Common Pb.” Chemical Geology 112, nos. 1–2 (25 January): 57–70.
Benninghoven, A., F. G. Rudenauer, and H. W. Werner. 1987. Secondary Ion Mass Spectrometry: Basic Concepts, Instrumental Aspects, Applications, and Trends. New York: Wiley.
Bigeleisen, Jacob. 1996. “Nuclear Size and Shape Effects in Chemical Reactions: Isotope Chemistry of the Heavy Elements.” Journal ofthe American Chemistry Society 118, no. 15: 3676–3680.
Black, Lance P. 2005. “The Use of Multiple Reference Samples for the Monitoring of Ion Microprobe Performance During Zircon 207Pb/206Pb Age Determinations.” Geostandards and Geoanalytical Research 29, no.2 (July): 169–182.
Black, Lance P., Sandra L. Kamoc, Charlotte M. Allen, Donald W. Davis, John N. Aleinikoff, John W. Valley, Roland Mundil, Ian H. Campbell, Russell J. Korsch, Ian S. and Chris Foudoulis. 2004. “Improved 206Pb/238U Microprobe Geochronology by the Monitoring of a Trace-Element-Related Matrix Effect; SHRIMP, ID–TIMS, ELA–ICP–MS and Oxygen Isotope Documentation for a Series of Zircon Standards.” Chemical Geology 205, nos. 1–2 (30 April): 115–140.
Boehnke, Patrick, and T. Mark Harrison. 2014. “A Meta-Analysis of Geochronologically Relevant Half-Lives: What’s the Best Decay Constant?” International Geology Review 56 no. 7 (14 April): 905–914.
Boltwood, Bertram B. 1907. “On the Ultimate Disintegration Products of the Radio-active Elements. Part II. The Disintegration Products of Uranium.” American Journal of Science, Series 4, 23 no. 134: 77–88.
Brennecka, Gregory A. 2011. “Uranium Isotope Variations in Nature: Mechanisms, Applications, and Implications.” PhD Thesis, Arizona State University, Tempe, Arizona. https://www.researchgate.net/profile/Greg_Brennecka/ publication/265987838_Uranium_Isotope_Variations_ in_Nature_Mechanisms_Applications_and_Implications/ links/54ca3ccf0cf2c70ce521a137/Uranium-Isotope-Variations-in-Nature-Mechanisms-Applications-and-Implications.pdf
Brennecka, Gregory A., and Meenakshi Wadhwa. 2012. “Uranium Isotope Compositions of the Basaltic Angrite Meteorites and the Chronological Implications for the Early Solar System.” Proceedings of the National Academy of Sciences USA 109, no. 24 (June 12): 9299–9303.
Chen, J. H., and G. J. Wasserburg. 1983. “The Least Radiogenic Pb in Meteorites.” Lunar and Planetary Science Conference 14 (March): 103–104.
Chen, Fukun, Wolfgang Siebel, and M. Satir. 2002. “Zircon U-Pb and Pb-Isotope Fractionation During Stepwise HF Acid Leaching and Geochronological Implications.” Chemical Geology 191, nos. 1–3 (15 November): 155–164.
Compston, W., and V. M. Oversby. 1969. “Lead Isotope Analyses Using a Double Spike.” Journal of Geophysical Research 74, no. 17 (15 August): 4338–4348.
Compston W., I. S. Williams, and C. Meyer. 1984. “U-Pb Geochronology of Zircons From Lunar Breccia 73217 Using a Sensitive High Mass-Resolution Ion Microprobe.” Journal of Geophysical Research 89, no. 502 (15 February): B525–B534.
Compston, W., P. D. Kinney, I. S. Williams, and J. J. Foster. 1986. “The Age and Pb Loss Behaviour of Zircons From the Isua Supracrustal Belt as Determined By the Ion Microprobe.” Earth and Planetary Science Letters 80, nos. 1–2 (October): 71–81.
Corfu, Fernando. 2000. “Extraction of Pb With Artificially Too-Old Ages During Stepwise Dissolution Experiments On Archean Zircon.” Lithos 53, nos. 3–4 (September): 279–291.
Cowan, George A. 1976. “A Natural Fission Reactor.” Scientific American 235, no. 1 (July): 36–47.
Cumming, G. L. 1973. “Propagation of Experimental Errors in Lead Isotope Ratio Measurements Using the Double Spike Method.” Chemical Geology 11, no. 3 (June): 157–165.
Davis, D. W., and T. E Krogh. 2000. “Preferential Dissolution of 234U and Radiogenic Pb From α-Recoil-Damaged Lattice Sites in Zircon: Implications For Thermal Histories and Pb Isotopic Fractionation in the Near Surface Environment.” Chemical Geology 172, nos. 1–2 (1 February): 41–58.
Dempster, A. J. 1918. “A New Method of Positive Ray Analysis.” Physical Review 11 (1 April): 316–325.
Dickin, Alan P. 2005. Radiogenic Isotope Geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Doucelance, R., and G. Manhès. 2001. “Reevaluation of Precise Lead Isotope Measurements by Thermal Ionization Mass Spectrometry: Comparison with Determinations by Plasma Source Mass Spectrometry.” Chemical Geology 176, nos. 1–4: 361–377.
Faure, Gunter. and Teresa M. Mensing. 2005. Isotopes: Principles and Applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Fujii, Toshiyuki, Frédéric Moynier, and Francis Albarède. 2006. “Nuclear Field vs. Nucleosynthetic Effects as Cause of Isotopic Anomalies in the Early Solar System.” Earth and Planetary Science Letters 247, nos. 1–2 (15 July): 1–9.
Goldmann, Alexander, Gregory Brennecka, Janine Noordmann, Stefan Weyer, and Meenakshi Wadhwa. 2015. “The Uranium Isotopic Composition of the Earth and the Solar System.” Geochimica et Cosmochimica Acta 148 (1 January): 145–158.
Guillong, Marcel, and Detlef Günther. 2002. “Effect of Particle Size Distribution on ICP-Induced Elemental Fractionation in Laser Ablation-Inductively Coupled Plasma-Mass Spectrometry.” Journal of Analytical Atomic Spectrometry 17, no. 8: 831–837.
Hayes, Robert B. 2017. “Some Mathematical and Geophysical Considerations in Radioisotope Dating Applications.” Nuclear Technology 197, no. 2 (26 February): 209–218.
Hiess, Joe, Daniel J. Condon, Noah McLean, and Stephen R. Noble. 2012. “238U/235U Systematics in Terrestrial Uranium-Bearing Minerals.” Science 335, no. 6076 (30 March): 1610–1614.
Hinthorne, J. R., C. A. Andersen, R. L. Conrad, and J.F. Lovering. 1979. “Single-Grain 207Pb/206Pb and U/Pb Age Determinations with a 10-μm Spatial Resolution Using the Ion Microprobe Mass Analyzer (IMMA).” Chemical Geology 25, no. 4 (June): 271–303.
Holmes, Arthur. 1913. The Age of the Earth. London, United Kingdom: Harper and Brothers.
Horn, Ingo, Roberta L. Rudnick, and William F. McDonough. 2000. “Precise Elemental and Isotope Ratio Measurement by Simultaneous Solution Nebulization and Laser Ablation-ICP-MS: Application to U–Pb Geochronology.” Chemical Geology 164, nos. 3–4 (27 March): 281–301.
Hoskin, Paul W. O., and Richard J. Wysoczanski. 1998. “In Situ Accurate and Precise Lead Isotopic Analysis of Ultra-Small Analyte Volumes (10-16 m3) of Solid Inorganic Samples by High Mass Resolution Secondary Ion Mass Spectrometry.” Journal of Analytical Atomic Spectrometry 13, no. 7: 597–601.
Ireland, T. R., and I. S. Williams. 2003. “Considerations in Zircon Geochronology by SIMS.” In Zircon. Edited by John M. Hanchar and Paul W. O. Hoskin, vol. 53, 215–241. Reviews in Mineralogy and Geochemistry. Washington DC: Mineralogical Society of America.
Klötzli, Urs, Eva Klötzli, Zekeriya Günes, and Jan Košler. 2009. “Accuracy of Laser Ablation U-Pb Zircon Dating: Results from a Test Using Five Different Reference Zircons.” Geostandards and Geoanalytical Research 33, no. 1 (March): 5–15.
Košler, Jan, Hege Fonneland, Paul Sylvester, Mike Tubrett, and Rolf-Birger Pedersen. 2002. “U–Pb Dating of Detrital Zircons for Sediment Provenance Studies—A Comparison of Laser Ablation ICPMS and SIMS Techniques.” Chemical Geology 182, nos. 2–4 (15 February): 605–618.
Košler, Jan, and Paul J. Sylvester. 2003. “Present Trends and the Future of Zircon in Geochronology: Laser Ablation ICPMS.” In Zircon. Edited by John M. Hanchar and Paul W. O. Hoskin, vol. 53, 243–275. Reviews in Mineralogy and Geochemistry. Washington DC: Mineralogical Society of America.
Kuroda, P. K. 1982. The Origin of the Chemical Elements and the Oklo Phenomenon. New York: Springer-Verlag.
Lancelot, Joel R., Annie Vitrac, and Claude J. Allègre. 1975. “The Oklo Natural Reactor: Age and Evolution Studies of U-Pb and Rb-Sr Systematics.” Earth and Planetary Science Letters 25, no. 2 (March): 189–196.
Li, Xian-Hua, Yu Z. Liu, Qiu-Li Li, Chun-Hua Guo, and Kevin R. Chamberlain. 2009. “Precise Determination of Phanerozoic Zircon Pb/Pb Age by Multicollector SIMS without External Standardisation.” Geochemistry, Geophysics, Geosystems 10, no. 4 (April). doi/abs/10.1029/2009GC002400.
Ludwig, K.R. 1993. “PBDAT 1.24: A Computer Program for Processing Pb-U-Th Isotope Data. Version 1.24.” USGS Open-File Report 88-542. Washington, D.C.: U.S. Geological Survey.
Manhès, G., and C. Göpel. 2007. “Mass-Independent Fractionation During TIMS Measurements: Evidence of Nuclear Shift Effect?” Geochimica et Cosmochimica Acta 71, no. 15 (August): A618.
Marillo-Sialer, E., J. Woodhead, J. Hergt, A. Greig, M. Guillong, A. Gleadow, N. Evans, and C. Paton. 2014. “The Zircon ‘Matrix Effect’: Evidence for an Ablation Rate Control on the Accuracy of U-Pb Age Determinations by LA-ICP-MS.” Journal of Analytical Atomic Spectrometry 29, no. 6: 981–989.
Marillo-Sialer, E., J. Woodhead, J. M. Hanchar, S. M. Reddy, A. Greig, J. Hergt, and B. Kohn. 2016. “An Investigation of the Laser-Induced Zircon ‘Matrix Effect’.” Chemical Geology 438 (2 November): 11–24.
Mattinson, James M. 1994. “A Study of Complex Discordance in Zircons Using Step-Wise Dissolution Techniques.” Contributions to Mineralogy and Petrology 116, nos. 1–2 (March): 117–129.
Mattinson, J. M. 1997. “Analysis of Zircon By Multi-Step Partial Dissolutions: The Good, The Bad, and The Ugly.” GAC/MAC Annual Meeting Abstracts Volume, A98. Ottawa, Ontario: Geological Association of Canada.
Mattinson, J. M. 2000. “Revising the ‘Gold Standard’, the Uranium Decay Constants of Jaffrey et al., 1971.” EOS, Transactions of the American Geophysical Union 81: abstract S444.
Mattinson, James M. 2010. “Analysis of the Relative Decay Constants of 235U and 238U by Multi-Step CA-TIMS Measurements of Closed-System Natural Zircon Samples.” Chemical Geology 275, nos. 3–4 (August): 186–198.
McLean, Noah M. 2014. “Straight Line Regression Through Data with Correlated Uncertainties in Two or More Dimensions, with an Application to Kinetic Isotope Fractionation.” Geochimica et Cosmochimica Acta 124 (1 January): 237–249.
Mehrer, Helmut. 2007. Diffusion in Solids. New York: Springer-Verlag.
Miller, Johanna L. 2012. “Time to Reset Isotopic Clocks? Two New Studies Revise Key Parameters in Radiometric Dating.” Physics Today = 65, no. 6 (26 April): 20–22.
Min Kyoungwon, Roland Mundil, Paul R. Renne, and Kenneth R. Ludwig. 2000. “A Test for Systematic Errors in 40Ar/39Ar Geochronology through Comparison with U-Pb Analysis of a 1.1 Ga Rhyolite.” Geochimica et Cosmochimica Acta 64, no. 1 (January): 73–98.
Nier, Alfred O. 1940. “A Mass Spectrometer for RoutineIsotope Abundance Measurements.” Review of Scientific Instruments 18: 398–411.
Paton, Chad, Jon D. Woodhead, John C. Hellstrom, JanetM. Hergt, Alan Greig, and Roland Maas. 2010. “Improved Laser Ablation U–Pb Zircon Geochronology Through Robust Downhole Fractionation Correction.” Geochemistry, Geophysics, Geosystems 11, no. 3 (March). Q0AA06; doi:10.1029/2009GC002618.
Potts, Philip J. 2012. “Glossary of Analytical and Metrological Terms from the International Vocabulary of Metrology (2008).” Geostandards and Geoanalytical Research 36, no. 3 (September): 231–246.
Rademacher, Laura K., Craig C. Lundstrom, Thomas M. Johnson, Robert A. Sanford, Juanzho Zhao, and Zhaofeng Zhang. 2006. “Experimentally Determined Uranium Isotope Fractionation During Reduction of Hexavalent U by Bacteria and Zero Valent Iron.” Environmental Science and Technology 40, no. 22 (October 20): 6943–6948.
Renne, Paul R., Daniel B. Karner, and Kenneth R. Ludwig. 1998. “Absolute Ages Aren’t Exactly.” Science 282, no. 5395 (4 December): 1840–1841.
Richards, J.R. 1981. “Some Thoughts on the Time-Dependence of Lead Isotope Ratios.” Geokhimiya [Geochemistry International] 1981: 17–36.
Roddick, J.C., and O. van Breemen. 1994. “U-Pb Zircon Dating: A Comparison of Ion Microprobe and Single Grain Conventional Analyses.” Radiogenic Age and Isotopic Studies: Report 8, Geological Survey of Canada, 1994-F, 1–9.
Rudnick, R. L., and S. Gao. 2005 “Composition of the Continental Crust.” In The Crust. Edited by R. L. Rudnick, vol. 3, 1–64. Treatise on Geochemistry. Edited by H. D. Holland and K. K. Turekian. Amsterdam, The Netherlands: Elsevier.
Russell, R. D. 1971. “The Systematics of Double Spiking.” Journal of Geophysical Research 76, no. 20 (10 July): 4949–4955.
Russell, R. D. 1975. “Mass Discrimination in the Measurement of Lead Isotope Reference Samples.” Geochemical Journal 9, no. 1 (March 20): 47–50.
Rutherford, Ernest. 1906. Radioactive Transformations. New York: Charles Scribner’s Sons.
Schauble, E. A. 2006. “Equilibrium Uranium Isotope Fractionation by Nuclear Volume and Mass-Dependent Processes.” American Geophysical Union, Fall Meeting, Abstract V21B-0570.
Schauble. Edwin A. 2007. “Role of Nuclear Volume in Driving Equilibrium Stable Isotope Fractionation of Mercury, Thallium, and Other Very Heavy Elements.” Geochimica et Cosmochimica Acta 71, no. 9 (1 May): 2170–2189.
Schmitz, M.D. 2012. “Radiogenic Isotope Geochronology.” In The Geologic Time Scale 2012. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg. vol. 1, chapter 6, 115–126. Amsterdam, The Netherlands: Elsevier.
Schoene, Blair, James L. Crowley, Daniel J. Condon, Mark D. Schmitz, and Samuel A. Bowring. 2006. “Reassessing the Uranium Decay Constants for Geochronology Using ID-TIMS U–Pb Data.” Geochimica et Cosmochimica Acta 70, no. 2 (15 January): 426–445.
Schoene, Blair, Daniel J. Condon, Leah Morgan, and Noah M. McLean. 2013. “Precision and Accuracy in Geochronology.” Elements 9,no. 1 (February): 19–24.
Schön, R., G. Winkler, and W. Kutschera. 2004. “A Critical Review of Experimental Data For the Half-Lives of the Uranium Isotopes 238U and 235U.” Geochimica et Cosmochimica Acta 60, nos. 2–4 (February–April): 263–273.
Shimizu, Naohiro, and S. R. Hart. 1982a. “Applications of the Ion Microprobe to Geochemistry and Cosmochemistry.” Annual Review of Earth and Planetary Sciences 10, no. 1 (November): 483–526.
Shimizu N. and S. R. Hart. 1982b. “Isotope Fractionation in Secondary Ion Mass Spectrometry.” Journal of Applied Physics 53, no.3 (1 March): 1303–1311.
Slodzian, G., J. C. Lorin, and A. Havette. 1980. “Isotopic Effect on the Ionization Probabilities in Secondary Ion Emission.” Journal de Physique Lettres 41, no. 23 (December): 555–558.
Snelling, Andrew A. 2000a. “Geochemical Processes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: A Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 123–304. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, Andrew A. 2000b. “Radiohalos.” In Radioisotopes and the Age of the Earth: A Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 381–468. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, Andrew A. 2005a. “Radiohalos in Granites: Evidence of Accelerated Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 101–207. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/radiohalos-granites-evidence-for-accelerated/.
Snelling, Andrew A. 2005b. “Fission Tracks in Zircons: Evidence for Abundant Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 209–324. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/fission-tracks-zircons-evidence-for/.
Snelling, Andrew A. 2005c. “Isochron Discordances and the Role of Mixing and Inheritance of Radioisotopes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/isochron-discordances-role-inheritance/.
Snelling, Andrew A. 2014a. “Determination of the Radioisotope Decay Constants and Half-Lives: Rubidium-87 (87Rb).” Answers Research Journal 7 (September 3): 311–322. https://answersingenesis.org/geology/radiometric-dating/ determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, Andrew A. 2014b. “Determination of the Radioisotope Decay Constants and Half-Lives: Lutetium-176 (176Lu).” Answers Research Journal 7 (December 3): 483–497. https://answersingenesis.org/geology/radiometric-dating/ determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, Andrew A. 2015a. “Determination of the Radioisotope Decay Constants and Half-Lives: Rhenium-187 (187Re).” Answers Research Journal 8 (February 25): 93–111. https://answersingenesis.org/geology/radiometric-dating/ determination-radioisotope-decay-constants-and-half-lives-rhenium-187/.
Snelling, Andrew A. 2015b. “Determination of the Radioisotope Decay Constants and Half-Lives: Samarium-147 (147Sm).” Answers Research Journal 8(June 10): 305–321. https:// answersingenesis.org/geology/radiometric-dating/ determination-radioisotope-decay-constants-and-half-lives-samarium-147/.
Snelling, Andrew A. 2016. “Determination of the Radioisotope Decay Constants and Half-Lives: Potassium-40 (40K).” Answers Research Journal 9 (August 3): 171–196. https://answersingenesis.org/geology/radiometric-dating/ determination-radioisotope-decay-constants-half-lives-potassium-40/.
Snelling, Andrew A. 2017a. “Determination of the Decay Constants and Half-Lives of Uranium-238 (238U) and Uranium-235 (235U), and the Implications for U-Pb and Pb-Pb Radioisotope Dating Methodologies.” Answers Research Journal 10 (January 18): 1–38. https://answersingenesis. org/geology/radiometric-dating/determination-decay-constants-half-lives-uranium/.
Snelling, Andrew A. 2017b. “Problems with the U-Pb Radioisotope Dating Methods—1. Common Pb.” Answers Research Journal 10 (July 26): 121–167. https:// answersingenesis.org/geology/radiometric-dating/ problems-radioisotope-dating-u-pb/.
Snelling, Andrew A. 2018. “Problems with the U-Pb Radioisotope Dating Methods—2. U and Pb Mobility.” Answers Research Journal 11 (June 13): 85–140. https:// answersingenesis.org/geology/radiometric-dating/ problems-with-u-pb-radioisotope-dating-methods-mobility/.
Steely, Alexander N., Jeremy K. Hourigan, and Erik Juel. 2014. “Discrete Multi-Pulse Laser Ablation Depth Profiling with a Single Collector ICP-MS: Sub-Micron U-Pb Geochronology of Zircon and the Effect of Radiation Damage on Depth-Dependent Fractionation.” Chemical Geology 372 (24 April): 92–108.
Steiger, R. H., and E. Jäger. 1977. “Subcommission on Geochronology: Convention on the Use of Decay Constants in Geo- and Cosmochronology.” Earth and Planetary Science Letters 36, no. 3 (October): 359–362.
Stern, Richard A. 1997. “The GSC Sensitive High Resolution Ion Microprobe (SHRIMP): Analytical Techniques of Zircon U-Th-Pb Age Determinations and Performance Evaluation.” Radiogenic Age and Isotopic Studies: Report 10, Geological Survey of Canada, 1997-F, 1–31.
Stern, Richard A., and Yuri Amelin. 2003. “Assessment of Errors in SIMS Zircon U-Pb Geochronology Using a Natural Zircon Standard and NIST SRM 610 Glass.” Chemical Geology 197, nos. 1–4 (15 June): 111–142.
Stern, Richard A., Simon Bodorkos, Sandra L. Kamo, Arthur H. Hickman, and Fernando Corfu. 2009. “Measurement of SIMS Instrumental Mass Fractionation of Pb Isotopes During Zircon Dating.” Geostandards and Geoanalytical Research 33, no. 2 (June): 145–168.
Stirling Claudine H., Morten B. Andersen, Emma-Kate Potter, and Alex N. Halliday. 2007. “Low-Temperature Isotopic Fractionation of Uranium.” Earth and Planetary Science Letters 264, nos. 1–2 (15 December): 208–225.
Tatsumoto, Mitsunobu, Roy J. Knight, and Claude J. Allègre. 1973. “Time Differences in the Formation of Meteorites as Determined From the Ratio of Lead-207 to Lead-206.” Science 180, no. 4092 (22 June): 1279–1283.
Thirlwall, M. F. 2000. “Inter-Laboratory and Other Errors in Pb Isotope Analyses Investigated Using a 207Pb-204Pb Double Spike.” Chemical Geology 163, nos. 1–4 (February): 299–322.
Thomson, J. J. 1911. “A New Method of Chemical Analysis.” Nature 86 (1 June): 466–469.
Tissot, François L. H., and Nicolas Dauphas. 2015. “Uranium Isotopic Compositions of the Crust and Ocean: Age Corrections, U Budget and Global Extent of Modern Anoxia.” Geochimica et Cosmochimica Acta 167(15 October): 113–143.
Vardiman, L., A. A. Snelling, and E. F. Chaffin. eds. 2000. Radioisotopes and the Age of the Earth: A Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E.F. Chaffin. eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Ver Hoeve, Thomas J., James S. Scoates, Corey J. Wall, Dominique Weis, and Marghaleray Amini. 2018. “Evaluating Downhole Fractionation Corrections in LA-ICP-MS U-Pb Zircon Geochronology.” Chemical Geology 483 (20 April): 201–217.
Villa, I. M., M. L. Bonardi, P. De Bièvre, N. E. Holden, and P. R. Renne. 2016. “IUPAC-IUGS Status Report on the Half-Lives of 238U, 235U and 234U.” Geochimica et Cosmochimica Acta 172 (1 January): 387–392.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nemov, and C. A. Bauman. 1969. “A Programmable Magnetic Field Mass Spectrometer with On-Line Data Processing.” Review of Scientific Instruments 40, no. 2 (February): 288–295.
Wetherill, George W. 1956. “Discordant Uranium-Lead Ages.” Transactions of the American Geophysical Union 37, no. 3 (June): 320–326.
Wetherill, G. W. 1963. “Discordant Uranium-Lead Ages—Pt. 2. Discordant Ages Resulting from Diffusion of Lead and Uranium.” Journal of Geophysical Research 68, no. 10 (15 May): 2957–2965.
Wetherill, George W. 1966. “Radioactive Decay Constants and Energies.” In Handbook of Physical Constants. Edited by S. E. Clarke, 514–519. Geological Society of America Memoir 97. Boulder, Colorado: Geological Society of America.
Weyer, S., A. D. Anbar, A. Gerdes, G. W. Gordon, T. J. Algeo, and E. A. Boyle. 2008. “Natural Fractionation of 238U/235U.” Geochimica et Cosmochimica Acta 72, no. 2 (15 January): 345–359.
White, L. T., and T. R. Ireland. 2012. “High-Uranium Matrix Effect in Zircon and Its Implication for SHRIMP U-Pb Age Determinations.” Chemical Geology 306–307 (4 May): 78–91.
Wiedenbeck, Michael George. 1992. “U-Pb Dating of Zircons by Ion Microprobe: Case Studies From the Northwestern Yilgarn Craton, Western Australia.” Ph.D. thesis, Research School of Earth Sciences, The Australian National University, Canberra.
Wiedenbeck, Michael, and Keith P. Watkins. 1993. “A Time Scale for Granitoid Emplacement in the Archean Murchison Province, Western Australia, by Single Zircon Geochronology.” Precambrian Research 61, nos. 1–2 (February): 1–26.
Williams, Ian S. 1998. “U-Th-Pb Geochronology by Ion Microprobe.” In Applications of Microanalytical Techniques to Understanding Mineralizing Processes. Edited by M. A. McKibben, W. C. Shanks III, and W. I. Ridley. Reviews in Economic Geology 7 (January 1): 1–35. San Diego, California: Economic Geology Publishing Company.
Wingate, M. T. D., and W. Compston. 2000. “Crystal Orientation Effects During Ion Microprobe U-Pb Analysis of Baddeleyite.” Chemical Geology 168, nos. 1–2 (July): 75–97.
Wunderlich, R. K., G. J. Wasserburg, I. D. Hutcheon, and Geoffrey A. Blake. 1993. “Laser-Induced Isotopic Effects in Titanium Resonance Ionization.” Analytical Chemistry 65, no. 10 (May 15): 1411–1418.
York, Derek. 1968. “Least Squares Fitting of a Straight Line with Correlated Errors.” Earth and Planetary Science Letters 5: 320–324.
Zumbro, J. D., E. B. Shera, Y. Tanaka, C. E. Bemis Jr., R. A. Naumann, M. V. Hoehn, W. Reuter, and R.M. Steffen. 1984. “E2 anti E4 Deformations in 233,234,235,238U.” Physical Review Letters 53, no. 20 (12 November): 1888–1892.