Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Over the last 78 years numerous determinations have been made of the total 40K decay half-life, obtained by direct counting experiments and by comparing radioisotope ages derived from more than one dating method applied to the same rocks or minerals. The determinations since 1997 have converged with close agreement toward the total 40K decay half-life value of 1.2524±0.0064Byr. But that determination in 2011 ignored the two liquid scintillation direct counting determinations in 2002 and 2004 which had agreed on a slightly lower total 40K decay half-life value of 1.248±0.003Byr. So neither of these values has yet been adopted for standard use by the uniformitarian geochronology community. There are important sources of systematic error in all 40Ar-39Ar (and K-Ar) ages that arise from uncertainties in the two 40K decay constants and the K-Ar isotopic data for neutron fluence monitors (the Ar-Ar dating standards). Even though it is crucial to determination of the total 40K decay half-life, the branching ratio between 40K β-decay to 40Ca and electron capture decay to 40Ar with γ-rays emitted is still not definitively agreed upon. The value of 0.1162 was used in 2011 in spite of the value of 0.1194±0.007 carefully determined in 2000, which confirmed the value of 0.1195±0.0014 determined in 1973. The uncertainties in the crucial 40K/K abundance ratio also need to be considered, because there is no agreement on it. The value of 0.011672±0.000041% determined in 1975 is still adopted, but the value of 0.011668±0.000008% determined in 2013 has yet to be recognized. Therefore, when all these factors are considered the total 40K decay half-life is thus known to no better than ±2% at the 2σ level, and the 40Ar*/40K ratios for individual standards are only known to better than ±2% in some cases, while interlaboratory discrepancies of more than 2% in the 40Ar/39Ar ages of secondary standards like the Fish Canyon Tuff sanidine suggest larger uncertainties. Thus independent determinations of the branching and 40K/K abundance ratios are still needed, as well as new laboratory investigations to determine the total 40K decay half-life. Yet, in spite of the many experiments directly measuring the total 40K decay half-life, the adopted value ultimately depends on deriving it by adjusting (that is, massaging) K-Ar and Ar-Ar ages to conform to U-Pb and Pb-Pb ages obtained from different minerals respectively in the same rocks. But many unprovable assumptions are also involved, not the least being that the radioisotope systems closed at the same time and subsequently remained closed. Furthermore, even this U-Pb “gold standard” has unresolved uncertainties due to the U decay constants being imprecisely known, and to measured variations of the 238U/235U ratio in terrestrial rocks, ores, and minerals, and in meteorites. Both of these factors are so critical to the U-Pb method, as well as the additional factor of knowing the initial concentrations of the daughter and index isotopes, so it should not be used as a standard to determine other decay constants. There is also evidence decay rates of the radioisotopes used for rock dating have not been constant in the past, as well as the possibility of a slight decline in the measured values of the total 40K decay half-life during the 78 years of determinations. This only serves to emphasize that if the K-Ar and Ar-Ar dating methods have been calibrated against the U-Pb “gold standard” with all its attendant uncertainties, then they cannot be absolute, and therefore they cannot be used to reject the young-earth creationist timescale. Indeed, current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Introduction
Radioisotope dating of rocks and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Many in both the scientific community and the general public around the world thus remain convinced of the earth’s claimed great antiquity.
However, accurate radioisotopic age determinations require that the decay constants (or half-lives) of the respective parent radionuclides be accurately known and constant in time. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is still not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with direct half-life determinations are, in most cases, still at the 1% level, which is still significantly better than any radioisotope method for determining the ages of rock formations. However, even uncertainties of only 1% in the half-lives lead to very significant discrepancies in the derived radioisotope ages. The recognition of an urgent need to improve the situation is not new (for example, Renne et al. 1998; Min et al. 2000a). It continues to be mentioned, at one time or another, by every group active in geo- or cosmochronology (Schmitz 2012).
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further inroads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was the issue of how reliable have been the determinations of the radioisotope decay rates, which are so crucial for calibrating these dating “clocks.” Indeed, before this present series of papers (Snelling 2014a, b, 2015a, b) there have not been any attempts in the creationist literature to review how the half-lives of the parent radioisotopes used in long-age geological dating have been determined and to collate all the determinations of them reported in the literature to discuss the accuracy of their currently accepted values. After all, accurate radioisotope age determinations depend on accurate determinations of the decay constants or half-lives of the respective parent radioisotopes. The reliability of the other two assumptions these supposed absolute dating methods rely on, that is, the starting conditions and no contamination of closed systems, are unprovable. Yet these can supposedly be circumvented somewhat via the isochron technique, because it is claimed to be independent of the starting conditions and is claimed to be sensitive to revealing any contamination, which is still significantly better than any radioisotope method for determining the ages of rock formations. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. That this is common practice is illustrated with numerous examples cited from the literature by Faure and Mensing (2005) and Dickin (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is arbitrary and therefore is not good science, because it is merely assumed the “aberrant” values are due to contamination rather than that being proven to be so. Indeed, in order to discard such outliers in any data set, one must establish a reason for discarding those data points which cannot be reasonably questioned.
In order to rectify this deficiency in the creationist literature, Snelling (2014a, b, 2015a, b) has documented the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes 87Rb, 176Lu, 187Re, and 247Sm which are used as the basis for the Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd long-age dating methods respectively. He showed that there is still some uncertainty in what the values for these measures of the 87Rb and 176Lu decay rates should be, in contrast to the apparent agreement on the 187Re and 247Sm decay rates. This uncertainty is especially prominent in determinations of the176Lu decay rate by physical direct counting experiments. Furthermore, the determined values of the 87Rb decay rate differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rates of isotopes such as 87Rb and 247Sm used for deep time dating that makes precise measurements of their decay rates so difficult. Thus it could be argued that direct measurements of their decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology employed by the secular community in their rock dating methods. Yet, the 87Rb, 176Lu, 187Re, and 147Sm decay half-lives have all ultimately been calibrated against the U-Pb radioisotope systems. This is the case even for the 147Sm decay half-life whose accepted value has not changed since it was calibrated against the U-Pb dating of two meteorites in the 1970s, in spite of the fact that more recent thorough physical direct counting experiments suggest a higher value. However, confidence in U-Pb radioisotope dating as the “gold standard” is very questionable, as there are now known measured variations in the 238U/235U ratio that is critical to that method (Brennecka and Wadhwa 2012; Hiess et al 2012), as well as uncertainties as to the 238U and 235U decay rate values (Mattinson 2010; Schön, Winkler, and Kutschera 2004; Schoene et al. 2006).
Therefore, the aim of this contribution is to further document the methodology behind and history of determining the present decay constants and half-lives of the parent radioisotopes used as the basis for the long-age dating methods. We need to explore just how accurate these determinations are, whether there really is consensus on standard values for the half-lives and decay constants, and just how independent, consistent, and objective the standard values are for each of the different methods. Of course, it is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life measurements because these are difficult measurements to make with concomitant high statistical errors. This would also apply to determination of the amount of daughter isotope produced via the decay process. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks, and the question remains as to whether the half-life values for each long-lived parent radioisotope are independently determined. We continue here with determinations of the potassium-40 (40K) decay rate, which is the basis for the K-Ar and Ar-Ar dating methods.
Potassium, Potassium-40 Decay and Potassium-Argon Dating
Potassium (Z=19) is an alkali metal (group IA), along with Li, Na, Rb, and Cs. It is one of the eight most abundant chemical elements in the earth’s crust and is a major constituent of many important rock-forming minerals, such as the micas, the feldspars, the feldspathoids, many clay minerals, and some evaporite (precipitite) minerals (Dickin 2005; Faure and Mensing 2005).
The isotopic composition of K was first studied by Aston (1921), who discovered 39K and 41K. The radioactivity of K salts was suggested by Thomson (1905) and was subsequently demonstrated by Campbell (1908) and Campbell and Wood (1906). However, the naturally-occurring radioisotope 40K was not identified until Nier (1935) presented conclusive evidence for its existence using a much more sensitive mass spectrometer than had been available to Aston. The possible modes of decay open to 40K were first discussed by Von Weizsäcker (1937), who concluded that 40K undergoes branched decay to 40Ca and to 40Ar, based partly on the fact that the abundance of Ar in the earth’s atmosphere is about 1000 times greater than expected when compared to the cosmic abundances of the other noble gases. Von Weizsäcker (1937) also postulated that radiogenic 40Ar should be present in old K-bearing minerals. Aldrich and Nier (1948) then confirmed that prediction by demonstrating that four geologically old minerals did contain radiogenic 40Ar. The theoretical basis for K-Ar dating method was thus established by 1950, and since then it has become an important and widely used method for dating K-bearing rocks and minerals (Dalrymple 1991; Dalrymple and Lanphere 1969; Hunziker 1979; Schaeffer and Zähringer 1966).
Potassium therefore has three naturally-occurring isotopes whose abundances have been determined as 39K = 93.2581 ± 0.0029%, 40K = 0.01167 ± 0.00004%, and 41K = 6.7302 ± 0.0029% (Garner et al. 1975). Since 40K makes up only 0.01167% of total potassium, it thus effectively falls in the low-ppm concentration range in rocks and minerals. The isotopic composition of Ar in the terrestrial atmosphere was measured by Nier (1950) as 40Ar = 99.60%, 38Ar = 0.063%, and 36Ar = 0.337%, so that the 40Ar/36Ar ratio is 99.60/0.337 = 295.5.
Naturally-occurring 40K exhibits a branched decay scheme to 40Ca and 40Ar (fig. 1). The major branch (89.52% of 40K) leads by negatron (β-particle) emission to 40Ca, but in most rocks the 40Ca daughter product is swamped by common (non-radiogenic) 40Ca, which makes up 97% of total calcium (Dickin 2005). Only about 10.48% of the 40K atoms decay to 40Ar, but by three different routes, two of which involve capture of an orbital electron by the nucleus. One of these two electron capture modes leaves the 40Ar nucleus in an excited state, which then de-excites by means of an energetic γ-ray (1.4608 MeV) (Faure and Mensing 2005). The second electron capture mode and the positron decay both reach the ground state of 40Ar directly. However, the third route by positron emission makes up only 0.001% of decays to 40Ar. Therefore, the electron capture (etc.) decay constant can be taken to represent all of the routes from 40K to 40Ar (Dickin 2005).

Fig. 1. The branched β-decay of 40K to 40Ar and 40Ca (after Faure and Mensing 2005). The decay to 40Ar proceeds by means of electron capture (e.c.) and positron decay. The maximum energy of the positrons (0.483 MeV) has been combined in this diagram with the energy of the annihilation γ-rays (1.02 MeV). The decay by negatron emission leads to the ground state of 40Ca. The energetic γ-rays (1.4608 MeV) that characterize the radiochemical properties of 40K are associated with the dominant electron capture mode. (Data from Dalrymple and Lanphere 1969; Lide and Frederikse 1995.)
The electron capture decay constant λec has a recommended value of 0.581 × 10-10 per year, equivalent to a half-life of 11.93 Byr (Steiger and Jäger 1977), based on a weighted mean of the six best counting determinations at the time evaluated by Beckinsale and Gale (1969). But the β-decay of 40K to 40Ca has its own decay constant λβ which has to also be taken into account. It has a recommended value of 4.962 × 10-10 per year, equivalent to a half-life of 1.397 Byr (Steiger and Jäger 1977). Thus the recommended value of the total decay constant λ for 40K decay, which is the sum of the two branches, is 5.543 × 10-10 per year, equivalent to a half-life of 1.25 Byr (Steiger and Jäger 1977).
As already indicated, there are two parameters by which the decay rate is measured and expressed, namely, the decay constant (λ) and the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, whereas the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:
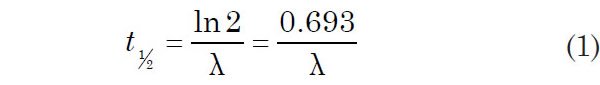
The branching ratio R is defined as λec/λβ and has a value of 0.117 (Faure and Mensing 2005). The fraction of 40K atoms that decay to 40Ar is given by (λec/λ) 40K, which is used to express the growth of radiogenic 40Ar atoms (40Ar*) in a K-bearing rock or mineral:
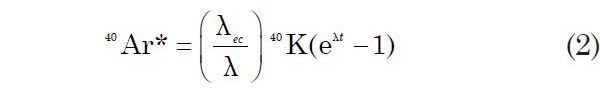
The total number of 40Ar atoms is:
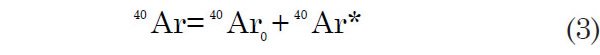
where 40Ar0 is the number of 40Ar atoms per unit weight of sample that were incorporated into the rock or mineral at the time of its formation. Since Ar is a noble (or inert) gas and since its solubility in silicate melts is thus low, 40Ar0 is assumed to be zero. It could be argued that this is a questionable assumption to verify, especially since only a relatively small amount of 40Ar is incorporated into the rock via radioactive decay.
To date a K-bearing rock or mineral by the K-Ar method, the number of 40K and 40Ar* atoms in a unit weight of sample must be measured and then used to solve equation 2 for t:
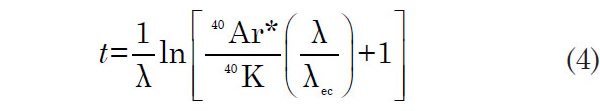
However, as Faure and Mensing (2005) emphasize, the value of t so calculated is the age (that is, the model age) of the rock or mineral only when the following assumptions are satisfied:
- No radiogenic 40Ar* produced by decay of 40K in the rock or mineral during its lifetime has escaped.
- The rock or mineral became closed to 40Ar soon after its formation, which means it must have cooled rapidly after crystallization, unless it formed at a low temperature.
- No 40Ar was incorporated into the rock or mineral either at the time of its formation or during a later metamorphic event.
- An appropriate correction is made for the presence of atmospheric 40Ar.
- The rock or mineral was closed to K, that is, it neither gained nor lost any K, throughout its lifetime.
- The isotopic composition of K in the rock or mineral is normal and was not changed by fractionation or other processes except by decay of 40K.
- The decay constants (or half-lives) of 40K are known accurately and have not been affected by the physical or chemical conditions of the environment in which the K has existed since it was incorporated into the earth.
- The concentrations of K and 40Ar* were determined accurately.
Even Faure and Mensing (2005) admit that these assumptions require careful evaluation in each case and place certain restrictions on the geological interpretation of K-Ar dates. Indeed, Dickin (2005), Faure and Mensing (2005), and Snelling (2000) provide numerous examples where spurious K-Ar and Ar-Ar dates have been obtained for various rocks and minerals due to the demonstrated failure of some of these assumptions. The last three assumptions are quite general in scope and express certain fundamental conditions of any radioisotope dating method. The isotopic composition of K in terrestrial samples is usually regarded as constant, even though fractionation of K isotopes has been observed on a small scale across contacts of igneous intrusions (Morozova and Alferovsky 1974; Verbeek and Schreiner 1967). However, if the total 40K half-life is not known accurately, then the calculated K-Ar age of any rock or mineral cannot be known accurately either. These problems led to the development of the argon-argon (Ar-Ar) dating method.
Argon-Argon Dating
In addition, the decay of 40K to 40Ar is also the basis for the 40Ar-39Ar dating method, which uses an unconventional approach to the problem of measuring the K concentrations in rocks and minerals (Dallmeyer 1979; Dalrymple 1991, 2004; Dalrymple and Lanphere 1971; McDougall and Harrison 1988).
The conventional K-Ar dating method depends on the assumptions that the sample contained no Ar at the time of its formation and all the radiogenic Ar produced within it was quantitatively retained (Faure and Mensing 2005). Because Ar may diffuse out of minerals even at temperatures well below their melting point, K-Ar dates can only possibly represent the time elapsed since cooling to temperatures at which diffusion loss of Ar is insignificant. However, under certain circumstances excess radiogenic 40Ar may also be present, which causes K-Ar dates to be too old. That this is a common problem has been well documented in the literature (Dickin 2005; Faure and Mensing 2005; Snelling 2000). Another problem is that in the conventional K-Ar method the concentrations of 40Ar and K are measured separately on different aliquots of the samples, which also significantly increases the probability of unknown systematic errors. Therefore, the samples being dated must be homogeneous with respect to both elements. But this requirement may not be satisfied in all cases, especially by fine-grained or glassy volcanic rocks.
The very different chemical affinities of potassium and argon also cause limitations in the K-Ar dating method (Dickin 2005). For all these reasons the 40Ar*-39Ar dating method was developed, first being described in detail by Merrihue and Turner (1966). This method can overcome some of the limitations of the conventional K-Ar dating method because K and Ar are determined on the same sample and only measurements of the isotope ratios of Ar are required. The problem of inhomogeneity of samples and the need to measure absolute concentrations of K and Ar are thus eliminated. This method is therefore claimed to be well suited to the dating of small or valuable samples such as meteorites or lunar rocks and minerals, especially when samples are heated stepwise with a continuous laser.
The 40Ar-39Ar dating method is based on the formation of 39Ar by converting 39K in K-bearing samples to 39Ar in a nuclear reactor by irradiation with thermal and fast neutrons. This causes the desired n, p (neutron capture, proton emission) reaction:
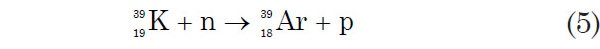
39Ar is unstable and decays to 39K by β-emission with a half-life of 269 years. Because of its slow decay rate (comparatively long half-life), 39Ar can be treated as though it were stable during the short time involved in the analyses of samples. Merrihue (1965) was the first to propose that the 40Ar*/39Ar ratio could be measured by mass spectrometry. Subsequently Merrihue and Turner (1966) described such a procedure and reported the Ar-Ar dates for several stony meteorites that appeared to be in good agreement with conventional K-Ar dates for the same meteorites. The principles of the 40Ar-39Ar dating method have been presented by Dallmeyer (1979), Dalrymple and Lanphere (1971), Dalrymple (1991, 2004), and McDougall and Harrison (1988).
When a K-bearing sample is irradiated with neutrons in a reactor, isotopes of Ar are produced by several reactions involving K, Ca, and Cl in the target. In the ideal case, 39Ar is produced only by the n, p reaction with 39K. In the formulation of Mitchell (1968), the number of 39Ar atoms formed in the sample by the neutron irradiation is
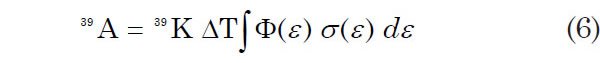
where 39K is the number of atoms of this isotope in the irradiated sample, ΔT is the duration of the irradiation, φ(ε) is the neutron flux density at energy ε, σ(ε) is the capture cross-section of 39K for neutrons having energy ε, and the integration is carried out over the entire energy spectrum of the neutrons. The number of radiogenic 40Ar atoms in the irradiated sample due to decay of 40K during its lifetime is given by equation 2 above, where 40Ar* is the radiogenic 40Ar, λec is the decay constant of 40K electron capture, and λ is the total decay constant of 40K. So after neutron irradiation of a sample, its 40Ar*/39Ar ratio is obtained by dividing equation 2 above by equation 6
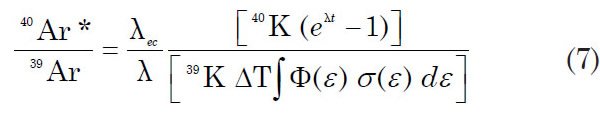
The neutron flux density and the capture cross-sections are difficult to evaluate from first principles because the energy spectrum of the incident neutrons and the cross-sections of 39K for capture of neutrons of varying energies are not well known. So equation 7 can be simplified by introducing the parameter J, defined as
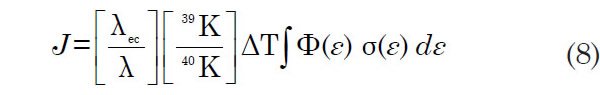
which leads to
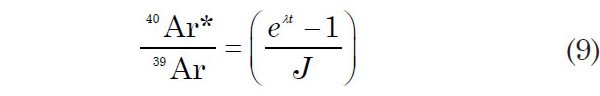
Equation 9 suggests that J might be determined by irradiating samples of known age (which are called the flux or fluence monitors) together with samples whose ages are unknown and are being determined. Technically the irradiation flux is not measured. In some sense one might consider that the fluence is being measured, but it is the 40Ar*/39Ar ratio that is really being measured by this methodology. So after the 40Ar*/39Ar ratio of the monitor has been measured, J can be calculated from equation 9
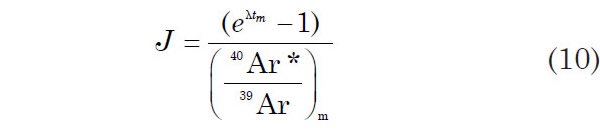
where tm is the known age of the flux monitor, and (40Ar*/39Ar)m is the measured value of this ratio in the flux monitor.
The energy spectrum of the neutron flux to which a particular sample is exposed during the irradiation depends on its position in the sample holder. For this reason, several samples of the flux monitor are inserted into the sample holder at known positions between unknown samples. The entire package is then irradiated for several days in a nuclear reactor to allow 39Ar to be produced. This of course assumes a consistent beam profile over a period of several days, which experience shows is a difficult task to achieve. After the irradiation the Ar in the flux monitors (of known age) is released by fusion in a vacuum system and their 40Ar*/39Ar ratios are measured by mass spectrometry. It is assumed that all the Ar, with no fractionation occurring, is released from the monitors and collected for mass spectrometry analyses. Their J values are then calculated using equation 9 and are plotted as a function of their position in the sample holder. The respective J values of the unknown age samples are then obtained by interpolation of the resulting graph according to their known positions in the sample holder. It is only possible to apply these J values to the samples of unknown ages because both those samples and the monitors were irradiated at the same time.
The 40Ar*/39Ar ratios of the irradiated unknown age samples are determined similarly by melting them individually in a vacuum chamber and by measuring the 40Ar*/39Ar ratio of the released Ar in a gas source mass spectrometer. The resulting 40Ar*/39Ar ratios of the unknown age samples are then used to calculate their ages using equation 9 rearranged as
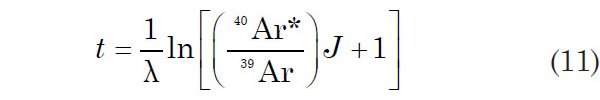
Several different mineral concentrates have been used as monitors. Their ages must be accurately known because they are used for calculating values of J using equation 10. Any errors in the ages of the monitors are therefore propagated from equations 10 and 11 and result in corresponding systematic errors in the calculated 40Ar*/39Ar ages of the samples of unknown ages that were irradiated with those flux monitors. “Precise” K-Ar ages of widely used flux (or fluence) monitors (Hb3gr, MMHb-1, LP-6, FY12a, FCs, WA1ms and others) have been published by Jourdan et al. (2014), Jourdan, Verati and Féraud (2006), Jourdan and Renne (2007), Renne et al. (1998, 2010), Schwartz and Trieloff (2007a), and Roddick (1983). Of course, no matter how precisely they are known, to use the K-Ar ages of the monitors to determine the Ar-Ar ages of the samples of unknown ages still involves circular reasoning.
The estimated analytical error in the calculated age using equation 11 according to Dalrymple and Lanphere (1971) is
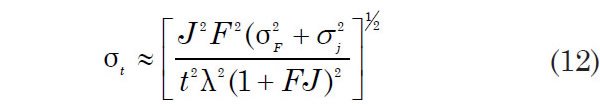
where F = 40Ar*/39Ar, σF2 and σj2 are the variances of F and J, respectively, expressed in percent, t is the age of the sample, and λ is the total decay constant of 40K. The ages so obtained are referred to as total argon release ages. Any errors in λ do not seem to be factored into such age determinations. Yet they are subject to the same limitations as conventional K-Ar ages because they depend on the assumption that no radiogenic 40Ar has escaped from the samples and no excess 40Ar is present. However, such ages avoid the problems arising from the inhomogeneous distribution of K and Ar in samples and require only the measurements of isotope ratios of Ar.
In the ideal case outlined above it is assumed that all of the 40Ar in the irradiated samples is either radiogenic or atmospheric, all of the 36Ar is atmospheric, and the 39Ar is produced only by the 39K (n, p) to 39Ar reaction during the irradiation process. In this case the measured values of the 40Ar/39Ar and 36Ar/39Ar ratios can be used to calculate the desired ratio of radiogenic 40Ar (40Ar*) to 39Ar by the relationship
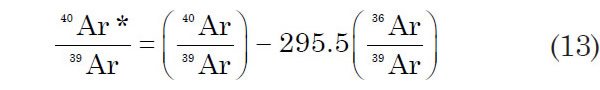
where 295.5 is the 40Ar/36Ar ratio of atmospheric Ar, assuming that this ratio has remained constant over hundreds of millions of years and the only non-radiogenic Ar in the unknown is due to atmospheric absorption at current isotopic abundance ratios.
Actually, Ar isotopes are also produced by several interfering reactions caused by interactions of neutrons with the isotopes of Ca, K, and Cl in the samples. Therefore, a series of corrections must be made that are especially important for apparently young samples (~106 years) and those having a Ca/K ratio > 10. The interfering reactions are listed in Table 1 and can be studied by reference to Fig. 2. Detailed discussions of these corrections have been provided by Mitchell (1968), Brereton (1970), Turner (1971), Dalrymple and Lanphere (1971), and Tetley, McDougall, and Heydegger (1980).
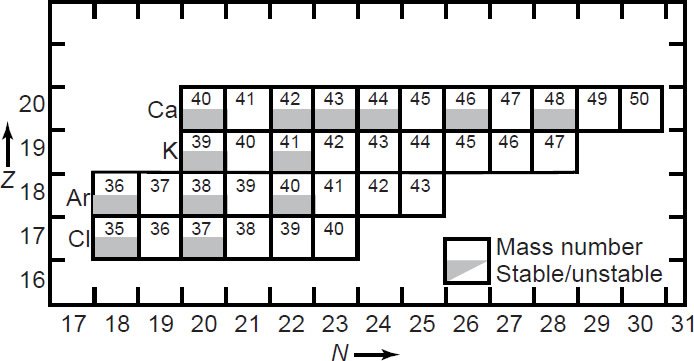
Fig. 2. Segment of the chart of the nuclides showing most of the stable and unstable isotopes of Ca, K, Ar, and Cl that participate in nuclear reactions with neutrons (after Faure and Mensing 2005).
The most important interfering reactions are those involving the isotopes of Ca. As listed in Table 1, Ca isotopes produce every one of the Ar isotopes, as discussed in more detail by Faure and Mensing (2005). These reactions interfere with the atmospheric Ar correction, which is based on 36Ar. It is claimed that the abundance of 37Ar in an irradiated sample is an indication of the extent of Ca interference, but this is not necessarily so if the production cross-sections for 37Ar are significantly different from those for 36Ar or 39Ar. Yet 37Ar is radioactive and decays to stable 37Cl with a short half-life of 35.1 days. Thus a correction for the decay of 37Ar after irradiation must be made because the 40Ca abundance derived from 37Ar is used to estimate the contributions to 40Ar. And 39Ar is also produced by Ca isotopes. Thus Brereton (1970) derived an equation that relates the age of an irradiated sample to its 40Ar*/39Ar ratio corrected for all interfering reactions. Furthermore, Dalrymple and Lanphere (1971) reported their measurements in a reactor to derive correction factors for Ca- and K-derived Ar isotopes, which they used to develop a more general expression for their parameter F in equation 12 above. However, there is not enough detail in how their measurements were made to assess their relevance to determining the amount of 40Ar in the unknown due to radioactive decay.
| Argon Produced | Calcium | Potassium | Argon | Chlorine |
|---|---|---|---|---|
| 36Ar | 40Ca (n, nα) | |||
| 37Ar | 40Ca (n, α) | 39K (n, nd) | 36Ar (n, γ) | |
| 38Ar | 42Ca (n, nα) | 39K (n, d) | 40Ar (n, nd, β-) | 37Cl (n, γ, β-) |
| 41K (n, α, β-) | ||||
| 39Ar | 42Ca (n, α) | 39K (n, p)a | 38Ar (n, γ) | |
| 43Ca (n, nα) | 40K (n, d) | 38Ar (n, d, β-) | ||
| 40Ar | 43Ca (n, α) | 40K (n, p) | ||
| 44Ca (n, nα) | 41K (n, d) |
It should be abundantly clear that both these dating techniques are dependent on knowing accurately the rate of 40K decay. In spite of the high respect in which the Ar-Ar dating technique is held by the geochronology community because it is claimed to provide such precise results, it is not independent of the same pitfalls as the K-Ar method for two reasons. First, it still depends on how accurate is the determination of the total half-life of 40K, because the total 40K decay constant still appears in the relevant equation 7 above that defines the 40Ar*/39Ar ratio used in the age equation 11 above. And second, the known ages of the fluence monitors irradiated with the samples of unknown age have sometimes been determined by using the K-Ar dating method, which of course depends on accurately knowing the 40K decay rate. So it is the determinations of the 40K total half-life on which we next focus, keeping in mind that this methodology is still subject to the eight assumptions listed above.
Determination Methods
Two approaches have been followed to determine the total decay constant and half-life of long-lived radioactive 40K.
Direct counting
Because of the branched decay of 40K (fig. 1) the total decay rate has to be determined. Thus there have been two techniques in direct counting experiments – measuring both the beta (β) and gamma (γ) activities of 40K.
In the first technique the beta (β) activity of 40K is counted in a source material, and divided by the total number of radioactive 40K atoms in the known quantity of K, based on Avogadro’s number and the isotopic abundance of 40K. Among the difficulties of this approach are the self-shielding of finite-thickness solid samples, the low specific activities, imprecise knowledge of the isotopic composition of the parent 40K, the detection of very low-energy decays, and problems with detector efficiencies and geometry factors (Begemann et al. 2001).
In the second technique the gamma (γ) activity of 40K, resulting from the electron capture decay mode, is measured in the relevant energy spectrum band and from the peak the number of γ-ray counts is determined, which is then divided by the total number of radioactive 40K atoms in the known quantity of K, based on Avogadro’s number and the isotopic abundance of 40K. Among the difficulties are the geometry and absorption properties of the detection assembly used, how the internal and external bremsstrahlung of the absorber and back scatter events are reduced and accounted for, how well the Compton interaction is calculated, and how narrow the energy peak is from which the number of γ-rays are counted (Leutz, Schulz, and Wenninger 1965). It is estimated that the accuracy of the absorption coefficients is usually better than ± 1%.
Many early experiments used both approaches, for example, Houtermans, Haxel and Heintze (1950), Leutz, Schulz, and Wenninger (1965), McNair, Glover and Wilson (1956), Saha and Gupta (1960), Sawyer and Wiedenbeck (1950), Spiers (1950), and Suttle and Libby (1955). And many of these and other experiments used a variety of source materials and measurement instrumentation. Several also attempted to measure the electron capture component of the 40K decay scheme (fig. 1), for example, Sawyer and Wiedenbeck (1950), and Leutz, Schulz, and Wenninger (1965). Typically, the β and γ activities in Tl-doped potassium iodide (KI) scintillation crystals were measured with the corrections of the counting rates for Tl contents, background, and dead time of the electronic equipment not exceeding 1%, but Leutz, Schulz, and Wenninger (1965) also measured the γ intensity of a 40K enriched potassium chloride (KCl) source with Tl-doped sodium iodide (NaI) and Tl-doped caesium iodide (CsI) crystals. The counting equipment used has included counting tubes or beta counters (Borst and Floyd 1948; Floyd and Borst 1949; Good 1951; Gräf 1948a, b; Houtermans, Haxel and Heintze 1950; Sawyer and Wiedenbeck 1950), Geiger-Müller tubes or counters (Bramley and Brewer 1938; Gopal, Sanjeevaiah, and Sanjeevaiah 1972; Gräf 1950; Hirzel and Wäffler 1948; Smaller, May, and Freedman 1950; Suttle and Libby 1955), an ionization chamber (Burch 1953), a proportional counter (McNair, Glover, and Wilson 1956), scintillation spectrometers (Kelly, Beard, and Peters 1959; Leutz, Schulz, and Wenninger 1965; Saha and Gupta 1960), and liquid scintillation counters (Glendenin 1961; Grau Malonda and Grau Carles 2002; Kossert and Günther 2004).
After Gopal, Sanjeevaiah, and Sanjeevaiah in 1972 used a Geiger-Müller counter in their direct counting experiment, there was a long time gap of 30 years until the most recent direct counting experiments which used liquid scintillation counters (Grau Malonda and Grau Carles 2002; Kossert and Günther 2004). Both experiments used the same methodology. However, Grau Malonda and Grau Carles (2002) first used Cerenkov (light photons generated by electrons) counting efficiencies for 40K and a calibrated solution of several other nuclides in 1 M hydrochloric acid (HCl) was measured in a liquid-scintillation spectrometer to verify the 40K β-ray transition shape-factor. They also calculated the counting efficiencies for 40K, including the contributions from both β-ray and electron capture γ-decay processes which will be different. Then they prepared seven 40K samples by adding measured amounts of potassium gel to 0.2 mg/l solutions of potassium nitrate (KNO3) in water. Additionally, to evaluate the background counting rate for each of the seven samples of 40K, 7 ml of distilled water was added to four other samples of potassium gel to produce unquenched blanks, to which were added increasing amounts of carbon tetrachloride (CCl4) to achieve a chemical quenching equivalent to the 40K samples. All samples were measured in a liquid scintillation counter (spectrometer). The final background counting rates for each one of the seven samples of 40K were obtained by interpolation into the previously measured four-point quench curve (from the four blanks) versus the background counting rate. The β-activity measurements for the seven 40K samples were then averaged. That average β-activity was then used, with the calculated number of 40K atoms obtained from the isotopic abundance in 40K samples, and the contribution of the electron capture γ-ray component determined from counting efficiencies using the tracer 3H (tritium), to calculate the total 40K half-life.
On the other hand, Kossert and Günther (2004) prepared four aqueous solutions each of potassium nitrate (KNO3, 99.995% purity) and potassium chloride (KCl, 99.5% purity) at a concentration of 2 g of salt per 10 g of water. To measure background counting rates, four similar solutions were prepared with small additions of sodium nitrate (NaNO3) and sodium chloride (NaCl) respectively instead of the potassium salts. To avoid errors in the weighing procedure due to hygroscopic behaviour of the salts, two samples were prepared with oven dried salts. Weighed portions of these 16 solutions were variously added to three different scintillators. The sample counting rates varied between 230 and 660 cpm, while all background counting rates were lower than 50 cpm. This means that the random error in the measurements had to vary from 6.6% to 3.9% at least simply due to counting statistics. The total counting time for potassium and background samples was more than 60 days, during which the counting rates of all samples were stable. The results of the dried salts agreed perfectly with results obtained with undried salts. The total 40K half-life was then calculated for each of the eight β-activity measurements, while the contribution of the electron capture γ-ray component was again determined from counting efficiencies using the tracer 3H (tritium). The individual uncertainty contributions to the calculated total 40K half-life were also meticulously determined and compared between the KNO3 and KCl salts. These included preparation of the solutions (weighing), preparation of the samples (weighing), purity of the salts, the statistics, the counting efficiencies (dead time, pile-up, time and adsorption), impurities of other radioisotopes, quenching, efficiency, decay scheme (branching ratio), atomic and nuclear data, quench indicator measurement (long periods), non-representative background measurement, and isotopic abundance. The quadratic sum of the uncertainty contributions was 0.23% for the total 40K half-life determinations using KNO3 and 0.38% using KCl, which seem to be small for liquid scintillation counting. The higher value for KCl was primarily due to higher uncertainties for salt purity and statistics. Thus the final total 40K half-life value was obtained by averaging the four determinations using KNO3, but the measurements using KCl confirmed the final result, which agreed perfectly with the total 40K half-life value obtained by Grau Malonda and Grau Carles (2002). Kossert and Günther (2004) noted in conclusion that the largest uncertainty contributions stem from the isotopic abundance of 40K (0.172%) and the branching ratios (0.104%). However, they appeared to gloss over the uncertainty contributions from the quenching curves of 1.05% using KNO3 and 0.05% using KCl.
Judged from the fact that many of the earlier direct counting experiments yielded results that are not compatible with one another within the stated uncertainties, it would appear that not all the measurement uncertainties may have been accounted for, and therefore the stated uncertainties may be unrealistically small. According to Begemann et al. (2001) many of those experiments were thus plagued by unrecognized systematic errors. As the nature of these errors is obscure, it is not straightforward to decide which of the, often mutually exclusive, results of such direct counting experiments is closest to the true value, although the independent Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004) determinations agree perfectly. Furthermore, the presence of unknown systematic biases makes any averaging of them all dangerous. It is possible that reliable results of careful workers, listing realistic uncertainties, will not be given the weights they deserve—this aside from the question of whether it makes sense to average numbers that by far do not agree within the stated uncertainties. In any case, there is a natural tendency for bias towards the most recent measurements as though the more “modern” equipment and methodologies (using computers, for instance) guarantee better results, when in fact the earlier experimenters may have been more intimately involved and careful with their equipment and methodologies to obtain excellent results rather than relying on computers. Also, the fact that the most recent attempts to “calibrate” the total 40K half-life value used in geochronology have not relied on the recent liquid scintillation counting experiments (see below) is indicative of how those experiments are viewed as potentially not being well planned.
Geological comparisons of methods
The second approach to the determination of the total decay constant (and half-life) of 40K has been to date geological samples whose ages have also been measured by other radioisotope dating methods with presumably more reliable decay constants (Dickin 2005; Faure and Mensing 2005). This approach in the case of 40K is especially appealing to secular geochronologists because of the large uncertainty contributions in direct counting total 40K decay half-life determinations from the isotopic abundance of 40K and the 40K branching ratios. However, this second approach essentially involves circular reasoning, because it is being assumed the other radioisotope dating methods, principally the U-Pb method, give the reliable dates to which the total 40K decay half-life can be calibrated to bring the K-Ar and Ar-Ar radioisotope ages into agreement. It should be noted, however, that this is hardly objective, because all the radioisotope ages of rocks could be wrong due to the underlying unprovable and suspect assumptions on which all the radioisotope methods are based.
Nevertheless, this approach was used as early as Smith (1964), but has become increasingly used since Renne et al. (1997), and almost exclusively used since the Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004) direct counting determinations. It would thus seem that most geologists have come to accept radioisotope dating as factual and therefore the only task left is to reconcile all of the methods into a coherent “deep time” picture of the solar system. Apart from Renne et al. (1997) who cross-calibrated their Ar-Ar date for the pumice from the AD 79 Vesuvius eruption with that historic date, and Renne et al. (1998) who cross-calibrated their Ar-Ar ages for Ar-Ar dating standards with the recognized absolute K-Ar and Ar-Ar ages for those standards, all the other geological comparisons have been with the U-Pb system. Only Renne et al. (2010, 2011) have evaluated the geological comparisons together with the most recent direct counting determinations.
This geological comparisons approach has the disadvantage that it involves the geological uncertainties, such as whether all radioisotopic systems closed at the same time and remained closed. However, it is claimed to still provide a useful check on the laboratory determinations by direct physical counting. Nevertheless, this approach entails multi-chronometric dating of minerals and components in individual rocks and meteorites and cross-calibration of different radioisotopic age systems by adjusting the decay constant of the K-Ar system so as to force agreement with the age obtained via another radioisotope dating system, usually U-Pb (Begemann et al. 2001). In essence, because the half-life of 238U is claimed to be the most accurately known of all relevant radionuclides, this usually amounts to expressing ages in units of the half-life of 238U.
Results of the Potassium-40 Decay Determinations
During the last 78 years numerous determinations of the total decay constant and half-life of 40K have been made using these two methods. The results are listed with details in Table 2. The year of the determination versus the value of the total 40K decay half-life is plotted in Fig. 3. In each case the data points plotted have been color-coded the same to differentiate the values as determined by the three approaches that have been used—direct counting, geological comparisons with other radioisotope dating methods, and a combination of these.
| Year | Half-Life (Byr) | Uncertainty (Byr) | Method | Instrument/Procedure | Source(s) |
|---|---|---|---|---|---|
| 1938 | 1.42 | ±0.3 | Direct Counting | Geiger-Müller Counter | Bramley and Brewer (1938) |
| 1948 | 1.54 | ±0.2 | Direct Counting | Beta Counter | Borst and Floyd (1948) |
| 1948 | 1.37 | ±0.15 | Direct Counting | Beta Counter | Gräf (1948a, b) |
| 1948 | 1.11 | ±0.19 | Direct Counting | Geiger-Müller Counter | Hirzel and Wäffler (1948) |
| 1949 | 1.61 | ±0.6 | Direct Counting | Beta Counter | Floyd and Borst (1949) |
| 1950 | 1.5 | ±0.07 | Direct Counting | Geiger-Müller Counter | Gräf (1950) |
| 1950 | 1.33 | ±0.08 | Direct Counting | Beta Counter | Houtermans et al. (1950) |
| 1950 | 1.27 | ±0.05 | Direct Counting | Beta Counter | Sawyer and Wiedenbeck (1950) |
| 1950 | 1.61 | ±0.2 | Direct Counting | Geiger-Müller Counter | Smaller, May, and Freedman (1950) |
| 1951 | 1.48 | ±0.05 | Direct Counting | Beta Counter | Good (1951) |
| 1953 | 1.31 | ±0.04 | Direct Counting | Ionization Chamber | Burch (1953) |
| 1955 | 1.25 | ±0.04 | Direct Counting | Geiger-Müller Counter | Suttle and Libby (1955) |
| 1956 | 1.28 | ±0.02 | Direct Counting | Proportional Counter | McNair, Glover, and Wilson (1956) |
| 1959 | 1.47 | ±0.03 | Direct Counting | Scintillation Spectrometer | Kelly, Beard, and Peters (1959) |
| 1960 | 1.4 | ±0.08 | Direct Counting | Scintillation Spectrometer | Saha and Gupta (1960) |
| 1961 | 1.41 | ±0.015 | Direct Counting | Liquid Scintillation Counter | Glendenin (1961) |
| 1964 | 1.31 | Geological Comparisons | Smith (1964) | ||
| 1965 | 1.266 | ±0.007 | Direct Counting | Scintillation Spectrometer | Leutz, Schulz and Wenninger (1965) |
| 1969 | 1.265 | ±0.002 | Direct Counting | Weighted Mean of Previous Determinations | Beckinsale and Gale (1969) |
| 1971 | 1.345 | ±0.055 | Direct Counting | Venkataramaiah, Sanjeevaiah, and Sanjeevaiah (1971) | |
| 1972 | 1.14 | ±0.08 | Direct Counting | Geiger-Müller Counter | Gopal, Sanjeevaiah, and Sanjeevaiah (1972) |
| 1973 | 1.277 | ±0.08 | Direct Counting | Adjusted Beckinsale and Gale 1967Value | Endt and Van der Leun (1973) |
| 1977 | 1.25 | Direct Counting | Adjusted Beckinsale and Gale 1967 Value | Steiger and Jäger (1977) | |
| 1997 | 1.277 | ±0.08 | Direct Counting | Repeated Reporting in Nuclear Physics Literature | Audi et al. (1997) |
| 1997 | 1.29 | Geological Comparisons Calibration against the 79AD Vesuvius eruption | Renne et al. (1997) | ||
| 1998 | 1.295 | Geological Comparisons | Calibration of Ar-Ar fluence monitor standards Renne et al. (1998) | ||
| 2000 | 1.255 | Direct Counting | Re-evaluation of Activities Determinations | Min et al. (2000b) | |
| 2000 | 1.269 | ±0.013 | Geological Comparisons | Calibration of ages for a rock unit and a meteorite | Min et al. (2000a); Renne (2000) |
| 2002 | 1.248 | ±0.004 | Direct Counting | Liquid Scintillation Counter | Grau Mahonda and Grau Carles (2002) |
| 2002 | 1.265 | ±0.004 | Geological Comparisons | Calibration of ages for five rock units | Kwon et al. (2002) |
| 2004 | 1.248 | ±0.003 | Direct Counting | Liquid Scintillation Counter | Kossert and Günther (2004) |
| 2006 | 1.265 | ±0.004 | Geological Comparisons | Adopted Kwon et al. 2002 value to recalibrate mineral Ar-Ar ages | Krumei et al. (2006) |
| 2007 | 1.255 | Geological Comparisons | Calibration using disparities in ages for rocks and meteorites | Schwarz and Trieloff (2007a) | |
| 2010 | 1.2476 | ±0.0064 | Combination of Re-evaluation of Direct Counting and Geological Comparisons | Calibration of U-Pb and Ar-Ar ages of fl uence monitor standards | Renne et al. (2010) |
| 2011 | 1.2524 | ±0.0064 | Combination of Re-evaluation of Direct Counting and Geological Comparisons | Revision of Renne et al. 2010 value without LSC data | Renne et al. (2011) |
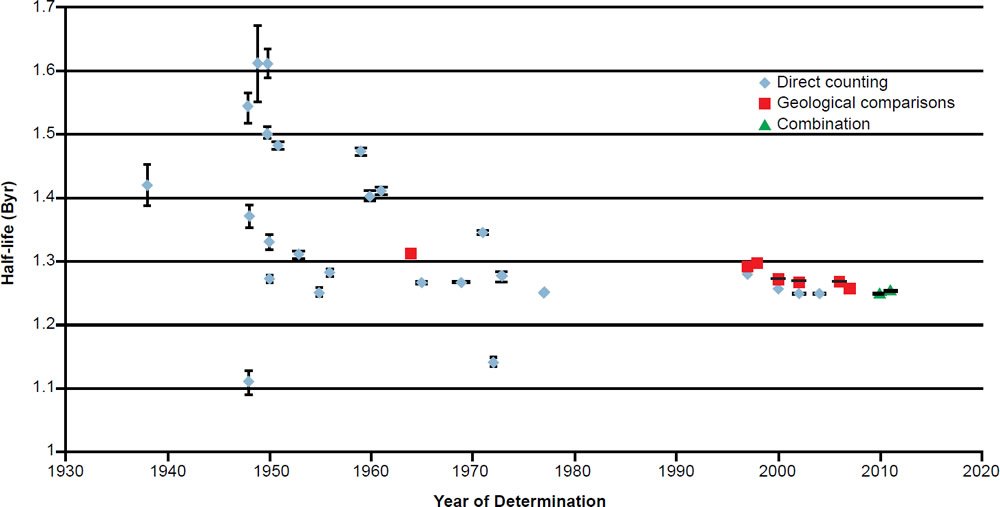
Fig. 3. Plot of each 40K half-life determination versus the year of its determination, color-coded according to the method of its determination. The error bars for each determination are also plotted from the error values listed in Table 2.
Discussion
The early determinations
The K-Ar (Aldrich and Nier 1948) and derivative 40Ar-39Ar (Merrihue and Turner 1966) dating methods are among the most widely applicable in terms of time range and geological environments. Owing to the branched decay of 40K to both 40Ca and 40Ar, two decay constants are relevant to the system. The values of these two decay constants in virtually universal use when Begemann et al. (2001) were calling for improved decay constants for geochronology, namely, 4.962 × 10-10 yr-1 and 0.581 × 10-10 yr-1 respectively, were those recommended by Steiger and Jäger (1977). Those values are based on β and γ activity data (28.27 ± 0.05 β/g × s and 3.26 ± 0.02 γ/g × s, respectively) for 40K summarized by Beckinsale and Gale (1969), updated to include 40K/K measurements (mean 0.01167%) by Garner et al. (1975). Beckinsale and Gale (1969) also included an estimated value of 5.0 × 10-2 dps/g for a hypothetical γ-less decay of 40K to the ground state of 40Ar. The total 40K decay constant recommended by Steiger and Jäger (1977) of 5.543 × 10-10 yr-1 corresponds to a half-life of 1.25 Byr.
A later compilation of 40K β and γ activity data by Endt and Van der Leun (1973) used a larger proportion of available data published before 1969, and determined activities of 27.89 ± 0.15 β/g × s and 3.31 ± 0.03 γ/g × s, respectively. Reliable β and γ activity data between 1969 and 2002 do not seem to exist. Results of Gopal, Sanjeevaiah, and Sanjeevaiah (1972) derive from an “experiment believed to be a good addition to an undergraduate laboratory with limited resources,” while the impressively precise γ-activity 3.21 ± 0.02 γ/g × s reported by Cesana and Terrani (1977) lists only “the standard deviation between different determinations” which “does not include the errors associated with efficiencies, geometry factors, chemical purity, etc.” In fairness, Begemann et al. (2001) claim that many of the previous studies utilized by Beckinsale and Gale (1969) also failed to quantify potential systematic errors in their measurements. Endt and Van der Leun (1973) used more appropriate statistical methods than Beckinsale and Gale (1969), and the resulting uncertainties for the total activity are much larger. The lower total activity combined with the use of a larger value for the 40K/K abundance of 0.01178% resulted in a total decay constant of 5.428 × 10-10 yr-1 (corresponding to a total decay half-life of 1.277 Byr) for 40K lower by 2.1% than that of Steiger and Jäger (1977). The data of Garner et al. (1975) for the isotope abundance of 40K were not incorporated in the compilation of Endt and Van der Leun (1973), nor was the hypothetical γ-less electron capture decay.
The more recent summary of 40K decay data by Audi et al. (1997) reported the same total decay constant of 5.428 × 10-10 yr-1 (total decay half-life of 1.277 Byr) as previously cited in the nuclear physics literature, but with a different branching ratio of 89.28% β/β + γ and a 40K/K abundance of 0.0117%. The implicit reevaluation of activity data was not discussed by Audi et al. (1997).
Begemann et al. (2001) noted that outstanding problems remaining to be addressed in evaluating the 40K decay constants included: (i) improving disintegration counting experiments to provide better data for β and γ activities; and (ii) verifying the existence and magnitude of the hypothetical γ-less electron capture decay directly to 40Ar in the ground state.
As shown by Min et al. (2000a), combining the Endt and Van der Leun (1973) compilation of activity data with other modern values of physical constants yields a total 40K decay constant of (5.463 ± 0.054) × 10-10 yr-1 corresponding to a half-life of 1.269 ± 0.013 Byr. Min et al. (2000a) also graphically illustrated how the use of different total 40K half-life values had a dramatic effect on the resultant K-Ar ages determined, varying by tens of millions of years for rocks supposedly more than 2 Byr old (fig. 4). Using these updated values, Renne (2000) showed that certain unshocked and rapidly cooled meteorites (acapulcoites) yield 40Ar-39Ar ages indistinguishable from ages determined with other radioisotope systems.
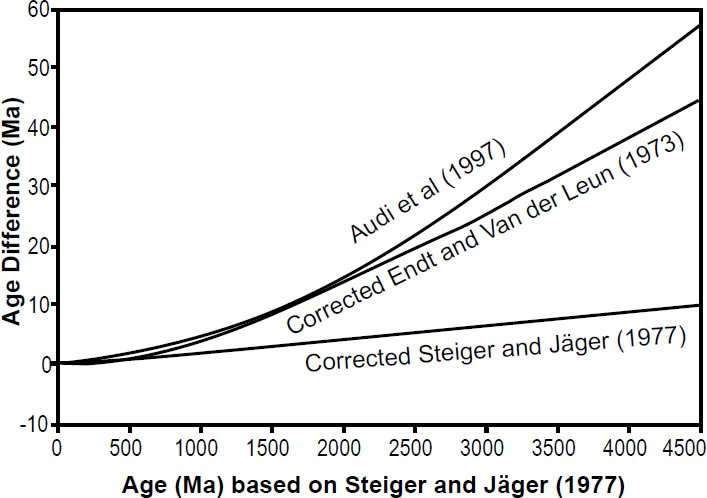
Fig. 4. Differences between K-Ar and Ar-Ar ages calculated from the decay constants of Audi et el. (1997) and of Endt and Van der Leun (1973) (corrected), and the “traditional age” based on the decay constant of Steiger and Jäger (1977) (corrected), after Min et al. (2000a).
The use and calibration of Ar-Ar standards
In the 40Ar-39Ar method, which has now largely supplanted K-Ar dating, only the total 40K decay constant is needed provided the absolute ages of the 40Ar-39Ar standards (neutron monitors) are known by means other than K-Ar dating (for example, Min et al. 2000a; Renne and Min 1998). Uncertainties in the 40K decay constants have gone unrecognized in part because they are difficult to deconvolve from the effects of the standards (see detailed discussion by Min et al. 2000a). Active programs have been underway now for more than a decade to improve the accuracy of both the total 40K decay constant and the ages of the 40Ar-39Ar standards, including development of appropriate statistical methods for their simultaneous determination from geological comparison data (Min et al. 2000b). Thus many attempts have been made to determine more accurately the absolute ages of the neutron fluence monitors or standards for 40Ar-39Ar dating (for example, Bachmann et al. 2007; Jourdan and Renne 2007; Jourdan et al. 2014; Kuiper et al. 2008; Lanphere and Baadsgaard 2001; Nomade et al. 2005; Phillips and Matchan 2013; Renne et al. 1998, 2010, 2011; Schwarz et al. 2011; Schwarz and Trieloff 2007b; Spell and McDougall 2003). Of particular focus in many of these studies has been the sanidine standard from the Fish Canyon Tuff in southwestern Colorado.
The methods used to determine and calibrate the absolute age of this Fish Canyon Tuff sanidine standard have included: K-Ar ages of the sanidine; Ar-Ar ages of the sanidine, plagioclase, hornblende, and biotite from the Fish Canyon Tuff; Ar-Ar ages of other standards of sanidine, plagioclase, biotite, muscovite, and hornblende analyzed concurrently with the Fish Canyon Tuff sanidine standard; Rb-Sr ages of sanidine, plagioclase, and biotite from the Fish Canyon Tuff; multiple U-Pb ages of many zircon grains from the Fish Canyon Tuff; and calibration of the Fish Canyon Tuff sanidine with the Ar-Ar ages of single sanidine crystals extracted from tephra layers at and near the K-T boundary intercalated in the astronomically “tuned” marine succession of the Melilla Basin in Morocco. Space here precludes detailed discussion of the objectivity of, and assumptions implicit in, these determinations and calibrations. However, in summary it must be emphasized that none of these calibrations is truly independent and thus objective due to the interwoven circular reasoning between all methods by which one method is calibrated against another and then that method is used to calibrate the original method, or another method which is then used to calibrate the original method. And all assumptions involved are not provable. Furthermore, the overriding assumption is that presently measured process rates can be extrapolated uniformly and indefinitely back into the remote past.
The usual rejoinder is that multiple radioisotope methods used on the same rocks and meteorites, and minerals from them, yield identical ages so the methods must work, which of course is the rationale for such calibration studies. However, Snelling (2000) has extensively documented with many examples from the literature of the numerous failures of each of the radioisotope dating methods because of inheritance and contamination, contrary to two of the three underlying assumptions involved in the methods. Furthermore, Austin (2005) and Snelling (2005) have studied and reported numerous examples where there are pronounced discordant ages between the radioisotope dating methods due to past accelerated radioisotope decay rates, and Snelling (2015c) has demonstrated that meteorite ages determined by the many different radioisotope methods have been calibrated against, to bring agreement with, their Pb-Pb model and isochron ages.
Nevertheless, the increasing popularity of the astronomical tuning method is based on its presumed independence of the radioisotope dating methods and the assumption that the orbital motions of the earth can be extrapolated back into the remote past uniformly because the earth is billions of years old and has to have been stable in such orbital behavior through much of that time. In other words, the billions of years are assumed so then the method can calibrate the rocks deposited during millions of years.
However, even the astronomical tuning method is calibrated against the radioisotope dating methods. For example, in the Kuiper et al. (2008) study the tephra layers intercalated in the marine succession were first Ar-Ar dated and then the astronomically tuned marine succession was used to revise the Ar-Ar ages of the tephra beds. Yet the astronomical tuning of this marine succession in Morocco had already been calibrated against the astronomical tuning of the composite sedimentary succession in the Sorbas and Nijar Basins in Spain, which in turn was calibrated against the geomagnetic polarity timescale. However, the geomagnetic timescale itself has been established and calibrated by the K-Ar and Ar-Ar radioisotope dating of the rocks, particularly volcanic rocks, which contain the geomagnetic polarity time intervals and which mark the geomagnetic polarity time boundaries (Ogg 2012). Thus this lengthy chain of reasoning begins with K-Ar and Ar-Ar radioisotope dating of the geomagnetic polarity timescale, and ends with the astronomically tuned marine succession calibrated by the geomagnetic polarity timescale being used to calibrate the Ar-Ar ages of the tephra layers, and the Ar-Ar age of the Fish Canyon Tuff sanidine standard so widely used as a fluence monitor in Ar-Ar dating. In other words, because there is no objective standard the Ar-Ar method is calibrated against itself! And the astronomical tuning or astrochronology method is not independent of radioisotope dating, as clearly documented by Hinnov and Hilgen (2012).
The branching ratio
It is claimed that there are two parameters for which accurate values are not needed in the Ar-Ar radioisotope dating method, namely, the branching ratio of 40K and the amount of 40K in, or the isotopic composition of, natural potassium (Renne et al. 2010; Vermeesch 2015). However, such is clearly not the case, as reiterated by Kossert and Günther (2004), and Schwarz et al. (2011), because both the branching ratio for 40K and the amount of 40K in natural potassium need to be known in order to determine the total 40K decay constant and half-life [see equation (4) above and the list of necessary assumptions (Faure and Mensing 2005)].
The branching ratio attempts to quantify how much 40K decays via electron capture to 40Ar compared to how much decays via β emission to 40Ca (see fig. 1 again). Early efforts to determine this branching ratio were undertaken by three methods. First, Ceccarelli, Quareni and Rostagni (1950), and Sawyer and Wiedenbeck (1950) used Geiger-Müller counters to measure the x-rays emitted by 40K in KF and KCl respectively decaying via electron capture to 40Ar compared to the measured β-rays as 40K decays to 40Ca. Second, Faust (1950), Floyd and Borst (1949), Sawyer and Wiedenbeck (1949), Smaller, May and Freedman (1950), and Spiers (1950) used scintillation counters or ionisation chambers to measure the γ-rays emitted by 40K in KCl for 40K decaying via electron capture to 40Ar compared to the measured γ-rays emitted by a known added amount of 42K or the measured β-rays as 40K decays to 40Ca. Third, Aldrich and Nier (1948), Inghram et al. (1950), Mousuf (1952), and Russell et al. (1953) used mass spectrometers to analyse for the 40Ar and 40Ca derived from 40K decay in K-bearing minerals such as sylvite (KCl) and multiple samples of microcline (K-feldspar) from various pegmatites of “known age,” as determined by their provenance and in many cases by U-Pb radioisotope dating of associated uraninite (UO2). Russell et al. (1953) noted that the x-ray measurements had yielded branching ratio to 40Ar values from <0.7 to 1.9, the γ-ray measurements had yielded values from 0.04 to 0.15, and the measurements by others of the 40Ar contents of “old” K-bearing minerals had yielded branching ratio to 40Ar values from 0.02 to 0.10. Their determinations using five different microcline samples yielded a value of 0.060 ± 0.006.
Beckinsale and Gale (1969) reviewed all the early measurements of the β and γ activities from 40K decay in order to determine the best estimates for the branching ratio, as well as the total 40K decay constant and half-life. Smith (1964) had estimated the branching ratio as 0.124, but Beckinsale and Gale (1969) from their analysis of all the then available data estimated it to be 0.117 ± 0.001. In their assessment Endt and Van der Leun (1973) concluded that from the direct measurements with the smallest stated errors of the ratio between the β and γ activities from 40K decay yield a weighted average for the branching ratio of 0.1195 ± 0.014. Subsequently, Steiger and Jäger (1977) made no recommendation for the value of the branching ratio but merely implied acceptance of the Beckinsale and Gale (1969) value of 0.117 ± 0.001, and Audi et al. (1997) merely reiterated the status quo except for claiming a branching ratio of 0.120.
Nägler and Villa (2000) utilized an entirely different approach to determine the branching ratio. They successfully attempted both 40K-40Ca and 39Ar-40Ar dating of the same samples of muscovite from an unsheared pegmatite intruded into a South African Archaean greenstone belt, and of sanidine from an Ordovician pegmatite in Madagascar. They determined the amounts of radiogenic 40Ar and 40Ca derived from the 40K decay they measured in these muscovite and sanidine samples by the normal 40Ar-39Ar dating procedure, and by using a double 43Ca-48Ca double spike added to the total Ca separated from the samples, respectively. Then using those amounts they calculated a branching ratio for 40Ar equivalent to 0.1194 ± 0.007. This is almost identical to the branching ratio of 0.1195 ± 0.0014 determined by Endt and Van der Leun (1973) as the weighted average of the direct measurements with the smallest stated errors of the ratio between the β and γ activities from 40K decay. But the Nägler and Villa (2000) value has a halved uncertainty. And it is also independent verification of the Endt and Van der Leun (1973) value.
Interestingly, subsequent efforts to determine the total 40K decay constant and half-life ignored this work by Nägler and Villa (2000). Instead, Grau Malonda and Grau Carles (2002), adopted a value of 0.1198 which they obtained from Browne, Dairiki, and Doebler (1978), while Kossert and Günther (2004) adopted a value of 0.1218 which they obtained from Helmer (1998). Then Renne et al. (2010) adopted a branching ratio value of 0.1157 adjusted from the value of 0.1188 suggested by Min et al. (2000a), likewise calculated from the individual decay constants for 40K decay to 40Ar via electron capture versus to 40Ca via β-decay. In response to comments from Schwarz et al. (2011), Renne et al. (2011) adjusted their estimate of the branching ratio to 0.1162 by ignoring the liquid scintillation counting determinations of the decay constants by Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004). But as Kossert and Günther (2004) asserted the branching ratio is one of the two major sources of uncertainty in determinations of the total 40K decay constant and half-life. Renne et al. (2010, 2011) agreed and suggested the uncertainty is ± 0.27%, which is why they and others are seeking to calibrate the total 40K decay constant and half-life using mineral standards and rocks of known ages, as determined by other radioisotope dating methods, principally the U-Pb method.
Isotopic composition of potassium
The other major source of uncertainty in determinations of the total 40K decay constant and half-life according to Kossert and Günther (2004) is the value for the 40K concentration in natural potassium. Renne et al. (2010) estimated that uncertainty as ± 0.35%. Nier (1950) used mass spectrometry on samples of the mineral sylvite (KCl) to determine the 40K/K abundance ratio as 0.0119 ± 0.0001%. Subsequently Burnett, Lippolt, and Wasserburg (1966) used multiple mass spectrometry analyses of three terrestrial samples (two mineral samples and a basalt sample) and eight meteorites (six chondrites and two eucrites) to determine whether there was any variation in their 40K/K abundance ratio. They found that the 40K/K abundance ratio varied in the three terrestrial samples between 0.0113 and 0.0121%, while the 40K/K abundance ratio varied in the meteorites between 0.0113 and 0.0118%.
Beckinsale and Gale (1969) adopted a 40K/K abundance ratio of 0.0118%, based on several determinations more recent than that by Nier (1950) as summarized by Lederer, Hollander, and Perlman (1967). However, Garner et al. (1975) subsequently analyzed the newly produced NIST standard reference material SRM 985, and reported a 40K/K abundance ratio of 0.011672 ± 0.000041%. This was the value then adopted by Steiger and Jäger (1977), whereas Endt and Van der Leun (1973) used a value of 0.01178 ± 0.00004%. Subsequently, Audi et al. (1997) adopted a 40K/K abundance ratio of 0.0117%, perhaps a rounding up of the Garner et al. (1975) value of 0.011672 ± 0.000041%. Nevertheless, De Laeter et al. (2003) similarly adopted a value of 0.0117 (1) % due to its adoption by the International Union of Pure and Applied Chemistry (IUPAC), whereas Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004) both used a 40K/K abundance ratio of 0.01167%, and Renne et al. (2010) a value of 0.011672 ± 0.000021% adopted from Garner et al. (1975). Thus to this day the Garner et al. (1975) value is the value for the terrestrial 40K isotope composition recommended by the IUPAC.
Concern about the level at which the 40K/K abundance ratio might vary was heightened as a result of Verbeek and Schreiner (1967) reporting significant light 39K isotope enrichments from within a few centimeters of potassium-metasomatized granitic contact rocks in South Africa. However, that concern over isotopic fractionation was greatly reduced, at least for terrestrial samples, by the measurements of Humayun and Clayton (1995) which indicated the complete absence of isotopic variations in δ41K among terrestrial materials at the 0.5% level and thus a near constancy in the 40K/K abundance ratio. By inference, Begemann et al. (2001) stated that variations in the relative abundance of 40K should be about half that determined by Humayun and Clayton (1995), although they considered it important to emphasize that the Humayun and Clayton (1995) study had clarified the extent of variation rather than the absolute value of the 40K/K abundance ratio.
Nevertheless, the geochronology community has continued its efforts to reduce the uncertainties in K-Ar and Ar-Ar radioisotope ages from around 2% down to around 0.1%. Thus Naumenko et al. (2013) obtained high precision 40K/39K data using thermal ionization mass spectrometry (TIMS) by three different measurement protocols for the two standard reference materials SRM 918b and SRM 985, the latter being the same standard reference material analyzed by Garner et al. (1975). As a result, they obtained a 40K/39K value for SRM 985 that within the uncertainties is coincident with the IUPAC value adopted since 1975 (De Laeter et al. 2003), but with a significantly improved measurement uncertainty. Their value corresponds to a 40K/K abundance ratio of 0.011668 ± 0.000008%. Naumenko et al. (2013) commented that this now reduced the uncertainty in the abundance of 40K from 0.35% to 0.05%, but that in order to reduce the goal of K-Ar and Ar-Ar ages with an absolute uncertainty of 0.1% there have to be further improvements in the determination of the total 40K decay constant and half-life.
The most recent 40K half-life determinations
So we need to return to the most recent determinations of the total 40K decay constant and half-life, as ultimately the K-Ar and Ar-Ar radioisotope dating methods depend on accurately knowing those values, as well as the electron capture/positron branching ratio. The only two recent direct counting determinations are those performed by Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004). Their methodologies have been described already in detail above. Unlike most previous direct counting experiments, these investigators used liquid scintillation counters to measure the specific activity of 40K β-decays, though how they went about their experiments were somewhat different. Nevertheless, they obtained essentially the same results, total 40K decay half-life values of 1.248 ± 0.004 Byr and 1.248 ± 0.003 Byr respectively.
Renne et al. (2010) initially included the Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004) data for 40K specific activity in their reassessment of the total 40K decay constant and half-life. But they primarily used K-Ar isotopic data and pairs of 238U-206Pb and 40Ar-39Ar data for rigorously selected rocks and minerals extracted from them, many utilized as Ar-Ar fluence monitor standards, to calibrate the total 40K decay constant and half-life, and the Fish Canyon Tuff sanidine Ar-Ar dating standard. They obtained a half-life value of 1.2476 ± 0.0064 Byr. However, Schwarz et al. (2011) pointed out that liquid scintillation counting data have a sensitive dependence for the determination of the total 40K decay half-life on the specifically adopted branching ratio for the probability of β--decay to 40Ca and electron capture to 40Ar, the latter including both possible decays (electron capture to the ground state and electron capture followed by γ-emission—see fig. 1 again). This dependence is embodied in a correction for the relative detection efficiency of γ versus β- radiation, and the equation(s) governing this efficiency dependence were not provided by either pair of experimenters. Thus Renne et al. (2011) noted that while those two liquid scintillation counting experiments obtained identical total 40K decay half-life values, the experimenters had used different values for the branching ratio without justifying their choices. Consequently, Renne et al. (2011) revised their Renne et al. (2010) determination of the total 40K decay half-life to 1.2524 ± 0.0064 Byr by discounting that liquid scintillation counting data.
In the meantime, several other studies had been done using geological comparisons, that is, calibrating the K-Ar isotopic system using other radioisotope ages, primarily U-Pb ages, for minerals from the same rock units. Indeed, apart from the two direct counting determinations performed by Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004), all determinations of the total 40K decay half-life in the last two decades have been done using such geological comparisons, with or without any reassessment of the earlier direct counting experiments.
Min et al. (2000a) obtained high precision U-Pb and Ar-Ar ages for zircon and alkali feldspar grains respectively separated from the Palisade Rhyolite of the North Shore Volcanic Group in the Keweenawan Province, Minnesota. Fourteen analyses of 11 zircon grains yielded a weighted mean Pb-Pb age of 1097.6 ± 5.3 Myr, or 1097.6 ± 2.1 Myr if decay constant errors are ignored. Nine single alkali feldspar phenocrysts providing undisturbed Ar-Ar age spectra yielded an error-weighted mean plateau Ar-Ar age of 1088.4 ± 4.0 Myr, distinctly different to the zircon Pb-Pb age. These ages could only be reconciled if the systematic errors were included so that their uncertainties overlapped. The mean Ar-Ar age was then recalculated to agree within the uncertainties to the Pb-Pb zircon age by “updating” decay constants and errors of Endt and Van der Leun (1973) and Audi et al. (1997). However, among the Ar-Ar standards used as fluence monitors in obtaining this alkali feldspar Ar-Ar data for the Palisades Rhyolite was the Fish Canyon Tuff sanidine standard, so using the published age data for it (Renne et al. 1998) the total 40K decay constant and half-life were determined from the Palisade Rhyolite data. And simultaneously using the Ar-Ar data for the historic Vesuvius eruption (Renne et al. 1997), the total 40K decay constant and half-life and the adjusted “absolute” age of the Fish Canyon Tuff sanidine standard were confirmed. This represents a series of convoluted steps in adjusting mineral ages and the total 40K decay constant and half-life to get the desired consilience, with many unstated assumptions in each step. Yet Min et al. (2000a) still opined for more concordant U-Pb analyses to provide much more powerful constraints by minimizing the effects of uncertainty in the U decay constants, and suggested additional 40K decay counting experiments would be desirable.
Kwon et al. (2002) did statistical analyses of the Ar-Ar dating data for five rock units with respect to the Fish Canyon Tuff sanidine standard compared with well-constrained “reference age” data for these five rock units (Min et al. 2000a; Min, Renne and Huff 2001; Renne 2000; Renne et al. 1995; Renne and Min 1998). The Vesuvius eruption is historically dated (Sigurdsson, Cashdollar, and Sparks 1982), whereas the Meishan basalt (China), Deicke K-bentonite, Palisade Rhyolite, and the Acapulco meteorite have been U-Pb dated (Göpel, Manhès and Allègre 1992; Min et al. 2000a; Mundil, Meier, and Oberli 1997; Tucker 1992). The problems of estimating the total 40K decay constant and half-life and “absolute” age of the Fish Canyon Tuff sanidine standard were studied using a (Gaussian) nonlinear errors-in-variables regression model, and the maximum likelihood method was applied for point estimates, while the parametric bootstrap method was used to estimate reasonable confidence regions for the estimates. These statistical analyses yielded what Kwon et al. (2002) regarded as the “most appropriate estimates” for the total 40K decay constant and half-life and “absolute” age of the Fish Canyon Tuff sanidine standard, which were in between previously reported values but had significantly smaller uncertainties. Their sensitivity analysis also showed them that their solution was reasonably robust against mis-specified error distributions.
Krumrei et al. (2006) Ar-Ar dated large K-rich amphibole crystals and U-Pb dated baddeleyite (ZrO2) crystals from augite syenite and alkali granite, and related rocks and pegmatite, in the Ilímaussaq complex of South Greenland. Using the decay constant of Steiger and Jäger (1977) and the fluence monitor (the MMhb standard) calibration of Renne et al. (1998) they obtained amphibole Ar-Ar ages that were systematically inconsistent with their baddeleyite U-Pb age, and with U-Pb results from previous studies (Upton et al. 2003). So in order to reconcile these disparate Ar-Ar and U-Pb ages Krumrei et al. (2006) chose to modify both the total 40K decay half-life they used in the calculation of their Ar-Ar ages, and the age of the Fish Canyon Tuff sanidine standard that had been used to calibrate the MMhb standard they used. This was the same approach as adopted by Kwon et al. (2002), so the new 40K decay half-life value proposed by Krumrei et al. (2006) was essentially identical to that proposed by Kwon et al. (2002). Again it should be noted that the resultant value chosen for the total 40K decay half-life depends on assumptions about both the U-Pb age, and the chosen age of the Fish Canyon Tuff sanidine standard.
Schwarz and Trieloff (2007a) similarly sought to revise the total 40K decay half-life by collating data on the apparent systematic offset of Ar-Ar and U-Pb mineral ages of various rocks. These included those that rapidly cooled, as studied by Kwon et al. (2002). Then using the supposed cooling history of the H chondrite parent body (Schwarz et al. 2006; Trieloff et al. 2003), it was possible for Schwarz and Trieloff (2007a) to calculate the apparent age offset of Ar-Ar and U-Pb ages for ~4.6 Byr old rocks at ~30 Myr (Trieloff, Jessberger, and Fiéni 2001), significantly smaller than 1%, which is also noted by Kwon et al. (2002) and Krumrei et al. (2006). Furthermore, biotite from the Great Dyke intrusion in Zimbabwe with an age of ~2.5 Byr had an K-Ar age discrepancy of ~20 Myr (Allsopp 1965), and the Ar-Ar age data for the ~2.0 Byr old Vredefort impact structure (Trieloff et al. 1994), recalculated using the new NL25 hornblende standard age (Schwarz and Trieloff 2007b), has a difference of ~17 Myr. From these data Schwarz and Trieloff (2007a) determined a revised total 40K decay constant and half-life (table 2), the latter only very slightly larger than that determined by Steiger and Jäger (1977). Their total 40K half-life value was also a little larger than the value determined by liquid scintillation counting by Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004), who used different 40K/K abundance and branching ratios in their calculations.
Schwarz and Trieloff (2007a) concluded that for conventional K-Ar and Ar-Ar dating, where the age calculation depends on mineral standards dated by the conventional K-Ar technique, the values of the total 40K decay constant and half-life, and the 40K/K abundance and branching ratios are all needed in the age equation, and that the accuracy of current K-Ar age calculations are seriously limited by the uncertainties of the total 40K decay constant and half-life. Subsequently Renne et al. (2010) insisted that, since their values for the total 40K decay constant and half-life and the 40Ar*/40K ratio of the Fish Canyon Tuff sanidine standard best fitted constraints from 40K activity-based measurements, independent measurements of the age of the Fish Canyon Tuff sanidine standard, and paired U-Pb and Ar-Ar ages of carefully selected rock units, their results implied approximately an order of magnitude improvement in the accuracy of the Ar-Ar method relative to previous calibrations, in spite of the principal sources of uncertainties in the systematic errors. But Schwarz et al. (2011) then claimed it was evident that the new total 40K decay constant and half-life proposed by Renne et al. (2010) should not be used for calculating Ar-Ar ages before issues such as the branching and 40K/K abundance ratios, the bias between Ar-Ar and U-Pb ages, and the need for more direct counting data on the 40K decay constants are clarified and resolved by general consensus being reached officially by the Subcommission on Geochronology of the International Union of Geological Sciences (IUGS). Even so, Renne et al. (2011) still insisted that their values for the 40K decay constants and the 40Ar*/40K ratio of the Fish Canyon Tuff sanidine standard, then revised by excluding the liquid scintillation counting data but by using an appropriate branching ratio, can still be used to compute Ar-Ar ages and uncertainties, and that their values provide the most accurate and precise comprehensive calibration of the 40Ar-39Ar system available. Yet Schmitz (2012) reported that in the compilation of the geochronological data for the 2012 version of the “official” geologic timescale by Gradstein et al. (2012) all the Ar-Ar ages utilized as timescale calibration points were recalculated to the Kuiper et al. (2008) age for the Fish Canyon Tuff sanidine monitor standard using the total 40K decay constant and half-life value of Min et al. (2000a) and Endt and Van der Leun (1973).
Quite clearly there is still much uncertainty in the geochronology community about the value of the total 40K decay constant and half-life. Thus according to Renne et al. (2011) independent determinations of the branching and 40K/K abundance ratios are still welcome, as well as new laboratory investigations to determine the total 40K decay constant and half-life. Yet there are still fundamental problems with the routine measurements of the isotope ratios of argon extracted from samples being dated that have gone unanswered. Trieloff et al. (2005) reported diffusion theory-based model calculations which predict that the routinely-used stepwise thermal extraction process from mineral phases induces isotope fractionation and, hence, adulterates the original argon isotopic compositions of the samples being dated. According to Trieloff et al. (2005) such effects are largely unconsidered, as they are small and a compelling experimental observation is lacking. Nevertheless, they reported the first unequivocal evidence for significant mass fractionation of argon isotopes during thermal extraction. They concluded that in 40Ar-39Ar stepwise heating, the isotope fractionation effect could cause systematic under-estimations of plateau ages, between 0.15 and 0.4% depending on age, or considerably higher if samples contain appreciable atmospheric Ar.
Is there a trend in the total 40K half-life data?
In spite of all the ongoing discussions in the geochronology community, as they try to increase the precision and decrease the uncertainties in the ages they obtain by the Ar-Ar and K-Ar techniques, it is clear from Table 2 and Fig. 3 that since 1997 the values determined for the total 40K decay half-life have converged towards a very narrow range of 1.2476– 1.295 Byr from eight geological comparisons studies, the former value being virtually indistinguishable from the 1.248 Byr value obtained by the two recent liquid scintillation counting experiments. Yet earlier total 40K decay half-life values determined before the twenty year (1977–1997) gap are scattered between 1.11 and 1.61 Byr. Of these only one determination was based on geological comparisons (Smith 1964), while the other 22 determinations were all based on direct counting experiments.
So it may be important to consider whether there is any trend in all these total 40K decay half-life data. As stated earlier there is a natural tendency for bias towards the most recent measurements as though the more “modern” equipment and methodologies (using computers, for instance) guarantee better results, when in fact the earlier experimenters may have been more intimately involved and careful with their equipment and methodologies to obtain excellent results rather than relying on computers. Indeed, as early as 1950 experimenters were reporting uncertainties in their measurements as low as ± 0.07, and by 1956 as low as ± 0.02. However, Begemann et al. (2001) claimed that judging from the fact that many of those earlier direct counting experiments yielded results that are not compatible with one another within the stated uncertainties, it appeared to them that not all the measurement uncertainties were accounted for, and therefore the stated uncertainties are unrealistically small. So according to Begemann et al. (2001) many of those experiments were apparently plagued by unrecognized random and/or systematic errors.
However, it needs to be emphasized here that from the perspective of uniformitarians the total 40K decay half-life is assumed to have been constant, at least from the time when the earth supposedly accreted from the solar nebula over 4.5 Byr ago. Thus they have to automatically assume these disparities between the results of the earlier direct counting experiments are due to the limitations of the “older” equipment and systematic errors unrecognized by the experimenters. On the other hand, biblical creationists are not bound by uniformitarian assumptions when examining these total 40K decay half-life data, especially in the light of the extensive evidence provided by Vardiman, Snelling, and Chaffin (2005) that nuclear decay rates were likely accelerated by orders of magnitude in at least one past catastrophic event, the global Flood cataclysm only about 4500 years ago. Thus if that were so, biblical creationists might expect that, at the end of that catastrophic event when the nuclear decay rates were drastically decelerating, some of that residual deceleration may have continued into our post-Flood era, even almost imperceptibly up to the present day.
So is there a trend in the total 40K decay half-life data? To determine if there is a trend and what it is, it first needs to be decided whether there are any outlying data points that need to be excluded from such an analysis. For example, are the determinations of 1.11 Byr in 1948, and 1.61 Byr in 1949 and 1950 too extreme and so should be considered outliers and discounted (see fig. 3)? However, considering them “extreme” is not sufficient reason to exclude them. A flaw in the experimental methodology or known errors in procedure by the experimenters would exclude them; otherwise they have to be considered as statistical outliers. Actually, the 1948 and 1950 determinations of 1.11 Byr and 1.61 Byr respectively were both obtained using Geiger-Müller counters, while the 1949 determination of 1.61 Byr was obtained using a beta disintegrations counter. Floyd and Borst (1949) did not describe the instrument they used, but given the sample was mounted in the counter on aluminium foil, the instrument may not have been unlike a Geiger-Müller or a gas proportional counter. Furthermore, if these three determinations are discounted as outliers, then the 1972 determination of 1.14 Byr should also be discounted as an outlier (see fig. 3 again). And then what about the 1948 determination of 1.54 Byr which also was obtained on a beta counter instrument, and by the same investigators (Borst and Floyd 1948) as the 1949 determination of 1.61 Byr which likely was obtained on the same instrument? Actually, the error uncertainties of these 1.61 Byr and 1.54 Byr determinations overlap, and since they were likely obtained on the same instrument, they could be potentially averaged at 1.575 Byr and be included in the analysis to determine any trends.
Ultimately every determination could be similarly scrutinized to decide whether it should be included in the analysis to determine any trends. Many of the 19 pre-1977 direct counting experiments were conducted using Geiger-Müller, beta and proportional counters or an ionization chamber, with four experiments using scintillation spectrometers or counters (table 1). Choices to exclude any determination would seem arbitrary. But even if the four extreme outliers are excluded, the two 1.61 Byr, and the 1.11 Byr and 1.14 Byr determinations, there are still some obvious possible trends, as the four depicted in Fig. 5. Then should the chosen trend be linear, or should it be akin to an exponentially declining curve? It all depends on which measurements are given the most “weight.” There appear to be two groupings of determinations— those that lie along the curved trend numbered 1 in Fig. 5, and those that are encompassed by the lower two of the linear trends numbered 3 and 4. If the half-life values along the upper curved trend are excluded, then the linear trends numbered 3 and 4 would approximate the overall trend in the remaining determinations, whereas if the half-life values along the upper curved trend are included, then the linear trend numbered 2 might approximate the overall trend.
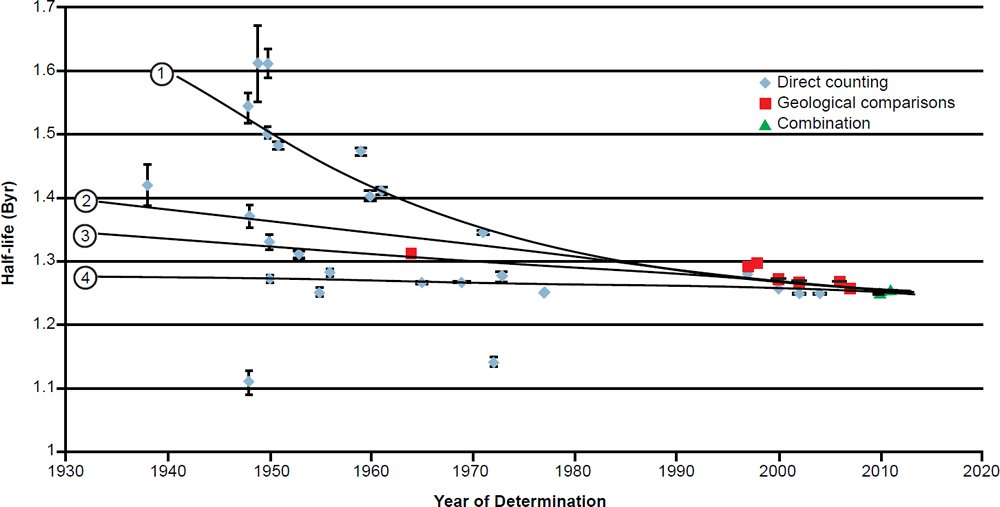
Fig. 5. Plot of the 40K half-life determinations versus the year of each determination, color-coded according to the method of its determination. The error bars for each determination are also plotted as in Fig. 3, but three possible lines depicting possible trends in the 40K half-life determinations have been added.
However, regardless of how a specific trend is chosen, the obvious conclusion is that it is conceivable the total 40K decay half-life may have declined slightly since measurements of it began in 1938. Obviously it is simply not possible to be dogmatic about this, since we cannot go back and redo the earlier experiments with the same more “modern” equipment to test whether the total 40K decay half-life was slightly higher in the past. Of course, the uniformitarian geochronology community has already discarded the earlier experimental determinations (for example, Begemann et al. 2001, Renne et al. 2010), although they are still embodied in the total 40K decay half-life vales adopted by Endt and Van der Leun (1973) and Steiger and Jäger (1977), and thus by Min et al. (2000b) and Schmitz (2012). Nevertheless, a slightly declining total 40K decay half-life over the last 78 years is not unexpected by biblical creationists, who have postulated based on available sound evidence that nuclear decay rates were accelerated by orders of magnitude during the global Flood cataclysm only about 4500 years ago, and then decelerated rapidly as that cataclysm ended (Vardiman, Snelling, and Chaffin 2005). Perhaps we can see confirmation of a slight residual decline in the total 40K decay half-life in the past 78 years of determinations to the present, as might be expected from being at the tail end of an exponential deceleration curve since the cataclysm ended only about 4500 years ago. If this is so, then it is further confirmation that nuclear decay rates have not always been constant at today’s measured rates as assumed by uniformitarians as a mandatory requirement for their radioisotope clocks to work reliably.
Dependence on the 238U and 235U half-lives and the 238U/235U ratio
The dependence of Ar-Ar (and hence K-Ar) dating on the U-Pb dating method, and thus the values of the 238U and 235U half-lives and the 238U/235U ratio, is well illustrated by an embarrassing example in the literature. Melchor, de Valais and Genise (2002) were studying fossilized bird-like footprints in the Santo Domingo Formation of northwest Argentina, and in order to date them they used the Ar-Ar method to date an interbedded basalt flow about 80 m above the fossil track-bearing horizons. They obtained a 40Ar/39Ar plateau age of 212.5 ± 7.0 Myr by step-heating analysis of an albite crystal, which made the fossilized bird-like footprints Late Triassic in age, which appeared to be consistent with fossil wood found lower in the same stratigraphic section. However, such an age was considered problematical, given that the “known history” of birds does not begin until the Late Jurassic. So further investigations were undertaken, particularly when it was realized the fossilized bird tracks were identical to the footprints made in sand by sandpipers today (Genise et al. 2009). Consequently, Melchor, Buchwaldt, and Bowring (2013) used the U-Pb method to date zircon crystals from a tuff (volcanic ash) bed also interbedded within the same stratigraphic unit and obtained a weighted mean 238U/206Pb age of 37 Myr. Furthermore, Vizán et al. (2013) used paleomagnetic measurements of samples of sandstones and conglomerates from the now revised red bed stratigraphic succession containing the fossilized bird tracks to further constrain the age of the formation hosting the fossil bird tracks to the Eocene. Thus the Ar-Ar date was abandoned without explanation because the U-Pb date was regarded as more reliable and superior, even though the paleomagnetic timescale also used to support the U-Pb date is mostly calibrated by K-Ar and Ar-Ar dating anchored to assumed projections of ocean floor spreading rates (Ogg 2012), another example of circular reasoning in the use of these various long-age dating methods.
In any case, Renne et al. (1998, 2010) undertook huge analytical programs of Ar-Ar analyses to attempt to accurately intercalibrate eight monitor standards routinely used in the Ar-Ar dating technique relative to the Fish Canyon Tuff sanidine standard. However, as admitted by Min et al. (2000a) the 40Ar*/40K ratios for individual standards are only known to better than ± 2% in some cases, and interlaboratory discrepancies of more than 2% in the 40Ar-39Ar ages of secondary standards like the Fish Canyon Tuff sanidine (FCTs) suggest larger uncertainties. Therefore, Renne, Karner, and Ludwig (1998) argued that the “precisely known” decay constants for 238U and 235U, as well as the existence of internal reliability criteria in the U-Pb systems, offer a “gold standard” for geochronology and cosmochronology, including K-Ar and Ar-Ar dating. They stated that this would be achieved by normalization of other radioactive systems’ decay constants to those of 238U and 235U, either directly or indirectly by comparison with the 207Pb-206Pb system, which they reasoned provides advantages over disintegration counting in experimentally difficult cases, such as in determining the total 40K decay constant and half-life. Thus all non-direct counting attempts since 1998 to more accurately determine the total 40K decay constant and half-life have ultimately used the U-Pb systems as the “gold standard” to be calibrated against (for example, Krumrei et al. 2006; Kwon et al. 2002; Min et al. 2000a; Schwarz and Trieloff 2007a; Schwarz et al. 2011). Furthermore, Snelling (2014a, b, 2015a, b) has already demonstrated in detail how the 87Rb, 176Lu, 187Re, and 147Sm decay half-lives have also all ultimately been calibrated against the U-Pb radioisotope system.
Nevertheless, even as they were promoting the adoption of the U-Pb system “gold standard,” Renne, Karner, and Ludwig (1998) admitted that because the 40Ar-39Ar system depends on two decay constants because of the branched decay of 40K and also on standards that introduce additional decay constant uncertainty, the age uncertainty in 40Ar-39Ar ages at 4.6 Byr due to decay constant effects alone is ~34 Myr, and therefore a critical value test requires a minimum difference of 35 Myr between 207Pb-206Pb and 40Ar-39Ar ages (neglecting analytical errors and errors in 40K-40Ar data for the standards) to infer that the ages are only resolvable at the 95% confidence level. This discrepancy between apparent 40Ar-39Ar and 207Pb-206Pb ages was also subsequently highlighted by Schwarz and Trieloff (2007a) and Schwarz et al. (2011). In all instances, to resolve this glaring discrepancy the total 40K decay half-life was “normalized” (that is, adjusted or massaged) so that the 40Ar-39Ar ages then agreed with, or conformed to, the 207Pb-206Pb ages. The Krumrei et al. (2006) study is a good example of how it has been done.
However, the U-Pb “gold standard” dating method has itself come under much scrutiny in the two last decades. Ludwig (2000) has demonstrated that, although almost universally ignored, the effect of the errors in the U decay constants on U-Pb concordia-Pb-Pb intercept ages are significant, being a 4.5 Myr error for a 500 Myr age, which amounts to almost a 1% error. The U-Pb method also depends on the crucial 238U/235U ratio, but discrepancies and variations have been found recently between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al 2012). Much earlier, Apt et al. (1978) had reported that the 235U/238U ratio in uranium ores in Canada, Brazil, Zaire and Australia varied from 0.7107 to 0.7144 when the recognized value is 0.72. Such variations in uranium ores have been further documented by Bopp et al. (2009). These discrepancies and variations remain unexplained, especially in the context of the 238U and 235U decay constants and half-lives. Furthermore, the fact that there are these variations in the crucial 238U/235U ratio in terrestrial minerals and rocks on which the U-Pb dating systems “gold standard” depends, which has been used to re-calibrate K-Ar and Ar-Ar radioisotope ages to determine the total 40K decay half-life and decay constant, only underscores that these radioisotope methods cannot provide the absolute invariable “dates” they are so confidently proclaimed to provide.
In any case, there is the additional assumption in all the radioisotope dating methods of having to know the original concentrations of the daughter and index isotopes, which is very significant in the U-Pb method because the original concentrations are assumed not to be zero, in contrast to the K-Ar method. Yet there must be great uncertainty as to what those initial values were in the unobserved past, despite the isochron and concordia techniques attempting to negate the necessity for knowing those initial values, and despite the assumption ever since Patterson (1956) and Tatsumoto, Knight, and Allègre (1973) that the Pb isotopic composition of the troilite (FeS) in the Canyon Diablo iron meteorite represents the initial “primordial Pb” of the earth and the solar system (Dickin 2005; Faure and Mensing 2005). Thus the U-Pb method should not, and cannot, be used as a supposedly objective standard to determine other parent radioisotope half-lives and decay constants.
Indeed, it would remain prudent to be very careful with these geological comparison methods for two other reasons. First, there are significant flaws in the basic assumptions on which all the radioisotope dating methods depend, not least being the assumption that the decay rates of the parent radioisotopes have always been constant in the past at today’s measured decay rates. And there is a hint of this non-constant nuclear decay rate in the possible slight decline in the total 40K half-life over the last 78 years of experimental measurements, as discussed above. Second, the U-Pb method relies primarily on α-decay, in contrast to the K-Ar and Ar-Ar methods which are based on β-decay. Yet both Austin (2005) and Snelling (2005) have reported that the parent U α-decaying radioisotopes seem to yield systematically different Pb-Pb isochron ages compared to K-Ar isochron ages from the parent β-decaying 40K for some earth rocks using the same samples with essentially the same methodology. Additionally, they suggested the pattern of differences was potentially related to the parent radioisotopes’ atomic weights and half-lives, which could be indicative of parent radioisotopes’ decay rates having not been constant in the past but instead were substantially faster. Furthermore, these different radioisotope ages yielded by the same earth rocks are often widely divergent, even up to 100–200% different, which is such a huge divergence that it renders these dating methods highly suspect, even if the differences in the determinations of the half-lives of the parent radioisotopes seem miniscule and therefore trivial by comparison. However, it was considered prudent to still document here these seemingly miniscule differences in half-life values, because they may be indicative of other underlying factors at work, and they can still lead to very significant discrepancies in the derived radioisotope ages that might otherwise appear to be acceptably accurate to uniformitarians.
Nevertheless, U-Pb and Pb-Pb radioisotope age comparisons have ultimately been used to determine the total 40K half-life, in spite of the two most recent high-quality direct counting experimental determinations being in agreement with a different total 40K decay half-life value. In any case, there is still disagreement in the uniformitarian geochronology community over whose value of the total 40K decay half-life should be adopted (compare Renne et al. 2011 with Schmitz 2012). Yet even then, when the U-Pb systems “gold standard” is used to calibrate the Ar-Ar and K-Ar systems, the total 40K decay half-life values of Min et al. (2000a), as preferred by Schmitz (2012), and of Renee et al. (2011) have uncertainties of 1.0% and 0.5% respectively. This is in part because the uncertainties contributed by the U-Pb systems “gold standard” depend on whether the U decay constants are accurately and precisely known, and on the crucial 238U/235U ratio. Indeed, discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites which remain unexplained. This only serves to highlight that if the K-Ar and Ar-Ar dating methods have been calibrated against the U-Pb “gold standard” with its own uncertainties, then the claimed accurately-determined total 40K decay half-life cannot be absolute, especially given the evidence in some earth rocks of past higher radioisotope decay rates and the evidence from the direct counting experiments that there may have been a slight decline in the total 40K half-life values over the past 78 years. Yet even though it is to be expected these half-life measurements vary because of the difficulties in measuring such a long half-life, the resultant calculated radioisotope ages end up being different from one another and so require adjustment, which is far too “inaccurate” in providing the absolute ages required by uniformitarians. Thus without an accurately known 40K decay half-life, K-Ar and Ar-Ar radioisotope ages cannot be accurately determined. Therefore, K-Ar and Ar-Ar dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Conclusions
There have been numerous attempts to determine the total 40K decay half-life in the last 78 years by two primary techniques—by physical direct counting experiments using Geiger-Müller and beta counters, ionization chambers and liquid scintillation counters; and by radioisotope age comparisons of rocks, minerals, and meteorites. The determinations since 1997 have converged with close agreement on the total 40K decay half-life value of 1.2524 ± 0.0064 Byr (Renne et al. 2011), although this value has not yet been adopted for standard use by the uniformitarian geological community which still prefers the Min et al. (2000a) determined total 40K decay half-life value of 1.269 ± 0.013 Byr (Schmitz 2012). The Renne et al. (2011) total 40K decay half-life value ignores the two recent liquid scintillation direct counting determinations by Grau Malonda and Grau Carles (2002) and Kossert and Günther (2004) which agreed on a slightly lower total 40K decay half-life value of 1.248 ± 0.003 Byr. Instead the total 40K decay half-life value preferred by Renne et al. (2011) depends on K-Ar isotopic data and pairs of 238U-206Pb and 40Ar-39Ar data for rigorously selected rocks and minerals extracted from them, many utilized as Ar-Ar fluence monitor standards, to calibrate it and the Fish Canyon Tuff sanidine Ar-Ar dating standard. Nevertheless, both the Min et al. (2000a) and Renne et al. (2011) total 40K decay half-life values ultimately depend on adjusting (that is, massaging) K-Ar and Ar-Ar ages to conform to U-Pb and Pb-Pb ages, often obtained from different minerals respectively in the same rocks.
Min et al. (2000a) stated that important sources of systematic error in 40Ar-39Ar (and K-Ar) dating arise from uncertainties in the two 40K decay constants and the K-Ar isotopic data for neutron monitors (standards). They admitted that the β and γ activity data underlying the decay constants used in geochronology since Steiger and Jäger (1977) are more dispersed than acknowledged by the geochronological-oriented summaries previous to theirs, and that compilations of essentially the same data in the nuclear physics and chemistry literature since Endt and Van der Leun (1973) have consistently produced lower estimates (and larger assigned uncertainties) of the constants for 40K → 40Ar and 40K → 40Ca decay and thus the branching ratio. Even though it is crucial to determination of the total 40K decay half-life, the branching ratio is still not definitively agreed upon, the value of 0.1162 being adopted by Renne et al. (2011) in spite of the carefully-determined Nägler and Villa (2000) value of 0.1194 ± 0.007, which confirmed the value of 0.1195 ± 0.0014 determined by Endt and Van der Leun (1973). Min et al. (2000a) then conceded that the uncertainties in the crucial 40K/K abundance ratio also need to be considered, because there is no agreement on it. Min et al. (2000a) adopted the Garner et al. (1975) determined value of 0.011672 ± 0.000041% which Renne et al. (2010, 2011) also adopted as per IUPAC recommendation, but the value of 0.011668 ± 0.000008% determined by Naumenko et al. (2013) has yet to be recognized. Added to that there is the uncertainty over the questionable existence of a γ-less electron capture 40K → 40Ar decay direct to ground state. Therefore, when all these factors are considered, Min et al. (2000a) concluded that the total 40K decay constant and half-life are thus known to no better than ± 2% at the 2σ level, and that 40Ar*/40K ratios for individual standards are known to better than ± 2% in some cases, while interlaboratory discrepancies of more than 2% in the 40Ar/39Ar ages of secondary standards like the Fish Canyon Tuff sanidine suggest larger uncertainties. Thus according to Renne et al. (2011) independent determinations of the branching and 40K/K abundance ratios are still welcome, as well as new laboratory investigations to determine the total 40K decay constant and half-life.
Yet even though there is now close agreement between the many recently determined values, ultimately the total 40K decay half-life has been determined by recalibrating the Ar-Ar (and K-Ar) ages of rocks and minerals with the U-Pb and Pb-Pb ages of minerals from the same rocks by adjusting (or massaging) the total 40K decay half-life. Thus such radioisotope age comparisons have been given preference over the values obtained by direct counting experiments which directly measure 40K decay. Yet the latter are independent of all the assumptions involved with the radioisotope dating methods. Indeed, model dependent results should not take precedence over the direct experimental evidence.
Since all but one of the age comparisons on rocks and minerals used to determine the total 40K decay half-life ultimately involved the U-Pb method, all K-Ar and Ar-Ar age calculations are thus calibrated against the U-Pb method. However, this U-Pb “gold standard” depends on having precisely determined 238U and 235U decay constants, as well as on the crucial 238U/235U ratio being known and constant. Yet there are still uncertainties in the measured U decay constants, and discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals, rocks, and uranium ores, and the 238U/235U ratio in meteorites. These discrepancies and variations remain unexplained. This only serves to highlight that if the K-Ar and Ar-Ar dating methods have been calibrated against the U-Pb “gold standard” with its own uncertainties, then they cannot be absolute.
Furthermore, there is evidence that nuclear decay rates have not been constant in the past, including the possibility of a slight decline in the measured values of the total 40K decay half-life during the 78 years of determinations. Thus without an accurately known 40K decay half-life, K-Ar and Ar-Ar radioisotope ages cannot be accurately determined. Therefore, K-Ar and Ar-Ar dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Acknowledgments
The invaluable help of my research assistant in compiling and plotting the data in the color-coded age diagrams is acknowledged. The three reviewers are also acknowledged for their helpful comments and input, though the final content of this paper is solely my responsibility. Our production assistant Laurel Hemmings is also especially thanked for her painstaking work in preparing this paper for publication.
References
Aldrich, L. T., and A. O. Nier. 1948. “Argon-40 in Potassium Minerals.” Physical Review 74 (8): 876–877.
Allsopp, H. L. 1965. “Rb-Sr and K-Ar Age Measurements on the Great Dyke of Southern Rhodesia.” Journal of Geophysical Research 70 (4): 977–984.
Apt, K. E., J. P. Balagna, E. A. Bryant, G. A. Cowan, W. R. Daniels, R. J. Vidale, and D. G. Brookins. 1978. “Search For Other Natural Fission Reactors.” In Natural Fission Reactors, Proceedings of a Meeting on Natural Fission Reactors, Paris, France, December 1977, IAEA-TC-119/37, 677–689. Vienna, Austria: International Atomic Energy Agency.
Aston, F. W. 1921. “The Mass Spectra of the Alkali Metals.” Philosophical Magazine 42, series 6 (249): 436–441.
Audi, G., O. Bersillon, J. Blachot, and A. H. Wapstra. 1997. “The NUBASE Evaluation of Nuclear and Decay Properties.” Nuclear Physics A 624 (1): 1–124.
Austin, S. A. 2005. “Do Radioisotope Clocks Need Repair? Testing the Assumptions of Isochron Dating Using K-Ar, Rb-Sr, Sm-Nd, and Pb-Pb Isotopes.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative, 325–392. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/do-radioisotope-clocks-need-repair.
Bachmann, O., F. Oberli, M. A. Dungan, M. Meier, R. Mundil, and H. Fischer. 2007. “40Ar/39Ar and U-Pb Dating of the Fish Canyon Magmatic System, San Juan Volcanic Field, Colorado: Evidence for an Extended Crystallization History.” Chemical Geology 236 (1–2): 134–166.
Beckinsale, R. D., and N. H. Gale. 1969. “A Reappraisal of the Decay Constants and Branching Ratio of 40K.” Earth and Planetary Science Letters 6 (4): 289–294.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. “Call for an Improved Set of Decay Constants for Geochronological Use.” Geochimica et Cosmochimica Acta 65 (1): 111–121.
Bopp, C. J., C. C. Lundstrom, T. M. Johnson, and J. J. G. Glessner. 2009. “Variations in 238U/235U in Uranium Ore Deposits: Isotopic Signatures of the U Reduction Process?” Geology 37 (7): 611–614.
Borst, L. B., and J. J. Floyd. 1948. “The Radioactive Decay of K40.” Physical Review 74 (8): 989.
Bramley, A, and A. K. Brewer. 1938. “The Radioactivity of Potassium.” Physical Review 53 (7): 502–505.
Brennecka, G. A., and M. Wadhwa. 2012. “Uranium Isotope Compositions of the Basaltic Angrite Meteorites and the Chronological Implications for the Early Solar System.” Proceedings of the National Academy of Sciences USA 109 (24): 9299–9303.
Brereton, N. R. 1970. “Corrections for Interfering Isotopes in the 40Ar/39Ar Dating Method.” Earth and Planetary Science Letters 8 (6): 427–433.
Browne, E., J. M. Dairiki, and R. E. Doebler. 1978. Table of Isotopes, 91. New York: Wiley.
Burch, P. R. J. 1953. “Specific γ-Activity, the Branching Ratio and Half-life of Potassium-40.” Nature 172 (4373): 361–362.
Burnett, D. S., J. H. Lippolt, and G. J. Wasserburg. 1966. “The Relative Abundance of K40 in Terrestrial and Meteoritic Samples.” Journal of Geophysical Research 71 (4): 1249–1269.
Campbell, N. R. 1908. “The Radioactivity of Potassium, with Special Reference to Solutions of its Salts.” Proceedings of the Cambridge Philosophical Society 14: 557–567.
Campbell, N. R., and A. Wood. 1906. “The Radioactivity of the Alkali Metals.” Proceedings of the Cambridge Philosophical Society 14: 15–21.
Ceccarelli, M., G. Quareni, and A. Rostagni. 1950. “On the Radioactivity of Potassium.” Physical Review 80 (5): 909–910.
Cesana, A., and M. Terrani. 1977. “Gamma-ray Activity Determination in Large Volume Samples with a Ge-Li Detector.” Analytical Chemistry 49 (8): 1156–1159.
Dallmeyer, R. D. 1979. “40Ar/39Ar Dating: Principles, Techniques, and Applications in Orogenic Terranes.” In Lectures in Isotope Geology, 77–105. Edited by E. Jäger and J. C. Hunziker. Berlin, Germany: Springer-Verlag.
Dalrymple, G. B. 1991. The Age of the Earth. Stanford, California: Stanford University Press.
Dalrymple, G. B. 2004. Ancient Earth, Ancient Skies: The Age of the Earth and Its Cosmic Surroundings. Stanford, California: Stanford University Press.
Dalrymple, G. B., and M. A. Lanphere. 1969. Potassium-Argon Dating: Principles, Techniques, and Applications to Geochronology. San Francisco, California: W.H. Freeman.
Dalrymple, G. B., and M. A. Lanphere. 1971. “40Ar/39Ar Technique of K/Ar Dating: A Comparison with the Conventional Technique.” Earth and Planetary Science Letters 12 (3): 300–308.
De Laeter, J. R., J. K. Böhlke, P. De Bièvre, H. Hidaka, H. S. Peiser, K. J. R. Rosman, and P. D. P. Taylor. 2003. “Atomic Weights of the Elements: Review 2000.” Pure and Applied Chemistry 75 (6): 683–800
Dickin, A. P. 2005. Radiogenic Isotope Geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Endt, P. M., and C. Van der Leun. 1973. “Energy Levels of A = 21-44 nuclei (V).” Nuclear Physics A 214: 1–625.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and Applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Faust, W. R. 1950. “Specific Activity of Potassium.” Physical Review 78: 624.
Floyd, J. J., and L. B. Borst. 1949. “Energy of Beta-Rays from K40.” Physical Review 75 (7): 1106.
Garner, E. L., T. J. Murphy, J. W. Gramlich, P. J. Paulsen, and I. L. Barnes. 1975. “Absolute Isotopic Abundance Ratios and the Atomic Weight of a Reference Sample of Potassium.” Journal of Research of the National Bureau of Standards—A. Physical Chemistry 79A (6): 713–725.
Genise, J. F., R. N. Melchor, M. Archangelsky, L. O. Bala, R. Straneck, and S. de Valais. 2009. “Application of Neoichnological Studies to Behavioural and Taphonomic Interpretation of Fossil Bird-like Tracks from Lacustrine Settings: The Late Triassic-Early Jurassic? Santo Domingo Formation, Argentina.” Palaeogeography, Palaeoclimatology, Palaeoecology 272 (3–4): 143–161.
Glendenin, L. E. 1961. “Present Status of the Decay Constants.” Annals of the New York Academy of Sciences 91: 166–176.
Good, M. L. 1951. “Beta-Ray Spectrum of K40.” Physical Review 83 (5): 1054–1055.
Gopal, K., H. Sanjeevaiah, and B. Sanjeevaiah. 1972. “A Laboratory Experiment for Determining the Partial Half-life of 40K for Beta Emission.” American Journal of Physics 40 (5): 721–723.
Göpel, C., G. Manhès, and C. J. Allegrè. 1992. “U-Pb Study of the Acapulco Meteorite.” Meteoritics 27 (3): 226.
Gradstein, F. M., J. G. Ogg, M. D. Schmitz, and G. M. Ogg, eds. 2012. The Geologic Time Scale 2012. Amsterdam, The Netherlands: Elsevier.
Gräf, T. 1948a. “On the Half-life of K40.” Physical Review 74 (7): 831.
Gräf, T. 1948b. “On the Total Half-life Period of K40.” Physical Review 74 (9): 1199–1200.
Gräf, T. 1950. “Electron Capture/Beta-Decay Ratio in K40.” Physical Review 79 (6): 1014.
Grau Malonda, A., and A. Grau Carles. 2002. “Half-life Determination of 40K by LSC.” Applied Radiation and Isotopes 56 (1–2): 153–156.
Helmer, R. G. 1998. Table de Radionucléides. Paris: Laboratoire de Metrologie des Rayonnements Ionisants, Bureau National de Metrologie, Commissariat a l’Energie Atomique.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. “238U/235U Systematics in Terrestrial Uranium-Bearing Minerals.” Science 335 (6076): 1610–1614.
Hinnov, L. A., and F. J. Hilgen. 2012. “Cyclostratigraphy and Astrochronology.” In The Geologic Time Scale 2012. Vol. 1, chapter 4, 63–83. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg. Amsterdam, The Netherlands: Elsevier.
Hirzel, O., and H. Wäffler. 1948. “On the Radioactivity of K40.” Physical Review 74 (10): 1553.
Houtermans, F. G., O. Haxel, and J. Heintze. 1950. “Die Halbwertszeit des K40.” Zeitschrift für Physik 128 (5): 657–667.
Humayun, M., and R. N. Clayton.1995. “Precise Determination of the Isotopic Composition of Potassium: Application to Terrestrial Rocks and Lunar Soils.” Geochimica et Cosmochimica Acta 59 (10): 2115–2130.
Hunziker, J. C. 1979. “Potassium-Argon Dating.” In Lectures in Isotope Geology, 52–76. Edited by E. Jäger and J. C. Hunziker. Berlin, Germany: Springer-Verlag.
Inghram, M. G., H. Brown, C. Patterson, and D. C. Hess. 1950. “The Branching Ratio of K40 Radioactive Decay.” Physical Review 80 (5): 916–917.
Jourdan, F., and P. R. Renne. 2007. “Age Calibration of the Fish Canyon Sanidine 40Ar/39Ar Dating Standard Using Primary K–Ar Standards.” Geochimica et Cosmochimica Acta 71 (2): 387–402.
Jourdan, F., A. Frew, A. Joly, C. Mayers, and N. J. Evans. 2014. “WA1ms: A ~2.61 Ga Muscovite Standard for 40Ar/39Ar Dating.” Geochimica et Cosmochimica Acta 141: 113–126.
Jourdan, F., C. Verati, and G. Féraud. 2006. “Intercalibration of the Hb3gr 40Ar/39Ar Dating Standard.” Chemical Geology 231 (3): 177–189.
Kelly, W. H., G. B. Beard, and R. A. Peters. 1959. “The Beta Decay of K40.” Nuclear Physics 11: 492–498.
Kossert, K., and E. Günther. 2004. “LSC Measurements of the Half-life of 40K.” Applied Radiation and Isotopes 60 (2–4): 459–464.
Krumrei, T. V., I. M. Villa, M. A. W. Marks, and G. Markl. 2006. “A 40Ar/39Ar and U/Pb Isotopic Study of the Ilímaussaq Complex, South Greenland: Implications for the 40K Decay Constant and for the Duration of Magmatic Activity in a Peralkaline Complex.” Chemical Geology 227 (3–4): 258–273.
Kuiper, K. F., A. L. Deino, F. J Hilgen, W. Krijgsman, P. R. Renne, and J. R. Wijbrans. 2008. “Synchronizing Rock Clocks of Earth History.” Science 320 (5875): 500–504.
Kwon, J., K. Min, P. J. Bickel, and P. R. Renne. 2002. “Statistical Methods for Jointly Estimating the Decay Constant of 40K and the Age of a Dating Standard.” Mathematical Geology 34 (4): 457–474.
Lanphere, M. A., and H. Baadsgaard. 2001. “Precise K-Ar, 40Ar/39Ar, Rb-Sr and U/Pb Mineral Ages from the 27.5 Ma Fish Canyon Tuff Reference Standard.” Chemical Geology 175 (3–4): 653–671.
Lederer, C. M., J. M. Hollander, and I. Perlman. 1967. Table of Isotopes. New York: Wiley.
Leutz, H., G. Schulz, and H. Wenninger. 1965. “The Decay of Potassium-40.” Zeitschrift für Physik 187 (2): 151–164.
Lide, D. R., and H. P. R. Frederikse. 1995. CRC Handbook of Chemistry and Physics. 76th ed. Boca Raton, Florida: CRC Press.
Ludwig, K. R. 2000. “Decay Constant Errors in U-Pb Concordia-Intercept Ages.” Chemical Geology 166 (3–4): 315–318.
Mattinson, J. M. 2010. “Analysis of the Relative Decay Constants of 235U and 238U by Multi-step CA-TIMS Measurements of Closed-System Natural Zircon Samples.” Chemical Geology 275 (3–4): 186–198.
McDougall, I., and T. M. Harrison. 1988. Geochronology and Thermochronology by the 40Ar/39Ar Method. New York: Oxford University Press.
McNair, A., R. N. Glover, and H.W. Wilson. 1956. “The Decay of Potassium-40.” Philosophical Magazine 1 (2): 199–211.
Melchor, R. N., S. de Valais, and J. F. Genise. 2002. “Bird-like Footprints from the Late Triassic.” Nature 417 (6892): 936– 938.
Melchor, R. N., R. Buchwaldt, and S. A. Bowring. 2013. “A Late Eocene Date for Late Triassic Bird Tracks.” Nature 495: E1–E2.
Merrihue C. M. 1965. “Trace-Element Determinations and Potassium-Argon Dating by Mass Spectrometry of Neutron-irradiated Samples.” Transactions of the American Geophysical Union 46: 125.
Merrihue C. M., and G. Turner. 1966. “Potassium-Argon Dating by Activation with Fast Neutrons.” Journal of Geophysical Research 71 (11): 2852–2857.
Miller, J. L. 2012. “Time to Reset Isotopic Clocks? Two New Studies Revise Key Parameters in Radiometric Dating.” Physics Today 65 (6): 20–22.
Min K., R. Mundil, P. R. Renne, and K. R. Ludwig. 2000a. “A Test for Systematic Errors in 40Ar/39Ar Geochronology through Comparison with U-Pb Analysis of a 1.1 Ga Rhyolite.” Geochimica et Cosmochimica Acta 64 (1): 73–98.
Min K., J. Kwon, P. R. Renne, and P. Bickel. 2000b. “Regression Model and Maximum Likelihood Method for Simultaneous Estimation of 40K Decay Constants and Age of a Standard.” EOS Transactions of the American Geophysical Union 81 (19): 445.
Min, K., P. R. Renne, and W. D. Huff. 2001. “40Ar/39Ar Dating of Ordovician K-bentonites in Laurentia and Baltoscandia.” Earth and Planetary Science Letters 185 (1–2): 121–134.
Mitchell, J. G. 1968. “The Argon-40/Argon-39 Method for Potassium-Argon Age Determination.” Geochimica et Cosmochimica Acta 32 (7): 781–790.
Morozova, I. M., and A. A. Alferovsky. 1974. “Fractionation of Lithium and Potassium Isotopes in Geological Processes.” Geokhimiya 1: 30–39.
Mousuf, A. K. 1952. “K40 Radioactive Decay: Its Branching Ratio and Its Use in Geological Age Determinations.” Physical Review 88 (1): 150–151.
Mundil, R., M. Meier, and F. Oberli. 1997. “Single Crystal U-Pb Dating of Permian/Triassic Boundary in SE China: Implications for Mass Extinction and Time-Scale Calibration.” Terra Nova 9 (2): 66.
Nägler, T. F., and I. M. Villa. 2000. “In Pursuit of the 40K Branching Ratios: K-Ca and 39Ar-40Ar Dating of Gem Silicates.” Chemical Geology 169 (1–2): 5–16.
Naumenko, M. O., K. Mezger, T. F. Nägler, and I. M. Villa. 2013. “High Precision Determination of the Terrestrial 40K Abundance.” Geochimica et Cosmochimica Acta 122: 353–362.
Nier, A. O. 1935. “Evidence for the Existence of an Isotope of Potassium of Mass 40.” Physical Review 48 (3): 283–284.
Nier, A. O. 1950. “A Redetermination of the Relative Abundances of the Isotopes of Carbon, Nitrogen, Oxygen, Argon, and Potassium.” Physical Review 77 (6): 789–793.
Nomade, S., P. R. Renne, N. Vogel, A. L. Deino, W. D. Sharp, T. A. Becker, A. R. Jaouni, and R. Mundil. 2005. “Alder Creek Sanidine (ACs-2): A Quaternary 40Ar/39Ar Dating Standard Tied to the Cobb Mountain Geomagnetic Event.” Chemical Geology 218 (3–4): 315–338.
Ogg, J. G. 2012. “Geomagnetic Polarity Time Scale.” In The Geologic Time Scale 2012. Vol. 1, chapter 5, 85–113. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg. Amsterdam, The Netherlands: Elsevier.
Patterson, C. 1956. “Age of Meteorites and the Earth.” Geochimica et Cosmochimica Acta 10 (4): 230–237.
Phillips, D., and E. L. Matchan. 2013. “Ultra-High Precision 40Ar/39Ar Ages for Fish Canyon Tuff and Alder Creek Rhyolite Sanidine: New Dating Standards Required?” Geochimica et Cosmochimica Acta 121: 229–239.
Renne, P. R. 2000. “40Ar/39Ar age of Plagioclase from Acapulco Meteorite and the Problem of Systematic Errors in Cosmochronology.” Earth and Planetary Science Letters 175 (1–2): 13–26.
Renne, P. R., G. Balco, K. R. Ludwig, R. Mundil, and K. Min. 2011. “Response to the Comment by W. H. Schwarz et al. on ‘Joint Determination of 40K Decay Constants and 40Ar*/40K for the Fish Canyon Sanidine Standard, and Improved Accuracy for 40Ar/39Ar Geochronology’ by P. R. Renne et al. (2010).” Geochimica et Cosmochimica Acta 75 (17): 5097– 5100.
Renne, P. R., D. B. Karner, and K. R. Ludwig. 1998. “Absolute Ages Aren’t Exactly.” Science 282 (5395): 1840–1841.
Renne, P. R., and K. Min. 1998. “40Ar/39Ar Dating of the 79 AD Eruption of Vesuvius: An ab initio Basis for Improved Accuracy in 40Ar/39Ar Geochronology.” Mineralogical Magazine 62A (2): 1255–1256.
Renne, P. R., R. Mundil, G. Balco, K. Min, and K. R. Ludwig. 2010. “Joint Determination of 40K Decay Constants and 40Ar*/40K for the Fish Canyon Sanidine Standard, and Improved Accuracy for 40Ar/39Ar Geochronology.” Geochimica et Cosmochimica Acta 74 (28): 5349–5367.
Renne, P. R., W. D. Sharp, A. L. Deino, G. Orsi, and L. Civetta. 1997. “40Ar/39Ar Dating into the Historical Realm: Calibration Against Pliny the Younger.” Science 277 (5330): 1279–1280.
Renne, P. R., C. C. Swisher, A. L. Deino, D. B. Karner, T. L. Owens, and D. J. DePaolo. 1998. “Intercalibration of Standards, Absolute Ages and Uncertainties in 40Ar/39Ar Dating.” Chemical Geology 145 (1–2): 117–152.
Renne P. R., Z. Zichao, M. A. Richards, M. T. Black, and A. R. Basu. 1995. “Synchrony and Causal Relations Between Permian-Triassic Boundary Crises and Siberian Flood Volcanism.” Science 269 (5229): 1413–1416.
Roddick, J. C. 1983. “High Precision Intercalibration of 40Ar-39Ar Standards.” Geochimica et Cosmochimica Acta 47 (5): 887–898.
Russell, R. D., H. A. Shillibeer, R. M. Farquhar, and A. K. Mousuf. 1953. “The Branching Ratio of Potassium 40.” Physical Review 91 (5): 1223–1224.
Saha, N. K., and J. B. Gupta. 1960 “The γ/β Branching Ratio in the Decay Scheme of 40K.” Proceedings of the National Institute of Sciences India A26 (5): 486–491.
Sawyer, G. A., and M. L. Wiedenbeck. 1949. “Gamma-ray of K40.” Physical Review 76 (10): 1535.
Sawyer, G. A., and M. L. Wiedenbeck. 1950. “Decay Constants of K40.” Physical Review 79 (3): 490–494.
Schaeffer, O. A., and J. Zähringer, eds. 1966. Potassium-Argon Dating. New York: Springer-Verlag.
Schmitz, M. D. 2012. “Radiogenic Isotope Geochronology.” In The Geologic Time Scale 2012. Vol. 1, chapter 6, 115–126. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg. Amsterdam, The Netherlands: Elsevier.
Schoene, B., J. L. Crowley, D. J. Condon, M. D. Schmitz, and S. A. Bowring. 2006. “Reassessing the Uranium Decay Constants for Geochronology Using ID-TIMS U-Pb Data.” Geochimica et Cosmochimica Acta 70 (2): 426–445.
Schön, R., G. Winkler, and W. Kutschera. 2004. “A Critical Review of Experimental Data for the Half-Lives of the Uranium Isotopes 238U and 235U.” Applied Radiation and Isotopes 60 (2–4): 263–273.
Schwarz, W. H., M. Trieloff, E. V. Korochantseva, and A. I. Buikin. 2006. “New Data on the Cooling History of the H Chondrite Parent Body.” Meteoritics and Planetary Science 41 (S8): A161.
Schwarz, W. H., K. Kossert, M. Trieloff, and J. Hopp. 2011. “Comment on the ‘Joint Determination of 40K Decay Constants and 40Ar*/40K for the Fish Canyon Sanidine Standard, and Improved Accuracy for 40Ar/39Ar Geochronology’ by Paul R. Renne et al. (2010).” Geochimica et Cosmochimica Acta 75 (17): 5094–5096.
Schwarz, W. H., and M. Trieloff. 2007a. “Constraints on the Revision of the K Decay Constants.” Geochimica et Cosmochimica Acta 71 (15) S1: A910.
Schwarz, W. H., and M. Trieloff. 2007b. “Intercalibration of 40Ar–39Ar Age Standards NL-25, HB3gr Hornblende, GA1550, SB-3, HD-B1 Biotite and BMus/2 Muscovite.” Chemical Geology 242 (1–2): 218–231.
Sigurdsson, H., S. Cashdollar, and R. S. J. Sparks. 1982. “The Eruption of Vesuvius in A.D. 79: Reconstruction from Historical and Volcanological Evidence.” American Journal of Archaeology 86 (1): 39–51.
Smaller, B., J. May, and M. Freedman. 1950. “Scintillation Studies on Potassium Iodide.” Physical Review 79 (6): 940–945.
Smith, A. G. 1964. “Potassium-Argon Decay Constants and Age Tables.” Quarterly Journal of the Geological Society of London 120S: 129–141.
Snelling, A. A. 2000. “Geochemical Processes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: A Young-Earth Creationist Research Initiative, 123–304. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, A. A. 2005. “Isochron Discordances and the Role of Mixing and Inheritance of Radioisotopes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative, 393–524. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr. org/article/isochron-discordances-role-inheritance/.
Snelling, A. A. 2014a. “Determination of the Radioisotope Decay Constants and Half-lives: Rubidium-87 (87Rb).” Answers Research Journal 7: 311–322. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, A. A. 2014b. “Determination of the Radioisotope Decay Constants and Half-lives: Lutetium-176 (176Lu).” Answers Research Journal 7: 483–497. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, A. A. 2015a. “Determination of the Radioisotope Decay Constants and Half-lives: Rhenium-187 (187Re).” Answers Research Journal 8: 93–111. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rhenium-187/.
Snelling, A. A. 2015b. “Determination of the Radioisotope Decay Constants and Half-lives: Samarium-247 (247Sm).” Answers Research Journal 8: 449–478. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-samarium-147/.
Snelling, A. A. 2015c. “Radioisotope Dating of Meteorites: V. Isochron Ages of Groups of Meteorites.” Answers Research Journal 8: 305–321. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-v-isochron-ages-groups-meteorites/.
Spell, T. L., and I. McDougall. 2003. “Characterization and Calibration of 40Ar/39Ar Dating Standards.” Chemical Geology 198 (3–4): 189–211.
Spiers, F. W. 1950. “Radioactivity of Potassium.” Nature 165: 356.
Steiger, R. H., and E. Jäger. 1977. “Subcommission on Geochronology: Convention on the Use of Decay Constants in Geo- and Cosmochronology.” Earth and Planetary Science Letters 36 (3): 359–362.
Suttle, A. D., Jr., and W. F. Libby. 1955. “Absolute Assay of Beta Radioactivity in Thick Solids: Application to Naturally Radioactive Potassium.” Analytical Chemistry 27 (6): 921–927.
Tatsumoto, M., R. J. Knight, and C. J. Allègre. 1973. “Time Differences in the Formation of Meteorites as Determined from the Ratio of Lead-207 to Lead-206.” Science 180 (4092): 1279–1283.
Tetley, N., I. McDougall, and H. R. Heydegger. 1980. “Thermal Neutron Interferences in the 40Ar/39Ar Dating Technique.” Journal of Geophysical Research 85 (B12): 7201–7205.
Thomson, J. J. 1905. “On the Emission of Negative Corpuscles by the Alkali Metals.” Philosophical Magazine 10, Series 6 (59): 584–590.
Trieloff, M., M. Falter, A. I. Buikin, E. Korochantseva, E. K. Jessberger, and R. Altherr. 2005. “Argon Isotope Fractionation Induced by Stepwise Heating.” Geochimica et Cosmochimica Acta 69 (5): 1253–1264.
Trieloff, M., E. K. Jessberger, and C. Fiéni. 2001. “Comment on ‘40Ar/39Ar Age of Plagioclase from Acapulco Meteorite and the Problem of Systematic Errors in Cosmochronology’ by Paul R. Renne.” Earth and Planetary Science Letters 190 (3–4): 267–269.
Trieloff, M., E. K. Jessberger, I. Herrwerth, J. Hopp, C. Fiéni, M. Ghélis, M. Bourot-Denise, and P. Pellas. 2003. “Structure and Thermal History of the H-Chondrite Parent Asteroid Revealed by Thermochronometry.” Nature 422 (6931): 502–506.
Trieloff, M., W. U. Reimold, J. Kunz, R. H. Boer, and E. K. Jessberger. 1994. “40Ar-39Ar Thermochronology of Pseudotachylite at the Ventersdorp Contact Reef, Witwatersrand Basin.” South African Journal of Geology 97 (3): 365–384.
Tucker, R. D. 1992. “U-Pb Dating of Plinian-Eruption Ashfalls by the Isotopic Dilution Method: A Reliable and Precise Tool for Time-Scale Calibration and Biostratigraphic Correlation.” Geological Society of America, Abstracts With Programs 24: A198.
Turner, G. 1971. “Argon 40-Argon 39 Dating: The Optimization of Irradiation Parameters.” Earth and Planetary Science Letters 10 (2): 227–234.
Upton, B. J. G., C. H Emeleus, L. M. Heaman, K. M. Goodenough, and A. A. Finch. 2003. “Magmatism of the Mid-Proterozoic Gardar Province, South Greenland: Chronology, Petrogenesis and Geological Setting.” Lithos 68 (1–2): 43–65.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the Age of the Earth: A Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Venkataramaiah, P., H. Sanjeevaiah, and B. Sanjeevaiah. 1971. “Specific Beta Activity of Potassium.” Indian Journal of Pure and Applied Physics 9: 133–134.
Verbeek, A. A., and G. D. L. Schreiner. 1967. “Variations in 39K:41K Ratio and Movement of Potassium in a Granite-Amphibolite Contact Region.” Geochimica et Cosmochimica Acta 31 (11): 2125–2163.
Vermeesch, P. 2015. “Revised Error Propagation of 40Ar/39Ar Data, Including Covariances.” Geochimica et Cosmochimica Acta 171: 325–337.
Vizán, H., S. Guena, R. N. Melchor, E. S. Bellosi, S. L. Lagorio, C. Vásquez, M. S. Japas, G. Ré, and M. Do Campo. 2013. “Geological Setting and Paleomagnetism of the Eocene Red Beds of Laguna Brava Formation (Quebrada Santo Domingo, northwestern Argentina).” Tectonophysics 583: 105–123.
Von Weizsäcker, C. F. 1937. “Über die Möglichkeit eines Dualen b-Zerfalls von Kalium.” Physikalische Zeitschrift 38: 623–624.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nenow, and C. A. Bauman. 1969. “A Programmable Magnetic Field Mass Spectrometer with On-Line Data Processing.” Review of Scientific Instruments 40 (2): 288–295.









