Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Minerals such as zircon are routinely used by geochronologists to confidently provide the U-Pb and Pb-Pb ages which underpin the conventional multi-millions-of-years’ timescale. These dating methods and the underlying assumptions are reviewed. The recognition of Pb loss from minerals after they form to explain discordant dates has resulted in the demonstration that both U and Pb mobility can occur in them. But how much U and Pb have been mobilized and how far they have migrated cannot be known with certainty. The radiation released by U decay damages crystal lattices and volume expansion generates micro-fractures, providing preferential pathways for U and Pb migration. Heat aids U and Pb mobility, but also causes recrystallization and defect recovery, locking migrated U and Pb atoms into their new locations. The current locations of U and Pb atoms within minerals can be studied at the atomic level. But there can be no certainty as to whether those atoms have always been in those locations, or whether they have migrated there. Also, there is no way of knowing what and how much migration happened in the past. Thus, even if the outer portions of crystals are removed before isotopic analysis and the U-Pb ages obtained for the cores of crystals are concordant, there can be no certainty that they represent the dates when the crystals formed. These uncertainties are compounded by the underlying unprovable assumptions on which the radioisotope dating methods are based, especially the assumption of time-invariant decay rates, built on the foundation of an assumed deep time history. The resultant U-Pb and Pb-Pb ages obtained are thus subjective, even though geochronologists take numerous precautions to make the U-Pb and Pb-Pb methods still have a strong semblance of validity. Nevertheless, since the amount of U and Pb mobility in most cases has been small, then the determinations can be used to provide useful relative ages. Thus, those absolute ages cannot be used to dismiss the history of the earth and its chronology provided in God’s infallible Word.
Introduction
Radioisotope dating of minerals, rocks, and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Many in both the scientific community and the general public around the world thus remain convinced of the earth’s claimed great antiquity.
The decay of 238U and 235U to 206Pb and 207Pb, respectively, forms the basis for one of the oldest methods of geochronology (Dickin 2005, Faure and Mensing 2005, Reiners et al. 2018, 171). While the earliest studies focused on uraninite (an uncommon mineral in igneous rocks), there has been intensive and continuous effort over the past five decades in U-Pb dating of more-commonly occurring trace minerals. Zircon (ZrSiO4) in particular has been the focus of thousands of geochronological studies, because of its ubiquity in felsic igneous rocks and its claimed extreme resistance to isotopic resetting (Begemann et al. 2001).
However, accurate radioisotopic age determinations require that the decay constants or half-lives of the respective parent radionuclides be accurately known and constant in time. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is still not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with direct half-life determinations are, in most cases, still at the 1% level, which is still significantly better than any radioisotope method for determining the ages of rock formations. However, even uncertainties of only 1% in the half-lives lead to significant discrepancies in the derived radioisotope ages due to how the half-life uncertainties are dealt with in the procedures for propagation of errors (Mattinson 2010; Schoene et al. 2006). The recognition of an urgent need to improve the situation is not new (for example, Min et al. 2000; Renne, Kamer, and Ludwig 1998). It continues to be mentioned, at one time or another, by every group active in geo- or cosmochronology (Boehnke and Harrison 2014; Schmitz 2012).
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates have not always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Ongoing research continues to make further inroads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One area the RATE project did not get to investigate was the issue of how reliable are the determinations of the radioisotope decay rates, which are so crucial for calibrating these dating “clocks.” Thus, as follow-on to the RATE effort, in a recent series of papers Snelling (2014a, 2014b, 2015a, 2015b, 2016, 2017a) reviewed how the half-lives of the parent radioisotopes used in long-age geological dating have been determined and collated all the determinations of them reported in the literature to discuss the accuracy of their currently accepted values. He documented the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes 87Rb, 176Lu, 187Re, 147Sm, 40K, 238U, and 235U which are used as the basis for the Rb-Sr, Lu-Hf, Re-Os, Sm-Nd, K-Ar, Ar-Ar, U-Pb, and Pb-Pb long-age dating methods respectively. He showed that there is still some uncertainty in what the values for these measures of the 87Rb, 176Lu, 40K, and 235U decay rates should be, in contrast to the apparent agreement on the 187Re, 147Sm, and 238U decay rates. This uncertainty is especially prominent in determinations of the176Lu decay rate by physical direct counting experiments. Furthermore, the determined values of the 87Rb decay rate differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rates of isotopes such as 87Rb, 176Lu, 187Re, and 147Sm used for deep time dating that makes precise measurements of their decay rates so difficult. Thus, it could be argued that direct measurements of their decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology employed by the secular community in their rock dating methods.
Ultimately, the 87Rb, 176Lu, 187Re, 147Sm, and 40K decay half-lives have all been calibrated against the U-Pb radioisotope systems. This is the case even for the 147Sm decay half-life whose accepted value has not changed since it was calibrated against the U-Pb dating of two meteorites in the 1970s, in spite of the fact that more recent thorough physical direct counting experiments suggest a higher value. However, confidence in U-Pb radioisotope dating as the “gold standard” is very questionable, as there are now known measured variations in the 238U/235U ratio that is critical to that method (Brennecka and Wadhwa 2012; Goldmann et al. 2015; Hiess et al. 2012; Tissot and Dauphas 2015), as well as uncertainties as to the 238U and 235U decay rate values (Boehnke and Harrison 2014; Mattinson 2010; Schoene et al. 2006; Schön, Winkler and Kutschera 2004; Snelling 2017a; Villa et al. 2016). It is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life measurements because these are difficult measurements to make. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks and minerals due to how the half-life uncertainties are dealt with in the procedures for propagation of errors (Mattinson 2010; Schoene et al. 2006). This, of course, in no way diminishes or casts uncertainties on the conclusions of the RATE project that radioisotope decay rates have not always been constant at today’s measured rates, and that as a result radioisotope ages can still be used as relative ages (Vardiman, Snelling, and Chaffin 2000, 2005). Yet the question still remains as to whether the half-life values for each long-lived parent radioisotope are independently determined.
Nevertheless, accurate radioisotope age determinations not only depend on accurate determinations of the decay constants or half-lives of the respective parent radioisotopes, but on the reliability of the three assumptions these supposed absolute dating methods rely on. Those are the starting conditions, no contamination of closed systems, and time-invariant decay rates. All of these assumptions are unprovable. Yet they can supposedly be circumvented somewhat via the isochron technique, because it is claimed to be independent of the starting conditions and sensitive to revealing any contamination, which is still significantly better than any of the model radioisotope age methods for determining the ages of rock formations. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. Often (if not usually for many investigators) discordant points are interpreted that the sample itself is thus problematic and should not be used for dating. That this is common practice is illustrated with numerous examples cited from the literature by Faure and Mensing (2005) and Dickin (2005). Nevertheless, the discarding discordant points by practitioners would appear to be justifiable in many cases. On the other hand, some may argue that this discarding of data points which do not fit the isochron is arbitrary and therefore is not good science, because it is merely assumed the “aberrant” values are due to contamination rather than that being proven to be so. Indeed, in order to discard such outliers in any data set, one must establish a reason for discarding those data points which cannot be reasonably questioned.
Undoubtedly the U-Pb and Pb-Pb radioisotope dating methods are now the cornerstone in current geochronology studies. Thus it is imperative every aspect of the methodology used in these methods be carefully examined to investigate whether the age results obtained by them are really as accurate and absolute as portrayed in the geological literature. Therefore, it is highly significant that Amelin et al. (2009) listed the potential problems which cause possible inaccuracies in obtaining reliable U-Pb and Pb-Pb ages. These are:
- Presence of non-radiogenic Pb of unknown isotopic composition;
- Deviations from closed system evolution (gain or loss of U, loss of intermediate daughters such as the inert gas Rn, and loss of Pb);
- Misidentification of the processes that start or reset the isotopic clocks;
- Analytical problems (fractionation, instrument specific, etc.) and blank subtraction;
- Fractionation of radiogenic Pb isotopes induced by leaching of alpha recoil tracks;
- Variations in the 238U/235U ratio;
- Uncertainties in the half lives of 238U and 235U; and
- Deviations of the 234U/238U ratio from secular equilibrium.
It should be noted that Amelin et al. (2009) totally ignored the “elephant-in-the-room” issue of the time-invariance of the decay rates, because as uniformitarians they regard decay rates as constant at today’s measured rates. Yet, of these eight potential problems, Amelin et al. (2009) admitted that the first five are important and common, whereas the last three they considered insignificant or unlikely. But recent research has even found that these last three problems are more critical than they estimated, not least the variations in the 238U/235U ratio (Goldmann et al. 2015; Tissot and Dauphas 2015), and the uncertainties in the half lives of 238U and 235U (Boehnke and Harrison 2014; Snelling 2017a). Goldmann et al (2015) stated that “the investigated meteorites show U isotope variation between 137.71 and 137.89 (1.3%).” And Tissot and Dauphas (2015) reported:
Using the mass fractions and isotopic compositions of various rock types in Earth’s crust, we further calculate an average δ238U isotopic composition for the continental crust of –0.29 ± 0.03‰ corresponding to a 238U/235U isotopic ratio of 137.797 ± 0.005. We discuss the implications of the variability of the 238U/235U ratio on Pb-Pb and U-Pb ages and provide analytical formulas to calculate age corrections as a function of the age and isotopic composition of the sample.
Thus, each of these potential problems needs to be investigated closely.
Snelling (2017b) has already closely examined the first of them, the problem of the presence of non-radiogenic Pb of unknown isotopic composition, that is, common, initial, or primordial Pb. So now we will turn to the second and third of these problems. The second problem listed was the deviations from closed system behaviour evident from loss of Pb, or gain or loss of U, which requires monitoring U-Pb discordance and studying distribution of U and radiogenic Pb. The third problem Amelin et al. (2009) listed was the misidentification of the processes that start or reset the isotopic clocks. That requires studying the distribution of U and radiogenic Pb to look for element migration caused by diffusion and alteration. But before that, there is a need to go over some important background informational issues germane to the subsequent focus on the issues of the distribution of U and radiogenic Pb that is indicative of Pb loss or U loss or gain, and on the effects of diffusion and/or alteration.
Uranium and Lead Geochemistry
Uranium is element 92 (Z= 92) and a member of the actinide series in which the 5f orbitals are progressively filled with electrons. It occurs naturally in the tetravalent oxidation state U4+ with an ionic radius of 1.05 Å. But under oxidizing conditions it forms the uranyl ion (UO22+) in which U has a valence of 6+. The uranyl ion forms compounds that are soluble in water, so U is a mobile element under oxidizing conditions. In contrast to U, Pb (Z= 82) is in period 6 and is a group 14 post-transitional metal. It is insoluble in water, but is a chalcophile element because it reacts with sulfur. It forms Pb2+ and Pb4+ ions with ionic radii of 1.32 Å and 0.91 Å respectively, so Pb ions cannot substitute for U ions in minerals.
In the course of the earth’s history, during partial melting of the rocks in the earth’s mantle U was concentrated in the liquid (melt) phase and thus became incorporated into the more silica-rich products. Therefore, the progressive geochemical differentiation of the earth’s upper mantle has enriched the rocks of the earth’s continental crust in U compared to those of the upper mantle. At an average of 1.3 ppm U is the 51st most abundant element in the earth’s crust, whereas Pb is regarded as quite a common element in the earth’s crust with an average of 11 ppm (Rudnick and Gao 2003). The concentrations of U and Pb increase from basaltic rocks (0.43 ppm U and 3.7 ppm Pb) to granites (4.8 ppm U and 23.0 ppm Pb) (Faure and Mensing 2005, 215). The concentrations of U in the common rock-forming silicate minerals are uniformly low, on the order of a few ppm or less. Instead, U occurs primarily in certain accessory minerals in which it is either a major constituent or replaces other elements. These minerals include uraninite, zircon, baddeleyite, monazite, apatite, and sphene (titanite).
All six naturally-occurring U isotopes are unstable and decay. Of these, 238U is the dominantly abundant isotope in natural U. It and 235U, the next most abundant isotope, are the starting radioisotopes in two decay chains or series (figs. 1 and 2), with 234U one of the early steps in the 238U decay chain. There are also several other trace U isotopes. 239U is formed when 238U undergoes spontaneous fission, releasing neutrons that are captured by other 238U atoms. 237U is formed when 238U captures a neutron but emits two more, which then decays to 237Np (neptunium). And then 233U is formed in the decay chain of that 237Np. 233U is also made from 232Th by neutron bombardment, usually in a nuclear reactor.
On the other hand, Pb has four stable isotopes, three of which (206Pb, 207Pb, and 208Pb) are the end members of decay chains (238U, 235U, and 232Th respectively). Only stable 204Pb has no radioactive precursor from which it is derived, and thus it is often called common Pb. Thus, the isotopic concentration of Pb in a natural rock sample depends on how much U and Th are also present. For example, the relative amount of 208Pb can range from 52.4% in normal samples to 90% in thorium ores. Similarly, the ratios of 206Pb and 207Pb to 204Pb increase in different samples, since the former two are supplemented by radioactive decay of U and the latter is not. For this reason, the atomic weight of lead is given to only one decimal place. Both 214Pb and 210Pb are short-lived intermediates in the 238U decay chain (fig. 1), while 211Pb and 212Pb are short-lived intermediates in the 235U and 232Th decay chains respectively (fig. 2). Lastly, very minute traces of 209Pb are also present from the cluster decay of 223Ra, one of the daughter products of natural 235U (fig. 2). Hence, natural Pb consists of not only the four stable isotopes, but also minute traces of another five short-lived radioisotopes.
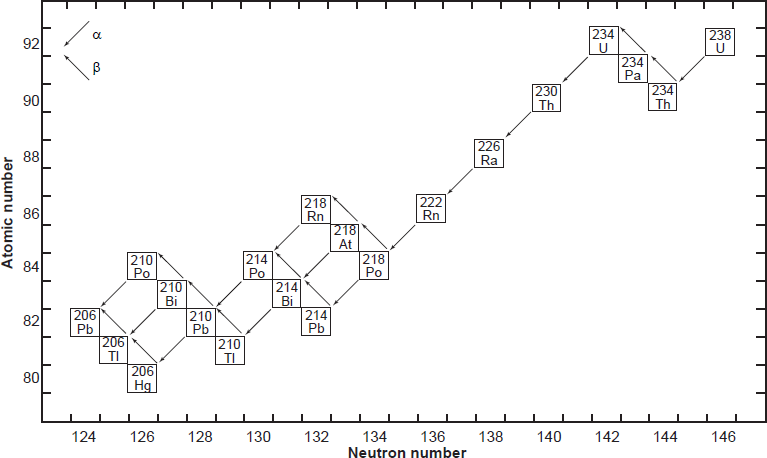
Fig. 1. The decay chain of 238U resulting from the successive emission of α-particles and β-particles from intermediate isotopes as indicated (after Faure and Mensing 2005). The final decay product is stable 206Pb.
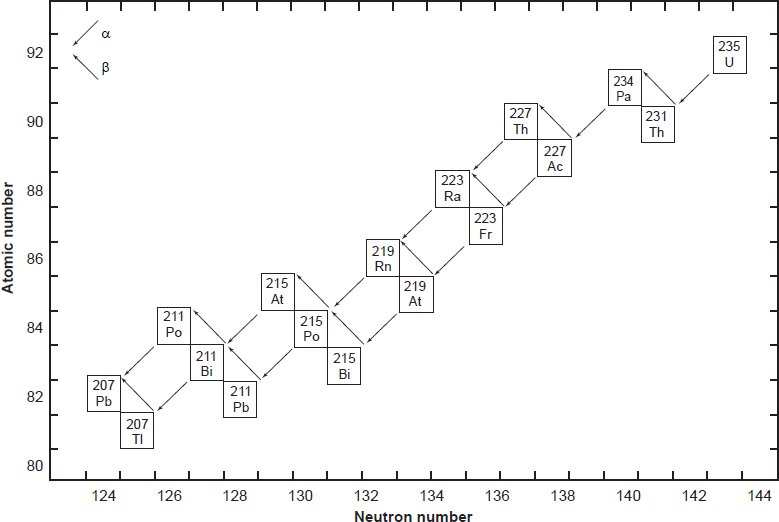
Fig. 2. The decay chain of 235U resulting from the successive emission of α-particles and β-particles from intermediate isotopes as indicated (after Faure and Mensing 2005). The final decay product is stable 207Pb.
Primordial Pb, which comprises the amounts of the isotopes 204Pb, 206Pb, 207Pb, and 208Pb at the time the earth formed, has been defined as the Pb isotopic composition of troilite (FeS) in the Canyon Diablo iron meteorite (Chen and Wasserburg 1983; Tatsumoto, Knight, and Allègre 1973). It is postulated to have been mostly “created” as a result of repetitive rapid and slow neutron capture processes occurring in stars. Yet there are serious questions about the so-called r-process in supernova which is postulated to generate all the elements heavier than Fe (Thielemann et al. 2011). Indeed, the supernova origin of heavy elements via the r-process has very recently fallen out of favor. Instead, the detection of merging neutron stars via gravitational waves and, concurrently, via electromagnetic radiation has resulted in the new view that merging neutron stars are the primary r-process site. Whether this is borne out in quantitative terms remains to be seen. Thus, it should be noted that this is not an absolute value, but merely an artifact of the reigning popular model for the naturalistic formation of the universe and its component stars and planetary systems.
238U and 235U Decay
The decay of the uranium isotopes 238U and 235U to the stable lead isotopes 206Pb and 207Pb respectively is the basis for the several most important methods of radioisotope dating. These not only derive from the transformation of 238U and 235U to 206Pb and 207Pb respectively, but also derive from the time-dependent “evolution” of common lead 204Pb from the decay of the intermediate daughters of 238U and 235U, and from the resulting isotopic composition of the accumulating daughter He (helium). Of course, 204Pb is not produced from 238U or 235U decay. However, 204Pb is assumed to be primordial and thus is hypothetically used as an indicator of the 206Pb, 207Pb, and 208Pb present due to radioactive decay. Age determinations of rocks based on the decay of U and the resulting accumulation of Pb and He were first attempted in the early years of the 20th century by Rutherford (1906) and Boltwood (1907). Subsequently, Holmes (1913) used chemical U-Pb and U-He dates to propose the first geological timescale based on radioisotope dating in his book on the age of the earth.
The invention of the first mass spectrometer by Thomson (1911) was followed by the work of Dempster (1918) and Ashton (1919), who designed the mass spectrographs which they used in subsequent years to discover the naturally-occurring isotopes of most of the elements in the periodic table and to measure their masses and abundances. The design of mass spectrographs was further improved in the 1930s, but it was the mass spectrometers based on a design by Nier (1940) that made possible the measurement and interpretation of variations in the isotopic composition of certain elements in natural materials such as minerals and rocks. Modern mass spectrometers follow his design and achieve a high level of accuracy and reliability of operation which enable isotope ratios to be measured for radioisotope dating, such as that based on the isotopic composition of Pb due to the decay of U to Pb, but also on the isotope ratios of common Pb. As a result of continuing refinement of the analytical procedures and of the sophistication of the instrumentation, the U-Pb and Pb-Pb methods of radioisotope dating are now regarded as the most precise and accurate geochronometers for determining the ages of terrestrial and extra-terrestrial minerals and rocks.
As already indicated, U has three naturally occurring isotopes, 238U, 235U, and 234U, all of which are radioactive. The decay of 238U gives rise to what is called the uranium series, which includes 234U as one of the intermediate daughters and ends in stable 206Pb (fig. 1). The decay of 238U to 206Pb can be summarized by the equation
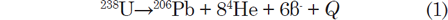
where Q = 47.4 MeV per atom or 0.71 calories per gram per year (Wetherill 1966). Each atom of 238U that decays produces one atom of 206Pb by emission of eight α-particles and six β-particles. The parameter Q represents the sum of the decay energies of the entire series in units of millions of electron volts and calories of heat produced per gram per year. Several intermediate daughters in this series (fig. 1) undergo branched decay involving the emission of either an α-particle or a β-particle. The chain therefore splits into separate branches but 206Pb is the stable end product of all possible decay paths.
The decay of 235U gives rise to what is called the actinium series (fig. 2), which ends with stable 207Pb after emission of seven α-particles and four β-particles, as summarized by the equation
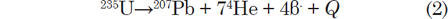
where Q = 45.2 MeV per atom or 4.3 calories per gram per year (Wetherill 1966). This series also branches as shown in Fig. 2.
In spite of there being 33 isotopes of 12 elements formed as intermediate daughters in these two decay series (not counting 4He), none is a member of more than one series. In other words, each decay chain always leads through its unique set of intermediate isotopes to the formation of a specific stable Pb isotope. The decay of 238U always produces 206Pb, and 235U always produces 207Pb.
The half-lives of 238U and 235U are very much longer than those of their respective intermediate daughter isotopes. Therefore, these decay series satisfy the prerequisite condition for the establishment of secular equilibrium, provided none of the intermediate daughters escaped from the U-bearing mineral or were added from external sources (Faure and Mensing 2005, 218). When secular equilibrium exists in a U-bearing mineral because it is a closed system, the decay rates of the intermediate daughters are equal to those of their respective parents, and thus the production rate of the stable daughter at the end of the decay chain is equal to the decay rate of its parent at the head of that chain. Therefore, the decay of 238U and 235U in minerals in which secular equilibrium has established itself can be treated as though it occurred directly to the respective 206Pb and 207Pb isotopes. As a result, the growth of these radiogenic Pb isotopes can be described by means of equations (1) and (2), which are similar to the equations used to represent the decay of 87Rb to 87Sr and 147Sm to 143Nd.
The U-Pb Dating Method
The accumulation of stable daughter atoms from the decay of parent atoms over time is expressed by the equation known as the law of radioactivity, namely
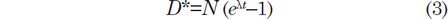
where D* is the number of measured stable radiogenic daughter atoms, N is the number of measured parent atoms remaining, λ is the decay constant (decay rate), and t is the time since decay of the parent atoms began (Faure and Mensing 2005). Since D* and N can be measured in a mineral, then if λ is known the equation can be solved for t, which is thus declared to be the age of the mineral. Thus the accumulation of stable radiogenic 206Pb and 207Pb by decay of their respective parents 238U and 235U in a mineral is governed by equations derivable from equation (3) as follows
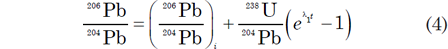
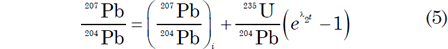
where λ1 and λ2 are the decay constants of 238U and 235U respectively; 238U/204Pb and 235U/204Pb are ratios of these isotopes calculated from the measured concentrations of U and Pb in the mineral; and the subscript i refers to the initial values of the 206Pb/204Pb and 207Pb/204Pb ratios.
To date U-bearing minerals by the U-Pb methods, the concentrations of U and Pb are measured by an appropriate analytical technique (usually isotope dilution), and the isotopic composition of Pb is determined by using a solid-source mass spectrometer, an ion-probe mass spectrometer, or an ICP mass spectrometer. The U-Pb dates are calculated by means of equations (4) and (5) being solved for t using assumed values of the initial isotope ratios of Pb (for example, Ludwig 1993) as follows
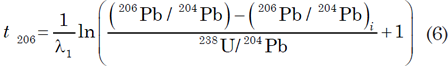
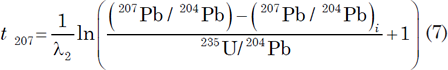
These are known as 206Pb and 207Pb model ages respectively. They are independent of each other, but will be concordant (that is, agree with each other) if the mineral samples satisfy the conditions for dating (Faure and Mensing 2005, 218–219):
- The mineral has remained closed to U and Pb, and all the intermediate daughters throughout its history;
- Correct values are used for the initial Pb isotope ratios;
- The decay constants of 238U and 235U are known accurately;
- The isotopic composition of U is normal and has not been modified by isotope fractionation or by occurrence of a natural chain reaction based on induced fission of 235U; and
- All analytical results are accurate and free of systematic errors.
The assumption that the samples being dated remained closed to U, Pb, and all intermediate daughters throughout their history “is satisfied only in rare cases because U is a mobile element in oxidizing environments and therefore tends to be lost during chemical weathering” (Faure and Mensing 2005, 219, emphasis in the original). In addition, the emission of α-particles causes radiation damage to the crystal structures of the U-hosting minerals, which facilitates the loss of Pb and the other intermediate daughters in both decay chains. Consequently, U-Pb dates for rocks and minerals are rarely concordant, so procedures have been devised to overcome that problem.
The choice of the initial Pb isotope ratios would seem to only be a problem for dating rocks and minerals that have low U/Pb ratios and additionally are young. It is claimed that the numerical values of the initial Pb isotope ratios do not appear to significantly affect the calculated U-Pb ages of Precambrian rocks and minerals having high U/Pb ratios because their present Pb isotope ratios in most cases reach large values.
The decay constants and half-lives of 238U and 235U were fixed by the International Union of Geological Sciences (IUGS) Subcommission of Geochronology in 1975 (Steiger and Jäger 1977). At the same time a value of 137.88 was adopted for the 238U/235U ratio. Since then these values have been used in almost all U-Pb age calculations so as to avoid any potential confusion by the use of different values. It has been continually claimed that the numerical values of the 238U and 235U decay constants and half-lives are probably more accurately known than those of other long-lived radionuclides because of their importance in the nuclear industry. Therefore, refractory U-bearing minerals such as zircon (ZrSiO4) that often yield concordant U-Pb ages have been used to refine (that is, adjust) the decay constants of other radionuclides used in geochronology (Begemann et al. 2001; Snelling 2014a, 2014b, 2015a, 2015b, 2016).
It should be mentioned here that decay rates are not just measured and expressed by the parameter known as the decay constant (λ), but also by the parameter called the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, whereas the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:
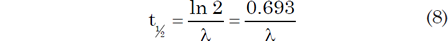
The issue of the abundances of the U isotopes and thus the adopted value of the 238U/235U ratio has already been discussed in detail by Snelling (2017a), so further comment is not warranted here. Suffice it to say, real differences in the isotopic composition of terrestrial and extra-terrestrial U have been reported in the past decade. So until very recently there has been no compelling evidence not to base age determinations of terrestrial and lunar rocks and minerals, and of meteorites and their minerals, by the U-Pb method on a value of 137.88 for the present-day 238U/235U ratio.
It is claimed that the effect of Pb loss on U-Pb dates can be minimized by calculating a date based on the 207Pb/206Pb ratio which is supposed to be insensitive to recent Pb loss provided that the Pb which was lost from the mineral had the same isotopic composition as the Pb which remained, that is, there has been no isotopic fractionation. The relationship between the 207Pb/206Pb ratio and time results from the difference in the half-lives of 238U and 235U. The desired equation is obtained by combining equations (4) and (5) above:
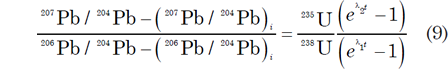
This equation has several interesting properties (Faure and Mensing 2005, 219–220):
- It involves the 235U/238U ratio which at 1/137.88 is regarded as a constant for all U of normal isotopic composition on and in the earth, the moon, Mars, and meteorites at the present time.
- The equation does not require knowledge of the concentrations of U and Pb and involves only isotope ratios of Pb.
-
The left hand side of equation (9) is equal to the 207Pb/206Pb ratio of radiogenic Pb:
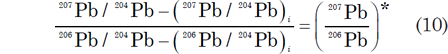
where the asterisk * identifies the radiogenic Pb isotopes produced since the “clock” was reset by a metamorphic or complete melting/recrystallization event.
- Equation (9) cannot be solved for t by algebraic means because it is transcendental, but it can be solved by iteration and by interpretation in a table.
A difficulty arises in the solution of equation (9) when t = 0, because it yields the indeterminate result 0/0 (Faure and Mensing 2005, 220). It is claimed thus that this difficulty is overcome by means of l’Hôpital’s rule, which requires that the differentiated functions in the ratio are differentiable over the entire open interval in question, that is, over millions to billions of years (Faure and Mensing 2005, 220). However, it appears questionable whether this is a proper application of l’Hôpital’s rule. This is because the decay rates of 235U and 238U are not equal, and therefore the quantities of 235U and 238U are functions of time and thus the 235U/238U ratio must be a function of time. Hence the right side of equation (9) is not in a form amenable to l’Hôpital’s rule, that is, there are four functions of time involved in the open interval 0 < t < ta, where t = the elapsed time since the “clock” was reset. However, only applying this rule to the value of (207Pb/206Pb)* at time t = 0 (the instant of clock reset) yields
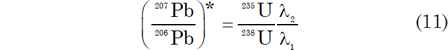
Equation (11) indicates that the (207Pb/206Pb)* which forms by the decay of 238U and 235U over the time interval equalling the age of the mineral is equal to the rates of decay of these two U isotopes at the present time. Substituting into equation (11) the relevant values for the 235U/238U ratio, and the decay constants λ1 and λ2, yields a value at time (t = 0) for (207Pb/206Pb)* of 0.04604 (see Table 1).
| t, × 109 y | eλ1t–1 | eλ2t–1 | 207Pb*/206Pb |
|---|---|---|---|
| 0 | 0.0000 | 0.0000 | 0.04604 |
| 0.2 | 0.0315 | 0.2177 | 0.05012 |
| 0.4 | 0.0640 | 0.4828 | 0.05471 |
| 0.6 | 0.0975 | 0.8056 | 0.05992 |
| 0.8 | 0.1321 | 1.1987 | 0.06581 |
| 1.0 | 0.1678 | 1.6774 | 0.07250 |
| 1.2 | 0.2046 | 2.2603 | 0.08012 |
| 1.4 | 0.2426 | 2.9701 | 0.08879 |
| 1.6 | 0.2817 | 3.8344 | 0.09872 |
| 1.8 | 0.3221 | 4.8869 | 0.11004 |
| 2.0 | 0.3638 | 6.1685 | 0.12298 |
| 2.2 | 0.4067 | 7.7292 | 0.13783 |
| 2.4 | 0.4511 | 9.6296 | 0.15482 |
| 2.6 | 0.4968 | 11.9427 | 0.17436 |
| 2.8 | 0.5440 | 14.7617 | 0.19680 |
| 3.0 | 0.5926 | 18.1931 | 0.22266 |
| 3.2 | 0.6428 | 22.3716 | 0.25241 |
| 3.4 | 0.6946 | 27.4597 | 0.28672 |
| 3.6 | 0.7480 | 33.6556 | 0.32634 |
| 3.8 | 0.8030 | 41.2004 | 0.37212 |
| 4.0 | 0.8599 | 50.3878 | 0.42498 |
| 4.2 | 0.9185 | 61.5752 | 0.48532 |
| 4.4 | 0.9789 | 75.1984 | 0.55714 |
| 4.6 | 1.0413 | 91.7873 | 0.63930 |
The numerical values of (eλ1t–1) and (eλ2t–1) are listed in Table 1 and yield the (207Pb/206Pb)* ratios for increasing values of t ranging from t = 0 to t = 4.6 Byr. This table can be used to solve equation (9) for t by linear interpolation based on the (207Pb/206Pb)* ratio calculated from equation (10). Conversely, by determining the (207Pb/206Pb)* ratio in a mineral from measurements of its Pb isotope ratios, the age (t) of the mineral can be calculated by linear interpolation between the (207Pb/206Pb)* ratio values in Table 1. This is known as the 207Pb-206Pb model age.
Although U occurs in a large number of minerals, only a few are suitable for dating by the U-Pb methods. To be useful for dating, a mineral must be retentive with respect to U, Pb, and the intermediate daughters, and it should be widely distributed in a variety of rocks. The minerals that satisfy these conditions include zircon, baddeleyite, monazite, apatite, and sphene (titanite). All of these minerals contain trace amounts of U but low concentrations of Pb, giving them high U/Pb ratios favourable for dating. For example, concentrations of U in zircons range from a few hundred to a few thousand parts per million and average 1350 ppm (Faure and Mensing 2005, 221). The presence of U in zircon is due to the isomorphous substitution within the zircon crystal lattice of U4+ (ionic radius 1.05 Å) for Zr4+ (0.87 Å), although this substitution is limited by the differences in their ionic radii and may well be an exothermic reaction due to the substitution sites having to expand by 20%. However, whereas U4+is admitted into zircon crystals, Pb2+ is regarded as being excluded because of its large ionic radius (1.32 Å) and its low charge (2+). Therefore, zircons are supposed to contain very little initial Pb at their time of formation and have high U/Pb ratios. This appears to enhance their sensitivity as a geochronometer, so zircons have for several decades become increasingly used for dating via the U-Pb methods.
The Wetherill Concordia and Pb-Loss Discordia
The effect of the loss of Pb or U and the gain of U on U-Pb dates of minerals can be compensated by a graphical procedure developed by Ahrens (1955) and Wetherill (1956, 1963). Equations (4) and (5), which govern the time-dependent increase of the 206Pb/204Pb and 207Pb/204Pb ratios of U-bearing minerals or rocks, can be rearranged to yield ratios of radiogenic 206Pb to 238U and of radiogenic 207Pb to 235U:
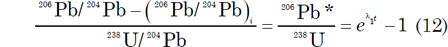
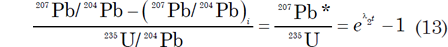
where the asterisk * is used to identify the radiogenic origin of the Pb isotopes. These equations assume that there is no 206Pb or 207Pb present when t = 0. Yet this begs the question as to whether t = 0 at the formation of the earth and solar system, or when the mineral forms and remains a closed system.
The values of eλ1t–1 and eλ2t–1 for different values of t are listed in Table 1 and were used to plot the curve in Fig. 3. The coordinates of all points on this curve are the 206Pb*/238U and 207Pb*/235U ratios that yield concordant U-Pb dates. Therefore, the curve in Fig. 3 is known as the concordia and is associated with its inventor (Wetherill 1956, 1963) in order to distinguish it from a different concordia diagram developed later by others. U-bearing minerals that contain no radiogenic 206Pb* and 207Pb* yield t = 0, while those containing radiogenic 206Pb* and 207Pb* will yield U-Pb ages of 1.0 Byr, 1.5 Byr, and so on, located sequentially along the concordia curve.
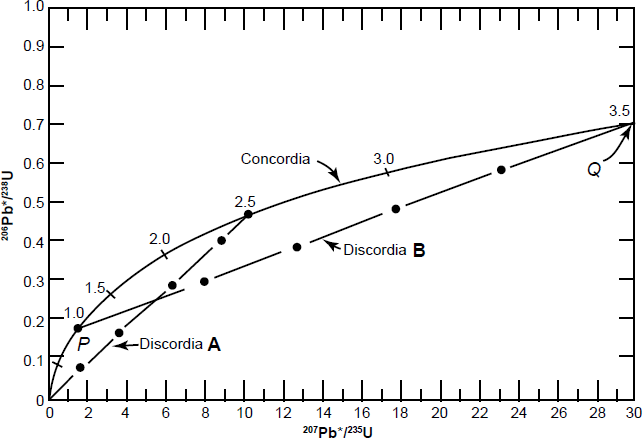
Fig. 3. The concordia diagram used for the interpretation of U-bearing minerals that lost radiogenic Pb and therefore discordant dates, as developed by Wetherill (1956, 1963).
Fig. 3 shows a hypothetical history of zircon grains that originally crystallized from a magma. At the time of crystallization, the zircons contained no radiogenic Pb and so plotted at the origin of the concordia diagram. During the subsequent 2.5 Byr the 206Pb*/238U and 207Pb*/235U ratios of the zircons increased by decay of 238U and 235U causing them to move upwards along the concordia. After 2.5 Byr there was an episode of thermal metamorphism during which some of the zircon grains lost all the radiogenic Pb they had accumulated and they therefore now plot back at the origin (t = 0). Yet it could be equally argued that these zircon grains may have lost more U than radiogenic Pb because U is more mobile. Furthermore, this happening introduces a discontinuity in the equations describing the process and hence could invalidate the application of l’Hôpital’s rule to the original equation. Meanwhile, the other grains lost varying amounts of radiogenic Pb, so they plot on a straight line chord, labelled as discordia A on Fig. 3 because all the zircon grains on this chord would yield discordant U-Pb dates. At the end of this short episode of thermal metamorphism the U in all the zircon grains continued decaying and so the grains resumed accumulating radiogenic Pb. At the present time 1 Byr after the episode of thermal metamorphism, the zircon grains that had previously lost all their radiogenic Pb have moved 1 Byr up along the concordia, while the other grains that had previously lost varying amounts of radiogenic Pb have maintained their linear relationship to one another. The net result is that the zircon grains now plot along discordia B in Fig. 3, extending from 1 Byr (the time elapsed since the thermal metamorphism) to 3.5 Byr (2.5 Byr + 1 Byr). Thus at 1 Byr after the episode of thermal metamorphism (which occurred at 2.5 Byr after the crystals formed) the zircon grains that previously defined discordia A now form discordia B, which intersects the concordia at two points, labelled P and Q in Fig. 3. The coordinates of point Q represent concordant U-Pb dates of 3.5 Byr which represents the time elapsed since the original crystallization of the zircon grains that now define discordia B.
Furthermore, the coordinates of point P yield concordant U-Pb dates of 1 Byr, but the interpretation of that date depends on the circumstances. If the loss of radiogenic Pb did occur during the short episode of thermal metamorphism, then the date of 1 Byr at point P is the time elapsed since that episode. This is called episodic loss of radiogenic Pb from the zircon grains. At the same time the thermal metamorphism should have caused loss of radiogenic 40Ar from other minerals in the same rock, which should thus yield a K-Ar date also of 1 Byr. Alternatively, radiogenic Pb loss may have occurred by continuous diffusion at elevated temperature. In that case, the trajectory of the U-Pb system in the zircons would follow a straight line that became non-linear near the origin (t= 0). As a result, linear extrapolation of discordias would yield a lower intercept with concordia that corresponds to a fictitious date. Therefore, the date calculated for the lower intercept point P of discordia B in Fig. 3 must be confirmed by a K-Ar date for another mineral in the same rock before it can be interpreted as the age of an episode of thermal metamorphism.
Thus the concordia diagram can indicate the U-bearing minerals that plot on a discordia line were altered. As well as loss of radiogenic Pb from a mineral, a discordia may represent a gain or loss of parent U. However, on this concordia diagram the gain of Pb by the mineral is not predictable unless the isotopic composition of the new Pb can be specified. The concordia model also includes a further constraint that the Pb loss must occur without discrimination between the Pb isotopes on the basis of their masses (that is, fractionation). Thus it has been shown by Faure and Mensing (2005) how both Pb loss and U gain will cause a mineral’s grains to plot along a discordia below the date of their original formation and yield younger discordant U-Pb dates. On the other hand, a loss of U from the mineral will cause its grains to plot along that same discordia above the date of their original formation and yield older discordant U-Pb dates.
The Tera-Wasserburg Concordia
The U-Pb dates of some lunar rocks were found to be significantly older than the Rb-Sr and K-Ar dates yielded by the same rocks (Tatsumoto and Rosholt 1970, compared with Tera and Wasserburg 1972, 1973). For example, a lunar basalt yielded 238U-206Pb and 235U-207Pb model ages of 4.24 Byr and 4.27 Byr respectively compared to Rb-Sr and K-Ar dates of only 3.88 Byr (Tera and Wasserburg 1972). The postulated reason for this discrepancy is that these lunar rocks contain excess radiogenic 206Pb and 207Pb that was incorporated into these lunar basalts at the time of crystallization, but no explanation is given as to where this excess radiogenic Pb came from. Tera and Wasserburg (1972) therefore devised a new concordia that does not require prior knowledge of the initial 206Pb/204Pb and 207Pb/204Pb ratios.
The number of 206Pb and 207Pb atoms in a unit weight of U-bearing rocks or minerals can be expressed by the equations:
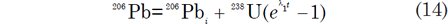
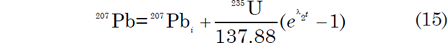
where 206Pbi and 207Pb i are the initial 206Pb and 207Pb respectively. Tera and Wasserburg (1972) used these equations to define a concordia in parametric form where the x-coordinate is derived from equation (14) as follows:
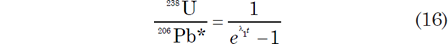
and the y-coordinate is obtained by combining equations (14) and (15) as follows:
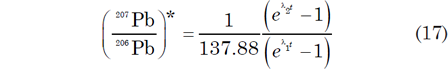
The concordia is constructed by solving equation (16) (x-coordinate) and equation (17) (y-coordinate) for selected values of t. However, in order to plot two such parameters against each other, a postulated relation must exist between them. Thus, it could be questioned as to whether these two parameters are actually in a linear relationship to begin with. Nevertheless, the results are listed in Table 2. The resulting graph in Fig. 4 is the locus of all points representing U-Pb systems that yield concordant dates.
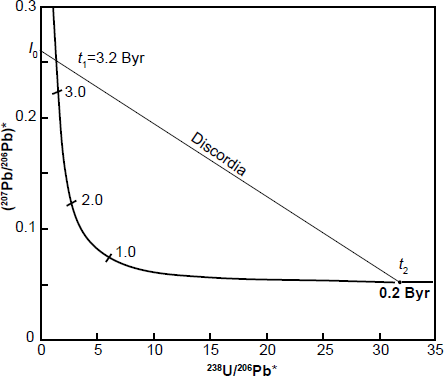
Fig. 4. The Tera-Wasserburg concordia based on equation (16) (x-coordinate) and equation (17) (y-coordinate) plotted from values in Table 2, assuming that ƛ1(238U) = 1.55125 × 10-10 yr-1, ƛ2 (235U) = 9.8485 × 10-10 yr-1, and 238U/235U = 137.88 (after Faure and Mensing 2005).
| t, Ga | x | y |
|---|---|---|
| 0.2 | 31.746 | 0.05012 |
| 0.4 | 15.625 | 0.05575 |
| 0.6 | 10.256 | 0.05992 |
| 0.8 | 7.570 | 0.06581 |
| 1.0 | 5.959 | 0.0725 |
| 1.2 | 4.887 | 0.0801 |
| 1.4 | 4.122 | 0.0887 |
| 1.6 | 3.549 | 0.0987 |
| 1.8 | 3.104 | 0.1100 |
| 2.0 | 2.748 | 0.1229 |
| 2.2 | 2.458 | 0.1378 |
| 2.4 | 2.216 | 0.1548 |
| 2.6 | 2.012 | 0.1743 |
| 2.8 | 1.838 | 0.1968 |
| 3.0 | 1.687 | 0.2226 |
| 3.2 | 1.555 | 0.2524 |
| 3.4 | 1.439 | 0.2867 |
| 3.6 | 1.336 | 0.3263 |
| 3.8 | 1.245 | 0.3721 |
| 4.0 | 1.162 | 0.4249 |
| 4.2 | 1.088 | 0.4862 |
| 4.4 | 1.021 | 0.5571 |
| 4.6 | 0.9603 | 0.6393 |
The discordia line in Fig. 4 intersects the Tera-Wasserburg concordia at two points corresponding to dates t1 (3.2 Byr) and t2 (0.2 Byr). Extrapolation of this discordia line beyond t1 yields an intersection point I0 on the y-axis where 238U/206Pb* = 0. Obviously, this means that the 206Pb* concentration must be non-zero when there is no 238U, and calculating the relevant values infers that the 206Pb* is approximately four times larger than the 207Pb* concentration. In any case, the numerical value of I0 is the radiogenic 207Pb/206Pb ratio that formed in the interval of time between t1 and t2 (Tera and Wasserburg 1974) as follows:
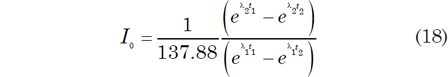
where λ1 and λ2 are the decay constants of 238U and 235U respectively, and t1 and t2 are the upper and lower intersections with the discordia as depicted in Fig. 4.
The U-Pb system whose postulated geological history is depicted in Fig. 4 originally contained no radiogenic Pb, that is, 238U/206Pb* = ∞ when it formed at t1 = 3.2 Byr. Subsequently, radiogenic 207Pb and 206Pb accumulated by decay of 235U and 238U respectively until the system apparently recrystallized or differentiated at t2 = 0.2 Byr. The radiogenic 207Pb/206Pb ratio of the Pb that had accumulated from t1 = 3.2 Byr to t2 = 0.2 Byr is equal to I0 in Fig. 4 and is expressed by equation (18). If the U-free mineral (for example, plagioclase) formed during the recrystallization event at t2, it would contain Pb whose radiogenic 207Pb/206Pb ratio is equal to I0.
The postulated U-bearing system represented by t2 on the Tera-Wasserburg concordia in Fig. 4 was apparently Pb-free at the end of the metamorphic event (that is, 238U/206Pb* = ∞). All the Pb it contains at the present time apparently formed by decay of the U isotopes after the end of the recrystallization event at t2 = 0.2 Byr. This interpretation implies that both t1 and t2 are valid dates in the geological history of a volume of U-bearing rocks. Keep in mind that t1 and t2 are obtained as result of where the discordia plotted on the Tera-Wasserburg diagram from the U and Pb isotope analyses of the rock unit being investigated intersects the Tera-Wasserburg concordia, as depicted in Fig. 4.
Alternately, the radiogenic 207Pb/206Pb ratio represented by I0 may be the result of a complex process unrelated to the U-Pb system that recrystallized at t2. In that case, the discordia is the locus of U-Pb systems that formed by mixing of two components. One of the components is I0 and the other component is the U-Pb system represented by the point of intersection at t2 in Fig. 4. In that case, the date derived from the coordinates of point t1 has no geological significance (Tera and Wasserburg 1974).
A follow-on example illustrates how the Tera-Wasserburg concordia diagram has been utilized to obtain a corrected age for a rock with discordant U-Pb model ages. One of the rock samples obtained by the Apollo 14 mission from the Fra Mauro region of the moon was lunar basalt 14053. This sample yielded highly discordant and improbable whole-rock U-Pb model ages of 5.60 Byr (238U-206Pb), 5.18 Byr (235U-207Pb), and 5.01 Byr (207Pb/206Pb), corrected for the postulated presence of primeval Pb which the moon supposedly inherited from the solar nebula (Tera and Wasserburg 1972). The same sample had yielded an internal (mineral and whole-rock) Rb-Sr isochron date of 3.88 ± 0.04 Byr (Papanastassiou and Wasserburg 1971). Furthermore, the same sample had been dated by Turner et al. (1971) by the 40Ar*/39Ar method applied to both the whole-rock and plagioclase. The partial-release spectra indicated well-defined plateau dates of 3.95 Byr (whole rock) and 3.93 Byr (plagioclase), using then current recommended decay constants.
The U-Pb data reported by Tera and Wasserburg (1972) for lunar basalt 14053 define a discordia line that intersects the y-axis (238U/206Pb* = 0) at (207Pb/206Pb)* = 1.46, as depicted in Fig. 5. The slope of the discordia line is –0.88366 based on an unweighted linear regression of three data points representing two whole-rock and one magnetite (the magnetic fraction) analyses. The slope m of the discordia is related to the initial (207Pb/206Pb)* ratio and to the age of the U-Pb system by the equation:
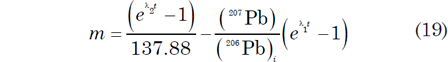
This equation was solved graphically by Tera and Wasserburg (1972) for (207Pb/206Pb) i = 1.46 for values of t between 3.87 and 4.00 Byr. Their graph indicates that a slope of –0.88366 corresponds to a date of 3.91 Byr, which represents the intersection point of the discordia with the Tera-Wasserburg concordia in Fig. 5. A more accurate date could be obtained by interpolating in a table values of the slope for selected values of t or by numerical iteration.
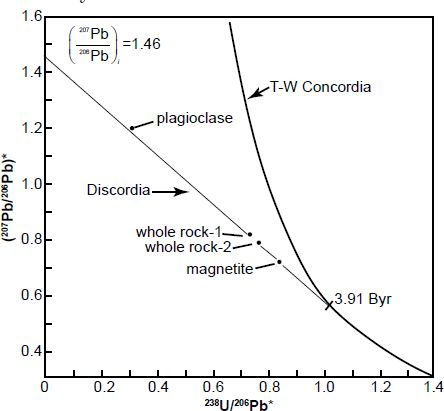
Fig. 5. Tera-Wasserburg concordia diagram for U-Pb data of lunar basalt 14053 (after Tera and Wasserburg 1972). The slope of the discordia line is m = –0.88366 and the intercept on the y-axis for 238U/206Pb = 0 is 1.46. The date that corresponds to the intersection point of the discordia with the Tera-Wasserburg concordia was determined graphically from equation (19).
This interpretation of the U-Pb data for lunar basalt 14053 by means of the Tera-Wasserburg concordia yielded a date that is in good agreement with the Rb-Sr and 40Ar*/39Ar dates for this same rock. The essential feature of this concordia is that it permits an explicit determination of the radiogenic 207Pb/206Pb ratio at 238U/206Pb* = 0 without requiring an estimate of the initial isotope ratios of Pb at the time of crystallization of the basalt.
Pb-Pb Isochron Dating
Equations (4) and (5) above describe the accumulation of the radiogenic 206Pb and 207Pb from 238U and 235U respectively. The same equations can be used with multiple samples to plot independent isochrons. The slopes of the 238U-206Pb and 235U-207Pb isochrons yield dates that are concordant only when the samples remained closed to Pb diffusion and had identical initial Pb isotopic ratios. However, in most cases, U-Pb isochrons based on whole-rock samples have not been successful, primarily because rocks which are exposed to chemical weathering lose a significant fraction of U. Thus the U-Pb isochron method of dating igneous and metamorphic rocks composed of silicate minerals does not work in most cases because of the variable losses of U by chemical weathering, which occurs not only at the earth’s surface, but also in the subsurface where rocks are in contact with oxygenated groundwater.
On the other hand, igneous and metamorphic rocks that have lost U by recent chemical weathering may also have lost Pb. However, the isotopic ratios of the remaining Pb may not have changed if the isotopes of Pb were not fractionated. In other words, the isotope ratios of Pb in the weathered rocks are not changed if the Pb that was lost had the same isotope composition as the Pb that was present before the loss occurred. If chemical behavior is the only consideration, then perhaps this assumption could be justified; however, there are other factors such as any movement of the various Pb isotopes within the material matrix containing the Pb isotopes. Nevertheless, it is maintained that a date can be calculated based on the slope of the Pb-Pb isochron obtained from samples of even weathered rocks.
The equation for Pb-Pb isochrons is derived from combining equations (4) and (5) above to yield equation (10) above, which expresses the ratio of radiogenic 207Pb to 206Pb and then yields equation (9) above:
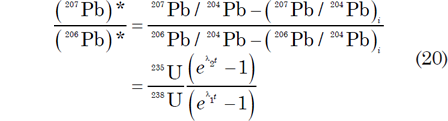
This is the equation for a straight line in coordinates of 206Pb/204Pb (x) and 207Pb/204Pb (y) whose slope m is
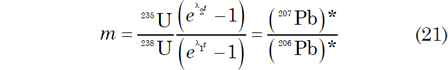
Age determinations by this Pb-Pb isochron method depend on the assumptions that all the samples that define the isochron (Faure and Mensing 2005, 241):
- Had the same initial Pb isotope ratios;
- Formed at the same time; and
- Remained closed to U and Pb until the recent past, when they were exposed to chemical weathering.
In addition, the 238U/204Pb and 235U/204Pb ratios of the samples must have sufficient variation to allow Pb having different isotope ratios to form within them. The slope of Pb-Pb isochrons can be used for dating by solving equation (21) for t by interpolating within Table 1. Alternately, equation (21) can be solved by iteration on a computer to any desired level of precision.
The Pb-Pb isochron method has been used very widely for dating igneous and metamorphic rocks, especially those of Precambrian age, as well as meteorites. The method is claimed to yield the time elapsed since the isotopic homogenization of Pb and subsequent closure of rocks to U and its intermediate daughters. However, this ignores the known measurable leakage of the intermediate daughter Rn gas, which thus reduces the amount of in situ final 206Pb and 207Pb. Furthermore, this Pb-Pb isochron method also ignores the demonstrable fact that what are interpreted as isochron lines may instead be mixing lines between two end-member Pb isotope compositions, and there is no known way to definitively tell the difference between an isochron and a mixing line.
The several assumptions involved in the various U-Pb and Pb-Pb model and isochron dating methods have a somewhat tenuous validity, because they are based on an unknown and unconfirmed uniformitarian evolutionary past history. Yet in spite of that, all these methods depend on the U-Pb system within the minerals and rocks being dated being closed to loss from within and to contamination from without. That condition might seem to be easily resolved if the multiple ages derived by these methods all agree (are concordant), but even then there is no guarantee loss and/or contamination has not occurred. So we need to look more closely at these issues.
Recognition of the Problem of Pb Loss
As noted earlier, two potential problems which cause possible inaccuracies in obtaining reliable U-Pb and Pb-Pb ages were listed by Amelin et al. (2009). They are “deviations from closed system evolution (gain or loss of U, loss of intermediate daughters such as the inert gas Rn, and loss of Pb),” and “misidentification of the processes that start and reset isotopic clocks.” Amelin et al. (2009) assessed these two problems as being “important and common.” Of the closed system problem, they commented that it “requires monitoring of U-Pb concordance and studying distribution of U and radiogenic Pb.” Similarly, they commented regarding the processes which start and reset isotopic clocks that it “requires studying distribution of U and radiogenic Pb” and “for element migration caused by diffusion, alteration and shock.” Furthermore, they admitted that the “significance of some potential problems cannot be estimated at the present level of knowledge,” and thus they require “detailed and theoretical studies.”
An additional problem related to “deviations from closed system evolution” that Amelin et al. (2009) assessed as “insignificant” is “deviations from the 234U/238U ratio from secular equilibrium.” To be fair, Amelin et al. (2009) made that assessment in the context of the radioisotope dating of meteorites and their components. And yet, Amelin and Zaitsev (2002) in their radioisotope dating study of minerals from phoscorites and carbonatites from the Kola Peninsula of Russia had warned of the “geochronological pitfalls of initial radioactive disequilibrium” and “differential migration of isotopes.”
The concordia diagram developed by Wetherill (1956) has been widely used by geochronologists to interpret discordant U-Pb ages where Pb appears to have been lost. However, Tilton (1960) offered an alternative explanation for the loss of radiogenic Pb based on continuous diffusion of Pb from crystals at a rate governed by the mineral’s diffusion coefficient, the effective radius of diffusion of the crystals, and the concentration gradient of Pb in them. He assumed that U is uniformly distributed throughout the crystals, that diffusion of U and its intermediate daughters is negligible compared to that of Pb, that the diffusion coefficient is constant independent of time, and that diffusion is governed by Fick’s law. The solutions of Tilton’s diffusion equation generate curves on the concordia diagram which are the loci of points that represent U-Pb systems of specific ages that have suffered continuous Pb loss by diffusion.
Thus Tilton (1960) demonstrated that a linear array of data points representing discordant U-Pb systems on a concordia diagram can be interpreted in two fundamentally different ways. If Pb loss was due to an episode of metamorphism, then the U-Pb date calculated from the lower intercept point on the concordia apparently indicates the time of closure after the Pb loss. On the other hand, if the Pb was lost continuously by diffusion, then the U-Pb date calculated from the lower intercept point would be fictitious. The problem is that both episodic and continuous Pb loss results in daughter-parent ratios that appear to fit a straight-line discordia. This is why the U-Pb date derived from the lower intercept of the discordia with concordia must be confirmed by K-Ar or Rb-Sr dates of other minerals in the same rock before it can be accepted as the time elapsed since cooling after an episode of metamorphism. This Pb loss by continuous diffusion model implicitly assumes the temperature has remained constant throughout the history of the mineral grains (for example, zircon) and thus the diffusion coefficient and the effective radius are invariant with time. The general case in which the diffusion coefficient is a function of time and both Pb and U diffused was subsequently considered by Wasserburg (1963) and Wetherill (1963).
Yet another alternative interpretation of the discordance of U-Pb dates for U-bearing minerals was proposed by Goldich and Mudrey (1972). Minerals such as zircon suffer radiation damage as a result of the kinetic energy of the α-particles ejected by α-decay of U, Th, and daughter atoms. The extent of that radiation damage increases with age and with the U and Th concentrations in the minerals. The apparent relationship between the radioactivity of zircons and the discordance of their U-Pb dates was first demonstrated by Silver and Deutsch (1963), and was used by Wasserburg (1963), who related the diffusion parameter D/a2 to the radiation damage of zircon crystals. Goldich and Mudrey (1972) thus postulated that radiation damage causes the formation of microcapillary channels which permit water to enter the crystals. They argued that this water is tightly held until uplift and erosion cause the pressure on the minerals to be released. The resulting dilatance of the zircons allows the water to escape together with dissolved radiogenic Pb. Consequently, the loss of radiogenic Pb from zircon crystals in the crystalline basement complexes of Precambrian shields may be related to the uplift and erosion of those complexes. Such relatively recent Pb loss is consistent with the observation that the 207Pb-206Pb dates commonly approach the conventional true age of the U-bearing minerals (Faure and Mensing 2005).
This dilatancy model therefore appeared to provide a rational explanation for the observation emphasized by Tilton (1960) that U-bearing minerals, particularly zircons, from different continents all seem to have lost radiogenic Pb supposedly 500–600 million years ago, even though no worldwide metamorphic event is recognized by secularists in that period of their version of the earth’s history. Yet according the dilatancy model, the 500–600 million-year date corresponding to the lower intercept of the discordia based on apparent cogenetic suites of U-bearing minerals from a particular region on Tilton’s (1960) concordia plot indicates the time of uplift and erosion of that region.
The rocks and minerals used for U-Pb dating are usually collected from surface outcrops where they have been exposed to chemical weathering. Therefore, the discordance of model U-Pb ages may also be due to disturbances of the daughter-to-parent ratios caused by chemical weathering. This was confirmed as a problem by Stern, Goldich, and Newell (1966) who U-Pb dated zircons removed from residual clay formed by weathering of the Morton Gneiss in Minnesota. Model U-Pb dates of three weathered zircon crystals were found to be grossly discordant, whereas the 207Pb-206Pb dates were the oldest dates in all cases and approached the conventional known original age of these zircons. The weathered zircons plotted on a straight-line that started from a discordia and projected to the origin. Thus the displacement of those weathered zircons from their original position on the discordia indicated that they had lost up to 85% of their radiogenic Pb as a result of the ongoing chemical weathering.
The Problem of Inherited and Discordant Age Zircons
Another significant problem for zircon U-Pb dating is that zircon crystals in some metamorphic and granitic rocks yield much older ages than the accepted ages of the rocks. During episodes of crustal anatexis, radiogenic isotopes and other trace elements contained within the mineral phases comprising the source rock are redistributed. Dependent upon the extent of melting and homogenization, the geochronologic (radiogenic daughter isotopes 206Pb, 207Pb, 208Pb, 143Nd, 147Hf) and geochemical (for example, REEs) information contained within these mineral phases may be perturbed, or in the extreme be completely lost. With specific reference to accessory minerals, this information is lost if the mineral is completely consumed during partial melting, or if diffusion of the element within the restitic fraction of the mineral of interest is sufficiently rapid to allow equilibration on the time scale of the partial melting event. Alternatively, restitic minerals may be transported from the source region by the departing melt fraction, and under some circumstances carry not only information characteristic of the source region, but also information characteristic of the time-temperature history of crustal melting and transport. In metamorphic rocks this has been interpreted as inheritance of those zircon grains from the original sediment sources, the zircons somehow surviving metamorphism without resetting of the U-Pb isotopic system (Froude et al. 1983; Kröner, Jaeckel, and Williams 1994). The older zircons in granitic rocks are likewise interpreted as being inherited from the source rocks that melted to produce the magmas (Chen and Williams 1990; Williams, Compston, and Chappell 1983).
Evidence of inherited U-Pb ages in zircon from Phanerozoic granites is common (Harrison et al. 1987; Muir et al. 1996; Parrish and Tirrul 1989; Pasteels 1970; Pidgeon and Aftalion 1978; Pidgeon and Johnson 1974; Williams 1992), indicating that zircon may not be totally soluble during the formation of some granitic magmas. Experimental measurements of zircon solubility under crustal conditions have confirmed this conclusion (Watson and Harrison 1983). In some published studies the inherited zircons are 5–10 times older than those matching the accepted ages of the granites—for example, up to 1753 Ma in a 21 Ma Himalayan granite (Parrish and Tirrul 1989), up to 3500 Ma in a 426 Ma southeast Australian granodiorite (Williams 1992), and up to 1638 Ma in a 370 Ma New Zealand granite (Muir et al. 1996). Significantly, monazite grains can also yield negative ages, such as –97 Ma in a 20 Ma Himalayan granite that also contains zircons yielding ages up to 1483 Ma (Parrish 1990), a discordancy of almost 7500%.
The literature abounds with evidence for extremely strong retentivity of radiogenic Pb in zircons at high grade temperatures and in melts (for example, Dunn et al. 2005; Pidgeon and Nemchin 2006; Pidgeon et al. 2007). In apparent contradiction to this, examples of severe discordance reflecting more than 50% loss of radiogenic Pb, are also very common. Discordia lower intercepts, in many cases ill-defined, range from zero age to ca. 800 Ma (for example, Dunn et al. 2005; Kröner et al. 1999; Pidgeon and Nemchin 2006). It is noteworthy that in Precambrian zircons from the Canadian Shield, such discordance can mostly be avoided by abrading zircon grains before analysis. Also, secondary ion mass spectrometry (SIMS) data on Canadian Shield or West Greenland Archaean zircons also show little discordance (for example, Bowring and Williams 1999; Nutman et al. 2004). [In the SIMS technique a beam of energetic primary O- ions is focused on the sample surface, where their impact breaks chemical bonds and liberates a mixture of molecules and different (secondary) ions, which are extracted by an electric field and thus introduced to the mass spectrometer for analysis (Reiners et al. 2018, 48–49).] Lunar zircons, even those with high U-contents, do not show discordance beyond the analytical uncertainty limits (Nemchin et al. 2006; Pidgeon et al. 2007). It has thus been suggested that this type of discordance may be caused by groundwater acting on a metamict structure (Black 1987; Mezger and Krogstad 1997; Stern, Goldich and Newell 1966).
Furthermore, if Pb is lost from some mineral grains, then it could be inherited by other crystals in the host rocks subsequent to the formation of those rocks. Thus Ludwig and Silver (1977) found that many K-feldspars in Precambrian rocks contained unsupported or excess radiogenic Pb (that is, no parent isotopes in the mineral), though the composition of the unsupported Pb was compatible with the supposed ages of the host rocks. On the other hand, Williams et al. (1984) found unsupported (excess) radiogenic Pb in a zircon crystal in an Antarctic gneiss, which thus produced anomalously high ages. Similar situations also result in ages hundreds of millions of years more than expected and are interpreted as due to excess radiogenic Pb, the origin of which is either explained as mixing from older source materials which melted to form the magmas, and/or due to subsequent migration as a result of fluids, temperature and pressure (Copeland, Parrish, and Harrison 1988; Zhang and Schärer 1996). This all begs the question—should “anomalously old” zircons be interpreted as inheritance of the zircon crystals, or as due to “excess” radiogenic Pb in the crystals?
Zircon is now the most widely-used mineral in U-Pb geochronology, due to a combination of favorable properties, including high U content (typically hundreds of ppm), assumed lack of initial (or common) Pb, apparent good retention of radiogenic Pb (up to 900°C), and a diversity of geological occurrences (Cherniak and Watson 2000; Corfu 2013; Davis, Williams, and Krogh 2003; Harley, Kelly, and Möller 2007). However, the Achilles’ heel of zircon is the accumulation of radiation damage over time, critically affecting its properties (Ewing et al., 2003). Self-irradiation enhances diffusion, facilitates mineral–fluid interaction, leads to possible reduction of Pb4+ to Pb2+, and more generally results in open system behavior at low temperatures (< 200°C) and discordance between the two decay chains of U, namely, 238U-206Pb and 235U-207Pb (Geisler, Schaltegger, and Tomaschek 2007; Nasdala et al. 2010; Xu et al. 2012). Of course, one way to avoid these problems is simply not to use heavily radiation damaged or metamict zircons for geochronological purposes, but there are many situations where that is not feasible.
Pioneering publications (for example, Silver and Deutsch 1963) established a correlation between U concentration and discordance in zircon. They inferred that episodic Pb loss, rather than U gain, is the most probable cause for discordance and it was promoted by structural radiation damage. Since then, three main reasons for discordance of analyses are commonly cited: loss or redistribution of radiogenic Pb, introduction of common Pb, and mixed sampling of more than one generation of zircon (Corfu 2013). In the literature, papers invoking U-gain to explain discordance are rare. Yet analyzing detrital zircon grains from a quartzite inclusion in pegmatite, Grauert, Seitz, and Soptrajanova (1974) proposed that U penetrated along tiny cracks, during metamorphism without new zircon growth.
Utilizing the SHRIMP (ion microprobe) in situ analytical technique, radiogenic Pb was found by Compston (1997) to vary within most tested zircon grains on a 20 µm spatial scale. Some spots were characterized by huge excess radiogenic Pb, up to 30 times the “expected” values. However, zircon is not the only U-bearing mineral suitable for U-Pb dating using the SHRIMP. Monazite, sphene (titanate), rutile, perovskite, and uraninite are all potential candidates. Baddeleyite was the first mineral to be U-Pb dated using an ion microprobe, but Wingate and Compston (2000) found a flaw—the measured 206Pb/238U values and thus the U-Pb dates varied by up to ± 10% depending on the orientation of the crystals relative to the ion beam. They also tested monazite and zircon, but found no indication that the orientation of those crystals affected the results. Yet the flaw using baddeleyite has not been explained.
Indeed, Wingate and Compston (2000) demonstrated that there were pronounced reproducible differences in radiogenic 206Pb/238U and thus apparent U-Pb ages between four differently oriented faces of a large baddeleyite crystal (fig. 6a), as well as correlated variation in radiogenic 208Pb/206Pb with 232Th/238U for the same four differently oriented faces (fig. 6b). They concluded that the latter effect could be a primary crystal growth feature. In a second experiment, Wingate and Compston (2000) measured the isotopic ratios on the same crystal faces of 47 baddeleyite crystals but at different orientations with respect to the SHRIMP’s beam over a 180° range, the results revealing a striking, approximately sinusoidal, variation in 206Pb/238U apparent ages with orientation (fig. 6c). However, similar significant differences in radiogenic 206Pb/238U or radiogenic 207Pb/206Pb related to orientation were not detected in zircon or monazite crystals (within the analytical statistics), although radiogenic 208Pb/206Pb and 232Th/238U both vary with orientation. These differences in radiogenic 208Pb/206Pb again correlated precisely with those in 232Th/238U, which could be a real compositional variation reflecting zones of anisotropic primary crystal growth.
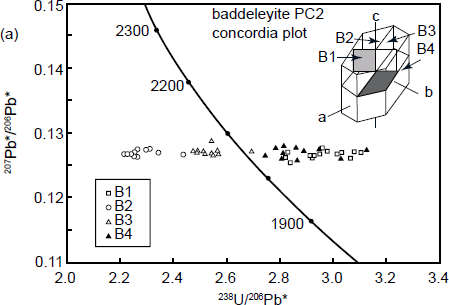
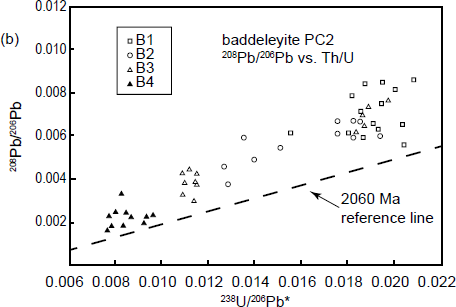
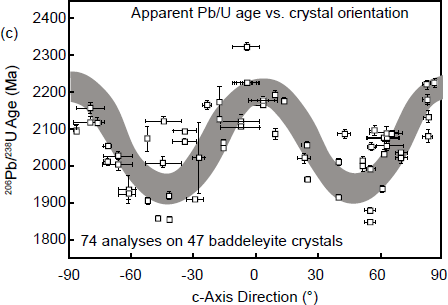
Fig. 6. SHRIMP analytical results for baddeleyite, illustrating observed orientation effects (after Wingate and Compston 2000). (a) A U-Pb evolution (concordia) diagram showing apparent ages for four different oriented surfaces (shown in the inset) of a single large baddeleyite crystal (PC2 from the Phalaborwa carbonatite, South Africa). (b) Correlated variation in total 208Pb/206Pb with 232Th/238U for the same surfaces measured in (a). (c) Variation of apparent 206Pb/238U age with orientation for (100) surfaces of 47 oriented baddeleyite crystals.
Furthermore, the problem of identifying in an igneous rock to be U-Pb dated which zircons were inherited by the magma and which crystallized from the magma is still fraught with difficulties due to the subjectivity of the criteria used. Siégel et al. (2018) have reviewed the techniques available to discriminate zircons crystallized from the magma from inherited zircons and proposed a new methodology to assist in the identification of the zircons crystallized from the magma for emplacement age determinations and a separate evaluation of inherited zircon components. Their approach used two strands of data:
- Zircon data such as zircon morphologies, textures, compositions, and U-Pb ages; and
- Whole-rock data, in particular SiO2 and coupled geothermometry (TZircsat and TMagma) to estimate whether the magma was zircon-saturated or undersaturated.
They tested this protocol using several Phanerozoic granitic rocks where contextual information was limited, and showed how zircons which didn’t crystallize from the granitic magmas could be distinguished. They also realized that where zircons are metamict (for example, high U and Th-rich zircons), much of the ability to discriminate between them is impacted because such zircons have suffered Pb loss and have modified compositions (for example, higher TZircTi). Thus, they recommended an integrated approach incorporating whole-rock chemistry, independent geothermometric constraints, zircon composition, textures, and U-Pb ages obtained by routine cathodoluminescence and LA-ICP-MS or ion microprobe analyses to provide increased confidence for the discrimination of inherited zircons from those zircons which crystallized from the magmas.
The Extent and Cause of Pb Mobility
Davis and Krogh (2000) undertook U and Pb isotopic analyses of HF-washed Archean zircon grains from a trondhjemite (dated at 2732 ± 2 Ma) and a dacite (dated at 2728 ± 1 Ma) and demonstrated that altered domains can be selectively removed by treatment with HF at moderate temperatures. The threshold value of radiation damage for solubility under these conditions is probably slightly in excess of 1.5 × 1015 α-decay events per mg. Residues appeared to contain no alteration but showed evidence of preferential leaching of radiogenic Pb isotopes and 234U from damaged crystal lattice sites.
Davis and Krogh (2000) found that the age of the HF-leached Pb, as calculated from its isotopic composition, was younger than the apparent crystallization age of the sample, resulting in anomalously old Pb in the residue fractions. They argued that this was likely to be due to the annealing of early radiation damage in the zircons. Their most plausible explanation for this was early burial and residence at temperatures above the long-term annealing point, followed by differential uplift and cooling. The supposed times when radiation damage began to accumulate were calculated at 2500 ± 20 Ma for the trondhjemite and 2295 ± 35 Ma for the dacite. Comparisons with temperatures of regional metamorphism and similar Ar-Ar uplift ages on biotite from nearby terrains suggested that the temperature for annealing of α-recoil damage is about 250–300°C.
Davis and Krogh (2000) also found that the two rock samples showed different relative proportions of leachability for accessible radiogenic Pb and 234U, but the average of the two was close to 1. This supported their suggestion that the leachability of different radiogenic isotopes from zircon is not significantly affected by the number of α-recoil events in the preceding decay chain.
The results of these experiments indicated to Davis and Krogh (2000) that leaching of radiogenic atoms from α-recoil-damaged sites in otherwise non-metamict and insoluble crystal domains is an important process during HF washing of Archean zircon grains as a pre-treatment to U-Pb analyses. There was also a suggestion that nitric acid leaches radiogenic atoms to a much lesser degree. These data combined with previous results of theirs using brines implied to Davis and Krogh (2000) that ancient geological leaching may be an important cause of discordance. They concluded that the typical Archean zircon grain population probably contains altered, leachable, and non-leachable domains, which must be considered in trying to interpret natural discordance due to low temperature processes, as well as in laboratory leaching experiments.
Furthermore, Davis and Krogh (2000) concluded that 234U and radiogenic Pb in damaged lattice sites are leachable to roughly the same extent. This conclusion, combined with the observation of significant 234U anomalies in groundwater and the oceans, seemed to imply that preferential leaching of radiogenic Pb must occur from zircon and other minerals in the natural environment. This in turn suggested that dissolved Pb in near-surface environments is biased toward 206Pb enrichment, especially in relatively recently metamorphosed or uplifted terrains. Such an enrichment mechanism may thus have implications for the interpretation of high 206Pb/204Pb lead in groundwater-precipitated ore deposits and perhaps for other aspects of the Pb cycle. Finally, Davis and Krogh (2000) maintained that their experiments, as well as those conducted by many others, demonstrated that leachability is a function of radiation dose level.
Geisler et al. (2002) reported the results of an investigation of the stability of partially metamict zircon in leaching experiments at 175°C with 2 M AlCl3 and 1 M HCl–CaCl2 solutions as hydrothermal fluids for 1340 hours (almost 56 days). Cathodoluminescence (CL) and backscattered electron (BSE) images showed that the zircon grains had developed either a reaction rim several micrometers thick, or deeply penetrating reticulated alteration zones with sharp boundaries to unaltered metamict zircon. Those zones had experienced severe loss of Si, U, Th, and Pb, and gain of Al or Ca, and a water species as revealed by electron microprobe, sensitive high-resolution ion microprobe (SHRIMP) analyses, and infrared spectroscopy. Micro-Raman and infrared measurements on the altered areas showed that disordered crystalline remnants of the partially metamict zircon structure were partially recovered, whereas recrystallization of the embedding amorphous phase was not observed. No detectable structural or chemical changes were found inside the unaltered areas. Intensive fracturing, which was most intense in the HCl–CaCl2 experiment, occurred inside the altered areas due to the volume reduction associated with the recovery of the disordered crystalline material, and probably with the leaching reactions.
Geisler et al. (2002) explained the formation of the deep penetrating alteration zones by a percolation-type diffusion model. That model assumes the existence of percolating interfaces or areas of low atomic density between crystalline and amorphous regions, as well as between amorphous domains, along which fast chemical transport is possible. The idea of the existence of these fast diffusion interfaces is supported by the sharp chemical gradients at the margins to unreacted zircon. This model was used to estimate for the first-time coefficients for U, Th, and Pb diffusion in amorphous zircon at 175°C by assuming that volume diffusion inside the amorphous domains is the loss-rate-limiting process. Their estimates showed that volume diffusion in metamict zircon can cause significant loss of U and Th, and especially loss of radiogenic Pb over presumed geological time scales, even at temperatures as low as 175°C. Their results showed that recent Pb loss discordias can be generated:
- By predominate Pb loss from metamict zircon through volume diffusion at low temperatures where thermal healing of the structure is insignificant; and
- By leaching of Pb (and U and Th) from metamict zircon by an external fluid.
Thus, it has been shown that the fast transport of chemical species from and into the metamict network can be well explained by the microstructure of a partially metamict zircon, that is, by the existence of percolating domain boundaries or areas of low atomic density, which act as fast diffusion pathways. According to the percolation-type model for diffusion proposed by Geisler et al. (2002), the effective diffusion of any species within the zircon lattice should vary with the α-decay dose, that is, the degree of metamictization. This model provided for the first time a physical explanation for the relationship between the degree of metamictization and age discordance as observed by SHRIMP and Micro-Raman measurements (Nasdala et al. 1998), and more generally for the correlation between the U content and age discordance in zircon often reported in U-Pb zircon studies (for example, Silver and Deutsch 1963). In addition, the stability of U and the higher degree of structural recovery observed in hydrothermal experiments, which were performed at higher temperatures (Geisler et al. 2001b), indicated that the dynamics of structural rearrangements of metamict zircon during fluid-zircon interaction play an important role in controlling the leaching process, and especially the loss of U and Th. The difference of the kinetics of rim formation in both experiments is evidence that the leaching kinetics (that is, rim formation) is not only controlled by structural properties, but also by the composition and the pH of the solution. All this only emphasizes the need to avoid metamict zircons for radioisotope dating of rocks if at all possible.
Although both solutions have no direct natural analogs and thus the experimental results of Geisler et al. (2002) cannot be directly transferred to natural conditions, they suggested that within presumed geological timescales, leaching of metamict zircon through natural waters can be significant even at temperatures below 200°C, as indicated by studies on natural zircons (for example, Högdahl, Gromet, and Broman 2001; Lumpkin 2001). This is further supported by reports of natural Ca- and Al-rich metamict zircons (for example, Geisler and Schleicher 2000; Speer 1980), some of which unambiguously have not suffered any high temperature metamorphic imprint (Geisler and Schleicher 2000). The results of Geisler et al. (2002) also suggested that volume diffusion of Pb in metamict zircon must be taken into account seriously as a possibility when interpreting recent Pb loss discordias, although a fluid is much more effective in resetting or disturbing the isotopic system of a metamict zircon.
Bowring and Schmitz (2003) reported that zircon analyses which are apparently too young and/or exhibit discordance attributable to Pb loss are also common in the study of volcanic ash beds. Such Pb loss had been inferred from large data sets obtained by both conventional and ion-microprobe analyses (for example, Compston 2000a, b), indicating the various spatial scales of the phenomenon. Experimental measurements of Pb diffusivity in zircon also indicate that Pb loss is not likely dominated by volume diffusion through crystalline zircon (Cherniak and Watson 2000; Lee, Williams, and Ellis 1997), but rather is related to loss from radiation-damaged domains through crystal defects and fractures. While the selection of the best quality, diamagnetic zircons for analyses and the aggressive abrasion of their outer portions would seem to minimize the effects of Pb loss, it is still a problem that can be difficult to recognize without a large number of analyses. Discordance of analyses is obviously the best indicator of Pb loss, but unfortunately, for Late Paleozoic and younger zircons the limited curvature of concordia combined with the imprecision in the measured 207Pb-235U dates can limit the discernment of discordance as an obvious signal of Pb loss.
Another problem is the apparently systematic analytical bias encountered in the application of laser ablation inductively-coupled-plasma mass spectrometry (LA-ICP-MS) to young (<100 Ma) zircons. Sliwinski et al. (2017) noted that where the majority of studied units are young, the LA-ICP-MS zircon U-Pb dates are often discordant with established 40Ar-39Ar eruption ages or high-precision ID-TIMS U-Pb crystallization ages. They argued that the zircon lattice properties, particularly the degree of lattice damage caused by the radioactive decay of U and Th, impart analytical bias by causing differential ablation rates and therefore differential fractionation of U and Pb throughout each analysis. They suggested that although it is possible to normalize the zircon lattice strengths to calibration reference zircons by thermal annealing to some extent, this may not entirely alleviate the problem. Therefore, Sliwinski et al. (2017) examined the effects of α-decay dose (that is, the degree of radiation damage) on analytical biases in age determination by analyzing a number of zircon reference materials under well-constrained analytical parameters. They demonstrated that a regression based, multi-standard correction method improved the accuracy of age data, particularly in young (Cenozoic) zircons. They also introduced a novel data reduction scheme which runs in conjunction with a widely-used platform and performs a correction for α-dose and Th disequilibrium. They found that their scheme improved the accuracy of presumed age data for unannealed zircons, and demonstrated its utility by applying it to zircons from several well-studied units.
Yet another problem is reversed discordance, that is, Pb is gained rather than lost, or U-Pb ages are greater than 207Pb-206Pb ages. (This is further discussed below in the section “Atomic Scale Studies of Diffusion of Pb and U.”) Kusiak et al. (2013) reported that in some well-documented cases (for example, Williams et al. 1984), zircon data are reversely discordant, with U-Pb ages older than 207Pb-206Pb ages. They interpreted this as corresponding to apparent “Pb gain” because strongly lattice-bound U is unlikely to be mobilized. A sub-class of reverse discordance in SIMS analyses, in which Pb/U ratios increase at constant 207Pb/206Pb ratio, is readily detected by horizontal arrays on the inverse (Tera-Wasserburg) concordia diagram (fig. 4) and is attributed to matrix-related ion yield effects in high-U and/ or metamict zircon (for example, White and Ireland 2012; Williams and Hergt 2000). More difficult to explain are cases of reverse discordance in which data points extend along a discordia line with correlated Pb/U and 207Pb/206Pb ratios opposite to the common Pb-loss discordia, as noted for example in SIMS studies of early Archean zircon from Mount Sones in Antarctica (Black, Williams, and Compston 1986; Williams et al. 1984). Such arrays define apparent “Pb gain,” which, in principle, can be explained by ancient redistribution of radiogenic Pb that locally “locks in” higher 207Pb/206Pb and Pb/U ratios than would be expected from the true age and U content (Hinton and Long 1979). Typically, analyses on these arrays are characterized by within-run fluctuations in the secondary Pb ion signal that are independent of the U and Th ion signals (for example, Kelly, Clarke, and Fanning 2004; Williams et al. 1984), indicating Pb heterogeneity on a scale much smaller than a typical SIMS analytical volume.
A number of mechanisms have been proposed to account for this behavior, including localized intra-grain accumulations of radiogenic Pb (Carson et al. 2002), radon migration through radiation damage (Suzuki 1987), U loss (the corollary of Pb gain) via 234U ejection from porous zircon (Romer 2003), or a sputtering effect due to Pb concentration in a silica glass phase in annealed zircon grains (McLaren, FitzGerald, and Williams 1994). Regardless of the precise mechanism, the documentation of reverse discordance and apparent Pb gain, primarily from high-spatial resolution studies, provides a clue to the scale of the process, as it must be small enough to escape detection in relatively high-sample-volume conventional methods of analysis but sufficiently large that heterogeneities will be manifest at the ~15–25 μm scale of a typical SIMS analysis.
Finally, zircon crystals in high-grade metamorphic rocks and igneous rocks of granitic composition, in some cases, contain cores (that are conventionally interpreted as xenocrystic) surrounded by zones of overgrowths which formed later during regional metamorphism or during crystallization of the magmas (Bickford et al. 1981; Silver and Deutsch 1963). Nasdala et al. (1999) reported that overgrowths of zircons in monzonites yielded concordant U-Pb dates which agreed with 40Ar-39Ar dates of amphiboles in the metamorphic rocks hosting those intrusions, whereas the U-Pb dates of the cores ranged from slightly discordant (low U and Th) to highly discordant (high U and Th) and indicated a Proterozoic age. It was concluded that the relationship between the discordance of the U-Pb isotope systematics of the cores and their U and Th concentrations was caused by radiation damage of the crystal lattices, which increases the diffusion rate of radiogenic Pb in zircon. Cherniak and Watson (2000) confirmed that the diffusion coefficient of Pb in zircon is very small, but increases with increasing radiation damage. Therefore, the U-Pb chronometers deviate from concordia depending on the extent of radiation damage. The low diffusion rate of Pb in undamaged zircon overgrowths evidently causes their U-Pb dates to be concordant and gives such zircons a closure temperature in excess of 900°C.
The Impact of Radiation Damage
Even though zircon has proved to be by far the most useful mineral for U-Pb geochronology because it is mechanically and chemically inert, and has one of the highest known blocking temperatures, significant Pb loss from it is common in low temperature environments. The blocking temperature is defined as the temperature at which the loss of Pb by diffusion out of the zircon becomes negligible compared to its rate of accumulation (Faure and Mensing 2005, 82). For zircon it is >1000°C (Flowers et al. 2005). This Pb loss is often correlated with accumulated radiation damage, which of course is related to U concentration. Physical property changes in damaged zircon were well documented by Holland and Gottfried (1955) and expanded on by Murakami et al. (1991).
Holland and Gottfried (1955) and Murakami et al. (1991) distinguished three stages of damage accumulation in zircon:
- A pre-metamict Stage I (<3 × 1015 α-decay events per mg);
- Stage II (3–8 × 1015 α-decay events per mg) during which crystal structure gradually becomes aperiodic and significant physical changes occur, such as reduction in density and refractive index; and
- Stage III (>8 × 1015 α-decay events per mg) in which the structure becomes entirely aperiodic.
Metamict zircons exhibit a 17% volume expansion, a decrease in refractive index and luster, a darkening of color, and an increasing susceptibility to chemical alteration and dissolution. Where zircons are highly zoned in U, volume changes produce cracks in adjacent less-damaged zones that are perpendicular to growth surfaces (Chakoumakos et al. 1987). Metamict zircon is susceptible to chemical alteration by fluids that can penetrate into the crystal along such fractures and preferentially remove radiogenic Pb (Krogh and Davis 1974, 1975).
Early work by Silver and Deutsch (1963) demonstrated that zircons with the lowest paramagnetic susceptibility (and U level) are the least discordant. Coupled substitution by REEs can potentially explain the correlation between U level and paramagnetism. Krogh (1982a) showed that altered domains tend to be higher in U and more paramagnetic, resulting in a correlation between Pb loss and magnetic susceptibility. Analyses of variably magnetic zircon grains commonly produce linear to quasi-linear arrays of discordant data. Upper concordia intercepts are usually close to the presumed ages of crystallization defined by concordant data from high quality zircons. On the other hand, lower concordia intercepts can be variable in rocks from the same area and usually correspond to no known geologic event (for example, Davis et al. 1985). They probably represent an average age for multiple Pb loss events and may depend on local factors such as the concentration and distribution of U in the crystals, as well as the nature of the host rock in providing access to fluids.
Another possible mechanism for Pb loss, in addition to chemical alteration, is preferential leaching of radiogenic atoms from damaged crystal lattice sites. Radiation damage is largely caused by recoil of nuclei during α-particle emission (Murakami et al.1991). This disrupts crystal bonds in the vicinity of a radiogenic atom, making Pb potentially more leachable than U, which is in undamaged sites. Pidgeon, O’Neil, and Silver (1966, 1973) demonstrated that up to 60% of the radiogenic Pb could be leached from zircon by 2 M NaCl at hydrothermal conditions in the laboratory with minor loss of U. In other studies, significant amounts of radiogenic Pb and U were leached from relatively low U zircon using NaCl and weak nitric acid solutions (Sinha, Wayne, and Hewitt 1992), and even spring water (Hansen and Friderichsen 1989). In some cases, residues moved up the Pb loss line, suggesting dissolution and removal of discordant, previously leached or altered domains. Ewing et al. (2003) helpfully reviewed the status of investigations of the radiation damage in zircons and the mechanisms involved. They reported that although the concentrations of U and Th are generally low in natural zircons (typically <5000 ppm), some zircon crystals are supposedly of great age (the claimed oldest zircon grains being >4 Ga), and thus have calculated doses of >1016 α-decay events per mg, well beyond the dose required for the radiation-induced transformation to the aperiodic, metamict state. In an α-decay event, the α-particle dissipates most of its energy (4–6 MeV for actinides) by ionization processes over the range of 10 to 20 µm, but undergoes enough elastic collisions along its path to produce approximately 100 isolated atomic displacements.
The largest number of atomic displacements occurs near the end of the α-particle trajectory. The more massive, but lower energy, α-recoil (70 keV 234Th from decay of 238U) dissipates nearly all its energy in elastic collisions over only 30–40 nm, transferring enough kinetic energy to cause ~1000 atomic displacements, as calculated by Weber (1993). This creates a “cascade” of atomic displacements in which the total energy can be as much as 1 eV per atom, and whose structure and evolution can only be modelled by computer simulations. The cascade duration is extremely short (<10-12 sec), after which displacements by elastic interactions cease and the cascade gradually loses energy as it cools to ambient temperature, typically “quenching” in nanoseconds. During this cooling phase, relaxation and diffusion reduce the number of displaced atoms in the cascade, and the final damage state consists of a small low-density core surrounded by a halo of interstitials (Brinkman 1954; Slater 1951; Trachenko, Dove, and Salje 2002, 2003).
A single α-decay event generates approximately 700–1200 “permanently” displaced atoms, significantly more than the 0.1 displacements generated per β-decay event (Weber 1993; Weber et al. 1998a). In the decay chain of 238U, there are eight α-decay events; 232Th has six. Because of the large number of atomic displacements during an α-decay event, the accumulation and overlap of individual cascades, as well as the presence of still crystalline but highly-strained domains, there is a dramatic decrease in density (17%), a decrease in birefringence until isotropic, a decrease in elastic moduli (69%), a decrease in hardness (40%), an increase in fracture toughness (Chakoumakos et al. 1987, 1991), and an increase in dissolution rate of one to two orders of magnitude (Ewing, Haaker, and Lutze 1982). Over extended time, the final damage microstructure is both time and temperature dependent because of annealing and recrystallization of damaged and strained domains (Weber, Ewing, and Meldrum 1997). Again, all this only emphasizes the need to avoid metamict zircons for radioisotope dating of rocks if at all possible.
Zircon figured prominently in the earliest studies of the metamict state and radiation damage (Ewing 1994). Von Stackelberg and Rottenbach (1940a, 1940b) had noted changes in density, refractive indices and birefringence with increasing α-decay dose, and even tried to test this hypothesis by irradiating a thin slab of zircon with α-particles. Metamict minerals though remained a mineralogical oddity for over a decade until the systematic review of radiation-induced property changes by Pabst (1952). Hurley and Fairbairn (1953) completed the first systematic study of a suite of increasingly damaged zircon crystals and quantified the amount of damage based on x-ray diffraction data. Although their interpretation was limited by a lack of experimental data (for example, they estimated that 5000 atoms were permanently displaced by each α-decay event), their approach was sound and laid the foundations of later work.
Holland and Gottfried (1955) completed a classic study of the effects of α-decay events on density, optical properties, and unit cell parameters as determined by x-ray diffraction. But further advances in knowledge had to await the development of more controlled irradiation experiments. Accelerated damage techniques, including doping with extremely short-lived actinides that transmuted by α-decay, such as 238Pu with a half-life of 87.7 years (Burakov et al. 2002; Exarhos 1984; Weber 1991; Weber, Ewing, and Wang 1994), neutron irradiation (Crawford and Wittels 1956; Hayashi et al. 1990), and ion beam irradiation (Cartz and Fournelle 1979; Ewing et al. 2000; Wang and Ewing 1992a, 1992b) have been used to great advantage in simulating the α-decay event damage in natural zircon. Ewing et al. (2003) concluded that we now have experimental data from irradiation experiments with dose rates that vary by more than 15 orders of magnitude (displaced atoms per sec) over a range of temperature from –260 to 800°C (Meldrum et al. 1999). Therefore, one can now safely state that there is no other mineral for which there is so much information on the process and effects of radiation damage.
During the1990s there was a small “explosion” of work on radiation damage effects in zircon specifically (Ewing et al. 2000). The experimental work was of three types:
- Natural zircon crystals—In these studies, there was generally no lack of material and a wide variety of analytical techniques used. However, the conclusions from them were always limited by a lack of knowledge of the thermal history of the zircon crystals.
- 238Pu-doped synthetic zircon crystals—These studies were generally conducted under ambient conditions, followed by thermal annealing studies. These were long-term studies lasting several decades. Because of restrictions handling Pu-bearing samples, analytical studies have been limited to simple density determinations, structural analysis using x-ray diffraction, electron microprobe analysis, and some spectroscopic studies.
- Ion-beam irradiated zircon crystals—In these studies, both heavy- and light-ion irradiations have been completed at precisely controlled temperatures. Although the physics of the damage process allows one to correlate the results to α-decay damage, the experimental configuration had limitations.
In situ irradiations combined with high resolution electron microscopy allowed changes in the atomic-scale structure to be observed in real time, and the dose to be determined at which the material became amorphous as a function of temperature. However, the high surface area to volume ratio of the thin wedge of the electron transparent region may have affected the damage accumulation process as defects migrated to the surface. More recent bulk irradiations, followed by examination of samples cut perpendicular to the surface (parallel to the trajectory of the ion), have allowed damage effects to be followed because the amount of damage varies along the trajectory of the implanted ion. These samples were generally examined by high-resolution transmission electron microscopy (HRTEM) (Lian et al. 2001, 2003) or utilized surface techniques such as x-ray photoelectron spectroscopy (XPS) (Chen et al. 2002). Such studies have provided critical information on oxidation states, defect deformation, and migration mechanisms.
Ewing et al. (2003) maintained that several observations can be drawn from TEM studies which support and clarify the x-ray diffraction results. First, the amorphization process is clearly heterogeneous. Even at low doses there are isolated regions that appear to be amorphous in high-resolution images. The rotated crystalline islands observed by TEM in highly damaged zircon also suggests the presence of considerable strain or shearing due to volume expansion of the amorphous material. Diffuse x-ray scattering also suggests the presence of shear waves in the crystalline lattice (Ríos and Salje 1999).
Furthermore, extended x-ray absorption fine structure (EXAFS) spectroscopy is a sensitive probe of the local coordination and bonding geometry at the nearest neighbor level. Thus, it has been very useful for characterizing the fully-damaged state of zircon. Farges and Calas (1991) and Farges (1994) completed the first detailed EXAFS study of radiation damaged natural zircon. With increasing α-decay events dose, the mean <Zr-O> distance decreased by 0.06 Å with respect to crystalline zircon. The next-nearest-neighbor <Zr-Zr> distances are shorter in metamict zircon than in crystalline zircon (3.34 Å versus 3.64 Å). For metamict zircon, Zr was in 7-fold coordination, as compared to 8-fold coordination in crystalline zircon. Based on bond-valence theory (Brown and Shannon 1973), the relatively smaller Zr4+ cation is expected to be in 7-fold coordination, suggesting that due to metamictization, there is a “relaxation” of the ZrO8 polyhedra to a more stable local configuration (Farges and Calas 1991). There was no evidence for radiation-induced decomposition into constituent oxides. Farges (1994) suggested that at temperatures below 900 K (627°C) the structure of naturally amorphized zircon consists of Zr- and Si-rich “nanodomains” with separate oxygen networks.
Farnan and Salje (2001) obtained a more complete picture using x-ray absorption spectroscopy (XAS) and nuclear magnetic resonance (NMR) by characterizing a suite of zircon samples ranging in dose from 1.0 × 1015 to 15.9 × 1015 α-decays per mg. They found a combination of changes which suggest that the structures of both the crystalline and amorphous regions are not constant but evolve continuously with increasing α-decay dose. Polymerization of the SiO4 tetrahedra, as implied by the NMR data, is consistent with the EXAFS results of Farges and Calas (1991) that indicated a decreased coordination of the Zr in metamict zircon. However, Farnan and Salje (2001) showed that in highly damaged or amorphous zircon there is an average of 2–3 bridging oxygens per silicon tetrahedron. These are too many bridging oxygen atoms to make up for the one removed from the Zr coordination polyhedron. In order to maintain the charge balance, they therefore suggested the presence of oxygen interstitials in metamict zircon.
Using all these data, Ewing et al. (2003) reported that there has also been a major effort to model the damage accumulation process in natural, Pu-doped, and ion-irradiated zircons. A critical aspect of such modelling has been the determination of the amorphous fraction, for which the measured value is different depending on the analytical technique used. The results from using a 7-circle diffractometer to measure the diffuse diffraction signals from single crystals of zircon (Ríos et al. 2000) provide strong evidence in support of the direct impact model of damage accumulation. Because of the close, although not perfect, correspondence between the results from U, Th, and Pu doping experiments and ion beam experiments (Weber, Ewing, and Wang 1994; Weber and Ewing 2000, 2002), substantial effort has been devoted to systematic ion beam experiments combined with in situ TEM examination because the irradiation conditions and temperature (–260 to 1000°C) can be carefully controlled. Those studies have provided important information on the formation of collision cascades and defect annealing mechanisms (Wang, Wang, and Ewing 1997, 2001; Weber, Ewing, and Wang 1994; Weber et al. 1998b). Weber (2000) provides a good summary of the different mathematical models.
Weber et al. (1998b) have summarized all the ion beam irradiation results for zircon. The general features of the damage process are clear. The amorphization dose for zircon exhibits two distinct stages with increasing temperature. The transition temperature between stages for natural zircon occurs at a much lower temperature (300 K or 27°C) than for synthetic zircon (500 K or 227°C), perhaps due to the impurities in the natural zircon. The amorphization dose also increases with damage energy density, which may reflect the effect of changes in the cascade size and geometry on relaxation and recrystallization processes. No single mathematical model has captured the behaviour of zircon from the three types of radiation experiments, so the three models of Weber, Ewing, and Wang (1994), Meldrum et al. (1999), and Wang, Wang, and Ewing (2001) are over simplifications of the damage accumulation process. Therefore, Weber (2000) presented a variety of mathematical models with some representing combinations of processes, because no single analytical technique provides the required resolution over all dose ranges. The critically missing information has been the description of cascade formation and relaxation processes, and the interactions between the cascades as they overlap.
Therefore, there has also been an increased effort to simulate cascade formation and the evolution of the damage microstructure using atomistic computer simulations to understand atomic-level processes related to the radiation damage during cascade formation (Ewing et al. 2003). Computational limitations initially restricted such dynamic calculations to cells that contained less than 400,000 atoms and time periods for cascade evolution of up to 20 picoseconds. Theoretical methods, such as ab initio calculations and molecular dynamics (MD) simulations, were used to study the behavior intrinsic defects (for example, interstitials and vacancies) and extrinsic defects associated with impurities, and to determine the minimum energies required to permanently displace atoms due to the transfer of kinetic energy. MD simulations have also been used to determine the distribution and nature of intrinsic defects, extended defect structures, and solid-state transformations resulting from the collision cascade produced by energetic ions, such as the α-particle and recoil nucleus produced in an α-decay event.
The formation energies of intrinsic defects and impurities in zircon are important to identifying the lowest energy configurations for interstitial and vacancy defects, to determining the probability for stable anti-site defects, and to identifying the stable configurations for incorporation of impurities such as U, Th, and Pu, and the decay products. In addition, the migration energies of intrinsic defects determine the nature of the damage recovery processes and self-diffusion mechanisms that occur as a function of time and temperature.
All these radiation damage effects are relevant to U and Pb mobility within the zircon crystal lattice and cause either loss or gain of the Pb and/or U isotopes within and from the zircon grains. Thus U-Pb ages can be reset. However, whether the U-Pb ages are then concordant or discordant is not an infallible guide to how much Pb and/or U loss or gain there has been, as the U-Pb and Pb-Pb isotope ratios cannot quantify the amounts of the Pb and/or U isotopes which have moved, even using the assumed “correct” ages for the zircons.
The Effects of Recrystallization
The final damaged microstructure of metamict zircon depends on the kinetics of damage accumulation and the kinetics of defect recovery and/or recrystallization. These processes are highly dependent on the ambient temperature and on the irradiation conditions (for example, dose rate, ion mass and energy, and the presence of impurities). In some instances, the recovery processes dominate, and crystallinity is preserved, even at low temperatures. Monazite remains crystalline despite extremely high α-decay doses (Meldrum et al. 1998; Meldrum, Boatner and Ewing 2000; Meldrum, Wang and Ewing 1996), whereas natural zircon is frequently found in a moderately- to highly-damaged state, suggesting that the kinetics of the recovery mechanisms are slower in zircon than monazite. Recrystallization of zircon therefore is a complex process in which several intermediate phase assemblages may form, depending on the annealing conditions and the initial microstructure. The combination of microstructural evolution studies on annealing of radiation-damaged zircon and thermodynamic results (Ellsworth, Navrotsky, and Ewing 1994) provides a more complete picture of the recrystallization mechanisms in zircon.
Ewing et al. (2003) reported that, in general, there are two broad types of recrystallization mechanisms. Type I recrystallization is purely thermal. It occurs on timescales longer than cascade quench times and is due to defect diffusion processes. Type I recovery processes generally dominate at longer times or at higher temperatures, and become particularly important in natural zircons stored at ambient conditions for “geologic” periods. Type II recrystallization occurs during irradiation. It is nearly an instantaneous process that either decreases the amount of residual damage produced by each displacement event or leads to the annihilation of pre-existing irradiation-induced defects or other types of damage. Type IIa recrystallization is due to the increased mobility or diffusion of interstitials and other point defects during irradiation. Type IIb recrystallization occurs within individual displacement cascades, and is increasingly effective as the temperature increases.
Type I recrystallization effects have been straightforwardly investigated and characterized in controlled experiments in which radiation-damaged zircon was thermally annealed in the laboratory (Farges 1994; Geisler et al. 2001a; Zhang et al. 2000a, 2000b). Capitani et al. (2000) performed in situ heating experiments in a transmission electron microscope in order to directly observe the damage recovery process. In a moderately damaged sample (7–8 × 1015 α-decays per mg), the initial microstructure consisted of nanoscale grains of crystallographically oriented zircon embedded in an amorphous matrix. These crystalline domains increased in size at a temperature of 827°C, the recrystallization occurring at the boundaries of the particles. At 927°C, these crystalline domains continued to grow, but nanoscale grains of ZrO2 nucleated in the still-amorphous regions. At 1127°C, there were no more amorphous domains or ZrO2 remaining, and the sample consisted of a single crystal of zircon. However, Pidgeon, O’Neil, and Silver (1966) and Geisler et al. (2001b) showed that annealing under hydrothermal conditions is much faster than in an ambient, dry atmosphere. In contrast, heavily damaged or amorphous zircon segregates into its constituent oxides (ZrO2 and SiO2) at high temperatures (Ellsworth, Navrotsky, and Ewing 1994; Zhang et al. 2000a).
Recrystallization and defect recovery are kinetic processes that are strongly dependent on time and temperature. Processes that are only apparent at high temperatures in the laboratory may be important at considerably lower temperatures over “geologic” time. Early results were somewhat contradictory. Lumpkin and Ewing (1988) found that the calculated dose for the amorphization of natural zircon increased with “geologic” time due to annealing. Using a model based on fission-track fading, they calculated a “half-life” of 400 Ma for the α-recoil damage in zircon, which should depend on the damage rate and the recovery kinetics (specifically, temperature). Weber, Ewing, and Wang (1994) showed that the amorphization dose for ion-beam-amorphized natural zircon is less than that for α-decay-amorphized Sri Lanka zircon, suggesting some recovery on geologic timescales.
Nasdala et al. (1998) found that U-Pb isotope discordance in zircon does not always correlate with the degree of damage as estimated by Raman spectroscopy, possibly the result of annealing at temperatures above 227°C (Geisler et al. 2001b). However, Nasdala et al. (2001) reported that most zircon specimens provided evidence of recrystallization over “geologic” time, with complete retention of damage being only observed at the lowest α-decay doses. Nevertheless, Geisler et al (2001b) suggested that “geologic” recrystallization is only significant at high temperatures. They calculated that it would take 370 Ma to recrystallize “metamict” zircon at 700°C.
Meldrum et al. (1998, 1999) found that the amorphization dose for natural zircon can be higher than that measured by the in-situ laboratory experiments. They observed that since thermal recrystallization is a diffusion-driven process, it occurs at all temperatures, but at different rates. They also derived a model that accounted separately for Type I and II recrystallization, which allowed the ion beam irradiation data to be compared to data on natural zircon over a wide range of “geologic” ages. Those data sets were broadly consistent, with the two structural states of zircon generally plotting in their expected fields according to α-decay doses and “geologic” ages, despite the different experimental techniques used to measure the degree of damage and the different thermal histories of the various specimens.
There are two implications. First, it is possible to extract information from the ion irradiation experiments that is directly applicable to the α-decay-damaged zircon, despite the enormous difference in dose rate. Second, given enough time, zircon can recrystallize at geologically “cool” temperatures. Temperatures as low as 100–200°C seem to be sufficient to produce measurable recovery effects over extremely long timescales. This result is consistent with the observation of recovery in various suites of zircons (Nasdala et al. 2001), and with the long-term annealing of damage cascades modelled by Lumpkin and Ewing (1988).
It should thus be abundantly evident that recrystallization and defect recovery in zircons are relevant to the mobility of Pb and/or U isotopes within zircons and therefore the reliability of the derived U-Pb ages. Since the Pb and/or U isotopes are made mobile by the radiation damage creating migration pathways, when subsequent recrystallization and/or defect recovery occurs, the Pb and/or U isotopes may either further migrate, and/or be locked into the places they have already migrated to, within the crystal lattices of the zircons. Thus U-Pb ages can again be reset. However, once again, whether the U-Pb ages are then concordant or discordant is not an infallible guide to how much Pb and/or U loss or gain there has been which has been locked in by the recrystallization and/or defect recovery, as the U-Pb and Pb-Pb isotope ratios cannot quantify the amounts of the Pb and/or U isotopes which have moved, even using the assumed “correct” ages for the zircons.
Quantifying the Diffusion and Leakage of Pb
The experiments of Shestakov (1969, 1972) and Magomedov (1970) relied upon bulk release methods, with the zircon crystals heated and the amount of Pb released recorded as a function of time. Such measurements encountered several difficulties, such as the presence of cracks, cleavage surfaces, dislocations, and other features that might provide shortcut pathways for Pb transport, as well as the mineral’s surfaces departing from the ideal smooth surface which would have increased the available surface area for exchange. In these studies, Pb did not obey a typical volume diffusion relationship, indicating the possibility of grain-boundary diffusion, and suggesting surface volatilization as well as Pb migration might be a factor influencing Pb release patterns. Nevertheless, Magomedov (1970) obtained an activation energy of 58 kcal (~243 kJ) mol-1 and a diffusion coefficient of 6.2 × 10-3 cm2 sec-1 based on Pb-loss measurements made at 1000°C and 1150°C.
The thermal evaporation experiments of Bogolomov (1991), which yielded quite high activation energies (790–1180 kJ mol-1) likely involved decomposition of zircon to ZrO2 + SiO2 during heating, as suggested by the work of Chapman and Roddick (1994). Pb loss in this case is not governed by simple volume diffusion, but is instead controlled by the decomposition process and movement of the reaction front.
Cherniak, Lanford, and Ryerson (1991) implanted Pb ions into natural zircon and annealed the implanted samples under a range of time-temperature conditions, and measured resultant profiles with Rutherford back scattering (RBS). The process of ion implantation, however, produced significant amounts of damage of the zircon crystal lattice, leading to elevated transport rates for Pb, and a low activation energy for diffusion (142 kJ mol-1). Interestingly, implantation of Pb at energies in the range of those used by Cherniak, Lanford, and Ryerson (1991) creates damage comparable to that produced by α-recoil events in the decay of U to Pb in natural zircon (for example, Headley, Arnold, and Northrup 1981; Petit, Dran, and Mea Della 1987), so their results, as the authors then noted, provided a determination of Pb transport rates in zircons that have experienced significant radiation damage.
Lee, Williams, and Ellis (1997) measured out-diffusion of Pb, as well as U and Th, in a natural zircon from Sri Lanka with SIMS. They obtained an activation energy of 675 kJ mol-1 and pre-exponential factor of 3.9 × 105 m2 sec-1. In the temperature range over which their study overlaps with the work of Cherniak and Watson (2000) (1000–1100°C), diffusivities determined by Lee, Williams, and Ellis (1997) are more than an order of magnitude faster. In fact, the variance approaches two orders of magnitude at 1100°C. The reasons for this discrepancy are unclear. The diffusion rates for U and Th measured by Lee, Williams, and Ellis (1997) are also four orders of magnitude larger than those of Cherniak, Hanchar, and Watson (1997b). Lee, Williams, and Ellis (1997) contend that this difference may be a consequence of the fact that their experiments were run on natural zircons and measured out-diffusion, while those of Cherniak, Hanchar, and Watson (1997b) were run with synthetic zircons and measured in-diffusion. But this explanation seems unconvincing for several reasons.
Both the work of Cherniak and Watson (2000) and that of Cherniak, Hanchar, and Watson (1997a) on REE diffusion in zircon indicate that there exists no appreciable difference in cation diffusion rates in synthetic zircons and natural zircon with little radiation damage. Variations in minor and trace element compositions, and differences in defect concentrations as a consequence of different growth conditions of the natural and synthetic zircons, appear to exert little influence on cation diffusion. The small amounts of radiation damage present in the Sri Lanka zircon, which as Lee, Williams, and Ellis (1997) noted exhibited “excellent crystallinity,” should have been annealed out readily, as the reported α-dose for the zircon (4.8 × 1014 α-decays per mg) is well within the Stage I regime of damage accumulation, zircon with <3 × 1015 α-decays per mg (Murakami et al. 1991). Therefore, radiation damage in that case should not have greatly affected Pb transport.
Furthermore, the out-diffusion experiments of Cherniak and Watson (2000), using a zircon similar to that used by Lee, Williams, and Ellis (1997) as well as a generally comparable experimental approach, yielded diffusivities consistent with the rest of their measurements rather than the faster diffusion rates measured by Lee, Williams, and Ellis (1997). Other than the analytical techniques used to measure Pb distributions, the medium employed as the sink for the diffusant was the salient difference between the out-diffusion experiments of Cherniak and Watson (2000) and those of Lee, Williams, and Ellis (1997). The material constituting the reservoir surrounding the sample in the Cherniak and Watson (2000) experiment, ground zircon, is quite refractory and was unreactive with the zircon specimen. NaCl exhibits quite different attributes. Although Lee, Williams, and Ellis (1997) failed to adequately address the possibility, it is not unreasonable to conjecture that reaction of the zircon surface with the molten salt reservoir might have produced near-surface (non-diffusional) Pb loss, since it has been noted elsewhere that NaCl solutions may enhance Pb loss through “chemical leaching” (Lee 1993).
Other aspects of the Lee, Williams, and Ellis (1997) study are problematic. They did not offer sufficiently strong evidence that what they were measuring was indeed volume diffusion of Pb. They mentioned two key “tests” undertaken to confirm the occurrence of volume diffusion. The first was the independence of the diffusion coefficient on the duration of the diffusion anneal. While the time series is a well-established test, anneal times must differ by an amount such that diffusion profiles are significantly different in length. Since diffusion distance scales as the square root of time, a difference in anneal times of a factor of 4, which would result in length scales differing by a factor of 2, is generally considered a minimum variance for this test. Anneal times at a given temperature differ by at most a factor of 1.8 in the Lee, Williams, and Ellis (1997) study. The second “test” mentioned by Lee, Williams, and Ellis (1997), that of Arrhenian behavior (that is, linear dependence of log D on 1/t), was not definitive, as the Arrhenius relation is empirical and kinetic processes other than volume diffusion might also exhibit some form of linear dependence in 1/t. Furthermore, profiles at the lowest temperature (900°C) are extremely short (only a few nanometers, given the durations of the diffusion anneals and reported diffusion coefficients) and thus carry much greater uncertainty in SIMS analysis than they suggested.
Cherniak and Watson (2000) maintained that their measurements yielded comparable diffusivities at a given temperature for a wide range of conditions, and for consistent diffusivities over a broad temperature span with a variety of experimental approaches and two different analytical techniques. This lends strong support to the conclusion that several factors which might have been heretofore suspected of affecting Pb diffusion in zircon do not seem to exert significant influence. Among them are out-diffusion versus in-diffusion, the presence of concentrations of Pb somewhat higher than natural Pb abundances, and the possibility that radiogenic Pb may not occupy lattice sites due to displacement as a consequence of the multi-stage decay process. Thus, radiogenic Pb could diffuse in a different manner than the Pb in their experiments with the PbSO4 source they used.
Further support for the reasonableness of the Pb diffusion findings of Cherniak and Watson (2000) came from a set of high-temperature ion implantation experiments on synthetic zircon, and a theoretical prediction of Pb diffusion rates (Cherniak, Hanchar, and Watson 1997b). The ion implantation experiments were conducted in a manner similar to that outlined by Cherniak, Lanford, and Ryerson (1991). In those experiments, zircon was implanted with Pb ions, and the initial Pb distributions depth-profiled with RBS. The samples were then annealed and subsequent depth profiles were fitted with a model to determine diffusion coefficients based on the spreading of the initial implanted Pb distributions.
This high-temperature implantation study by Cherniak and Watson (2000) differed from the experiments of Cherniak, Lanford, and Ryerson (1991) in that implantation took place with samples mounted on a heated stage (held at 800°C), rather than at room temperature. Heating the sample during implantation permitted radiation damage produced by the implantation to anneal out rather than accumulating as rapidly as it would during implantation at room temperature, so the ion doses required to induce amorphization of the material increased with increasing temperature of implantation. At temperatures of 800°C, zircon will resist amorphization even for relatively high implant doses of heavy ions (for example, Wang and Ewing 1992b; Weber, Ewing, and Wang 1994). For the heated-stage experiments, synthetic zircons were implanted with Pb+ ions with an energy of 250 keV. Implant doses were 1 × 1015 Pb ions/cm2, a similar dose to that used in the Cherniak, Lanford, and Ryerson (1991) experiments. Over the temperature range 1200–1350°C, Cherniak and Watson (2000) obtained from these diffusion data an activation energy of 456 ± 109 kJ mol-1 (10,926 kcal mol-1) and a pre-exponential factor of 1.6 × 10-4 m2 sec-1 (log D = –3.80 ± 3.69). While these data extend over a fairly short range in 1/T and carry a relatively large amount of uncertainty, they are consistent with the Pb diffusion measurements they reported, despite a very different means of introducing Pb into the zircons.
The theoretical prediction, based on observed trends for diffusion of trivalent and tetravalent cations in zircon, was reported by Cherniak, Hanchar, and Watson (1997b). Among tetravalent cations, Hf diffuses more rapidly than U or Th, but these differences are not as pronounced as those found between trivalent cations. The influence of cation charge is also great, as the (trivalent) REEs diffuse 3–5 orders of magnitude faster than tetravalent cations in zircon. Pb likely existed in the divalent state in those experiments, and in zircons in nature as well, since Pb is stable in the 4+ valence state at elevated temperatures only under conditions of very high fO2 (for example, Otto 1966; Watson et al., 1997). At the same time, the ionic radius of Pb2+ is quite large (1.29 Å in eightfold coordination; Shannon 1976). In the trends broadly obtained for cations in zircon, it appears that these two factors, that is, lower charge tending to increase diffusion rates and larger ionic radius tending to reduce them, provide competing influences.
Cherniak and Watson (2000) concluded that Pb loss due to diffusion is more likely in metamict zircons, since Pb diffusion has been found to be much more rapid in zircon that has been severely radiation-damaged (Cherniak, Lanford, and Ryerson 1991). Radiation damage at today’s U and Th decay rates, however, takes significant amounts of time to accumulate because of the natural annealing that would seem to occur on presumed geologic time scales (for example, Lumpkin and Ewing 1988; Meldrum et al. 1998). The annealing process is such that zircons residing at temperatures above a “critical amorphization temperature” will not become metamict. The critical amorphization temperature is a weak function of activity, that is, zircon U content and conventional age (Meldrum et al. 1998). The critical amorphization temperature for zircons with 1000 ppm U is about 360°C, and only about 20°C higher for zircons with as much as 10,000 ppm (that is,1%) U. It also appears to vary as a function of the supposed zircon age by less than a degree per billion years for a given U content. Zircons exposed to temperatures below the critical amorphization temperature can accumulate damage, but only over long timescales.
Added complexities, such as the possibility that Pb transport rates may change with differing degrees of radiation damage, and the two-stage annealing kinetics of zircon (for example, Meldrum et al.1998; Weber, Ewing, and Wang 1994) were not considered in the simple model of Cherniak and Watson (2000). In severely radiation-damaged zircon, in contrast to crystalline zircon, significant amounts of diffusional Pb loss are possible, even at relatively low temperatures given the enhanced transport rates in the damaged material. Complete resetting of Pb isotopes through volume diffusion could also occur if zircon possessing significant amounts of radiation damage (in residing at low temperatures) were rapidly heated, since the zircon structure is slow to recover crystallinity after experiencing radiation damage beyond certain levels (for example, Murakami et al. 1991; Weber 1990; Weber, Ewing, and Wang 1994), and Pb diffusion would remain relatively rapid.
It has long been argued (for example, Silver and Deutsch 1963) that there exists a correlation between U content and discordance, although there are cases where this relationship does not seem to apply (for example, Schärer and Allègre 1982). However, the work of Sanborn, Stern, and Carr (1998) and Stern, Sanborn, and Bleeker (1998) continued to point to the complexity of the phenomenon of “Pb loss” in natural zircon. On the one hand, some correlation between U content and degree of discordance in mildly discordant (<10%) zircons studied has been found, which suggests a possible role of enhanced volume diffusion in radiation-damaged zircon. However, on the other hand, there is often no such correlation in severely discordant zircon, which indicates the possible influence of other (non-diffusional) processes, such as recrystallization and various fluid-assisted processes, including physical deformation that could significantly alter Pb isotope ratios and zircon U contents (for example, Pidgeon, Nemchin, and Hitchen 1998; Sinha, Wayne, and Hewitt 1992). The zircon composition itself can be an important factor influencing the probability of recrystallization. Pidgeon, Nemchin, and Hitchen (1998) argued that recrystallization (and consequent exclusion of trace elements from the zircon lattice) is more likely in zircon (or regions of zircon) with high trace element concentrations, as the zircon lattice, experiencing strain due to the significant substitution of these other elements, can become metastable upon cooling from magmatic temperatures.
Indeed, Davis and Krogh (2000) demonstrated by experiments with zircon that radioactive daughter elements can be preferentially leached from zircon crystal lattice sites that had been damaged by α-recoil. This results in significant loss of 206Pb, 207Pb, and 234U from damaged crystal sites, which thus perturbs the zircon U-Pb and Pb-Pb ages. Similarly, Pidgeon, O’Neil, and Silver (1966) found that the U-Pb system in zircon was perturbed under experimental hydrothermal conditions, with up to 61% loss of radiogenic Pb within 13 days, and most of the Pb loss occurring in the first ten hours. They concluded that episodic Pb loss is a significant process and explains many discordant U-Pb isotope relations and ages observed in natural zircon suites.
Cherniak and Watson (2003) reviewed the results of all these experimental studies of cation diffusion, as well as theoretical determinations of energies of formation and migration of various defects in zircon (Crocombette 1999; Meis and Gale 1998; Williford et al. 1999), and speculated on possible mechanisms for diffusion. For a few reasons, it appeared most likely to them that cations such as Pb diffuse via an intrinsic vacancy mechanism. Diffusivities for both synthetic and natural zircon crystals with varying concentrations of aliovalent impurities are quite similar, which suggests that extrinsic cation vacancies are an unlikely mechanism, because the concentrations of these defects would be proportional to the concentration of the dominant aliovalent impurity (for example, P5+). Furthermore, theoretically-determined Zr vacancy migration energies (Williford et al. 1999) range from 1.16 eV to 1.38 eV (110–130 kJ mol-1), considerably smaller than the activation energies for cation diffusion. However, energies for creation of Zr vacancies by so-called Schottky defect formation are 6.2 eV per defect (600 kJ mol-1) compared to 12.28 eV per defect (1190 kJ mol-1) for so-called Frenkel defect formation (He and Cormack 1999; Williford et al. 1999). Thus, the experimental activation energies are consistent with an intrinsic regime reflecting energies of both formation and migration of Zr vacancies. Zr interstitials can be reasonably ruled out as unfavorable because of their very high estimated energy of formation (18 eV or 1740 kJ mol-1; Crocombette 1999). Calculations by Meis and Gale (1998), using empirical potentials for zircon and applying static transition state theory, estimated an activation energy for diffusion of U4+ (via a vacancy mechanism) in zircon of 5.9–9.4 eV (590–900 kJ mol-1), consistent with experimentally determined activation energies for diffusion of tetravalent cations (for example, 726–812 kJ mol-1).
Cherniak and Watson (2003) also noted that sharp compositional zoning in zircon is often observed, as slow diffusivities characteristic of most elements in zircon can influence both the likelihood of formation of such zoning (Watson and Liang 1995), and its preservation under a broad range of geologic conditions (Cherniak, Hanchar, and Watson 1997a, 1997b). Zoning down to micron and sub-micron scales of high-Z elements incorporated into zircon in relatively high abundance (Hf, and to a lesser extent, U) are observable in back-scattered electron (BSE) and in cathodoluminescence (CL) spectra (Corfu et al. 2003). While zoning in Pb generally cannot be observed by these means because of its low abundance and the fact that its electronic structure militates against its being a CL activator in zircon, marked variations in Pb isotopes across individual grains, presumably representing different stages (and ages) of zircon growth, have been detected in ion probe analyses (Ireland and Williams 2003). Because of the width of the ion beam, discordances in U-Pb ages in many cases have been attributed to presumed “mixing” as a consequence of combining isotope information from distinct regions into single analyses.
Therefore, Cherniak and Watson (2003) claimed that given the slow diffusion rates of Pb, REEs, and the tetravalent cations in crystalline zircon under most geologic conditions, distinct zones, even on relatively fine scales, will quite often be preserved. Although they maintained that the diffusion rates of Pb in zircon do not differ greatly from those of the REEs over the investigated temperature range, the differences in activation energy for diffusion (550 kJ mol-1 for Pb versus 690–840 kJ mol-1 for the REEs) result in significant differences in diffusion rates at most temperatures of geologic interest. For example, at 800°C, diffusion rates of Dy and Pb will differ by more than two orders of magnitude, with diffusion distances differing by a factor of ~20. Differences become even more pronounced with decreasing temperature. Hence, the preservation of REE zoning observable with CL spectroscopy does not guarantee preservation of Pb isotope signatures on the same scale. Furthermore, preservation of BSE-observable zoning in Hf or U offers even less evidence for simultaneous preservation of Pb zoning, as diffusion of the tetravalent cations is considerably slower than that of the REEs (Cherniak, Hanchar, and Watson 1997b).
However, Cherniak and Watson (2003) made it clear that these diffusion data apply strictly to crystalline zircon. Diffusion may be significantly enhanced in severely radiation-damaged zircon (Cherniak, Lanford, and Ryerson 1991), thus permitting the obliteration of zoning under much less extreme thermal conditions. Nevertheless, Cherniak and Watson (2003) admitted that the effects of radiation damage on diffusion are still to be systematically investigated. For Pb diffusion, there exist measurements of the “end member” cases—severely radiation-damaged zircon (Cherniak, Lanford, and Ryerson 1991), and fully crystalline zircon (Cherniak and Watson 2000). Yet it is not clear how intermediate amounts of radiation damage in the zircon structure would affect diffusivities. However, the fact that there are two simultaneously occurring kinetic processes, that is, atomic diffusion and repair of the damaged zircon lattice, with quite different activation energies and rates, complicates characterization of diffusivities under these circumstances, not to mention the degree of radiation damage.
Tetravalent Pb and its Distribution
Kramers et al. (2009) attempted to critically discuss the paradoxical behaviour of radiogenic Pb in zircon, and suggested that it can be explained by the hypothesis that this Pb is tetravalent. They reviewed several strong indications for this. These all suggested that the peculiarities of U-Pb behavior in zircon can be understood using a tetravalent-Pb working hypothesis, coupled to an important role of water as a conductor and agent for isotope transport.
In their study on titanite, Frei et al. (1997) had suggested that a primary tetravalent state of radiogenic Pb can be understood from the decay process itself, but they did not propose a specific mechanism to explain this. The last α-decays leading to 206Pb and 207Pb have energies between 5.3 and 7.5 MeV. Therefore, the α-recoiled nucleus has a kinetic energy of 100–150 keV. The initial velocity of a 206 atomic mass units nucleus (such as 206Pb) recoiling with 100 keV is ~3 × 105 m sec−1, and the energy needed for an electron to reach this velocity is only ~0.27 eV, much lower than the first ionization energy. Thus, the recoiling atom does not lose extra valence electrons initially. However, a highly oxidized state of radiogenic Pb in silicates is probably reached in a way analogous to the hexavalent state of 234U, which is formed via two β-decays from α-recoiled 234Th early in the 238U decay chain.
Ordonez Regil et al. (1989) had studied the effects of the recoil of actinide atoms on a lattice by collision cascade modeling in MgO and UO2. In the former matrix, they found that at recoil energies around 100 keV (typical of α-decays in the 238U, 235U, and 232Th decay chains) more than 10% of the recoil energy is lost in an inelastic way, not only destroying the lattice but also displacing specifically the lighter atoms, that is, oxygen, towards the end of the 20–30 nm recoil trajectory. Thus, the recoiled atom would come to rest in a highly oxidizing environment. In the case of recoiled 234Th, this leads to its oxidation to the highest valence state of 4+ (while, without interaction, ejecting an α-particle, 2+, out of 238U4+ would yield 234Th2+). The two subsequent β-decays then increase the charge of the nucleus by 2+, so that 234U6+ results. Ordonez Regil et al. (1989) and Adloff and Roessler (1991) extrapolated this model result to oxygen-rich minerals consisting mainly of elements much lighter than U and having <1% U, thus including silicates such as zircon. They also noted the oxidized nature of the products of hot atom target experiments, and cited the higher mobility of 234U compared to 238U as evidence for its hexavalent state.
Cherniak and Watson (2000) noted that it is impossible for Pb to be tetravalent in redox equilibrium with other elements in a rock or silicate magma. However, Kober (1987) had argued that zircon grains should, through their radioactivity, maintain a positive charge relative to their environment. The decay chains of U and Th involve 7 to 8 α-decays and 4 to 6 β-decays. The β-particles travel between 0.05 and 1 mm and therefore have a high probability of leaving a zircon grain. In contrast, the paths of α-particles in the lattice are only 10–30 μm long and they will thus mostly remain trapped in an average-sized, datable zircon grain. With a net outflow of negative charge and a deficit of electrons, the interior of a zircon grain is thus a highly oxidizing environment, not in redox equilibrium with other minerals and the elements in them. Combining these arguments, the 4+ valence state in radiogenic Pb should be produced by the radioactive decay itself and maintained through “geological” time in the highly oxidizing environment created by β-decays.
If the above conclusions are correct, then radiogenic Pb cannot be lost from zircon crystals except by being reduced to the divalent state, after which it would become both incompatible in the lattice and highly mobile in solution. Kramers et al. (2009) proposed that not only hydrothermal fluids, but also natural leaching by groundwater in weathering can both reduce the Pb to the divalent state, and transport it. Countless observations on natural cases of discordance of zircon U-Pb dates, as well as the leaching experiments already discussed, help to test this proposition.
If radiogenic Pb in silicates is primarily tetravalent, as argued, it would remain immobile as long as zircon grains are kept oxidized by a combination of α-decays and β-decays (Kober 1987). Electrolyte-rich groundwater in deep pre-weathering would then penetrate the sieve-like structure of a zircon having recoil tracks, and establish redox equilibrium with the surrounding minerals. As Pb would be reduced to the divalent state in the process, it would become both incompatible and soluble. In this scenario, easy loss of Pb from zircons in weathering is not in contradiction to its previous extreme retentivity, even at very high temperatures.
If this is true, and the probability of escaping from a zircon crystal is equal for all radiogenic Pb isotope species, then these Pb-loss discordia cords related to weathering would trend to the zero point in the Wetherill Concordia diagram (or at least to a relatively recent time of paleoweathering). This is frequently observed, but in the case of early Proterozoic and Archean zircons a range of lower intercepts up to 800 Ma is more common for such recent or sub-recent Pb loss (Kramers et al. 2009). Negative lower intercept ages are never seen, and the bias to positive ones calls for an explanation.
Kramers et al. (2009) suggested that α-recoil tracks hosting 207Pb are more accessible to the permeating, reducing solutions than those with 206Pb. As a working hypothesis, they proposed that the reason for this lies in the different energies of the last α-decays leading to the two isotopes (see figs 1 and 2), which are:
- 206Pb is wholly produced by α-decay of 210Po (E = 5.31 MeV).
-
207Pb is produced in two ways:
- 68% via α-decay of 211Bi (E = 6.62 MeV [83%] or 6.27 MeV [17%]), and β-decay of 207Tl.
- 2% via α-decay of 211Po (E = 7.43 MeV [99.5%] or 6.9 MeV [0.5%]).
The 206Pb and 207Pb are thus expected to be oxidized to their highest valence state (4+) by analogy to 234Th (Ordonez Regil et al. 1989). 207Tl is expected to be oxidized to its highest valence state (3+) in the recoil cascade, and as the proton number in the nucleus is increased by +1 by the β-decay, this translates to 207Pb4+. Furthermore, the weighted average energy of the last α-decays leading to 207Pb is thus 6.834 MeV. The ratio of the last α-decay energies for 207Pb relative to 206Pb is 1.29, and the ratio of recoil velocities is 1.14. Tentatively, Kramers et al. (2009) used these ratios as guidelines for the ratios of the amount of recoil damage, and therefore accessibility to groundwater and likelihood of mobilization, for these two Pb isotopes.
In zircon U-Pb systematics, extreme robustness up to the temperatures of granulite facies and anataxis contrasts with apparently easy loss of radiogenic Pb at low temperatures, often without any metamorphic event being in evidence. This is why Kramers et al. (2009) proposed that this paradoxical behaviour can be understood by the radiogenic Pb in zircon being tetravalent. They maintained the data are in favor of this. For example, diffusion profiles calculated for Pb2+ in a 25 μm radius zircon xenocryst in a melt at 1000°C, combined with the incompatibility of Pb2+, and for a zircon core inside a younger zircon rim at this temperature, showed age effects that should have been observed in SIMS dating. Furthermore, in zircon evaporation experiments, as well as in leaching experiments, so-called common Pb appears to be generally released preferentially to radiogenic Pb. After removal of the less radiogenic Pb, the evaporation record generally shows pure radiogenic Pb during the final evaporation steps. The distribution of residual Pb in a leached titanite, revealed by PIXE, was similar to that of Ti. Furthermore, XANES spectra of a 1 Ga old titanite (predominantly radiogenic Pb) and an Alpine titanite (presumed to contain predominantly common Pb) were significantly different, although the former does not resemble that of PbO2 (Kramers et al. 2009).
As for why radiogenic Pb should be tetravalent, Kramers et al. (2009) based their arguments on analogies with studies relating to the tetravalent state of 234Th and the hexavalent state of 234U, which show that α-recoil in silicates generates a strongly oxidizing environment at the site where the recoiling nucleus comes to rest (Ordonez Regil et al. 1989). Further, a zircon grain, being small, should remain highly oxidizing in its interior by the constant loss of β-particles, maintaining the 4+ state of radiogenic Pb. From its effective ion radius, similar to that of Zr4+, and its charge, Pb4+ has to be compatible in the zircon lattice. Also, by analogy with U4+, Th4+, and Hf4+, its diffusivity should be several orders of magnitude lower than that measured for Pb2+ in zircon. These factors can account for the apparent extreme retentivity of U–Pb clocks even at high temperatures. On the other hand, radiogenic Pb situated in α-recoil damaged sites could be leached out by any electrolyte solution that reduces it to the divalent state, making it both incompatible and soluble. Thus, discordia can be generated in weathering. The curious observation that discordant Archean zircon suites generally define trends to lower intercepts at up to 800 Ma instead of zero, appears to reflect an approximate14 to 28% better average accessibility to leaching of radiogenic 207Pb compared to 206Pb, in accord with the somewhat higher recoil energy of the last (branched) α-decays in the 235U chain.
Short of showing beyond doubt that radiogenic Pb in zircon is tetravalent, Kramers et al. (2009) thus assembled considerable circumstantial evidence and arguments in favor of that working hypothesis. The arguments are that α-recoil in silicates generates a strongly oxidizing environment at the site where the recoiling nucleus comes to rest, and that a zircon grain, being small, remains highly oxidizing in its interior by the constant loss of β-particles. They further argued that with this hypothesis, some of the major apparent paradoxes of zircon geochronology can be accounted for.
Atomic Scale Studies of Diffusion of Pb and U
Kusiak et al. (2013) presented the results of a multi-faceted ion microprobe study of zircon grains from the Napier Complex, East Antarctica, a region affected by pervasive high-temperature metamorphism at 2.5 Ga, and from which previous zircon geochronological interpretations had been problematic. Both U-Pb spot analyses (~15 μm) and high spatial resolution (~2 μm) scanning ion imaging of Pb isotopes were applied in an attempt to quantify the effects of metamorphism. Spot analyses spread along the concordia yielding 207Pb/206Pb ages from 2.5 Ga to 3.9 Ga, with the oldest grains reversely discordant. Ion images of uranogenic Pb revealed a surprising micrometer-scale patchy distribution that was unrelated to crystal morphology or damage. The 207Pb/206Pb ratios within these sub-domains corresponded to apparent zircon ages as old as 4.2 Ga. These were interpreted as artifacts of ancient redistribution of radiogenic Pb, a process that can generate meaningless ages, and are not relicts of ancient (including Hadean) zircon.
Considering the full U-Pb analyses plotted on a concordia diagram, Kusiak et al. (2013) found that the isolation of the radiogenic Pb from its parent isotopes over time resulted in a sloping linear array, with ratios reflecting Pb loss projecting toward a lower intercept representing the time of Pb mobilization, and ratios affected by Pb gain projecting away from concordia in the opposite direction. In their examples from the Napier Complex, this lower intercept appeared to correspond to the well-documented episode of UHT (ultra-high temperature) metamorphism at ca. 2.5 Ga (Kelly and Harley 2005) suggesting that radiogenic Pb mobilization occurred at that reputed time, while the upper intercept approximated the likely protolith age of the rock. However, Kusiak et al. (2013) found that precise age determinations were problematic, because the within-run fluctuations in the Pb-isotope signals caused by the Pb micro-domains degraded the quality of the analyses.
Kusiak et al. (2013) commented that where ancient Pb mobilization concentrated radiogenic Pb, measured 207Pb/206Pb ratios were elevated because the total signal was a combination of unsupported radiogenic Pb (or common/initial Pb) and radiogenic Pb that has evolved since the time of redistribution. As a result, radiogenic Pb-enriched patches yielded spuriously old 207Pb-206Pb ages that are not true ages, but the result of sampling (either with a spot analysis or via age calculations from ion images) that integrated areas with both unsupported and supported radiogenic Pb. The same applied for areas that had experienced ancient Pb loss leading to spuriously young ages. Both types of ages were revealed in the examples Kusiak et al. (2013) investigated from the Napier Complex by the combination of ion imaging of Pb isotopes and area calculation. Although Pb redistribution in their study mainly occurred at sites <5 μm in diameter, when Pb-enhanced domains were incorporated in a typical ion microprobe spot (~15 μm in diameter), the age was up to 300 Ma older.
Kusiak et al. (2013) explained the reverse discordance is especially problematic for very ancient zircon investigated by high-spatial-resolution methods (for example, by ion microprobes). For such methods, 207Pb-206Pb ages are regarded as generally more precise than U-Pb ages and consequently form the primary basis of geochronological interpretations. Kusiak et al. (2013) thus discussed an example of the effect of a metamorphic event generating discordant zircons for three hypothetical but geologically reasonable scenarios, assuming a typical U-Pb measurement uncertainty of ± 2%. In the first scenario, chosen to be broadly analogous with events in the Napier Complex, a discordia would have been generated by a metamorphic event at 2.5 Ga affecting zircons originally crystallized at 3.6 Ga. Reversely discordant zircon grains could then be readily identified at apparent 207Pb-206Pb ages that are only slightly older than that first discordia. In the second scenario, reversely discordant zircon grains lying along a second discordia, generated by supposed 3.8 Ga metamorphism of 4.0 Ga zircons, are resolvable as discordant at the 2% uncertainty level only at apparent 207Pb-206Pb ages >4.2 Ga. In the last scenario, Hadean-aged zircon grains with a supposed age of 4.2 Ga affected by metamorphism at 4.0 Ga lay along a third discordia and are only resolved as discordant when the apparent 207Pb-206Pb age exceeded 4.4 Ga. Kusiak et al. (2013) noted that the last two scenarios are especially relevant to Hadean detrital zircon grains such as those from the Jack Hills, Australia, where the absence of an original host rock context hinders interpretations. The possibility that apparently concordant 207Pb-206Pb ages might be too old by tens to hundreds of millions of years can only be tested by multiple analyses in the same zircon yielding the same age (for example, Nemchin et al. 2006).
Kusiak et al. (2013) concluded that a causal mechanism for the redistribution of radiogenic Pb remained elusive and progress toward this would require investigations on a scale smaller than they had undertaken, for example, using transmission electron microscopy (TEM). Nonetheless, they still suggested that some observations from their ion imaging provided important constraints. The micrometer scale domains were essentially randomly distributed, indicating that the process was unrelated to cracks or primary radiation damage, which tended to form linear patterns (for example, Utsunomiya et al. 2004). Their location was unrelated to the concentration of U or Th in the zircon, which appeared to rule out a direct correlation with radiation damage. They did not observe inclusions in the imaged grains that corresponded to the patches. Examples of unsupported Pb in monazite had been demonstrated by TEM (Seydoux-Guillaume et al. 2003), but the nanometer-scale Pb-rich domains were explained by fluid circulation under lower amphibolite-facies conditions with no obvious analogy to UHT metamorphism. Ion imaging could thus identify the presence of unsupported Pb with anomalous 207Pb-206Pb ages and might be used to test the validity of ages from very old zircons known to have a supposed long and complicated history.
Subsequently, Valley et al. (2015) used atom-probe tomography (APT) and secondary ion mass spectrometry (SIMS) to provide complementary in situ element and isotope data from within zircon grains. The APT technique combines a field ion microscope with a mass spectrometer, so that a highly curved electric field removes ions from a sample surface in order to image and identify them (Miller 2000). This generates magnifications sufficient to observe individual atoms as they are removed from the sample surface using a position-sensitive detector to deduce the lateral location of atoms. In the Valley et al. (2015) study the SIMS measured isotope ratios and trace elements from 1–20 μm spots with excellent accuracy and precision. The APT identified the mass/charge and three-dimensional position of individual atoms (± 0.3 nm) in 100 nm-scale samples, with volumes up to one million times smaller than SIMS. The APT data provided unique information for understanding element and isotope distribution, crystallization and thermal history, and mechanisms of mineral reaction and exchange. This atomistic view enabled evaluation of the fidelity of the geochemical data for zircon, because it provided a new understanding of radiation damage, and tested for intra-crystalline element mobility. Indeed, nano-geochronology is one application of APT in which Pb isotope ratios from sub-micrometer domains of zircon provide model ages of crystallization, and potentially identify later magmatic and metamorphic reheating.
Based on SEM imaging and SIMS analyses, 11 needle-shaped specimens ~100 nm in diameter were sampled by Valley et al. (2015) from one Archean and two Hadean zircons by focused ion-beam milling and analyzed with APT. The three-dimensional distribution of Pb and nominally incompatible elements (Y, REEs) differed at the atomic scale in each zircon. Zircon JH4.0 (dated at 4.007 Ga, from Jack Hills, Western Australia) was homogeneous in Pb, Y, and REEs. In contrast, Pb, Y, and REEs were clustered in sub-equant ~10 nm diameter domains, spaced 10–40 nm apart, in zircons ARG2.5 (dated at 2.542 Ga, from Grouse Creek Mountains, Utah) and JH4.4 (dated at 4.374 Ga, from Jack Hills, Western Australia). Most clusters were flattened parallel to the (100) or (010) crystallographic orientations. U and Th were not co-located with Pb in these clusters and appeared to be homogeneously distributed in all three zircons. The analyzed domains had evidently experienced 4 to 8 × 1015 α-decay events per mg due to U and Th decay, and yet all zircons yielded U-Pb ages by SIMS that were better than 97% concordant, consistent with annealing of most radiation damage.
The 207Pb/206Pb ratios for the 100 nm-scale specimens measured by APT averaged 0.17 for ARG2.5, 0.42 for JH4.0, and 0.52 for JH4.4. These ratios were less precise (± 10–18% 2σ) due to the ultra-small sample size, but in excellent agreement with values measured by SIMS (0.1684, 0.4269, and 0.5472, respectively) and the crystallization ages of the zircons. Thus, Pb in these clusters appeared to be radiogenic, but unsupported, meaning that the Pb was not spatially associated with its parent isotopes of U and Th. For the domain outside of the clusters in JH4.4, the 207Pb/206Pb ratio was 0.3, consistent with the SIMS value of 0.2867 for the zircon overgrowth rim and a conventional age of 3.4 Ga. In ARG2.5, all Pb was concentrated in clusters and there was no detectable Pb remaining outside of the clusters. The Pb-Y-REE-rich clusters and lack of correlation with U in ARG2.5 and JH4.4 were best explained by diffusion of Pb and other elements into ~10 nm amorphous domains formed by α-recoil. Diffusion distances of ~20 nm for these elements in crystalline zircon were consistent with heating at temperatures of 800°C for ~2 m.y. Such later reheating events were identified and dated by APT from 207Pb-206Pb model ages of clusters in JH4.4 and by the absence of detectable Pb outside of clusters in ARG2.5.
SIMS dates for the zircon rims independently confirmed apparent reheating of ARG2.5 and JH4.4, which were assumed to be xenocrysts in younger magmas when the rims formed. Valley et al. (2015) proposed that most domains damaged by α-recoil were annealed at ambient temperatures above 200–300°C before the apparent reheating, and only a small number of domains were amorphous and available to concentrate Pb at the time of that reheating. The size, shapes, and orientations of clusters were apparently altered by annealing after formation. The absence of enriched clusters in JH4.0 showed that this zircon was apparently not similarly reheated. Thus, the APT data provided apparent thermochronologic information about potential crustal reworking, even for zircons where no overgrowths were recognized. The clusters in JH4.4 documented Pb mobility at the sub-50 nm scale, but showed that the much larger 20 μm-scale domains analyzed by SIMS were apparently closed systems.
The complementary data from SIMS and APT thus enabled Valley et al. (2015) to document atom-scale isotope and trace element distribution in these Hadean and Archean zircons. The APT showed that Pb, Y, and REEs were concentrated in ~10 nm clusters in the two supposed xenocryst zircons (4.4 and 2.5 Ga), which have younger rims that potentially document magmatic reheating. Quantitative measurements of the 207Pb/206Pb ratios provided nano-geochronological information. Pb in the clusters appeared to be radiogenic and unsupported by parent isotopes, as predicted by the α-recoil model for their genesis. That model proposes that incompatible elements diffused during reheating into amorphous domains damaged by α-recoil (Valley et al. 2014). In addition to zircon JH4.0 used in the Valley et al. (2015) study, a fourth zircon (14Q4 from the Moon, dated at 4.35 Ga) has been studied by APT (Blum et al. 2014), and neither of these zircons appear to have younger rims or contain clusters, likely ruling out later supposed magmatic reheating or high-grade metamorphism.
This first combined nano- and micro-geochronology study of multiple zircons by Valley et al. (2015) provided enhanced confidence in the criteria used for evaluating the fidelity of their geochemical records. The demonstration that Pb mobility occurred at sub-50 nm-scale to form clusters showed that longer-distance Pb transport likely did not occur, and that the much-larger 20 μm-scale volumes analyzed by SIMS were apparently closed systems. The existence of supposedly 4.4 Ga zircons, the oldest known on the earth, was thus believed confirmed. Likewise, the REE spectra and stable isotope ratios in these zircons were confirmed as primary, thus potentially reflecting magmatic compositions.
In contrast, Seydoux-Guillaume et al. (2015) studied selected zircon crystals from a pegmatite from Iveland, Norway, combining “in situ” and “in context” analyses by scanning electron microscopy (SEM), electron microprobe, and scanning transmission electron microscopy (STEM), as well as U-Pb isotopic analyses by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS). They provided nanoscale evidence for U-mobility during alteration of zircon. This has important consequences for the understanding of discordance of U-Pb geochronological systems.
The discordance observed by Seydoux-Guillaume et al. (2015) was characterized by a positive correlation between U content, Ca content, and the 238U/206Pb ratios paired with near-constant Pb content. It could have resulted from both U gain or Pb loss. Pb diffusion in crystalline zircon is very slow, according to Cherniak and Watson (2000). However, as already discussed, several studies have documented radiogenic Pb mobility, at least at local-scale. They have shown patchy distribution of Pb in the zircon structure, with Pb-rich clusters ranging from the micrometer scale (Kusiak et al. 2013) down to the nanometer scale (Utsunomiya et al. 2004; Valley et al. 2014, 2015). In monazite, Seydoux-Guillaume et al. (2003) also revealed small approximate 50 nm Pb-rich domains. If such clusters were over-represented in a microanalytical volume, then the analyses would be affected by apparent Pb gain, and the analyses would plot reversely discordant. If they were under-represented, then Pb loss would be apparent. Similarly, Fougerouse et al. (2018) investigated the nanoscale distribution of Pb in monazite from granulite facies rocks of the Sandmata Metamorphic Complex (Rajasthan, India) by atom probe microscopy. They found distinct 10 nm clusters in the monazite, enriched in Ca and with a bulk composition consistent with them being apatite (Ca5(PO4)3(OH)), that are also enriched in Si and Pb relative to the monazite host. Their 208Pb/232Th ratios indicated that the clusters hold unsupported Pb. The 208Pb/232Th ratios of the whole specimen (including clusters) and the matrix alone are similar (<6% difference), indicating that the clusters formed shortly after monazite crystallization by a phase exsolution mechanism that partitioned the initial common Pb and the minor radiogenic Pb into apatite. A volume-dependent analysis of the bulk monazite composition showed that a large variability in the Ca and, by proxy, Pb composition at small volumes (125 to 10,000 nm3) due to its heterogeneous distribution in the clusters, which Fougerouse et al. (2018) concluded may thus have detrimental effects on radiometric dating with small analytical volumes. At larger volumes, including those used in EPMA and traditional isotopic dating methods (LA-ICPMS, SIMS), the variability of Pb content is negligible. However, the measured composition may result from the mixing of multiple reservoirs.
Contrary to expectations, the zircon crystals from Iveland, Norway, analyzed by Seydoux-Guillaume et al. (2015) did not reveal any Pb-enriched anomalies, suggesting homogeneous behavior of Pb in radiation-damaged zircon. However, U is known to be less mobile than Pb in radiation damaged zircon. Nasdala et al. (2010) showed retention of original U oscillatory zoning in complexly altered zircon, supporting lack of preferential leaching of U. On the other hand, the main result of the Seydoux-Guillaume et al. (2015) study was to reveal that there are U-rich nano-domains, possessing a uraninite structure associated with the porosity of radiation-damaged zircon. These U-rich clusters could be interpreted as a product of solid-state separation (known as demixion) of a coffinite component (USiO4) from the magmatic zircon. However, three qualitative arguments suggested that the U was introduced into the zircon, which is included within plagioclase:
- Alteration of euxenite crystals (average UO2 = 11 wt%) into pyrochlore (average UO2 = 2.5 wt%) within the rock resulted in the liberation of a large amount of U and its transfer via fluid circulation though cracks;
- The negative correlations between Zr and U and between Zr and Ca, and the corresponding positive correlation between U and Ca support the model that U was then introduced into the zircon together with Ca in increasingly porous zircon; and
- The spatial association of U-rich domains with pores and especially the formation of a dense U-rich and/or Ca-rich layer coating the wall of some of the pores provided strong evidence that the U and Ca were both introduced into the zircon via the pores.
Seydoux-Guillaume et al. (2015) found that the zircon crystals included in xenotime were less altered than crystals included in plagioclase. Either they had a distinct initial magmatic composition, or they were partly sheltered by xenotime from open system exchange with the matrix. In any case, the zircon included in xenotime lacked U-clusters (in the less porous zone cut with the focused ion beam [FIB] and analyzed by STEM), lacked a negative correlation between the U and ZrO2, and therefore lacked indubitable evidence for U-gain.
The Iveland pegmatite is not foliated nor metamorphosed. However, Seydoux-Guillaume et al. (2015) found that swelling of the zircon and euxenite had occurred in response to radiation damage, which had resulted in the development of a network of brittle fractures formed over time, at the scale of the sample. A variety of platy micro-phases in the fractures, and of pyrochlore around euxenite, attested to alteration in low temperature conditions in the presence of a fluid phase. In these conditions, transport of the U in the fluid from euxenite to other minerals was realistic. Secondary monazite and xenotime found elsewhere in the Iveland–Evje area suggest that fluid-present alteration took place at a temperature below approximately 320°C (Seydoux-Guillaume et al. 2012).
The physical mechanisms of interaction between zircons and fluids have been the topic of a lively discussion. Geisler, Schaltegger, and Tomasc (2007) proposed two distinct mechanisms, called coupled dissolution-precipitation and diffusion-reaction, to account for the recovery of zircon in the presence of a fluid. They demonstrated that the active mechanism is highly dependent on the initial structural state of the zircon crystals. Crystalline zircon will be transformed by a coupled dissolution-precipitation process, whereas metamict zircon (with amorphous fraction > 30%) re-equilibrates by a diffusion-reaction process. Two crucial implications from these mechanisms concern the porosity and the chemical changes after reaction. Zircon crystals with undamaged structure interacting with a fluid results in new zircon crystals that may contain micrometer-sized pores and inclusions of U, or Th-silicate phases (for example, Corfu et al. 2003; Poitrasson et al. 1998; Soman et al. 2010). In the case of a diffusion-reaction process, a nano-porosity is developed, and non-formula elements like Ca, Al, Fe, and common (or initial) Pb are gained, and radiogenic Pb is lost (Geisler et al. 2003a, 2003b).
The development of the zircon crystals in the Seydoux-Guillaume et al. (2015) study may be described in two stages. First, zircon crystals containing high amounts of U became amorphous and swelled. This volume increase was responsible for the formation of cracks around the zircon crystals. Partial recrystallization of such structure resulted in the formation of nano-pores, which provided a preferential pathway for fluids. During a second alteration episode, euxenite crystals (also self-irradiated) interacted with the fluids, which resulted in the liberation of U and Ca (via alteration of euxenite into pyrochlore). The fluids then transported the U and Ca through cracks at the zircon-fluid interface within the zircon crystals. Hydrous species diffused inwards allowing structural recovery and formation of nano-pores. The close association of the U and Ca with such nano-pores demonstrated that both elements were transported together by the fluids inward into the zircon and precipitated as UO2 and CaO within these nano-pores, sometimes coating the walls of the pores. Thus the U was neither incorporated into the zircon structure, nor exsolved from the zircon as a U-silicate phase. Common (or initial) Pb was also probably transported by the fluids at the same time as the Ca and U, as demonstrated by the high 207Pb/206Pb ratios in some of the analyses. The Seydoux-Guillaume et al. (2015) study may thus be the only one that has demonstrated nano-evidence of U-enriched domains in zircon.
The pegmatite sample from Iveland used by Seydoux-Guillaume et al. (2015) in their study was an atypical U-rich rock containing radiation-damaged zircons. In contrast, for the purpose of a targeted geochronological study, it is thus clear that such zircons would be typically avoided. However, these zircons carried important information on the discordance process. For the Iveland pegmatite, the discordance on the U-Pb concordia diagram combined radiogenic Pb loss and the introduction of unradiogenic Pb and U. The scattered discordia trends with upper and lower intercept ages (approximately 825–240 Ma and 640–250 Ma) are distinctly younger than the supposed intrusion age of the pegmatite field (approximately 920 Ma), and indicate that more than one of these processes likely took place during several episodes or periods. Extracting meaningful geochronological information from such data is highly speculative. The data suggested that minor U-uptake in zircon from other radiation-damaged minerals, for example, allanite, euxenite, or thorite, is possible, and probably more common than generally assumed. Cumulated with the effect of Pb-mobility, U-mobility results in scatter or inaccuracy of discordia lines and consequently in the potential geochronological information.
Subsequently, Piazolo et al. (2016) were quick to point out that although experimental determinations of diffusion rates within pristine zircons have shown that substantial Pb diffusion should only occur at extreme temperatures (Cherniak and Watson 2003), there is some evidence that Pb diffusion can take place at lower temperatures (Geisler 2002). This is often attributed to the annealing of regions of radiation damage within the crystalline lattice (Mezger and Krogstad 1997; Williams et al. 1984). Such damaged (metamict) domains are only partially crystalline, may be porous (Hay and Dempster 2009; Mezger and Krogstad 1997), and are usually cited as the cause of either relative Pb-loss (discordance) or Pb-gain (reverse discordance) recorded on the μm scale (Hay and Dempster 2009; White and Ireland 2012; Williams et al. 1984). Yet studies have shown diffusion only over small distances (<100 nm) resulting in Pb clusters (Gray and Zeitler 1997) and some μm-scale redistribution (Kusiak et al. 2013). Although measurable changes in trace element concentrations have been linked to μm-scale deformation structures (Piazolo, Austrheim, and Whitehouse 2012; Reddy et al. 2007; Timms, Kinny, and Reddy 2006), atomic-scale evidence of the relevant processes is lacking. Consequently, Piazolo et al. (2016) maintained that it is not yet possible to predict how these changes may influence the accuracy of U-Pb dating.
Piazolo et al. (2016) therefore presented an atomic-scale study of a ~2.5-Ga-old zircon grain using a range of high-end microanalytical techniques including atom probe tomography (APT) (Larsen et al. 2013), high-resolution electron backscatter diffraction (EBSD), transmission Kikuchi diffraction (TKD) (Trimby 2012), and a sensitive high-resolution ion microprobe (SHRIMP). The zircon selected for their study needed to satisfy three main criteria:
- A sufficiently high U and Pb content to allow reliable, statistically robust detection of radiogenic isotopes using APT;
- A known crystal-plastic deformation history to enable an understanding of the link between deformation and element mobility; and
- A sufficiently long time after the main deformation event(s) to allow an assessment of the importance of pre-existing deformation structures on trace element/isotope mobility in a static regime.
Previous studies had shown that the chosen zircons met these criteria.
The correlation between the deformation microstructures and the atomic-scale distribution of trace elements in this zircon allowed Piazolo et al. (2016) to determine the mechanisms of trace element movement and segregation in a deformed mineral. The zircon analyzed had apparently been affected by a series of high temperature deformation events at common “geological” strain rates (~10-11–10-16 sec-1) with peak temperatures exceeding 980°C (Harley 1985, 1987; Hokada 2001; Lund, Piazolo, and Harley 2006). The exact timing of these events had been the subject of much discussion, but the general conventional consensus was that there was high temperature formation and deformation of these zircons at around 2.55–2.45 Ga, followed by some weaker, lower temperature (~500–600°C) retrograde deformation.
Piazolo et al. (2016) believed that the dislocation array (an alignment of crystallographic defects due to atoms being dislocated) in their APT traverse 1 was formed during the early stages of deformation at relatively high temperatures (>800°C) enabling dislocation movement through the lattice by both glide and climb. Thus, the high temperatures had resulted in higher lattice diffusion rates within the crystal lattice, which enlarged the capture zone, although the bonding of trace elements to the dislocation core may have been weakened. At the same time, at high temperatures, the elastic strain may have been dissipated by increased dislocation movement. The higher level of dislocation movement, together with an enlarged capture zone (outweighing the effect of a possible weak element-dislocation bond), meant that much of the zircon lattice volume was at some point in time in a dislocation capture zone, resulting in large volumes becoming solute depleted (see fig. 7, Stage I). At the same time, the dislocations themselves became enriched (fig. 7, Stage I), as at the geologically slow strain rates the solutes remained captured.
Fig. 7. Schematic diagram showing the link between element redistribution and dislocations (after Piazolo et al. 2016). This diagram illustrates their proposed stages of dislocation formation and movement and associated trace element mobility within this zircon grain. Only the trace elements U, Pb, and Al are considered, with active processes shown in italics.
Piazolo et al. (2016) regarded the absence of detectable Pb in the dislocation array in their APT traverse 1 as striking. However, the presence of a relatively high amount of U in that array, presumably swept into the array during its formation, would have necessitated the presence of a significant amount of radiogenic Pb (see fig. 7, Stage II). Given the presumed age of this zircon and the concentration of U in the array, they expected ~550 ppm of Pb to be present in that array. The Pb must therefore have diffused along the dislocation array into the structural sink at either end—namely, the porous metamict domains. In effect, the Pb was “successfully” lost from the dislocation array (see fig. 7, Stage III). SHRIMP analyses of such metamict domains did indeed show a reverse discordance with higher than expected Pb levels. This process must have been ongoing throughout the history of this sample, even after the deformation event and at lower temperatures. This was unequivocal evidence for pipe diffusion (the process of relatively rapid diffusion of atoms through dislocation cores) along a dislocation array in zircon, resulting in relatively fast and continuous redistribution of Pb over >10 μm.
Reverse discordance had been the subject of a number of studies (Butera et al. 2001; Hay and Dempster 2009; McLaren, FitzGerald, and Williams 1994; White and Ireland 2012; Williams et al. 1984) and is generally observed in high-U zircons (above a threshold of ~2500 ppm U). The phenomenon had been attributed to possible matrix effects, causing increased relative sputtering of Pb from high-U, metamict regions, and resulting in a 1–3% increase in 206Pb-238U ages for every 1000 ppm U (White and Ireland 2012). However, in the zircon analyzed by Piazolo et al. (2016), the relationship between U content and reverse discordancy was not simple. Several points showed a degree of reverse discordance despite having U concentrations below 2000 ppm, whereas the highest measured reverse discordancy (21%) was from a location with 3102 ppm U, only just above the threshold for which reverse discordancy is normally attributable to matrix effects. In contrast to analyses exhibiting some degree of reverse discordance, they interpreted that the chemical signal of that spot represented a domain that was completely metamict. Although they could not rule out some matrix effects in the high-U metamict zones, the complex relationship between U content and reverse discordancy in this zircon was further evidence for an additional process of Pb-enrichment—namely, the pipe diffusion of Pb along dislocation arrays into adjacent metamict zones.
In their ATP traverse 2, the dislocations had not formed into well-ordered arrays, indicating little high-temperature recovery had taken place. The lack of Al in both the matrix and dislocations in traverse 2 and its proximity to the low-angle boundary in traverse 1 suggested that the dislocations forming the array in traverse 1 had already passed through this volume, collecting the majority of the solute atoms, especially Al, and to a lesser extent U and Pb. As a consequence, there was only a slight enrichment of “swept” U in the dislocations of their traverse 2 (see fig. 7, Stage II). In the dislocations, Pb concentrations were too high to be explained by radioactive decay of U alone. Piazolo et al. (2016) believed that the Pb clustering in particular areas along that dislocation was further evidence for its localized redistribution through pipe diffusion along dislocation cores (see fig. 7, Stage III). However, in contrast to their traverse 1, the lack of a physically continuous connection to a sink led to “unsuccessful” pipe diffusion, that is, there was no loss of Pb from the dislocation (fig. 7, Stage III). Consequently, at the μm scale, no element redistribution took place. Radiation damage may have enhanced this pipe diffusion/clustering behavior. The phenomena they observed here was quite similar to the segregation and clustering behaviour around dislocations in metals (Xie et al. 2012).
Even though, in the field of materials science, pipe diffusion plays a very important role in governing the properties of advanced materials, affecting nucleation, corrosion, creep, and dynamic strain-ageing (Luo, Shen, and Wang 2007; Picu and Zhang 2004), it has proven to be extremely difficult to demonstrate or measure its effects experimentally, as processes are too fast to allow a time-resolved study. The zircon studied by Piazolo et al. (2016) provided a unique opportunity to investigate this phenomenon with a control on timing, as the continuous production of elements through radioactive decay was time dependent. Consequently, the Piazolo et al. (2016) study was as close as possible to an “in situ” study, which allowed the construction of a robust model with regard to ongoing processes through time. Therefore, they were able to provide unprecedented evidence of pipe diffusion along a dislocation array.
The results from the Piazolo et al. (2016) study demonstrated the importance of deformation processes and microstructures on the localized trace element concentrations and continuous redistribution from the nm to μm scale in zircon. Dislocation movement through the zircon lattice can effectively sweep up and concentrate solute atoms at “geological” strain rates. Dislocation arrays can act as fast pathways for the diffusion of incompatible elements such as Pb across distances of >10 μm if they are connected to a chemical or structural sink. Hence, nominally immobile elements can become locally extremely mobile. And not only did their study confirm recent speculation that an understanding of the deformation microstructures within zircon grains is a necessity for subsequent, robust geochronological analyses, but it also sheds light on potential pitfalls when utilizing element concentrations and ratios for geological studies.
However, Villa (2016) maintained that Kusiak et al. (2013) and Valley et al. (2014) have clearly demonstrated, by high-resolution imaging and spatially resolved U-Pb dating, that radiogenic Pb likely only moves by a few nm at most in zircon, even under extremely high temperature conditions. This would appear to force a complete overhaul of the concept of discordant U-Pb ages in metamorphic rocks as due to “diffusive Pb loss” (Tilton 1960). In that view, which still partly persists, data points plotted on a concordia diagram are shifted towards the origin of the coordinates as they lose radiogenic Pb by volume diffusion. The discordia arrays in concordia diagrams are thus considered as indicating the movement of the Pb isotopes. However, as radiogenic Pb is claimed to be essentially immobile (Cherniak and Watson 2000; Kramers et al. 2009), Villa (2016) maintained that radiogenic Pb ions are held in the zircon grain with a near-infinite energy barrier to diffusion. Therefore, Villa (2016) argued that what can happen instead during chemically open-system metamorphism is the accretion of a discrete, heterochemical ZrSiO4 rim. Thus, he claimed that the two radiogenic Pb populations never exchange, but when the rim and the core of a grain are analyzed together their sum lies on a discordia. In his view, discordia arrays are static effects of phase mixing. Points do not plot towards the origin due to diffusion but stay fixed in the location indicated by mass balance of the mixture and co-rotate rigidly with the concordia as time passes. By co-rotate is meant that the points on each discordia rotate in lock step with the rotation of the concordia as time passes.
Of course, with the technology now available, it is possible to acquire spatially resolved analyses and/or produce the stepwise release of the relevant isotopes in the U-Pb system. However, as Villa (2016) pointed out, one very sensitive issue is whether the spatial resolution that is ultimately achieved in a U-Pb dating experiment is sufficient to reliably resolve the petrological structures of the analyzed mineral. In principle, lasers can be focused to beam diameters of < 1 µm, which is similar to the spatial resolution with which electron microprobes allow the identification of heterochemical sub-grains. In practice, however, present-day mass spectrometers require a sample volume of at least 1000 µm3 to achieve sufficient precision. This has the consequence that very often the size of the ionizing beam must be made larger than the microstructures of the analyzed sample, resulting in mixed isotope signatures and blurring the connection between textures and ages.
Furthermore, cathodoluminescence (CL) images, now routinely used in most U-Pb laboratories worldwide, often reveal discrete growth zones that can be texturally very different in grains of zircon, monazite, allanite, titanite, rutile, etc. To Villa (2016) the question that thus arises is whether this petrologic evidence can be linked to dating the formation of the different sub-grains. The 208Pb/206Pb ratios are presumably a measure of the Th/U ratio of the zircon grain, and are easily accessible by TIMS measurements. Additional information on the chemical signature of the zircon’s growth zones is possible using microbeam analyses (SIMS or LA-ICP-MS) by measuring the radiogenic Pb/U ratio in a 20 µm diameter spot, and on the same spot also the REE pattern (Whitehouse, Kamber, and Moorbath 1999). The significance of this interplay of petrology and isotope geochemistry cannot be overstated (Vance, Müller, and Villa 2003; Villa and Williams 2013; Whitehouse 2003; Williams, Jercinovic, and Hetherington 2007). What emerges is a pattern whereby virtually all mineral chronometers analyzed in sufficient detail reveal the admixture of heterochemical phases and thus an admixture of their U-Pb data, which blurs the resultant geochronological interpretations.
More recently, recognizing that lattice defects in zircon can cause disturbance of isotopic systems, Kovaleva and Klötzli (2017) investigated in detail how seismically induced deformation microstructures in zircon correlate with isotope re-equilibration. They studied zircons from felsic mylonites with pseudotachylite veins in northern Italy and found in them post-growth deformation microstructures, namely, planar deformation bands (PDBs), planar fractures (PFs), non-planar fractures (both healed and open), and finite strain patterns. Several grains, in which PDBs were observed, were analyzed with an ion microprobe. Ion maps indicated redistribution of radiogenic Pb isotopes associated with PDB formation. The 207Pb/206Pb ratios demonstrated systematic Pb loss in the PDB-bearing lattice domains with respect to PDB-free domains. In some cases, Pb gain was observed where the PDBs had apparently sourced radiogenic Pb from older detrital cores. Kovaleva and Klötzli (2017) concluded that their results have important implications for geochronology, as zircons found in seismically deformed rocks may demonstrate distorted and even reset isotopic ages.
Finally, Ge et al. (2018) investigated a detrital zircon grain from the Jack Hills, Western Australia, with 4425–4486 Ma concordant ion microprobe ages that yielded a concordia age of 4463 ± 17 Ma (2σ), the oldest zircon age recorded on the earth. However, scanning ion imaging revealed that this >4.4 Ga apparent age had resulted from incorporation into the zircon grain of micrometer-scale patches of unsupported radiogenic Pb with extremely high 207Pb/206Pb ratios and >4.5 Ga 207Pb/206Pb ages. Using isotopic modeling, Ge et al. (2018) sought to demonstrate that these radiogenic Pb enriched patches likely resulted from redistribution of radiogenic Pb in a ca. 4.3 Ga zircon during a ca. 3.8 Ga or older event. They concluded that this highlights that even a concordia age can be spurious, and thus should be carefully evaluated before being interpreted as the crystallization age of an ancient zircon grain. However, how many investigators have had these sophisticated tools available to them to use to check every concordia age obtained? If this one zircon grain had its radiogenic Pb mobilized and concentrated in micrometer-scale patches that caused its concordia age to be apparently older by almost 4%, then how many other concordant ages may have been similarly affected? Clearly, the mobility of radiogenic Pb atoms at the μm scale has been demonstrated as a potential problem for obtaining reliable concordant absolute ages.
Differential Mass Diffusion
Hayes (2017) has asserted that there is a key flaw in the radioisotope dating methodology, which thus far has been overlooked. It would have resulted in over-estimation of isochron ages, including those obtained from U-Pb isotopic data. The Pb isotope ratios are reasonably assumed to be influenced only by radioactive decay of U and Th into Pb. However, as Hayes (2017) has pointed out, that assumption does not take into account differential mass diffusion—the tendency of different atoms to diffuse through materials at different rates. Thus 206Pb atoms can diffuse (or leak) more readily than 207Pb and 208Pb atoms, simply because 206Pb atoms are smaller. Hayes (2017) claimed that this differential diffusion of 206Pb, 207Pb, and 208Pb may contribute to a linear distribution of the 207Pb/206Pb and 208Pb/206Pb ratios, as in an isochron. Any such linear bias that might occur from this isotope diffusion effect would then have to be corrected in applying the isochron radiometric dating methodology to the isotopic ratios.
There are two mathematical models for diffusion through a solid. These are steady state and dynamic diffusion corresponding to the well-studied Fick’s first and second laws, respectively (Mehrer 2007). The driving force in diffusion is a concentration gradient attempting to homogenize all substances at microscopic scales. Until the concentration gradient is allowed to taper off to closely approach zero due to the diffusion process, the diffusion of each isotopic species can be expected to follow Fick’s second law. Of course, geochronologists would argue the close-to-zero condition would be slowly approached over geological timescales, so such diffusion has not been considered a problem in isochron dating.
However, the diffusion coefficient is expected to be different for each isotope for a given matrix in accordance with each’s differences in mass, chemical bonding, defect types, and concentrations. Diffusion from and around grain boundaries can be expected to be the dominant effect when the samples being dated include grain boundaries in the rock matrix. This would be the case for all rock samples, even those from which the minerals such as zircon are separated for U-Pb dating. All rock samples have large fractions of grain boundaries, so they would all suffer from these more egregious diffusion effects.
There are multiple approximations to account for the mass effect, beginning with the approximation that the vibrations in a crystal lattice all have the same harmonic frequencies. The atomic bonding between like atoms in a crystal having the same strength is also a good approximation, although the approximation of a mass dependence may give better overall results. In either case, the approximation of a classical spring being the atomic bond between adjoining atoms gives rise to the mass effect of the oscillation frequency. Thus the square of the vibrational frequency is inversely proportional to the isotopic mass of a diffusing atom.
A frequency distribution gives the basic mechanism driving lower mass isotopes to diffuse faster than larger mass isotopes. This means the frequency for 206Pb vibrations is slightly greater than that for 207Pb at all temperatures for which the material is solid (which includes room temperature). Over supposed geological timescales, Hayes (2017) maintained that this should not simply be assumed to result in a negligible frequency factor without sufficiently supporting measurement verification. This becomes particularly true for samples that include large fractions of grain boundaries. The relative scale of increasing diffusion effects in solids is smallest for vacancy diffusion followed by interstitial diffusion, with grain boundary diffusion being the largest potential mechanism when it is available. This contributes to a sample-specific isotopic mass diffusion effect, since impurities, defects, and grain boundary contributions can vary substantially within a single rock sample if granular inclusions are present.
Hayes (2017) discussed how solid-state diffusion can take place through multiple means. These include interstitial, vacancy, and even multi-vacancy mechanisms. Diffusion can occur on the surface of a rock, through grain boundaries, and directly through the volume of a rock (albeit at much slower rates). The most significant of these sites is along the surface of the rock, followed by transport along grain boundaries. These diffusion mechanisms generally all follow a diffusion coefficient temperature dependence. When multiple diffusion mechanisms are taking place, the product of the individual diffusion coefficients leaves the overall temperature dependence unchanged. Similarly, because the diffusion is exponential, the resultant overall activation energy for the diffusion is the sum of the individual activation energies.
This mass diffusion of isotopes effect is not widely discussed in the geochronology literature. In solids, the diffusivity of one material through another still depends on mass. This means that depending on the chemical bonding of the Pb isotopes, the 206Pb should in general diffuse faster than the 207Pb and 208Pb through a material. A similar difference in diffusion rates is known between 234U and 238U, the lighter 234U (which decays to 206Pb) more readily diffusing than the heavier 238U. Hayes (2017) noted that the atomic radius of Rb is 20% larger than that of Sr, making both Sr isotopes in general more diffusive (Mantina et al. 2009). Because 86Sr is smaller in mass than 87Sr, 86Sr is the more diffusive of these three isotopes. So he focused his subsequent discussion on the Rb-Sr system, though still applying the demonstrated differential mass diffusion effect to the U-Pb system. Indeed, the separation of these isotopes by such differential mass diffusion has the potential to create a natural isotopic distribution independent of radioactive decay in a sample being dated.
To assess the effects of this isotope diffusion based on considering all these discussed mechanisms, Hayes (2017) carefully performed numerical simulations of diffusion from a point source. Evaluating the effects of only the 87Rb/86Sr and 87Sr/86Sr ratios, he found that the basic principles at play are the mass effect and chemical bonding related effects. For the 87Sr/86Sr ratio, 86Sr has a smaller mass, which results in the distribution of the lighter isotope being represented by a higher standard deviation parameter than that of the heavier isotope after diffusion. A similar result is also true for the 87Rb/86Sr ratio, although it is reasonable to expect that under unique circumstances, chemical bonding forces could provide the dominant effect in the diffusion coefficient. Because the radius of Rb is larger than that of elemental Sr by approximately 20% (Mantina et al. 2009), so that in general Sr isotopes should all diffuse measurably faster than those of Rb. However, Hayes (2017) found that the only fundamental statement that can be applied to all scenarios is that there is no reason to expect in general that any of these isotopes will diffuse at the same rate through any material with time and that this effect should be considered in isotopic dating of rock samples.
There were three different potential regimes for the magnitude of the diffusion coefficients and activation energies in Hayes’ numerical simulations. It was a requirement that the diffusion of 86Sr was greater than the diffusion of 87Sr due to the isotope effect on identical elements. Still, in principle, the diffusion could end up in any relationships, although the most expected case is that of 86Sr > 87Sr > 87Rb because of the larger atomic size of Rb relative to Sr making Sr more diffusive in general. Assuming equal concentrations and activation energies having negligible differences, Hayes’ results produced almost linear plots. What was rather revealing though was that these could easily be mistaken for linear relationships, as in isochron lines, if only a few data points were chosen from the 50 defining each plot. Hayes (2017) emphasized how significantly this applied to isochron dating studies, because in the dating literature it is usually normal for a geological age to be ascribed using fewer than seven data points to define the isochrons. Based on his analysis, obtaining an isochron-like linear plot is virtually guaranteed based on this differential isotope diffusion effect alone!
Hayes (2017) established that almost all rock and mineral samples which are affected by differential diffusion of isotopes will have some non-linearity in the distribution of their isotopic ratios. That distribution can then be related back to the bias from this differential diffusion effect independent of the purely linear distribution caused by radioactive decay. Unless that is done, Hayes (2017) demonstrated that the resultant isochrons will be wrongly estimating the true ages of the rocks and minerals. He emphasized that such differential diffusion is an inescapable reality in rocks and minerals, including in the U-Pb system. This is because the parent radioisotopes (238U, 235U, and 232Th) and their daughter products (206Pb, 207Pb, and 208Pb respectively) are not the elements which form the minerals in the rocks being dated (for example, zircon), but are merely trace elements that substitute into, or are trapped inside, the crystal lattices of rock-forming minerals. As such they are held more loosely in the crystal lattices and thus are much more likely to diffuse than any of the major elements that are more tightly bonded to form the mineral crystals. This is exactly what the many studies already discussed have shown. Hayes (2017) concluded he had demonstrated that the simplest approach to remove solid-state mass diffusion effects that would have occurred would be not to use isotopic ratios in dating samples, an assertion at direct odds with the work done by geochronologists.
Hayes (2017) proposed two solutions. First, the differential diffusion effects on the parent and daughter isotopes in each sample (rock or mineral) to be used in a U-Pb dating study should first be individually assessed and potentially quantified. Only then can such effects be removed when using the isotopic ratios in question to plot isochrons and determine the ages of rocks and minerals. And second, alternately, careful statistical analyses should be undertaken of the isotopic ratios obtained and of the isochrons they plot on to determine and eliminate the differential diffusion effects. Only then could the “corrected” isotopic ratios be used to plot “corrected” isochrons to obtain seemingly more reliable ages for the rocks. But this is a very subjective approach, because such statistical tools are designed to weed out isotopic ratios that do not plot tightly on isochron and concordia plots, and yield what are then considered viable ages for the rocks. It could be instead that the isotopic ratios which plot on the isochron or concordia are actually the ones most affected by differential diffusion, which produces the linear plots resembling isochrons and discordias! Furthermore, Hayes (2017) also suggested that a rigorous statistical analysis sufficient to discriminate a linear from a nonlinear distribution is generally not possible without a much larger number of sample points, as many as 30, a number of sample points rarely achieved in U-Pb dating studies.
The only other alternative Hayes proposed is to remove the edges of the mineral grains separated for isotopic analyses before proceeding to the mass spectrometer determinations of their isotopic ratios. This suggestion is based on the premise that the two dominant components of differential diffusion occur along the surfaces of rocks and the edges of minerals, and between and along the grain boundaries. By removing the grain boundaries, one effectively removes those two dominant components of the differential isotopic diffusion that has occurred. Yet even then there is no guarantee that all grain boundaries have been removed and thus the effects of the dominant differential isotopic diffusion have been eliminated.
Sample Treatments Before U-Pb Dating
In practice, these problems of discordance and differential mass diffusion in zircon are regarded as having been solved by geochronologists, who are careful to select well-crystalline zircons for dating, and who apply mechanical or chemical abrasion to the grains before isotope analyses (Krogh 1982b; Kryza et al. 2012; Mattinson 2005). It is claimed these methods efficiently remove radiation-damaged zircon grain rims, leading to concordant analyses of grain cores (Corfu 2013). However, the development of microanalytical methods addressing large populations of zircon grains in both magmatic and sedimentary rocks (Gehrels et al. 2011), and for both geochronological and isotopic tracing purposes (Scherer, Whitehouse, and Münker 2007; Valley et al. 2005), justifies more detailed investigations of the mobility of elements and their isotopes during alteration of zircon.
Those investigations have provided insights which suggest yet another possible mechanism for the discordance of U-Pb dates derived from bulk zircon samples consisting of several hundred crystals each. Such samples are mixtures of cores and overgrowths in different proportions that define straight lines between points on a concordia diagram, which represent mixing between the isotopic Pb compositions of the cores (upper intercept) and that of the overgrowths (lower intercept). In such cases, the position of a particular zircon sample on the discordia is controlled by the proportion of cores and overgrowths in that sample. Various approaches attempt to overcome this problem. First, physical abrasion of zircon grains to remove altered (metamict) grains and altered outer layers of grains, after they have been magnetically sorted and handpicked from heavy liquid separates from the crushed rock (Krogh 1982a, 1982b; Goldich and Fischer 1986). Subsequently, Mattinson (2005) developed the chemical abrasion technique to similarly pre-treat zircon grains prior to their isotopic analysis. And second, by the development and use of secondary-ion mass spectrometry (SIMS) in instruments such as the SHRIMP (Sensitive High Resolution Ion Micro Probe) (Compston 1999) that are capable of focusing a collimated O2- ion beam on a small spot of a polished cross-section of a zircon grain (Smith et al. 1998; Williams 1998). However, one must be certain the small analytical spots are hopefully wholly within cores and overgrowth zones of the zircon crystals. So the polished cross-sections are often checked by back-scattered electron images after the SHRIMP analyses are done, because the pits left by the ion beam are visible and thus their locations within the zircons’ growth zones are verified.
The isolation and analysis of zircon crystal domains that have remained closed systems have been the major challenge for U-Pb geochronology. Most of the radiation-induced property changes previously discussed would appear to have been taken into account when selecting the least damaged zircon material for dating. Exposing a large number of grains to NaOH or hydrofluoric acid (HF) for several hours at 220°C makes altered and damaged domains visible and allows selection of grains that yield concordant U-Pb systems (Krogh 1994, 1998; Krogh, McNutt, and Davis 1982). Another approach is laboratory abrasion of crack and alteration-free zircon grains to remove geologically exposed surfaces. This typically produces data within 1% of concordia (Krogh 1982b) and is thus the most widely used method in isotope dilution analyses. Ion microprobes (for example, Compston et al. 1986) have also been used to isolate and analyze 30-μm-sized domains but at a reduced precision. These methods are difficult to apply in cases where all zircon grains are severely cracked or where alteration has extensively penetrated along thin high-U crystal zones.
Chemical dissolution has also been used to isolate least-damaged, more concordant crystal domains. Highly-damaged and altered zircon dissolves in minutes in HF at room temperature, whereas undamaged grains require several days at 220°C in high pressure Teflon capsules (Krogh 1973). Using a step-wise HF dissolution method, Mattinson (1994) was able to isolate near-concordant fractions from Cretaceous zircons by chemically removing most of the sample. In later studies, Mattinson (1997) noted that excess radiogenic Pb and 234U were leached by this dissolution method from α-recoil-damaged crystal sites in some samples, leaving a discordant residue with fractionated Pb isotopes. Partial HF dissolution is an attractive method because it can dissolve out damaged domains at the micron scale. However, it might also leach radiogenic Pb from damaged crystal lattice sites in domains that have not achieved a metamict, soluble state, thereby inducing discordance. Such effects have been documented by Mattinson (1997) and Corfu (2000).
Von Quadt et al. (2014) reviewed the methodology in current use in chemical abrasion isotope-dilution thermal ionization mass spectrometry (CA-ID-TIMS), which is well known as a high precision technique for resolving Pb loss and improving the interpretation of U-Pb zircon age data. Von Quadt et al. (2014) then argued that combining CA with the widely applied laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) improves the precision and accuracy of zircon dates, while removing the substantial parts with Pb loss, reducing data scatter, and providing potentially more meaningful geological interpretations.
To demonstrate this, von Quadt et al. (2014) chose for their investigations samples of magmatic rocks from different geological time periods (one Paleozoic, one Mesozoic, and three Cenozoic). All the zircon separates were analysed by LA-ICP-MS before and after CA, and the resultant age data were compared with CA-ID-TIMS 206Pb-238U dates, which were considered the most accurately obtainable ages. All CA-treated zircon crystals showed up to 50% less data scatter compared to the non-CA-treated zircon grains. Thus reduction of the calculated uncertainties was apparent. The obtained weighted average LA-ICP-MS 206Pb-238U ages of the CA-treated zircon grains were up to 4–6% higher than those of the non-CA treated crystals, exceeding the analytical uncertainties of the LA-ICP-MS dating technique of 1–2%. The damaged crystal parts, caused by U-decay with Pb loss, had been removed, so that they could potentially exclude younging from the possible geological scenarios. Thus, because the CA-LA-ICP-MS age data were in good agreement with the CA-ID-TIMS dates, von Quadt et al. (2014) suggested that using CA-LA-ICP-MS has advantages in defining accurate ages. They also concluded that the use of the CA technique for very young zircons seemed optional, as the obtained mean 206Pb-238U ages of non-CA and CA treated young zircons coincided within the uncertainty. The negligible relative time to produce the lattice damage by α-decay and spontaneous fission made Pb loss less important for age dating and data interpretation of very young zircons (<1 Ma).
Crowley et al. (2014) also warned that although the U-Pb system in zircons has proven to be a robust chronometer, it can suffer from Pb loss or elevated common (or initial) Pb, both of which impede precision and accuracy of age determinations. Thus the chemical abrasion of zircon methodology was developed, which involves thermal annealing followed by relatively low temperature partial dissolution in HF acid. It was specifically developed to minimize or eliminate the effects of Pb loss prior to analysis using TIMS. Crowley et al. (2014), like von Quadt et al. (2014), tested the application of chemical abrasion to LA-ICP-MS by analyzing zircons from both untreated and chemically abraded samples. They found that rates of ablation for high α-dose non-treated zircons were up to 25% faster than chemically abraded equivalents. Ablation of the 91500-zircon reference material demonstrated an approximate 3% greater fractionation of 206Pb/238U ratios down inside the ablation pits (holes) in non-treated zircons. Crowley et al. (2014) concluded that these disparities thus necessitated using chemical abrasion for both primary reference material and unknowns to avoid applying an incorrect laser-induced fractionation correction. Since all treated samples displayed a marked increase in the degree of concordance and/or the lowering of so-called common Pb, they argued that this thereby illustrated the effectiveness of chemical abrasion to LA-ICP-MS U-Pb zircon geochronology.
Solari, Ortega-Obregón, and Bernal (2015) also commented how U-Pb zircon dating by LA-ICP-MS is now one of the most popular geochronological techniques. However, they admitted that it still suffers from some accuracy and precision problems. These problems, they suggested, are mostly due to the slight differences in behavior between zircons, and the differential coupling of isotopes by the laser radiation, which probably results from the crystal damage induced by the radioactive decay of U and Th. These problems, they admitted, thus result in difficult-to-predict and even irreproducible matrix effects, impinging on the precision and accuracy of the technique.
Therefore, Solari, Ortega-Obregón, and Bernal (2015) explored the effect that thermal annealing has on the analyses of zircons by LA-ICP-MS, in order to improve the U-Pb age dating results obtained. They documented the advantages of thermal annealing by means of two experiments on zircon standards and several igneous zircons, spanning different degrees of crystallization history complexity. In general, they found that the pre-treatment of the zircons by thermal annealing yielded more accurate ages—for example, 336.87±0.49 Ma for the annealed Plešovice standard zircon, versus 340.24 ± 0.49 Ma when not annealed, with significantly less dispersion, the MSWD (the mean weighted squared deviates statistical measure) decreasing as much as 80%. They also demonstrated that the thermal annealing significantly reduced the scatter of the trace element data in zircon, yet it preserved the primary characteristics, such as the differences in overgrowth compositions. They concluded that this method enabled the production of more accurate U-Pb ages.
Huyskens, Zink, and Amelin (2016) also reiterated that the partial loss of radiogenic Pb and the presence of older grains or cores (presumably by assumed inheritance) are the main obstacles for accurate and precise U-Pb geochronology of magmatic zircons by ID-TIMS. Sequential annealing and leaching, otherwise known as chemical abrasion (Mattinson 2005), is thus aimed at restoring crystallinity to zircons with low to medium radiation damage, and removing parts of the zircons with strongly radiation-damaged crystal lattices, hoping to effectively eliminate Pb loss. Huyskens, Zink, and Amelin (2016) noted that the original version of chemical abrasion (Mattinson 2005) was designed for determination of precise 206Pb-238U plateau ages of multi-grain zircon populations, free from inheritance, using multiple dissolution steps. However, currently, the main application of chemical abrasion is to date zircon grain populations potentially affected by both Pb loss and inheritance, and this is commonly achieved by analyses of single zircon grains. The procedure involves the chemical abrasion of single zircon grains via only one high temperature leaching step, since stepwise leaching is rarely possible or practical due to the small sample sizes. Yet despite the widespread use of single zircon chemical abrasion, Huyskens, Zink, and Amelin (2016) noted that the optimal temperature and duration of annealing in single step leaching had thus far not been reported. Furthermore, the temperature and time durations of chemical abrasion (apparently ad hoc adaptations of the findings of multi-grain, multi-step leaching experiments) varied substantially between published geochronological studies, leaving the possibility of incomplete removal of zones affected by Pb loss and hence a potential bias in the comparison of the resultant U-Pb ages.
Therefore, Huyskens, Zink, and Amelin (2016) reported the results of their systematic study, which was aimed at determining the optimal conditions for the chemical abrasion of single zircon grains in a single high temperature leaching step to ensure the complete removal of zones affected by Pb loss. Their tests were performed on three different zircon standards with various conventional ages (~418 to 3465 Ma) using a three-step partial dissolution technique. They found that the optimal conditions for low to moderately radiation-damaged zircons are annealing at 900°C for 48 hours and subsequent leaching at 190°C (or slightly higher) in concentrated HF in a pressurized vessel for 15 hours. Additionally, leaching at a lower temperature did not completely remove zones affected by Pb loss. And annealing at a higher temperature might have restored crystallinity to those parts of zircon crystals that had been affected by Pb loss.
Discussion
Amelin et al. (2009) commented that it is necessary to study the distribution of U and radiogenic Pb in order to understand the processes which start and reset isotopic clocks, as well the migration of U and radiogenic Pb caused by diffusion, alteration, and shock. Furthermore, they admitted that the significance of some potential problems of deviations from closed system behavior “cannot be estimated at the present level of knowledge,” and thus they require “detailed and theoretical studies.” Yet such detailed studies have been undertaken, including those at atomic scale, and the significance of potential problems of deviations from closed system behavior still cannot be estimated. In fact, open system behavior has been demonstrated to be a common persistent problem that cannot be consistently identified and quantified, and which varies from sample to sample. This casts some doubt on the second foundational assumption of closed-system history on which U-Pb radioisotope dating is built. Thus, these uncertainties call into question all the absolute U-Pb and Pb-Pb ages which uniformitarians so confidently use to build their multi-millions-of-years’ timescale and proclaim the absurdity of the biblical timescale.
Given the conflicting claims as to the effects on U and Pb mobility due to radiation damage, diffusion, and recrystallization in many recent detailed studies, it is clear these issues are not fully resolved in the conventional geochronology community and its literature. Nor is it clear whether the sample pre-treatments currently in use are effective in removing only those outer portions of zircon grains reputed to have been affected by Pb loss. There is no way of knowing for sure, as all 206Pb atoms are the same whether they are in the location in a zircon crystal being analysed due to in situ decay from 238U, or whether they have migrated from elsewhere in the same crystal to that location. And it has been demonstrated that fluids with various chemistries percolating through rocks and penetrating around grain boundaries and into grains along microfractures are capable of leaching both U and radiogenic Pb isotopes to move them within grains and even remove them entirely. Yet current methods by the conventional community to detect these pitfalls include rather aggressive measures to detect when these problems are present.
Furthermore, the 206Pb atoms measured in any location may also be a component of the common or initial Pb, having been inherited by the mineral when it crystallized. This is particularly the case when the 206Pb atoms are found within primary micro and nano domains in the zircon and monazite crystals to be U-Pb dated. Since these micro and nano domains formed when these minerals crystallized, these are inherited common or initial 206Pb atoms not related to subsequent decay of 238U that was also incorporated at the time of crystallization. Snelling (2017b) has discussed this at length. The presence, amount, and isotopic composition of common or initial Pb is not always readily evident, as Pb of various isotopic compositions is well known to be inherited from the earth’s mantle by crustal rocks and minerals, and once in the crust Pb isotopes are recycled (Snelling 2000). Yet it is insisted in the geochronological community that the zircon crystal lattice excludes Pb when zircons form. They claim that the problem of inherited or initial does not apply to zircons, which is why they insist zircons are perfect candidates for geochronometers. However, Snelling (2017a) documented there is experimental evidence that initial or inherited Pb can be incorporated in zircons when they form (Watson et al. 1997). And some of the atomic scale studies already cited above have confirmed this (for example, Fougerouse et al. 2018; Seydoux-Guillaume et al. 2015). Thus, there is no way of knowing which 206Pb and 207Pb atoms in zircons are due to U decay, or whether some atoms were inherited in the zircons when they formed. Yet in many cases the level of inheritance may be no more than a few percent, so U-Pb and Pb-Pb methods may still provide approximate relative ages.
It has also been demonstrated conclusively that radiation damage occurs to mineral crystals, and such damage facilitates Pb loss and U and Pb mobility within those crystals. But it all depends on the chemistry of any fluids percolating around and through the crystals, as the fluid chemistry affects the degree of U and/or Pb mobility. It is also true that the outer zones of mineral crystals will be more affected by radiation damage and Pb loss, particularly due to the volume expansion causing microfractures there, which facilitate U and Pb mobility and Pb loss. So, removing the outer zones of such crystals certainly removes the areas most affected by Pb loss, but it does not guarantee that the remaining cores have not also been affected by migration of Pb isotopes, or U mobility. And removing outer zones of crystals may also remove important information if the outer zones consist of growth zones formed subsequent to crystallization of the cores. But again, there is no way of knowing which 206Pb atoms measured in any location are there by being derived from in situ decay or by having migrated from elsewhere. Of course, when appropriate precautions are taken such uncertainties do not render worthless the U-Pb and Pb-Pb zircon methods.
These circumstances are complicated by the fact that repair of radiation damage does occur by recrystallization. Since the Pb isotopes (and sometimes U) are made mobile by the radiation damage creating migration pathways, when subsequent recrystallization and/or defect recovery occurs, the Pb (and U) isotopes may either further migrate, and/or be locked into the places they have already migrated to, within the crystal lattices of the zircons. Thus U-Pb ages can again be reset. However, once again, whether the final U-Pb ages are then concordant or discordant is not an infallible guide as to how much Pb loss or gain there has been, or if U has or hasn’t been mobile. Whatever Pb (and U) isotopes have been locked in by the recrystallization and/or defect recovery, the U-Pb and Pb-Pb isotope ratios cannot quantify the amounts of the Pb and/or U isotopes which have moved, even using the assumed “correct” ages for the zircons.
The major stimulus that causes recrystallization to occur is heat. The source of that heat is usually the external environment in which the mineral is located, such as due to deep burial and/or tectonics. However, heat is also generated within minerals such as zircon due to the radioactive decay of their contained U and Th. At today’s decay rates, which uniformitarians extrapolate as constant in the past, the heat generated by radioactive decay would likely have had little effect on the U-hosting minerals, although it would have assisted the volume expansion and fracturing of mineral grains which has been observed under the microscope (for example, in high U-bearing mineral grains by Ramdohr 1960 and Chakoumakos et al. 1987). Such fracturing aids the escape of daughter isotopes such as radium and radon, especially the latter which is an inert gas, and thereby Pb loss from those fractured mineral grains.
If instead, as it has been proposed, radioisotope decay rates were grossly accelerated during the recent global Flood cataclysm, then it is generally postulated that there would have been a massive amount of heat released in an intense sustained burst (Vardiman, Snelling, and Chaffin 2005). Indeed, it has been suggested that there would have been enough heat released to have vaporized granite. However, there are many lines of evidence that indicate the heating of the crustal rocks during the Flood was minimal. Any sudden sustained burst of heat would be expected to have caused considerable damage to U-bearing mineral grains with sudden massive volume expansion and fracturing, but there is almost no evidence of that. Any massive volume expansion and fracturing, and the heat, would have also potentially caused significant U and Pb mobility and thus redistribution of these isotopes within the grains, and even U and Pb loss out of them. But the heat would also have potentially annealed much of the damage and caused recrystallization, setting in place whatever U and Pb redistribution which had previously occurred, and thus making U-Pb ages derived from subsequent isotopic analyses somewhat meaningless. Indeed, the amount of heat potentially released by this grossly accelerated radioisotope decay has been deemed a “heat problem” because of the gross impacts it would have had (Vardiman, Snelling, and Chaffin 2005).
On the other hand, the very existence of radiohalos associated with zircons and fission tracks in zircons (Snelling 2005a, 2005b) indicates that this supposed “heat problem” was not as severe as supposed. This is because heat anneals both radiohalos and fission tracks, even at temperatures as low as 150°C. In other words, such heat would have obliterated the radiohalos and fission tracks. Thus, their survival to the present indicates that the host minerals could not have suffered from excessive heating since they formed. Yet as Snelling (2005a) has demonstrated, the formation of the Po radiohalos required grossly accelerated U decay.
Taken together, these considerations thus suggest that there was no major heat problem, because whatever heat was produced by the grossly accelerated U decay to generate the Po radiohalos had to be simultaneously dissipated so that the Po radiohalos were not annealed. Humphreys (2005, 2018) has proposed mechanisms for rapidly dissipating this heat. Alternatively, as Chaffin (2017) pointed out, there is a possible mechanism for giving an appreciable fraction of the 238U decay energy to antineutrinos which then would escape into space. However, this does not rule out the potential for both U and Pb mobility during an accelerated U-decay event and thus the redistribution of U and Pb isotopes in and out of minerals, and the fixing in place of those redistributed isotopes by recrystallization and defect recovery. The net result still makes the absolute U-Pb ages derived from subsequent isotopic analyses somewhat subjective.
Ultimately, there is still no agreement on how much Pb and U mobility there has been, and how far U and Pb isotopes might have travelled within and out of minerals. Nor is agreement possible, simply because there is no way of knowing with certainty the location of any particular atom in the past based on its present location, especially for Pb atoms which are not bonded within the crystal lattices of minerals such as zircon. Even the very recent atomic scale studies using the most sophisticated instruments now available can only be demonstrated where U and Pb atoms now reside in the crystal lattice of zircon. Yet it is often claimed that Pb loss can be established, and how much, by discordia on a concordia diagram and by discordant U-Pb and Pb-Pb ages. However, that assumes a deep time history for the earth and its constituent rocks and minerals, for which the proof given by uniformitarians and evolutionists is the claimed U-Pb ages derived by assuming a constant U decay rate at today’s measured very slow rate. That is circular reasoning. But as Snelling (2017a, 2017b) has also documented, there are uncertainties about today’s measured 238U and 235U decay rates (especially the latter), the crucial 238U/235U ratio (which can even vary in the same mineral in different rocks), and the amount and composition of inherited, initial and/or common Pb (which is known to be contributed from the mantle). All these uncertainties coupled with the uncertainties of U and especially Pb mobility, and resetting due to recrystallization and defect recovery, make the claimed absolute multi-millions-of-years U-Pb and Pb-Pb ages highly subjective based on unprovable dubious assumptions and a priori interpretations, the most crucial of which is still the assumption of time-invariant decay rates.
If instead we assume the biblical timescale is the correct history for the earth, which includes the events recorded in God the Creator’s eyewitness testimony in Genesis, then we derive a radically different interpretation of the U-Pb isotope data obtained from the earth’s rocks and minerals. The concordant multi-millions-of-years U-Pb ages for rocks and minerals that are systematically younger up through the rock record are the direct result of the grossly accelerated U decay which occurred during the global Flood cataclysm (Vardiman, Snelling, and Chaffin 2005). And the Flood began with a cataclysmic upheaval as “the fountains of the great deep” were broken up (Genesis 7:11), which has been proposed as a description of the rupturing and cleaving of the earth’s crust to commence the break-up of the pre-Flood supercontinent which started catastrophic plate tectonics (Austin et al. 1994), and which would have likely also coincided with the ramping up of grossly accelerated radioisotope decay rates (Vardiman, Snelling, and Chaffin 2005).
It may thus be somewhat coincidental that Tilton (1960) found that U-bearing minerals, particularly zircons, from different continents, all seem to have lost radiogenic Pb supposedly 500–600 million years ago. That is about the same conventional time in the geologic record that is proposed for the commencement of the catastrophic plate tectonics and the grossly accelerated radioisotope decay which triggered the Flood cataclysm (Snelling 2009). Tilton (1960) suggested that this conventional time frame coincided with uplift of continents and their weathering and erosion. More recently, Kramers et al. (2009) found that Precambrian zircons frequently have a range of lower concordia intercepts up to 800 Ma which commonly marked the onset of more recent Pb loss. Coincidentally perhaps, this corresponds to the conventional time in the geologic record when the supercontinent Rodinia, which has been proposed as the pre-Flood supercontinent (Snelling 2014c), may have begun to break apart (Li et al. 1999). And in this conventional period from 800 Ma to 500–600 Ma was a time of continental-wide weathering and erosion (denudation) that culminated in the almost global formation of the “Great Unconformity” (Peters and Gaines 2012). Alternately, within the biblical Creation-Flood model of earth history that conventional time period is consistent with the beginning phase of the Flood when erosion of the continental land surfaces began, culminating in the tsunami-driven rising Flood waters at their most intense point producing the almost worldwide “Great Unconformity” on which the fossil-bearing Flood sediments were then deposited (Snelling 2009).
Conclusions
Minerals such as zircon are routinely used by geochronologists to confidently provide the U-Pb and Pb-Pb ages which underpin the conventional multi-millions-of-years’ timescale. However, U and Pb mobility have been demonstrated to have occurred in these minerals, but how much and how far the U and Pb have been mobilized cannot be known with certainty. The radiation released by U decay damages the crystal lattices of the minerals and volume expansion generates micro-cracks, providing preferential pathways for U and Pb to migrate. Heating can also aid U and Pb mobility, but it also aids recrystallization and defect recovery. To wherever the U and Pb atoms have migrated, when recrystallization occurs it potentially locks those U and Pb atoms into those new locations. Yet even though the current locations of the U and Pb atoms within minerals such as zircons can be studied at the atomic level, there can be no certainty as to whether those atoms have always been in those locations since the original crystals formed, or whether they have migrated within the crystals or have even been added from outside the crystals. There is no way of knowing what and how much migration happened in the past. Thus, even if the outer portions of crystals are removed before isotopic analysis and the U-Pb ages obtained for the cores of crystals are concordant, there can be no certainty that they represent the absolute dates when the original crystals formed.
These uncertainties are compounded by the uncertainties in the measured 238U and 235U decay rates, the crucial 238U/235U ratio, and the amount and composition of inherited, initial and/or common Pb. Even though these uncertainties are inadequately acknowledged by geochronologists, when they take numerous precautions the U-Pb and Pb-Pb methods still have a strong semblance of validity. However, all these uncertainties are overshadowed by the underlying unprovable assumptions on which the radioisotope dating methods are based, especially the assumption of time-invariant decay rates, built on the foundation of an assumed deep time history. The resultant U-Pb and Pb-Pb ages obtained are thus subjective and only provide relative ages. Therefore, those absolute ages cannot be used to dismiss the history of the earth and its approximately 6000-year chronology provided in God’s infallible Word.
Acknowledgments
The three reviewers are acknowledged for their helpful comments and input, though the final content of this paper is solely my responsibility. Our production assistant Laurel Hemmings is also especially thanked for her painstaking work in preparing this paper for publication.
References
Adloff, J. P., and K. Roessler. 1991. “Recoil and Transmutation Effects in the Migration Behaviour of Actinides.” Radiochimica Acta 52/53: 269–274.
Ahrens, L. H. 1955. “Implications of the Rhodesian Age Pattern.” Geochimica et Cosmochimica Acta 8 (1–2): 1–15.
Amelin, Y., and A. N. Zaitsev. 2002. “Precise Geochronology of Phoscorites and Carbonatites: The Critical Role of U-Series Disequilibrium in Age Interpretations.” Geochimica et Cosmochimica Acta 66 (13): 2399–2419.
Amelin, Y., J. Connelly, R. E. Zartman, J. H. Chen, C. Göpel, and L. A. Neymark. 2009. “Modern U-Pb Chronometry of Meteorites: Advancing to Higher Time Resolution Reveals New Problems.” Geochimica et Cosmochimica Acta 73 (17): 5212–5223.
Ashton, F. W. 1919. “A Positive Ray Spectrograph.” Philosophical Magazine 38 (series 6): 707–714.
Austin, S. A., J. R. Baumgardner, D. R Humphreys, A. A. Snelling, L. Vardiman, and K. P. Wise. 1994. “Catastrophic Plate Tectonics: Global Flood Model of Earth History.” In Proceedings of the Third International Conference on Creationism. Edited by R. E. Walsh, 609–612. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. “Call for an Improved Set of Decay Constants for Geochronological Use.” Geochimica et Cosmochimica Acta 65 (1): 111–121.
Bickford, M. E., R. B. Chase, B. K. Nelson, R. D. Shuster, and E. C. Arruda. 1981. “U-Pb Studies of Zircon Cores and Overgrowths, and Monazite: Implications for the Age and Petrogenesis of the Northeastern Idaho Batholith.” Journal of Geology 89 (4): 433–457.
Black, L. P. 1987. “Recent Pb Loss in Zircon: A Natural or Laboratory-Induced Phenomenon?” Chemical Geology 65 (1): 25–33.
Black, L. P., I. S. Williams, and W. Compston. 1986. “Four Zircon Ages From One Rock: The History of a 3930 Ma-Old Granulite from Mount Sones, Enderby Land, Antarctica.” Contributions to Mineralogy and Petrology 94 (4): 427–437.
Blum, T. B., D. Reinhard, M. Spicuzza, D. Olson, M. A. Coble, A. J. Cavosie, T. Ushikubo, D. J. Larson, T. F. Kelly, and J. W. Valley. 2014. “Nanoscale Isotope Mapping of Terrestrial and Lunar Zircons by Atom Probe Tomography.” EOS, Transactions of the American Geophysical Union, Fall Meeting, Abstract V34A-06.
Boehnke, P., and T. M. Harrison. 2014. “A Meta-Analysis of Geochronologically Relevant Half-Lives: What’s the Best Decay Constant?” International Geology Review 56 (7): 905–914.
Bogolomov, Y. S. 1991. “Migration of Lead in Non-Metamict Zircon.” Earth and Planetary Science Letters 107 (3–4): 625–633.
Boltwood, B. B. 1907. “On the Ultimate Disintegration Products of the Radio-active Elements (Part II).” American Journal of Science 23 (4): 77-88.
Bowring, S. A., and I. S. Williams. 1999. “Priscoan (4.00–4.03 Ga) Orthogneisses from Northwestern Canada.” Contributions to Mineralogy and Petrology 134 (1): 3–16.
Bowring, S. A., and M. D. Schmitz. 2003. “High-Precision U-Pb Zircon Geochronology and the Stratigraphic Record.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry, 53 (1): 305–326. Washington, DC: Mineralogical Society of America.
Brennecka, G. A., and M. Wadhwa. 2012. “Uranium Isotope Compositions of the Basaltic Angrite Meteorites and the Chronological Implications for the Early Solar System.” Proceedings of the National Academy of Sciences USA 109 (24): 9299–9303.
Brinkman, J. A. 1954. “On the Nature of Radiation Damage in Metals.” Journal of Applied Physics 25 (8): 961–970.
Brown, I. D., and R. D. Shannon. 1973. “Empirical Bond Strength-Bond-Length Curves for Oxides.” Acta Crystallographica A29: 266–282.
Burakov, B. E., J. M. Hanchar, M. V. Zamoryanskaya, V. M. Garbuzov, and V. A. Zirlin. 2002. “Synthesis and Investigation of Pu-Doped Single Crystal Zircon, (Zr, Pu)SiO4.” Radiochimica Acta 90 (2): 95–97.
Butera, K. M., I. S. Williams, P. L. Blevin, and C. J. Simpson. 2001. “Zircon U-Pb Dating of Early Palaeozoic Monzonitic Intrusives from the Goonumbla Area, New South Wales.” Australian Journal of Earth Sciences 48 (1): 457–464.
Capitani, G. C., H. Leroux, J. C. Doukhan, S. Ríos, M. Zhang, and E. K. H. Salje. 2000. “A TEM Investigation of Natural Metamict Zircons: Structure and Recovery of Amorphous Domains.” Physics and Chemistry of Minerals 27 (8): 545–556.
Carson, C. J., J. J. Ague, M. Grove, C. D. Coath, and T. M. Harrison. 2002. “U-Pb Isotopic Behaviour of Zircon During Upper-Amphibolite Facies Fluid Infiltration in the Napier Complex, East Antarctica.” Earth and Planetary Science Letters 199 (3–4): 287–310.
Cartz, L., and R. Fournelle. 1979. “Metamict Zircon Formed by Heavy Ion Bombardment.” Radiation Effects 41 (4): 211–217.
Chaffin, E. F. 2017. “Variable Neutrino Mass, Supernovae, and Accelerated Decay.” Creation Research Society Quarterly 53 (3): 180–190.
Chakoumakos, B. C., T. Murakami, G. R. Lumpkin, and R. C. Ewing. 1987. “Alpha Decay-Induced Fracturing in Zircon: The Transition from Crystalline to the Metamict State.” Science 236 (4808): 1556–1559.
Chakoumakos, B. C., W. C. Oliver, G. R. Lumpkin, and R. C. Ewing. 1991. “Hardness and Elastic Modulus of Zircon as a Function of Heavy-Particle Irradiation Dose: I. In Situ α-Decay Event Damage.” Radiation Effects and Defects in Solids 118 (4): 393–403.
Chapman, H. J., and J. C. Roddick 1994. “Kinetics of Pb Release During the Zircon Evaporation Technique.” Earth and Planetary Science Letters 121 (3–4): 601–611.
Chen, J. H., and G. J. Wasserburg. 1983. “The Least Radiogenic Pb in Iron Meteorites.” Lunar and Planetary Science Conference 14: 103–104.
Chen, J., J. Lian, L. M. Wang, R. C. Ewing, R. G. Wang, and W. Pan. 2002. “X-Ray Photoelectron Spectroscopy Study of Disordering in Gd2(Ti1-xZrx)2O7 Pyrochlores.” Physical Review Letters 88 (10): 105901-1–105901-4.
Chen, Y. D., and I. S. Williams. 1990. “Zircon Inheritance in Mafic Inclusions from Bega Batholith Granites, South-Eastern Australia: An Ion Microprobe Study.” Journal of Geophysical Research: Solid Earth 95 (B11): 17,787–17,796.
Cherniak, D. J., W. A. Lanford, and F. J. Ryerson. 1991. “Lead Diffusion in Apatite and Zircon Using Ion Implantation and Rutherford Backscattering Techniques.” Geochimica et Cosmochimica Acta 55 (5): 1663–1673.
Cherniak, D. J., J. M. Hanchar, and E. B. Watson. 1997a. “Rare-Earth Diffusion in Zircon.” Chemical Geology 134 (4): 289–301.
Cherniak, D. J., J. M. Hanchar, and E. B. Watson. 1997b. “Diffusion of Tetravalent Cations in Zircon.” Contributions to Mineralogy and Petrology 127 (4): 383–390.
Cherniak, D. J., and E. B. Watson. 2000. “Pb Diffusion in Zircon.” Chemical Geology 172 (1–2): 5–24.
Cherniak, D. J., and E. B. Watson. 2003. “Diffusion in Zircon.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry 53 (1): 113–143. Washington, DC: Mineralogical Society of America.
Compston, W. 1997. “Variation in Radiogenic Pb/U within the SL13 Standard.” Research School of Earth Sciences Annual Report 1996, 118–121. Canberra, Australia: Australian National University.
Compston, W. 1999. “Geological Age Determination by Instrumental Analysis: The 29th Halmond Lecture.” Mineralogical Magazine 63: 297–311.
Compston, W. 2000a. “Interpretation of SHRIMP and Isotope Dilution Zircon Ages for the Geological Time-Scale. 1. The Early Ordovician and Late Cambrian.” Mineralogical Magazine 64 (1): 43–57.
Compston, W. 2000b. “Interpretation of SHRIMP and Isotope Dilution Zircon Ages for the Geological Time-Scale. II. Silurian to Devonian.” Mineralogical Magazine 64: 1127–1146.
Compston, W., P. D. Kinney, I. S. Williams, and J. J. Foster. 1986. “The Age and Pb Loss Behaviour of Zircons from the Isua Supracrustal Belt as Determined by the Ion Microprobe.” Earth and Planetary Science Letters 80 (1–2): 71–81.
Copeland, P., R. R. Parrish, and T. M. Harrison. 1988. “Identification of Inherited Radiogenic Pb in Monazite and Its Implications for U-Pb Systematics.” Nature 333: 760–763.
Corfu, F. 2000. “Extraction of Pb with Artificially Too-Old Ages During Stepwise Dissolution Experiments on Archean Zircon.” Lithos 53 (3–4): 279–291.
Corfu, F. 2013. “A Century of U-Pb Geochronology: The Long Quest Towards Concordance.” Geological Society of America Bulletin 125 (1–2): 33–47.
Corfu, F., J. M. Hanchar, P. W. O. Hoskin, and P. Kinny. 2003. “Atlas of Zircon Textures.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry 53 (1): 469–500. Washington, DC: Mineralogical Society of America.
Crawford, J. H., and M. C. Wittels. 1956. “A Review of Investigations of Radiation Effects in Covalent and Ionic Crystals.” In Proceedings of International Conference on Peaceful Uses of Atomic Energy, vol. 7, 654–665. New York, United Nations.
Crocombette, J. P. 1999. “Theoretical Study of Point Defects in Crystalline Zircon.” Physics and Chemistry of Minerals 27 (2): 138–143.
Crowley, Q. G., K. Heron, N. Riggs, B. Kamber, D. Chew, B. McConnell, and K. Benn. 2014. “Chemical Abrasion Applied to LA-ICP-MS U-Pb Zircon Geochronology.” Minerals 4 (2): 503–518.
Davis, D. W., T. E. Krogh, J. Hinzer, and E. Nakamura. 1985. “Zircon Dating of Polycyclic Volcanism at Sturgeon Lake and Implications for Base Metal Mineralization.” Economic Geology 80 (7): 1942–1952.
Davis, D. W., and T. E Krogh. 2000. “Preferential Dissolution of 234U and Radiogenic Pb From α-Recoil-Damaged Lattice Sites in Zircon: Implications for Thermal Histories and Pb Isotopic Fractionation in the Near Surface Environment.” Chemical Geology 172 (1–2): 41–58.
Davis, D. W., I. S. Williams, and T. E. Krogh. 2003. “Historical Development of Zircon Geochronology.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry 53 (1): 145–181. Washington, DC: Mineralogical Society of America.
Dempster, A. J. 1918. “A New Method of Positive Ray Analysis.” Physical Review 11: 316–325.
Dickin, A. P. 2005. Radiogenic Isotope Geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Dunn, S. J., A. A. Nemchin, P. A., Cawood, and R. T. Pidgeon. 2005. “Provenance Record of the Jack Hills Metasedimentary Belt: Source of the Earth’s Oldest Zircons.” Precambrian Research 138 (3–4): 235–254.
Ellsworth, S., A. Navrotsky, and R. C. Ewing. 1994. “Energetics of Radiation Damage in Natural Zircon (ZrSiO4).” Physics and Chemistry of Minerals 21 (3): 140–149.
Ewing, R. C. 1994. “The Metamict State: 1993—The Centennial.” Nuclear Instruments and Methods in Physics Research B: Beam Interactions with Materials and Atoms 91 (1–4): 22–29.
Ewing, R. C., R. F. Haaker, and W. Lutze. 1982. “Leachability of Zircon as a Function of Alpha Dose.” In Scientific Basis for Nuclear Waste Management V. Edited by W. Lutze, 389–397. Amsterdam, The Netherlands: Elsevier.
Ewing, R. C., A. Meldrum, L. M. Wang, and S. X. Wang. 2000. “Radiation-Induced Amorphization.” In Transformation Processes in Minerals. Edited by S. A. T. Redfern and M. A. Carpenter, Reviews in Mineralogy and Geochemistry, vol. 39, 319–361. Washington, DC: Mineralogical Society of America.
Ewing, R. C., A. Meldrum, L. Wang, W. J. Weber, and L. R. Corrales. 2003. “Radiation Effects in Zircon.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry 53 (1): 387–425. Washington, DC: Mineralogical Society of America.
Exarhos, G. J. 1984. “Induced Swelling in Radiation Damaged ZrSiO4.” Nuclear Instruments and Methods in Physics Research B: Beam Interations with Materials and Atoms 1 (2–3): 538–541.
Farges, F. 1994. “The Structure of Metamict Zircon: A Temperature-Dependent EXAFS Study.” Physics and Chemistry of Minerals 20 (7): 504–514.
Farges, F., and G. Calas. 1991. “Structural Analysis of Radiation Damage in Zircon and Thorite: An X-Ray Absorption Spectroscopic Study.” American Mineralogist 76 (1–2): 60–73.
Farnan, I., and E. K. H. Salje. 2001. “The Degree and Nature of Radiation Damage in Zircon Observed by 29Si Nuclear Magnetic Resonance.” Journal of Applied Physics 89 (4): 2084–2090.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and Applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Flowers, R. M., S. A. Bowring, A. J. Tulloch, and K. A. Klepeis. 2005. “Tempo of Burial and Exhumation Within the Deep Roots of a Magmatic Arc, Fiordland, New Zealand.” Geology 33 (1): 17–20.
Fougerouse, D., S. M. Reddy, D. W. Saxey, T. M. Erickson, C. L. Kirkland, W. D. A. Rickard, A.-M. Seydoux-Guillaume, C. Clark, and I. S. Buick. 2018. “Nanoscale Distribution of Pb in Monazite Revealed by Atom Probe Microscopy.” Chemical Geology 479: 251–258.
Frei, R., I. M. Villa, J. D. Kramers, T. F. Nägler, W. J. Przybylowicz, V. M. Prozeski, B. A. Hofmann, and B. S. Kamber. 1997. “Single Mineral Dating by the Pb-Pb Step-Leaching Method: Assessing the Mechanisms.” Geochimica et Cosmochimica Acta 61 (2): 393–414.
Froude, D. O., T. R. Ireland, P. D. Kinny, I. S. Williams, W. Compston, I. R. Williams, and J. S. Myers. 1983. “Ion Microprobe Identification of 4100–4200 Myr-Old Terrestrial Zircons.” Nature 304: 616–618.
Ge, R., S. A. Wilde, A. A. Nemchin, M. J. Whitehouse, J. J. Bellucci, T. M. Erickson, A. Frew, and E. R. Thern. 2018. “A 4463 Ma Apparent Zircon Age from the Jack Hills (Western Australia) Resulting from Ancient Pb Mobilization.” Geology 46 (4): 303–306.
Gehrels, G., P. Kapp, P. DeCelles, A. Pullen, R. Blakey, A. Weislogel, L. Ding, J. Guynn, A. Martin, N. McQuarrie, and A. Yin. 2011. “Detrital Zircon Geochronology of Pre-Tertiary Strata in the Tibetan-Himalayan Orogen.” Tectonics 30 (5): TC5016-1–TC5016-27.
Geisler, T. 2002. “Isothermal Annealing of Partially Metamict Zircon: Evidence for a Three-Stage Recovery Process.” Physics and Chemistry of Minerals 29 (6): 420–429.
Geisler, T., and H. Schleicher. 2000. “Improved U-Th-Total Pb Dating of Zircons by Electron Microprobe Using a Simple New Background Modeling Procedure and Ca as a Chemical Criterion of Fluid-Induced U-Th-Pb Discordance in Zircon.” Chemical Geology 163: 269– 285.
Geisler, T., R. T. Pidgeon, W. van Bronswijk, and R. Pleysier. 2001a. “Kinetics of Thermal Recovery and Recrystallization of Partially Metamict Zircon: A Raman Spectroscopy Study.” European Journal of Mineralogy 13 (6): 1163–1176.
Geisler, T., M. Ulonska, H. Schleicher, R. T. Pidgeon, and W. van Bronswijk. 2001b. “Leaching and Differential Recrystallization of Metamict Zircon Under Experimental Hydrothermal Conditions.” Contributions to Mineralogy and Petrology 141 (1): 53–65.
Geisler, T., R. T. Pidgeon, W. van Bronswijk, and R. Kurtz. 2002. “Transport of Uranium, Thorium, and Lead in Metamict Zircon Under Low-Temperature Hydrothermal Conditions.” Chemical Geology 191 (1–3): 141–154.
Geisler, T., R. T. Pidgeon, R. Kurtz, W. van Bronswijk, and H. Schleicher. 2003a. “Experimental Hydrothermal Alteration of Partially Metamict Zircon.” American Mineralogist 88 (10): 1496–1513.
Geisler, T., A. A. Rashwan, M. K. W. Rahn, U. Poller, H. Zwingmann, R. T. Pidgeon, H. Schleicher, and F. Tomaschek. 2003b. “Low-Temperature Hydrothermal Alteration of Natural Metamict Zircons from the Eastern Desert, Egypt.” Mineralogical Magazine 67 (3): 485–508.
Geisler, T., U. Schaltegger, and F. Tomaschek. 2007. “Re-Equilibration of Zircon in Aqueous Fluids and Melts.” Elements 3 (1): 43–50.
Goldich, S. S., and M. G. Mudrey. 1972. “Dilatancy Model for Discordant U-Pb Zircon Ages.” In Contributions to Recent Geochemistry and Analytical Chemistry. Edited by A. I. Tugarinov, 415–418. Moscow, Russia: Nauka.
Goldich, S. S., and L. B. Fischer. 1986. “Air-Abrasion Experiments in U-Pb Dating of Zircon.” Chemical Geology 58 (3): 195–215.
Goldmann, A., G. Brennecka, J. Noordmann, S. Weyer, and M. Wadhwa. 2015. “The Uranium Isotopic Composition of the Earth and the Solar System.” Geochimica et Cosmochimica Acta 148: 145–158.
Grauert, B., M. G Seitz, and G. Soptrajanova. 1974. “Uranium and Lead Gain of Detrital Zircon Studied by Isotopic Analyses and Fission-Track Mapping.” Earth and Planetary Science Letters 21 (4): 389–399.
Gray, M. B., and P. K. Zeitler. 1997. “Comparison of Clastic Wedge Provenance in the Appalachian Foreland Using U/Pb Ages of Detrital Zircons.” Tectonics 16 (1): 151–160.
Hansen, B. T., and J. D. Friderichsen. 1989. “The Influence of Recent Lead Loss on the Interpretation of Disturbed U-Pb Systems in Zircons from Igneous Rocks in East Greenland.” Lithos 23 (3): 209–223.
Harley, S. L. 1985. “Garnet-Orthopyroxene Bearing Granulites from Enderby Land, Antarctica: Metamorphic Pressure-Temperature-Time Evolution of the Archaean Napier Complex.” Journal of Petrology 26 (4): 819–856.
Harley, S. L. 1987. “A Pyroxene-Bearing Meta-Ironstone and Other Pyroxene-Granulites from Tonagh Island, Enderby Land, Antarctica: Further Evidence for Very High Temperature (>980°C) Archaean Regional Metamorphism in the Napier Complex.” Journal of Metamorphic Geology 5 (3): 341–356.
Harley, S. L., N. M. Kelly, and A. Möller. 2007. “Zircon Behaviour and the Thermal Histories of Mountain Chains.” Elements 3 (1): 25–30.
Harrison, T. M., J. N. Aleinikoff, and W. Compston. 1987. “Observations and Controls on the Occurrence of Inherited Zircon in Concord-Type Granitoids, New Hampshire.” Geochimica et Cosmochimica Acta 51 (9): 2549–2558.
Hay, D. C., and T. J. Dempster. 2009. “Zircon Behaviour During Low-Temperature Metamorphism.” Journal of Petrology 50 (4): 571–589.
Hayashi, M., I. Shinno, S. Tagushi, and S. Sugihara. 1990. “ESR Signals of Zircon Irradiated with Thermal Neutrons and γ-Rays.” Journal of Mineralogy, Petrology and Economic Geology 85 (1): 27–33.
Hayes, R. B. 2017. “Some Mathematical and Geophysical Considerations in Radioisotope Dating Applications.” Nuclear Technology 197 (2): 209–218.
He, Y., and A. N. Cormack. 1999. “Atomistic Simulation Study of Defect Structure of Zircon as a High-Level Nuclear Waste Host Form.” Journal of the China University of Geosciences 10: 309–313.
Headley, T. J., G. W. Arnold, and C. J. M. Northrup. 1981. “Dose-Dependence of Pb-Ion Implantation Damage in Zirconolite, Hollandite, and Zircon.” In Scientific Basis for Radioactive Waste Management V. Edited by W. Lutze, 379–388. Amsterdam, The Netherlands: Elsevier.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. “238U/235U Systematics in Terrestrial Uranium-Bearing Minerals.” Science 335 (6076): 1610–1614.
Hinton, R. W., and J. V. P. Long. 1979. “High-Resolution Ion-Microprobe Measurement of Lead Isotopes: Variations Within Single Zircons from Lac Seul, Northwestern Ontario.” Earth and Planetary Science Letters 45 (2): 309–325.
Högdahl, K., L. P. Gromet, and C. Broman. 2001. “Low P-T Caledonian Resetting of U-Rich Paleoproterozoic Zircons, Central Sweden.” American Mineralogist 86 (4): 534–546.
Hokada, T. 2001. “Feldspar Thermometry in Ultrahigh-Temperature Metamorphic Rocks: Evidence of Crustal Metamorphism Attaining ~1100°C in the Archean Napier Complex, East Antarctica.” American Mineralogist 86 (7): 932–938.
Holland, H. D., and D. Gottfried. 1955. “The Effect of Nuclear Radiation on the Structure of Zircon.” Acta Crystallographica 8: 291–300.
Holmes, A. 1913. The Age of the Earth. London: Harper and Brothers.
Hurley, P. M., and H. W. Fairbairn. 1953. “Radiation Damage in Zircon: A Possible Age Method.” Geological Society of America Bulletin 64 (6): 659–674.
Humphreys, D. R. 2005. “Young Helium Diffusion Age of Zircons Supports Accelerated Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 25–100. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/young-helium-diffusion-age-zircons/.
Humphreys, D. R. 2018. “New Mechanism for Accelerated Cooling of Excessive Radiogenic Heat.” In Proceedings of the Eighth International Conference on Creationism. Edited by J. H. Whitmore, in prep. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Huyskens, M. H., S. Zink, and Y. Amelin. 2016. “Evaluation of Temperature-Time Conditions for the Chemical Abrasion Treatment of Single Zircons for U-Pb Geochronology.” Chemical Geology 438: 25–35.
Ireland, T. R., and I. S. Williams. 2003. “Considerations in Zircon Geochronology by SIMS.” In Zircon. Edited by J. M Hanchar and P. W. O. Hoskin, Reviews in Mineralogy and Geochemistry 53 (1): 215–241. Washington, DC: Mineralogical Society of America.
Kelly, N. M., and S. L. Harley. 2005. “An Integrated Microtextural and Chemical Approach to Zircon Geochronology: Refining the Archaean History of the Napier Complex, East Antarctica.” Contributions to Mineralogy and Petrology 149 (1): 57–84.
Kelly, N. M., G. L. Clarke, and C. M. Fanning. 2004. “Archaean Crust in the Rayner Complex of East Antarctica: Oygarden Group of Islands, Kemp Land.” Earth and Environmental Science Transactions of the Royal Society of Edinburgh–Earth Sciences 95 (3–4): 491–510.
Kober, B. 1987. “Single-Zircon Evaporation Combined with Pb+ Emitter Bedding for 207Pb/206Pb-Age Investigations Using Thermal Ion Mass Spectrometry, and Implications to Zirconology.” Contributions to Mineralogy and Petrology 96 (1): 63–71.
Kovaleva, E., and U. Klötzli. 2017. “NanoSIMS Study of Seismically Deformed Zircon: Evidence of Y, Yb, Ce, and P Redistribution and Resetting of Radiogenic Pb.” American Mineralogist 102 (6): 1311–1327.
Kramers, J. D., R. Frei, M. Newville, B. Kober, and I. Villa. 2009. “On the Valency State of Radiogenic Lead in Zircon and Its Consequences.” Chemical Geology 261 (1–2): 4–11.
Krogh, T. E. 1973. “A Low-Contamination Method for Hydrothermal Decomposition of Zircon and Extraction of U and Pb for Isotopic Age Determinations.” Geochimica et Cosmochimica Acta 37 (3): 485–494.
Krogh, T. E. 1982a. “Improved Accuracy of U-Pb Zircon Dating by Selection of More Concordant Fractions Using a High Gradient Magnetic Separation Technique.” Geochimica et Cosmochimica Acta 46 (4): 631–635.
Krogh, T. E. 1982b. “Improved Accuracy of U-Pb Zircon Ages by the Creation of More Concordant Systems Using an Air Abrasion Technique.” Geochimica et Cosmochimica Acta 46 (4): 637–649.
Krogh, T. E. 1994. “Identification of Concordant Zircons Using Etch Techniques.” Abstracts of the 8th International Conference on Geochronology, Cosmochronology and Isotope Geology. Edited by M. A. Lanphere, G. B. Dalrymple, and B. D. Turrin, 180.
Krogh, T. E. 1998. “Etch Selection and Abrasion Techniques Applied to Complex Populations and Revealed Spurious Ion Probe Ages.” Mineralogical Magazine 62: A816–A817.
Krogh, T. E., and G. L. Davis. 1974. “Alteration in Zircons with Discordant U-Pb Ages.” Carnegie Institution of Washington, Year Book 73: 560–567.
Krogh, T. E., and G. L. Davis. 1975. “Alteration in Zircons and Differential Dissolution of Altered and Metamict Zircon.” Carnegie Institution of Washington, Year Book 74: 619–623.
Krogh, T. E., R. H. McNutt, and G. L. Davis. 1982. “Two High Precision U-Pb Zircon Ages for the Sudbury Nickel Irruptive.” Canadian Journal of Earth Sciences 19 (4): 723–728.
Kröner, A., P. Jaeckel, and I. S. Williams. 1994. “Pb-Loss Patterns in Zircons from a High-Grade Metamorphic Terrain as Revealed by Different Dating methods, U-Pb and Pb-Pb Ages for Igneous and Metamorphic Zircons from Northern Sri Lanka.” Precambrian Research 66 (1–4): 151–181.
Kröner, A., P. Jaeckel, G. Brandl, A. A. Nemchin, and R. T. Pidgeon. 1999. “Single Zircon Ages for Granitoid Gneisses in the Central Zone of the Limpopo Belt, Southern Africa and Geodynamic Significance.” Precambrian Research 93 (4): 299–337.
Kryza, R., Q. G. Crowley, A. Larionov, C. Pin, T. Oberc-Dziedzic, and K. Mochnacka. 2012. “Chemical Abrasion Applied to SHRIMP Zircon Geochronology: An Example from the Variscan Karkonosze Granite (Sudetes, SW Poland).” Gondwana Research 21 (4): 757–767.
Kusiak, M. A., M. J. Whitehouse, S. A. Wilde, A. A. Nemchin, and C. Clark. 2013. “Mobilization of Radiogenic Pb in Zircon Revealed by Ion Imaging: Implications for Early Earth Geochronology.” Geology 41 (3): 291–294.
Larson, D. J., T. J. Prosa, R. M. Ulfig, B. P. Geiser, and Th. F. Kelly. 2013. Local Electrode Atom Probe Tomography: A User’s Guide. Berlin, Germany: Springer.
Lee, J. K. W. 1993. “Problems and Progress in the Elucidation of U and Pb transport Mechanisms in Zircon.” In Defects and Processes in the Solid State: Geoscience Applications. Edited by J. N. Boland and J. D. FitzGerald, 423–446. Amsterdam, The Netherlands: Elsevier.
Lee, J. K. W., I. S. Williams, and D. J. Ellis.1997. “Pb, U and Th Diffusion in Natural Zircon.” Nature 390 (6656): 159–162.
Li, Z. X., X. H. Li, P. D. Kinny, and J. Wang. 1999. “The Breakup of Rodinia: Did it Start with a Mantle Plume beneath South China?” Earth and Planetary Science Letters 173 (3): 171–181.
Lian, J., L. M. Wang, S. X. Wang, J. Chen, L. A. Boatner, and R. C. Ewing. 2001. “Nanoscale Manipulation of Pyrochlore: New Nanocomposite Ionic Conductors.” Physical Review Letters 87 (14): 145901-1–145901-4.
Lian, J., S. Ríos, L. A. Boatner, L. M. Wang, and R. C. Ewing. 2003. “Microstructural Evolution and Nanocrystal Formation in Pb+-Implanted ZrSiO4 Single Crystals.” Journal of Applied Physics 94 (9): 5695–5703.
Ludwig, K. R. 1993. “Pb Dat 1.24: A Computer Program for Processing Pb-U-Th Isotope Data.” USGS Open-File Report 88-542. Washington, D.C.: US Geological Survey.
Ludwig, K. R., and L. T. Silver. 1977. “Lead Isotope Inhomogeneity in Precambrian Igneous K-Feldspars.” Geochimica et Cosmochimica Acta 41 (10): 1457–1471.
Lumpkin, G. R. 2001. “Alpha-Decay Damage and Aqueous Durability of Actinide Host Phases in Natural Systems.” Journal of Nuclear Materials 289 (1–2): 136–166.
Lumpkin, G. R., and R. C. Ewing. 1988. “Alpha-Decay Damage in Minerals of the Pyrochlore Group.” Physics and Chemistry of Minerals 16 (1): 2–20.
Lund, M. D., S. Piazolo, and S. L. Harley. 2006. “Ultrahigh Temperature Deformation Microstructures in Felsic Granulites of the Napier Complex, Antarctica.” Tectonophysics 427 (1–4): 133–151.
Luo, W., C. Shen, and Y. Wang. 2007. “Nucleation of Ordered Particles at Dislocations and Formation of Split Patterns.” Acta Materialia 55 (8): 2579–2586.
Magomedov, Sh. A. 1970. “Study of Migration Mechanism of Radiogenic Products in Zircon.” Geokhimiya 2: 263–268.
Mantina, M., A. C. Chamberlin, R. Valero, C. J. Cramer, and D. G. Truhlar. 2009. “Consistent van der Waals Radii for the Whole Main Group.” Journal of Physical Chemistry A 113 (19): 5806–5812.
Mattinson, J. M. 1994. “A Study of Complex Discordance in Zircons Using Step-Wise Dissolution Techniques.” Contributions to Mineralogy and Petrology 116 (1–2): 117–129.
Mattinson, J. M. 1997. “Analysis of Zircon by Multi-Step Partial Dissolutions: The Good, the Bad, and the Ugly.” Geological Association of Canada Annual Meeting Abstracts, p. A98.
Mattinson, J. M. 2005. “Zircon U-Pb Chemical Abrasion (‘CA-TIMS’) Method: Combined Annealing and Multi-Step Partial Dissolution Analysis for Improved Precision and Accuracy of Zircon Ages.” Chemical Geology 220 (1–2): 47–66.
Mattinson, J. M. 2010. “Analysis of the Relative Decay Constants of 235U and 238U by Multi-Step CA-TIMS Measurements of Closed-System Natural Zircon Samples.” Chemical Geology 275 (3–4): 186–198.
McLaren, A. C., J. D. FitzGerald, and I. S. Williams. 1994. “The Microstructure of Zircon and Its Influence on the Age Determination from Pb/U Isotopic Ratios Measured by Ion Microprobe.” Geochimica et Cosmochimica Acta 58 (2): 993–1005.
Mehrer, H. 2007. Diffusion in Solids. New York: Springer-Verlag.
Meis, C., and J. D. Gale. 1998. “Computational Study of Tetravalent Uranium and Plutonium Lattice Diffusion in Zircon.” Materials Science and Engineering B57 (1): 52–61.
Meldrum, A., L.M. Wang, and R.C. Ewing. 1996. “Ion Beam-Induced Amorphization of Monazite.” Nuclear Instruments and Methods in Physics Research B 116 (1–4): 220–224.
Meldrum, A., L. A. Boatner, W. J. Weber, and R. C. Ewing. 1998. “Radiation Damage in Zircon and Monazite.” Geochimica et Cosmochimica Acta 62 (14): 2509–2520.
Meldrum, A., S. J. Zinkle, L. A. Boatner, S.-X. Wang, L.-M. Wang, and R. C. Ewing. 1999. “Effects of Dose Rate and Temperature on the Crystalline-to-Metamict Transformation in ABO4 Orthosilicates.” Canadian Mineralogist 37: 207–221.
Meldrum, A., L. A. Boatner, and R. C. Ewing. 2000. “A Comparison of Radiation Effects in Crystalline ABO4-Type Phosphates and Silicates.” Mineralogical Magazine 64 (2): 185–194.
Mezger, K., and E. J. Krogstad. 1997. “Interpretation of Discordant U-Pb Zircon Ages: Am Evaluation.” Journal of Metamorphic Geology 15 (1): 127–140.
Miller, J. L. 2012. “Time to Reset Isotopic Clocks? Two New Studies Revise Key Parameters in Radiometric Dating.” Physics Today 65 (6): 20–22.
Miller, M. K. 2000. Atom Probe Tomography: Analysis at the Atomic Level. Dordrecht, The Netherlands: Kluwer Academic/Plenum Publishers.
Min K., R. Mundil, P. R. Renne, and K. R. Ludwig. 2000. “A Test for Systematic Errors in 40Ar/39Ar Geochronology through Comparison with U-Pb Analysis of a 1.1-Ga Rhyolite.” Geochimica et Cosmochimica Acta 64 (1): 73–98.
Muir, R. J., T. R. Ireland, S. D. Weaver, and J. D. Bradshaw. 1996. “Ion Microprobe Dating of Paleozoic Granitoids: Devonian Magmatism in New Zealand and Correlations with Australia and Antarctica.” Chemical Geology 127 (1–3): 191–210.
Murakami, T., B. C. Chakoumakos, R. C. Ewing, G. R. Lumpkin, and W. J. Weber. 1991. “Alpha-Decay Event Damage in Zircon.” American Mineralogist 76 (9–10): 1510–1532.
Nasdala, L., R. T. Pidgeon, D. Wolf, and G. Irmer. 1998. “Metamictization and U-Pb Isotopic Discordance in Single Zircons: A Combined Raman Microprobe and SHRIMP Ion Probe Study.” Mineralogy and Petrology 62 (1–2): 1–27.
Nasdala, L., T. Wenzel, R. T. Pidgeon, and A. Kronz.1999. “Internal Structures and Dating of Complex Zircons from Meissen Massif Monzonites, Saxony.” Journal of Chemistry and Geology 156 (1–4): 331–341.
Nasdala, L., M. Wenzel, G. Varva, G. Irmer, T. Wenzel, and B. Kober. 2001. “Metamictization of Natural Zircon: Accumulation Versus Thermal Annealing of Radioactivity-Induced Damage.” Contributions to Mineralogy and Petrology 141 (2): 125–144.
Nasdala, L., J. M. Hanchar, D. Rhede, A. K. Kennedy, and T. Váczi. 2010. “Retention of Uranium in Complexly Altered Zircon: An Example from Bancroft, Ontario.” Chemical Geology 269 (3–4): 290–300.
Nemchin, A. A., R. T. Pidgeon, and M. J. Whitehouse. 2006. “Re-evaluation of the Origin and Evolution of >4.2 Ga Zircons from the Jack Hills Metasedimentary Rocks.” Earth and Planetary Science Letters 244 (1–2): 218–233.
Nemchin, A. A., M. J Whitehouse, R. T. Pidgeon, and C. Meyer. 2006. “Oxygen Isotopic Signature of 4.4–3.9 Ga Zircons as a Monitor of Differentiation Processes on the Moon.” Geochimica et Cosmochimica Acta 70 (7): 1864–1872.
Nier, A. O. 1940. “A Mass Spectrometer for Routine Isotope Abundance Measurements.” Reviews of Scientific Instruments 18: 398–411.
Nutman, A. P., C. R. L. Friend, S. L. L. Barker, and V. R. McGregor. 2004. “Inventory and Assessment of Palaeoarchaean Gneiss Terrains and Detrital Zircons in Southern West Greenland.” Precambrian Research 135 (4): 281–314.
Ordonez R. E., J. J. Schleiffer, J. P. Adloff, and K. Roessler. 1989. “Chemical Effects of α-Decay in Uranium Minerals.” Radiochimica Acta 47 (4): 177–185.
Otto, E. M. 1966. “Equilibrium Pressures of Oxygen Over Oxides of Lead at Various Temperatures.” Journal of the Electrochemistry Society 113 (6): 525–527.
Pabst, A. 1952. “The Metamict State.” American Mineralogist 37 (3–4):137–157.
Papanastassiou, D. A., and G. J. Wasserburg. 1971. “Rb-Sr Ages of Igneous Rocks from the Apollo 14 Mission and the Age of the Fra Mauro Formation.” Earth and Planetary Science Letters 12 (1): 36–48.
Parrish, R. R. 1990. “U-Pb Dating of Monazite and Its Application to Geological Problems.” Canadian Journal of Earth Sciences 27 (11): 1431–1450.
Parrish, R. R., and R. Tirrul. 1989. “U-Pb Age of the Baltoro Granite, Northwest Himalaya, and Implications for Monazite U-Pb Systematics.” Geology 17 (12): 1076–1079.
Pasteels, P. 1970. “Uranium-Lead Radioactive Ages of Monazite and Zircon from the Vire-Carolles Granite (Normandy): A Case of Zircon-Monazite Discrepancy.” Eclogae Geologicae Helvetiae 63 (1): 231–237.
Peters, S. E., and R. R. Gaines 2012. “Formation of the ‘Great Unconformity’ as a Trigger for the Cambrian Explosion.” Nature 484 (7394): 363–366.
Petit, J. C., J. C. Dran, and G. Della Mea. 1987. “Effects of Ion Implantation on the Dissolution of Minerals. II. Selective Dissolution.” Bulletin de Minéralogie 110: 25–42.
Piazolo, S., H. Austrheim, and M. J. Whitehouse. 2012. “Brittle-Ductile Microfabrics in Naturally Deformed Zircon: Deformation Mechanisms and Consequences for U-Pb Dating.” American Mineralogist 97 (10): 1544–1563.
Piazolo, S., A. LaFontaine, P. Trimby, S. Harley, L. Yang, R. Armstrong, and J. M. Cairney. 2016. “Deformation-Induced Trace Element Redistribution in Zircon Revealed Using Atom Probe Tomography.” Nature Communications 7: 10490-1—10490-7; doi: 10.1038/ncomms10490.
Picu, R. C., and D. Zhang. 2004. “Atomistic Study of Pipe Diffusion in Al-Mg Alloys.” Acta Materialia 52 (1): 161–171.
Pidgeon, R. T., J. R. O’Neil, and L. T. Silver. 1966. “Uranium and Lead Isotopic Stability in a Metamict Zircon under Experimental Hydrothermal Conditions.” Science 154 (3756): 1538–1540.
Pidgeon, R. T., and M. R. W. Johnson. 1974. “A Comparison of Zircon U-Pb and Whole-Rock Rb-Sr Systems in Three Phases of the Carn Chuinneag Granite, Northern Scotland.” Earth and Planetary Science Letters 24 (1): 105–112.
Pidgeon, R. T., J. R. O’Neil, and L. T. Silver. 1973. “Observations on the Crystallinity and the U-Pb System of a Metamict Ceylon Zircon Under Experimental Hydrothermal Conditions.” Fortschritte der Mineralogie 50: 118.
Pidgeon, R. T., and M. Aftalion. 1978. “Cogenetic and Inherited Zircon U-Pb Systems in Granites: Paleozoic Granites of Scotland and England.” In Crustal Evolution in Northwestern Britain and Adjacent Regions. Edited by D. R. Bowes and B. E. Leake, Geological Journal Special Issue 10: 183–220.
Pidgeon, R. T., A. A. Nemchin, and G. J. Hitchen. 1998. “Internal Structures of Zircons from Archaean Granites from the Darling Range Batholith: Implications for Zircon Stability and the Interpretation of Zircon U-Pb Ages.” Contributions to Mineralogy and Petrology 132 (3): 288–299.
Pidgeon, R. T., and A. A. Nemchin. 2006. “High Abundance of Early Archaean Grains and the Age Distribution of Detrital Zircons in a Sillimanite-Bearing Quartzite from Mt Narryer, Western Australia.” Precambrian Research 150: 201–220.
Pidgeon, R. T., A. A. Nemchin, W. van Bronswijk, T. Geisler, C. Meyer, W. Compston, and I. S. Williams. 2007. “Complex History of a Zircon Aggregate from Lunar Breccia 73235.” Geochimica et Cosmochimica Acta 71 (5): 1370–1381.
Poitrasson, F., J.-L. Paquette, J.-M. Montel, C. Pin, and J.-L. Duthou. 1998. “Importance of Late-Magmatic and Hydrothermal Fluids on the Sm-Nd Isotope Mineral Systematics of Hypersolvus Granite.” Chemical Geology 146 (3–4): 187–203.
Ramdohr, P. 1960. “New Observations on Radioactive Halos in Various Minerals with Critical Remarks for the Evaluation of Halos for Age Determinations.” Geologische Rundschau 49 (1): 253–263.
Reddy, S. M., N. E. Timms, W. Pantleon, and P. Trimby. 2007. “Quantitative Characterization of Plastic Deformation of Zircon and Geological Implications.” Contributions to Mineralogy and Petrology 153 (6): 625–645.
Renne, P. R., D. B. Karner, and K. R. Ludwig. 1998. “Absolute Ages Aren’t Exactly.” Science 282 (5395): 1840–1841.
Reiners, P. W., R. W. Carlson, P. R. Renne, K. M. Cooper, D. E. Granger, N. M. McLean, and B. Schoene. 2018. Geochronology and Thermochronology. Hoboken, New Jersey: John Wiley & Sons.
Ríos, S., and E. K. H. Salje. 1999. “Diffuse X-Ray Scattering from Weakly Metamict Zircon.” Journal of Physics: Condensed Matter 11 (45): 8947–8956.
Ríos, S., E. K. H. Salje, M. Zhang, and R. C. Ewing. 2000. “Amorphization of Zircon: Evidence for Direct Impact Damage.” Journal of Physics: Condensed Matter 12 (11): 2401–2412.
Romer, R. L. 2003. “Alpha-Recoil in U-Pb Geochronology: Effective Sample Size Matters.” Contributions to Mineralogy and Petrology 145 (4): 481–491.
Rudnick, R. L., and S. Gao. 2003. “Composition of the Continental Crust.” In The Crust. Edited by R. L. Rudnick, Treatise on Geochemistry. Edited by H. D. Holland and K. K. Turekian, vol. 3, 1–64. Amsterdam, The Netherlands: Elsevier.
Rutherford, E. 1906. Radioactive Transformations. New York: Charles Scribner’s Sons.
Sanborn, N., R. A. Stern, and S. D. Carr. 1998. “Discordance and Pb-Loss Mechanisms in 3.5 Ga Zircon from the Acasta Gneiss Complex, N.W.T., Canada: A SHRIMP Ion Microprobe Study.” Geological Society of America Abstracts with Programs A240.
Schärer, U., and C. J. Allègre. 1982. “Uranium-Lead System in Fragments of a Single Zircon Grain.” Nature 295 (5850): 585–587.
Scherer, E. E., M. J. Whitehouse, and C. Münker. 2007. “Zircon as a Monitor of Crustal Growth.” Elements 3 (1): 19–24.
Schmitz, M.D. 2012. “Radiogenic Isotope Geochronology.” In The Geologic Time Scale 2012. Edited by F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 1, chapter 6, pp. 115–126. Amsterdam, The Netherlands: Elsevier.
Schoene, B., J. L. Crowley, D. J. Condon, M. D. Schmitz, and S. A. Bowring. 2006. “Reassessing the Uranium Decay Constants for Geochronology Using ID-TIMS U-Pb Data.” Geochimica et Cosmochimica Acta 70 (2): 426–445.
Schön, R., G. Winkler, and W. Kutschera. 2004. “A Critical Review of Experimental Data for the Half-Lives of the Uranium Isotopes 238U and 235U.” Applied Radiation and Isotopes 60 (2–4): 263–273.
Seydoux-Guillaume, A. M., P. Goncalves, R. Wirth, and A. Deutsch. 2003. “Transmission Electron Microscope Study of Polyphase and Discordant Monazites: Site-Specific Specimen Preparation Using the Focused Ion Beam Technique.” Geology 31 (11): 973–976.
Seydoux-Guillaume, A.-M., J. M. Montel, B. Bingen, V. Bosse, P. de Parseval, J.-L. Paquette, E. Janots, and R. Wirth. 2012. “Low-Temperature Alteration of Monazite: Fluid Mediated Coupled Dissolution—Precipitation, Irradiation Damage, and Disturbance of the U-Pb and Th-Pb Chronometers.” Chemical Geology 330–331: 140–158.
Seydoux-Guillaume, A.-M., B. Bingen, J.-L. Paquette, and V. Bosse. 2015. “Nanoscale Evidence for Uranium Mobility in Zircon and the Discordance of U-Pb Chronometers.” Earth and Planetary Science Letters 409: 43–48.
Shannon, R. D. 1976. “Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides.” Acta Crystallographica A32: 751–767.
Shestakov, G. I. 1969. “On Diffusional Loss of Lead from a Radioactive Mineral.” Geokhimiya 9: 1103–1111.
Shestakov, G. I. 1972. “Diffusion of Lead in Monazite, Zircon, Sphene, and Apatite.” Geokhimiya 10: 1197–1202.
Siégel, C., S. E. Bryan, C. M Allen, and D. A. Gust. 2018. “Use and Abuse of Zircon-Based Thermometers: A Critical Review and a Recommended Approach to Identify Antecrystic Zircons.” Earth-Science Reviews 176: 87–116.
Silver, L. T., and S. Deutsch. 1963. “Uranium-Lead Isotopic Variations in Zircons: A Case Study.” Journal of Geology 71 (6): 721–758.
Sinha, A. K., D. M. Wayne, and D. A. Hewitt. 1992. “The Hydrothermal Stability of Zircon: Preliminary Experimental and Isotopic Studies.” Geochimica et Cosmochimica Acta 56 (9): 3551–3560.
Slater, J. C. 1951. The Effect of Radiation on Materials.” Journal of Applied Physics 22 (3): 237–256.
Sliwinski, J. T., M. Guillong, C. Liebske, I. Dunkl, A. von Quadt, and O. Bachmann. 2017. “Improved Accuracy of LA-ICP-MS U-Pb Ages of Cenozoic Zircons by Alpha Dose Correction.” Chemical Geology 472: 8–21.
Smith, J. B., M. E. Barley, D. I. Groves, B. Krapez, N. J. McNaughton, M. J. Bickle, and H. J. Chapman. 1998. “The Sholl Shear Zone, West Pilbara: Evidence for a Domain Boundary Structure from Integrated Tectonostratigraphic Analyses, SHRIMP U-Pb Dating and Isotopic and Geochemical Data of Granitoids.” Precambrian Research 88 (1–4): 143–171.
Snelling, A. A. 2000. “Geochemical Processes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: A Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 123–304. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, A. A. 2005a. “Radiohalos in Granites: Evidence of Accelerated Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 101–207. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/radiohalos-granites-evidence-for-accelerated/.
Snelling, A. A. 2005b. “Fission Tracks in Zircons: Evidence for Abundant Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 209–324. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/fission-tracks-zircons-evidence-for/.
Snelling, A. A. 2009. Earth’s Catastrophic Past: Geology, Creation and the Flood. Green Forest, Arkansas: Master Books; and Petersburg, Kentucky: Answers in Genesis.
Snelling, A. A. 2014a. “Determination of the Radioisotope Decay Constants and Half-Lives: Rubidium-87 (87Rb).” Answers Research Journal 7: 311–322. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, A. A. 2014b. “Determination of the Radioisotope Decay Constants and Half-Lives: Lutetium-176 (176Lu).” Answers Research Journal 7: 483–497. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, A. A. 2014c. “Noah’s Lost World.” Answers 9 (2): 80–85.
Snelling, A. A. 2015a. “Determination of the Radioisotope Decay Constants and Half-Lives: Rhenium-187 (187Re).” Answers Research Journal 8: 93–111. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rhenium-187/.
Snelling, A. A. 2015b. “Determination of the Radioisotope Decay Constants and Half-Lives: Samarium-147 (247Sm).” Answers Research Journal 8: 305–321. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-samarium-147/.
Snelling, A. A. 2016. “Determination of the Radioisotope Decay Constants and Half-Lives: Potassium-40 (40K).” Answers Research Journal 9: 171–196. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-half-lives-potassium-40/.
Snelling, A. A. 2017a. “Determination of the Decay Constants and Half-Lives of Uranium-238 (238U) and Uranium-235 (235U), and the Implications for U-Pb and Pb-Pb Radioisotope Dating Methodologies.” Answers Research Journal 10: 1–38. https://answersingenesis.org/geology/radiometric-dating/determination-decay-constants-half-lives-uranium/.
Snelling, A. A. 2017b. “Problems with U-Pb Radioisotope Dating—1. Common Pb.” Answers Research Journal 10: 121–167. https://answersingenesis.org/geology/radiometric-dating/problems-radioisotope-dating-u-pb/.
Solari, L. A., C. Ortega-Obregón, and J. P. Bernal. 2015. “U-Pb Zircon Geochronology by LAICPMS Combined with Thermal Annealing: Achievements in Precision and Accuracy on Dating Standard and Unknown Samples.” Chemical Geology 414: 109–123.
Soman, A., T. Geisler, F. Tomaschek, M. Grange, and J. Berndt. 2010. “Alteration of Crystalline Zircon Solid Solutions: A Case Study on Zircon from an Alkaline Pegmatite from Zomba-Molosa, Malawi.” Contributions to Mineralogy and Petrology 160 (6): 909–930.
Speer, J. A. 1980. “Zircon.” In Orthosilicates. Edited by P. H. Ribbe, Reviews in Mineralogy, vol. 5, pp. 67–122. Washington, DC: Mineralogical Society of America.
Steiger, R. H., and E. Jäger. 1977. “Subcommission on Geochronology: Convention on the Use of Decay Constants in Geo- and Cosmochronology.” Earth and Planetary Science Letters 36 (3): 359–362.
Stern, R. A., N. Sanborn, and W. Bleeker. 1998. “Exploiting the High Spatial Sensitivity of the Ion Microprobe in Studying Pb-Loss Mechanisms and U-Pb Ages of Metamict and Altered Zircon.” EOS, Transactions of the American Geophysical Union 79: F951.
Stern, T. W., S. S. Goldich, and M. F. Newell. 1966. “Effects of Weathering on the U-Pb Ages of Zircon from the Morton Gneiss, Minnesota.” Earth and Planetary Science Letters 1 (6): 369–371.
Suzuki, K. 1987. “Discordant Distribution of U and Pb in Zircon of Naegi Granite: A Possible Indication of Rn Migration Through Radiation Damage.” Geochemical Journal 21 (4): 173–182
Tatsumoto, M., and J. N. Rosholt. 1970. “Age of the Moon: An Isotopic Study of U-Th-Pb Systematics of Lunar Samples.” Science 167 (3918): 461–463.
Tatsumoto, M., R. J. Knight, and C. J. Allègre. 1973. “Time Differences in the Formation of Meteorites as Determined from the Ratio of Lead-207 to Lead-206.” Science 180 (4092): 1279–1283.
Tera, F., and G. J. Wasserburg. 1972. “U-Th-Pb Systematics in Three Apollo 14 Basalts and the Problem of Initial Pb in Lunar Rocks.” Earth and Planetary Science Letters 14 (3): 281–304.
Tera, F., and G. J. Wasserburg. 1973. “A Response to a Comment on U-Pb Systematics in Lunar Basalts.” Earth and Planetary Science Letters 19 (2): 213–217.
Tera, F., and G. J. Wasserburg. 1974. “U-Th-Pb Systematics on Lunar Rocks and Inferences About Lunar Evolution and the Age of the Moon.” Proceedings of the 5th Lunar Conference, Geochimica et Cosmochimica Acta 2 (Supplement 5): 1571–1599.
Thielemann, F.-K., A. Arcones, R. Käppeli, M. Liebendörfer, T. Rauscher, C. Winteler, C. Fröhlich, et al. 2011. “What are the Astrophysical Sites for the r-Process and the Production of Heavy Elements?” Progress in Particle and Nuclear Physics 66 (2): 346–353.
Thomson, J. J. 1911. “A New Method of Chemical Analysis.” Nature 86 (2170): 466–469.
Tilton, G. R. 1960. “Volume Diffusion as a Mechanism for Discordant Lead Ages.” Journal of Geophysical Research 65 (9): 2933–2945.
Timms, N. E., P. D. Kinny, and S. M. Reddy. 2006. “Enhanced Diffusion of Uranium and Thorium Linked to Crystal Plasticity in Zircon.” Geochemical Transactions 7: 1–16.
Tissot, F. L. H., and N. Dauphas. 2015. “Uranium Isotopic Compositions of the Crust and Ocean: Age Corrections, U Budget and Global Extent of Modern Anoxia.” Geochimica et Cosmochimica Acta 167: 113–143.
Trachenko, K. O., M. T. Dove, and E. K. H. Salje. 2002. “Structural Changes in Zircon Under α-Decay Irradiation.” Physical Review B 65: 180102.
Trachenko, K. O., M. T. Dove, and E. K. H. Salje. 2003. “Large Swelling and Percolation in Irradiated Zircon.” Journal of Physics: Condensed Matter 15 (2): L1–L7.
Trimby, P. W. 2012. “Orientation Mapping of Nanostructured Materials Using Transmission Kikuchi Diffraction in the Scanning Electron Microscope.” Ultramicroscopy 120: 16–24.
Turner, G., J. C. Huneke, F. A. Podosek, and G. J. Wasserburg. 1971. “40Ar-39Ar Ages and Cosmic-Ray Exposure Ages of Apollo 14 Samples.” Earth and Planetary Science Letters 12 (1): 19–35.
Utsunomiya, S., C. S. Palenik, J. W. Valley, A. J. Cavosie, S. A. Wilde, and R. C. Ewing. 2004. “Nanoscale Occurrence of Pb in an Archean Zircon.” Geochimica et Cosmochimica Acta 68 (22): 4679–4686.
Valley, J. W., J. S. Lackey, A. J. Cavosie, C. C. Clechenko, M. J. Spicuzza, M. A. S. Basei, I. N. Bindeman, et al. 2005. “4.4 Billion Years of Crustal Maturation: Oxygen Isotope Ratios of Magmatic Zircon.” Contributions to Mineralogy and Petrology 150 (6): 561–580.
Valley, J. W., A. J. Cavosie, T. Ushikubo, D. A. Reinhard, D. F. Lawrence, D. J. Larson, P. H. Clifton, et al. 2014. “Hadean Age for a Post-Magma-Ocean Zircon Confirmed by Atom-Probe Tomography.” Nature Geoscience 7: 219–223.
Valley, J. W., D. A. Reinhard, A. J. Cavosie, T. Ushikubo, D. F. Lawrence, D. J. Larson, T. F. Kelly, D. R. Snoeyenbos, and A. Strickland. 2015. “Nano- and Micro-Geochronology in Hadean and Archean Zircons by Atom-Probe Tomography and SIMS: New Tools for Old Minerals.” American Mineralogist 100 (7): 1355–1377.
Vance, D., W. Müller, and I. M. Villa. 2003. “Geochronology: Linking the Isotopic Record with Petrology and Textures—An Introduction.” In Geochronology: Linking the Isotopic Record With Petrology and Textures. Edited by D. Vance, W. Müller, and I. M. Villa, Geological Society of London Special Publication 220: 1–24.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the Age of the Earth: A Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Villa, I. M. 2016. “Diffusion in Mineral Geochronometers: Present and Absent.” Chemical Geology 420: 1–10.
Villa, I. M., and M. L. Williams. 2013. “Geochronology of Metasomatic Events.” In Metasomatism and the Chemical Transformation of Rock. Edited by D.E. Harlov and H. Austrheim, 171–202. Heidelberg, Germany: Springer.
Villa, I.M., M.L. Bonardi, P. De Bièvre, N.E. Holden, and P.R. Renne. 2016. “IUPAC-IUGS Status Report on the Half-Lives of 238U, 235U and 234U.” Geochimica et Cosmochimica Acta 172: 387-392.
von Quadt, A., D. Gallhofer, M. Guillong, I. Peytcheva, M. Waelle, and S. Sakata. 2014. “U-Pb Dating of CA/Non-CA Treated Zircons Obtained by LA-ICP-MS and CA-TIMS Techniques: Impact for their Geological Interpretation.” Journal of Analytical Atomic Spectrometry 29 (9): 1618–1629.
von Stackelberg M., and E. Rottenbach. 1940a. “Dichte und Struktur des Zirkons. III Die Natur der Lamellen-Zirkone.” Zeitschrift für Kristallographie 102 (1–6): 173–182.
von Stackelberg M., and E. Rottenbach. 1940b. “Dichte und Struktur des Zirkons, IV: Die Ursache der Isotopisierung des Zirkons.” Zeitschrift für Kristallographie 102 (1–6): 207–208.
Wang, L. M., and R. C. Ewing. 1992a. “Ion-Beam-Induced Amorphization of Complex Ceramic Materials—Minerals.” Materials Research Society Bulletin 17 (5): 38–44.
Wang, L.M., and R.C. Ewing. 1992b. “Detailed In Situ Study of Ion Beam-Induced Amorphization of Zircon.” Nuclear Instruments and Methods in Physics Research B 65: 324–329.
Wang, S. X., L. M. Wang, and R. C. Ewing. 1997. “A Model for Irradiation-Induced Amorphization.” In Symposium KK-Atomistic Mechanisms in Beam Synthesis & Irradiation of Materials, vol. 504. Edited by J. C. Barbour, S. Roorda, D. Ila, and M. Tsujioka, 165–170. Warrendale, Pennsylvania: Materials Research Society.
Wang, S. X., L. M. Wang, and R. C. Ewing. 2001. “Irradiation Induced-Amorphization: Effects of Temperature, Ion Mass, Cascade Size, and Dose Rate.” Physical Review B 63: 024105.
Wasserburg G. J., 1963. “Diffusion Processes in Lead-Uranium Systems.” Journal of Geophysical Research 68 (16): 4823–4846.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nemov, and C. A. Bauman. 1969. “A Programmable Magnetic Field Mass Spectrometer with On-Line Data Processing.” Reviews of Scientific Instruments 40 (2): 288–295.
Watson, E. B., and T. M. Harrison. 1983. “Zircon Saturation Revisited: Temperature and Composition Effects in a Variety of Crustal Magma Types.” Earth and Planetary Science Letters 64 (2): 295–304.
Watson, E. B., and Y. Liang. 1995. “A Simple Model for Sector Zoning in Slowly Grown Crystals: Implications for Growth Rate and Lattice Diffusion, with Emphasis on Accessory Minerals in Crustal Rocks.” American Mineralogist 80 (11–12): 1179–1187.
Watson, E. B., D. J. Cherniak, J. M. Hanchar, T. M. Harrison, and D. A. Wark. 1997. “The Incorporation of Pb in Zircon.” Chemical Geology 141 (1–2): 19–31.
Weber, W. J., 1990. “Radiation-Induced Defects and Amorphization in Zircon.” Journal of Materials Research 5 (11): 2687–2697.
Weber, W. J. 1991. “Self-Radiation Damage and Recovery in Pu-Doped Zircon.” Radiation Effects and Defects in Solids 115 (4): 341–349.
Weber, W. J. 1993. “Alpha-Decay-Induced Amorphization in Complex Silicate Structures.” Journal of the American Ceramic Society 76 (7): 1729–1738
Weber, W. J. 2000. “Models and Mechanisms of Irradiation-Induced Amorphization in Ceramics.” Nuclear Instruments and Methods in Physics Research B: Beam Interactions with Materials and Atoms 166–167: 98–106.
Weber, W. J., R. C. Ewing, and L. M. Wang. 1994. “The Radiation-Induced Crystalline-to-Amorphous Transition in Zircon.” Journal of Materials Research 9 (3): 688–698.
Weber, W. J., R. C. Ewing, and A. Meldrum. 1997. “The Kinetics of Alpha-Decay-Induced Amorphization in Zircon and Apatite Containing Weapons-Grade Plutonium or Other Actinides.” Journal of Nuclear Materials 250 (2–3): 147–155.
Weber, W. J., R. C. Ewing, C. R. A. Catlow, T. D. de la Rubia, L. W. Hobbs, C. Kinoshita, H. J. Matzke, et al. 1998a. “Radiation Effects in Crystalline Ceramics for the Immobilization of High-Level Nuclear Waste and Plutonium.” Journal of Materials Research 13 (6): 1434–1484.
Weber, W. J., R. Devanathan, A. Meldrum, L.A. Boatner, R.C. Ewing, and L.M. Wang. 1998b. “The Effect of Temperature and Damage Energy on Amorphization in Zircon.” In Microstructural Processes in Irradiated Materials. Edited by S. J. Zinkle, G. E. Lucas, R. C. Ewing, and J. S. Williams, Symposium on Microstructural Processes in Irradiated Materials, vol. 540, pp. 367–372. Warrendale, Pennsylvania: Materials Research Society.
Weber, W. J. and R. C. Ewing. 2000. “Plutonium Immobilization and Radiation Effects.” Science 289 (5487): 2051–2052.
Weber, W. J. and R. C. Ewing. 2002. “Radiation Effects in Crystalline Oxide Host Phases for the Immobilization of Actinides.” In Symposium on the Scientific Basis for Nuclear Waste Management XXV. Edited by B. P McGrail and G. A. Cragnolino, Symposium Proceedings, vol. 713, pp. 443–454. Warrendale, Pennsylvania: Materials Research Society.
Wetherill, G. W. 1956. “Discordant Uranium-Lead Ages, I.” Transactions of the American Geophysical Union 37: 320–326.
Wetherill, G. W. 1963. “Discordant Uranium-Lead Ages: 2. Discordant Ages Resulting from Diffusion of Lead and Uranium.” Journal of Geophysical Research 68 (10): 2957–2965.
Wetherill, G. W. 1966. “Radioactive Decay Constants and Energies.” In Handbook of Physical Constants. Edited by S. E. Clarke, Geological Society of America Memoir 97: 514–519. Boulder, Colorado: Geological Society of America.
White, L. T., and T. R. Ireland. 2012. “High-Uranium Matrix Effect in Zircon and Its Implications for SHRIMP U-Pb Age Determinations.” Chemical Geology 306–307: 78–91.
Whitehouse, M. J. 2003. “Rare Earth Elements in Zircon: A Review of Applications and Case Studies from the Outer Hebridean Lewisian Complex, NW Scotland.” In Geochronology: Linking the Isotopic Record With Petrology and Textures. Edited by D. Vance, W. Müller, and I. M. Villa. Geological Society of London Special Publication 220: 49–64.
Whitehouse, M. J., B. S. Kamber, and S. Moorbath. 1999. “Age Significance of U-Th-Pb Zircon Data from Early Archaean Rocks of West Greenland—A Reassessment Based on Combined Ion-Microprobe and Imaging Studies.” Chemical Geology 160 (3): 201–224.
Williams, I. S. 1992. “Some Observations on the Use of Zircon U-Pb Geochronology on the Study of Granitic Rocks.” Transactions of the Royal Society of Edinburgh: Earth Sciences 83 (1–2): 447–458.
Williams, I. S. 1998. “U-Th-Pb Geochronology by Ion Microprobe.” In Applications of Microanalytical Techniques to Understanding Mineralizing Processes. Edited by M. A. McKibben, W. C. Shanks III, and W. I. Ridley. Reviews in Economic Geology 7: 1–35. San Diego, California: Economic Geology Publishing Company.
Williams, I. S., W. Compston, and B. W. Chappell. 1983. “Zircon and Monazite U-Pb Systems and Histories of I-Type Magmas, Berridale Batholith, Australia.” Journal of Petrology 24 (1): 76–97.
Williams, I. S., W. Compston, L. P. Black, T. R. Ireland, and J. J. Forster. 1984. “Unsupported Radiogenic Pb in Zircon: A Cause of Anomalously High Pb-Pb, U-Pb and Th-Pb Ages.” Contributions to Mineralogy and Petrology 88 (4): 322–327.
Williams, I. S., and J. M. Hergt. 2000. “U-Pb Dating of Tasmanian Dolerites: A Cautionary Tale of SHRIMP Analysis of High-U Zircon.” In Beyond 2000: New Frontiers in Isotope Geoscience. Edited by J. D. Woodhead and W. P. Noble, 185–188. Melbourne, Australia: University of Melbourne.
Williams, I. S., M. L. Jercinovic, and C. J. Hetherington. 2007. “Microprobe Monazite Geochronology: Understanding Geologic Processes by Integrating Composition and Chronology.” Annual Review of Earth and Planetary Sciences 35: 137–175.
Williford, R. E., W. J. Weber, R. Devanthan, and A. N. Cormak. 1999. “Native Vacancy Migrations in Zircon.” Journal of Nuclear Materials 273 (2): 164–170.
Wingate, M. T. D., and W. Compston. 2000. “Crystal Orientation Effects During Ion Microprobe U-Pb Analysis of Baddeleyite.” Chemical Geology 168 (1–2): 75–97.
Xie, K. Y., T. Zheng, J. M. Cairney, H. Kaul, J. G. Williams, F. J. Barbaro, C. R. Killmore, and S. P. Ringer. 2012. “Strengthening from Nb-Rich Clusters in a Nb-Microalloyed Steel.” Scripta Materialia 66 (9): 710–713.
Xu, X.-S., M. Zhang, K.-Y. Zhu, X.-M. Chen, and Z.-Y. He. 2012. “Reverse Age Zonation of Zircon Formed by Metamictisation and Hydrothermal Fluid Leaching.” Lithos 150: 256–267.
Zhang, L.-S., and U. Schärer. 1996. “Inherited Pb Components in Magmatic Titanite and Their Consequence for the Interpretation of U-Pb Ages.” Earth and Planetary Science Letters 138 (1–4): 57–65.
Zhang, M., E. K. H. Salje, R. C. Ewing, I. Farnan, S. Ríos, J. Schlüter, and P. Leggo. 2000a. “α-Decay Damage and Recrystallization in Zircon: Evidence for an Intermediate State from Infrared Spectroscopy.” Journal of Physics: Condensed Matter 12 (24): 5189–5199.
Zhang, M., E. K. H. Salje, G. C. Capitani, H. Leroux, A. M. Clark, J. Schlüter, and R. C. Ewing. 2000b. “Annealing of α-Decay Damage in Zircon: A Raman Spectroscopic Study.” Journal of Physics: Condensed Matter 12 (13): 3131–3148.











