The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
Wood and co-workers (Robinson and Cavanaugh, 1998; Wood 2002, 2005a) have devised and promoted the application of some statistical methods to the taxonomy of various biological organisms. Principally, they rely on a technique described as Baraminic Distance Correlation (BDC) or a version of multi-dimensional scaling (BDISTMDS). This paper will argue that these methods are based on a shaky understanding of statistical principles, and that their use ought to be abandoned.
Keywords: statistical baraminology, distance metrics, distance correlation, bootstrapping
Introduction
Whereas Darwinian evolution assumes a monophyletic relationship between all life, as depicted in his famous “tree of life,” creationists interpret the differences between biological organisms in terms of original baramins, or “created kinds,” followed by a subsequent polyphyletic development. Statistical baraminology (SB) assumes it can uncover the discontinuities between groups of known taxa, which may be a route to determining the original kinds. To identify relationships between taxa, we can enumerate a set of characters that are shared by subsets of the particular organisms being studied. From a statistical viewpoint, we have a set of data comprising measurements of p variables (also called characters or attributes in the literature) for each of n objects (taxa) {xi }, where xi is a row vector (xi1, . . ., xip). We can denote the data set by
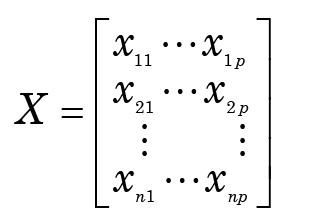
The first step of the BDC procedure is then to define a n-dimensional dissimilarity matrix
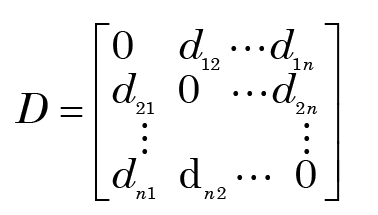
where the notation dij is shorthand for a function d(xi,xj) that measures the dissimilarity or “distance” between taxon i (xi) and taxon j (xj). Note that in practice the distances are nearly always symmetric (i.e., dij = dij), so only the upper or lower triangle of this matrix needs to be stored.
The BDC technique
Baraminic Distance Correlation (BDC) typically uses a distance metric that simply counts the number of “matches” between every pair of taxa across all characters1 and subtracts this from the maximum number of matches possible (p). Indeed, this is sometimes called a simple matching distance. Mathematically, if we have two taxa x and y this is equivalent to the formula
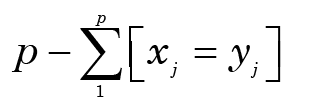
or, equivalently
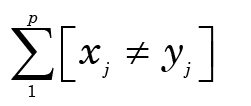
where the notation [expr] denotes the value 1 if the expression expr is logically true, and 0 if it is false, and xj (resp. yj) is the value of the jth character for the taxon x (resp. y). Of course this needs to be normalized, so the “distance” between x and y is defined as
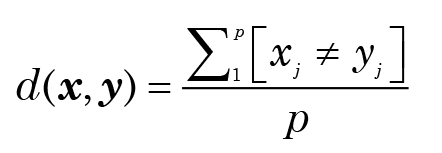
Having calculated this function for all taxa, a n × n matrix is obtained. The columns of this dissimilarity matrix are then treated as variables from which a set of pairwise correlation coefficients r can be computed. This is the origin of the term Baraminic Distance Correlation. The values of r are then assessed for significance using a t-test, and the resulting “significance matrix” inspected for patterns. A considerable creationist industry of baraminological data-mining has developed in the last decade in which this idea is applied to many different datasets, of which (Aaron 2014; Cavanaugh and Wood 2002; Garner 2004, 2014; Ingle and Aaron 2015; Wood 2002, 2010, 2011, 2016) form just a sample. Some of the results are equivocal, others problematic (particularly Wood 2010, 2011), which comes to unexpected conclusions in the area of putative human ancestry), but the statistical validity of the method has just been assumed. Some years ago, Wilson (2010) made a plea for better scrutiny of the underlying assumptions of statistical baraminology, but as far as I can tell, this hasn’t happened. On examining SB from a conventional statistical perspective, I have discovered several problems, some of them very serious. These will now be discussed in detail.
Problematic Aspects of BDC
Distance metrics
BDC assumes we can assign a precise meaning to the idea that (say) object x is closer to y than to z. Wood (2002) makes a virtue of the “simplicity” of the distance metric described above, but it is hardly unique. (For some background on distance metrics, see Appendix A.) Nor is it necessarily the most appropriate one, as the data type of the variable under consideration may be an important factor. (For background on data types, see Appendix B.) It is very often the case that the underlying variables are nominal: that is, they express which of a set of discrete characters is possessed by the taxon of interest. Often, indeed, the variables are strictly binary, having just two values—the presence (1) or absence (0) of a character. Thus, if we imagine the p-dimensional character space which the taxa inhabit, the set of feasible points in this space consists only of the “corners,” and is a tiny fraction of the space as a whole. (For example, if there are 3 binary characters, there are just 8 possible points, corresponding to the corners of a cube. Points along an edge, or in the interior, correspond to no physical reality at all.) Sometimes, however, they may be ordinal—different objects may have smaller or larger instances of a character. It is conceivable, too, that some variables are quantitative—measurable on an interval or even a ratio scale. Defining a suitable measure of distance for a mixture of types of variable then becomes a highly subjective matter. Of course, it is always possible to reduce a numerical variable to a mere category, but there is inevitably a loss of information or—even worse—the potential to mislead the distance function.2 There may also be some idea as to the relative importance of the characters, in which case a weighted matching distance can be defined; for example, in the case of simple matching this might be
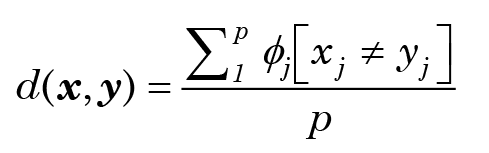
where ϕj is the weight of the jth variable.
Moreover, even if we assume the simplest case—purely nominal variables and the simple matching definition—we are still implicitly assuming that presence and absence of characters is of equal significance. This may not be true, and if a character is expressed by an ordinal variable, it becomes highly dubious. Statisticians are not unaware of this, and several alternative measures have been suggested. Consider first the specific case of binary variables: by counting the presences and absences separately, the distance formula can be rewritten as
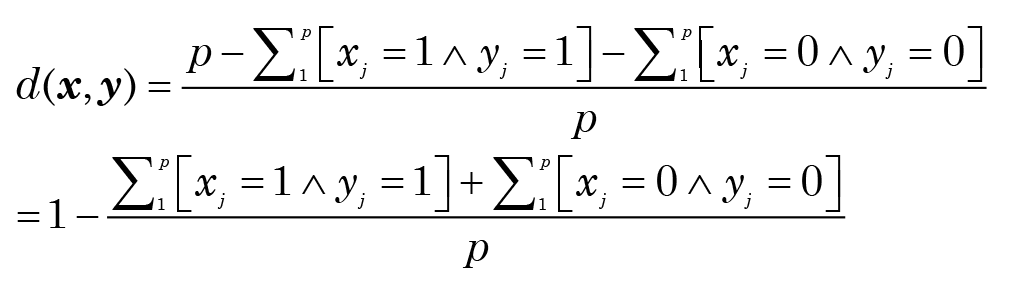
where ˄ is the standard symbol for logical “and.” Building on this, some obvious extensions can be seen. If the presence of a character (xj = 1) is more significant than its absence (xj = 0), the distance measure preferred is often the Jaccard distance:
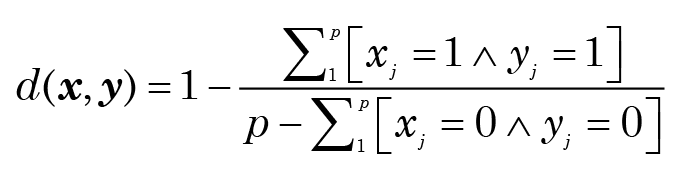
Still other ideas have been suggested: the Dice distance, which gives twice as much weight to the case where both characters are present, has the value
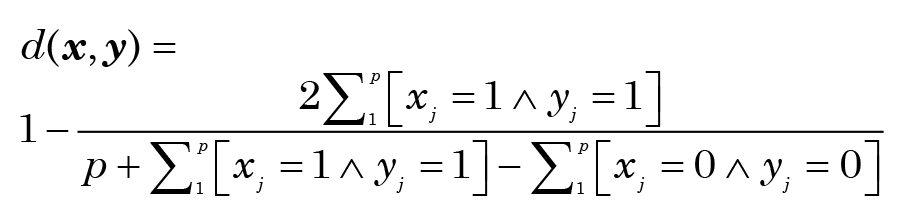
(This could be further generalized to reflect subjective opinions on the importance of presence or absence by using some other value than 2.) These formulae can be extended to the non-binary case if necessary, and weighted versions of all of them can also be defined. For an example of some calculations using these metrics, see Appendix C. A recent study by Finch (2005) concluded that the Jaccard and Dice distances tend to do better than simple matching, in terms of cluster recovery for simulated binary data where the “true” taxonomic structure was known.
For non-binary variables, an obvious modification is to normalize the set of possible values to lie in the range [0, 1], and to modify the contribution made by such components by calculating the absolute distance |xj − yj| between the relevant pairs of variables whenever xj and yj are both non-zero.
Turning now to the various techniques described in Robinson and Cavanaugh (1998) and Wood (2002, 2005a), which can be collectively identified under the heading “statistical baraminology,” we should note that they all assume the computation of a suitable distance metric, although generally only results using the simple matching distance were reported in these papers. In fact, the question of whether this is appropriate appears to be ignored in the SB literature.
Distance correlation
The “novel” tool developed in Robinson and Cavanaugh (1998), and routinely employed in papers on SB via a piece of online software known as BDIST (Wood 2001, 2008a, 2008b), is the use of baraminic distance correlation. The columns of the dissimilarity matrix are treated as variables from which a set of pairwise correlation coefficients r can be computed using the well-known Pearson product-moment formula. The values of r are then assessed for significance using a t-test, and the resulting “significance matrix” inspected for patterns.
There are some serious questions about the validity of this procedure. A correlation coefficient measures the strength of a postulated linear relationship between two variables, assuming we have obtained a set of independent random samples of each. Implicitly, we suppose a model
Y = α + βX + ε
where y and x here represent the “response” and “explanatory” variables, respectively, and ε represents a random error term. The values of α and β (and hence the correlation between Y and X) are estimated by minimizing the sum of squared errors, which is a L2 norm. (See Appendix A on norms.) These errors are assumed to be independently and identically distributed. In particular, if the distribution of the errors is Normal, it is possible to test for “significance” of the coefficient β by means of a t-test with n − 2 degrees of freedom and a pre-specified “P-value,” which is the probability of rejecting a null hypothesis that β is zero if the hypothesis is true.3 (Testing β is equivalent to testing r.) Firstly we should realize that the Pearson formula assumes the data are continuous random variables, although formally one can always apply the formula and obtain a result even if this is not so. In any case, it gets worse.
In the application to a distance matrix, the underlying assumptions for correlation are invalid, for the “variables” are simply the columns4 of the distance matrix D, which are also just the rows transposed! These values are certainly not independent realizations of a random variable: they are values of a distance metric, which inherently connects the columns (and rows) together in a particular way. Consider columns 1 and 2, for example: the first two rows would read
0 d
d 0
where d = d(x1, x2) = d(x2, x1). It is obvious that these rows are not independent, yet every pair of columns will contain such a 2-row subset. In effect, the nature of the data (as values of a distance metric) imposes constraints, which means that in the underlying linear model the errors, by definition, cannot be independent random variables. Moreover, if nominal variables form the basis for the distance matrix, there can only be a finite set of values (i.e., {0, 1/p, 2/p,. . . , (p–1)/p,1}) for distance, whereas linear regression requires continuous variables. When the response is binary and the explanatory variables continuous we can use a generalized linear model (GLM) by means of a transformation (for example, logistic regression), but when both response and explanatory variables are discrete, we are really leaving the realms of linear regression altogether. Putting it another way, BDC commits a category error, using variables that are L1 distances, but minimizing a L2 norm! We can certainly carry out a “regression” in a formal sense—i.e., we can plug numbers into some statistical formulae and calculate some “correlations,” but what it means is highly debatable. And as the errors cannot be Normally distributed, the use of a t-test is completely invalid. Generally, in such cases, a “nonparametric” test might be recommended, but it is hard to say what would be appropriate here.
Now clearly this procedure does something, but as the “correlations” do not have a well-defined distribution, we cannot tell which ones are “significant;” that is, we have no idea what the distribution of these values would be under either a null or an alternative hypothesis. Generally, we assign significance to a value that is highly unlikely to arise by chance—usually defined as exceeding the pre-specified critical value. But how can we obtain such values in the absence of Normally distributed variables? In the simplest case, we can sketch a possible answer. If we have a n × p matrix of 1s and 0s, the density of the matrix X can be defined as
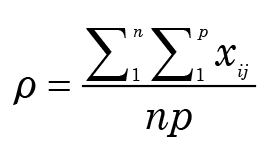
In other words, ρ tells us the fraction of 1s in the matrix X. Let us think about what would influence the distribution of values of the distance between 2 taxa under a null hypothesis that there is no pattern, i.e., if the 1s were assigned at random such that the average density is ρ. In this case, a match between these taxa implies that for each character we must have either two 1s or two 0s. This happens by chance with probability θ = ρ2 + (1 − ρ)2. If there are k matches, the normalized “distance” between these taxa would be (n − k) ⁄ p, and the probability of k matches can be found from the binomial distribution as
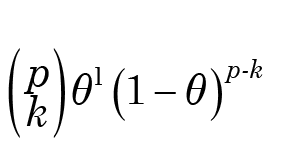
which thus provides us with the distribution of “distances.” It’s difficult, however, to make further progress: what is really needed is a joint hypothesis test of a set of correlations, but to evaluate the joint distribution of the “correlations” obtained from a set of n such variables is an even harder problem! At any rate, it should be clear that this isn’t simply a matter of a t-test with degrees of freedom n − 2. Even if we could find it, a “critical value” for r will depend not only on n, but also on p and ρ.
Compounding the problems, however we obtain a critical value, is the non-independence of the columns of D. But even suppose they were independent: in any set of n variables, there are
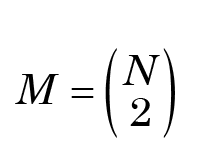
two-way comparisons between them, which implies that the chance of false positives is substantially inflated above the prescribed critical value.5 What constitutes “significance” is therefore exceedingly hard to determine, and in reality, independence is an impossible condition to satisfy anyway.
These problems have been routinely ignored in SB literature—indeed, there is no evidence that they have really been considered. Wood (2011), for example, has argued in favor of statistical baraminology in the case of humanoid species as follows:
With statistical baraminology, the correlation test can be used to estimate the significance of organismal similarity or difference . . . . [so that] we can assign statistical probabilities to the differences that divide human from non-human and to the similarities that unite humans with other non-sapiens human species.
which he regards as the clinching argument against “qualitative” approaches. It would be nice if this statement were true, but until a truly rigorous probability model has been formulated and estimated, the jury must stay out.
Pattern recognition
The BDC procedure can only be seen, then, as a heuristic technique that may help to visualize the structure of the data—but we have no reliable way of knowing whether it does or not, whereas we do know that the assumptions underlying it are false. It would be possible to improve the BDC approach by carrying out a randomization test; that is, having calculated ρ, we could simulate a large number of distance matrices with the same statistical characteristics, calculate all the r values, and use these to find critical values. But every set of {n, p, ρ} parameters would generate different critical values, so the computational burden would be heavy. And there is a further problem: even when we have obtained “significant” correlations, we still have to interpret the pattern, if any.
At this point, the multi-dimensional scaling (MDS) procedure is generally invoked. Earlier SB literature (Cavanaugh and Wood 2002) used a technique called Analysis of Patterns (ANOPA), but since the publication of Wood (2005b), MDS seems to have become the standard approach.6 Unlike BDC, MDS is a well-documented, principled, tried-and- tested statistical technique for visualizing high-dimensional data in 2 (or occasionally 3) dimensions; it does, however, imply a possibly considerable loss of information. In 2 dimensions, the basic idea is to find a set of coordinates (ui,vi) for taxon i such that the distances δij between taxa i and j (derived by using some distance metric in the (u, v) space) are in some sense jointly as close as possible to the actual distances dij. (There are many different versions of MDS, but I assume the one meant is the “classical” approach, which involves minimizing a sum of squared differences—the L2 norm again. There are also versions that use the L1 norm, which are harder to fit, but less susceptible to outliers.) Plotting the coordinates on a graph then helps to suggest which taxa belong together and which do not. Sometimes, a 3D version is used with coordinates (ui, vi, wi) which can be helpful if sophisticated visualization software is available. There is still an inescapable subjectivity to the exercise, however: different people may see different groupings, and these may in any case depend on what distance metric is used to define δij. In fact, the issue of appropriate distance metrics remains unresolved—both for the original dataset, and for the MDS coordinates. Moreover, as Wilson (2010) points out, an unthinking attachment to the results of an MDS analysis may give rise to very strange conclusions. One of the most startling of these, Wood’s claim that the hominim Australopithecus sediba is human, has been severely critiqued by Menton, Habermehl and DeWitt (2010).
Whether their additional criticisms regarding the use of statistical techniques in general are truly justified, however, cannot be definitively answered when the BDC/MDS methodology is itself a flawed and unprincipled7 procedure. There are alternative statistical approaches, based on a much firmer foundation, such as cluster analysis. The question as to whether and how this can be applied to baraminology is considered in a separate paper (Reeves 2021).
Bootstrapping
Wood (2008a) has proposed a modified version of BDC that involves the idea of bootstrapping. Efron and Tibshirani (1993) is still the best introduction to this concept, which is in essence rather simple (although the mathematics that justifies it is rather less so). Bootstrapping is most commonly used to estimate the variability of an original single parameter estimate by means of a confidence interval. Classical statistics does this by making certain assumptions about the sampling distribution of the estimate of such a parameter—most commonly, that it can be approximated by a Normal (or occasionally some other well-defined) distribution, but in many cases this assumption is invalid. The bootstrap method is a solution for such cases. Our original dataset could have been different, but it is in fact, the best estimate we have of the underlying probability mass function, so we generate a large number B of pseudoreplicates, the same size as the original sample, by resampling from that original sample with replacement. (As it is with replacement, some elements of the original sample will appear more than once, while some won’t appear at all. It is this that makes the pseudoreplicates different from the original, and from each other.) Appendix D provides a simple example of the idea, but the critical assumption is this principle:
- Bootstrapping Principle: the sampling distribution of the sample around the population parameter can be approximated by the sampling distribution of the resample around the sample parameter.
But what are we (re-)sampling? The normal approach would be to focus on the taxa: assume there are more kinds of creatures than we have employed in the standard BDC analysis. (Perhaps there are even new species out there, or—more likely—we know of other species but just don’t have data on them.) For example, consider the data matrix X as a set of rows as follows:
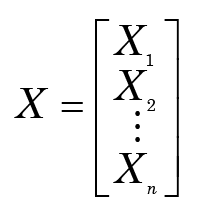
A resample of the row indices in the case n = 6 might generate {1, 2, 1, 4, 2, 5}, so the corresponding pseudoreplicate would consist of the rows
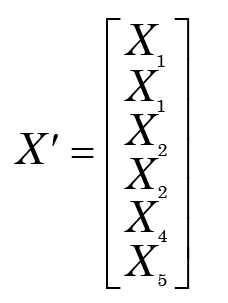
from which a distance matrix could be calculated, and the BDC procedure followed through—a process repeated B times, each time with a different set of “pseudo-taxa.” But if the datasets are fairly complete in terms of taxa, they effectively are a population, not a sample, so what we might gain is puzzling: the groupings that we find are what they are. In fact, any “pseudo-taxon” introduced will be identical to some other real taxon. Consequently, “distances” between them are zero, somewhat distorting the whole process. Nonetheless, as a formal procedure, we could compute a measure of consistency from the pseudoreplicates—for example, how many times each pair of (real) taxa is in the same grouping. (For a review of other ideas, see Hennig 2007).
In any event, Wood’s description of the process he uses in Wood (2008a), though rather opaque, appears to make the primary focus on the characters (i.e. the columns), which he regards as a sample from a larger set of characters that might have been used if we had measured them, so the pseudoreplicates are obtained by sampling with replacement B times from the set of p columns. Effectively, if I have understood Wood (2008a) correctly, the normal roles of objects and variables are reversed. I understand Wood is worried as to whether the groupings found are influenced by the particular characters selected, which is certainly a valid subject for inquiry, and the use of “random perturbations in the character data” would be one way to test the robustness of a statistical procedure in this area. But is bootstrapping BDC a statistically principled way of accomplishing this?
To see the problems with this approach, consider an example from Efron and Tibshirani (1993). The dataset consists of values of two measures of performance (LSAT and GPA)—these correspond to characters (columns)—for students entering 15 US law schools (rows)—these correspond to taxa. They create pseudoreplicates by resampling the rows (taxa) 15 times, and calculate the correlation between LSAT and GPA for each pseudoreplicate.8 But if they were to resample the columns, in many cases this would mean calculating the correlation between LSAT and LSAT, or GPA and GPA, which would obviously be nonsensical! Yet by analogy this is, I think, what Wood is doing.
Now, for a valid application of the bootstrapping concept the (re-)sample values are required to be independently and identically distributed (iid). This is usually a reasonable approximation when the sample values are scalar quantities. But here each taxon would in general be a multi-dimensional vector, comprising values from different domains: dichotomies, multiple categories, ordinal, discrete, or even continuous (see Appendix B). Even when all the characters are dichotomous, so that each of the n elements of the vector has a Bernoulli distribution, they are not all guaranteed to have the same Bernoulli parameter. More generally, if there are different types of distribution, it is self-evident that the resamples are not identically distributed.9 Moreover, while it seems to be an article of faith in SB that all characters are equal (see Wood and Murray 2003, 115–136), what if some really are “more equal than others?” Even evolutionists such as Conroy (2005, 235–237) recognize that morphological characters (in his case, in hominims) are inextricably dependent on each other, so the values of the sample variables are very likely not independent either. Even if the original columns are independent, the resamples are guaranteed not to be, and the fundamental Bootstrapping Principle is in doubt even for the most basic dichotomies-only case. And of course, all the problems with the BDC procedure itself remain. The question of character selection deserves attention, but this approach has too many unexamined assumptions, and some obviously incorrect ones.
Conclusions
The methods used by statistical baraminology have multifarious flaws, despite the surface appearance of rigor and sophistication.
• The basic assumption that all characters are equal appears to be untested. In fact, if Wilson is correct to argue (2010) that it is nearly always the case that all characters are not equally important,10 the analysis would be affected in important ways.
• The choice of distance metric is rarely discussed in the context of the nature of the variables involved.
• Typically the distance metric used assumes, without justification, that equal weight should be attached to the presence and absence of characters.
• The BDC technique is not based securely on statistical principles, and the question of true statistical significance of the “correlations” is sidestepped.
• While MDS has a better statistical pedigree than BDC, the inherent subjectivity of the choice of distance metric, and the loss of information in the dimensionality reduction, mean that results should be treated with more than usual caution.
• In a formal sense the application of bootstrapping is uncontroversial, but it is not clear that the bootstrap is correctly applied, nor that the Bootstrapping Principle can hold for SB methods.
As is shown in Reeves (2021), it is possible—and in fact—fairly simple, to apply cluster analysis to the sort of questions being asked by proponents of SB. Statistical software such as the r language is readily available (at no cost) with a wide choice of principled algorithms using well-defined statistical tests of significance. BDC really should be abandoned. But even this isn’t the end of the matter: in Reeves (2021), I discuss the important conceptual and practical considerations that arise when a large number of characters are evaluated across a range of taxa. This again is something routinely ignored by SB, as it remains under the spell of a “holistic” treatment of the data in order to facilitate a statistical analysis. Whether the analysis has a rigorous foundation or not, there are some important questions to be asked of the data before any software is applied.
I don’t wish to be too hard on the proponents of statistical baraminology; the goal is worthy and the fundamental idea commendable, even if the techniques applied are inadequate, and the treatment of the data too often perfunctory. Moreover, some excellent and painstaking—even heroic—work has clearly been done in preparing and editing a growing collection of very useful datasets. But it is a shame to see much effort ploughed into a mistaken enterprise that may only give ammunition to unfriendly critics of creationist research. Not that creationists are alone in misapplying statistics; evolutionists are no sure guide themselves. (See Mannion et al. 2011 for a fairly recent example of poor statistical understanding.11) If as creationists we wish to apply statistics to the identification of created kinds, just plugging numbers into a computer program (even if as in Reeves (2021) it is more firmly based than BDC) is inadequate. I would suggest we need to
- understand better the nature of the data we have collected and the assumptions upon which rests our measure of “distance”
- understand better the assumptions underlying statistical methods such as multi-dimensional scaling, cluster analysis, randomization tests and bootstrapping
- realize the importance of testing our assumptions and checking results for robustness (e.g., does changing a distance metric alter the conclusions?)
- treat conclusions with much greater caution than has sometimes been the case (cf. Australopithecus sediba).
Finally, I am no geneticist, but it seems highly likely to me that the exclusive focus on phenotypic information is a mistake. Perhaps there aren’t enough sequenced genomes for comparison, and defining “distance” at the level of DNA has its own collection of problems, some even more difficult than in the phenotype. But we surely expect the creatures within the kinds to be related on a genetic level.
References
Aaron, M. 2014. “Discerning Tyrants from Usurpers: A Statistical Baraminological Analysis of Tyrannosauroidea Yielding the First Dinosaur Holobaramin.” Answers Research Journal 7 (November 26): 463−481. https://answersingenesis.org/dinosaurs/discerning-tyrants-usurpers-statistical-baraminological-analysis-tyrannosauroidea-yielding-first-din/.
Cavanaugh, David P., and Todd Charles Wood. 2002. “A Baraminological Analysis of the Tribe Heliantheae senso latu (Asteraceae) Using Analysis of Pattern (ANOPA).” Occasional Papers of the Baraminology Study Group 1, 1−11.
Conroy, Glenn C. 2005. Reconstructing Human Origins. New York: W. W. Norton & Company.
Efron, Bradley. and Robert J. Tibshirani. 1993. An Introduction to the Bootstrap. San Francisco, California: Chapman & Hall.
Finch, Holmes. 2005. “Comparison of Distance Measures in Cluster Analysis with Dichotomous Data.” Journal of Data Science 3: 85−100.
Garner, Paul A. 2004. “Is the Equidae a Holobaramin?” In Proceedings of the Third BSG Conference. Edited by Roger W. Sanders. Occasional Papers of the BSG 4 (June 9): 10.
Garner, P. A. 2014. “Baraminological Analysis of the Picidae (Vertebrata:Aves:Piciformes) and Implications for Creationist Design Arguments.” Journal of Creation Theology and Science Series B: Life Sciences 4 (July 7): 1−11.
Hennig, C. 2007. “Cluster−wise Assessment of Cluster Stability.” Computational Statistics and Data Analysis 52, no. 1: 258−271.
Ingle, Matthew E., and M. Aaron. 2015. “A Baraminic Study of the Blood Flukes of Family Schistosomatidae.” Answers Research Journal 8 (June 24): 327–337. https://answersingenesis.org/creation-science/baraminology/baraminic-study-blood-flukes-family-schistosomatidae/.
Mannion, Philip D., Paul Upchurch, Matthew T. Carrano, and Paul M. Barrett. 2011. “Testing the Effect of the Rock Record on Diversity: A Multidisciplinary Approach to Elucidating the Generic Richness of Sauropodomorph Dinosaurs Through Time.” Biology Reviews 86, no. 1 (February): 157−181.
Menton, David A., Anne Habermehl, and David DeWitt. 2010. “Baraminological Analysis Places Homo habilis, Homo rudolfensis, and Australopithecus sediba in the Human Holobaramin: Discussion.” Answers Research Journal 3 (August 25): 153–158. https://answersingenesis.org/creation-science/baraminology/homo-habilis-homo-rudolfensis-australopithecus-sediba-discussion/.
Reeves, Colin R. 2021. “A Critical Evaluation of Statistical Baraminology: Part 2.” Answers Research Journal 14: 271–282.
Robinson, D. Ashley, and David P. Cavanaugh. 1998. “A Quantitative Approach to Baraminology with Examples from Catarrhine Primates.” Creation Research Society Quarterly 34, no. 4 (March): 196−208.
Wilson, Gordon. 2010. “Classic Multidimensional Scaling Isn’t the Sine Qua Non of Baraminology.” Answers in Depth 5 (September 29). https://answersingenesis.org/creation-science/baraminology/classic-multidimensional-scaling-and-baraminology/.
Wood, Todd Charles. 2001. BDIST software, v.1. Dayton, Tennessee: Center for Origins Research and Education, Bryan College. Distributed by the author. http://www. coresci.org/bdistinfo.html.
Wood, Todd Charles. 2002. “A Baraminology Tutorial with Examples from the Grasses (Poaceae).” Journal of Creation 16, no. 1 (April): 15−25.
Wood, Todd Charles. 2005a. A Creationist Review and Preliminary Analysis of the History, Geology, Climate, and Biology of the Galápagos Islands. Center for Origins Research Issues in Creation, no. 1 (June 15). Eugene, Oregon: Wipf & Stock.
Wood, Todd Charles. 2005b. “Visualizing Baraminic Distances using Classical Multidimensional Scaling.” Origins 57: 9−29.
Wood, Todd Charles. 2008a. “Baraminic Distance, Bootstraps, and BDISTMDS.” Occasional Papers of the Baraminology Study Group 12: 1−17.
Wood, T. C. 2008b. BDISTMDS Software, v.2.0. Dayton, Tennessee: Center for Origins Research and Education, Bryan College. Distributed by the author. http://www. coresci.org/bdist.html.
Wood, Todd Charles. 2010. “Baraminological Analysis Places Homo habilis, Homo rudolfensis, and Australopithecus sediba in the Human Holobaramin.” Answers Research Journal 3 (May 5): 71−90.
Wood, Todd Charles. 2011. “Baraminology, the Image of God, and Australopithecus sediba.” Journal of Creation Theology and Science Series B: Life Sciences 1 (July 8): 6–14.
Wood, T. C. 2016. “An Evaluation of Homo naledi and ‘Early’ Homo from a Young-Age Creationist Perspective.” Journal of Creation Theology and Science, Series B: Life Sciences 6: 14–30.
Wood, Todd Charles, and Megan J. Murray. 2003. Understanding the Pattern of Life: Origins and Organization of the Species. Nashville, Tennessee: Broadman & Holman.
Appendix A
Mathematically, a distance metric has the following properties:
Given points (or vectors) x, y, and z in a p-dimensional vector space X, a function
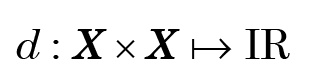
(where IR is the real line )
is a distance metric if
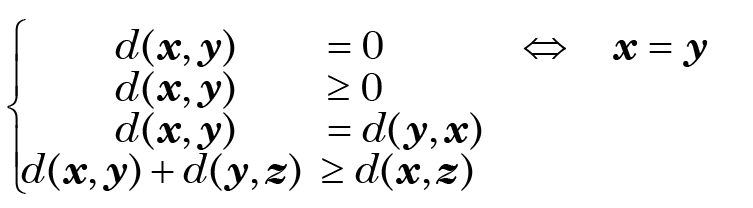
If this looks threatening, consider it intuitively.
Really this is just stating the obvious: the first three conditions say (respectively) that a distance may be zero (but if and only if the points are coincident), but can’t be negative, and that it shouldn’t depend on the direction of travel. The last (the triangle inequality) says that taking a detour can’t make the route between two points any shorter. Distances in cluster analysis may not always obey this last condition— the Dice distance, mentioned in the main text, is a case in point. When any condition is not true, we may speak more generally of a distance measure.
Closely related to the idea of distance is that of a vector norm, ║x║, which measures the “size” of a vector x. The most common norms are the L1 norm ║x║1 = Σi|xi| and the L2 norm ║x║2 = √(Σixi2). As the norm of x is effectively its distance from the zero vector 0—the origin of its coordinate system, it can be seen that d(x, y) = d( x − y, 0) = ║x − y║. Thus, we can also speak of L1 or L2 distances depending on the underlying norm.
Appendix B
It is a mistake to assume that all statistical techniques can be used on any type of statistical data. Statisticians commonly distinguish between at least 4 types of data: When the categories into which objects can be placed are simply “names” without underlying order (e.g., red/blue/green), the data are nominal; if there are only two categories (e.g., male/female), we further denote them as binary or dichotomous. If the categories can be ordered they are ordinal (e.g., small/medium/large). When they can be measured on a scale, they are quantitative. We distinguish quantitative variables as discrete if they are the result of counting, or continuous if they are the result of a measurement. The latter may be further divided: If the measuring scale is merely an interval scale (e.g., Fahrenheit temperature), there is no true zero and we can only compare differences, but if it is a ratio scale (e.g., blood pressure), we can calculate ratios and percentages. (If my diastolic blood pressure has decreased from 100 to 97, I can say either by 3 units or by 3%, but if my body temperature has decreased from 100° F to 97° F only the difference of 3° F makes sense. Try converting the ratios to Celsius!)
Appendix C
As an example for constructing different distance measures, consider the following table of 2 objects (taxa) and 9 binary variables (characters):
| Taxon | Character | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| y | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Comparing x and y, we find that
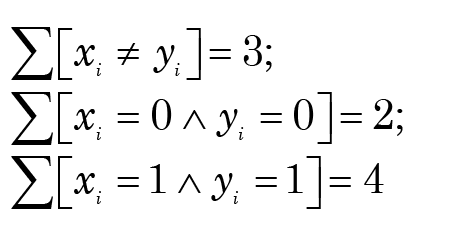
Thus the simple matching distance is
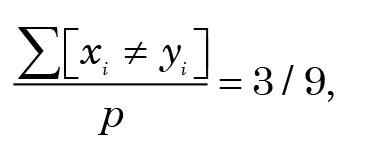
the Jaccard distance is
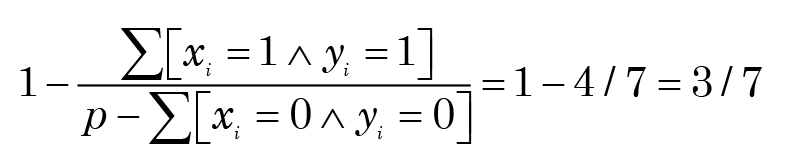
while the Dice distance is
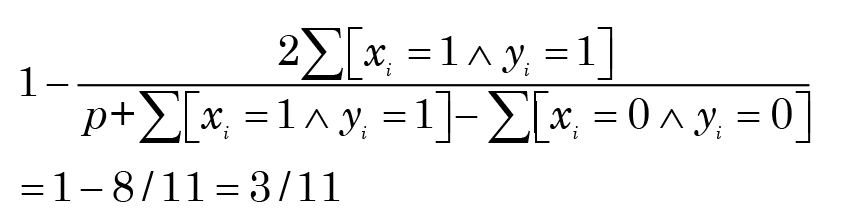
Notice how the distance between x and y is changed by the choice of distance measure.
Appendix D
The bootstrap estimator of a statistical parameter assumes that the best “guess” for the true probability distribution of a random variable is the probability mass function obtained from the actual data. For example, if we toss a fair coin (i.e. prob. of a head = prob. of a tail = 0.5) three times and record the number of heads, we can calculate the expected probability distribution analytically using the Binomial distribution, as in the following table:
| No. of heads | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Prob. | 1/8 | 3/8 | 3/8 | 1/8 |
But what if we suspect the coin is biased? Theoretical calculations are no good; we need data. Suppose we do 8 experiments, each time tossing the coin 3 times and counting the number of heads. Suppose they were distributed as shown below:
| No. of heads | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Prob. | 2/8 | 4/8 | 1/8 | 1/8 |
This is the empirical probability distribution. There are 4+2+3 = 9 heads in these 24 coin tosses, so the probability of a head is estimated as p̂H = 9/24 = 3/8 for this coin, but with what degree of confidence? We could use the Binomial distribution again to find a confidence interval, but we could also estimate the variability of the estimate by drawing (say) 1,000 samples of size 8 with replacement from the empirical mass function, configured as the set {0, 0, 1, 1, 1, 1, 2, 3}. From each resample, calculate an estimate p̂H, and sort all the estimates into ascending order. To get (say) a 95% confidence interval, just eliminate the largest 25 p̂H values to find an upper limit, and the smallest 25 to find a lower limit. This is bootstrapping.



