The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
Wood and co-workers (Cavanaugh and Wood 2002; Robinson and Cavanagh 1998; Wood 2005; Wood and Murray 2003) have pioneered the application of some statistical methods to the taxonomy of various biological organisms, an approach that has become known as statistical baraminology (SB). For example, in Wood (2005), the report of an analysis of patterns of morphological characters in 30 turtle species, there appeared to be two distinct groups. From a statistical perspective, however, these methods are flawed in several ways, as was argued in an earlier paper Reeves (2019), where the question as to whether a conventional statistical approach—cluster analysis—could provide a more securely based alternative was left open. Part 2 of this research, reported herein, presents a formal reanalysis of the turtle data using some well-known clustering techniques.
The results suggest that the original conclusion in Wood (2005)—that there are two distinct clusters—can be supported, as well as the detailed cluster composition. Nevertheless, clustering techniques, being more soundly based, should be preferred. In addition, they also enable the identification of how well individual taxa fit into their clusters by means of silhouette plots. Some further suggestions are made for the evaluation of cluster stability that have a sounder statistical basis than the type of bootstrapping commonly applied in SB. Finally, answers to some important questions concerning the original dataset are still needed, and these are used to highlight some important conceptual and practical issues within SB research.
Keywords: statistical baraminology, distance metrics, cluster analysis, missing values, collinearity
Introduction
In Wood (2005, 71), he reported, inter alia, on the analysis of a database of 30 turtle species (originally published in Shaffer, Meyland, and McKnight (1997), for each of which 115 morphological characters have been used to distinguish the species from each other. The objective was to assign species to reasonably homogeneous groups on the basis of these characters, and a method known as “baraminic distance correlation” (BDC) was used in an attempt to identify what are termed baramins, or “created kinds,” on the hypothesis of a polyphyletic development of biological organisms, rather than the standard monophyletic “tree of life” associated with Darwinism. In Reeves (2021), I argued that BDC is not securely based on a principled statistical methodology, and should be abandoned. In this paper, taking the turtle data as an illustrative example, I report on an alternative approach, and discuss some of the conceptual and practical issues that arise. From a statistical perspective, regardless of the underlying motivation, statistical baraminology (SB) is simply a problem of clustering. The generic clustering problem can be described as follows:
We have a set of data comprising measurements of p variables for each of n objects xi, where xi is a row vector (xi1, …, xip). We can denote the data set by
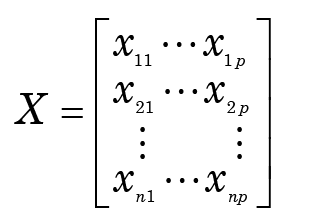
A wide variety of clustering techniques is available in the statistical literature.1 Some are based on the raw data, but most make use of an n-dimensional dissimilarity matrix
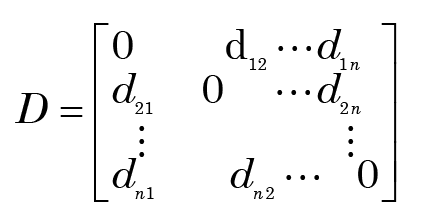
The notation dij is shorthand for a function d(xi, xj), which measures the dissimilarity or “distance” between the objects xi and xj. (Theoretical concepts associated with the idea of distance are outlined in Reeves (2021, Appendix A). Note that in practice the distances are nearly always symmetric (i.e., dij = dji), so only the upper or lower triangle of this matrix needs to be stored.
The objective is to assign the objects to one of m clusters, so that “close” objects belong to the same cluster, while “distant” objects are in different clusters. Generally, in statistics we decide such questions by invoking some principle or criterion whereby “good” and “bad” assignments can be distinguished. (It is the lack of such a principle that makes BDC problematic.) In the case of clustering, a natural principle is to use a “minimum total distance” criterion: if the set of objects in cluster k is denoted by Ck, we search for assignments that minimize an objective function
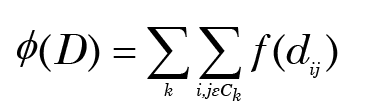
(1)
where f is some function of the interobject distances. The number of partitions of n objects into m(< n) groups such that each group has at least one member is given by the Stirling number of the second kind
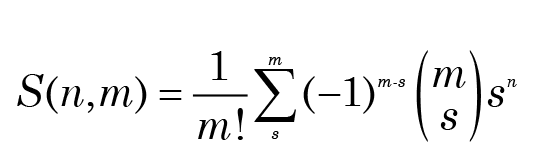
This is a very large number, even for moderate values of n and m (e.g., S(10, 4) ≈ 4.5 × 1010), so enumeration of all possible partitions is impossible, and heuristic methods are necessary to find a quasioptimal partition. Furthermore, as the value of m is unknown a priori, several trials with different values of m are usually undertaken.
The nature of f in Eqn. (1) depends on the type of data contained in X. For continuous numerical variables, the most commonly used function is the square of the distance between the objects (i.e., the L2 norm (Reeves (2021, Appendix A), weighted by the relevant cluster size. It can be shown (see Späth 1985, Chapter 2, for example) that this is equivalent to minimizing the sum of squared distances from the centroid of each cluster, i.e.
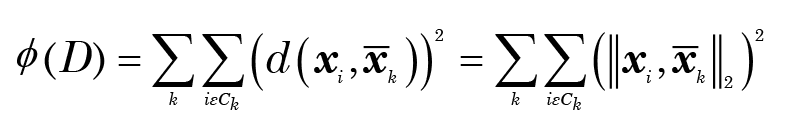
where x̄ is the centroid of cluster k. The centroid, of course, only rarely coincides with any actual point, but need not be computed separately because of the equivalence of equations (1) and (2) in this case. This is less satisfactory when some or all of the variables are ordinal or nominal. (There is a discussion on variable types and their appropriate methods of statistical analysis in Reeves 2021 Appendix B.) In such cases it is hard to assign any meaning to the idea of a centroid, but they may be replaced by “medoids” (the medoid is the vector whose elements are the middle values of the sorted elements of the vectors belonging to Ck). These are clearly more meaningful as centers for nominal data as they do coincide with actual values; moreover, if the function f in equation (2) is an identity function instead of the square of the distances, and the distance is based on the L1 norm, it can be shown (Späth 1985, Chapter 6) that the medoids do in fact minimize
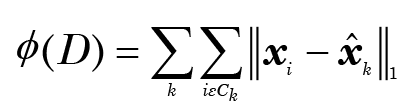
where x̂ is the medoid of cluster k. Not only is this appropriate for non-quantitative data, but it is also more robust and less influenced by outliers.
One of the most comprehensive studies of clustering techniques is that of Kaufman and Rousseeuw (1990), many of whose algorithms have been implemented (Struyf, Hubert, and Rousseeuw 1997) in recent versions of the statistical computing languages S-Plus and R, which therefore make a convenient starting point for any exploration of the data.
Distance metrics
Central to the clustering problem is the definition of a suitable distance metric, so that we can assign a precise meaning to the idea that (say) object x is closer to y than to z. (For background on distance metrics and examples of their use, see Reeves 2021, Appendices A and C). For convenience, two of the metrics most commonly used are reintroduced below.
The simple matching coefficient
This uses a simple count of the number of cases in which the two objects do not coincide. If xj (resp. yj) is the value of the jth variable for the object x (resp. y), this is
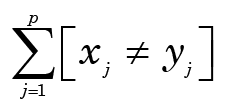
where the notation [expr] denotes the value 1 if the logical expression expr is true, and 0 if it is false. Normalizing, the “distance” between x and y becomes
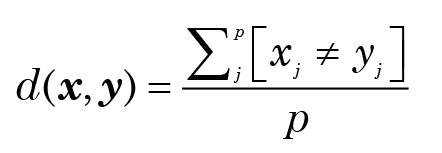
For the specific case of binary variables, there is another way of writing this which points the way towards alternative measures:
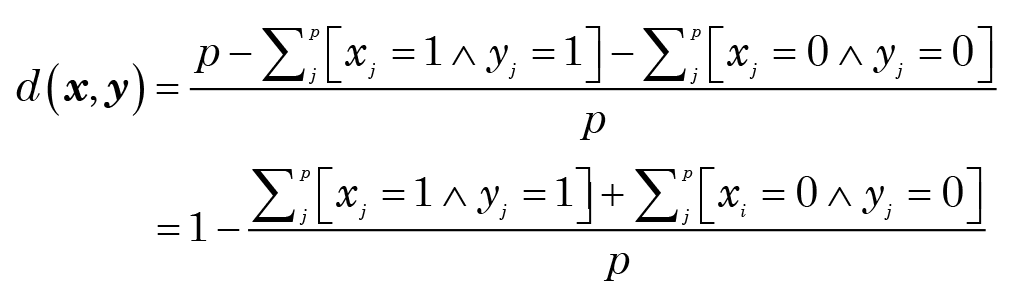
where ˄ is the standard symbol for logical “and”.
The Jaccard coefficient
In the case of binary variables in particular, the presence of a character (xj = 1) may be more significant than its absence (xj = 0). For asymmetric cases such as this, the distance measure preferred is often the Jaccard coefficient:
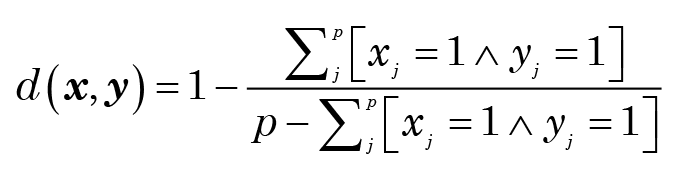
These formulae can also be generalized to the nonbinary case if necessary.
Distances using daisy
A procedure called daisy is available in S-Plus and R to compute a variety of distances, including the simple matching and Jaccard cases. It copes with mixed data where some variables are non-binary by normalizing such components to lie in the range [0, 1]. It deals with missing values, too, by simply excluding them from the counts in both numerator and denominator. (This assumes that the denominator does not become zero.) It does not, however, compute other metrics such as the Dice coefficient, nor does it enable the possibility of asymmetric non-binary variables. Should such cases occur, it might be necessary to develop a specific function.
Cluster Analysis of the Turtle Dataset
In Wood (2005) the data were analyzed by some novel methods based on the concept of distance correlation, using simple matching to define distance. The dataset comprises 30 taxa and 115 characters; as some of the characters are sparsely distributed, a relevance value of 0.9 was used to reduce the number of characters to 93. (A preliminary analysis with a relevance value of 0.95 eliminated another 33 characters, but—in accordance with the belief in the importance of a large holistic set of characters—this was deemed to be too drastic.) For a cluster analysis it is unnecessary to eliminate such data explicitly, as missing values are handled by default in the daisy function. (See the discussion in Conceptual and Practical Issues, however.) There are some serious questions about the validity of the BDC procedure, as discussed in Reeves (2021), so this paper explores cluster analysis as an alternative.
Clustering with pam
There are many possible clustering methods that are based on sound statistical principles. One that is relevant to the type of data commonly found in taxonomical problems is partitioning around medoids (pam), which is available in S-Plus and R. This procedure has the additional benefit of in providing so-called silhouette plots. These compare the average distance of a point x to the other points within its cluster
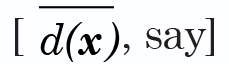
to its average distance to points in its second-best cluster
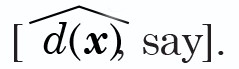
The normalized width
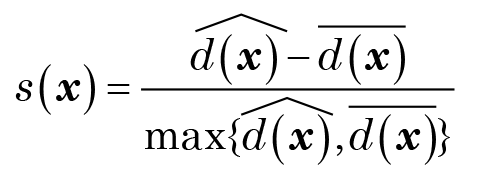
lies in the range [−1, 1], and measures how well x fits into its cluster. In this way, individual “outlier” objects are easily identified by a visual display of silhouette widths in descending order. The average silhouette width of a cluster is also an indicator of the strength of a particular partition.

Fig. 1. A 2D visualization of the clusters obtained from pam for m = 2. The medoids are Elseya (cluster 1) and Lindholmemys (cluster 2). According to the silhouette plots, the most out-of-place taxa are Proganochelys and Meiolania respectively.
Following the computation of the D matrix from the turtle dataset, using daisy to produce the simple matching distance, the pam procedure was applied, with the results shown in fig. 1. The 2D visualization is obtained by first carrying out a multidimensional scaling (MDS), and then plotting the first two components against each other. Although we should bear in mind the caveats expressed in Reeves (2021) against interpreting MDS too enthusiastically, it would appear from both plots that Proganochelys, although assigned to cluster 1, is substantially different from any other point in that cluster. In the case of cluster 2 the most out-of-place taxon is Meiolania.
3 clusters
In the case of 3 clusters, the results are shown in fig. 2. The third cluster is a small one, comprising three very similar taxa. As a result, group 2 is now much more compact, but group 1 is the same as before, with Proganochelys remaining an outlier. The average silhouette width s has actually decreased, suggesting that m = 2 is probably to be preferred to m = 3 (Kaufman and Rousseeuw 1990). That the cluster memberships also coincide with those reported in Wood (2005), despite the flaws in the BDC methodology, may assuage some of the doubts as to the validity of the cluster compositions produced therein.
An attempt with 4 clusters produced a further fall in s, so there is little support for the idea that there are 4 groups.
Jaccard metric
As mentioned above, there is often merit in treating coincident values of two variables differently, in terms of constructing a distance, depending on whether the coincidence is one of presence or absence of a character. As nearly all of the variables in the turtle dataset are dichotomous, this is an area that invites exploration. (See, however, the discussion in Conceptual and Practical Issues.) Accordingly, the distances were re-calculated using daisy with the asymmetric setting. When pam was applied, similar results were obtained for m = 2, as displayed in fig. 3.
For the case m = 3, there are some interesting differences in cluster composition, as a comparison between figs. 2 and 4 demonstrates. The average silhouette width in fact suggests that 2 clusters are sufficient for describing the taxonomic structure— the fact that there is a slight increase in the average value of s is due to the fact that the 3rd cluster is actually Proganochelys on its own. And while the taxa contained in each cluster are the same as with the simple matching distance, there are some notable differences in the rank ordering of the taxa within the second (larger) cluster. The most substantial change involves Adocus, which moves from 3rd most well classified in the case of simple matching to 7th when the Jaccard coefficient is used. Despite this and other changes in ordering, however, the overall agreement between the ranks is very good, with a rank correlation of 0.95.

Fig. 2. A 2D visualization of the clusters obtained from pam for m = 3. The medoids are Elseya, Lissemys and Lindholmemys. Proganochelys is still wildly different from the other taxa in cluster 1.

Fig. 3. A 2D visualization of the clusters obtained from pam for m = 2 using the Jaccard distance metric. The medoids are still Elseya (cluster 1) and Lindholmemys (cluster 2), and the most out-of-place taxa are Proganochelys and Meiolania respectively.

Fig. 4. A 2D visualization of the clusters obtained from pam for m = 3 using the Jaccard distance metric.
Fuzzy Clustering
Another approach that is becoming increasingly popular is the use of fuzzy clustering. In this case, rather than assigning a point unequivocally to one cluster, it is given a membership value
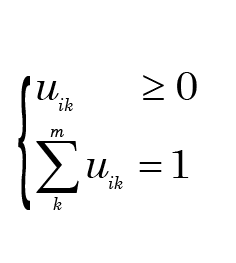
uik satisfying the requirements.
That is, uik indicates the degree to which object i “belongs” to Ck. This idea is implemented by a procedure called fanny in S-Plus and R. Figs. 5 and 6 display the results of applying fanny with simple matching.

Fig. 5. A 2D visualization of the clusters obtained from fanny for m = 2 using the simple matching distance metric.

Fig. 6. A 2D visualization of the clusters obtained from fanny for m = 3 using the simple matching distance metric.
It should be noted that in order to obtain such plots, the fuzzy clusters must first be “defuzzified” into their “crisp” or “hard” form, where each object i is assigned to the cluster k for which uik is largest. This would not necessarily coincide with the clustering produced by pam, although it does in the case m = 2. The case m = 3 is interesting: although a third cluster is assumed in the fuzzy procedure, the crisp version collapses to 2 clusters, providing further evidence that a 3-cluster solution is implausible.
Jaccard metric
As with pam, it is also possible to use fanny with the Jaccard distance. The results of this investigation are shown in figs. 7 and 8.

Fig. 7. A 2D visualization of the clusters obtained from fanny for m = 2 using the Jaccard metric.

Fig. 8. A 2D visualization of the clusters obtained from fanny for m = 3 using the Jaccard metric.
Again, for m = 2 the structure revealed on converting from fuzzy to crisp clusters is identical to that found in the corresponding case of pam, with the same silhouette rank ordering within each cluster. The case m = 3 again collapses to 2 clusters on defuzzification, although the silhouette width for Proganochelys is negative, which suggests it really does not belong to either cluster and should be treated as a distinct taxon.
Extensions
The analysis reported above has suggested that the inference of Wood (2005) that the turtle taxa comprise two distinct groups is valid. There is, however, a distinct lack of statistical principles in some of the methodology used in that earlier research, and those findings may therefore be merely fortuitous. Given the firmer statistical foundations for clustering techniques such as pam and fanny than for baraminic distance correlation, clustering algorithms would seem safer for analyses of taxonomic datasets.
For the turtle data, there is on the whole more statistical support for a 2-cluster model than for 3 or 4 clusters, in that the average silhouette widths are mostly larger in the case m = 2. (Using pam with m = 3 is an exception, where the fossil species Proganochelys is revealed as an outlier, in a cluster of its own.) The fuzzy approach adds weight to this interpretation, as the crisp clusters produced number 2 even when a 3-cluster fuzzy model is fitted. There is little doubt as to the group membership of nearly all taxa, although Proganochelys is really unlike anything else. Whether the use of the Dice or other distance measures adds anything to the discussion is a possible extension to this research; it would entail writing a simple function to replace daisy in applying pam and fanny to the problem. There are several other possibilities for extending the analysis. Some of these are discussed in outline below.
Missing values
There are considerable gaps in some parts of the turtles database. For some objects, there are many variables whose values are either not known, or are not considered relevant. In terms of distance calculations, variables with missing values are simply disregarded by daisy, which may lead to a loss of confidence in the validity of a particular distance.
This is, of course, a familiar problem in many areas of data analysis, and a variety of techniques have been suggested for filling in the gaps in a data matrix. For example, it is possible to fit a linear model of the dependence of values of one variable on values of others for which a complete record is available. (In cases of dichotomous variables, a logistic regression model would be more appropriate, giving rise to a value that can be read as a probability.) Another possibility is to use k-nearest neighbour methods to infer missing values. Neither has been attempted in the analysis reported here.
Bootstrapping
One of the problems in cluster analysis is often the difficulty of assessing the degree of robustness of the groups that result. Would things have been very different if certain objects (taxa) had been excluded from the analysis?
For example, in the turtle data set, the fossil species Proganochelys, which is difficult to fit into either of the two major groups identified, may create a bias in their composition simply because it is included. An obvious approach is simply to repeat the analysis with this species excluded, and decide to which (if any) of the resulting clusters it can be assigned. But then why not examine the effect of leaving out every object, one at a time? We can then build up a picture of the robustness of the assignments. This procedure is often called a jack-knife. The generalization of this procedure is known as cross-validation, but while the amount of computation required is acceptable if restricted to single objects, it becomes prohibitive to extend the analysis to every pair, every trio, etc. In general, cross-validation tends to be used by selectively sampling the pairs, trios etc.
An alternative that has become almost ubiquitous in many areas of statistics is to use the bootstrap (Efron and Tibshirani 1993), where the set of taxa is sampled with replacement to create a set of “pseudoreplicates” the same size as the original sample. The issue here is that each pseudoreplicate contains many pseudo-taxa, which are merely clones of real taxa. Asymptotic probability theory can be used to show that about 63% of the taxa in a pseudoreplicate occur as clones, so bootstrapping would induce a large degree of collinearity (see Conceptual and Practical Issues for a discussion of the problems this causes). Bootstrapping has also been applied in a rather idiosyncratic way in SB. For the reasons delineated in Reeves (2021), the SB approach to bootstrapping is unlikely to satisfy the underlying assumptions necessary for applying it.
Discussion
It should be noted that, notwithstanding the criticisms aimed at the BDC-based methodology in Reeves (2019), the results of the cluster analysis here are the same. Does this mean that BDC is justified after all? Not so: the ad hoc approach of BDC still has no valid statistical foundation, so any conclusions reached will always be subject to debate, criticism, or even (from evolutionists) ridicule. Furthermore, cluster analysis can be carried out by standard statistical software (available for free in the case of R) with the capacity for using a much wider range of distance metrics and specific techniques. It is also likely that conclusions drawn from a cluster analysis would gain more credence from a skeptical anti-creationist majority than those obtained by using novel methods used nowhere else. And cluster analysis is only one example of a growing set of “unsupervised learning” methods that have been developed in the last 30 years, many of which will also be applicable—so why not explore them? It would still be a mistake, however, to assume that the only change needed for SB research is to plug
a dissimilarity matrix into some R functions instead of BDIST. Cluster analysis still has some subjective elements—as stressed above, finding a globally “optimal” clustering is not a realistic aim. Thus, the goal that Wood (2011) mentions of being able to ‘‘assign statistical probabilities to the differences that divide [groups] and to the similarities that unite [them]’’ is unattainable. For example, while silhouette plots are handy visual aids, we cannot start attributing “P-values” to them.
Conceptual and Practical Issues
Applying statistical methodology should never be done in a routine way. Nothing is more important than engaging properly with the data, especially when the data come from secondary sources. Going to the source paper Shaffer, Meylan, and McKnight (1997) for the turtle analyses is actually a salutary example of some of the problems that can arise. Two things become clear:
1. There is an older source for the first 39 characters listed (Gaffney, Meylan, and Wyss (1991).
2. The description of characters 40–115 raises a fresh set of problems, the implications of which are discussed in table 1.
Collinearity
It is easy to see, even from a cursory examination of the data in Shaffer, Meylan, and McKnight (1997) that many characters or variables (the columns of the data matrix X) are collinear—that is, they are highly correlated. In fact, in many cases they are actually entirely identical. As a toy example of this problem, consider the example:
| Taxon | Character | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| x | 1 | 1 | 0 | 0 | 1 | 0 |
| y | 0 | 1 | 0 | 1 | 1 | 1 |
| z | 1 | 1 | 0 | 1 | 1 | 1 |
It is immediately evident that characters {2, 5} and {4, 6} contain exactly the same information with respect to the 3 taxa. These two sets of variables are perfectly collinear. What does this mean? Obviously, (for instance) it means that whenever character 4 is present in a taxon, so is character 6, and whenever character 4 is absent, so is character 6. So character 6 adds no more information about the taxon than character 4 (and vice-versa). But what are the statistical implications? We might regard characters 4 and 6 as representing instances of some “higher” concept that has these specific properties of presence/ absence in a generic sense, one that subsumes these particular cases. (This idea is behind such methods as factor analysis, principal components and MDS, where the aim is to reduce the dimensionality of the space in which the taxa sit.) But if we retain both of them (and likewise characters 2 and 5), we are implicitly giving this concept a higher weight (2 in this case) than those concepts represented by a single instance, such as characters 1 and 3. And this may alter the distance matrix in interesting ways; for example, using simple matching, d(x, z) = 2/6. Or is it? Perhaps, if we only count one of {2, 5} and {4, 6}, it should really be 1⁄4. And should d(y, z) = 1⁄6, or 1/4? In one case, the distance decreases, in the other it increases. How we regard collinearity has implications—and ignoring it does too.
In the case of the turtles, a pairwise comparison of all 115 columns was carried out. Some of these columns had missing values, which raises another problem. If two columns are identical everywhere the values are known, should they be declared identical, even if some characters are unknown? Arguably, it depends on how many missing values there are; most common techniques used to estimate a single missing value would probably impute an identical value to that of its twin column anyway. It is therefore reasonable to treat them as identical if the proportion of missing values is small. (NB The missing value proportion is the complement of what Wood (2005) calls the “relevance” criterion.) If all columns are included in the comparison, the set of 115 characters reduces to just 51 distinct characters in the sense of supplying unique information.
More generally, we may not have exact identity of variables, but some sets may still be highly correlated. Again, the information contained in such sets of variables is implicitly less than that contained in the same number of non-correlated variables, so leaving them in the dataset has the effect of inflating the implied weight of each concept represented by a set of multi-collinear variables. This raises further questions as to the meaning of a “holistic” set of characters. If we know—or at least suspect—that some characters are effectively describing the same thing, should we proceed as if we were ignorant of the fact? There is also a practical issue for clustering techniques that make use of matrix manipulations in order to cluster a data matrix: such a matrix will not be of full rank, and this may cause numerical stability problems.
Inconsistent labelling
Most standard implementations of cluster analysis assume the convention that 1 means the presence and 0 the absence of a character. On investigating the turtles dataset it appears that this is emphatically not the case. In some cases 0 is assigned to presence and 1 to absence, in what appears to be an almost arbitrary fashion. Closer inspection, however, shows that there is a rationale—an evolutionary one! Whether 0 means presence or absence depends on the status of the character as either “primitive” or “derived.” Thus the splenial bone (character 40) is present in the fossil turtle species Proganochelys, but absent in most modern turtles; its absence being considered “derived,” presence is coded as 0. On the other hand, cervical vertebrae 5 and 8 (character 48) are biconvex only in modern turtles, so presence is considered derived, and is therefore coded as 1. Moreover, this is in some cases extended further where degrees of derivation are believed to be evident—for example, a primitive character is coded as 0, a fully derived one as 2, and an intermediate one as 1. Although none of this is matters in the case of simple matching, it will clearly affect more sophisticated distance measures.
This also raises the question as to how much credence we should place on values that are based squarely on an evolutionary account in trying to elicit information about created kinds. Evolutionary biases are being injected into the very coding of the data. Of course, the original object of the coding was to subject the data to a cladistic analysis in order to build a phylogeny, but it may be that very phylogeny that, as creationists, we wish to question. At least, we should carefully scrutinize the data before blindly applying a particular clustering method, and if necessary consider modifying the coding.
Inappropriate scaling
Another example of possible coding bias is seen in character 43 (diploid number of chromosomes), for which there are nine possible values {28, 34, 36, 50, 52, 54, 56, 66, 68}, coded as 1–9. For distance-based clustering, this raises significant questions. If simple matching is used, the implication is that the distance between (say) 28 and 68 is the same as between 28 and 34 (and, of course, the same as presence/absence of any dichotomous character). If a more sophisticated metric is used, it may try to take account of the ordinal nature of the variables. But now we have a problem of incommensurability—is the relative difference between (say) 28 and 34 [which would be (|2 − 1|)/(|9 − 1|) = 1 ⁄ 8] less important (by a factor of 8) than the difference between presence and absence of some other dichotomous character? Answering such questions may not be easy, but they need to be considered when using statistical software; bespoke distance functions may have to be designed.
Unnecessary discretization
A similar problem is seen in a particularly acute way in another paper (O’Micks 2016), which attempts a baraminological analysis of the recent hominim discovery know as Homo naledi. All the characters in the underlying study (see Berger et al. 2015) are actually measurements, i.e., continuous variables. Yet in order to be able to apply the BDIST program, each variable has been discretized using the equation:2
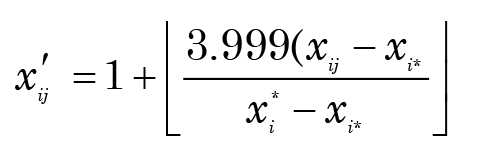
where xi* (resp. xi*) = maxjxij, (resp. minjxij), and [x] is the “floor” function, i.e., the largest integer not greater than x. With the greatest respect, this is crazy! All these data can be viewed as being generated from a set of probability density functions with their own characteristics (mean, standard deviation, skewness, etc.). Indeed, perhaps some characters have the same distribution—which might indicate they are markers for the same baramin. Why would we want to throw away the possibility of estimating such useful information by imposing a crude homogeneous discretization—one that doesn’t even acknowledge the nature of the centers of, and variations within, the continuous character values? Moreover, as discussed in Reeves 2021, 261, this may impute a “distance” between two characters that are almost identical but on opposite sides of these arbitrary borders. And why just four discrete characters? These data are crying out for a continuous clustering model—something like a “k-means” algorithm, perhaps.
Character selection
The issue of character selection is one that has occupied proponents of SB—in fact, it is the main thrust of the bootstrapping approach taken in BDIST. Wood (see for example, Wood and Murray 2003, 115–130) contends that baraminology should be based on the holistic value of a large set of attributes rather than a handful. This “refined baraminic concept” is just an assumption, however, and it does not appear to have been tested—Wood wants to address the question ‘‘have we got enough?’’ rather than ‘‘do we really need them all?’’. Yet it is an interesting question whether all the independent variables used in the clustering procedure are actually relevant. For the turtles dataset it is suggestive, just from the fact that the first two MDS components typically account for a fairly large fraction of the variation, that many variables may contribute very little. A deeper investigation (see Collinearity) reveals the existence of a large degree of collinearity. But such an in-depth examination is time-consuming, and may not always be possible (e.g., if we only had a dissimilarity matrix). A possible alternative to MDS would be to estimate discriminant functions to assign points to one or other of the clusters, iteratively eliminating characters whose coefficients are near zero. However, MDS loses information, the meaning of its components is often hard to interpret, and methods such as discriminant analysis are fragile in the presence of missing values. One way to answer this question in a more robust way might be to use a classification tree (Breiman et al. 1984), which also copes better with missing values.3 This may be a fruitful line of enquiry for further research.
Conclusions
Specifically in regard to the analysis of the turtles dataset, the questions raised above with respect to the nature of the data may make the conclusions reported above (and, a fortiori, those found in Wood 2005) debatable. A much deeper analysis is needed of the effect of the assumptions (embedded in the original papers) on the distance matrix. I suspect the examples discussed above could be multiplied many times. If we want to know whether statistical baraminology is giving reliable answers, the first step is to ask the right questions of the data. Having answered these questions it is then necessary to apply well-founded statistical methods, of which clustering techniques are an example, and a much safer one than BDC. I take it that the goal is to build a scientific research field founded on an acknowledgement of biblical data, a goal which I sincerely applaud. But that doesn’t obviate the need to treat the scientific data carefully and thoughtfully, to use statistical methods that are securely based, and to carry out appropriate robustness and sensitivity tests on the results. As currently practised, statistical baraminology lacks these elements, at least in some degree, and until it acquires them it is not a plausible research program.
Postscript
As the final version of this paper was being prepared, my attention was drawn to a recent paper (Doran et al. 2018). This uses another multivariate technique—principal components analysis (PCA), which produces a set of rotated axes to help visualize high-dimensional spaces from a covariance or correlation matrix. Is this likely to be a fruitful alternative to BDC? Probably not. PCA is generally used with quantitative (i.e., interval or ratio-scale) data, and its use for binary, and especially nominal or ordinal data, is anathema to many statisticians; it should at least be approached with caution. The use of polychoric correlation4 rather than the standard Pearson correlation coefficient has been suggested as one way of mitigating these problems. Standard PCA methods usually subtract centroids from the actual variables, about which the axes are rotated. As observed in Introduction, centroids are inappropriate for discrete data. Alternative centers (e.g., medoids) have been advocated, but these need to take into account the type of the variables explicitly. Indeed, for non-quantitative data, many statisticians advise that a technique called multiple correspondence analysis (MCA) should always be preferred to PCA. Once again, all such questions point up the need to ask the right questions of the data.
Acknowledgements
I would like to thank Todd Wood for supplying me with the turtles dataset as a spreadsheet, thus saving me from having to transcribe the original data from Shaffer, Meylan, and McKnight (1997).
References
Berger, Lee R., John Hawks, Darryl J. de Ruiter, Steven E. Churchill, Peter Schmid, Lucas K. Delezene, Tracy L. Kivell, et al. 2015. “Homo naledi, A New Species of the Genus Homo From the Dinaledi Chamber, South Africa.” CUNY Academic Works. Online at https://academicworks.cuny.edu/le_pubs/22/.
Breiman, Leo, Jerome Friedman, Charles J. Stone, and R. A. Olshen. 1984. Classification and Regression Trees. Monterey, California: Wadsworth & Brooks.
Cavanaugh, David P., and Todd Charles Wood. 2002. “A Baraminological Analysis of the Tribe Heliantheae senso latu (Asteraceae) Using Analysis of Pattern (ANOPA).” Occasional Papers of the BSG 1 (June 17): 1–11.
Doran, Neal A., Matthew A. McLain, N. Young, and A. Sanderson. 2018. “The Dinosauria: Baraminological and Multivariate Patterns.” In Proceedings of the Eighth International Conference on Creationism, edited by J. H. Whitmore, 404–457. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Efron, Bradley, and Robert J.Tibshirani. 1993. An Introduction to the Bootstrap. Monograph on Statistics and Applied Probability 57. San Francisco, California: Chapman & Hall.
Gaffney, Eugene S., Peter A. Meylan, and Andre R.Wyss. 1991. “A Computer Assisted Analysis of the Relationships of the Higher Categories of Turtles.” Cladistics 7, no. 4 (December): 313–335.
Kaufman, Leonard, and Peter J. Rousseeuw. 1990. Finding Groups in Data: An Introduction to Cluster Analysis. New York: Wiley.
O’Micks, J., 2016. “Preliminary Baraminological Analysis of Homo naledi and Its Place Within the Human Baramin.” Journal of Creation Theology and Science, Series B: Life Sciences 6: 31–39.
Reeves, Colin R. 2021. “A Critical Evaluation of Statistical Baraminology: Part 1—Statistical Principles.” Answers Research Journal 14: 271–282.
Robinson, D. Ashley, and David P. Cavanaugh. 1998. “A Quantitative Approach to Baraminology with Examples from Catarrhine Primates.” Creation Research Society Quarterly 34, no. 4 (March): 196–208.
Shaffer, H. Bradley, Peter Meylan, and Mark L. McKnight. 1997. “Tests of Turtle Phylogeny: Molecular, Morphological, and Paleontological Approaches.” Systematic Biology 46, no. 2 (1 June): 235–268.
Späth, Helmut. 1985. Cluster Dissection and Analysis—Theory FORTRAN Programs Examples. Chichester, United Kingdom: Ellis Horwood.
Struyf, Anja, Mia Hubert, and Peter J.Rousseeuw. 1997. “Clustering in an Object-Oriented Environment.” Journal of Statistical Software 1, no. 4 (February): 1–30. http://www.jstatsoft.org/v001/i04/.
Wood, Todd Charles. 2005. A Creationist Review and Preliminary Analysis of the History, Geology, Climate, and Biology of the Galápagos Islands. Center for Origins Research Issues in Creation 1 (June 15). Eugene, Oregon: Wipf & Stock.
Wood, T. C. 2011. “Baraminology, the Image of God, and Australopithecus sediba.” Journal of Creation Theology and Science, Series B: Life Sciences 1: 6–14.
Wood, Todd Charles, and Megan J. Murray. 2003. Understanding the Pattern of Life: Origins and Organization of the Species. Nashville, Tennessee: Broadman & Holman.





