The Philosophy of Science 4: A Brief History of Science from the Scientific Revolution to Modern Physics

Introduction

In two earlier papers, (Faulkner 2022a [hereafter Paper 1]; Faulkner 2023a [hereafter Paper 2]), I concentrated discussion on astronomy and later on physics in the development of science, to the exclusion of other sciences. The reason for this was twofold. First, as an astronomer, astronomy and physics are my fields of expertise. Second, astronomy, along with study of motion (the subdiscipline of physics known as mechanics), were very instrumental in the development of science. This is not to suggest that other sciences were unimportant or were not beginning to develop with astronomy and physics. However, Copernicus’ De Revolutionibus and Newton’s Principia, which were foundational in the development of science, were primarily about astronomy and mechanics. I leave it to other scientists more qualified than me to discuss the history of other sciences and the roles they may have played in the development of science.

In the previous paper in this series (Faulkner 2023b, [hereafter Paper 3]), I briefly traced the development of science in its transition from the Middle Ages to modern times. One could consider the beginning of the transition to be publication of the Copernican model in 1543, and the transition’s end could be dated to the 1687 publication of Newton’s Principia. I concluded that discussion with the observation that science is largely a product of Protestant Europe. It is no accident that at the time of Newton, England was blessed with a veritable Who’s Who of science: Edmund Halley, Robert Hooke, Christopher Wren, John Flamsteed, Robert Boyle, and Brook Taylor, to name just a few.

Classical Physics

For two centuries after the publication of the Principia, the implications of Newtonian, or classical, physics were worked out. Many of these implications involved intricate orbital calculations. Simple orbit calculations involve the interaction of only two bodies, such as the moon orbiting the earth. The two body interaction, as this has come to be called, has a relatively simple, closed form. It results in definite orbits of the earth and moon around one another. Many people may be surprised to learn that as the moon orbits the earth each month, the earth also orbits the moon. This is an inescapable result of Newton’s third law of motion. Both bodies orbit around a common center of mass called the barycenter. The distance of either body from the barycenter depends upon their relative masses. More specifically, the distance of a body from the barycenter is inversely proportional to its mass. Since the earth has 81 times more mass than the moon, the moon is 81 times farther from the barycenter than the earth is. The average distance between the earth and moon is nearly 240,000 miles, so the barycenter is about 3,000 miles from the earth’s center. Because the earth’s radius is 4,000 miles, the barycenter of the earth-moon system is about 1,000 miles below the earth’s surface.

The computed orbit of the moon assuming a two body interaction is a good approximation of the orbit of the moon around the barycenter. However, there are differences between the moon’s observed orbit and the simple one computed with the two-body problem. This is because the gravity of other objects in the solar system act on the moon in addition to the earth’s gravity. These little tweaks cause the moon’s orbit to vary from what it would be if the earth’s gravity acted alone on the moon. Once the gravity of three or more bodies is involved in an interaction, the problem becomes far more complicated than the two-body problem. Physicists call this the n-body problem, with n being an integer greater than two. Unlike the two-body problem, the n-body problem does not have a simple, closed form. That means that the n-body problem cannot be definitively solved in terms of algebraic equations. The orbit of each planet around the sun is easily solved as a two-body problem, which was Newton’s derivation of Kepler’s three laws of planetary motion discussed in Paper 3 (Faulkner 2023b). However, as the moon’s exact orbit cannot be solved as a two-body problem, neither can the planets’ exact orbits be solved as a two-body problem. However, like the moon’s orbit, treating the planets’ orbits as two-body problems results in very good approximations of the true orbits of planets. L4 L1L2L3

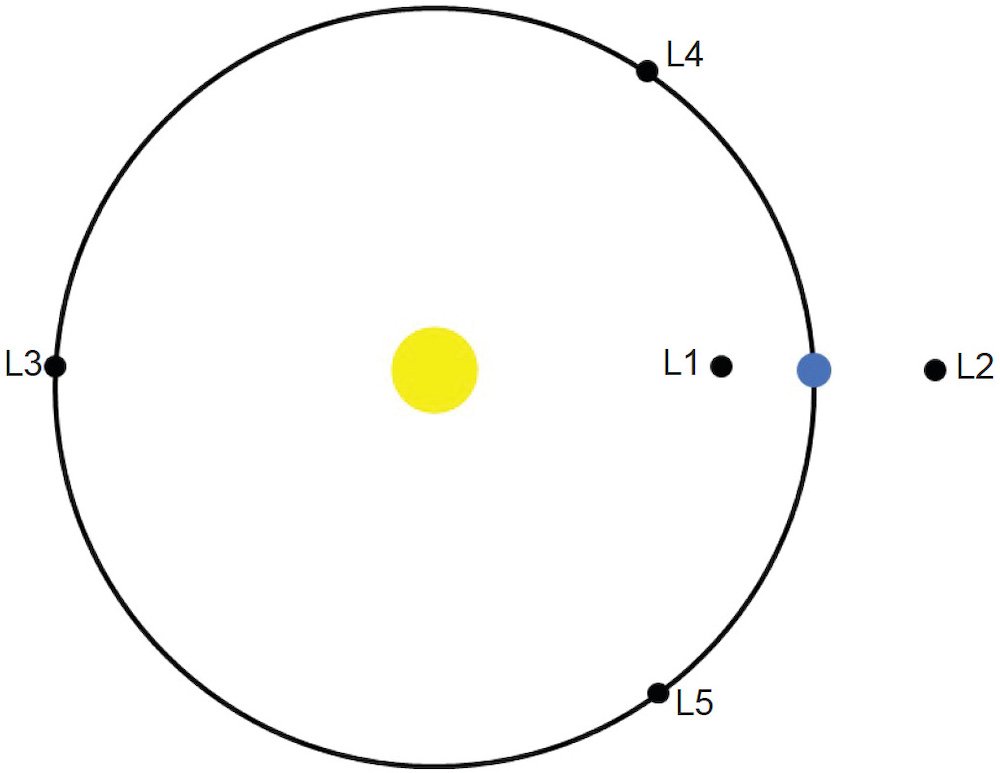
Fig. 1. An illustration of the five Lagrange points for the sun-earth system. The yellow dot represents the sun, and the blue dot represents the earth. The large circle represents the earth’s orbit around the sun.

Newton was aware of the n-body problem, and though he spent some time investigating it, he never reached a satisfactory resolution of the problem. This may be because Newton didn’t expect to find a resolution. Newton thought that the gravitational tugs in the solar system eventually would result in chaos that required God periodically to intervene to set things aright once again. This fitted well with Newton’s theology. Shortly after Newton, other mathematicians were able to demonstrate that Newton had overestimated the effects of gravitational perturbations, as the gravitational tugs beyond the two-body problem came to be called. Perturbations cause slight variations in the motions of the moon and planets, but those variations are quite modest, not leading to the level of chaos that Newton had envisioned. Mathematicians ever since have developed techniques to handle gravitational perturbations of the n-body problem. This is an iterative process of corrections to the two-body process that converges toward zero corrections. For instance, the best current model of the moon’s motion is that of Chapront-Touzé and Chapront (1983).

A key figure in the development of handling perturbations was Joseph-Louis Lagrange (1736 1813). In his study of orbital mechanics, Lagrange discovered that there are five positions where small masses are in equilibrium when under the gravitational influence of two much larger masses. Fig. 1 illustrates the five Lagrange points in the sun-earth system. The L₃ , L₄ , and L₅ points are in the same orbit as the earth around the sun, but with L₃ being 180° from the earth as measured from the sun, and the L₄ and L₅ points being respectively 60° ahead and behind the earth. The L₁ and L₂ points are respectively inside and outside the earth’s orbit colinear with the sun and earth. The distances of the L₁ and L₂ points from the earth and sun depend upon the masses of the sun and earth. The James Webb Space Telescope is at the earth’s L₂ point. There is a collection of asteroids near the L₄ and L₅ points of Jupiter’s orbit around the sun. These are called the Trojan asteroids. As of this writing, there are nearly 10,000 known Trojan asteroids in Jupiter’s orbit. Several other planets have some asteroids orbiting near their L₄ and L₅ points.

About a century after publication of the Principia, Lagrange reformulated classical mechanics in terms of energy. The advantage of working with energy rather than forces is that forces are vectors while energy is a scalar. Scalars have only magnitude (an amount), while vectors are characterized by both magnitude and direction. Consideration of direction in the general case of three dimensions can be very complicated. Using Lagrangian techniques, very complicated problems in mechanics can be reduced to a relatively simple form. A physics undergraduate major usually is introduced to Lagrangian techniques in a classical mechanics course during his junior or senior year. However, the full treatment of Lagrangian technique is found in a graduate level classical mechanics course.

About a half century after Lagrange, William Rowan Hamilton (1805–1865) reformulated Lagrangian mechanics in terms of momentum rather than energy. Many complex orbital dynamics problems in astronomy today, such as galactic structure and star clusters, are solved using Hamiltonian mechanics. Hamiltonian mechanics played a key role in the development of quantum mechanics. In 1926, Erwin Schrödinger (1887–1961) published his famous Schrödinger equation by converting the Hamiltonian equation to its quantum mechanical analog.

The point is that the development of classical mechanics for two centuries after publication of the Principia was done primarily by considering astronomical problems of orbital mechanics. This tremendous success of classical mechanics in describing the world led physicists of the nineteenth century to conclude that classical mechanics was the ultimate description of physical reality. All that remained was to work out the details, such as in the microscopic world.

Determinism, Deism, and the Enlightenment

This confidence in classical mechanics eventually led to the philosophical conclusion of determinism. In classical mechanics, if one knows the initial condition (positions and velocities) of all particles in the universe, then application of classical mechanics leads to knowledge of the positions and velocities of all particles in the future. All one needs to do is consider the forces of interaction of all particles in the universe to trace their motions throughout time. Of course, we cannot know with infinite precision the positions and velocities of all particles in the universe at any time, let alone at the beginning. Furthermore, the staggering number of particles in the universe makes it humanly impossible to compute these things. But that does not matter. Our inability to know all relevant information and our lacking the computational ability to follow all particles through time does not negate the fact that in classical mechanics, particles follow trajectories that are predetermined by the initial conditions and the laws of mechanics. There are no exceptions to these laws. While we may not have sufficient information with infinite precision, in classical physics the particles’ positions and velocities are infinitely precise at all moments.

Such faith in classical mechanics leads to the conclusion that all outcomes were predetermined by the initial state of the universe. In this sense, the universe is like a clock that was wound up and set in its initial state that led to all subsequent physical states since the beginning of the universe. But if the universe behaves like a clock, then there must have been a Clockmaker who set the universe in place. If all is determined by classical physics, then all outcomes are predetermined. If humans are no more than physical beings with each human the mere sum of his parts, then all is predetermined for us too. Thus, free will does not exist. This even led some to conclude that God, the great Clockmaker, was bound by classical physics, and God Himself could not intervene to change outcomes, even if He wanted to.

The question of whether God wanted to intervene in His creation was a point brought up by deism, a theology that developed in parallel with determinism. Deism was a movement spawned by the so-called Enlightenment. The Enlightenment made all sorts of beliefs tolerable that prior to the Enlightenment were unacceptable in Western culture. These beliefs included agnosticism and atheism, as well as deism. Deism did not reject theism, but it did reject organized religion and sacred texts. The Enlightenment claimed that an age of reason had dawned. Since deists rejected direct (especially written) divine revelation, deists relied upon general revelation (nature) to learn about God. They emphasized the use of observation and empirical reasoning were sufficient to conclude that there is a Creator.1 This approach is sometimes called natural theology.

Interestingly, Hutchings and Ungureanu (2021, 168–169) claim that the Reformation led to deism. They argue that the Reformation established the priesthood of the believer, with believers able to interpret the Bible rather than relying upon an authority (the Roman Catholic Church) to interpret Scripture for them. This led to all sorts of novel biblical interpretations and eventually led to deism. The problem with this analysis is that deists generally reject the inspiration and authority of the Bible. Consequently, deism hardly derives from biblical interpretation.

Deism reached its peak as a philosophical/ theological movement in the eighteenth century. It is often claimed that most of the founding fathers of the United States were deists. That is a debatable point. However, no one can deny that deism heavily influenced many of the United States’ founding fathers (one does not have to consciously embrace a movement to be influenced by that movement). Outstanding in this regard is Thomas Jefferson, who largely wrote the text of the Declaration of Independence. Several statements in the Declaration of Independence reflect Enlightenment and deistic thinking.2 Jefferson’s The Life and Morals of Jesus of Nazareth, commonly referred to as the Jefferson Bible, was literally a cut-and-paste job of the gospels, removing all references to miracles, the supernatural, and the deity of Jesus Christ.3

As a movement, deism waned considerably in the nineteenth century. Deism remains in the Unitarian Church (since 1961 in the United States known as the Unitarian Universalist Association), though it is doubtful that any Unitarians today call themselves deists. In fact, it is unlikely that anyone calls himself a deist anymore. However, that does not mean that the tenets of deism are not held today. Most people in the United States are what I would call practical deists. There are relatively few atheists in the United States and in the rest of the West today. While many theists in the West may identify with a particular Christian denomination, relatively few are active members of those denominations. In addition to not being active members of any organized church, many Western theists do not concern themselves with the authority of the Bible. They believe that God is responsible for creation, but that God isn’t very concerned with the affairs of men. That is a classic definition of deism. Hence, deism is alive and well today.

While deism as a movement soon disappeared after its peak in the seventeenth century, the attitude of deism had a profound effect on science. This thinking heavily influenced the development of geology in the early and mid-nineteenth century (Mortenson 2004, 234–236). This was followed by the wide acceptance of biological evolution even by those in the church. Theistic evolution is wholly compatible with deism, though few theistic evolutionists would call themselves deists.

The so-called Enlightenment began about the same time that science as we know it blossomed in the West. As I pointed out in Paper 2 (Faulkner 2023a), the scientific revolution was largely a product of Protestant Europe. This was no accident, as the Protestant Reformation provided a worldview that made science possible. In the Protestant worldview, there was a unity of nature both on earth and in the heavens. God upholds the creation by the power of His word (Colossians 1:16–17; Hebrews 1:3). Since God is a God of order and decrees, then we might expect there to be an orderly pattern in the way the world operates. The study of the natural world could be a holy calling just as much as being a member of the clergy could be a calling. Thus, by studying the world looking for the God-ordained order, one can give due honor and reverence to God. With this fertile soil, it was inevitable that natural science would flourish.

Positivism and the Conflict Thesis

Unfortunately, the architects of the so-called Enlightenment hijacked science. They ignored the biblical worldview that formed the foundation of science, and incorrectly claimed that the Enlightenment finally freed man’s intellect from the strictures of the church. In the nineteenth century, this thinking gradually grew in influence among scientists, as consideration of God’s role in the world diminished among scientists. A key figure in this shift in thinking was Auguste Comte (1798–1857), who I mentioned in Paper 1 (Faulkner 2022a). In the 1830s and 1840s, Comte founded a school of thinking that he called positivism. The Oxford dictionary defines positivism as

a philosophical system that holds that every rationally justifiable assertion can be scientifically verified or is capable of logical or mathematical proof, and that therefore rejects metaphysics and theism.

Positivism’s rejection of theism in science was much more explicit than that of the humanistic philosophy of the Enlightenment. Enlightenment thinking permitted belief in God but limited God’s concern or influence in the world. Since God is irrelevant in Enlightenment thinking, then Comte’s positivism was merely the logical next step beyond the Enlightenment. Under the leadership of James Hutton (1726–1797) and Charles Lyell (1797–1875), the revolution in geology from flood geology to uniformitarianism was well underway at the time Comte was developing positivism (Mortenson 2004; 2007). Theories of biological evolution proposed by Jean-Baptist Lamarck (1724–1829) and others were already being discussed, and Charles Darwin (1809–1882) was formulating his ideas about biological evolution. Though many leaders in these developments were not atheists, the ideas that they promulgated were consistent with atheism. So, Comte was both reflecting and influencing the changing attitude of many scientists.

This change in thinking was controversial. For instance, the devout Christian physicist James Clerk Maxwell (1831–1879) strongly opposed positivism. Alas, positivism soon won, transforming science so that any consideration of God was no longer welcome. If there is no God, then humanity and the world around us must have had a natural origin. Thus, the purview of science came to include origins rather than just the description of how the world now works. It didn’t matter that one cannot test what may have happened in the past the same way that one uses science to test processes in the present. This was the doorway that led to the blending of the rigid testing of scientific hypotheses that may describe the present world with speculations about what might have happened in the past.

Positivism in the philosophy of science peaked in the early twentieth century. Later philosophers of science such as Popper and Kuhn (discussed in Paper 1 [Faulkner 2022a]) replaced positivism, but positivism’s rejection of theism remained. Positivism has largely disappeared in discussions of the philosophy of science, though a version of positivism is still debated in social sciences. This dramatic shift in thinking resulted in the conflict thesis in the second half of the nineteenth century that I mentioned in Paper 2 (Faulkner 2023a). The conflict thesis is the idea that religion (read that as Christianity) had hindered progress during the Middle Ages and that it was only after the power of the church waned that progress could resume once again. There were two major players in the conflict thesis. One of these was John William Draper (1811–1882), who in 1875 published History of the Conflict between Religion and Science. The other was Andrew Dickson White (1832–1918), who published his two-volume A History of Warfare of Science with Theology in Christendom in 1896.

In 1860, Draper delivered a paper on the influence of Darwinism on the intellectual development of Europe at the annual meeting of the British Association for the Advancement of Science (now the British Science Association). This was only months after the publication of Darwin’s Origin of Species. Draper’s presentation sparked a lively discussion that has become known as the “Oxford evolution debate” between Samuel Wilberforce (1805–1873) and Thomas H. Huxley (1825–1895). Contrary to popular misconceptions, it wasn’t a debate but a discussion, and there were other participants in the discussion besides Wilberforce and Huxley. There was no record of the discussion, so the details of this supposed debate were recreated later from recollections of those in attendance. Consequently, much of what was allegedly said in this discussion is more legend than true, and people ought to be cautious in referencing or quoting details of the “Oxford evolution debate.”

In his book, Draper primarily focused his criticism on the Roman Catholic church, though he also criticized Islam and Protestants. White’s two volumes argued that Christianity (both Catholic and Protestant) was the culprit in holding back progress. Since Draper’s book was published two decades before White’s work, he initially had more influence than White. However, White’s work was more voluminous and had numerous references, giving it an air of scholarship, so White eventually became more influential than Draper. History has not been kind to the conflict thesis and its major proponents, Draper and White. Modern historians of science have discredited the conflict thesis (Hutchings and Ungureanu 2021). An example of the shoddy scholarship of the conflict thesis is the creation of the Columbus myth that I discussed in Paper 2 (Faulkner 2023a). Unfortunately, the conflict thesis remains alive and well in popular perception. Combined with the Galileo affair (which the conflict thesis mischaracterized), many people today, scientists included, think Christianity has been and still is an impediment to science.

Physics in the Nineteenth Century

The unparalleled success of classical mechanics continued in the nineteenth century. In 1781, William Herschel (1738–1822) discovered Uranus, the first planet discovered since antiquity. Uranus had escaped detection previously because it generally is too faint to be seen with the naked eye. In 1787, Herschel discovered two natural satellites of Uranus. Based upon observations, the orbit of Uranus around the sun and orbits of the two natural satellites around Uranus were computed, and they all followed their computed orbits well. However, by 1840, the observed orbit of Uranus departed slightly from the computed orbit. Two mathematicians, John Couch Adams (1819–1892) and Urbain Le Verrier (1811–1877), independently approached the problem by invoking the hypothesis that an eighth planet beyond the orbit of Uranus was perturbing Uranus in its orbit. From the discrepancies between the observations of Uranus’ position and its calculated orbit, the mathematicians were able to predict the position of the hypothetical planet. In 1846, a search by astronomers at the predicted position quickly confirmed the existence of the eighth planet, now named Neptune. Once again, classical mechanics had triumphed.

The discovery of Neptune accounted for most of the discrepancies in Uranus’ orbit. The remaining discrepancy was only 1/60 of the original amount. This led several astronomers to hypothesize a ninth planet beyond the orbit of Neptune to account for the remaining discrepancy. In the early 1900s, there were several published predictions for the position of Planet X, as this hypothetical planet came to be called. Due to the small size of the discrepancies, the predictions of the position of Planet X varied widely, making its position much more uncertain than Neptune’s position at the time of its discovery. This made the search for Planet X problematic. Most tenacious in the search for Planet X was Percival Lowell (1855–1916), who searched for it until his death. In 1929, Percival’s brother donated a new telescope to Lowell Observatory to facilitate the search. With this new telescope, Clyde Tombaugh (1906–1997) famously found Pluto the following year. Once again, it appeared that classical mechanics had triumphed.

However, astronomers quickly realized that there was a problem—Pluto was extremely faint, suggesting that it was very small and hence its mass was much less than required to explain the discrepancies in Uranus’ orbit. The mass of Pluto was not known until 1979, when Pluto’s largest natural satellite, Charon, was discovered. This allowed determining the mass of Pluto from Charon’s orbital motion, using the generalized form of Kepler’s third law obtained from Newtonian mechanics. Pluto’s mass turned out to be 1 /400 the mass of earth, whereas most predictions of its mass to account for the perturbations of Uranus exceeded the mass of the earth. What had gone wrong? Recall that the discrepancies in Uranus’ orbit were very small. It is now recognized that the discrepancies were on the order of the uncertainty in measuring the position of Uranus. That is, there probably is no discrepancy to explain. What is Pluto then? Since the 1990s, astronomers have discovered many more small bodies orbiting the sun at an average distance greater than that of Neptune. At the time of this writing, the number of confirmed trans-Neptunian objects (TNOs) is nearly 1,000, with more than 3,000 TNOs awaiting confirmation. Pluto was just the first TNO discovered, six decades before any more TNOs were found. Hence, once again Newtonian mechanics was confirmed.

About the same time as the discovery of Neptune (1846), Le Verrier noticed a small discrepancy in the orbit of Mercury, leading him to hypothesize the existence of another planet interior to Mercury’s orbit around the sun. However, searches for this hypothetical planet were unsuccessful. As the observations of Mercury’s orbit improved, others joined the search for Vulcan, as this hypothesized planet came to be called. By the end of the nineteenth century, attention was focused on the precession of perihelion of Mercury’s orbit. Most of the precession could be explained by gravitational perturbations, but there remained 43 arcseconds per century in the precession of Mercury’s perihelion that were unaccounted for. As we shall see soon, this would become very important later.

By 1866, 90 asteroids had been discovered, all in the asteroid belt. That year, Daniel Kirkwood (1814 1895) noticed that there were gaps in the distribution of asteroids within the belt. Kirkwood also explained the gaps by resonances between the orbital periods of objects in the gaps and the orbital period of Jupiter. These resonances are integral multiples of the orbital periods with Jupiter, such as 2:1, 3:1, and 5:2. For instance, if a small object orbits the sun three times every time Jupiter orbits once (a 3:1 resonance), then the gravity of Jupiter regularly perturbs the orbit of the small body, lifting its orbit higher, resulting in a longer orbital period. Once the period of the asteroid increases sufficiently, the resonance no longer exists, and the effect ceases. This process efficiently cleans out asteroids with certain orbital periods (and consequently distances, according to Kepler’s third law). The resonances with the lower integers tend to be more influential. Once again, Newtonian mechanics had triumphed.

In 1857, the University of Cambridge awarded the Adams Prize to James Clerk Maxwell for demonstrating that the rings of Saturn are composed of many solid particles orbiting in the same plane but at various distances from Saturn. It quickly followed that the Cassini Division, a break in rings, was caused by a 2:1 resonance with Saturn’s natural satellite Mimas. Again, classical mechanics appeared to triumph.

Other areas of physics made great progress in the nineteenth century. For instance, thermodynamics and statistical mechanics became recognized sciences. William Thomson (aka Lord Kelvin, 1824–1907) made many significant contributions to thermodynamics. Maxwell also contributed to the development of thermodynamics and statistical mechanics, such as the Maxwell-Boltzmann distribution. Some aspects of statistical mechanics seem to undermine the determinism that some scientists had surmised from classical mechanics. For instance, Ludwig Boltzmann pointed out that the collisions of particles, such as in a cooling cup of coffee, follow classical physics and so are time reversible, yet the cooling of the cup of coffee is not time reversible (Robertson 2021). This question still does not have a satisfactory answer. Ludwig Boltzmann (1844–1906) was the first to equate entropy with a measure of disorder.

Or consider an idea formulated by Maxwell and later expanded by Kelvin that has become known as Maxwell’s demon. A small demon controls a massless door between two chambers of gas initially at the same temperature. As the gas particles collide in their respective chambers, they occasionally approach the door. The demon briefly opens the door to permit fast moving particles to pass through the door in one direction, and the demon briefly opens the door to permit slow moving particles to pass through the door in the opposite direction. This eventually would result in the gas particles in one chamber moving faster than the gas particles in the other chamber. According to the kinetic theory of gases, the temperature of a gas depends upon the speed of the gas particles. Therefore, through this process one chamber will warm and the other chamber will cool, which is a decrease in entropy. Since the demon manipulated a massless door, there was no work required to do this. According to the second law of thermodynamics, work is required to decrease entropy of a system. Therefore, Maxwell’s demon would violate the second law of thermodynamics.

Maxwell’s demon is still debated among scientists and philosophers alike, with no satisfactory resolution. Some people see resolution in the link between Maxwell’s demon and information theory (the demon uses both intelligence and information), a topic of much interest to many creationists. This link was first formulated in 1929 by Leo Szilard (1898–1964) in the form of a hypothetical engine operated by a Maxwellian demon. The relationship between information theory and entropy was further developed by Ralph Hartley (1888–1970 and Claude Shannon (1916–2001) in the 1940s. Maxwell’s demon seemed to undermine determinism. Maxwell ended up concluding that thermodynamics is anthropocentric, requiring an observer. As we shall see, this thinking is similar to the Copenhagen interpretation that emerged a half century later. Thus, these quirky conclusions about thermodynamics and statistical mechanics presaged the starker oddities of quantum mechanics decades later.

Maxwell’s greatest contribution was to the physics subdiscipline of electromagnetism. Electricity and magnetism had been known since ancient times, but they had been viewed as two unrelated phenomena. However, in the first half of the nineteenth century there were numerous experiments conducted that demonstrated there was an intimate relationship between electricity and magnetism. In 1865, Maxwell unified electricity and magnetism into one theory of electromagnetism by publishing four equations that described the relationship between the two. When Maxwell solved the four equations simultaneously, he found a wave equation featuring electric and magnetic fields that oscillated perpendicular to one another, with the wave propagating in a direction perpendicular to the plane defined by the two oscillating fields. Maxwell was astonished to find that the predicted speed of the wave matched the measured speed of light. Maxwell hid his enthusiasm by dryly commenting that this didn’t seem to be a coincidence. Maxwell had set out to unify electricity and magnetism, and he unexpectedly ended up providing a good understanding of what the medium of light is.

The nature and medium of light had been hotly debated throughout the nineteenth century and would be into the early twentieth century. Newton subscribed to the corpuscular theory of light, that light consisted of particles. Due to Newton’s looming influence, scientists of the eighteenth century largely agreed with Newton on the nature of light. One person unconvinced of the corpuscular theory of light was Thomas Young (1773–1829), who began to test the two ideas. Young presented his first paper advocating the wave nature of light in 1800. In 1803, Young shared the results of an interference experiment that suggested light is a wave. At first, Young’s arguments were met with skepticism, but within a decade or two, Young had won most scientists over.

A wave is a periodic disturbance in a medium. Therefore, once physicists came to realize that light is a wave phenomenon, they knew that light required a medium. On the earth, the medium was easy enough to see—it was air, glass, water, or whatever transparent medium light was in. But what was the medium for light outside the earth that would transmit light from the sun and distant stars to the earth? In the nineteenth century, physicists viewed space as being the idealized perfect vacuum, totally void of anything. That is not the modern concept of space. We now know that all space contains a tiny amount of matter, though the density is incredibly low. Furthermore, in modern physics, even space void of matter isn’t exactly empty. A total vacuum, if it existed, would still be chock full of fields and virtual particles required in quantum mechanics. Consequently, quantum mechanics would seem to forbid an absolutely empty vacuum.

Physicists of the nineteenth century eventually developed the idea that space was permeated by some medium. They resurrected the Aristotelian term aether for the stuff of heaven (discussed in Paper 2 [Faulkner 2023a]) for this hypothetical medium for light in empty space. Aether had some peculiar properties, totally unknown for any other substance. Aether had to be massless. It also had infinite tensile strength. As the earth moved, aether had to instantly close in behind the earth or else we would not see stars on the backside of the earth as it moved. These extreme properties that had no analog in real substances should have been an indication that something was seriously wrong with the aether hypothesis, but physicists continued with this flawed theory. There were different versions of aether theory. In some versions, aether remained fixed in space as the earth moved through it. In other versions, aether was dragged along by the earth as the earth moved. In still other versions, aether was partially entrained by the earth’s motion. Why were there different versions of aether theory? It was because experiments were developed to test these different aether possibilities, each giving null results.

The First Failure of Classical Physics

There are two famous aether experiments worthy of mention. In 1727, James Bradley (1692–1762) discovered the aberration of starlight. As the earth moves in its orbit, telescopes must be pointed slightly in the direction of the earth’s motion for stars to be seen. This is often compared to tilting an umbrella in the direction one is walking in the rain if there is no wind and rain falls vertically. The maximum amount of tilt is 20.5 arcseconds, but the amount of aberration of starlight depends upon a star’s ecliptic latitude. Aberration of starlight causes the observed positions of stars to periodically shift throughout the year. Bradley’s discovery was the first direct evidence of the earth’s orbital motion around the sun. The 20.5 arcsecond amplitude of aberration of starlight depends upon the ratio of the earth’s orbital speed to the speed of light. In 1871, George Airy (1801–1892) conducted an experiment to test for the theory of aether drag. Since the speed of light in water is 2/3 the speed of light in vacuum or air, if a telescope is filled with water, then according to aether drag theory, the amount of aberration of starlight will be different from an empty telescope. Airy found that the amount of observed aberration of starlight was the same whether the telescope was empty or filled with water. This experiment eliminated the possibility of aether drag.

The second experiment worth mentioning is the Michelson-Morley experiment conducted in 1887 by Albert A. Michelson (1852–1931) and Edward W. Morley (1838–1923). If the aether is not dragged by the earth, then the aether must be at rest as the earth moves through it. In classical physics, the observed speed of a wave depends upon the speed of the wave in the medium and the motion of the observer through the medium. Thus, if one measured the speed of light in the direction of the earth’s motion around the sun and measured the speed of light in the direction perpendicular to the direction of the earth’s motion, then there ought to be a difference in these two measured speeds. The best way to make this measurement was by using the interference of light. Waves interfere with one another. If light from a monochromatic (one wavelength) source is split into two beams and the beams are brought together, then the two different waves can arrive at the same place in phase, completely out of phase, or some phase in between. When the two beams are in phase, the waves will combine (constructive interference), producing a wave having twice the amplitude of either wave. However, if the waves are completely out of phase, they will cancel out one another (destructive interference), producing no wave. For phase differences in between, there will be a combined wave with varying amplitude. Light has a short wavelength, so examination of the interference pattern requires magnification. One will see a series of closely spaced light and dark fringes. This observed interference pattern will depend upon how out of phase the two light sources are.

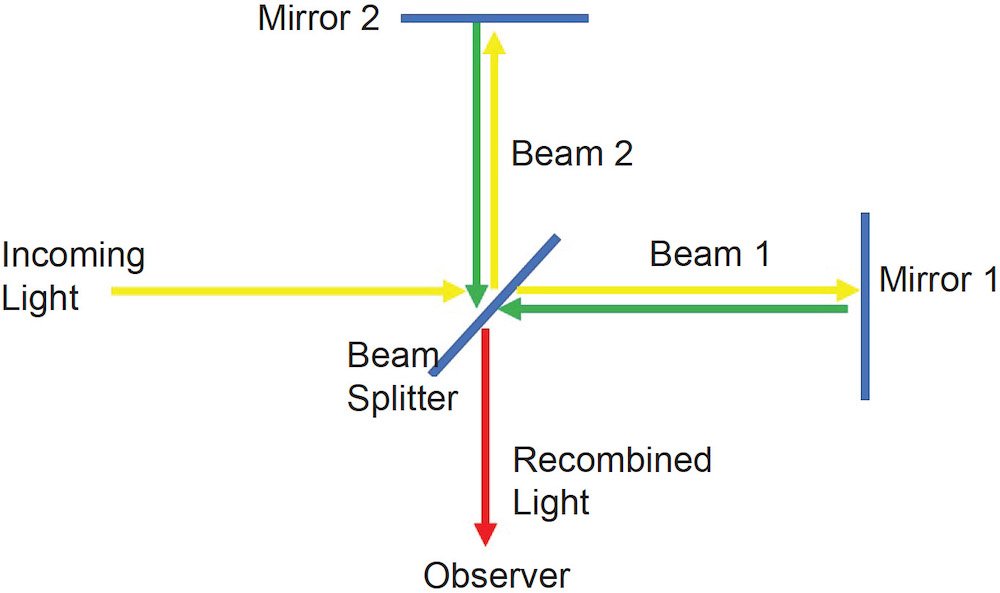
Fig. 2. The Michelson-Morley apparatus. Incoming light is split into two beams at right angles to one another. After the two beams are reflected off mirrors, they are recombined into a single beam.

The Michelson-Morley apparatus (see fig. 2) had a monochromatic light source and a collimator to produce a narrow beam. The beam passed through a beam splitter, a half-silvered piece of glass at a 45° angle to the beam that split the original beam into two beams, with one beam passing straight through the beam splitter along a pipe, and the other beam passing down an identical pipe perpendicular to the first pipe. The pipes were oriented with one pipe parallel to the earth’s orbital motion, and the other pipe perpendicular to the earth’s orbital motion. The two pipes had mirrors at their other ends, which sent the two beams back toward the beam splitter. The two beams were allowed to interfere with one another, and the fringe pattern was observed. The fringe pattern depended upon the different speeds of light along either pipe. However, the fringe pattern also depended upon the difference in the lengths of the two pipes. Ideally, the two pipes had the same lengths to well within the wavelength of light used. Since light has a very short wavelength, this wasn’t practical.

To account for the difference in the lengths of the pipes, once the experiment was conducted, the apparatus was rotated 90° so that the pipe originally oriented parallel to the earth’s motion was now perpendicular to the earth’s motion, and the pipe originally perpendicular to the earth’s motion was now parallel to the earth’s motion, and the experiment was repeated. This was expected to produce an entirely different fringe pattern, so a comparison between the different fringe patterns of the two runs of the experiment would reveal the difference in the speed of light between the two orientations. Michelson and Morley were astonished to see that the two interference patterns were the same.

There were two possible explanations. One possibility was that the earth is not moving. However, there was abundant evidence (aberration of starlight, stellar parallax, annual changes in Doppler shifts observed in stars) that the earth indeed orbits the sun, so that possibility did not seem likely. The other possibility was that the aether theory the Michelson Morley experiment was designed to test was disproved. That possibility was not palatable to many physicists because other experiments had ruled out other versions of aether theory. The Michelson Morley was the final nail in the coffin of aether theory, but established ideas do not go away easily, so few physicists were ready to abandon aether theory. Many physicists continued to cast about for some mechanical medium for light. In the 1890s, Hendrik Lorentz (1853–1928) and George Fitzgerald (1851 1901) found that they could explain the Michelson Morley experiment if length contracted, and time dilated with increased speed. However, this was sort of plucked out of the air.

In 1905, Albert Einstein (1879–1955) took a different tack at the problem. We observe phenomena and make measurements from frames of reference. There are two types of reference frames, those that are accelerating and those that are not accelerating. In nonaccelerating reference frames, objects obey Newton’s three laws of motion. More specifically, they obey Newton’s first law of motion, the law of inertia: an object at rest remains at rest and an object in motion remains in straight line motion unless acted upon by an outside force. Because objects in nonaccelerating reference frames obey the law of inertia, we call them inertial reference frames. Objects in accelerating reference frames do not obey the law of inertia, so we call them non-inertial reference frames. Consequently, in non-inertial reference frames, we must make up fictitious forces to explain what we see. The classic example of a non-inertial reference frame is a spinning merry-go-round. Riders on a spinning merry-go-round experience an outward force along the radius of the merry-go-round. We call this outward force “centrifugal force.” Any motion along a curved path, such as a turning automobile, also gives one the sensation of a centrifugal force. Linear acceleration gives rise to another type of a non-inertial reference frame, such as an automobile that is speeding up or an aircraft taking off on a runway. Passengers aboard these accelerating vehicles feel a force pushing them back into their seats. One may observe accelerating vehicles and their contents from an external inertial reference frame. From such a frame, mechanics is correctly described without resorting to fictitious forces. We may transform from an inertial frame to a non-inertial frame by using these fictitious forces. It doesn’t matter which inertial reference frame one uses because mechanics will be the same in all inertial reference frames. We say that mechanics is invariant with respect to inertial reference frames.

I previously mentioned Maxwell’s four equations that completely describe electromagnetism. These equations and electromagnetic phenomena are observed to be invariant with respect to inertial reference frames. For instance, if a coil of conducting wire is moved at a constant rate in the vicinity of a magnetic field, a current is induced in the coil of wire. But if the coil is held still while the magnetic field is moved so that the relative motion between the two is the same as before, the observed current in the wire is the same. It follows that since light is an electromagnetic phenomenon, then the speed of light will be invariant with respect to motion between the source of the light and the observer of the light, provided the observer is in an inertial reference frame. Otherwise, the electromagnetic phenomenon of light would not be invariant. Einstein took the invariance of light with respect to motion in inertial reference frames as a given and worked out the details. The details included the effects that Lorentz and Fitzgerald had pulled out of the air. Einstein derived those effects as consequences of the invariance of electromagnetic phenomena.

The invariance of the speed of light with respect to inertial reference frames was shocking to most physicists at the time because no other known wave behaved this way. However, Maxwell had already shown that light is not an ordinary wave—light is a vibration of electric and magnetic fields, not a vibration of a mechanical medium like all other waves then known. Once one comes to understand that light is an electromagnetic phenomenon and that electromagnetic phenomena are invariant with respect to inertial reference frames, then the constancy of the speed of light in inertial reference frames is inescapable. This is the foundation of Einstein’s theory of special relativity.4 Many physicists at the time had difficulty accepting this revolutionary concept, and there are a few physicists today who still struggle with it.

If the speed of light is invariant in inertial reference frames, then what about non-inertial reference frames? Just as mechanics is not invariant in non-inertial reference frames, so are electromagnetic phenomena. Therefore, the prediction of special relativity is that the speed of light is not invariant in a non-inertial reference frame. In 1913, Georges Sagnac (1869–1928) performed an experiment with an interferometer in a rotating reference frame, and he found that the speed of light was not invariant, just as Max von Laue (1879–1960) had predicted from special relativity two years earlier, in 1911. Admittedly, Sagnac was attempting to demonstrate aether drag in his experiment. However, other experiments had ruled out the possibility of aether drag. The only theory that could account for all the relevant experiments (Airy’s experiment, Michelson Morley, Sagnac, etc.) was special relativity. The phenomenon demonstrated by Sagnac is called the Sagnac effect, which is the operating principle of laser ring gyroscopes. In 1925, Michelson and Henry G. Gale (1874–1942) performed an experiment using a large Sagnac interferometer to test for the earth’s rotation. Since rotation is a non-inertial reference frame, the prediction of special relativity was that such an experiment would be positive rather than null as in the case of the Michelson-Morley experiment. The Michelson-Gale experiment had a positive result, as predicted.5

But Einstein was not finished. A problem with Newtonian gravity had existed since Newton first formulated his law of universal gravity. All other forces appeared to act through direct contact of the bodies involved, but gravity seemed to operate through empty space. When asked about how gravity does this, Newton famously responded that he framed no hypothesis about that. That sort of question is more about why phenomena happen rather than how phenomena happen. As I pointed out in Paper 1 (Faulkner 2022a), science doesn’t really address the question of why things happen. Rather, science is more about the description of how things happen. Newtonian gravity does a very good job describing how gravity works but does not address why gravity works at all.

After Newton, scientists began to realize that electromagnetic phenomena happen through empty space as well. In 1785, Charles-Augustin de Coulomb (1736–1806) published his famous law of force between charges that follows an inverse square law of the distance as gravity does. Others had noticed this behavior previously, but Coulomb was the first to publish it. The inverse squared relationship probably was suggested by Newton’s law of gravity. A major difference between electrostatic forces and gravity is that electric charges come in two types and so can be either attractive or repulsive, but gravity is only attractive. As pointed out in Paper 1 (Faulkner 2022a), field theory was eventually created to explain the forces of electromagnetism and gravity. Similarly, physicists often use a gravitational field to explain how gravity works. With field theory, there isn’t a problem with gravity acting through empty space with no direct contact between the bodies involved. However, there remained another problem. The gravitational force on a body is observed to depend upon the body’s mass. We can define this as a body’s gravitational mass. Newton’s second law states that when a force acts on a body, its acceleration depends upon the body’s mass. We can define this as a body’s inertial mass. There is no reason why these two masses are the same, but experiments demonstrate that they are. The only other time we see forces that depend upon the masses of objects is when we create fictitious forces to explain what we observe in non-inertial reference frames. Fictitious forces in non-inertial reference frames, such as centrifugal force, always depend on the masses of the bodies involved. This is because all bodies in non-inertial reference frames are subject to the same accelerations. Since gravity also acts on objects so that they experience the same acceleration, this raised the possibility that gravity is a fictitious force that is due to being in a non-inertial reference frame. A person in free fall in a closed container without windows cannot detect gravity. For instance, astronauts orbiting in the International Space Station are continually falling around the earth, so they are in free fall. That is why we say they are in zero gravity, even though it is gravity that keeps them in orbit. This is a difference between Newtonian gravity and general relativity’s explanation of gravity. In Newtonian theory, gravity is a real force that is present and accounts for orbital motion. In the theory of general relativity, a person orbiting the earth is not subject to the fictitious force of gravity, but a person on the earth’s surface is.

It took a decade for Einstein to work through his theory of general relativity. He published it in 1915–1916. It was a radical departure not only from the Newtonian concept of gravity, but also from the Newtonian concepts of space and time. In Newtonian mechanics, space and time are independent of one another, and they are merely the stage upon which the real actors, matter and energy, act out their roles. However, in general relativity, space and time are real entities that play significant roles in conjunction with matter and energy. Also, space and time are intimately related to one another. By multiplying time by the speed of light, time is transformed into a fourth dimension of what we now call space-time, or Minkowski space-time. As the three dimensions of space are mutually perpendicular, the coordinate of time is perpendicular to each of the three spatial coordinates (this is possible in dimensionality that is greater than three dimensions). One difference between time and the three spatial coordinates is that one may move in either direction of each dimension of space, but motion in the time direction is only in one direction. This motion carries objects through space-time. The presence of matter and/or energy curves space-time. As objects move on geodesics (straight lines) in curved space-time, we perceive those geodesics as accelerations of gravity. This not only explains why gravitational and inertial masses are the same, but it also provides a mechanism by which gravity appears to act through empty space.

Such an extraordinary proposal required extraordinary evidence. Einstein proposed three tests. The first evidence was already in hand, the 43 arcseconds per century anomaly in the precession of Mercury’s orbit. Einstein’s theory beautifully explained the observed discrepancy. The second test was deflection of starlight during a total solar eclipse. There was a total solar eclipse in 1919 that was suitable to test the prediction of general relativity. Though the measurements were a bit noisy, they did conform to the prediction of general relativity. With subsequent eclipses, technology improved, as did the quality of measurements, providing additional confirmation of general relativity’s prediction. Since the 1960s, pulsar timings as they pass behind the sun have provided much more precise verification of this test of general relativity. Einstein’s third test was gravitational redshift, but it was several decades before this was confirmed. Over the years, many additional tests of general relativity have been conducted. General relativity has passed each test, making it one of the most tested theories in physics.

It is sometimes claimed that general relativity has replaced classical mechanics, and especially Newtonian gravity. While technically true, it is not practically true (Faulkner 2022b). In most applications, classical mechanics provides a very good description of the physical world. It is not until extremely large mass and/or energy or extremely high velocities are encountered that the predictions of the two theories differ. Therefore, in most situations, classical physics and Newtonian gravity are preferred, if nothing else because the description is much easier in classical physics. In this context, some physicists say that gravity is not a force. However, general physics textbooks always call gravity a force and treat it as such. Is this a contradiction? No. Physicists often look at situations in different ways. General relativity is one way of looking at the world, but there are other ways of looking at the world. As we shall see, in quantum mechanics, gravity is a force.

The Second Failure of Classical Physics

As just discussed, various experiments to test aether theories in the nineteenth century led to a sort of downfall of classical mechanics on at least one front. At the same time, the application of classical mechanics to very small systems led to perhaps a greater crisis for classical physics. There were several key experiments on this path.

When solid objects are heated, they begin to glow. Throughout the nineteenth century various people invented filament lamps based upon heating the filament to incandescence, though it was not until the last few decades of the nineteenth century that incandescent lights became feasible. One problem was the inefficiencies involved. Therefore, there was much interest in studying the nature of the radiation given off by heated objects in hopes of improving efficiency of nascent light bulbs. Dark objects tend to be good absorbers and good emitters of energy. This led physicists to hypothesize an ideal blackbody, a perfect absorber and emitter of light. Though no real object is an ideal blackbody, it is possible to construct ovens that come very close to being ideal blackbodies. Experimenters found that the emission from these approximations to ideal blackbodies had certain characteristics.

First, the spectrum of an ideal blackbody has a unique shape. For very short wavelengths, there is no emission. However, as wavelength increases, there is a quick rise to peak emission followed by a much more gradual decline toward longer wavelengths. Second, the wavelength where the peak emission occurs is inversely proportional to the blackbody temperature, expressed on an absolute scale (Wien’s law). Third, the total energy emitted by a blackbody (graphically, the areas under the intensity vs. wavelength curve) is proportional to the fourth power of the temperature (Stefan-Boltzmann law).

At the beginning of the twentieth century, Lord Rayleigh (1842–1919) and Sir James Jeans (1877 1946) applied classical physics to explain blackbody spectra. Their work produced a very good fit at longer wavelengths. However, at shorter wavelengths, the Rayleigh-Jeans law predicted that blackbody emission would increase without bound. Since observed blackbody spectra rapidly declined with decreasing wavelength beyond the peaks of their curves, there was a very bad mismatch between theory and observations.

At about the same time, Max Planck (1858–1947) was able to derive a mathematical expression that correctly described blackbody spectra. Planck did this with classical physics, but with one small modification. Instead of the light absorbed and emitted by blackbodies being continuous, Planck assumed the light is absorbed and emitted in discrete packets that are proportional to the frequency of radiation, or, alternately, inversely proportional to wavelength of light. In equation form, this is

where E is the energy of a packet of light, h is Planck’s constant, υ is frequency, c is the speed of light, and λ is wavelength. Setting the derivative of Planck’s expression describing blackbody spectra to zero resulted in Wien’s law, while integration of the expression produced the Stefan-Boltzmann law. In short, Planck’s simple assumption about energy being quantized rather than being continuous beautifully described all the known characteristics of blackbody spectra. However, quantization of energy made no sense in classical physics. Like the assumptions of Lorentz and Fitzgerald, Planck’s assumption was merely plucked out of the air.

In the 1880s, other experimenters discovered the photoelectric effect. If light falls onto a metal surface in a vacuum, electrons are dislodged from the metal surface. Experiments revealed that the total number of electrons liberated is proportional to the intensity of light falling on the surface. That much agreed with the prediction of classical physics. However, no electrons were dislodged unless the frequency of light exceeded a minimum value. The threshold frequency required to produce photoelectrons varied according to which metal the surface was made of. That made no sense in classical physics—photoelectrons should be produced regardless of the frequency of the light if the intensity was sufficient.

In 1905, Einstein explained the photoelectric effect by applying Planck’s simple assumption about light being quantized. But Einstein took Planck’s assumption a step further. Einstein suggested that light has a particle nature, with the energy of each photon (as light particles came to be called) proportional to its frequency. Just a century before, physicists had resisted the wave theory of light in favor of Newton’s corpuscular theory but eventually were won over. After a century of believing light is a wave, physicists were then asked to switch back to corpuscular theory. As before, there was resistance reverting to the corpuscular theory of light. Confirmation of Einstein’s proposal came in 1921 when Arthur Compton (1892–1962) demonstrated the particle nature of electromagnetic radiation by bouncing x rays off graphite crystals.

If things were getting confusing whether light was a wave or a particle, things were getting cloudy for entities that clearly seemed to be particles too. In the second half of the nineteenth century, scientists studied the spectra of hot gases at low pressure. They found that unlike solids, liquids, and gases at high pressure (which have blackbody spectra), hot, low-pressure gases emit energy only at discrete wavelengths or frequencies. When the spectra of low-pressure gases are observed, they have bright lines that correspond to the wavelengths of emission, so we call them bright line spectra. Every element produces a unique set of emission lines, which allows for chemical analysis. Emission line spectra generally are complex, but the spectrum of hydrogen is relatively simple. In 1885, Johann Balmer (1825–1898) found an empirical numerical relationship that described the set of spectral lines visible in the visual and ultraviolet part of the spectrum of hydrogen. Balmer’s equation made use of two positive integers. A few years later, Johannes Rydberg (1854–1919) generalized Balmer’s relationship for other gases that had one electron (such as singly ionized helium). No one knew why these relationships worked.

In 1913, Niels Bohr (1885–1962) published his model of the hydrogen atom that explained the relationships that Balmer and Rydberg had found. In the Bohr model, the electron orbits the nucleus in a circular orbit caused by the electrostatic attraction between the negatively charged electron and the positively charged nucleus. This much comes straight from classical physics. However, in classical physics, the orbit of an electron could have any radius, but the Bohr model imposed a restriction—the electron is constrained to orbits that have angular momentum that are integral multiples of ħ, Planck’s constant divided by 2π. This restriction has no analogue in classical physics. Furthermore, in classical physics, an accelerated charge radiates, but even though the electron in the Bohr model is continually accelerated as it orbits the nucleus, it does not radiate. Therefore, in the Bohr model an orbiting electron maintains constant energy as it orbits the nucleus. The energy of an orbiting electron can be calculated using classical physics. The orbits may be numbered with a positive integer, n. The value of n for the lowest, and hence least energetic energy, is 1, with n incrementing by one for each successive orbit. We may number the energy of each orbit E_n. An electron may discontinuously jump from a higher orbit, n = i, to a lower orbit, n = f, by emitting a photon having frequency

This final equation matched the empirical relationships of Balmer and Rydberg. Notice that the Bohr model incorporated the quantization of energy by quantizing the orbits of electrons. Why would electrons, which are particles, behave this way?

In 1924, Louis de Broglie (1892–1987) answered this question by proposing that all matter, including electrons, have a wave nature. The electrons in the Bohr model orbited with integral multiples of ħ because they constructively interfered. Any other orbit resulted in destructive interference, thus eliminating those orbits. Particles are not prone to interference this way, but waves are. Electrons were independently confirmed to have a wave nature in 1927, when Clinton Davisson (1881–1958) and Lester Germer (1896–1971) passed electrons through a double slit similar to Young’s experiment with light more than a century earlier. The electrons produced an interference pattern, indicating that they were waves. Just as Young’s experiment had shown light has a wave nature, it was demonstrated that electrons have a wave nature too. In 1925, Schrödinger incorporated de Broglie’s bold hypothesis to develop his wave equation that became the foundation of quantum mechanics. The formalism of quantum mechanics soon followed, with physicists working out the consequences of this new physics over the past century, much as mathematicians had worked out the consequences of classical mechanics for two centuries after Newton.

The Aftermath of Modern Physics

Relativity theory (both the special and general theories) and quantum mechanics were radical departures from classical physics. Together, they form the twin pillars of modern physics. The notions of absolute space and time had to be surrendered.6 Light and matter are now recognized to have both a wave and particle nature. Physicists a century ago struggled with this new physics, and some physicists continue to struggle with it today.

What does it mean for matter to have a wave nature? When one solves the Schrödinger equation for a particle, a wave function of position results. What is the medium of this wave? The answer to that question is not entirely clear. Physicists quickly came to realize that the wave function of a particle can be used to produce a probability function. If the wave function is squared, it results in a prediction of the probability of where the particle may be found. Where the probability function has a high value, the probability of finding the particle there is high. Where the probability function has a low value, the probability of finding the particle function is low. Consider the Davisson-Germer experiment. When many electrons are directed at two closely spaced apertures, the distribution of detections on the other side is an interference pattern, consistent with the electrons going through both openings, as if the electrons are waves. The solution of the Schrödinger equation for electrons passing through a double opening setup matches the observed interference pattern. Therefore, we have confidence that quantum mechanics accurately describes the behavior of electrons.

What if the experiment is rerun, this time with a detector placed immediately behind one slit or the other rather than behind both slits simultaneously? When this is done, each electron is detected individually, as if the electrons went through one slit or the other. How can this be? Doesn’t this contradict the observation of an interference pattern? Physicists have spent the past century pondering this question, and several answers to the question have arisen. The most common resolution of this paradox has become known as the Copenhagen interpretation, so named for the city where Bohr and Werner Heisenberg (1901–1976) lived when they developed it. The Copenhagen interpretation of quantum mechanics posits that prior to observing a particle, the particle exists in a state of probability occupying all possible states. It is not until the particle is observed that the wave function collapses, and the particle assumes one of the possible states. The numerical value of a physical quantity has no meaning until it is measured. If many identical particles in the same experiment (such as a double slit) are observed, the states that particles assume conform to the prediction of the interference pattern.

Many physicists find the Copenhagen interpretation unsettling. There have been many negative responses to the Copenhagen interpretation, often in the form of thought experiments. The most famous of these has become known as Schrödinger’s cat (Schrödinger was so troubled with the Copenhagen interpretation that he eventually came to express regret that he ever had anything to do with quantum mechanics). Schrödinger proposed placing a cat in a sealed container with a vial of poison gas, along with a hammer that is set to break the vial to release the gas and kill the cat. Included in the box is a subatomic particle governed by quantum mechanics that can exist in two possible states, and its state is monitored by a detector that triggers the hammer to break the glass when the particle assumes one of the two possible states. The life (or death) of the cat is now entangled with the state of the subatomic particle. Therefore, just as the subatomic particle exists in two different states simultaneously, the cat exists simultaneously in the state of being alive and being dead. This absurd situation is not resolved until the box is opened, and someone observes which state the cat is in. Presumably, the wave function of the particle did not collapse until the observation occurred, yet the cat, if alive, emerges with some memory of being in the box even though the cat was in the state of both living and being dead.

The situation gets even more absurd. Some people have suggested that in a sense the observer who opens the box now is a part of the experiment, which requires a second observer to observe the first observer to collapse the wave function. But then isn’t the second observer part of the experiment requiring yet a third observer? Or even a fourth observer, in the early steps of an infinite series? It seems we have returned to Zeno’s paradoxes (Paper 1 [Faulkner 2022a] and Paper 2 [Faulkner 2023a]). But if objects are simply sums of their parts, aren’t even macroscopic objects subject to this fuzzy world of existence in multiple states? That has prompted some physicists to ask the question whether the moon exists if no one is looking at it, such as when the moon is in its new phase. Some physicists have proposed that the universe is the ultimate quantum mechanical experiment. Since the Copenhagen interpretation of quantum mechanics requires the action of an observer to collapse the wave function, if there were no one in the universe, would the universe exist? That is, without an observer, wouldn’t the universe simultaneously be in a state of existing and not existing? This leads to the conclusion that the universe requires our existence to collapse the wave function of the universe so that the universe assumes the state of existence. This is a variation of the anthropic principle, the observation that the universe appears to be designed for our existence. Thus, the Copenhagen interpretation could be invoked to explain why we exist. If so, then there is no need for God in this view of the universe.

As I have previously argued (Faulkner 2020), the Copenhagen interpretation is a stupid answer to a stupid question. Never in the history of modern science have scientists asked what our physical theories mean. For instance, when Newton wrote his Principia, no one asked what it meant because the meaning was obvious—what Newton wrote was a very good description of how the physical world worked. No one asked what Maxwell’s four equations meant because everyone understood the four equations were a good description of how electricity and magnetism work. Even with the controversy sparked by Einstein’s two theories of relativity, none of the theories’ critics asked what the theories meant. It seems that only quantum mechanics is placed in a special category, requiring a meaning or philosophical interpretation of some sort. Quantum mechanics provides a very good description of how atomic and subatomic particles behave. Why ask for anything else? As I’ve pointed out in Paper 1 (Faulkner 2022a) and Paper 2 (Faulkner 2023a), science is good at telling us how, but it is not too keen at telling us why. The why questions are philosophical, metaphysical, and/or theological; scientists usually are not very well prepared to discuss such matters.

Waves are extended objects—they rise from a minimum to a maximum before falling back to a minimum. Where is the wave? This question is particularly problematic if the wave is a part of a series of waves, such as most waves in water or most sound waves. Since each wave is flanked by waves on either side, it is an arbitrary choice where one wave ends and another wave begins—is it at the maximum, the minimum, or at the point halfway between the maximum and minimum of a wave? If the latter, is it the point of zero amplitude where the wave is ascending or descending? Even if there is a single wave, such as with a pulsed wave or a standing wave, can one say that the wave is localized at one point? If so, isn’t it arbitrary where on the wave one chooses that point? By their nature of being spread out, waves are inherently fuzzy.

Applying this logic to quantum mechanical waves of particles, the positions of particles are inherently fuzzy. But this indeterminate nature is not limited to position alone. In 1927, Heisenberg derived the first expression of the uncertainty principle. Let Δp be the uncertainty in a particle’s momentum and let Δx be the uncertainty in a particle’s position. Then

An equivalent expression can be derived in terms of the uncertainty in the energy of a particle, ΔE, and the uncertainty in the measurement of the time of the measurement, Δt:

The uncertainty principle means that as one more precisely knows the momentum of a particle, the less precisely one knows the particles’ position. Likewise, the more precisely one knows the energy of a particle, the less precisely one knows the time of the measurement of the particle’s energy. This uncertainty only shows up in the atomic and subatomic world where quantum mechanics applies. It does not show up in the macroscopic world because ħ is so small. This is not an uncertainty of ignorance, as with the limiting precision discussed earlier in discussion of determinism. Rather, this is a fundamental uncertainty. Even if we could measure with infinite precision, this fundamental uncertainty would limit our ability to measure so precisely. Thus, modern physics has killed the determinism that Newtonian mechanics apparently had led to.

This uncertainty and many other quirky aspects of quantum mechanics are at odds with Western thinking, but they are not foreign to Asian mysticism. In 1975, the physicist Fritjof Capra wrote The Tao of Physics: An Exploration of the Parallels Between Modern Physics and Eastern Mysticism. Four years later, nonscientist Gary Zukav wrote The Dancing Wu Li Masters: An Overview of the New Physics. Both books noted parallels between eastern mysticism and quantum mechanics. Capra went on to write three more books expanding upon his ideas. While there was some criticism of Capra’s thesis, there were many who praised his work. Many physicists who were active at the time quantum mechanics was developing were aware of these parallels, though they didn’t publish on it. J. Robert Oppenheimer famously quoted from Bhagavad Ghita when the first atomic bomb was tested. Bohr reportedly was much interested in this topic, as was Heisenberg.

Modern physics has had an impact on popular culture. When general relativity was tested during the 1919 total solar eclipse, it was heralded with much press attention. The astronomer Arthur Eddington (1882–1944), who led the eclipse expedition, became the primary promoter of general relativity. This is what propelled Einstein into the pop icon that he has become. Moral relativists picked up on relativity theory to support their worldview. However, this is a misappropriation because modern relativity theory does not support the premise that “everything is relative” (Faulkner 2004, 66). To the contrary, modern relativity theory posits several absolutes, such as the invariance of the speed of light in inertial reference frames. Similarly, many references to quirky aspects of quantum mechanics are found in popular culture. Noting the dual nature of particles and waves that physicists eventually came to embrace, some practitioners of dualism have misappropriated that in support of their beliefs much as moral relativists misappropriated relativity theory.

Later Trends in Modern Science

In the second half of the twentieth century, scientists began to discuss what has become known as chaos theory. By the 1980s, chaos theory began to show up in popular culture. There are several roots of chaos theory. One route is the n-body problem briefly discussed earlier in this paper. The n-body problem cannot be solved in a closed form. One way of handling this difficulty is with perturbation theory. A step beyond perturbation is statistical studies that determine average behavior of systems and the limits of that behavior. Other statistical studies use Monte Carlo simulations to model changes in systems over time (these changes often are called “evolution,” though many times this evolution does not carry the connation about origins).

Another route to chaos theory is the study of complex systems, such as storms. Such systems have many variables of which we have incomplete knowledge. If we had complete knowledge of these variables, then our theory of how these systems operate ought to produce accurate models of their behavior. While weather models are fairly accurate in the immediate future, these models are well known to be incapable of predicting behavior at greater times into the future. This recognition has led to the famous butterfly effect. A shift in thinking occurred from the linear approach that imprecision or noise in data were not significant to the belief that these were components of the system. Soon chaos theory was expanded from the physical sciences to economics and social sciences.

Fractals, a term coined by the mathematician Benoît Mandelbrot in 1975, are used extensively in chaos theory. Fractals are geometrical figures that have the same character in the whole as they have in their parts. Snowflakes are good examples of fractals. Snowflakes assemble from the six-sided shape that ice crystals naturally have. Snowflakes begin as microscopic crystals that grow following the same pattern as the initial crystal, giving snowflakes their aesthetically pleasing symmetry. Since there is a very large (yet finite) way in which ice crystals can form, each snowflake forms and grows in a pattern that is probably unique. I say that all snowflakes are probably unique because the number of snowflakes that have formed over time is dwarfed by the number of different ways they could assemble. Obviously, this is a statistical likelihood, as it is impossible to test whether all snowflakes are indeed unique. Fractals have a myriad of applications, such as the study of coastlines and galactic structure.

Naturally, chaos theory has been enlisted to account for the origin and evolution of life. Since what appear to be chaotic trends can result in apparent complexity, many scientists assume that the same must be true of living things. But are things that appear to be chaotic truly chaotic? Physical systems, such as orbiting planets (the n-body problem) and storms, obey physical laws. There is nothing inherently chaotic in how these physical laws operate. The apparent chaos arises only because of human inability either to know all the relevant information or to possess the mathematical tools necessary for proper analysis. No structure is derived from truly random processes.

Conclusions and Further Comments

Classical physics was an integral part of the scientific revolution four centuries ago. Classical physics soon gave rise to determinism. The development of modern physics a century ago in turn gave rise to indeterminism. Not only is modern physics in conflict with classical physics, but the philosophical implications of modern physics are in tremendous conflict with Western thought, which gave rise to science as we know it. The conflict between classical and modern physics is resolved by understanding that classical mechanics is a special case, whereas quantum mechanics and general relativity are more general treatments of the physical world. In the everyday world that we experience, physical conditions are far out of the range where quantum mechanical and relativistic effects are important, so quantum mechanical and relativistic treatments morph into descriptions consistent with those of classical mechanics. This is why the effects of modern physics were hidden from man’s knowledge for so long. It is best to describe classical mechanics as an incomplete theory—correct in the bounds to which it applies but not outside those bounds. We must recognize that as impressive as quantum mechanics and general relativity are, they too are incomplete theories.

Maxwell’s unification of electricity and magnetism into a single theory had a profound impact upon how physicists view the world. In the twentieth century, physicists came to realize that there are four fundamental forces in nature:

1. Strong nuclear force
2. Electromagnetism
3. Weak nuclear force
4. Gravity

The forces are listed in order of decreasing strength. It is believed that all four fundamental forces can be unified into a single theory, much as Maxwell unified electromagnetism. In the 1960s, a theory unifying electromagnetism and the weak force was developed, and over the next two decades, many of the predictions of this theory were experimentally verified. It is now generally accepted that these two forces are unified in the electroweak force, though they usually are still listed as distinct forces, as here.

What about the other two forces? Unification of the two remaining forces with the electroweak interaction is hotly pursued by theoretical physicists. It is believed that the strong interaction will be unified with the electroweak interaction first. If done, this new force will be called the grand unified theory (GUT, for short). Because gravity is so much weaker than the other forces, it is believed that it will be the last fundamental interaction to be unified with the other fundamental forces. Such a future theory is called the theory of everything (TOE, for short).

Unification thus far is based upon a quantum mechanical approach in which forces operate over distance through the exchange of mediating particles between the particles experiencing the forces. For the strong force, the mediating particles are gluons. The electromagnetic force is mediated by the exchange of photons. The weak force is mediated by exchange of either the W⁺, W^-, or Z⁰ particles. The existence of all these particles have been verified in the lab. These ideas are a major part of the standard model of particles.

Left out of the standard model is gravity, though the way to include gravity in the standard model is sketched out. The hypothetical mediating particle for gravity is called the graviton. Though some of the properties of gravitons are believed to be known, other properties are unknown. Graviton energy is thought to be very low, making direct detection extremely difficult. But the theory is not well developed either. There are several impediments to developing the proper theory of gravitons, the chief being how to unify quantum mechanics with general relativity.

This brings up the tension between quantum mechanics and general relativity. Both seem to be true, yet they are so fundamentally different as to appear contradictory. For instance, in general relativity, gravity is mediated by the bending of space time. That is, there is no need for a mediating particle, as required by quantum mechanics. As I previously pointed out, in general relativity, gravity is not a true force. However, in quantum mechanics, gravity is a force because it requires mediation with an exchange particle. How might these two contradictory notions be reconciled in TOE? They may be reconciled in the way the particle and wave nature of everything has been reconciled—there is simply a dual nature.

Impressed with the success of Newtonian physics, in the nineteenth century, there developed an attitude among physicists that they had arrived at ultimate knowledge of the physical world. All that remained was to work out the details. By labeling a possible future theory “the theory of everything,” aren’t physicists today in their hubris committing the same error? No one knows what the future holds. There is much evidence for the reality of dark matter (Faulkner 2017). Tests for dark matter have ruled out dark matter consisting of particles that we already know about. Consequently, if dark matter is real, then it must be a form of matter that we have not yet contemplated. But the standard model of particles worked out more than a half century ago has no place for such a particle. Thus, dark matter may require a complete revision of the standard model. I seriously doubt that TOE, if it is ever elucidated and confirmed, will be the final word.

I am pessimistic about the future of science. Like Western culture, science has drifted from its foundation in a worldview that reflected biblical principles. Modern physics increasingly reflects an Eastern rather than Western worldview, even though most physicists still retain some elements of Western thinking. This is the reason many physicists f ind aspects of modern physics unsettling. Add to this the increasing assumption of naturalism among scientists, an assumption that undermines the foundation that gave rise to modern science in the first place. How should the Christian respond to this? It is best I address that question in the next and final paper in this series.

References

Barton, David. 2012. The Jefferson Lies: Exposing the Myths You’ve Always Believed about Thomas Jefferson. Nashville, Tennessee: Thomas Nelson.

Capra, Fritjof. 1975. The Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern Mysticism. Boston, Massachusetts: Shambhala.

Chapront-Tousé, M., and J. Chapront. 1983. “The Lunar Ephemeris ELP 2000.” Astronomy and Astrophysics 124 (August): 50–62.

Danny Faulkner. 2004. Universe by Design: An Explanation of Cosmology and Creation. Green Forest, Arkansas: Master Books.

Faulkner, Danny R. 2017. “The Case for Dark Matter.” Answers Research Journal 10 (March 22): 89–101. https:// answersresearchjournal.org/case-for-dark-matter/.

Faulkner, Danny R. 2020. “Quantum Mechanics and Creation: A Brief Overview.” https://answersingenesis.org/physics/quantum-mechanics-and-creation/.

Faulkner, Danny R. 2022a. “The Philosophy of Science 1: What is Science, and How is Science Done?” Answers Research Journal 15 (November 2): 359–376. https://answersresearchjournal.org/science/philosophy-science/.

Faulkner, Danny R. 2022b. “Is Newtonian Physics Outdated? What Do Flat-Earthers Say?” https://answersingenesis.org/blogs/danny-faulkner/2022/12/21/newtonian-physics-outdated-what-flat-earthers-say/.

Faulkner, Danny R. 2023a. “The Philosophy of Science 2: A Brief History of Science from the Ancient Greeks through the Middle Ages.” Answers Research Journal 16 (March 29): 155–173. https://answersresearchjournal.org/science/philosophy-science-2/.

Faulkner, Danny R. 2023b. “The Philosophy of Science 3: The Transition to Modern Science.” Answers Research Journal 16 (April 19): 189–200. https://answersresearchjournal.org/science/philosophy-science-3/.

Hutchings, David, and James C. Ungureanu. 2021. Of Popes and Unicorns: Science, Christianity, and How the Conflict Thesis Fooled the World. Oxford, United Kingdom: Oxford University Press.

Mortenson, Terry. 2004. The Great Turning Point: The Church’s Catastrophic Mistake on Geology—Before Darwin. Green Forest, Arkansas: Master Books.

Mortenson, Terry. 2007. “The History of the Development of the Geological Column.” https://answersingenesis.org/age-of-the-earth/the-history-of-the-development-of-the-geological-column/.

Robertson, Katie. 2021. “The Demons Haunting Thermodynamics.” Physics Today 74, no. 11 (November): 44–50.

Zukav, Gary. 1979. The Dancing Wu Li Masters: An Overview of the New Physics. New York, New York: William Morrow and Company.