The Philosophy of Science. 2: A Brief History of Science from the Ancient Greeks through the Middle Ages

Introduction

In my previous paper (Faulkner 2022, hereafter Paper 1), I briefly discussed the philosophy of science, what science is, and how science is done. It is difficult to discuss the philosophy of science without including some history of science. I avoided discussion of the history of science in the earlier paper because it would have greatly increased its length and likely would have detracted from my main points. I turn now in this second paper to briefly describe the history of science through the Middle Ages, taking care to implement some of the points I discussed in Paper 1. For instance, in Paper 1, I contrasted the different ways in which science can be done. I will evaluate developments in the history of science in terms of those different methodologies.

As with so many other products of the West, science as we know it dates to the ancient Greeks, so I shall pick up the story there. However, people have always practiced some form of science, even before the ancient Greeks. It is no accident that astronomy was one of the first sciences developed. Though relatively brief, George Abel’s astronomy textbook gives a good history of ancient Greek astronomy (Abel 1964). Much more detailed is the history of astronomy by Berry (1898), which has long been treated as an authority on the subject. Less known is a history of astronomy by Dreyer (1906). Much of my discussion draws from these sources.

Throughout history, most people were farmers, and agriculture is highly dependent upon weather and seasonal changes. Therefore, development of calendars is essential in knowing when to plant crops. Indeed, recognition of the passing of the seasons, and days, and years is one of the purposes of the heavenly bodies ordained Day 4 of Creation week (Genesis 1:14). A fundamental understanding of astronomy is necessary in developing calendars. There are many megalithic structures around the world with astronomical alignments that predate the ancient Greeks, the most famous being Stonehenge. Since the builders of these structures left no written records, what function(s) these structures served is only a matter of conjecture. However, building these structures obviously required some astronomical knowledge and development of calendars.

Early Ancient Greek Astronomy

Given the prehistoric roots of astronomy, it is no accident that some of the best science the ancient Greeks developed was astronomy. Ancient Middle Eastern and Asian cultures were collecting astronomical observations long before the Ancient Greeks were. So why were the ancient Greeks the first to advance astronomy as a science? According to Berry (1898, 24), the Greeks were not content to merely observe astronomical phenomena but were much more interested in enquiring into causes of those phenomena. We often fail to appreciate the difference worldview can make. While civilizations prior to the ancient Greeks had the data at their disposal to advance astronomy as a science, they lacked the prerequisite worldview that made looking at the world scientifically possible.

An example of the importance of worldview in interpreting the world is the Maya, the only pre-Columbian American civilization with a written language. The Maya Classical Period was A.D. 250–900, followed by decline. The Spanish conquered most Mayan territory by 1546, though a small Mayan civilization in the Petén Basin did not fall until 1697. Unfortunately, the Spanish destroyed nearly all Mayan documents they could find, including those that detailed Mayan astronomy and cosmology. However, beginning in the nineteenth century scholars began to study the remaining documents, which has revealed much about the Mayan culture. While it is well known that the Maya had a very sophisticated calendar that required extensive astronomical observations, Mayan cosmology is only hinted at in their records (Anonymous n.d.). It is generally surmised that the Maya thought the world was flat. However, the Maya knew about the saros cycle. Several civilizations in the Old World independently discovered the saros cycle from knowledge of the lengths of the synodic and draconic months. Such knowledge indicated that each civilization that discovered the saros cycle knew the two requirements for eclipses: the moon being at the proper phase (new for a solar eclipse and full for a lunar eclipse) and the moon near a node. From this information, it ought to be obvious that a solar eclipse occurs when the moon passes in front of the earth and a lunar eclipse happens when the earth’s shadow falls on the moon. From the observation that the shape of the earth’s shadow on the moon during lunar eclipses always is a circle easily leads to the conclusion the earth is a globe (only a sphere will consistently produce a circular shadow under these circumstances). Yet, the Maya did not reach this conclusion, or if they did, they did not think it worth mentioning. Some Old-World civilizations with knowledge of the saros cycle apparently did not reach this conclusion about the earth’s shape either, but the Greeks quickly did after learning of the saros cycle from the Babylonian civilization. The difference likely was the aforementioned worldview of the Greeks that was very different from other civilizations, including the Babylonians and Egyptians.

The primary difference was that the Greeks were far more analytical than other ancient civilizations. For instance, the Babylonians, and to a lesser extent the Egyptians, recorded extensive astronomical observations, such as positions of the moon, sun, and planets. The Babylonians were even able to make some predictions of future positions of heavenly bodies from their observations. However, the Babylonians did not seem as interested as the Greeks were in the underlying reasons for the patterns that they saw in the sky. Once the Greeks learned astronomy from the Babylonians, they began to innovate with cosmological models that exceeded anything that the Babylonians had done. Both the Egyptians and Babylonians developed mathematics, such as trigonometry and geometry, long before the Greeks, but it was the Greeks who demonstrated a passion for mathematics that permitted them to develop mathematics more fully. Without this analytical approach, the Babylonians and Egyptians may have not even noticed the circular shape of the earth’s shadow during lunar eclipses, and even if they did, they likely did not enquire as to what that implied. However, to the Greek mind, the earth’s shadow during a lunar eclipse was obvious, along with the implication that the earth is a globe. Since many ideas of the West trace back to the ancient Greeks, we identify with the worldview of the ancient Greeks, making it difficult for people in the West today to understand why other civilizations failed to make this connection about the earth’s shape.

Unlike earlier cultures in the West, the Greeks left written records. However, there are no surviving copies of works by many early Greek authors. We know of these earlier works either from mere fragments or from later sources that attributed accomplishments to them. With a few exceptions, these later accounts are generally considered reliable. A notable exception is Herodotus’ (c. 484–425 B.C.) report that Thales (c. 624/623–548/545 B.C.) accurately predicted a total solar eclipse in the early sixth century B.C. Greek cosmology in Thales’ time had not advanced to the point to be able to predict eclipses even crudely with the saros cycle,¹ let alone the precision implied by Herodotus. Therefore, modern historians of science discount Herodotus’ account of Thales’ eclipse prediction.

Speaking of Thales, he is considered the first traditional Greek philosopher, and he founded the Ionian school of philosophy. Thales is also credited with being the first to develop what we would recognize as a scientific way of looking at the world, so he is often called the father of science. Prior to Thales, the Greeks generally used mythology to explain the world. Rather than the world being random and haphazard, which is what mythological explanations generally result in, Thales saw unity and regularity in natural phenomena. One should not conclude that the ancient Greeks immediately abandoned their mythology through the influence of Thales. Rather, mythology and what we would recognize as a scientific approach to explain the world continued side by side for centuries. However, trust in the explanatory power of mythology gradually waned. This is a good examples of Kuhn’s paradigm shift discussed in Paper 1 (Faulkner 2022).

Thales made contributions to geometry and astronomy. Thales knew of the ecliptic, the apparent path of the sun through the stars each year. Consequently, Thales measured the length of the year and determined when the equinoxes and solstices occurred. In Thales’ cosmology, the earth was a flat disk. The stars (including the planets), sun, and moon orbited the earth each day, allowing astronomical objects to pass under the earth as they set and rose. About cosmogony, Thales taught that water was the primordial matter of earth’s creation. This is consistent with biblical cosmogony (Genesis 1:2; Psalm 24:1–2; Psalm 136:6; 2 Peter 3:5). Could Thales have been influenced by a vestige of the true Creation account that was otherwise lost to his people?

What type of science did Thales engage in? He used observations to learn about the ecliptic. He used metrology to measure the year’s length and when the times of equinoxes and solstices were. Thales used abductive reasoning to develop his cosmology. There is no evidence that Thales tested his cosmology, so he did not use inductive reasoning in studying his cosmology. Therefore, Thales’ cosmology had explanatory power but no predictive power.

Anaximander (c. 610–546 B.C.) succeeded his master, Thales. Anaximander’s cosmology had the height of the earth’s flat disk one-third its diameter. The known world of Europe, Asia, and Africa surrounding the Mediterranean Sea was bordered by a vast ocean that extended to the edge of the disk. Anaximander may have been the first to conceive of the celestial sphere, a large distant shell surrounding the earth. Beyond his celestial sphere was fire. Holes in the celestial sphere admitted light of the fire toward the earth. The light seen through these holes were the sun, moon, stars, and planets. The daily rotation of the celestial sphere caused astronomical bodies to rise and set. Soon after Anaximander, his model was modified so that astronomical bodies were attached to the celestial sphere. The celestial sphere remained in Western cosmology for two millennia. Anaximander speculated on the relative distances of the astronomical bodies. Most of Anaximander’s approach could be described as abductive reasoning. He refined and built upon what Thales had built, but as before, there were no tests of his model.

Pythagoras (c. 570–495 B.C.) was also from the Ionian school, though he eventually left Ionia and established his own school in modern day Crotone in southern Italy. Famous for his developments in mathematics and music, Pythagoras also is credited with being the first to argue that the earth is spherical. Unfortunately, we do not have a record of Pythagoras’ reasons for believing the earth is spherical. Pythagoras also believed that the sun and moon are spherical, so some have speculated that Pythagoras concluded that the earth is a globe by analogy. Pythagoras appears to have similarly reasoned that other astronomical bodies, the stars and planets, are spherical by analogy to the sun and moon. However, it may be that Pythagoras simply reasoned on aesthetic grounds that since the circle is the perfect two-dimensional object and the sphere is the perfect three-dimensional object, then the earth must be spherical. Since we do not know the reason Pythagoras opined the earth is a globe, it is not possible to assess what type of science, if any, that he employed to reach this conclusion. Pythagoras was well respected in his time and thereafter, so his influence on Western thought is immense. The fact that the earth is a globe appears to have been rapidly embraced by ancient Greek thought after Pythagoras.

Among the Pythagoreans, Philolaus (c. 470–385 B.C.) is credited as the first to suggest the earth is in motion. Philolaus had the earth orbit a central fire, with a counter-earth orbiting the central fire exactly 180° opposite the earth, so the counter-earth could not be seen from earth. The earth orbited the central fire once a day, with the Greek world on the opposite side of the spherical earth from the central fire, preventing anyone he knew from seeing the central fire. The other astronomical bodies orbited the central fire as well. Why did Philolaus concoct this system? It may be that, true to the Pythagorean mystical belief in numbers, Philolaus thought ten was the perfect number for such a cosmology. There were seven moving objects (sun, moon, and five naked-eye planets), plus the earth, requiring two more objects, the central fire and the counter earth. Few people would recognize any science in this, but some have suggested this was the first step on the road to heliocentrism. Keep in mind that this is geokinetism (as opposed to geocentrism), not heliocentrism.² Two other Pythagoreans, Hicetas (c. 400–335 B.C.) and Ecphantus (fourth century), thought the daily rotation of the sun, moon, and stars were due to the earth rotating on its axis, though they likely believed the earth was the center of the universe and hence did not orbit anything else.

The Pythagorean school developed the idea that there were eight concentric spheres, one for the stars, and one each for the seven moving objects, the sun, moon, and five naked-eye planets. As these spheres rotated independently, friction between them produced the music of the spheres that only the most gifted could hear. This notion persisted for two millennia. It is not clear if Pythagoras originated this or if it was developed by his followers. Though not of the Pythagorean school, Eudoxus of Cnidus (c. 408–355 B.C.) appears to have built upon it. Eudoxus proposed a system of nested, moving spheres to explain the motion of the sun, moon, and planets. This system required a total of 27 spheres to work. A few decades later, Callippus (c. 370–300 B.C.) improved Eudoxus’ system by adding an additional seven spheres. Since these schemes attempted to explain the observed motions of heavenly bodies, they are examples of abductive reasoning. Since we don’t have complete information about these two models, it is not clear how predictive these models were. These works were precursors of Ptolemy’s model nearly five centuries later.

Aristotle

Aristotle (384–322 B.C.) epitomized ancient Greek science. Aristotle discussed many topics in nature, but since I am concentrating on astronomy, for now I shall focus on Aristotle’s teachings on astronomy. Aristotle correctly inferred that the cause of lunar phases is the changing amount of the moon’s lit half we see throughout the moon’s monthly orbit of the earth. This required understanding that the moon is a globe that is not self-luminous but reflects the sun’s light. Aristotle also understood the cause of eclipses. It is likely that the causes of eclipses and lunar phases were already known to the ancient Greeks, but Aristotle is the earliest source we have that discusses the causes of eclipses and lunar phases.

In his On the Heavens, written about 350 B.C., Aristotle taught that the earth is a globe. Again, Aristotle did not introduce the idea of a spherical earth. Rather, Aristotle built on that knowledge, and gave four reasons for that belief. Two of these arguments are very good, so I use them today. One argument is to note that during lunar eclipses, the earth’s shadow is always circular. A flat, circular earth could cast a circular shadow, but only when a lunar eclipse happened at midnight in early winter. Given the circumstances of a lunar eclipse, the only shape that consistently casts a circular shadow regardless of its orientation is a sphere. The other argument involves the appearance of stars as one travels north or south on the earth. From southern locations, stars due south in the sky appear higher than they do at northern locations. Indeed, some stars that are perpetually below the southern horizon at more northern locations are above the southern horizon farther south. Meanwhile, stars in the northern part of the sky appear lower in the sky at southern locations than at northern locations. Likewise, stars that are above the northern horizon at northern locations may be below the northern horizon at southern locations. This is best explained by the earth being curved in the north-south direction. This is not direct evidence that the earth is a globe. For instance, the earth could be curved north-south but not curved east-west, resulting in a shape like a speedbump. However, there is no record of an ancient speedbump-shaped cosmology. A spherical earth is the simplest explanation for this observation.

A third argument that Aristotle had for the earth’s curvature is from analogy with the moon. The moon appears round in the sky, but what we see is two-dimensional. At the very least, the moon must be circular, but what is the moon’s shape in our line of sight? The moon’s terminator, the division between light and dark on the moon, is generally curved (the terminator is straight only at the quarter phases, when the moon appears half lit). Understanding the cause of lunar phases, the curved terminator indicates that the moon is curved in our line of sight, making the moon a sphere. The sun also appears circular, but is it two-dimensional round (a circle) or three-dimensional round (a sphere)? Aristotle lacked information to conclude the sun’s shape in our line of sight, but he thought the sun was a globe as the moon is. As mentioned before, this conclusion is consistent with the ancient Greeks’ concept of perfection in the heavens and the belief that a sphere is the perfect shape. By analogy, Aristotle reasoned that the earth must be a globe too. This is a weak argument because it requires assuming that the earth is somehow similar to the moon and sun. While this turns out to be a correct assumption and may seem obvious to people today, it was an assumption on Aristotle’s part.

What sort of reasoning did Aristotle use? Much of his reasoning was abductive. This is the case with the conclusion he reached about eclipses and lunar phases, as well as his first two reasons for the earth’s spherical shape. In each of these cases, Aristotle reached the most probable explanation for what he observed. His third argument for the earth’s spherical shape is more of a deductive approach. It took this form:

1. The earth is like the moon;
2. The moon is spherical;
3. Therefore, the earth is spherical.

If the two premises are true, then the conclusion is true. Aristotle arrived at the minor premise using abductive reasoning, but he assumed the major premise as being reasonable. We may question the first premise. It is virtually undeniable that the earth and moon have some similarities, but it is abundantly clear that they have differences as well. Therefore, how can one be sure that the characteristic raised in the minor premise (being spherical) is a trait that the earth and moon share?

As discussed in Paper 1 (Faulkner 2022), some people are fixated upon experimentation being the only methodology of science. If that is one’s standard for science, then Aristotle did not engage in scientific reasoning. But since very little of astronomy is based upon experiments, then this attitude results in the conclusion that astronomy is not a science, along with other disciplines that are generally recognized as sciences. The fact that most people, including scientists, consider astronomy and these other fields to be sciences exposes the error of a philosophy that demands an exclusively experimental approach to science. As argued in Paper 1 (Faulkner 2022), operational science, properly understood, is the drawing of inferences about how the natural world operates based upon empirical data. With this broader, proper understanding of science, Aristotle clearly engaged in scientific reasoning to reach his conclusions.

Aristotle’s influence on the opinions of those in the West about the shape of the earth was immense. While there were a few mentions of the earth being a globe prior to Aristotle, his writing on the earth’s shape in On the Heavens (c. 350 B.C.) is the earliest clear primary source on the subject. After Aristotle, there was widespread agreement of scientists in Western antiquity that the earth is spherical. Given the general lack of primary sources in the West earlier than the time of Aristotle, the understanding that the earth is a globe was probably widespread among ancient Greeks prior to Aristotle’s On the Heavens.

Measurements of the Earth’s Size

Furthermore, Aristotle commented on the earth’s size, for he wrote that

those among the mathematicians who attempt to calculate the extent of the circumference maintain that it is about 400,000 stadia, from which it follows that the bulk of the earth must not only be spherical, but not large in comparison with the size of the other stars. (Dreyer 1906, 118)

There was more than one stadium in use. The stadium by which Aristotle most likely expressed the earth’s circumference results in an earth diameter of about 12,500 miles, 58% larger than the correct value. It is not known who these mathematicians were or what method they used to measure the earth’s size. It is likely that they used a method similar to that of Eratosthenes, who measured the earth’s size around 200 B.C.

Eratosthenes (c. 276–195/194 B.C.) lived in Alexandria, working at the famous Great Library there. Eratosthenes was aware that at local noon on the June solstice, the bottom of a deep well in the city of Syene in southern Egypt (near modern-day Aswan) was briefly bathed in sunlight and thus could be seen. Whether Eratosthenes knew this from personal experience or from the testimony of others is not clear. Normally, the bottom of a deep well is not visible because it is perpetually in shade. Being situated on the Tropic of Cancer, it is possible to see the bottom of a deep well in Syene, but only at noon on the June solstice. Eratosthenes knew such a thing wasn’t possible in Alexandria because, being outside the tropics, the sun is never directly overhead there. Eratosthenes lived a century and a half after Aristotle, by which time it was widely known in the Greek world that the earth is a globe and that the sun is at a great distance from the earth compared to the earth’s size. Therefore, the difference in the sun’s altitude between Alexandria and Syene was a consequence of the earth being spherical rather than a parallax effect due to observing the sun at two different locations. Furthermore, it was possible to make use of this observation to measure the earth’s size.

In Alexandria, Eratosthenes constructed a gnomon (a vertical column to cast the sun’s shadow on a horizontal surface). At noon on the June solstice, Eratosthenes measured the length of the gnomon’s shadow. From the known height of the gnomon, it was a straightforward application of basic trigonometry to find the zenith distance of the sun, the angle the sun made with the vertical. Fig. 1 illustrates the method. Eratosthenes found that the sun’s zenith distance was 1/50 of a circle, about 7.2°. From geometry, one can readily see that this angle is the same as the difference in latitude between Alexandria and Syene. Eratosthenes reasoned that the linear north-south distance between the two cities is also 1/50 of the earth’s circumference, so dividing the known distance between the two cities (as the father of geography, Eratosthenes had commissioned much surveying and mapmaking of Egypt) by this fraction yielded the earth’s circumference. Division by 2π produced the earth’s radius. Like Aristotle, Eratosthenes expressed his result in stadia. If Eratosthenes used the more commonly used stadium, his answer was 20% too great. However, if he used the less commonly used stadium, his answer was off by only an astonishing ½%.

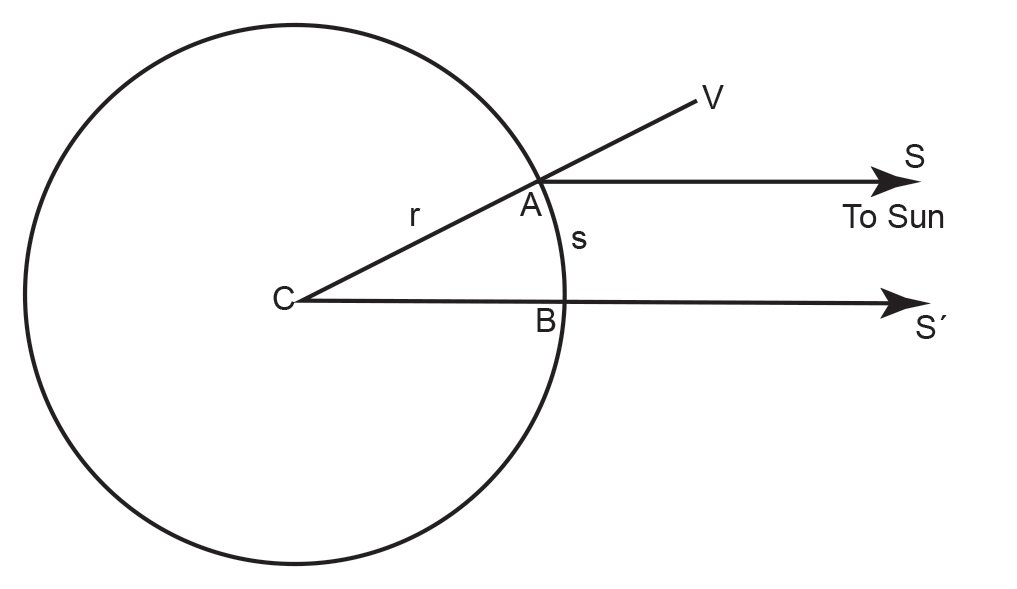
Fig. 1. Eratosthenes’ method of measuring the earth’s size. The angles VAS and ACB are the same. Eratosthenes measured the former angle to be 1/50 of a circle, and the arclength BA is 1/50 of the earth’s circumference. Therefore, multiplying the measured distance between points B and A on the earth by 50 yields the earth’s circumference.

A century later, Posidonius (c. 135–51 B.C.) used a different method to measure the earth’s size. Posidonius observed that where he lived on the island of Rhodes, the bright star Canopus was visible just on the southern horizon, never rising above the horizon. On the other hand, when Posidonius traveled to Alexandria a few hundred miles to the south, Canopus was a few degrees above the southern horizon. Realizing this too was a consequence of the earth being a globe, Posidonius divided what he thought was the distance between the two locations by the altitude of Canopus (the angle it made with the horizontal, expressed as a fraction of a circle) to obtain the earth’s circumference. As with Aristotle and Eratosthenes before him, there is uncertainty about which stadium Posidonius used, so there is some doubt as to the exact radius for the earth Posidonius found.

Unlike Aristotle, no intact works of either Eratosthenes or Posidonius survive. We know of their work through later, secondary sources. For instance, the earliest extant mention of Eratosthenes’ result is from several centuries after Eratosthenes lived. This has added confusion about the exact size of the earth that either man obtained. While Eratosthenes’ measurement is better known today, that has not always been the case. In the first century, Pliny the Elder (A.D. 23/24–79) mentioned Posidonius as one of his sources and described his method of measuring the earth’s size. In the second century, Ptolemy included a lower value of Posidonius’ result in his Almagest (1984). It was this one-third too small size of the earth that Christopher Columbus used to argue that India was not that far west of Europe. While Eratosthenes’ measurement has been known since antiquity, it is only in the past couple of centuries that Eratosthenes’ measurement received more attention than Posidonius’ measurement.

What kind of science did Eratosthenes and Posidonius employ? It certainly wasn’t experimental science. Nor did they use inductive or abductive reasoning. Rather, building upon what was already known, these two men engaged in metrology, measuring the properties of natural things—in this case, the earth’s size. As pointed out in Paper 1 (Faulkner 2022), this is a legitimate type of scientific research.

Measuring the Sizes of the Sun and Moon, Development of Spherical Astronomy

Between Aristotle and Eratosthenes was Aristarchus of Samos (c. 310–330 B.C.). Aristarchus attempted to measure the distances and sizes of the sun and moon in terms of the earth’s size. Aristarchus made three assumptions:

1. The moon’s orbit is circular;
2. The moon moves on its orbit at a uniform rate;
3. The sun is farther from the earth than the moon is, but the sun is sufficiently close so that its rays reach the first quarter moon and the third quarter moon from slightly different directions.

The first two assumptions are not strictly true but are approximately true. The third assumption is technically true but practically speaking is not true. What I mean by that is that the sun is far enough away (400 times the moon’s distance) that the difference in the direction of sunlight on either side of the moon’s orbit is too small for Aristarchus to have made meaningful measurements. Even today such a measurement would be difficult, if possible at all. With these assumptions, Aristarchus reasoned that the distance along the moon’s orbit from first to third quarter is greater than the distance between third and first quarter (see fig. 2). With assumptions 1 and 2, these different distances would be in direct proportion to the different times it takes the moon to pass from the first quarter to the third quarter and from the third quarter to the first quarter. Aristarchus precisely observed when he thought the respective quarter phases occurred, and from the pair of time intervals was able to construct the two triangles as shown in fig. 2. Aristarchus concluded that the sun was 18–20 times farther away than the moon is. This is off by a factor of 20, but it was the first attempt to measure the relative distances of the sun and moon.

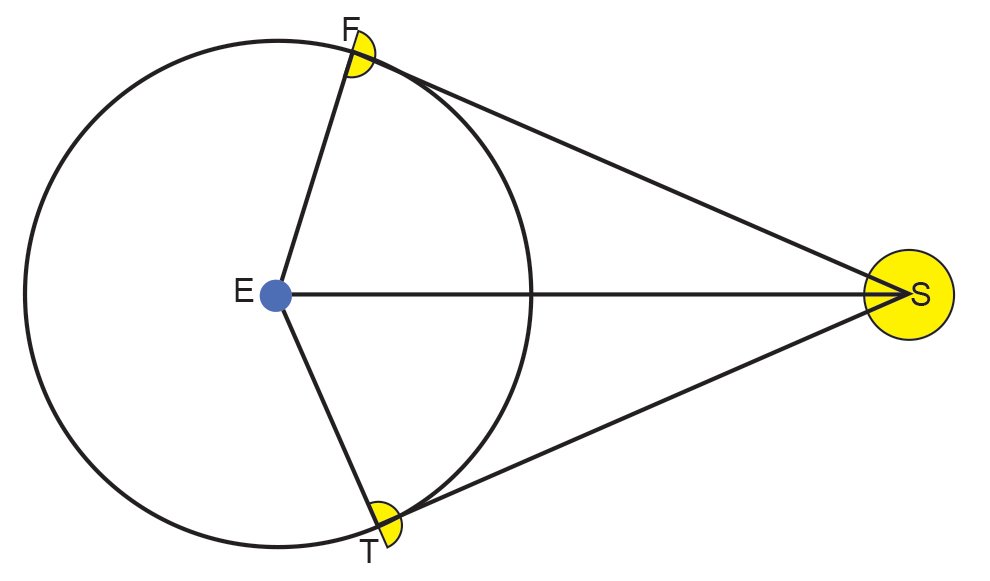
Fig. 2. Aristarchus’ method for finding the relative distances of the moon and sun. The blue circle at point E represents the earth, and the yellow circle at point S represents the sun. First quarter moon is at point F, and third quarter moon is at point T. Since the rays from the sun are tangent to the moon’s orbit at the quarter phases, the angles at points F and T are 90°. Aristarchus found that it took less time for the moon to travel CCW from point T to point F than it took to travel CCW from point F to point T. Assuming the moon moved at a constant rate in its orbit, Aristarchus knew the two arclengths. From geometric construction, Aristarchus was able to determine the relative distances of the moon and sun.

Aristarchus also was able to measure the sizes of the sun and moon relative to the earth. He started with the observation that the sun and moon have the same angular diameter.³ Since Aristarchus determined the sun is 20 times farther from the earth than the moon is, then the sun must be about 20 times larger than the moon. Aristarchus also observed that during a lunar eclipse, the earth’s umbra (shadow) at the moon’s distance from earth appears around 8/3 the moon’s diameter. From this information, Aristarchus used geometric construction to determine that the moon is approximately 1/3 the earth’s size, and the sun is about seven times the earth’s size. Combining with the other information, Aristarchus concluded that the moon’s distance is about 10 times the earth’s diameter, and the sun’s distance is 200 times the earth’s diameter. Aristarchus’ size for the moon is slightly larger than the moon’s true diameter, but his distances for the sun and moon are far too low.

Aristarchus taught that the earth orbited the sun each year. This is the earliest clear record of anyone proposing such a thing, so Aristarchus is considered the father of the heliocentric theory. We do not know Aristarchus’ reasons for his heliocentrism. It is likely that given the large size of the sun, it made more sense for the sun to be the center of the solar system rather than the much smaller earth. I shall return below to discussion of the geocentric and heliocentric models in antiquity.

What sort of reasoning did Aristarchus employ? He did not conduct any experiment in which he manipulated an independent variable. Rather, Aristarchus performed observations of the appearance and movement of the moon and sun to measure their relative sizes and distances. Therefore, much of his work was metrology rather than any formal inductive or abductive reasoning. Aristarchus’ conclusion about heliocentrism could perhaps be best described as being deductive.

Known as the father of geometry, Euclid flourished around 300 B.C. While Euclid did not invent geometry, Euclid’s great contribution was his Euclid’s Elements (1926), in which he collected and laid out what was already known about geometry in a logical, concise manner. However, Euclid completed other works, such as Phaenomena, a treatise on spherical geometry. Again, Euclid did not invent spherical geometry,⁴ but credit goes to him for organizing spherical geometry into the subdiscipline of math that it is. Being on a spherical surface, spherical geometry is non-Euclidian geometry. Spherical geometry, and especially spherical trigonometry, is very useful in expressing separations of celestial objects in the sky and solving problems involving celestial objects, such as determining the times of sunrise and sunset. While Euclid did not make any contributions to astronomy per se, his development of spherical geometry provided a very valuable mathematical tool for ancient Greek astronomers.

Hipparchus

The most important astronomer among the ancient Greeks was the second century astronomer Hipparchus (c. 190–c. 120 B.C.). Often called the father of astronomy, Hipparchus made many important contributions to astronomy. Unfortunately, Hipparchus’ only work to survive is his Commentary on the Phaenomena of Eudoxus and Aratus (Faulkner 2013a). This is a pity because this probably is the least significant of Hipparchus’ works. Consequently, most of what we know about Hipparchus’ work comes from many secondary sources, such as Strabo and Pliny the Elder in the first century and Ptolemy in the second century A.D.

Hipparchus carried out many observations from his observatory on the island of Rhodes. This required construction of instruments he used to accurately measure the positions of the stars, planets, the moon, and the sun. But more importantly, Hipparchus compared his observations to those of Timocharis and Aristyllus, who worked in Alexandria in the third century B.C. This allowed Hipparchus to make some of his most significant discoveries. Hipparchus compiled a star catalog with about a thousand entries. For each star, he recorded its position in the sky along with an estimate of how bright it is. To express the latter, Hipparchus developed the system of apparent magnitude, a system that astronomers still use after more than two millennia. Alas, Hipparchus’ star catalog was lost, but shortly before this paper went to press, discovery of a portion of Hipparchus’ famous star catalog came to light (Gysembergh, Williams, and Zingg 2022). It reveals that Hipparchus’ star catalog had more precise star positions than Ptolemy’s later catalog.

For a long time, it was assumed that, like Ptolemy two centuries later, Hipparchus used ecliptic coordinates to record the positions of the stars in his catalog. However, the newly discovered manuscript mentioned above shows that Hipparchus used equatorial coordinates.⁵ Ecliptic latitude is measured with respect to the plane of the ecliptic, with the range of –90° and +90°. Ecliptic longitude is measured eastward from the vernal equinox, with the range of 0° to 360°. Whatever coordinates one may use, it is relatively easy to transform from one system to the other. When Hipparchus compared his measurements to those measured by Timocharis a century and a half earlier, he found a shift of 2° in ecliptic longitude. However, there was no change in the ecliptic latitudes of those stars. Hipparchus concluded that the equinoxes (the intersections of the equator and ecliptic) gradually slide along the ecliptic. We call this effect the precession of the equinoxes (Faulkner 2013b). The ecliptic had not moved, but rather the celestial equator had moved through the stars. Consequently, the celestial poles, which are perpendicular to the celestial equator, move through the stars too. The celestial poles are the two points around which the stars appear to spin each sidereal day. Currently, Polaris is within ¾° of the north celestial pole, so Polaris hardly appears to move at all, making it the pole star. However, in antiquity, Polaris was not a pole star (the name Polaris goes back only a few centuries).

Hipparchus reattempted Aristarchus’ method of finding the moon’s distance. He determined that the moon is 29½ earth diameters from the earth. This is amazingly close to the correct value of 30. This value would remain the accepted distance to the moon until Tycho Brahe slightly improved upon it more than 17 centuries later. Hipparchus continued to refine measurements. For instance, Hipparchus determined the length of the year to within six minutes of the correct value. But Hipparchus also performed error analysis to conclude that his answer could not be off by more than 15 minutes. From his careful observations of the positions of the sun and moon, Hipparchus developed a method of predicting the sun’s position with at least the precision of measurements then possible. Hipparchus was able to calculate the position of the moon nearly as accurately. From this information, Hipparchus was able to predict lunar eclipses to within an hour or so. Hipparchus also made a major advancement in predicting roughly where on earth a solar eclipse might be visible. This had eluded earlier astronomers.

Hipparchus also made major advancements in design and construction of instruments to measure positions of astronomical objects as well as angles in the sky. To interpret his data, Hipparchus either invented or made innovations in plane and spherical trigonometry. Like most other Greek scientists of the time, Hipparchus was a geocentrist, and he thought it most likely that the sun moved on a circle at a uniform rate. However, Hipparchus was aware that the sun did not appear to move at a uniform rate throughout the year. He solved this problem by proposing the sun moved at a uniform rate on a circle that was not centered on the earth. An off-center circle such as this is called an eccentric. An eccentric is a good approximation to the elliptical shape of planetary orbits. If the sun moved uniformly on an eccentric, it would appear to move most quickly when nearest the earth and most slowly when most distant from the sun, much as what one observes with elliptical orbits. From the observed nonuniform apparent motion of the sun, Hipparchus was able to figure out when perihelion, the smallest distance between the earth and sun, was. Hipparchus realized that he could match the sun’s motion with an epicycle, but he thought the use of the eccentric was better. More than two centuries later, Ptolemy made use of these innovations in his model.

Fitting the moon’s motion around the earth proved to be more difficult. Hipparchus was able to fit the moon’s orbit with an eccentric, but unlike the sun, Hipparchus found that the moon’s eccentric in turn orbited the earth over nine years. Furthermore, Hipparchus measured the 5° tilt of the moon’s orbit to the ecliptic, and he found that the nodes (the two intersections of the moon’s orbit with the ecliptic) precess with a 19-year period. Thus, Hipparchus was the first to discover the moon’s apsidal and nodal precession.

What kind of science did Hipparchus employ? With his star catalog, and measurements of the positions of the sun and moon, from which he learned much about the moon’s orbit and the length of the year and the seasons, much of Hipparchus’ work was in metrology. These measurements proved invaluable for later astronomers. But Hipparchus also developed some models of the motions of the sun and moon. Later astronomers built upon these models.

Ptolemy

Working in the early second century A.D., Claudius Ptolemy (c. A.D. 100–c. 170) was the final word in ancient Greek astronomy. His greatest contribution is a 13-volume work that he called the Syntaxis but is usually known today as the Almagest. The name change came from the history of this work. Originally written in Greek, Ptolemy’s book virtually disappeared in western Europe in the early Middle Ages. Meanwhile, it remained in use in the remains of the eastern Roman Empire. In the wake of the Muslim Conquest in the seventh and eighth centuries, Arab astronomers encountered works of the ancient Greeks, including Ptolemy. They were much impressed with Ptolemy’s work, so they translated it into Arabic, calling it Al Magisti, meaning “the greatest” in Arabic (we get our word “majestic” from the same root). Read and used widely in the Arab world, the Almagest made its way back into the West a few centuries later, where it was translated from Arabic into several European languages. Along the way, the Arabic title was transliterated into Latin and finally into English as Almagest. Consequently, many late medieval manuscripts of the Almagest survive. Textual criticism reveals that we have something very close to the original autograph.

What about the Almagest so impressed medieval Arab astronomers? Ptolemy devised a clever geometric method of predicting the motion of the five naked-eye planets. While planetary orbits are relatively simple, the motions of the planets that we observe are not. The problem is that we observe the other planets from the earth, which is also orbiting the sun. Therefore, the observed motion of the planets is a combination of our motion and their motion around the sun. Most of the time, the planets appear to move eastward near the ecliptic. We call this direct, or prograde, motion. However, from time to time, the planets reverse direction and move westward along the ecliptic, in what we call indirect, or retrograde motion.

What causes retrograde motion? In the heliocentric model it is easy enough to understand. Superior planets are planets with orbits larger than the earth’s orbit. Among the five naked-eye planets, the superior planets are Mars, Jupiter, and Saturn. Since their orbits are larger than earth’s orbit, superior planets must travel a greater distance than earth does to complete one circuit around the sun. Furthermore, since superior planets are farther from the sun, they also move more slowly in their orbits. Consequently, the earth overtakes and passes superior planets when they are near opposition, the point where superior planets appear opposite the sun in our sky. When you overtake or pass a vehicle on a highway, the other vehicle appears to move backward even though it is moving forward the entire time. Similarly, superior planets undergo retrograde motion as we overtake them when they are near opposition (see fig. 3). A similar thing happens with inferior planets, planets with orbits smaller than earth’s orbit (Mercury and Venus), except this time it is the inferior planet, moving in a faster, smaller orbit, that overtakes the earth, producing retrograde motion of inferior planets.

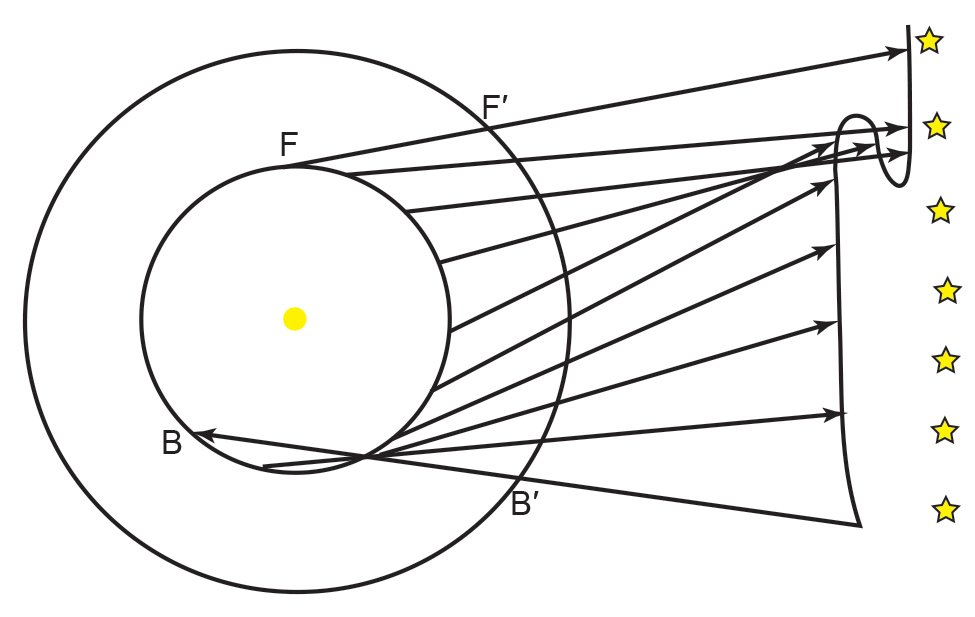
Fig. 3. How retrograde motion occurs in the heliocentric model. The yellow circle represents the sun. The smaller black circle represents the earth’s orbit, and the larger black circle represents the orbit of a superior planet. Beginning at points B and B′, the two planets move CCW toward points F and F′. Since the earth is moving more quickly on a smaller orbit, it overtakes the other planet. The series of straight lines extended to the right illustrate the apparent motion from earth that the other planet undergoes against a backdrop of stars.

As I said, it is easy enough to comprehend what is going on within the heliocentric model, but how can one explain this in a geocentric model? One could hypothesize that planets just change speed and direction in their motions around the earth. However, that would violate the concept of perfection in the heavens, with heavenly bodies required to move on circles at uniform rates. Furthermore, such a conjecture has no predictive power. Hipparchus and others had already offered suggestions of how to explain retrograde motion within a geocentric model while preserving some semblance of heavenly perfection. We don’t know if Ptolemy was the originator of what has become called the Ptolemaic model. If Ptolemy did not propose the model outright, he does deserve credit for codifying it and writing it in complete detail that survives today in many manuscripts. For now, I will assume that most, if not all, of the Ptolemaic model was conceived by Ptolemy, building on the works of his predecessors, of course.

The first problem that Ptolemy had to solve was retrograde motion. He did this by invoking motion on two circles, one larger and one smaller for each planet (see fig. 4). A planet moved at a uniform rate along the smaller circle, called an epicycle. The center of the epicycle in turn moved at a uniform rate on the larger circle, called the deferent. The original intent was to have all seven deferents (one for each of the five naked eye planets and one each for the sun and moon) centered on the earth. By adjusting the sizes of the epicycles and deferents and the speeds of the planets on their epicycles and the speeds of their epicycles on their deferents, Ptolemy had much success in fitting the observed motions of the planets.

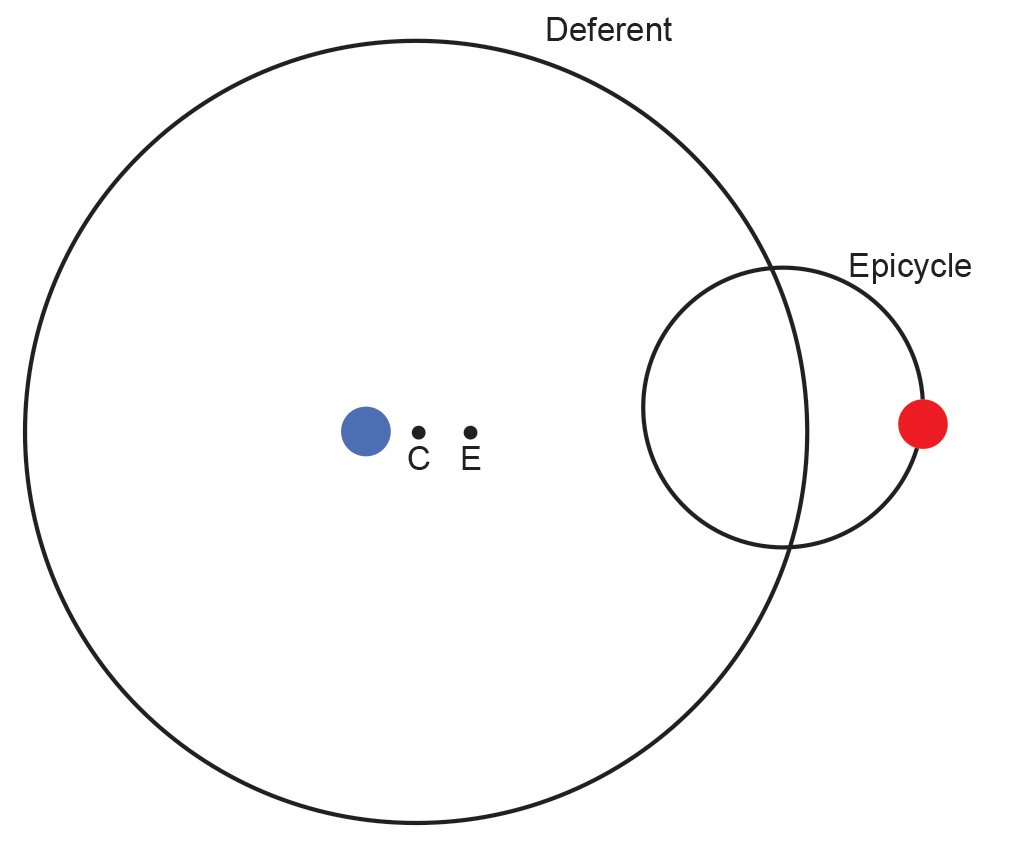
Fig. 4. The Ptolemaic explanation for retrograde motion. The blue dot represents the earth, and the red dot represents another planet. That planet moves along the epicycle at a uniform rate, while the epicycle moves along the deferent at a uniform rate around the equant at point E. Point C is the center of the deferent. These two simultaneous motions produces retrograde motion each time the planet passes on the epicycle closest to earth.

However, an exact fit required additional adjustments. For instance, the five naked-eye planets and the moon bob up and down slightly with respect to the ecliptic. Today we would say this is due to their orbits being inclined to the ecliptic. Ptolemy described this motion with an additional smaller epicycle for the moon and each planet. These smaller epicycles were in a plane perpendicular to the plane of the original epicycles.

But further refinements were necessary because strictly uniform motion centered on the earth was not sufficient to fully explain planetary motion. Ptolemy found that a better fit resulted when he slightly displaced the deferent of each planet from being centered on the earth. This is similar to Hipparchus’ small correction. Ptolemy also found that the uniform motion of the epicycles around either the centers of each deferent or the earth was not a good match to what was observed. Rather, the best match was found when each planet’s epicycle orbited at a uniform rate with respect to its equant. The equant of a deferent is the point colinear with earth and the center of the deferent, but on the side of the center opposite the earth. With these adjustments, the Ptolemaic model worked very well to describe planetary motion.

Why were these latter two refinements necessary? As we shall see in the next paper, the first adjustment of moving the earth off center was necessitated by the fact that planetary orbits are ellipses, with the center of motion being one focus of the ellipses. This is Kepler’s first law of planetary motion. Since the planets’ orbits are low-eccentricity ellipses, a good fit can be obtained by approximating the true situation with off-centered circles. The second adjustment is because planets do not orbit at uniform rates, but instead move most quickly when at perihelion (the closest approach to the sun) and most slowly when at aphelion (when most distant from the sun). Kepler’s second law of planetary motion expresses this fact in a very precise way. Therefore, Ptolemy was approximating Kepler’s description of planetary motion 15 centuries before Kepler.

Notice that these refinements were a retreat from the starting assumptions of the Ptolemaic model: uniform motion on circles centered on the earth (and hence the Ptolemaic model was not strictly geocentric). That didn’t seem to matter to many people. All that mattered was that the Ptolemaic model did a good job of explaining planetary motion, and it could be used to predict planetary positions far into the future with confidence, as well as into the past. That is, the Ptolemaic model had both explanatory power and predictive power, the hallmarks of a good theory, as pointed out in Paper 1 (Faulkner 2022). This power of the Ptolemaic model accounts for the preservation of the Almagest.

Until about four centuries ago, astrology was a seriously considered theory. The practice of astrology required the ability to predict planetary positions into the past and future, and the Ptolemaic model was the only theory that could do this. While astrology is false and is something Christians ought to avoid, it is good for us today that this motivation likely preserved the Almagest, for it contained far more than the Ptolemaic model. Ptolemy also included discussion of much of earlier Greek astronomy, giving us information about that history we would not otherwise know. The Almagest also contains a star catalog with 1,022 entries. There were earlier star catalogs such as that of Hipparchus, but none of them survive. Ptolemy’s catalog is arranged according to the 48 recognized constellations of the time. For each star, its brightness, position in its respective constellation, and ecliptic coordinates were listed. This allows us to unambiguously identify most stars in the catalog, as well as to accurately know how the Greeks pictured each constellation. The positions of the stars provided a baseline for measuring the rate of the precession of the equinoxes as well as searching for high proper motion stars.

Over much of the ensuing two millennia, it was assumed that Ptolemy did most of the work in the Almagest himself. However, over the past half century, there has been some debate among historians of astronomy about whether Ptolemy measured much of anything himself. Some historians have claimed that Ptolemy copied much of his work, such as his star catalog, from earlier sources and merely made some updates to the previous work. That reasoning calls into question whether the Ptolemaic model was truly Ptolemy’s work. At the very least, one can conclude that even if Ptolemy was more of a chronicler than an innovator, his recording in one place virtually all ancient Greek astronomical knowledge was a major accomplishment.

How can we categorize the scientific work of Ptolemy? The Almagest contains important information about the construction and use of astronomical instruments of the time. Ptolemy provided measurements (whether he made the measurements himself). Both these are significant contributions to metrology, which is an important part of science. However, Ptolemy is best remembered for his geocentric model, which best fits in the category of abductive reasoning. In terms of longevity (15 centuries), the Ptolemaic model probably is the most successful scientific theory in history. Since science is an attempt to understand the natural world and models frequently are part of that process, Ptolemy should be regarded as an outstanding scientist.

Before moving on, I ought to discuss how Ptolemy may have viewed his model and thus how he may have expected others to view his model. Mathematics is very important in science. The more quantitative a science is, the more robust that science is likely to be. To the ancient Greeks, geometry was the most advanced mathematics. So naturally, Greeks often expressed their scientific ideas in terms of geometry. And no one can doubt that the Ptolemaic model is a geometric model. But does that mean that Ptolemy intended the geometry of his model to be taken as reality? That is, did Ptolemy think that the planets literally spun around on some sort of large, invisible wheels? Perhaps not. Burtt (1932, 43–51) has argued that during the transition from the Middle Ages to modern times there was a profound shift in the mathematics used in science from geometry to algebra. Models in physics and astronomy today are expressed with mathematical equations that are at least algebraic but often are calculus equations. Does that mean that the equations themselves are tangible reality? No. It means that the equations are mathematical expressions of how some physical processes work.

For example, as I briefly discussed in Paper 1 (Faulkner 2022), our understanding of electricity and magnetism is based upon the theory of fields. A field is an alteration of space. Charges produce electric fields, and moving charges produce magnetic fields. That is, charges and magnets alter space in a way that allows other charges and magnets to detect the presence of the original charges and magnets and respond in a predictable way. In 1865, James Clerk Maxwell published four equations that describe these fields and how charges and magnets react to those fields. Note that these four equations don’t tell us why electromagnetism behaves the way it does; the four equations merely tell us how electromagnetism operates. Maxwell’s equations often are written in the form of differential equations using vector calculus. Does anyone think these equations are reality? Of course not. We understand that Maxwell’s equations merely are descriptions of reality.

In similar manner, did Ptolemy think that his system of epicycles and deferents were reality? Perhaps not. Ptolemy may have offered his model as a utilitarian sort of model, a model that could be used to predict planetary positions without it necessarily being physical reality. That is, perhaps Ptolemy intended his model to describe how the planets moved but not necessarily why the planets moved. If so, then to treat the Ptolemaic model as reality commits the reification fallacy. As I pointed out in Paper 1 (Faulkner 2022), science is very good at telling us how something happens but is not too keen on telling why something happens. We err when we attempt to answer the question of why too deeply when using science. Whether Ptolemy intended his model to be taken literally, that is the way his Ptolemaic model eventually came to be viewed. This possible reification led to some bad consequences four centuries ago.

In 1901, divers found an orrery in a first-century BC shipwreck off the coast of Antikythera. At the time, it was realized that the Antikythera mechanism, as the device came to be called, contained a gear, but interest in this relic soon faded. It was not until the 1970s that scientists began to realize the sophistication of the Antikythera mechanism. It is now recognized as the earliest known analog computer. It could be used to predict the positions of the sun, moon, and planets, as well as eclipses (Freeth 2019). Construction of the Antikythera mechanism obviously predates the shipwreck (usually dated 70–60 B.C.), but how much earlier? The range of estimates vary as far back as 200 B.C. The shipwreck was two centuries prior to publication of Ptolemy’s model. Therefore, the Antikythera mechanism bears testimony to the degree to which pre-Christian era Greek astronomy had developed, largely through the influence of Hipparchus.

Geocentrism vs. Heliocentrism

I will conclude my account of ancient Greek astronomy with a brief discussion of the ancient Greeks’ attitude toward the question of geocentrism vs. heliocentrism. As I have pointed out, a few ancient Greeks believed the heliocentric model. Their conclusion generally stemmed from their measurements that showed the sun is much larger than the earth. Even without understanding gravity, it makes more sense that smaller objects will orbit larger objects, not the other way around. However, geocentrism remained the dominant cosmology among the ancient Greeks, and it would remain so in the West until four centuries ago.

The ancient Greeks gave several reasons why they thought the earth was stationary. One reason was that we don’t feel the earth moving. Certainly, all motion that the ancient Greeks experienced could be felt, and so they reasoned that if the earth is moving, then we ought to feel that movement. It is a common misconception that we can feel motion. While we can’t feel motion, we can readily feel acceleration, which is change in motion. Until modern times, steady (non-accelerating) motion was not easy to experience. Most motion, such as riding in a cart or riding in an automobile, is not uniform. Such motion undergoes little bumps and sways. It is these small deviations from constant motion that we detect and misinterpret as detection of motion.

Another objection to heliocentrism attributed to Aristotle is that if the earth were moving around the sun, then the moon would be left behind as it tried to orbit the earth. It is not clear where the ancient Greeks got the idea that this is a problem. It didn’t seem to occur to them that the moon could be orbiting the sun along with the earth (which indeed is the case). But that requires knowledge of Newton’s law of gravity, which the ancient Greeks obviously did not possess. Perhaps the ancient Greeks just thought this made sense: that the moon’s motion is independent of the earth’s motion, and thus the moon would be left behind if the earth moved.

However, the best evidence the ancient Greeks had against the heliocentric model was the lack of parallax. The ancient Greeks correctly deduced that if the heliocentric model were true, then the stars would appear to assume different directions throughout the year as the earth changed its position. Attempts to measure parallax proved to be negative, so, being good scientists, most ancient Greeks rejected the heliocentric model. Therefore, the common misconception today that the ancient Greeks did not perform tests of hypotheses is not true. The ancient Greeks who persisted in heliocentrism did so against the best available evidence. Their response to the negative results of attempts to measure parallax was that the stars were too far away for measurable parallax. This turned out to be true, but the first successful parallax measurements were not made until the 1830s.

The Ancient Greeks and Physics

The ancient Greeks separated the terrestrial and the celestial realms. The rules that governed these two realms were very different. Perfection was the norm in the heavenly realm, so heavenly bodies followed perfect motion. As discussed in the previous section, this worldview required that heavenly bodies move uniformly around circles because circles were deemed the perfect shape and uniform motion was deemed to be perfect motion. Uniform circular motion is perpetual motion.

The rules of how things operated on earth were very different from the heavenly realm. Objects on earth do not move perpetually. Instead, on earth, effort (a force) must be expended to cause an object to move. A moving object will continue to move only if effort is continually expended to keep it moving. If one stops exerting a force on a moving object, the object soon comes to rest. This led Aristotle to conclude that on earth, rest is the natural state. Aristotle said that an object at rest will remain at rest unless an outside force acts upon it. Furthermore, Aristotle said that an object in motion will come to rest unless a force acts upon the object. As we shall see in the next paper, this contradicts Newton’s first law of motion.

The one exception to this rule was the propensity for objects to fall downward, a phenomenon that we today call gravity. Aristotle’s answer to the question of why things fall downward is that it is the nature of things on earth to fall downward. That is, things fall downward because that is what they do. To the modern mind, that may seem like a trivial answer to the question of why things fall, but keep in mind that science isn’t very good at answering “why” questions.

The usual answer today to the question of why things fall downward is Newton’s law of universal gravity. I shall discuss Newton’s law of gravity in the next paper, but suffice it to say for now that Newton’s law of gravity requires that mass attract mass. Why does mass attract mass in accordance with Newton’s law of gravity? Newton didn’t know, and neither does anyone else. All Newton’s law of gravity concerns itself with is a description of how masses attract one another, not why they do. Therefore, when we invoke gravity as the answer to the question of why things fall downward, aren’t we ultimately saying that things fall downward because they fall downward? How is that fundamentally different from Aristotle’s answer? Perhaps we ought not to be so harsh on Aristotle. Aristotle’s observation that things fall downward on earth is not fundamentally different from the more modern view of gravity. Both Aristotelian and Newtonian gravity are descriptions of how things operate, not why things operate the way they do.

So far, Aristotelian physics does a good job explaining our everyday world. Objects do tend to stay at rest unless we compel them to move by applying a force. And if we cause an object to move by applying a force to it, the object soon comes to rest once again unless we keep applying a force to maintain its motion. And an object tends to fall downward unless a force is applied to it to prevent that from happening. It’s no wonder that Aristotelian physics remained the status quo for two millennia.

Aristotle had other things to say about motion. Aristotle said that heavier things fall faster than lighter things. Where did Aristotle get such a notion? One readily observes that feathers and leaves fall far more slowly than stones do. What is the difference between a stone and a feather or leaf? A stone obviously is heavier than feathers and leaves. Ergo, heavier things fall more quickly than lighter things. That is a reasonable inference based upon the information given. However, further study, such as comparing the rates of fall of stones of various weights, would have revealed how wrong that inference is. As incorrect as some of Aristotle’s conclusions were, they are examples of abductive and inductive reasoning.

By the time of Aristotle, it was widely accepted among the ancient Greeks that there were four fundamental elements that comprised matter on earth: fire, air, water, and earth. While these substances existed in their pure forms, some substances were made of combinations of these four elements. These four elements fit well with Aristotle’s theory of gravity. Earth, being the densest element, tends to fall downward, as does water, though less so because, as Aristotle reasoned, water is not as heavy as earth. Since air is lighter than both earth and water, it tends to be atop the first two elements, and fire, being the lightest of the four elements, ascends far above the other three. Aristotle added a fifth element, aether, as the substance of the heavenly realm. It would not suffice for the perfect heavenly realm to consist of the same material that the imperfect terrestrial realm is made of. As Latin became the dominant language in the West, the Greek term aether was replaced with a Latin word from which we get the English word quintessence.

Over the years, the teaching on the heavenly substance varied. Often it was taken as the material substance of which heavenly bodies were made, but in other contexts it was the medium that permeated the heavenly realm. This latter meaning was the sense when early nineteenth century physicists appropriated the term “aether” to refer to the mechanical medium of light. There are a few people today who continue to argue for a nineteenth century version of the aether. However, Maxwell’s theory of electromagnetism provided a much more satisfactory non-mechanical medium for light, and quantum mechanics in the early twentieth century gave yet another entirely different medium for light. I have encountered people in the flat-earth movement who advocate an Aristotelian view of quintessence as the physical substance of astronomical bodies, completely divorcing them from any physical similarity to things on earth. This belief may be unique to flat-earthers today, but it was commonly believed through the Middle Ages due to the popularity of Aristotle’s teachings.

One major impediment to progress of ancient Greek physics was Zeno’s paradoxes, attributed to Zeno of Elea (c. 495–c. 430 B.C.), who lived about a century before Aristotle. Zeno’s most famous paradox involves a race between Achilles and a tortoise. Since Achilles can run much faster than the tortoise can, the tortoise is given a head start. If the head start does not place the tortoise too close to the finish line of the race, Achilles can easily overtake the tortoise and thus reach the finish line before the tortoise and can win the race. “Hold on!” Zeno says. Before Achilles can overtake the tortoise, he must first reach the starting point of the tortoise. But during the time it takes Achilles to reach the tortoise’s starting point, the tortoise has moved to a new position. Therefore, before Achilles can overtake the tortoise, he must close the distance between the tortoise’s starting point and the new position of the tortoise. But during the time it took Achilles to reach this new position of the tortoise, the tortoise has progressed to yet another new position. As you can readily see, this process goes on indefinitely. Zeno argued that since Achilles must exhaust an infinite number of parts of a journey to overtake the tortoise, then Achilles can never pass the tortoise and thus cannot win the race.

You might say this is ridiculous and propose an alternate race, this time with two heats so Achilles and the Tortoise do not directly compete with one another. But once again Zeno says, “Hold on!” Zeno argues that before Achilles can reach the finish line, Achilles must first traverse half the distance to the finish line. But before Achilles can reach the halfway point, he must first go halfway to the halfway point (one-quarter the way to the finish line). And before Achilles can run one-quarter of the way, he must run one-eighth of the way, and so forth. Once again, Achilles must exhaust an infinite number of parts of a journey before he can even start running. It would seem then that not only can Achilles not complete the race, he also can’t even start it!

This reasoning would seem to imply that motion is impossible, which was indeed Zeno’s point. Zeno drove this home by yet another paradox. Consider an arrow in flight. At each instant of time, the arrow cannot be moving to where it is because it is already there. Nor can the arrow be moving to where it is not because there is no time elapsed for that to happen. Therefore, at every instant there is no motion. Since time is composed of instants, in which there is no motion, then motion is impossible. Zeno’s point was that motion is an illusion. Since motion is a foundational part of our physical world, then the world is an illusion too. This approach to philosophy is not a good foundation for physics or for any other field of science. Therefore, Zeno’s paradoxes require an answer.

It is said that when the skeptic Diogenes heard of Zeno’s paradoxes, he simply rose and walked. To many people, this would suffice as a refutation, but Zeno would merely say that Diogenes’ movement was an illusion and hence Diogenes dodged the problem rather than answering it. A paradox is a proposition that leads to an apparent contradictory or absurd result. The key term is the word “apparent.” A proper answer to a paradox is called a resolution, in which one explains what is incorrect about the paradox, such as false premises, fallacious reasoning, or simply misinterpreting what one sees. While Diogenes’ response may seem brilliant, it hardly amounts to a resolution of Zeno’s paradox. Consequently, it is no surprise that there have been many attempts to resolve Zeno’s paradoxes, ranging in time from the ancient Greeks to today.

Most resolutions to Zeno’s paradoxes fall along the lines of Aristotle’s response. Aristotle noted that in the first two paradoxes, each portion of the trip covered ever-diminishing distances. Since the assumption was that the person was traveling at a uniform rate, then the amount of time required for each portion of the trip also was ever diminishing. Therefore, as the amount of distance required to travel approaches zero, so does the amount of time required to do so. Therefore, there is no problem.

While some philosophers accept this resolution, or variations thereof, apparently many philosophers do not. Though I had heard some versions of Zeno’s paradoxes while growing up, I did not learn of its full and proper discussion until I took an ancient and medieval philosophy course as an undergraduate student. Having completed the first semester of calculus and in my second semester of calculus, I immediately saw the resolution that was similar to Aristotle’s, raised my hand, and when the professor called upon me, I shared the answer. With a polite smile, the philosophy professor proceeded to disagree with me. At the time, I thought he was earnest in his opposition to what I still think is a refutation of the problem Zeno supposedly posed. Now I’m not so sure. Perhaps he didn’t disagree with me (remember the slight smile) and was merely playing devil’s advocate to keep the conversation going so that we students could learn to think through things and defend our positions. Philosophers love to do that.

While we can recognize parts of what we now know as science today in Aristotle’s work, some of his work seems to be counter to how science is done. Furthermore, the work of some other respected ancient Greek philosophers runs counter to science as we know it, and counter to Aristotelian thinking. This difference in attitude is reflected in Raphael’s fresco, “The School of Athens” (fig. 5). Plato and Aristotle are depicted at the center of the fresco, with Plato pointing upward while Aristotle gestures downward with a flat hand. This has led to many interpretations of what this contrast means. Most people understand this is showing Plato’s emphasis on his theory of forms while Aristotle was more concerned with the physical nature of our world.

Fig. 5. Raphael’s fresco, The School of Athens. Plato and Aristotle are at the center, with Plato pointing upward while Aristotle gestures downward with a flat hand. https://commons.wikimedia.org/wiki/File:%22The_School_of_ Athens%22_by_Raffaello_Sanzio_da_Urbino.jpg. Raphael, Public domain, via Wikimedia Commons

Plato insisted that things in this world conform to ideal forms. For instance, how do we recognize that a horse is a horse? It is because horses conform to a concept of what a horse is. Most people are content with a concept of a horse being a mental abstraction based upon our experience of what properties horses have, but Plato thought that the relationship worked in reverse order. That is, rather than the concept of a horse deriving from our experiences with horses, the concept came first and the horses we experience merely reflect that reality. That final word “reality” is a key term in this discussion. For the concept of a horse to come first, there must be an objective reality related to it. It was this objective reality of the concept that Plato called the form. Idealized forms do not exist in this world—things in this world merely imperfectly reflect the idealized form that exists elsewhere. The elsewhere could be described as heaven. This ultimately led to the belief that physical matter is evil, which in turn was absorbed by the Gnostics. This aspect of Gnosticism led to heresy about the nature of Jesus because of a question of whether He had a physical body. It also led to Christians in the first century having questions about the resurrection. The Apostle Paul addressed or referred to Gnostic ideas several times (2 Corinthians 10:5; Colossians 2:8;
1 Thessalonians 4:13–18; 1Timothy 6:20–21), as well as the Apostle John (1 John 1:1–4; 2 John 7–11).

Plato believed in a creator, though he never addressed who or what this creator is. This aspect of Plato’s teaching may have been the reason why many early church fathers came to embrace Neoplatonism. Examples include Clement of Alexandria, Origen in the early third century, and Augustine in the early fifth century. Consequently, these church fathers tended to interpret the Bible in terms of Neoplatonism, and many of these Neoplatonic ideas are still present in the church today. An examination of these Neoplatonic influences within the church today would be a very worthy study, but is far beyond the purposes of this paper.

Plato’s theory of forms had a profound impact upon how people viewed the world. It jibed with the ancient Greek idea that this world is imperfect, but the heavenly realm is perfect. Thus, it bolstered the notion that there were two different sets of rules for the two domains, a belief that even Aristotle agreed with. However, unlike Aristotle, who had interest in this physical world, Plato’s emphasis on the primacy of heaven left the world in which we live unworthy of real interest. Besides, as Heraclitus had observed a century before Plato, our world is in flux, so the rules of how our world operates are constantly changing, so why bother trying to figure out the order of this world when it was destined to change continually? As the church came to dominance in the West during the early Middle Ages, the interest in Neoplatonism over Aristotelian thought by many in the church led to the loss of Aristotelian thinking in the West.

Before moving beyond antiquity, I ought to contrast the Greek and Roman views toward science. You may have noticed that I have omitted any discussion of Roman scientists. There is a good reason for that—there were no notable Roman scientists as there had been among the ancient Greeks. There were some scientists within the Roman Empire, such as Ptolemy, but Ptolemy was thoroughly Greek in his language and culture. The Romans were concerned with more practical matters, such as commerce and effective governance—their attention to these at least partially accounts for the longevity of the Roman Empire. The Greeks were more theoretical in their approach, which fostered a curiosity about the world. Many Greeks thought the natural world was worth studying just for the pleasure of learning how the world worked. However, to the Roman mind, the motivation for learning about how the world worked was more practical—how can I use this knowledge? While the Greeks constructed some grand buildings, the Romans exceeded Greek architecture and construction in every way. It is amazing that after two millennia many Roman roads and some Roman aqueducts are still used today. Or consider Rome’s Pantheon, constructed 19 centuries ago. While the Greeks were much better than the Romans in doing science, the Romans were superior engineers.

This brings up an important distinction between pure science and applied science. Pure scientists (as exemplified by the ancient Greeks) are more motivated by curiosity about the natural world without much regard for how practical knowledge may be gained from their studies. On the other hand, applied scientists (as exemplified by the ancient Romans) are motivated more by the goal of how useful knowledge may be gained by studying the world. Examples of pure sciences are physics, chemistry, and biology. Examples of applied sciences are engineering and medical sciences.⁶ Pure and applied scientists tend to view the world a bit differently, though there is considerable overlap. For instance, many geologists are employed in mineral exploration. The uses of minerals are obvious, so there is considerable available money for funding the search for mineral resources. In contrast, funding for pure geology research where there is no clear economic impact are much more meager. Since astronomy doesn’t appear to be of much practical application, it is perhaps the most extreme example of a pure science. However, this has not always been the case. As discussed earlier, astronomy probably was originally developed to produce calendars to aid in agriculture, though for religious purposes too.⁷ Since those problems were solved long ago, astronomy has developed into a far less directly practical science today.

Medieval Science

The Middle Ages have been improperly portrayed for a long time. They are often called the “dark ages,” a term coined by Petrarch, a fourteenth century Italian poet and scholar who is recognized as an early humanist. Soon other Renaissance figures were using the term. However, it was post-Enlightenment thinkers who took this term to new depths. This culminated in the conflict thesis of the nineteenth century, the notion that Christianity had held back progress during the Middle Ages and that progress reemerged in Europe only as the influence of the church weakened (Faulkner 2017, 29–30). Exhibit A in this argument was the claim the church taught the earth is flat and that this thinking was overturned by Christopher Columbus a little more than five centuries ago. The medieval scholar Jeffrey Burton Russell (1991) masterfully disproved this claim. I call this false narrative about Columbus the “Columbus mythology.”

Was there a general reversal of progress in the early Middle Ages? Yes. Did the church have anything to do with this decline? No. As the Roman Empire disintegrated due to its decaying culture and under the onslaught of Barbarian invasions, the unique features of the Roman Empire that fostered prosperity crumbled too. Wherever Rome conquered, it promoted commerce by constructing aqueducts, roads, ports, and other infrastructure that enabled trade and supported large cities. Rome also vigorously prosecuted piracy and highway robbery, making travel throughout its empire relatively safe. These factors provided peace and prosperity within the empire and probably accounted for much of the success and longevity of the Roman Empire. As the Empire ceased to exist, so did the relative peace and prosperity. Consequently, there was retrenchment in standards of living, which undermined the ability of economies to support research, study, and the dissemination of knowledge.

In the early fourth century, Christianity became a tolerated religion within the Roman Empire, effectively ending official persecution of the church. By the end of the fourth century, Christianity had become the official state religion of the empire. While many professing Christians undoubtedly welcomed this change of policy at the time, it ended up having a deleterious effect on the church. It further encouraged participation of false believers in the church and eventually wedded civil and religious authority. As the security of the Roman government eroded, people clamored for some semblance of order. Many leaders in the church were more than happy to provide governance, while civil leaders found it advantageous to use the growing influence of the church for political gain. This set the stage for the intertwining of church and state that would prevail for the next millennium. It is no accident that religious leaders consolidated power in Rome, as they were modeling their governance after that of the former Roman Empire. The growing influence of the Roman Catholic Church amidst the perceived decline of progress in the Middle Ages led to the false conclusion that the former caused the latter. In reality, both were the result of the fall of the Roman Empire.

Nor were the Middle Ages quite as dark as often portrayed. For instance, the Venerable Bede (672/3–735) is considered the most learned man of the seventh and eighth centuries. There certainly were many other scholars during the Middle Ages, but unfortunately much of their writings and teachings remained within the walls of their institutions, mostly monasteries. The monastic philosophy did not encourage dissemination of intellectual accomplishments obtained within institutions. This is the opposite to how science is practiced today.

Much of medieval education focused on the seven liberal arts developed by Martianus Capella (c. 410–420) in the early fifth century, but reflecting much earlier ancient Greek thought, such as that of Plato. The seven liberal arts were divided into the trivium, followed by the quadrivium. The trivium consisted of grammar, logic, and rhetoric. Grammar was the proper use and understanding of language. Logic taught students how to properly form sound arguments and identify fallacious arguments. Rhetoric was the art of persuading others. Upon completion of the trivium, students progressed to the quadrivium, consisting of arithmetic, geometry, music, and astronomy. It is interesting that of the seven liberal arts, the only science we would recognize today is astronomy. That is likely due to the fact that other sciences, such as chemistry and physics, were not nearly as developed as astronomy (encapsulated by the Ptolemaic model).

The situation in western Europe began to change dramatically around A.D. 1100. By the time of the fall of Rome six centuries earlier, the empire had already split east-west. In the east, Greek remained the lingua franca, but in the west, Latin had replaced Greek as the common language. Eventually, Latin developed into the various Romance languages in the western end of the former empire. With the disuse of Greek in the west, Greek texts largely disappeared, with only some of them being replaced by Latin translations. Because of the influence of Neoplatonists in the Western church, the writings of some ancient Greeks, such as Aristotle and Ptolemy largely disappeared in the West. Meanwhile, the Muslim conquest of portions of the former eastern part of the Roman Empire brought some of these works to the attention of Muslim scholars. Of notable attention was the Almagest. While Muslim astronomers preserved and disseminated Ptolemy’s work, they made no significant improvements upon it. By A.D. 1100, many of these ancient Greek works largely lost in the West began to make their way back to the West, where they were translated into Latin and sometimes into common languages. This rekindled interest in the works of ancient Greek science had a profound impact on the West.

In the thirteenth century, Thomas Aquinas (1225–1274) did for Aristotle what Augustine had done for Plato eight centuries earlier. Aquinas wedded many of the teachings of Aristotle to Roman Catholic teaching. Since Aristotle was a geocentrist, the Bible was interpreted as being geocentric, which set up the Galileo affair a few centuries later. Many people understand this, but apparently are ignorant of the fact that Aristotle also taught that the earth is a globe, which also became the interpretation that Aquinas gave to the Bible, though that probably was already a widespread belief. This alone is an effective refutation of the Columbus mythology about the Middle Ages.

Much of this renewed emphasis on Aristotle’s work focused on his logic rather than his science. This gave rise to the myth that people in the Middle Ages did not do empirical science but relied upon deductive reasoning to reach conclusions about the world. A related myth is that during the Middle Ages people didn’t seek answers to questions about the world themselves but looked to Aristotle or other authorities to find answers to such questions. While this attitude was common in the Middle Ages, is it not common today as well? For instance, if a person today wanted to know how many teeth a horse has, would that person find the answer by counting the number of teeth horses have? Probably not. The most likely course of action today would be to look up the answer, usually online. How is that different from looking up the answer in Aristotle? Even scientists today look up the answers to questions they have. Only after a scientist finds that a question he has asked has not been answered satisfactorily might he set out to investigate the answer for himself with original research.

Roger Bacon (c. 1219–1292), a contemporary of Aquinas, challenged this emphasis on logical deduction to study the world and high reliance upon Aristotle as an ultimate human authority on nature. Bacon advocated an empirical approach to studying the world, an approach very similar to that of Francis Bacon (no relation) more than 300 years later. Apparently, the work of Roger Bacon was not entirely successful in changing the medieval philosophy of science. Perhaps the time was not quite right, for three centuries later, Francis Bacon was far more successful in establishing science as we now know it. Roger Bacon’s own investigations had led him to the conclusion that Aristotle was wrong about a few things. In addition to the philosophy of science, Roger Bacon made major contributions in linguistics, optics, and alchemy. He proposed a reform to the Julian calendar that was similar to the Gregorian calendar four centuries later. Roger Bacon was the first European to publish the formula for gunpowder.

A few decades later, the early fourteenth century scholastic philosopher and theologian William of Ockham (c. 1287–1347) developed the principle of parsimony. Though not recognized as a scientist, Occam’s razor, as his principle of parsimony is often called, is very important in science. Occam’s razor is a rule that when presented with two competing hypotheses that make the same correct prediction, the hypothesis with the fewest assumptions is more likely to be true. This principle is recognized to be reliable in any type of inductive (or perhaps more properly, abductive) reasoning. For example, in a court case, the attorneys on either side provide their versions of events that they claim explain the evidence presented in the trial. It often is the responsibility of the jury to decide which version is more likely to be true. Occam’s razor is a valuable tool in reaching a verdict. In similar manner, scientists often consider competing hypotheses that may equally explain the available evidence. Applying Occam’s razor, the simplest hypothesis is usually accepted. As we shall see in the next paper, application of Occam’s razor was a crucial test in deciding between the Ptolemaic model and the heliocentric model.

Since I have focused on astronomy in this discussion of the history of science, I must make mention of Johannes de Sacrobosco (c. 1195–1256). Around A.D. 1230, Sacrobosco wrote De Sphaera Mundi, (On the Sphere of the World). This was a treatment of the Ptolemaic model, and it remained the standard text on astronomy in the West for four centuries, making the transition from copying manuscripts by hand to the printing press. What eventually caused Sacrobosco’s work to fall into disuse was the general rejection of the Ptolemaic model in the seventeenth century. Many people misunderstand the title of this work, thinking the spherical world refers to the earth. Rather, the spherical world of the title is a reference to the celestial sphere that surrounds the earth. However, like Ptolemy before him, Sacrobosco made it very clear the earth is a globe and gave several reasons why we know this.

The Muslim conquest made one other inadvertent contribution to knowledge in the West. When Constantinople fell in 1453, many Greek texts were rapidly transported to the West, causing revival of interest in ancient Greek texts. Many of these were New Testament manuscripts, but many others were devoted to science and philosophy.

Born a year before the fall of Constantinople, Leonardo da Vinci (1452–1519) is recognized as a true Renaissance man. While most known for his art, da Vinci also made contributions to architecture, engineering, and science. Da Vinci’s only notable contribution to astronomy was his explanation of earthshine on the moon, something that apparently no one before him explained.

I wish to mention one other person in the transition from late medieval to modern times. In 1528, Jean Fernel (1497–1558) published Cosmotheoria, in which he made a major step in the development of geodesy. Fernel accurately measured the length of a degree of arc along a meridian of longitude. In modern navigation parlance, this distance is 60 nautical miles. Multiplying Fernel’s measurement by 360 yields the earth’s circumference, and the earth’s radius easily follows. Fernel’s result was within 1% of the correct value. Given that Fernel accomplished this before the invention of the telescope is remarkable.

Building upon an ancient Greek notion, there developed in the Middle Ages a sort of philosophical or theological geocentrism that mirrored physical geocentrism. In the Aristotelian worldview, things fall downward because that is the way the world operates. There is no need to further investigate the matter. It was also recognized that moral depravity tends to progress from bad to worse. That is, morality goes downward much as objects fall downward. Therefore, there was an equation between the physical falling of objects and declining morality. Since the earth is the center of the universe, it is fitting that hell is below the earth’s surface, perhaps even at the earth’s center. Like physical objects, once one is at the earth’s center, no further fall is possible.

Where is man’s place in this cosmology? Man is perched right above perdition in a very imperfect world. Much higher, in the heavenly realm, things are perfect. Thus, man is located at the least favorable place in God’s creation. However, the revisionism of the nineteenth century conflict thesis reversed man’s position. The claim was made that medieval theologians placed man at the center of creation because this was God’s most favored location, when the reality was precisely the opposite.

Conclusion

I have briefly reviewed the history of science from its roots among the ancient Greeks through the Middle Ages. At each stage, I have endeavored to classify the type of science important individuals did in terms of the discussion of Paper 1 (Faulkner 2022). It is interesting that there were no ancient Roman scientists of note. This indicates a difference in worldview between the ancient Greeks and Romans. As the order of the Roman Empire disintegrated into the chaos of the early Middle Ages, the church in Rome assumed greater power, leading to the blending of church and state and eventually to the authority of Rome to dictate other matters, such as the conduct of science. The loss of order contributed to the stalling of science in the early Middle Ages, but the dominance of Neoplatonism over other Greek philosophers changed the worldview, which played a role too. The revival of interest in Aristotle and other Greek sources in the late Middle Ages sparked renewal in science, though this was tempered by the worldview of the Middle Ages that contrasted to that of the ancient Greeks. This set the stage for conflict as science as we know it began to emerge in the seventeenth century. I shall review this conflict and the transition to modern science in the next paper in this series.

References

Abel, George O.1964. Exploration of the Universe. New York, New York: Holt, Rhinehart, and Winston.

Aristotle. (350 B.C.) 1807. The Treatises of Aristotle, on the Heavens, on Generation and Corruption, and on Meteors. Translated by Thomas Taylor. London, United Kingdom: Robert Wilks.

Anonymous. n.d. “Maya Civilization.” Canadian Museum of History. https://www.historymuseum.ca/cmc/exhibitions/civil/maya/mmc03eng.html#:~:text=The%20ancient%20Maya%20believed%20in,lasting%20about%205%2C200%20modern%20years.&text=Some%20Maya%20also%20believed%20that,physical%20strength%20called%20%22Bacabs%22.

Autolycus of Pitane. (335–300 B.C.) 1885. On the Moving Sphere. Translated by F. Hultsch. Leipzig, Germany: no publisher.

Berry, Arthur. (1898) 1961. A Short History of Astronomy from Earliest Times Through the Nineteenth Century. New York, New York: Dover Press.

Burtt, Edwin Arthur. 1932. The Metaphysical Foundations of Modern Science (second edition). Garden City, New York, Anchor Books.

de Sacrobosco, Johannes. 1488. De Sphaera Mundi. Venice, Italy: Per Magistrum Gullielmum de Tridino de Monteferrato.

Dreyer, John Louis Emil. 1906. A History of the Planetary Systems from Thales to Kepler. Cambridge, England: Cambridge University Press.

Euclid. (300 B.C.) 1926. Euclid’s Elements. Vols. 1–13). Translated by Thomas L. Heath. Cambridge, United Kingdom: Cambridge University Press.

Faulkner, Danny R. 2013a. “A Further Examination of the Gospel in the Stars.” Answers Research Journal 6 (February 6): 35–62. https://answersresearchjournal.org/further-examination-gospel-stars/.

Faulkner, Danny R. 2013b. “An Analysis of the Dodwell Hypothesis.” Answers Research Journal 6 (May 15): 179–191. https://answersresearchjournal.org/analysis-of-the-dodwell-hypothesis/.

Faulkner, Danny R. 2017. The Expanse of Heaven: Where Creation and Cosmology Intersect. Green Forest, Arkansas: Master Books.

Faulkner, Danny R. 2022. “The Philosophy of Science 1: What is Science, and How is Science Done?” Answers Research Journal 15 (November 2): 359–376. https://answersresearchjournal.org/science/philosophy-science/.

Fernel, Jean François. 1528. Cosmotheoria, libros duos complexa. Paris, France: Simon de Colines.

Freeth, Tony. 2019. “Revising the Eclipse Prediction Scheme in the Antikythera Mechanism.” Palgrave Communications 5, no. 7 (22 January): 1–12.

Gysembergh, Victor, Peter J. Williams, and Emanuel Zingg. 2022. “New Evidence for Hipparchus’ Star Catalogue Revealed by Multispectral Imaging.” Journal for the History of Astronomy 53, no. 4 (November): 383–393.

Petroski, Henry. 2010. “Engineering is Not Science: And Confusing the Two Keeps Us From Solving the Problems of the World.” IEEE Spectrum. https://spectrum.ieee.org/engineering-is-not-science#toggle-gdpr.

Ptolemy, Claudius. (150) 1984. Almagest. Translated and annotated by G. J. Toomer. London, United Kingdom: Gerald Duckworth and Co Ltd.

Russell, Jeffrey Burton. 1991. Inventing the Flat Earth: Columbus and Modern Historians. New York, New York: Praeger.