The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
The relative ages of rocks are often known from field relationships. If a dolerite intrudes a succession of rocks, the dolerite must be younger than the succession it intrudes. This relationship can be written as the inequality:
Age (Dolerite) ≤ Age (Intruded succession)
If the Radioisotope Age (Dolerite) > Radioisotope Age (intruded succession) then there is a violation of the relative age inequality. Many violations of a similar kind are described in this paper. These violations cannot be explained by constant half-lives, since constant half-lives would always produce radioisotope ages that are in sequence from old to young. This indicates that there is either a problem with the data or with the understanding of radioactivity. Since discrepancies occur in most of the data, it is thought that it is the latter. Therefore, a hypothesis is proposed to explain the discrepancies between the relative ages from geological field relationships and radioisotope ages:
There exists fractionation in radioactive atoms of the same atom mass based on proton neutron configurations in their nuclei, causing faster and slower decaying atoms of the same atom mass.
This hypothesis could explain why there is a general trend from old to young in radioisotope ages from the bottom of the stratigraphic profile to the top of the stratigraphic profile, and why discrepancies can occur.
Keywords: geochronology, geological field relationships, relative ages, radioactivity, radiometric ages
Introduction
Charles Darwin is one of the most influential figures in human history. His theory of evolution, the evolution of more complex organisms developing from less complex organisms through natural selection over millions of years, is accepted as fact by most scientists. The oldest fossil stromatolites (fossil bacteria) are radiometrically dated to be 3.45 billion years old. Evolution is taught to students at schools and universities as fact. Many people’s worldview is based on this perception of science. There are also many people in the church who wonder if evolution is true, especially when one looks at the fossil record. As believers, however, we need to look at what the Word of God reveals.
Before the Fall, there was no death in all creation. The wages of sin is death. Death entered the world through sin (Romans 5:12). To accept that death was the normal course of events in creation before the Fall is to say that Christ’s work was not necessary. Through Jesus Christ, God’s wrath is turned away from us and we are saved from sin and death.
After the Fall, however, the whole creation was addicted to perishability. When we look at creation and we see signs of death, we know that fallen man must have already existed. Fossils are plants and animals that are dead. Fossils are thus the proof of death and not the proof that more complex organisms evolved from less complex organisms. If one looks at dead bones, the thought of death is logical. So, if we look at fossils in the geological record, we know that fallen man already existed. This is contrary to the theory of Darwinian evolution which states that most fossils existed before man, and that man evolved from the organisms that are preserved as fossils.
If the biblical point of view is accepted and that fallen man already existed when the organisms from which the fossils are constituted died, the theory of evolution as a whole becomes falsified (Von Lindheim-Westerink 2010). The great ages for the fossils can also not be true, because the whole history of man has been documented, totaling about 7,000 years long. So, there must be something incomplete with our understanding radioactivity, the theory on which the great ages are based. This paper will look at some examples that demonstrate this incomplete understanding of radioactivity.
In 1905, Ernest Rutherford suggested that radioactivity can be used to find the exact age of a rock. The idea to determine absolute ages for rocks grew from work done by Rutherford in the early twentieth century when he described the process of radioactivity (see for example Rutherford and Soddy 1902).
Often, relative time relationships are known in different types of rocks. In an upright succession of sedimentary rocks, the youngest rock is at the top and the oldest rock at the bottom, and if molten material, like a dolerite, intrudes a package of rocks, the dolerite is clearly younger than the youngest rock it intrudes. Radiometric isotope ages should follow these relative geological relationships, otherwise there is a discrepancy between the relative ages from field relationships and the radiometric isotope ages.
The relative time relationships of field geology can be written as simple inequalities and equalities. For example, if a dolerite intrudes a succession of rocks, the dolerite must be younger than the succession it intrudes. This relationship can be written as the inequality:
Age (Dolerite) ≤ Age (Intruded succession) (1)
There is a violation of that relative age inequality if:
Radiometric Age (Dolerite) > Age Intruded succession) (2)
The discrepancies between relative ages known from field relationships and radiometric ages questions the fundamental understanding of radioactivity and challenges if the method of radiometric age dating is appropriate to determine the ages of rocks.
There are explanations for these discrepancies, such as contamination, Pb loss, and xenocrystic minerals, to argue why there are zircons that are both younger and older than they should be (Andersen, Elburg, and Magwaza 2019; Cherniac and Watson 2000). To be reasonably certain that contamination did not occur, zircons need to be analyzed in thin section. However, after studying zircons from several rocks, nine types of discrepancies are identified that have a strong likelihood or being primary isotope signatures.
Therefore, a hypothesis is proposed to explain the discrepancies between the relative ages from geological field relationships and radioisotope ages. The hypothesis is as follows:
There exists fractionation in radioactive atoms of the same atom mass based on proton neutron configurations in their nuclei, causing faster and slower decaying atoms of the same atom mass.
This hypothesis could explain why there is a general trend from old to young in radioisotope ages from the bottom of the stratigraphic profile to the top of the stratigraphic profile, and why discrepancies can occur. It is possible to verify or falsify this hypothesis with experiments.
Instances of Discrepancies Found
A few instances of discrepancies that were found are discussed below. More work needs to be done, but these examples may indicate the widespread existence of groups of discrepancies.
Discrepancies in a Sedimentary Succession
The Transvaal Supergroup, South Africa, is a succession of chemical, siliciclastic and volcanic rocks for which a significant amount of U-Pb age dating on zircon and baddeleyite have been performed (fig. 1, Gumsley et al. 2017; Schröder, Beukes, and Armstrong 2016). The Ongeluk lava (fig. 2), that has a U-Pb age of 2424 ± 32 Ma on baddeleyite overlies the Makganyene diamictite for which detrital zircons have been dated.
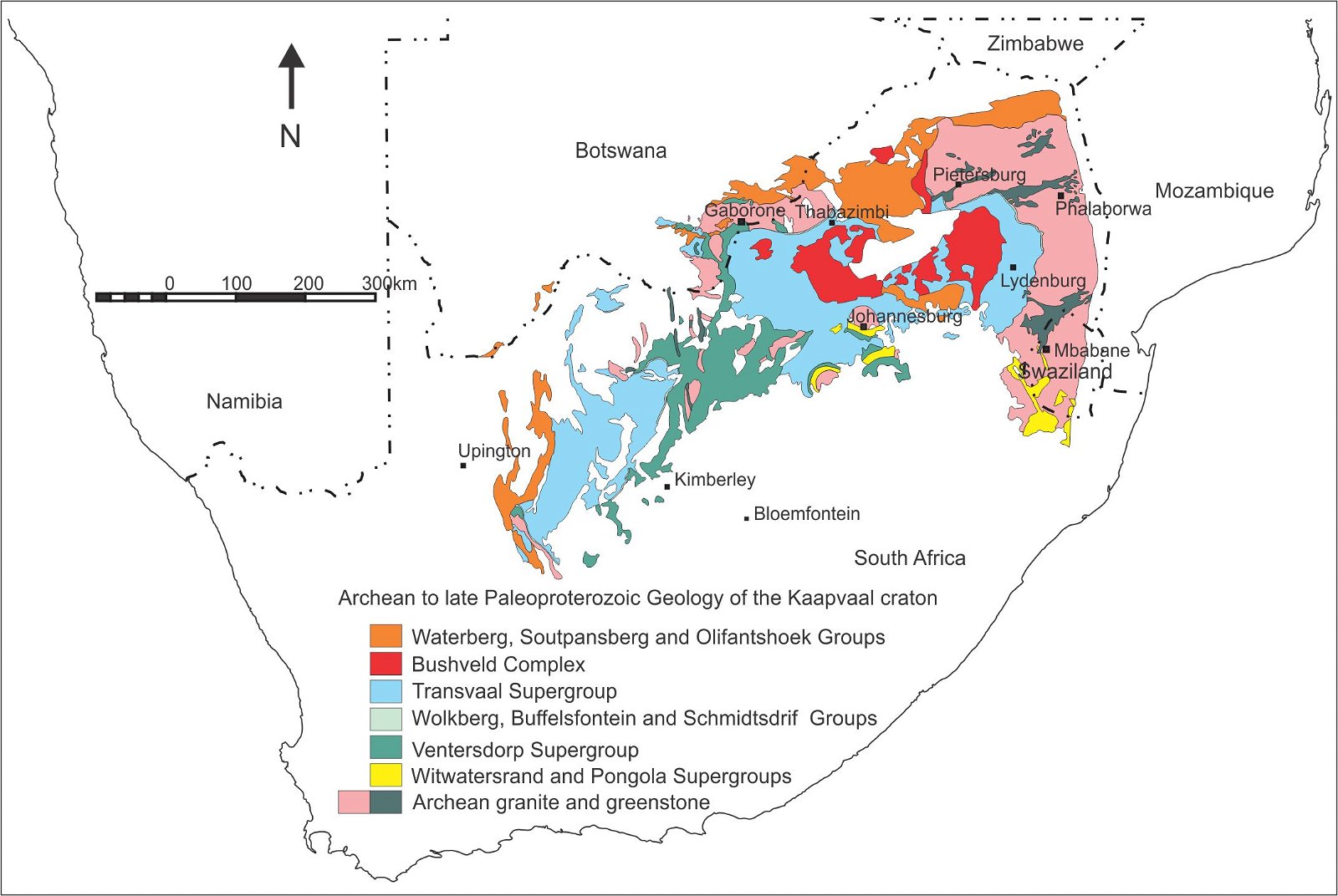
Fig. 1. Geological map indicating Archean to late Paleoproterozoic geology of South Africa (after Cairncross 2005).
The youngest of these detrital zircons in the Makganyene diamictite have ages of 2226 ± 42 Ma (Beukes, Vorster, and Frei 2013). Since 2013 the U-Pb isotopes of the Makganyene diamictite detrital zircons have been analyzed several times at different places with different machines, and the detrital zircon population that contains concordant 2220 Ma old zircons was found during each analytical attempt (Ngobeli 2019, 352). So far, 47 concordant or nearly concordant zircons younger than the baddeleyite in the Ongeluk lava have been found. The Ongeluk lava that is younger by stratigraphical relationship seems to have an older radioisotope age than the underlying diamictite. Perhaps the baddeleyite is xenocrystic, but the occurrence of the baddeleyite as described from petrography demonstrates that it is not (Gumsley et al. 2017). Also, the Pb-Pb age of 2392 ± 22 Ma on the Mooidraai dolomite above the lava (Bau et al. 1999, fig. 2) indicates that the ≈ 2400 Ma age is persistent. There are very few rocks stratigraphically below the Ongeluk lava on the Kaapvaal craton that have a 2420 Ma age where the baddeleyite may have been sourced from. These are arguments that the baddeleyite is not xenocrystic.
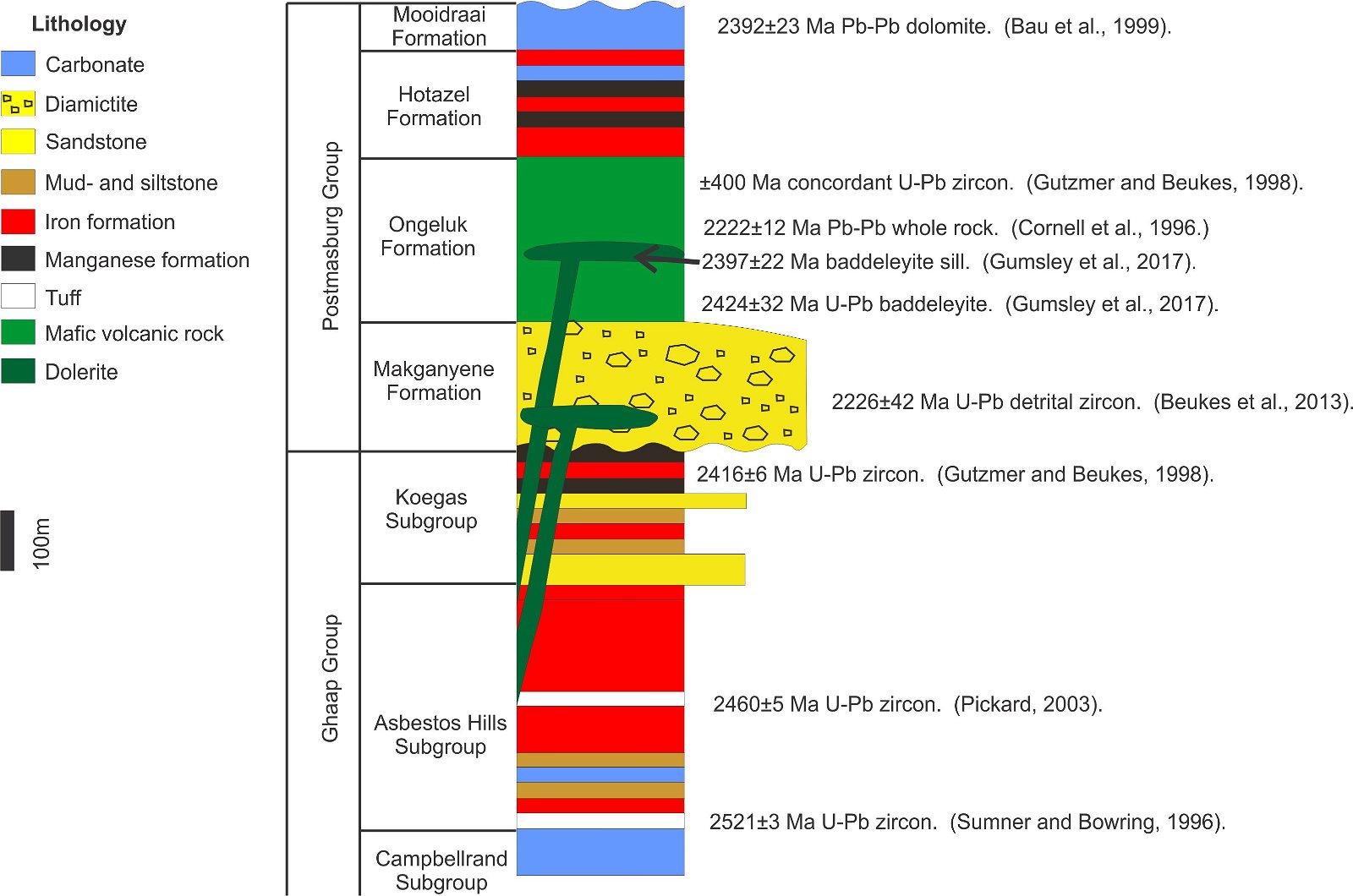
Fig. 2. Rocks of the Transvaal Supergroup with relevant isotope ages. Sketch after Gumsley et al. (2017).
What is observed about the relative stratigraphic ages of the rock in a sedimentary succession can be written as a simple inequality.
Age (Ongeluk lava) ≤ Age
(Youngest zircon in Makganyene diamictite) (3)
However, in terms of isotope ages, it is observed that:
Radiometric Age (Ongeluk lava) > Radiometric Age
(Youngest zircon in Makganyene diamictite) (4)
Therefore, there is a violation of the inequality in equation (3).
Discrepancies of Dolerite Intruding Sedimentary Successions
In the Transvaal Supergroup, dolerite that has a U-Pb baddeleyite age of 2397 ± 22 Ma (Gumsley et al. 2017, fig. 2) intrudes the Ongeluk lava, that overlies the Makganyene diamictite that have detrital zircon U-Pb ages of 2226 ± 42 Ma (Beukes, Vorster, and Frei 2013; Ngobeli 2019, 352). The baddeleyite in the dolerite may be xenocrystic. However, again the way the baddeleyite occurs in the dolerite, and the Pb-Pb age of the overlying Mooidraai dolomite of 2392 ± 23 Ma indicates that the ≈ 2400 Ma age is persistent and provides an argument that the baddeleyite in the dolerite is not xenocrystic. Apparently, the dolerite has an isotope age that is older than the rock it intrudes.
The relative ages of the rocks can be written as a simple inequality:
Age (Dolerite) ≤ Age
(youngest detrital zircon in Makganyene diamictite) (5)
However, when the isotope ages are observed it is seen that:
Radiometric Age
(Dolerite) > Radiometric Age
(youngest detrital zircon in Makganyene diamictite) (6)
Therefore, there is a violation of the inequality in equation (5).
Discrepancies in Volcanic Rock
Quartz porphyritic lavas are present near the base of the Waterberg Group in South Africa (figs. 1 and 3). A combination age of 2051 ± 7.9 Ma from several euhedral magmatic zircons has been reported for one of these lavas (Dorland et al. 2006). However, when single zircons are analyzed, zircons that are near concordant (less than 10% discordance), have 207Pb/206Pb ages of between 2059 ± 16 Ma and 1957 ± 14 Ma. This is a difference in age of 100 Ma. The 206Pb/238U ages on single zircons have a far greater spread, with the oldest zircon at 2083 ± 16 Ma and the youngest zircon at 514.7 ± 4.8 Ma, a difference of 1566 Ma in zircons that were extracted from a single sample that had a diameter of approximately 20 cm. Perhaps some of the zircons in this sample are xenocrysts that were picked up from the Bushveld Complex rocks these lavas overlie. The age of the Bushveld Complex has been defined between approximately 2060 Ma to 2057 Ma (Buick, Maas, and Gibson 2001; Harmer and Armstrong 2000; Mungall, Kamo, and McQuade 2016). Therefore, the zircons that have ages less than 2050 Ma are probably not xenocrysts from the Bushveld Complex. The age difference between the youngest and the oldest zircons that are less than 10% discordant, in this sample is 93 Ma between 2050 Ma (defined by the upper age limit of the 2% discordant 2040.7 ± 9.7 Ma zircon) and the 1957 ± 14 Ma zircon. In terms of morphology, cathodoluminescence indicates that the zircons are all euhedral, and do not appear to have been rounded by travel as xenocrysts (Dorland et al. 2006).
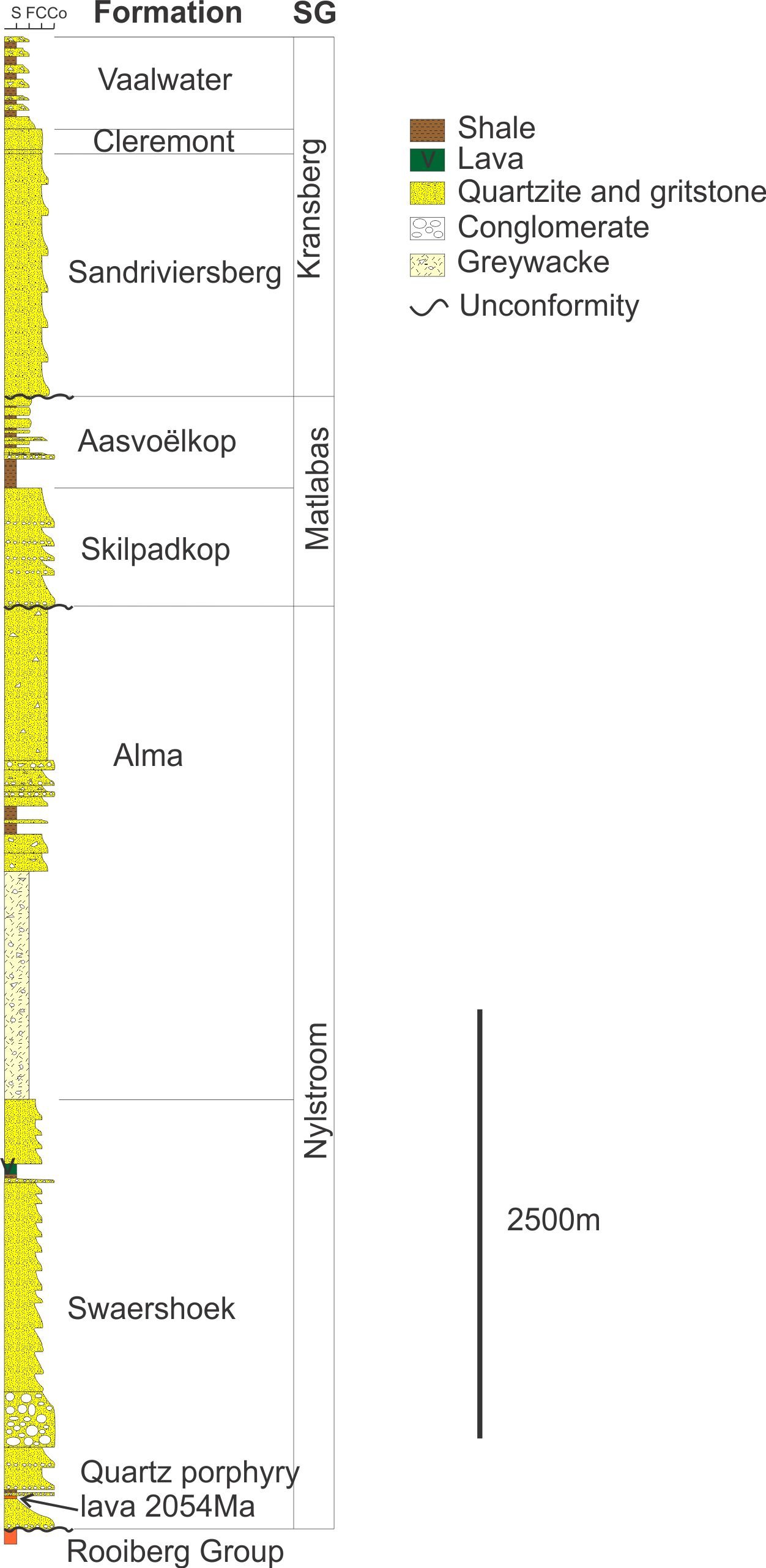
Fig. 3. Stratigraphy of the Waterberg Group (after Dorland et al. 2006).
The relative expected age relationship between zircons in a volcanic rock that crystallized at the same time can be written as the equality:
Age (Zircon A) = Age (Zircon B) = Age (Zircon C) (7)
However, in the quartz porphyry lavas of the Waterberg Group:
Radiometric Age (Zircon A) ≠ Radiometric Age (Zircon B) ≠ Radiometric Age (Zircon C) (8)
In Waterberg Group volcanic rocks, the equality in equation 7 is violated.
An isotope stratigraphic discrepancy is also displayed where the oldest concordant zircon in another sample of this porphyritic lava at the base of the Waterberg Group is 2075.9±10 Ma (Dorland et al. 2006), about 18 Ma older than the volcanic rocks of the Rooiberg Group of the Bushveld Complex they overlie (figs. 1 and 3, Harmer and Armstrong 2000). This zircon is statistically different from the 2060 Ma to 2057 Ma age for the Bushveld Complex and is therefore likely not a xenocryst.
Interesting enough, the Magaliesberg quartzite of the Transvaal Supergroup (fig. 1) contains zircon that has a 207Pb/206Pb age of 1809±9 Ma and is 5% discordant with a U content of 792 ppm (Schröder, Beukes, and Armstrong 2016). Schröder, Beukes, and Armstrong (2016) rejected this zircon because of high U content. However, after viewing several U-Pb datasets where U concentrations in zircons were reported (Dorland 2004, 326), 792 ppm U is rather a medium concentration of U as based on SHRIMP analytical points in zircon, and it can be argued that this zircon provides a valid data point. This zircon indicates (in radiometric age terms) that not only are the volcanic rocks of the Bushveld Complex overlain by a sedimentary succession that is older than it, but they also intrude rocks that are younger than it. Geologically, this is impossible.
Discrepancy Between Analytical Spots in the Same Zircon in Volcanic Rocks and Dolerite
In a volcanic or intrusive rock that cooled and crystallized rapidly, the age in two different analytical spots on the same zircon should give the same age in terms of U/Pb geochronology.
This relative age relationship can be written as the equality:
Radiometric Age (Spot 1) = Radiometric Age
(Spot 2) = Radiometric Age (Spot 3) (9)
However, when the radiometric ages of two spots in the same zircon of a rock that cooled rapidly is examined (Shumlyanskyy et al. 2016; Wingate 2001):
Radiometric Age (Spot 1) ≠ Radiometric Age
(Spot 2) ≠ Radiometric Age (Spot 3) (10)
Experimentally, the equality in equation (9) is therefore often violated when two spots are analyzed in zircon in volcanic and intrusive rocks that cooled rapidly. Another way to see this discrepancy is to evaluate analytical spots in zircon standards that are used during SHRIMP or other micro analyses. The equality in equation (9) is demonstrated to be violated in zircon standards in Wiedenbeck. et al. (1995).
Discrepancy Between Different Mineral Types in a Lava
The much-dated Ongeluk lava in the Transvaal Supergroup (figs. 1 and 2) is again used as an example where two different mineral types have been dated by U-Pb single crystal methods. Concordant U-Pb ages on ≈ 50 μm length, slightly rounded zircons vary between 200–800 Ma (table 1, fig. 4; Gutzmer and Beukes 1998, 221). There is also a nearly concordant zircon at 1819±3 Ma and one at 2009±6 Ma (table 1, fig. 4). The data for zircons from the Ongeluk lava are shown in table 1.
| Spot | U (ppm) | Th (ppm) | Th/U | 204Pb/206Pb | 4f206 | 207Pb*/206Pb* | 208Pb*/206Pb* | 206Pb*/238U | 207Pb*/235U | 208Pb/232Th | 206Pb* Age |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C.1-1 | 210 | 85 | 0.405 | 0.00007 | 0.12 | 0.0643±14 | 0.1230±31 | 0.124±2 | 1.10±3 | 0.0377±11 | 752±45 |
| C.2-1 | 89 | 7 | 0.079 | 0.00023 | 0.37 | 0.0616±43 | 0.0408±95 | 0.095±2 | 0.81±6 | 0.0502±118 | 660±149 |
| C.3-1 | 99 | 216 | 2.182 | 0.00202 | 3.24 | 0.0513±62 | 0.7135±168 | 0.086±2 | 0.61±8 | 0.0281±8 | 252±257 |
| C.4-1 | 1779 | 810 | 0.455 | 0 | 0 | 0.1274±2 | 0.1284±3 | 0.332±5 | 5.83±8 | 0.0937±13 | 2063±3 |
| C.5-1 | 212 | 130 | 0.613 | 0.00003 | 0.06 | 0.0567±16 | 0.2005±40 | 0.093±1 | 0.72±2 | 0.0303±8 | 482±61 |
| C.6-1 | 1355 | 36 | 0.027 | 0.00002 | 0.03 | 0.1109±3 | 0.0071±3 | 0.226±3 | 3.46±5 | 0.0614±27 | 1814±5 |
| C.7-1 | 342 | 97 | 0.284 | 0 | 0 | 0.0654±9 | 0.0920±20 | 0.131±2 | 1.18±2 | 0.0425±11 | 786±29 |
| C.8-1 | 2516 | 109 | 0.043 | 0 | 0.01 | 0.1112±2 | 0.0130±1 | 0.334±5 | 5.12±7 | 0.1003±17 | 1819±3 |
| C.9-1 | 519 | 14 | 0.027 | 0 | 0 | 0.1177±4 | 0.0076±3 | 0.374±5 | 6.07±9 | 0.1055±50 | 1921±6 |
| C.10-1 | 459 | 12 | 0.026 | -0.00001 | 0 | 0.1036±5 | 0.0091±2 | 0.195±3 | 2.79±4 | 0.0694±20 | 1689±9 |
| C.11-1 | 719 | 117 | 0.163 | 0.00021 | 0.33 | 0.1236±4 | 0.0391±8 | 0.359±5 | 6.12±9 | 0.0859±21 | 2009±6 |
| C.12-1 | 2237 | 170 | 0.076 | 0.00001 | 0.02 | 0.1181±2 | 0.0243±2 | 0.278±4 | 4.53±6 | 0.0886±14 | 1928±3 |
| C.13-1 | 1455 | 84 | 0.058 | 0.00004 | 0.06 | 0.1094±3 | 0.0093±3 | 0.260±4 | 3.92±6 | 0.0417±15 | 1790±4 |
| C.14-1 | 516 | 12 | 0.023 | -0.00001 | 0 | 0.0586±5 | 0.0056±2 | 0.088±1 | 0.71±1 | 0.0211±9 | 552±18 |
| C.15-1 | 401 | 108 | 0.269 | -0.00001 | 0 | 0.1066±3 | 0.0737±4 | 0.425±6 | 6.25±9 | 0.1167±18 | 1743±6 |
| C.16-1 | 616 | 79 | 0.128 | 0.00003 | 0.05 | 0.0573±7 | 0.0383±13 | 0.088±1 | 0.69±1 | 0.0262±10 | 502±25 |
| C.17-1 | 1917 | 198 | 0.103 | 0.00008 | 0.13 | 0.1102±2 | 0.0114±3 | 0.245±3 | 3.73±5 | 0.0270±9 | 1802±4 |
| C.18-1 | 143 | 60 | 0.42 | 0 | 0 | 0.0576±9 | 0.1334±23 | 0.082±1 | 0.65±2 | 0.0263±6 | 514±35 |
| C.19-1 | 4204 | 775 | 0.184 | 0.00005 | 0.09 | 0.1329±1 | 0.0516±2 | 0.344±5 | 6.31±9 | 0.0964±14 | 2137±2 |
The group of 200–800 Ma concordant zircons in fig. 4 is more than 1600 Ma younger than the ages from the baddeleyite grains in the same lava reported by Gumsley et al. (2017). The 1819±3 Ma nearly concordant zircon is 600 Ma younger than the baddeleyite. It has a U content of 2516 ppm, that is high. The zircon at 2009±6 Ma (table 1) is more than 400 Ma younger than the baddeleyite and has a U content of 719 ppm. The zircon and baddeleyite crystals therefore apparently give several different crystallization ages for the Ongeluk lava, and this is geologically not possible since the lava flowed out, cooled, and crystallized rapidly.
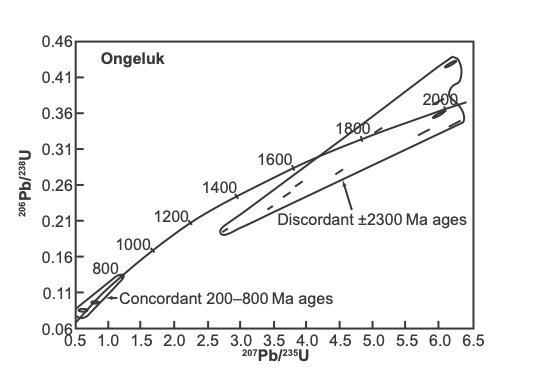
Fig. 4. Concordia plots of zircons from the Ongeluk lava analyzed by SHRIMP (after Gutzmer and Beukes 1998).
Baddeleyite is very susceptible to chemical weathering and therefore is thought to be a primary signature, indicating that the lava has not been altered significantly, thereby indicating that the zircons also give primary signatures. Young concordant populations of zircons have been observed in many tuff units throughout the Transvaal Supergroup (Gutzmer and Beukes 1998, 221).
In volcanic rocks or lava flows it is expected that single grains of zircons and baddeleyites from the lava should have the same ages because they crystallized at the same instant in time. The expected relative ages of single grains of zircons and baddeleyites in, for example, a lava flow can be written as an equality:
Age (Mineral A) = Age (Mineral B) = Age (Mineral C) (11)
However, as is seen in the Ongeluk lava example:
Radiometric Age (Mineral A) ≠ Radiometric Age (Mineral B) ≠ Radiometric Age (Mineral C) (12)
Therefore, as was observed in the examples, the equality in equation (11) is violated when the isotope ages are determined for single grains of zircons and baddeleyites in volcanic rocks.
Young Core, Old Rim Discrepancies
When geologists think about zircons that have experienced more than one period of growth, the core of the zircon is thought to be older than the rim. However, in many examples the isotope age of the core is younger than the rim. In the Limpopo metamorphic belt of southern Africa, Zeh et al. (2008) show zircon grains that, for example, have a rounded detrital core with an age of 2938 ± 49 Ma and a rim of 3231 ± 16 Ma. Another example is in the Jack Hills (Western Australia) zircon, where Cavosie et al. (2004) show a cathodoluminescence image of a zircon that has a core age of 3950 ± 20 Ma and a first inside rim of 4324 ± 6 Ma, and a second outside rim of 3676 ± 7 Ma. Cores can be younger than rims, if the cores had become metamict and the rims did not. However, the Pb escaping from the core would likely migrate into the crystal structure of the rim surrounding the core, causing the rim to look older. In zircons that display this type of isotope behavior, it may be very difficult to judge what is primary isotope behavior.
However, under normal circumstances the following inequality can be written based on the relative ages of cores and rims:
Age (Core) ≥ Age (Rim) (13)
However, as was seen in the above examples, often:
Radiometric Age (Core) < Radiometric Age (Rim) (14)
Therefore, the inequality in equation (13) is violated.
Zircon with High U Concentration that Does Not Display Visible Radiation Damage
During radioactive decay, gamma rays (Villard 1900) are emitted when alpha particles escape a nucleus of an atom (Rutherford and Soddy 1902). High amounts of alpha particles over a long period of time will damage the crystal structure of the zircon (Palenik, Nasdala, and Ewing 2003). The higher the concentration of radioactive elements in the zircon, the more alpha particles and gamma rays will be emitted because of more atoms decaying, increasing the likelihood of radiation damage to the crystal structure. However, often zircons are handpicked because they appear fresh (not discolored brown), and radiation damage is not indicated by cathodoluminescence or high magnification scanning electron microscope work on the zircons. For examples of this, see Dorland et al. (2006), analyses 7.1 (1177 ppm U), 8.1 (1899 ppm U), 12.1 (1337 ppm U), 13.1 (2171 ppm U, 3256 ppm Th), 14.1 (1346ppm U) of zircons from the Rust de Winter quartz porphyry of the lower Waterberg Group and several detrital zircons in Dorland (2004, 326) and Shröder, Beukes, and Armstrong (2016), from the Transvaal Supergroup, and red bed successions on the Kaapvaal craton (fig. 1).
These zircons that display no visible crystal damage by alpha particles are then analyzed by mass spectrometry and yet they can still have very high U concentrations (above 1000 ppm). For zircons in old rocks that have very high U and Th contents, there was sufficient time for alpha particles to damage the crystals. However, often high U and Th zircons in old rocks do not display damaged crystal structures.
Discordant Ages
Often when the radiometric ages from two isotope systems such as 206Pb/238U and 208Pb/232Th from the same analytical point are compared, the ages vary significantly. This difference in ages from two isotope systems is called discordance (Wetherill 1956), because the two isotope systems disagree.
Discordance is usually calculated as follows in older rocks (Vermeesch 2021):
Discordance %
= [1-(206Pb/238U age)/(207Pb/206Pb age)] × 100 (15)
Discordance is often associated with the high U concentrations in old rocks that have low Pb concentrations that do not reflect the old age of the rock. The common explanation for this is that Pb loss has occurred (Andersen, Elburg, and Magwaza 2019). There are however many examples of zircons that have high U that show less than 10% discordance (Huthmann et al. 2016).
Discordance also occurs in zircons that have a low U content. This can be seen in an example of analyzed detrital zircons from the Schelem Formation, Wolkberg Group (fig. 1), South Africa (Dorland 2004, 326). Fig. 5 shows the Concordia plot, fig. 6 shows the cathodoluminescence images, and table 2 shows the U-Pb data for the points that was analyzed by SHRIMP for these zircons.
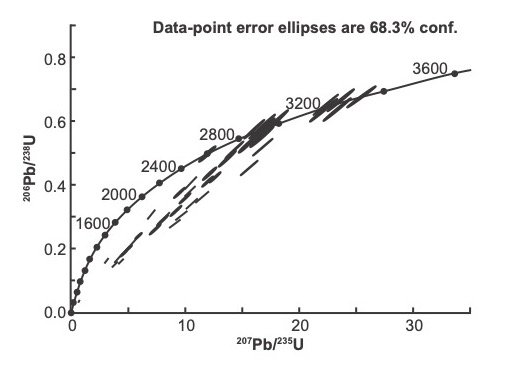
Fig. 5. Concordia plot of detrital zircons from the Schelem Formation, Wolkberg Group (after Dorland 2004).

Fig. 6. Cathodoluminescence images of zircons from the Schelem Formation, Wolkberg Group (from Dorland 2004).
There are many examples of zircons that have a medium to low U concentration (less than 300 ppm) that show greater than 10% discordance (see grain 19.1 that has 54 ppm U, 37 ppm Th) and is 46% discordant according to the equation (15) above, that is usually used for older rocks (table 2). At that level of U and Th concentrations it is unlikely that ejected alpha particles damaged the zircon crystal structure sufficiently to allow Pb loss. The low Pb concentrations in these zircons are a discrepancy.
| Grain Spot | (1) % 206Pbc | Ppm U | ppm Th | 232Th/238U | ppm 206Pb* | (1) 206Pb/238U Age | (1) 207Pb/206Pb Age | (1) 208Pb/232Th Age | % Discordant | (1) 207Pb*/206Pb* | ±% | (1) 207Pb*/235U | ±% | (1) 206Pb/238U | ±% | Err corr | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.1 | — | 38 | 13 | 0.35 | 18.9 | 2,964 | ±89 | 2,923 | ±18 | 3,030 | ±140 | -1 | 0.2123 | 1.1 | 17.08 | 3.9 | 0.584 | 3.8 | .960 |
| 2.1 | 0.10 | 146 | 56 | 0.40 | 65.3 | 2,697 | ±76 | 3,097.4 | ±9.8 | 939 | ±59 | 13 | 0.2366 | 0.62 | 16.95 | 3.5 | 0.519 | 3.5 | .985 |
| 3.1 | 0.09 | 130 | 82 | 0.65 | 74.4 | 3,279 | ±87 | 3,241.0 | ±8.1 | 3,239 | ±110 | -1 | 0.2591 | 0.52 | 23.68 | 3.4 | 0.663 | 3.4 | .988 |
| 4.1 | — | 32 | 16 | 0.51 | 15.0 | 2,830 | ±89 | 3,000 | ±19 | 2,742 | ±120 | 6 | 0.2226 | 1.2 | 16.91 | 4.0 | 0.551 | 3.9 | .956 |
| 5.1 | 0.37 | 333 | 256 | 0.79 | 99.8 | 1,923 | ±55 | 3,020.6 | ±8.4 | 1,105 | ±42 | 36 | 0.2255 | 0.52 | 10.81 | 3.3 | 0.348 | 3.3 | .988 |
| 6.1 | 0.37 | 273 | 232 | 0.88 | 72.8 | 1,735 | ±51 | 3,072.0 | ±8.8 | 2,549 | ±87 | 44 | 0.2329 | 0.55 | 9.92 | 3.4 | 0.309 | 3.3 | .987 |
| 7.1 | 0.21 | 792 | 734 | 0.96 | 152 | 1,297 | ±38 | 2,684.9 | ±6.9 | 383 | ±14 | 52 | 0.18351 | 0.42 | 5.64 | 3.3 | 0.2228 | 3.2 | .992 |
| 8.1 | 0.30 | 423 | 112 | 0.27 | 58.2 | 953 | ±30 | 2,735 | ±17 | 857 | ±44 | 65 | 0.1892 | 1.0 | 4.16 | 3.5 | 0.1594 | 3.4 | .957 |
| 9.1 | 0.05 | 54 | 37 | 0.70 | 12.6 | 1,544 | ±57 | 2,882 | ±17 | 1,426 | ±65 | 46 | 0.2069 | 1.0 | 7.72 | 4.3 | 0.271 | 4.1 | .971 |
| 11.1 | 0.41 | 187 | 261 | 1.45 | 58.3 | 1,991 | ±57 | 2,874 | ±11 | 469 | ±21 | 31 | 0.2060 | 0.70 | 10.28 | 3.4 | 0.362 | 3.3 | .979 |
| 12.1 | 0.17 | 384 | 863 | 2.32 | 107 | 1,809 | ±52 | 2,913.5 | ±7.0 | 657 | ±22 | 38 | 0.21103 | 0.43 | 9.42 | 3.3 | 0.324 | 3.3 | .991 |
| 13.1 | 0.36 | 364 | 166 | 0.47 | 116 | 2,021 | ±57 | 3,058.9 | ±6.9 | 1,780 | ±96 | 34 | 0.23099 | 0.43 | 11.73 | 3.3 | 0.368 | 3.3 | .992 |
| 15.1 | 0.28 | 256 | 217 | 0.88 | 84.1 | 2,083 | ±59 | 2,837.7 | ±9.3 | 2,332 | ±80 | 27 | 0.2014 | 0.57 | 10.59 | 3.3 | 0.381 | 3.3 | .985 |
| 16.1 | 0.98 | 506 | 549 | 1.12 | 130 | 1,670 | ±48 | 2,883 | ±11 | 987 | ±37 | 42 | 0.2071 | 0.69 | 8.45 | 3.4 | 0.2958 | 3.3 | .979 |
| 17.1 | 0.04 | 231 | 18 | 0.08 | 114 | 2,932 | ±78 | 2,990.7 | ±6.9 | 659 | ±150 | 2 | 0.22137 | 0.43 | 17.57 | 3.3 | 0.576 | 3.3 | .992 |
| 18.1 | 0.58 | 239 | 325 | 1.40 | 85.8 | 2,240 | ±63 | 2,940 | ±12 | 955 | ±36 | 24 | 0.2146 | 0.75 | 12.29 | 3.4 | 0.415 | 3.3 | .976 |
| 19.1 | 0.13 | 156 | 56 | 0.37 | 39.8 | 1,670 | ±51 | 2,866 | ±21 | 1,523 | ±69 | 42 | 0.2049 | 1.3 | 8.36 | 3.7 | 0.296 | 3.5 | .935 |
| 20.1 | 0.06 | 108 | 55 | 0.53 | 47.3 | 2,663 | ±73 | 2,873 | ±11 | 2,812 | ±100 | 7 | 0.2058 | 0.65 | 14.51 | 3.4 | 0.511 | 3.4 | .982 |
| 21.1 | 0.80 | 492 | 170 | 0.36 | 71.6 | 1,002 | ±30 | 2,867 | ±14 | 1,473 | ±59 | 65 | 0.2050 | 0.83 | 4.75 | 3.4 | 0.1681 | 3.3 | .969 |
| 22.1 | 0.26 | 236 | 102 | 0.45 | 85.9 | 2,271 | ±63 | 2,958 | ±14 | 2,350 | ±92 | 23 | 0.2170 | 0.86 | 12.63 | 3.4 | 0.422 | 3.3 | .968 |
| 23.1 | 0.17 | 281 | 265 | 0.98 | 123 | 2,655 | ±71 | 2,869.0 | ±7.4 | 2,618 | ±87 | 7 | 0.20533 | 0.45 | 14.43 | 3.3 | 0.510 | 3.3 | .991 |
| 24.1 | 0.37 | 343 | 197 | 0.59 | 112 | 2,075 | ±59 | 2,715 | ±16 | 2,565 | ±98 | 24 | 0.1869 | 0.99 | 9.79 | 3.5 | 0.380 | 3.3 | .958 |
| 25.1 | 0.19 | 157 | 103 | 0.68 | 61.7 | 2,419 | ±67 | 3,194.4 | ±9.2 | 1,967 | ±74 | 24 | 0.2515 | 0.58 | 15.79 | 3.4 | 0.455 | 3.3 | .985 |
| 26.1 | 0.26 | 2817 | 238 | 0.09 | 116 | 299.9 | ±9.4 | 2,512.7 | ±6.5 | 669 | ±25 | 88 | 0.16550 | 0.39 | 1.087 | 3.2 | 0.0476 | 3.2 | .993 |
| 27.1 | 0.52 | 624 | 98 | 0.16 | 133 | 1,421 | ±41 | 2,685 | ±21 | 2,341 | ±92 | 47 | 0.1835 | 1.3 | 6.24 | 3.5 | 0.2467 | 3.3 | .929 |
| 28.1 | — | 143 | 89 | 0.65 | 33.3 | 1,548 | ±46 | 2,890 | ±19 | 1,448 | ±53 | 46 | 0.2081 | 1.1 | 7.79 | 3.6 | 0.2714 | 3.4 | .946 |
| 29.1 | 0.04 | 68 | 42 | 0.64 | 34.2 | 2,971 | ±82 | 2,989 | ±11 | 3,059 | ±110 | 1 | 0.2211 | 0.70 | 17.86 | 3.5 | 0.586 | 3.5 | .980 |
| 30.1 | 0.09 | 158 | 178 | 1.17 | 55.6 | 2,214 | ±62 | 2,744 | ±10 | 2,609 | ±120 | 19 | 0.1902 | 0.64 | 10.75 | 3.4 | 0.410 | 3.3 | .982 |
| 31.1 | 0.86 | 491 | 404 | 0.85 | 81.5 | 1,129 | ±34 | 2,689 | ±15 | 540 | ±28 | 58 | 0.1839 | 0.88 | 4.86 | 3.4 | 0.1915 | 3.3 | .966 |
| 32.1 | 0.50 | 373 | 205 | 0.57 | 105 | 1,813 | ±51 | 2,925.4 | ±7.6 | 548 | ±30 | 38 | 0.2126 | 0.47 | 9.52 | 3.3 | 0.325 | 3.3 | .990 |
| 33.1 | 2.20 | 280 | 122 | 0.45 | 51.4 | 1,225 | ±37 | 2,699 | ±36 | 282 | ±94 | 55 | 0.1851 | 2.2 | 5.34 | 4.0 | 0.2094 | 3.3 | .838 |
| 34.1 | — | 122 | 63 | 0.53 | 62.9 | 3,040 | ±81 | 2,972 | ±10 | 3,043 | ±120 | -2 | 0.2189 | 0.64 | 18.18 | 3.4 | 0.603 | 3.3 | .982 |
| 35.1 | 0.39 | 499 | 338 | 0.70 | 123 | 1,616 | ±47 | 3,114 | ±12 | 1,864 | ±84 | 48 | 0.2391 | 0.74 | 9.39 | 3.4 | 0.2849 | 3.3 | .976 |
| 36.1 | 0.22 | 85 | 32 | 0.39 | 49.4 | 3,313 | ±88 | 3,336.3 | ±8.4 | 3,124 | ±120 | 1 | 0.2753 | 0.54 | 25.50 | 3.4 | 0.672 | 3.4 | .988 |
| 37.1 | 0.22 | 88 | 43 | 0.50 | 43.4 | 2,931 | ±80 | 2,905 | ±14 | 2,854 | ±120 | -1 | 0.2099 | 0.88 | 16.66 | 3.5 | 0.576 | 3.4 | .968 |
| 38.1 | 0.27 | 106 | 76 | 0.74 | 44.1 | 2,540 | ±71 | 2,894 | ±11 | 2,420 | ±90 | 12 | 0.2085 | 0.71 | 13.88 | 3.4 | 0.483 | 3.4 | .979 |
| 39.1 | 0.12 | 46 | 26 | 0.58 | 22.3 | 2,882 | ±81 | 2,941 | ±18 | 2,876 | ±120 | 2 | 0.2146 | 1.1 | 16.68 | 3.7 | 0.564 | 3.5 | .951 |
| 40.1 | — | 226 | 15 | 0.07 | 123 | 3,154 | ±82 | 3,201.7 | ±5.1 | 2,890 | ±110 | 1 | 0.25269 | 0.32 | 21.99 | 3.3 | 0.631 | 3.3 | .995 |
| 41.1 | 1.07 | 460 | 363 | 0.82 | 68.3 | 1,018 | ±31 | 2,675 | ±12 | 713 | ±26 | 62 | 0.1825 | 0.71 | 4.30 | 3.3 | 0.1710 | 3.2 | .977 |
| 42.1 | — | 64 | 17 | 0.28 | 35.5 | 3,220 | ±87 | 3,189 | ±10 | 3,596 | ±140 | -1 | 0.2506 | 0.66 | 22.39 | 3.5 | 0.648 | 3.4 | .982 |
| 43.1 | 0.03 | 171 | 54 | 0.33 | 84.7 | 2,934 | ±78 | 2,937.9 | ±7.3 | 2,888 | ±110 | 0 | 0.21423 | 0.45 | 17.03 | 3.3 | 0.576 | 3.3 | .991 |
| 44.1 | 0.04 | 34 | 14 | 0.41 | 14.6 | 2,602 | ±78 | 2,635 | ±18 | 2,548 | ±110 | 1 | 0.1780 | 1.1 | 12.20 | 3.8 | 0.497 | 3.6 | .959 |
| 45.1 | — | 67 | 26 | 0.41 | 36.4 | 3,159 | ±86 | 3,291 | ±12 | 3,239 | ±130 | 4 | 0.2675 | 0.76 | 23.32 | 3.5 | 0.632 | 3.4 | .977 |
| 46.1 | 0.27 | 202 | 303 | 1.55 | 53.2 | 1,721 | ±50 | 2,833.9 | ±9.3 | 224 | ±10 | 39 | 0.2009 | 0.57 | 8.48 | 3.4 | 0.306 | 3.3 | .985 |
| 47.1 | 0.01 | 115 | 137 | 1.22 | 57.1 | 2,930 | ±78 | 2,860.4 | ±7.7 | 2,893 | ±98 | -2 | 0.20425 | 0.47 | 16.21 | 3.4 | 0.575 | 3.3 | .990 |
| 48.1 | — | 59 | 30 | 0.53 | 31.8 | 3,163 | ±86 | 3,210.8 | ±9.5 | 3,080 | ±110 | 1 | 0.2542 | 0.60 | 22.20 | 3.5 | 0.633 | 3.4 | .985 |
| 49.1 | 0.36 | 82 | 42 | 0.53 | 30.9 | 2,336 | ±67 | 2,869 | ±15 | 932 | ±57 | 19 | 0.2054 | 0.89 | 12.36 | 3.5 | 0.437 | 3.4 | .967 |
| 50.1 | — | 96 | 95 | 1.02 | 47.6 | 2,940 | ±79 | 2,954.4 | ±8.6 | 2,929 | ±100 | 0 | 0.2164 | 0.53 | 17.24 | 3.4 | 0.578 | 3.4 | .988 |
| 51.1 | 0.01 | 303 | 18 | 0.06 | 145 | 2,863 | ±75 | 2,926.8 | ±5.0 | 2,730 | ±130 | 2 | 0.21277 | 0.31 | 16.40 | 3.3 | 0.559 | 3.3 | .996 |
| 52.1 | 0.01 | 199 | 29 | 0.15 | 95.1 | 2,855 | ±76 | 2,921.9 | ±5.9 | 2,809 | ±110 | 2 | 0.21213 | 0.37 | 16.29 | 3.3 | 0.557 | 3.3 | .994 |
| 53.1 | 0.02 | 592 | 46 | 0.08 | 159 | 1,752 | ±50 | 2,561.9 | ±5.1 | 1,726 | ±70 | 32 | 0.17043 | 0.31 | 7.34 | 3.2 | 0.312 | 3.2 | .996 |
Discordance may be calculated between radioisotope systems for which the isotope concentrations have been analyzed. For example, discordance can be calculated between the 208Pb/232Th age and the 206Pb/238U age with the following formula:
Discordance %
= [1-(208Pb/232Th age)/(206Pb/238U age)] × 100 (16)
If equation (16) is applied to calculate discordance for the data presented in table 2, many of the grains that are more than 10% discordant according to the equation (15) become less than 10% discordant. Grain 8.1 has a 206Pb/238U age of 953±30 Ma and is 10% discordant with the 208Pb/232Th age, and 65% discordant with 207Pb/206Pb age. Analysis 19.1, that has a 206Pb/238U age of 1670±51 Ma (table 2) is less than 8% discordant in terms of equation (16) but is 42% discordant in terms of equation (15). Another example of this is grain 53.1 that has a 206Pb/238U age of 1752±50 Ma (table 2) and is less than 2% discordant in terms of equation (16) but is 32% discordant in terms of equation (15). Therefore, depending on which isotope systems are being compared, different amounts of discordance are observed.
An equality can be written from what is known about relative ages of different isotope systems:
Radiometric Age (Isotope system 1)
= Radiometric Age (Isotope system 2)
= Radiometric Age (Isotope system 3) (17)
However, in ALL data sets produced on U/Pb ages:
Radiometric Age (Isotope system 1)
≠ Radiometric Age (Isotope system 2)
≠ Radiometric Age (Isotope system 3) (18)
Therefore, equality in equation (17) is often violated, practically in every dataset ever produced of U/Pb radiometric ages. Here, references can be made to all of these datasets in literature.
An age of 953±30 Ma in the Wolkberg Group (fig. 1) will cause a stratigraphical isotope discrepancy with the overlying Transvaal Supergroup that is thought to be older than 2600 Ma (Schröder, Beukes, and Armstrong 2016), and a discrepant intrusive isotope relationship with the Bushveld Complex that is thought to have been intruded at around 2057 Ma (Mungall, Kamo, and McQuade 2016).
Distribution or Mixing Pattern of Elements in Zircon Crystals Where It is Expected that Pb Loss has Occurred
In a zircon that looks “young,” and it is suspected that loss of radiogenic Pb has occurred, the spatial distribution of the Pb, and the other elements in the zircon can be analyzed. It is likely that there will be a disturbance in the spatial distribution pattern of the Pb that indicates that Pb loss took place. However, if the distribution pattern of the Pb is even and undisturbed compared to known Pb distribution patterns in zircons present in different rocks, it can be inferred that Pb loss did not take place, and that the zircon is truly “young.”
Discussion
Nine types of discrepancies between the relative ages and the radioisotope ages have been described. These include:
- In a normal sedimentary rock succession, older radioisotope ages are on top of younger radioisotope ages
- Dolerite that has older radioisotope ages than the youngest rock it intrudes
- Zircons in lava where the radioisotope age difference between the oldest and the youngest zircon is more than 100 Ma
- Discrepancy between analytical spots in the same zircon in volcanic rocks and dolerite
- Radioisotope age differences between baddeleyite and zircon in the same lava of more than 1500 Ma
- Metamorphic zircons which have cores that are hundreds of Ma younger radioisotope ages than rims, where the cores developed first
- Zircons with high U concentrations (above 1000 ppm) that do not display visible radiation damage to the crystals by alpha particles
- Discordant data where the radioisotope ages from two isotope systems do not agree
- Zircon is young due to supposed Pb loss but there is no disturbance in the spatial distribution pattern of elements
There is a strong likelihood that the discrepancies presented are occurring due to primary isotope behavior. It is easier to explain relative geological age relationships than it is to force radioisotope ages based on calculations from measurements of U-Pb isotopes to fit these relationships. If the radioisotope age relationships do not follow the relative geological age relationships, it is likely that the relative geological age relationships still give the correct interpretation. This leaves the discrepant isotope relationships difficult to explain.
In the past it has been concluded that the radioactive decay rate and therefore half-life is constant under all conditions (Rutherford, Chadwick, and Ellis 1930). However, in recent years, decay rates have been measured that vary and a correlation has been described between the sun’s distance from the earth and the sun’s activity and nuclear decay rates (Jenkins et al. 2008; O’Keefe et al. 2012). Reduced radioactivity has also been described for tritium surrounded by small titanium particles (Reifenschweiler 1994).
Solar activity and distance, and chemical compounds in the crystal structure of zircon could therefore be investigated to explain the discrepancies between relative geological ages and radioisotope ages from zircon. However, an entirely new hypothesis could also be possible for the discrepant radioisotope ages.
Hypothesis
Gamow (1928) described radioactivity as a quantum tunneling process, where alpha particles escape the strong nuclear force due to their wave function extending beyond the reach of the strong nuclear force. This creates the possibility that the alpha particles can be found outside the nuclei of radioactive atoms, which occur when alpha decay takes place. It would therefore appear that alpha decay would be more likely to occur when the protons and neutrons in the nuclei of radioactive atoms are in specific configurations. For example, some 238U atoms may have a nuclei proton-neutron configuration where alpha decay is more likely to take place than in other 238U atoms. For 238U there may therefore exist slower and faster decaying atoms. Gentry et al. (1974) noted that 210Po halos indicate that radioactive decay took place in the past at much faster rates than today. From the general trends in radiometric ages, it may then follow that the faster decaying 238U atoms go first into the crystal structures of minerals such as zircon, and the slower decaying 238U atoms later in a fractionation process. Such a fractionation process would explain why volcanic rocks at the bottom of the stratigraphic column give older radiometric ages than those at the top. However, because fractionation is not a 100% efficient process, the discrepancies could be explained, where some faster decaying 238U atoms may go into the crystal structures after some slower decaying 238U atoms went into the crystal structures before, causing the discrepant radiometric ages, and the radiometric ages appear to be inverted. The consequence of this is that there may not be a lot of time between the oldest basement rocks in the South African geology and the youngest rocks in the stratigraphy if fractionation of this sort occurs.
Local fractionation could explain the differences that are seen in radioisotope ages of single zircons in volcanic rocks that crystallized at the same instant. In a localized area, fast decaying 238U atoms may have gone into the crystals that crystallize first, and the crystals that cool and crystallize a few moments later may have more of the slow decaying 238U atoms so that when they are analyzed they appear younger.
Minerals that have high U content but do not show crystal damage due to the ejection of alpha particles may be that way because they are much younger than the radioisotope ages indicate, and radioactive decay has not had time to damage the crystal structures.
The discrepancies cannot be explained by constant half-lives, since constant half-lives would always produce radiometric ages that are always in sequence from old to young. During radioisotope age determinations, only atomic mass is considered. However, fractionation of this sort cannot be detected by atomic mass alone. Since it would be impossible to measure proton-neutron configuration in the nuclei of atoms due to the Heisenberg uncertainty principle, only the effects of this type of fractionation could be detected where it would manifest itself as discrepancies between the relative ages that we know from the geology, and the radiometric isotope ages.
Therefore, a hypothesis is proposed as follows:
There exists fractionation in radioactive atoms of the same atomic mass based on proton-neutron configurations in their nuclei, causing faster and slower decaying atoms of the same atomic mass.
Proposed Experiments
Experiments may be performed that could falsify or verify the proposed hypothesis. These experiments could be performed on naturally occurring rocks and in salt crystals produced under controlled conditions in a laboratory.
Experiments in lavas that flowed out recently
If a lava flowed out very recently it would be expected that there would be undetectable concentrations of 207Pb and 206Pb in the zircon and baddeleyite crystals found in the lava. It would also be expected that there would be very few fission tracks in the zircon and baddeleyite crystals. If larger than expected concentrations of 207Pb, 206Pb, and fission tracks are found in the zircon and baddeleyite crystals of these lavas, it would indicate that 235U and 238U decayed faster than expected. Measurements of these very young zircon and baddeleyite crystals can be repeated several times over a period of a few weeks to see if the concentrations of 207Pb and 206Pb change. If the concentrations of 207Pb and 206Pb increase perceptibly between measurements it would be conclusive evidence that faster decaying 235U and 238U atoms exist because very little change would be expected in the concentrations of 207Pb and 206Pb during such a short period.
Laboratory experiment
It is proposed that an experiment can be set up in a laboratory to create and monitor possible discrepancies under controlled conditions. The experiment could be set up as outlined in figs. 7 and 8.
Salt crystals would be grown that incorporate radioactive elements into their crystal structures (fig. 7). The growth of the crystal structures would be carefully observed with a camera. The actual growth time of the crystals would therefore be accurately known. The grown crystals would then be subjected to micro-analysis as shown in fig. 8. The radiometric ages from different positions on the crystals would then be compared to the actual ages as documented by the camera to evaluate if discrepancies exist between the actual and radioisotope ages. A radioactive element with a short enough half-life whose decay rate can be measured over perhaps a few months needs to be utilized. It would be best if such an element that undergoes alpha decay could be used, but perhaps elements that undergo beta decay could also be used. Due to the difficulties with working with radioactive material, it must first be evaluated how such an experiment could be performed safely.
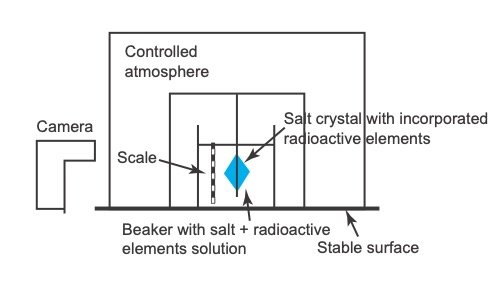
Fig. 7. Laboratory experiment set up.
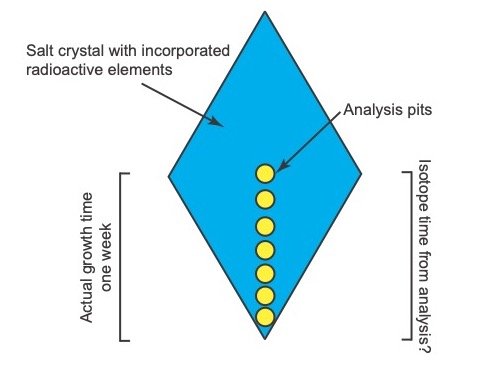
Fig. 8. Configuration of micro-analysis of a grown salt crystal.
Evaluation of analytical data of standards
Zircons used as standards in SHRIMP or other micro-analyses have many analytical spots in the same zircon crystals. These zircon standards are from rocks that cooled rapidly and therefore all the analytical spots should have the same radiometric age in terms of U/Pb geochronology, as predicted by the theory of radioactivity. An analysis could be performed on standard zircons to evaluate if there are radiometric age discrepancies between spots and thus between isotope systems.
Element distribution patterns in “young” Makganyene zircon
It is claimed that Pb loss occurred following the concordia in the “young” detrital zircons of the Makganyene Formation (Ngobeli 2019. 352). As a result of that process there could be concordant analytical spots in zircons in which Pb loss occurred. However, it can be reasonably assumed that Pb loss would impact the element distribution pattern in the zircons. If Pb loss did occur in these zircons, the element distribution pattern would not be even, but show disturbances.
14C in coal beds
Some coal beds contain measurable amounts of 14C (Giem 2001). The half-life of 14C is 5,730 years. Theoretically, there would therefore not be enough 14C in the coal beds to measure it, because those coal beds are dated at millions of years old. There are some claimed explanations for this, such as contamination from young sources. However, if some 14C in these coals could be isolated and concentrated, the half-life of this 14C could be measured. If the half-life of this 14C is longer than that of modern 14C, it would be evidence that there are fast and slow decaying 14C atoms.
Conclusions
The geological timescale is regarded by most geologists as the key to understanding how different geological processes took place over supposed millions of years. It is based mostly on U-Pb radiometric ages from minerals such as zircon and baddeleyite found in many rocks. One of the key assumptions of radiometric dating is that radioactive elements of the same atomic mass have the same stable lengths of their half-lives. This assumption is challenged by nine problems of discrepancies that exist between the relative geological ages and radiometric ages, as documented here. A hypothesis has been proposed that questions if radiometric age dating is properly understood in light of the changes that the science of radioactive decay has undergone. First, the deterministic outlook of particle behavior has changed towards a wave-particle dualistic-probabilistic model. And second, the analytical techniques have advanced to give more details about radioactive and stable daughter isotopes on a single crystal basis. An objective experiment under controlled conditions could be performed to test the hypothesis of slow and fast decaying atoms with the same atomic mass. This might be an interdisciplinary study, as chemists and physicists could potentially resolve the problems found by geologists in their exhaustive work of measuring the radioisotope ages of rocks.
Acknowledgements
I want to thank my wife, Maria, for her patience and the many discussions we have had about radioactivity. My native language is Afrikaans, and this causes many difficulties to reviewers and editors. I thank Cliff Delaporte who reviewed the paper before I submitted it, and the reviewers Andrew Snelling, Ken Coulson and an anonymous reviewer for their patience with my English, and also for helpful advice and editorial assistance. I am thankful for their sincere and humble guidance.
Soli Deo Gloria
References
Andersen, Tom, Marlina A. Elburg, and Boniswa N. Magwaza. 2019. “Sources of Bias in Detrital Zircon Geochronology: Discordance, Concealed Lead Loss and Common Lead Correction.” Earth-Science Reviews 197 (October): 1–15.
Bau, Michael, Rolf L. Romer, Volker Lüders, and Nicolas J. Beukes. 1999. “Pb, O, and C Isotopes in Silicified Mooidraai Dolomite (Transvaal Supergroup, South Africa): Implications for the Composition of Paleoproterozoic Seawater and ‘Dating’ the Increase of Oxygen in the Precambrian Atmosphere.” Earth and Planetary Science Letters 174, nos. 1–2 (December 30): 43–57.
Beukes, Nicolas Johannes, Clarissa Vorster, and Dirk Frei. 2013. “Detrital Zircon Age Constraint of the Makganyene Snowball Earth Event (South Africa) at 2.25–2.22 Ga: The Youngest of Four Huronian Glaciations?” Poster presented at GSA Annual Meeting 2013, Denver, USA.
Buick, Ian S., Roland Maas, and Roger Gibson. 2001. “Precise U-Pb Titanite Age Constraints on the Emplacement of the Bushveld Complex, South Africa.” Journal of the Geological Society of London 158, no. 1 (January): 3–6.
Cairncross, Bruce. 2005. A Field Guide to Rocks and Minerals of Southern Africa. Pretoria, South Africa: Struik Publishers.
Cavosie, Aaron J., Simon A. Wilde, Dunyi Liu, Paul W. Weiblen, and John W. Valley. 2004. “Internal Zoning and U–Th–Pb Chemistry of Jack Hills Detrital Zircons: A Mineral Record of Early Archean to Mesoproterozoic (4348–1576 Ma) Magmatism.” Precambrian Research 135, no. 4 (December 15): 251–279.
Cherniak, D. J. and E. B. Watson. 2000. “Pb Diffusion in Zircon”. Chemical Geology 172, nos. 1–2 (February 1): 5–24.
Cornell, David H., S. S. Schütte, and Bruce L. Eglington. 1996. “The Ongeluk Basaltic Andesite Formation in Griqualand West, South Africa: Submarine Alteration in a 2222 Ma Proterozoic Sea.” Precambrian Research 79, nos. 1–2 (July): 101–123.
Dorland, Herman C. 2004. “Provenance Ages and Timing of Sedimentation of Selected Neoarchean and Paleoproterozoic Successions on the Kaapvaal Craton.” PhD diss. Rand Afrikaans University, Johannesburg.
Dorland, Herman C., Nicolas J. Beukes, Jens Gutzmer, David A. D. Evans, and Richard A. Armstrong. 2006. “Precise SHRIMP U-Pb Zircon Age Constraints on the Lower Waterberg and Soutpansberg Groups, South Africa.” South African Journal of Geology 109, nos. 1–2 (June): 139–156.
Gamow, George. 1928. “The Quantum Theory of Nuclear Disintegration.” Nature 122, no. 3082 (24 November): 805– 806.
Gentry, Robert V., L. D. Hulett, S. S. Cristy, J. F. Mclaughlin, J. A. McHugh, and M. Bayard. 1974. “‘Spectacle’ Array of 210Po Halo Radiocentres in Biotite: A Nuclear Geophysical Enigma.” Nature 252, no. 5484 (13 December): 564–566.
Giem, Paul A. 2001. “Carbon-14 Content of Fossil Carbon.” Origins 51 (January1): 6–30
Gumsley, Ashley P., Kevin R. Chamberlain, Wouter Bleeker, Ulf Söderlund, Michiel O. de Kock, Emilie R. Larsson, and Andrey Bekker. 2017. “Timing and Tempo of the Great Oxidation Event.” Proceedings of the National Academy of Sciences of the United States of America 144, no. 8 (February 21): 1811–1816.
Gutzmer, Jens, and Nicholas J. Beukes. 1998. “High Grade Manganese Ores in the Kalahari Manganese Field: Characterisation and Dating of the Ore-forming Events.” Unpublished Report. Rand Afrikaans University, Johannesburg.
Harmer, Robin E. and Richard A. Armstrong. 2000. “New Precise Dates on the Acid Phase of the Bushveld and Their Implications.” Abstract. Workshop on the Bushveld Complex, 18–21 November. Burgersfort: University of Witwatersrand, Johannesburg.
Huthmann, Florian M., Marina A. Yudovskaya, Dirk Frei, and Judith A. Kinnaird. 2016. “Geochronological Evidence for an Extension of the Northern Lobe of the Bushveld Complex, Limpopo Province, South Africa.” Precambrian Research 280 (July): 1–29.
Jenkins, Jere H., Ephraim Fischbach, John B. Buncher, John T. Gruenwald, Dennis E. Krause, and Joshua J. Mattes. 2008. “Evidence for Correlations Between Nuclear Decay Rates and Earth-Sun Distance.” Astroparticle Physics 32, no. 1 (August): 42–46.
Mungall, James E., Sandra L. Kamo, and Steward McQuade. 2016. “U–Pb Geochronology Documents Out-of-Sequence Emplacement of Ultramafic Layers in the Bushveld Igneous Complex of South Africa.” Nature Communications 7 (November). https://doi.org/10.1038/ncomms13385.
Ngobeli, Rebeun. 2019. “A Comparison Between Detrital Zircon Age Populations of the Koegas Subgroup of the Ghaap Group and Overlying Makganyene Diamictite of the Postmasburg Group, Transvaal Supergroup, Griqualand West Area.” MSc diss. University of Johannesburg, South Africa.
O’Keefe, D., B. L. Morreale, R. H. Lee, John B. Buncher, Ephraim Fishbach, T. Gruenwald, J. H. Jenkins, D. Javorsek II, and P. A. Sturrock. 2012. “Spectral Content of 22Na/44Ti Decay Data: Implications for a Solar Influence.” Astrophysics and Space Science 344 (5 January), 297–303.
Palenik, Christopher S., Lutz Nasdala, and Rodney C. Ewing. 2003. “Radiation Damage in Zircon.” American Mineralogist 88, nos. 5–6 (May 1): 770–781.
Pickard, April L. (2003). “SHRIMP U-Pb Zircon Ages for the Palaeoproterozoic Kuruman Iron Formation, Northern Cape Province, South Africa: Evidence for Simultaneous BIF Deposition on Kaapvaal and Pilbara Cratons.” Precambrian Research 125, nos. 3–4 (25 August): 275–315.
Reifenschweiler, Otto. 1994. “Reduced radioactivity of tritium in small titanium particles.” Physics Letters A 184, no. 2 (January 3): 149–153.
Rutherford, Ernest, and Frederick Soddy. 1902. “The Cause and Nature of Radioactivity.” Philosophical Magazine 4: 370–396.
Rutherford, Ernest, James Chadwick and Charles D. Ellis. 1930. Radiations from Radioactive Substances. Cambridge, United Kingdom: Cambridge University Press.
Schröder, Stefan, Nicholas J. Beukes, and Richard A. Armstrong. 2016. “Detrital Zircon Constraints on the Tectonostratigraphy of the Paleoproterozoic Pretoria Group, South Africa.” Precambrian Research 278 (June): 362–393.
Shumlyanskyy, Leonid, Anna Nosova, Kjell Billström, Ulf Söderlund, Per-Gunnar Andréasson, and Oksana Kuzmenkova. 2016. “The U-Pb Zircon and Baddeleyite Ages of the Neoproterozoic Volyn Large Igneous Province: Implication for the Age of the Magmatism and the Nature of a Crustal Contaminant.” GFF 138, no. 1: 17–30.
Sumner, Dawn Y., and Samuel A. Bowring. 1996. “U-Pb Geochronologic Constraints on Deposition of the Campbellrand Subgroup, Transvaal Supergroup, South Africa.” Precambrian Research 79, nos. 1–2 (July): 25–35.
Vermeesch, Pieter. 2021. “On the Treatment of Discordant Detrital Zircon U-Pb Data.” Geochronology 3: 247–257.
Villard, Paul U. 1900. “Sur la Réflexion et la Réfraction des Rayons Cathodiques et des Rayons Déviables de Radium.” Comptes rendus de l’Académie des Sciences 130: 1010–1012.
Von Lindheim-Westerink, W. A. M. 2010. “Rondblik. Bewijsen of Geloven?” Nader Bekeken 17, no. 11 (November): 1–6.
Wetherill, George W. 1956. “Discordant Uranium-Lead Ages, I.” EOS, Transactions American Geophysical Union, 37. no. 3 (June): 320–326.
Wiedenbeck, M., P. Allé, F. Corfu,W. L. Griffen, M. Meier, F. Oberli, A. Von Quadt, J. C. Roddick, and W. Spiegel. 1995. “Three Natural Zircon Standards for U–Th–Pb, Lu–Hf, Trace Element and REE Analyses.” Geostandards and Geoanalytical Research 19, no. 1 (April): 1–23.
Wingate, Michael T. D. 2001. “SHRIMP Baddeleyite and Zircon Ages for an Umkondo Dolerite Sill, Nyanga Mountains, Eastern Zimbabwe.” South African Journal of Geology 104, no. 1 (March): 13–22.
Zeh, Armin, Axel Gerdes, Reiner Klemd, and Jackson M. Barton Jr. 2008. “U–Pb and Lu–Hf Isotope Record of Detrital Zircon Grains from the Limpopo Belt—Evidence for Crustal Recycling at the Hadean to Early-Archean Transition.” Geochimica et Cosmochimica Acta 72, no. 21 (November 1): 5304–5329.





