Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Over the last 66 years numerous determinations have been made of the 187Re half-life and decay constant. With the measurement technology having improved, the determinations over the last 20 years have resulted in close agreement between the four determination methods—direct physical counting and in-growth experiments, and radioisotope age comparisons using molybdenites and groups of meteorites. Thus the 187Re half-life and decay constant values of 41.577 ± 0.12 Byr and 1.6668 ± 0.0034 × 10-11 per year respectively have now been adopted for standard use by the uniformitarian geological community. These values are based on determinations recalibrating Re-Os model ages of molybdenites by forcing them (essentially by circular reasoning) to agree with the U-Pb concordia-Pb-Pb intercept ages of zircons from the same 11 magmatic-hydrothermal systems dating from ca. 90 Ma to ca. 2670 Ma. This value is essentially identical to the best of the recent determinations using groups of iron meteorites. It is also within the ± uncertainty range of the half-life values obtained by the best of the physical direct counting and in-growth experiments. Yet, in spite of such experiments directly measuring 187Re decay and its decay product 187Os respectively, preference has been given to the half-life value determined by forcing the Re-Os data to agree with U-Pb dates. But many unprovable assumptions are also involved, not least being that the radioisotope systems closed at the same time and subsequently remained closed. Furthermore, even this “gold standard” has unresolved uncertainties due to the U decay constants being imprecisely known, and to measured variations of the 238U/235U ratio in terrestrial rocks and minerals and in meteorites. Both of these factors are so critical to the U-Pb method, as well as the additional factor of knowing the initial concentrations of the daughter and index isotopes, so it should not be used as a standard to determine other decay constants. In any case, the half-life of 187Re has been shown to be dependent on environmental conditions such as the degree of ionization. Fluctuations in nuclear decay rates have also been observed to correlate with solar activity for a few other isotopes, while there is evidence decay rates of the radioisotopes used for rock dating have not been constant in the past. This only serves to highlight that if the Re-Os dating method has been calibrated against the U-Pb “gold standard” with all these uncertainties, then it cannot be absolute, and therefore it cannot be used to reject the young-earth creationist timescale. Indeed, current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Keywords: radioisotope dating, decay constants, half-lives, rhenium-187, 187Re, β decay, direct counting, in-growth experiments, geological comparisons, molybdenites, iron meteorites, U-Pb “gold standard,” U decay constants, 238U/235U ratio, environmental conditions
Introduction
Radioisotope dating of rocks and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks. Many in both the scientific community and the general public around the world thus remain convinced of the earth’s claimed great antiquity.
However, accurate radioisotopic age determinations require that the decay constants of the respective parent radionuclides be accurately known and constant in time. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with direct half-life determinations are, in most cases, still at the 1% level, which is still significantly better than any radioisotope method for determining the ages of rock formations. However, even uncertainties of only 1% in the half-lives lead to very significant discrepancies in the derived radioisotope ages. The recognition of an urgent need to improve the situation is not new (for example, Min et al. 2000; Renne, Karner, and Ludwig 1998). It continues to be mentioned, at one time or another, by every group active in geo- or cosmochronology (Schmitz 2012).
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further inroads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was the issue of how reliable have been the determinations of the radioisotope decay rates, which are so crucial for calibrating these dating “clocks.” Indeed, before this present series of papers (Snelling 2014a, b) there have not been any attempts in the creationist literature to review how the half-lives of the parent radioisotopes used in long-age geological dating have been determined and to collate their determinations to discuss the accuracy of their currently accepted values. After all, accurate radioisotope age determinations depend on accurate determinations of the decay constants or half-lives of the respective parent isotopes. The reliability of the other two assumptions these absolute dating methods rely on, that is, the starting conditions and no contamination of closed systems, are unprovable. Yet these can supposedly be circumvented somewhat via the isochron technique, because it is independent of the starting conditions and is sensitive to revealing any contamination, which is still significantly better than any radioisotope method for determining the ages of rock formations. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. That this is common practice is illustrated with numerous examples from the literature by Faure and Mensing (2005) and Dickin (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is arbitrary and therefore is not good science, because it is merely assumed their “aberrant” values are due to contamination rather than that being proven to be so. Indeed, in order to discard such outliers in any data set, one must establish a reason for discarding those data points which cannot be reasonably questioned.
In order to rectify this deficiency, Snelling (2014a,b) has documented the methodology behind and history of determining the decay constants and half-lives of the parent radioisotopes 87Rb and 176Lu used as the basis for the Rb-Sr and Lu-Hf long-age dating methods respectively. He showed that there is still some uncertainty in what the values for these measures of the 87Rb and 176Lu decay rates should be. This is especially the case with determinations of the 176Lu decay rate by physical direct counting experiments. Furthermore, the determined values differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rate of isotopes such as 87Rb used for deep-time dating that makes a precise measurement of that decay rate so difficult. Thus it could be argued that direct measurements of their decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology employed by the secular community in their rock dating methods. Indeed, both the 87Rb and 176Lu decay half-lives have ultimately been calibrated against the U-Pb radioisotope systems, yet there are now known measured variations in the 238U/235U ratio that is critical to that method (Brennecka and Wadhwa 2012; Hiess et al 2012).
Therefore, the aim of this contribution is to further document the methodology behind and history of determining the present decay constants and half-lives of the parent radioisotopes used as the basis for the long-age dating methods. We need to explore just how accurate these determinations are, whether there really is consensus on standard values for the half-lives and decay constants, and just how independent and objective the standard values are from one another between the different methods. Of course, it is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life measurements because these are difficult measurements to make. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks, and the question remains as to whether the half-life values for each long-lived parent radioisotope are independently determined. We continue here with determinations of the rhenium-187 (187Re) decay rate, which is the basis for the Re-Os dating method.
Rhenium and Rhenium-187 Decay
With an atomic number Z of 75, rhenium (Re) is element number 75 and appears in the sixth period on the periodic table. Although Re is chemically related to Mn and Tc in the group or column VIIB, its chemical properties are more similar to those of Mo (Z = 42), which it replaces in Mo-bearing minerals such as molybdenite (MoS2) (Faure and Mensing 2005). Rhenium radioactively decays to osmium (Z = 76), its neighboring element, yet Os is a member of the platinum group elements (PGEs) in group VIII of the periodic table—ruthenium (Ru), rhodium (Rh), palladium (Pd), osmium (Os), iridium (Ir), and platinum (Pt). Both Re and Os have several valences consistent with their electron configurations—Re (7+, 6+, 4+, 2+, and 1-) and Os (8+, 6+, 4+, 3+, and 2+). Additionally, their ionic radii in the 4+ valence state are identical at 0.71 Å, and both elements are strongly siderophile (iron-loving). The ionic radius of Re4+ (0.71 Å) is also similar to that of Mo4+ (0.68 Å), and their electronegativities are virtually identical (1.9 for Re and 1.8 for Mo), which explains why Re4+ can replace Mo4+ in molybdenite and other Mo-bearing sulfide minerals (Faure and Mensing 2005). Furthermore, Re4+ tends to occur in Cu sulfide minerals, presumably because Re4+ is captured in place of Cu2+ (ionic radius of 0.69 Å and electronegativity of 1.9).
Re and Os concentrations are generally much higher in chondrite and iron meteorites, in which they are highly correlated, than in most terrestrial rocks (Faure and Mensing 2005). Iron meteorites have average concentrations of 987 ppb Re and 15,260 ppb Os, whereas ordinary chondrites contain on average only 62.6 ppb Re and 690 ppb Os. Thus it has been feasible to use the Re-Os dating method on iron meteorites. On the other hand, the average concentrations of Re and Os in terrestrial igneous rocks are less than 1 ppb for Re and less than 3 ppb for Os. However, granitic gneisses and shales have elevated Re concentrations ranging up to 200 ppb, making it possible to use the Re-Os dating method on organic-rich black shales with their high Re concentrations (Schmitz 2012), the only example of radioisotope dating methods having been used directly on sedimentary rocks. Whereas most rock-forming silicate minerals have low Re and low Os concentrations, molybdenite (MoS2) and Cu-Ni-PGE sulfides (for example, pentlandite, chalcopyrite, and pyrrhotite) have high Re and low Os concentrations of 100–100,000 ppb and 6–900 ppb respectively, which has enabled their use for Re-Os dating of sulfide ore deposits. Re typically exists at the ppm level in molybdenite, whereas no Os is believed to be incorporated into molybdenite during its formation (Stein et al. 2001). Thus measured Os is assumed to be radiogenic 187Os accumulated in situ from 187Re decay, and thus model molybdenite Re-Os ages can presumably be calculated from the Re-Os isotopic analyses of single samples. For multiple molybdenite samples assumed to have the same paragenesis the Re-Os isochron approach is employed to supposedly verify zero initial or common 187Os and document presumed isochroneity of the supposedly related samples. The minerals magnetite, ilmenite, and garnet with average Re concentrations of 4–13 ppb have been suggested as having future potential for radioisotope dating by the Re-Os method. Of course, this implies that the technique used has to accurately measure very miniscule amounts of Os in small samples supposedly hundreds of millions of years old and then separate and measure from that miniscule amount the radiogenic Os compared to the primordial and cosmogenic Os.
Rhenium has two naturally occurring isotopes 185Re and 187Re whose abundances are 37.4% and 62.6% respectively (Shirey and Walker 1998). 187Re is radioactive and emits β--particles as it decays to 187Os, which is one of the seven naturally occurring isotopes of Os. The relevant decay scheme is depicted as:
187Re → 187Os + β- + v̄ + Q
where β- is a negatively charged β-particle, ν is an anti-neutrino, and Q is the total decay energy (0.00265 MeV).
There are two parameters by which the decay rate is measured and expressed, namely, the decay constant (λ) and the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, whereas the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:-
t½ = ln 2 / λ = 0.693 / λ
The decay rate of 187Re has been difficult to determine because the endpoint energy of the β-spectrum is only about 2.6 keV. Similarly, the total decay energy is extremely low at 2.65 keV, even compared with that for 87Rb at 275 keV. This makes measurement of the decay rate by direct counting very difficult, just as it has always caused problems in the accurate determination of the 87Rb decay rate (Dickin 2005; Faure and Mensing 2005).
Determination Methods
Three approaches have been followed to determine the β-decay constant and half-life of the long-lived radioactive 187Re since Naldrett and Libby (1948) made the first attempt.
Direct counting
In this technique, the beta (β) activity of 187Re is counted in a source material over a designated time period, and divided by the total number of radioactive atoms in the known quantity of Re, based on Avogadro’s number and the isotopic abundance of 187Re. However, detectors with an entrance window are not suitable for the detection of the spectral shape and half-life of 187Re because of the long half-life of 187Re’s unique first-forbidden β-decay and its β endpoint energy of only 2.6 keV, the lowest known in nature (Ashktorab et al. 1993). Furthermore, accurate counting of solid samples has proved to be almost impossible, due to the absorption of β-particles by surrounding Re atoms (Dickin 2005). An alternative technique was thus developed which uses either a gaseous Re compound to replace the gas filling of a proportional counter, or a liquid Re compound in a scintillation detector. In both cases it was difficult to find compounds with suitable properties, but Brodzinski and Conway (1965) using biscyclopentadienylrhenium hydride vapor obtained a 187Re half-life of 66 ± 13 Byr by the former method, and Naldrett (1984) using oxotrichlorobis (tri-phenylphosphine) rhenium V obtained a value of 35 ± 4 Byr by the latter method.
The precision of such direct counting studies was subsequently improved by the use of microcalorimetric determinations in which all the energy released in the β-decay of 187Re is measured except that of the emitted neutrino (Alessandrello et al. 1999; Arnaboldi et al. 2003; Ashktorab et al. 1993; Galeazzi et al. 2001). Ashktorab et al. (1993) used a high-temperature quartz proportional counter with metallo-organic biscyclopentadienylrhenium hydride vapors (containing natural rhenium) added to the counting gas (90% argon 10% methane) to determine a half-life for 187Re of 43.5 ± 1.3 Byr. On the other hand, Alessandrello et al. (1999), Galeazzi et al. (2001), and Arnaboldi et al. (2003) used cryogenic microcalorimeters or low-temperature bolometers, which consisted of a rhenium-containing absorber that converted the energy of the incident radiation into heat, a sensor that detected the temperature variations of the absorber, and a weak thermal link between the detector and the heat sink. All three experiments used neutron transmutation doped germanium thermistors with silicon chips, but whereas Galeazzi et al. (2001) used a metallic rhenium crystal for the absorber, Alessandrello et al. (1999) and Arnaboldi et al. (2003) used silver perrhenate (AgReO4) crystals instead. However, in spite of using similar protocols, even all these experiments using modern methods yielded results for the half-life of 187Re with uncertainties at the several percent level (Galeazzi et al. 2001) that are significantly different—43.0 ± 3.5 Byr (Alessandrello et al. 1999), 41.2 ± 0.6 Byr (Galeazzi et al. 2001), and 43.2 ± 0.15 Byr (Arnaboldi et al. 2003). This makes these half-life values unsuitable for high resolution Re-Os geochronology, particularly when compared with other radioisotopic systems in use in the earth sciences.
Judged from the fact that these direct counting experiments have yielded results that are not compatible with one another within the stated uncertainties (see below), it would appear that not all the measurement uncertainties are accounted for, and therefore the stated uncertainties are unrealistically small and typically are underestimated. Many of such experiments are likely plagued by unrecognized systematic errors (Begemann et al. 2001). As the nature of these errors is obscure, it is not straightforward to decide which of the, often mutually exclusive, results of such direct counting experiments is closest to the true value. Furthermore, the presence of unknown systematic biases makes any averaging dangerous. It is possible that reliable results of careful workers, listing realistic uncertainties, will not be given the weights they deserve—this aside from the question of whether it makes sense to average numbers that by far do not all agree within the stated uncertainties.
In-Growth Experiments
An alternative approach to determining the 187Re decay constant and half-life is to measure the amount of 187Os produced by the decay of a known quantity of 187Re in the laboratory over a known period of time. This method has only been attempted by Lindner et al. (1986, 1989), who used five batches of a concentrated solution of perrhenic acid (HReO4) for which the precise quantity of contained Re was carefully determined and from which all residual contaminant Os was removed. To three of the five batches were added precise measured quantities of independent spikes of the stable Os isotopes 190Os and 192Os in an effort to improve the precision of their determination of the 87Re half-life. To one of the other batches only a 192Os spike was added, and then a 190Os spike was only added to selected aliquots as they were withdrawn after the respective growth periods. To the last batch only a 190Os spike was added, and then a 192Os spike was only added just before testing after the respective growth periods. This procedure was adopted as an internal test of chemical equilibrium and isotopic exchange. Since one spike was added at the onset of 187Os growth and the other at the end of the growth period, any significant lack of isotopic exchange between the radiogenic 187Os and either spike would have caused a clear discrepancy between the results based on the two spikes. The time for the start of in-growth accumulation of daughter 187Os was measured from the end of the removal of the contaminant Os. The first batch was removed for testing after 400 days and the other batches were progressively removed for testing in intervals of approximately 200 days, the last batch being removed after almost five years. The 187Re/187Os, 187Re/190Os, and 187Re/192Os ratios in the final solutions at each time interval were measured by isotope dilution using inductively coupled plasma mass spectrometry. The unweighted average of all these determinations of the 187Re half-life, stated at the 95% confidence level, was 42.3 ± 1.3 Byr, with the stated uncertainties amounting to ± 3% and allowing for the known systematic uncertainties in the calibrations of the spikes and standard solutions, as well as the random uncertainties (Lindner et al. 1989).
This technique thus relies on measuring the β-decay product 187Os of a carefully measured amount of radioactive 187Re accumulated over a well-defined period of time. Where feasible, this is the most straightforward technique (Begemann et al. 2001). In-growth measurement overcomes the problems encountered with direct counting of large fractions of low-energy 187Re-emitted β-particles. It also comprises the direct 187Os product of any radiation-less decays (which otherwise cannot be measured at all). Among the drawbacks of this approach is that the method is obviously not instantaneous. The experiment must be started long before the first results can be obtained because long periods of time are required for sufficiently large amounts of the decay products to accumulate. In this case the period was only five years, which it could be argued might have been too short a length of time for sufficient daughter 187Os to have accumulated for the most accurate measurements to be made. In-growth experiments further require an accurate determination of the ratio of the two chemical elements (parent/daughter, 187Re/187Os) as well as an accurate determination of the isotopic composition of parent and daughter elements Re and Os at the start of the accumulation (Begemann et al. 2001). And Lindner et al. (1989) did not take into account the effect of the neutron capture cross section of 187Os on 187Re decay, which we now know would have been high during this five-year measurement period at the experiment’s temperature and thus facilitating the decay process (Segawa et al. 2007).
Geological Comparisons of Methods
The third approach to the determination of the 187Re decay constant (and half-life) has been to date geological samples whose ages have also been measured by other methods with presumably more reliable decay constants (Dickin 2005; Faure and Mensing 2005). This essentially involves circular reasoning, because it is being assumed the other radioisotope dating methods, principally the U-Pb method, gives the reliable dates to which the 187Re half-life can be calibrated to bring the Re-Os radioisotope ages into agreement. It should be noted, however, that this is hardly objective, because all the radioisotope ages of rocks could be wrong due to the underlying unprovable and suspect assumptions on which all the radioisotope methods are based. Nevertheless, geological determinations of the 187Re half-life have been made over the past 60 years using the terrestrial mineral molybdenite (MoS2) and groups of iron meteorites.
The first attempt to determine the 187Re half-life using Re-Os molybdenite dating studies could only estimate the value as being between 5 and 250 Byr because the age of the molybdenite was unknown (Herr, Hintenberger, and Voshage 1954; Hintenberger, Herr, and Voshage 1954). Further work by Herr and Merz (1955, 1958) on molybdenites of known ages, that is, by assuming the ages of the molybdenites were identical to their host rocks, narrowed the estimate of the 187Re half-life value to between 55 and 68 Byr. Then only several years later, Hirt, Herr, and Hoffmeister (1963) and Hirt et al. (1963) determined a 187Re half-life value of 43 Byr using molybdenites of known ages, which is in good agreement with the value of 41.577 Byr via a similar determination more than 40 years later (Selby et al. 2007), a remarkable achievement given the poor age constraints for the studied molybdenites and the ore deposits from which they came, and the very low precision of the analytical techniques available at the time.
The 187Re decay constant and half-life have also been defined by the generation of Re-Os isochrons for groups of iron meteorites of presumed age, first attempted by Luck, Birck, and Allègre (1980) and Luck and Allègre (1983), who obtained half-life values of 42.8 Byr and 45.6 Byr respectively. The value for the 187Re decay rate has been subsequently refined using new chemical separation and mass spectrometric techniques in order to generate Re-Os isochrons with higher precision for groups of iron meteorites with presumed ages. Thus Smoliar, Walker, and Morgan (1996), Shen, Papanastassiou, and Wasserburg (1996), and Shukolyukov and Lugmair (1997) obtained 187Re half-life values of 41.6 Byr, 41.7 Byr, and 41.8 Byr respectively, which are almost identical to the determination of 41.577 Byr by Selby et al. (2007) using molybdenites of known ages (according to uniformitarian assumptions). This method has the disadvantage that it involves geological uncertainties, such as whether all isotopic systems closed at the same time and remained closed. However, it is claimed to still provide a useful check on the laboratory determinations by direct physical counting and in-growth experiments. Nevertheless, this approach entails multi-chronometric dating of a mineral or groups of meteorites and cross-calibration of different radioisotopic age systems by adjusting the decay constant of the Re-Os system so as to force agreement with the age obtained via another dating system, usually U-Pb (Begemann et al. 2001). In essence, because the half-life of 238U is claimed to be the most accurately known of all relevant radionuclides, this usually amounts to expressing ages in units of the half-life of 238U.
Results of the Rhenium-187 Decay Determinations
During the last 66 years numerous determinations of the 187Re decay constant and half-life have been made using these three methods. The results are listed with details in Table 1. The year of the determination versus the value of the half-life is plotted in Fig. 1, and the year of the determination versus the value of the decay constant is plotted in Fig. 2. In each case the data points plotted have been color-coded the same to differentiate the values as determined by the three approaches that have been used—direct counting, in-growth experiments, and geological comparisons with other radioisotope dating methods.
Discussion
It is obvious from Table 1 that, in spite of the remarkable achievements involved, the earliest determinations of the 187Re decay rate were grossly inflated, due of course to the rudimentary technology available at the time. That is why most of them were not plotted on Figs. 1 and 2. Indeed, the only determinations prior to 1963 plotted were those of Herr and Merz (1958) and Watt and Glover (1962), because they were within the same range as all the later determinations. Those 187Re half-life values are 61.5 Byr and 30 Byr respectively, and they were obtained via comparison of the Re-Os ages of molybdenites of known ages determined by other radioisotope systems, and via direct counting with a proportional counter, respectively. However, the error bars on the pre-1963 data (see table 1) should have reflected the uncertainties due to the available technology, so it may be difficult to justify discarding that pre-1963 data based only on the technology argument. If that early data were retained, then it may conceivably be possible to postulate that the early measurements are reflecting a real shift in the decay constant with time.
Table 1. Determinations of the 187Re decay rate expressed in terms of the half-life and the decay constant using direct physical counting experiments, in-growth experiments, and comparisons of radioisotope ages of terrestrial minerals and rocks, and meteorites.
| Date | Half-Life (Byr) | Error (Byr) | Decay Constant (yr-1) | Error | Method | Source |
|---|---|---|---|---|---|---|
| 1948 | 4000 | ± 1000 | Direct counting by gas-filled Geiger counter | Naldrett and Libby (1948) | ||
| 1948 | 5000 | Direct counting by gas-filled Geiger counter | Sugarman and Richter (1948) | |||
| 1952 | 5000 | Direct counting by proportional counter | Curran (1952) | |||
| 1953 | 5000 | Direct counting of tracks in photographic emulsion | Gauthe and Blum (1953) | |||
| 1954 | 100 | Direct counting by Geiger counter | Suttle and Libby (1954) | |||
| 1954 | 5 | → 250 | Comparison of Re-Os age with unknown age of molybdenite | Hintenberger, Herr, and Voshage (1954); Herr, Hintenberger, and Voshage (1954) | ||
| 1954 | 1,300,000 | Direct counting by proportional counter | Dixon and McNair (1954) | |||
| 1957 | 240 | ± 50 | Direct counting by Geiger counter of internal gas-tube | Walton (1957) | ||
| 1958 | 61.5 | ± 6.5 | 1.13 × 10-11 | ±0.12 × 10-11 | Comparison of Re-Os ages of molybdenites with known ages | Herr and Merz (1958) |
| 1958 | 320 | ± 70 | Direct counting by Geiger counter | Naldrett (1958) | ||
| 1962 | 120 | ± 40 | Direct counting by Geiger counter of internal gas-tube | Wolf and Johnston (1962) | ||
| 1962 | 30 | Direct counting by proportional counter | Watt and Glover (1962) | |||
| 1963 | 43 | ± 5 | 1.61 × 10-11 | Comparison of Re-Os ages of molybdenites of known ages | Hirt, Herr, and Hoffmeister (1963); Hirt et al. 1963) | |
| 1965 | 66 | ± 13 | Direct counting of internal gas by proportional counter | Brodzinski and Conway (1965) | ||
| 1965 | 47 | ± 5 | Direct counting of internal gas by proportional counter | Payne and Drever (1965) | ||
| 1980 | 42.8 | ± 1 | 1.62 × 10-11 | ±0.03 × 10-11 | Comparison of Re-Os ages of iron meteorites with Rb-Sr, U-Pb, and Sm-Nd ages | Luck, Birck, and Allègre (1980) |
| 1982 | 45.5 | ± 1.8 | 1.52 × 10-11 | ±0.06 × 10-11 | Comparison of Re-Os ages of molybdenites of known ages (Rb- Sr, K-Ar, U-Pb) | Luck and Allègre (1982) |
| 1983 | 45.6 | ± 1.2 | 1.53 × 10-11 | ±0.08 × 10-11 | Comparison of Re-Os and Pb-Pb ages of meteorites | Luck and Allègre (1983) |
| 1984 | 35 | ± 4 | Direct counting by liquid scintillation counter | Naldrett (1984) | ||
| 1986 | 43.5 | ± 1.3 | 1.59 × 10-11 | ±0.05 × 10-11 | In-growth experiment by liquid scintillation counter | Lindner et al. (1986) |
| 1989 | 42.3 | ± 1.3 | 1.64 × 10-11 | ±0.05 × 10-11 | In-growth experiment by isotope dilution and ICP mass spectrometer | Lindner et al. (1989) |
| 1992 | 42 | ± 0.4 | 1.65 × 10-11 | ±0.011 × 10-11 | Comparison of Re-Os ages of iron meteorites with Pb-Pb ages | Horan et al. (1992) |
| 1993 | 45 | ± 3 | 1.54 × 10-11 | ±0.10 × 10-11 | Direct counting of internal gas by proportional counter | Ashktorab et al. (1993) |
| 1996 | 41.6 | ± 0.13 | 1.666 × 10-11 | ±0.017 × 10-11 | Comparison of Re-Os ages of iron meteorites with Pb-Pb ages | Smoliar, Walker, and Morgan (1996) |
| 1996 | 41.7 | ± 0.9 | 1.66 × 10-11 | ±0.027 × 10-11 | Comparison of Re-Os ages of iron meteorites with Pb-Pb ages | Shen, Papanastassiou, and Wasserburg (1996) |
| 1997 | 41.8 | ± 0.1 | 1.658 × 10-11 | ±0.003 × 10-11 | Comparison of Re-Os ages of iron meteorites with Pb-Pb ages | Shukolyukov and Lugmair (1997) |
| 1999 | 43 | ± 3.5 | 1.61 × 10-11 | ±0.26 × 10-11 | Direct counting by microbolometer detectors | Alessandrello et al. (1999) |
| 2001 | 41.2 | ± 0.6 | 1.682 × 10-11 | ±0.045 × 10-11 | Direct counting by cryogenic microcalorimeter | Galeazzi et al. (2001) |
| 2003 | 43.2 | ± 0.15 | 1.604 × 10-11 | ±0.004 × 10-11 | Direct counting by microbolometer detectors | Arnaboldi et al. (2003) |
| 2007 | 41.577 | ± 0.12 | 1.6668 × 10-11 | ±0.0034 × 10-11 | Comparison of Re-Os ages of molybdenites and U-Pb ages of zircons from same orebodies | Selby et al. (2007) |
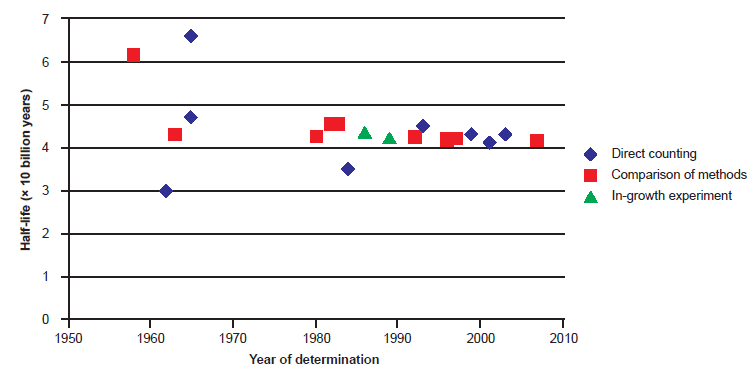
Fig. 1. Plot of each 187Re half-life determination versus the year of its determination, color-coded according to the method of its determination.
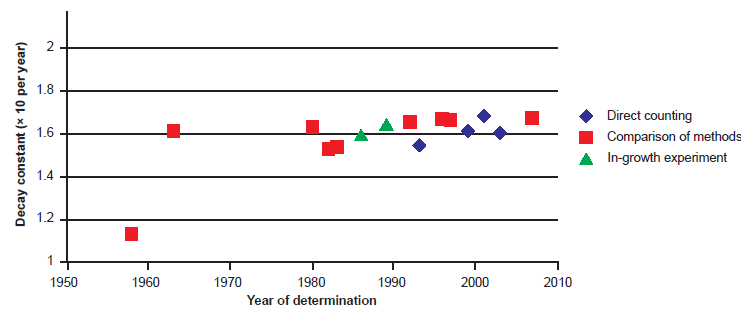
Fig. 2. Plot of each 187Re decay constant determination versus the year of its determination, color-coded according to the method of its determination.
Fig. 3 is a plot of all the post-1980 determinations of the 187Re half-life, color-coded the same to differentiate the values as determined by the three approaches that have been used. All the half-life values fall within a narrow range between 41.2 Byr (Galeazzi et al. 2001) and 45.6 Byr (Luck and Allègre 1983), except for the value of 35 Byr obtained by Naldrett (1984) (see table 1). The values of 43 Byr obtained by Hirt, Herr, and Hoffmeister (1963) and Hirt et al. (1963) via comparison of the Re-Os ages of molybdenites of known ages and 47 Byr obtained by Payne and Drever (1965) via direct counting of internal gas by proportional counter are also within the narrow range of values obtained from the post-1980 determinations, although their uncertainties of ± 5 Byr make them too imprecise to be seriously considered. Yet by the same standard the uncertainties of ± 3 Byr and ± 3.5 Byr in the direct counting determinations by Ashktorab et al. (1993) and Alessandrello et al. (1999) respectively would render their half-life values of 45 Byr and 43 Byr similarly imprecise.
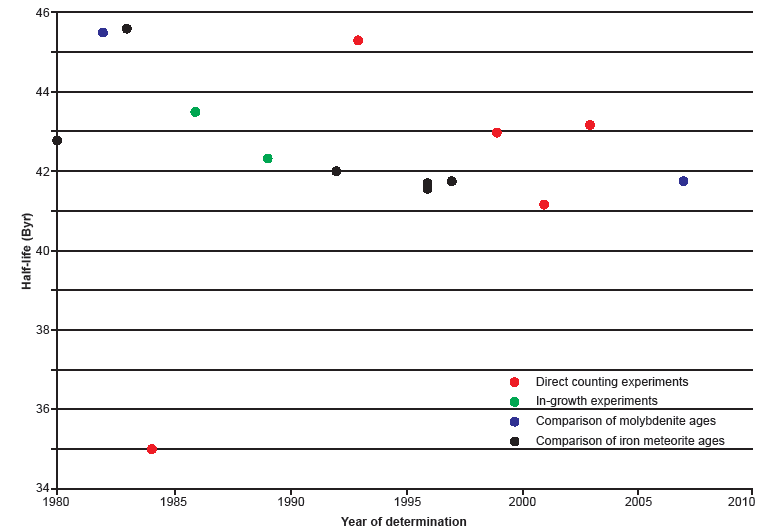
Fig. 3. Enlarged plot of the 187Re half-life determinations since 1980 versus the year of their determination, color-coded according to the method of its determination.
Therefore, to be able to better assess the post-1980 half-life determinations, only those values that fell within the narrow 41–46 Byr range were plotted with their ± uncertainties in Fig. 4 according to their method of determination. A distinction was also made between determinations obtained by radioisotope age comparisons of molybdenites and those obtained by radioisotope age comparisons of groups of iron meteorites.
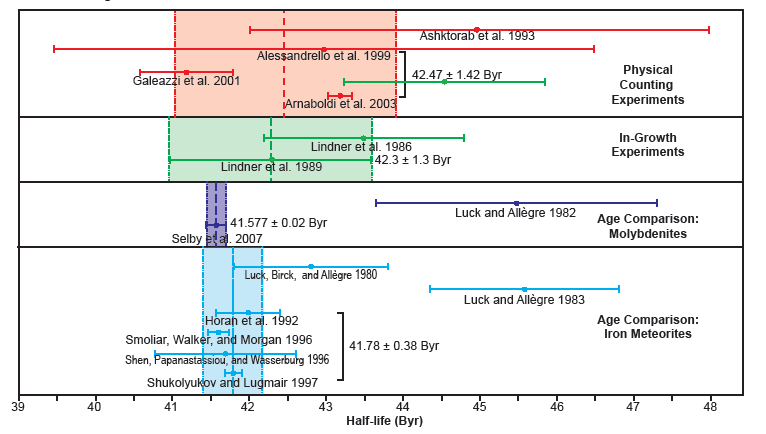
Fig. 4. Comparison of all the 187Re half-life determinations since 1980 in the range of 41–46 Byr grouped and color-coded according to the determination method. The vertical color-shaded areas indicate the two standard deviations (2σ) from the mean values (colored vertical lines) for the groupings of determinations in each method.
Among the physical direct counting determinations, the large uncertainties in the Ashktorab et al. (1993) and Alessandrello et al. (1999) experiments causes the four results to overlap throughout the 39–48 Byr range. Yet the Alessandrello et al. (1999) result of 43 Byr falls between the Galeazzi et al. (2001) and Arnaboldi et al. (2003) results of 41.2 Byr and 43.2 Byr respectively, but the ± uncertainties of these latter results are small so that their uncertainty ranges do not overlap. Nevertheless, the three most recent physical direct counting results were grouped to produce a mean 187Re half-life value of 42.47 ± 1.42 Byr, which is marked by a vertical dashed line in Fig. 4 together with the uncertainty range shaded. This mean 187Re half-life value is virtually identical to the value of 42.3 ± 1.3 Byr obtained by Lindner et al. (1989) in their in-growth experiment, which was a refinement of their initial experiment (Lindner et al. 1986) and so it is ignored in this discussion of the best determination results.
The 45.5 ± 1.8 Byr 187Re half-life value obtained in the earlier Luck and Allègre (1982) determination via radioisotope age comparisons of molybdenites is almost completely outside the range of the mean half-life value from the most recent physical direct counting experiments and the range of the half-life value from the Lindner et al. (1989) in-growth experiment (fig. 4), so for this discussion is ignored. On the other hand, the very precise Selby et al. (2007) 187Re half-life value of 41.577 ± 0.12 Byr plots on Fig. 4 within the left side of the range envelopes of the mean half-life value from the most recent physical direct counting experiments and of the half-life value from the Lindner et al. (1989) in-growth experiment. It is also almost identical to the Galeazzi et al. (2001) physical direct counting value for the 187Re half-life of 41.2 ± 0.6 Byr and within its uncertainty range.
Among the determinations obtained by radioisotope age comparisons of groups of iron meteorites, the Luck and Allègre (1983) 187Re half-life value of 45.6 ± 1.2 Byr plots in Fig. 4 well outside the range envelopes of the mean half-life value from the most recent physical direct counting experiments and of the half-life value from the Lindner et al. (1989) in-growth experiment. Furthermore, it does not in any way overlap with any other determination obtained by radioisotope age comparisons of groups of iron meteorites, so in this discussion it has been ignored. Similarly, the Luck, Birck, and Allègre (1980) 187Re half-life value of 42.8 Byr falls outside the ± uncertainties range envelopes of the four post-1990 determinations by the same method, even though the left-hand limit of its uncertainty range of ± 1 Byr overlaps with some of the post-1990 determinations and their ± uncertainties ranges. The post-1990 determinations utilized improved chemical separation and mass spectrometric techniques, so those four determinations plot close together in Fig. 4 and together yield a mean 187Re half-life value of 41.78 ± 0.38 Byr. This mean value is very close to and between the 187Re half-life values of 41.577 Byr of Selby et al. (2007) obtained by radioisotope age comparisons of molybdenites and 42.3 Byr of Lindner et al. (1989) obtained by an in-growth experiment. Its uncertainty envelope of ± 0.38 Byr also fully encloses the Selby et al. (2007) 187Re half-life value of 41.557 ± 0.12 Byr (fig. 4), and is itself fully enclosed within the uncertainty envelopes of the Lindner et al. (1989) in-growth experiment half-life value and of the mean half-life value of the three most recent physical direct counting experiments. Thus unlike the determinations of the 87Rb and 176Lu half-lives (Snelling 2014a, b), here there is essential agreement on the 187Re half-life value obtained by these four different determination methods, but only if the pre-1963 determinations are ignored.
But how was such agreement obtained? In particular, how objective were the determinations by the radioisotope ages comparisons? The Selby et al. (2007) half-life value of 41.557 ± 0.12 Byr and decay constant value of 1.6668 ± 0.034 × 10-11 per year are now regarded as well-established and thus used by the geochronology community (Schmitz 2012). Yet these are derived values subject to geological uncertainties and cross-calibration with other radioisotope systems that are equally subject to similar geological uncertainties and assumptions, as already noted (Begemann et al. 2001). Furthermore, direct physical counting of decay events should be the best measure of the decay rate, followed closely by in-growth measurements of the resultant decay products over a given time period. However, these more direct methods are relegated to only potentially affirming the determinations obtained by the radioisotope age comparisons of molybdenites and groups of iron meteorites, whereas due to the direct nature of the physical counting methods the age comparison methods with their inherent assumptions involved should be subject to confirmation by them.
If we consider only the post-1990 determinations via radioisotope age comparisons which utilized improved chemical separation and mass spectrometric techniques, then the first such determination was by Horan et al. (1992). They performed Re-Os isotopic analyses on eleven iron meteorites and constructed a Re-Os isochron for a group of six iron IIA meteorites, obtaining a Re-Os isochron age for them of 4596 ± 31 Ma using the Lindner et al. (1989) 187Re decay half-life of 42.3 Byr. However, according to the conventional naturalistic model for the formation of the solar system (even though there are several good reasons to not accept this model) these iron meteorites could not be older than the age of the solar system, as defined by Chen and Wasserburg (1981) at 4559 ± 15 Ma based on the mean 207Pb/206Pb model age of five coarse-grained Ca-Al inclusions (CAIs) in the Allende carbonaceous chondrite meteorite. So Horan et al. (1992) adjusted the 187Re decay half-life to 42.0 Byr in order to “force” the Re-Os isochron age of these iron IIA meteorites to agree with the Chen and Wasserburg (1981) Pb-Pb model age. This then was how the Horan et al. (1992) determination of the 187Re half-life was obtained, with several accompanying assumptions, not least being the presumed age of the solar system, the presumed identical age of the Allende CAIs and these iron IIA meteorites, and the reliability of the Pb-Pb radioisotope systems, all of which cannot be proven.
Subsequently, Smoliar, Walker, and Morgan (1996) used Re-Os isotopic data for six IIIAB “magmatic” iron meteorites, which they assumed formed as part of the primary sequence of crystallization of an asteroidal core, to generate a Re-Os isochron with a slope of 0.07887 ± 22 (2σ). They then assumed that the age of these IIIAB iron meteorites was 4557.8 ± 0.4 Ma, identical to the Pb-Pb model age of pyroxene separates from two angrite meteorites as determined by Lugmair and Galer (1992). Note that the uncertainty in the Pb-Pb age for the angrites did not, however, take into account uncertainties in the decay constants for 235U and 238U and the critical 238U/235U ratio. The assumption of a similar age for both these IIIAB iron meteorites and the two angrite meteorites was made because of the similar 53Mn-53Cr ages of IIIAB iron and angrite meteorites (Hutcheon et al. 1992; Hutcheon and Olsen 1991). However, that assumption is based on the further assumption that the 53Mn-53Cr ages of those IIIAB iron and angrite meteorites can be calibrated against the Pb-Pb model ages of two eucrite meteorites and Allende CAIs (Chen and Wasserburg 1985, Manhès, Göpel, and Allègre 1986, 1988, Birck and Allègre 1988). The high-precision Re-Os iron IIIAB isochron obtained by Smoliar, Walker, and Morgan (1996), combined with the assumed Pb-Pb model age for the IIIAB irons, permitted them to force the Re-Os isochron to agree with the Pb-Pb model age in order to determine a more precise and accurate decay constant for 187Re of 1.666 × 10-11 per year, corresponding to a half-life of 41.6 Byr.
Smoliar, Walker, and Morgan (1996) calculated a ± 0.31% uncertainty for the derived decay constant value from the regression statistics of their Re-Os isotopic data for those iron IIIAB meteorites. However, calibration of the Os spike they used included a systematic uncertainty of up to ± 1.2% (2σ), associated with the non-stoichiometry of the Os salt used to prepare the standard solution (Morgan et al. 1995), so this ± 0.31% uncertainty based just on the regression statistics is likely much lower that it really should be. Furthermore, in assuming that the iron IIIAB meteorites have an identical Re-Os isochron age to the Pb-Pb model age for the angrite meteorites, Smoliar, Walker, and Morgan (1996) were assuming that the Re-Os, Pb-Pb, and Mn-Cr radioisotope systems all isotopically closed at the same time and have not been subsequently disturbed. Those assumptions cannot be proved. Nevertheless, the uncertainties in the decay constants for the U isotopes, and the assumption of identical closure ages for Pb-Pb in angrites and Re-Os in IIIAB irons, perhaps contribute less to the overall uncertainty in the decay constant than the stoichiometry issue.
The results from the Smoliar, Walker, and Morgan (1996) study are in good agreement (within ± 0.4%) with results published subsequently by Shen, Papanastassiou, and Wasserburg (1996), who obtained a 187Re decay constant of 1.66 × 10-11 per year and a half-life of 41.7 Byr, but who used a different Os standard for spike calibration. Shen, Papanastassiou, and Wasserburg (1996) produced a Re-Os isochron for several iron IIAB meteorites on which other iron meteorites they analyzed also plotted. They estimated a ± 1.6% uncertainty in their tracer Os calibration and a combined uncertainty of about ± 4% in converting an isochron slope to an absolute age. Nevertheless, in order to determine the 187Re decay constant of 1.66 × 10-11 per year and half-life of 41.7 Byr they assumed that the Os tracer calibration was correct, and assumed that the IIAB irons’ whole-rock Re-Os isochron age should be adjusted to correspond to the same age as the 4566 Ma Pb-Pb model age for Allende CAIs (Chen and Wasserburg 1985; Manhès, Göpel, and Allègre 1988), the same age as that for the oldest Pb-Pb model ages obtained for phosphates from ordinary chondrite meteorites, and the same age as that for angrite and eucrite meteorites (Chen and Wasserburg 1985; Göpel, Manhès, and Allègre 1994; Lugmair and Galer 1992).
Shen, Papanastassiou, and Wasserburg (1998) reported that their Re-Os isotopic data for pallasite meteorites plotted along their same well-defined Re-Os isochron for the IIAB iron meteorites. So using their preliminary Re-Os data for pallasite meteorites, Shukolyukov and Lugmair (1997) had thus calculated a 187Re decay constant of 1.658 × 10-11 per year and a half-life of 41.8 Byr, by adjusting the Re-Os isochron to a Mn-Cr isochron age of 4558 Ma for the Omolon pallasite meteorite obtained by calibrating that age against the Pb-Pb model age of pyroxene separates from the angrite meteorite LEW86010 (Lugmair and Galer 1992). This calculation also involved the assumptions that the Omolon pallasite meteorite formed contemporaneously with other pallasite meteorites, and that the Mn-Cr and Re-Os radioisotope systems closed at the same time, as well as the assumption that the Omolon pallasite meteorite is the same age as the Pb-Pb model age as the angrite meteorite LEW86010. Once again, all those assumptions cannot be proved.
Subsequently, Birck and Allègre (1998) obtained a Re-Os isochron age of 4624 Ma for a mixed collection of iron meteorites, which they interpreted as too high compared to the age of the solar system of 4566 Ma as determined by the U-Pb systematics of Allende CAIs (Manhès, Göpel, and Allègre 1986, 1988). They thus concluded that a better measurement of the 187Re decay constant and half-life was highly desirable, but in the meantime the value of the 187Re decay constant should be adjusted to a value between 1.66 × 10-11 per year and 1.666 × 10-11 per year.
It is interesting to note that these groups of iron meteorites have sometimes yielded Re-Os isochron ages older than the presumed age of the solar system, so that the 187Re decay constant has had to be adjusted based on recalibrating the Re-Os isochron ages with the accepted age of the solar system based on Pb-Pb model ages of other meteorites and their components. However, there is also the possibility that instead this disparity between Re-Os isochron ages and Pb-Pb model ages is perhaps related to the extreme sensitivity of the 187Re half-life to the strength of the nuclear force, and to variations in fundamental couplings and the fine-structure constant, as first discussed by Dyson (1972), and more recently discussed by Olive et al. (2002, 2004) and Olive and Qian (2004). This is obviously worthy of further investigation, but is beyond the scope of this present contribution.
Consequently, in order to resolve this lingering disagreement over the 187Re decay constant and half-life and to obtain a better measurement, Selby et al. (2007) embarked on a different approach, using cross calibration of the Re-Os molybdenite and U-Pb zircon chronometers from magmatic-hydrothermal ore systems. This approach was taken because the Re-Os molybdenite geochronometer has been claimed to be highly robust (Stein et al. 2001), and because the U-Pb zircon method is widely acclaimed by uniformitarians as the most accurate and precise method of geochronology as a result of the claimed highly robust nature of zircon, the dual U-Pb decay scheme utilized, and the claimed most precisely determined decay constants (Bowring and Schmitz 2003; Heaman and Parrish 1991; Jaffey et al. 1971; Schoene et al. 2006). Selby et al. (2007) thus assembled the Re-Os model ages for molybdenites and U-Pb concordia-Pb-Pb intercept ages for zircons from 11 magmatic-hydrothermal ore deposits apparently spanning from ca. 90 Ma to ca. 2670 Ma. The analytical uncertainties were at least 0.2 Ma for both the Re-Os molybdenite and U-Pb zircon age determinations, and yet they assumed that the timing of crystallization of magmatism causing these magmatic-hydrothermal systems as recorded by the U-Pb zircon ages must be slightly older than the sulfide mineralization (which includes the molybdenites) in the magmatic-hydrothermal systems themselves. Nevertheless, they still found agreement between the U-Pb zircon and Re-Os molybdenite ages with an excellent correlation of 1.0004 ± 0.0023 (2σ) and probability of 0.99, using the 187Re and U decay constants of Smoliar, Walker, and Morgan (1996) and Jaffey et al. (1971) respectively. This was statistically indistinguishable from a correlation of 0.9984 ± 0.0021 (2σ) with a probability of 0.98, using the 238U decay constant of Jaffey et al. (1971) and the 235U decay constant of Schoene et al. (2006). Then using the Re-Os molybdenite data together with the U-Pb zircon ages for each deposit, new individual 187Re decay constant values were calculated for each of the 11 magmatic-hydrothermal systems, by forcing the Re-Os ages to agree with the U-Pb ages. In this way Selby et al. (2007) declared the weighted average of these 11 values of 1.6668 ± 0.0034 × 10-11 per year (2σ, with a probability of 0.97) to be the new 187Re decay constant (equivalent to a half-life of 41.577 Byr), which is now in standard use by uniformitarians in geochronology (Schmitz 2012).
Selby et al. (2007) claimed their cross calibration between the U-Pb zircon and Re-Os molybdenite chronometers provides an important independent test of the previously used 187Re decay constant, because the methodology, sample materials, and preparation of the Os standard solution differ greatly from the study of Smoliar, Walker, and Morgan (1996). Indeed, in many cases the molybdenites and zircons analyzed were found together in the same rock specimens, supposedly eliminating the need to infer genetic relationships that was necessary in analyses of different meteorite groups. However, it is well-established that minerals even found side-by-side in the same rock specimens may not have formed at the same time (for example, Bucher and Frey 2002; Cox, Bell, and Pankhurst 1995), yet that is the assumption that was necessary for this U-Pb/Re-Os cross calibration study. Nevertheless, Selby et al. (2007) did show that their weighted average 187Re half-life value of 41.557 ± 0.12 Byr using the U decay constants of Jaffey et al. (1971) is identical within the calculated uncertainty limits to the value of 41.6 ± 0.13 Byr obtained by Smoliar, Walker, and Morgan (1996), which is also based on the U decay constants of Jaffey et al. (1971) (fig. 5).
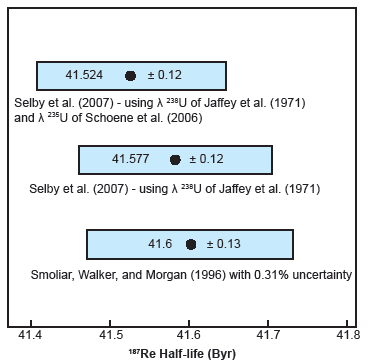
Fig. 5. Plot comparing the 187Re half-life values derived from Selby et al. (2007) to the value of Smoliar, Walker, and Morgan (1996). The uncertainties are at the 2σ level.
Furthermore, their weighted average 187Re half-life value of 41.524 ± 0.12 Byr using the 238U decay constant of Jaffey et al. (1971) but the 235U decay constant of Schoene et al. (2006) is also within the calculated uncertainty to the value of 41.6 ± 0.13 Byr obtained by Smoliar, Walker, and Morgan (1996) (fig. 5). Moreover, they also showed that calculating the Re-Os molybdenite ages using the 187Re half-life values obtained by other meteorite radioisotope age comparison studies resulted in Re-Os molybdenite ages widely divergent from the U-Pb zircon ages for the same magmatic-hydrothermal systems.
However, this U-Pb “gold standard” dating method has come under similar scrutiny in the two last decades. Even in their study, Selby et al. (2007) admitted that in many of the magmatic-hydrothermal systems they U-Pb zircon dated, the data were discordant and showed scatter, which likely impacted the accuracy and precision of the U-Pb concordia-Pb-Pb intercept ages used in the cross calibration with the Re-Os molybdenite ages. Indeed, most of the reported U-Pb ages were obtained by analyses of multi-grain zircon fractions, which can accentuate the effects of any Pb loss and/or inheritance. Furthermore, Ludwig (2000) has demonstrated that, although almost universally ignored, the effect of the errors in the U decay constants on U-Pb concordia-Pb-Pb intercept ages are significant, being a 4.5 Ma error for a 500 Ma age, which amounts to almost a 1% error. The U-Pb method also depends on the crucial 238U/235U ratio, but discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al 2012). These discrepancies and variations remain unexplained, especially in the context of the 238U and 235U decay constants and half-lives. Furthermore, the fact that there are these variations in the crucial 238U/235U ratio in terrestrial minerals and rocks on which the U-Pb dating “gold standard” depends, which has been used to re-calibrate Re-Os isochron ages to determine the 187Re half-life and decay constant, only underscores that these radioisotope methods cannot provide the absolute invariable “dates” they are so confidently proclaimed to provide. In any case, there is the additional assumption in all the radioisotope dating methods of having to know the original concentrations of the daughter and index isotopes which is very significant in the U-Pb method because the original concentrations are assumed not to be zero, in contrast to the K-Ar method. Yet there must be great uncertainty as to what those initial values were in the unobserved past, despite the isochron and concordia techniques attempting to negate the necessity for knowing those initial values. Thus the U-Pb method should not be used as a standard to determine other radioisotope decay constants.
Indeed, it would remain prudent to be very careful with these geological comparison methods for two other reasons. First, there are significant flaws in the basic assumptions on which all the radioisotope dating methods depend. Second, the U-Pb method relies primarily on α decay, whereas the Re-Os method relies on β decay. As observed by both Austin (2005) and Snelling (2005), these different decay modes seem to yield different ages for some earth rocks using the same samples with essentially the same methodology. Furthermore, these different ages yielded by the same earth rocks are often widely divergent, even up 100–200% different, which is such a huge divergence that it renders these dating methods highly suspect, even if the differences in the determinations of the half-lives of the parent radioisotopes seem miniscule and therefore trivial by comparison. However, it was considered prudent to still document here these seemingly miniscule differences in half-life values, because they may be indicative of other underlying factors at work (as already discussed briefly), and they can still lead to very significant discrepancies in the derived radioisotope ages that might otherwise appear to be acceptably accurate to uniformitarians.
In any case, as with 176Lu, there is a dependence of the half-life of 187Re on environmental conditions such as the degree of ionization (Begemann et al. 2001). And the effects are not entirely negligible, as is often assumed, so they must significantly impact the dating of terrestrial and meteoritic samples. Indeed, Bosch et al. (1996) and Bosch (1999) successfully measured by two independent methods the bound state β- decay of fully ionized bare 187Re nuclei and determined a half-life of only 32.9 ± 2.0 yr, compared to the nine orders of magnitude greater 41.577 ± 0.12 Byr half-life for neutral 187Re atoms. More relevant is the report from Jenkins, Mundy, and Fischbach (2010) confirming that the previously detected correlations between solar activity and nuclear decay rates were likely not due to seasonal variations in the sensitivities of the respective laboratory detectors, which were too small to produce the observed fluctuations. Thus they concluded that the observed fluctuations between solar activity and nuclear decay rates could arise from a direct interaction between the decaying nuclei and some particles or fields emanating from the sun. However, calculated solar neutrino absorption cross sections are too small to explain the observed effect, and other mechanisms have been investigated, such as gravitational effects (Chown 2009; Kostlecký and Tasson 2009). With such environmental influences established, it begs the question of how certain can anyone be that the nuclear decay rates of 187Re and other parent radioisotopes used in rock dating by uniformitarians have remained constant at today’s measured slow rates through the claimed >4.5 Byr history of the earth and solar system.
Nevertheless, all the age comparisons on terrestrial rocks and minerals, and the age comparisons on meteorites, used the U-Pb method to finally determine the 187Re decay constant of 1.6668 × 10-11 per year and half-life of 41.577 Byr, which are within the ranges determined by both physical direct counting and in-growth experiments. Thus Re-Os age calculations are ultimately calibrated against the U-Pb method. However, this U-Pb “gold standard” depends on whether the U decay constants are accurately and precisely known, and on the crucial 238U/235U ratio. Yet discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites. These discrepancies and variations remain unexplained. This only serves to highlight that if the Re-Os dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then the claimed accurately-determined 187Re decay rate cannot be absolute, especially given the environmental influences known to alter nuclear decay rates. Without an accurately known 187Re decay constant and half-life, accurate Re-Os radioisotope ages cannot be determined. Therefore, Re-Os dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Conclusions
There have been numerous attempts to determine the 187Re half-life and decay constant in the last sixty-six years by four methods—direct physical counting and in-growth experiments, and radioisotope age comparisons using molybdenites and groups of iron meteorites. With the measurement technology having improved, the determinations over the last 20 years have finally resulted in close agreement. Thus the 187Re half-life and decay constant values of 41.577 ± 0.12 Byr and 1.6668 ± 0.0034 × 10-11 per year respectively have now been adopted for standard use by the uniformitarian geological community. These adopted values are the weighted averages of eleven determinations in which the Re-Os model ages of molybdenites were re-calibrated by forcing them to be the same as the U-Pb concordia-Pb-Pb intercept ages of zircons from the same 11 magmatic-hydrothermal systems spanning from ca. 90 Ma to ca. 2670 Ma.
This adopted half-life value of 41.577 ± 0.12 Byr is virtually identical to the 41.6 ± 0.13 Byr value obtained by forcing the Re-Os isochron age of a group of iron meteorites to agree with the presumed Pb-Pb model age for the solar system obtained from pyroxene separates from two angrite meteorites. Furthermore, the ± uncertainty range of the adopted 41.577 ± 0.12 Byr half-life value lies within the ± uncertainty range of the 41.78 ± 0.38 Byr mean half-life value of the four post-1990 determinations using Re-Os/Pb-Pb age comparisons for groups of iron meteorites. And the adopted value also lies within the ± uncertainty range of the 42.3 ± 1.3 Byr half-life value obtained by an in-growth experiment, and within the ± uncertainty range of the 42.47 ± 1.42 Byr mean half-life value of the three most recent physical direct counting experiments. Yet even though there is this close agreement between these four determination methods, the half-life value obtained by comparison of Re-Os molybdenite ages with U-Pb zircon ages has been given preference over the values obtained by direct counting and in-growth experiments which directly measure 187Re decay and the 187Os product of 187Re decay respectively, and so are independent of all the assumptions involved with the radioisotope dating methods. Indeed, model dependent results should not take precedence over the direct experimental evidence.
All the age comparisons on molybdenites and groups of iron meteorites used the U-Pb method to determine the 187Re decay half-life, and thus all Re-Os age calculations are ultimately calibrated against the U-Pb method. However, this U-Pb “gold standard” depends on having precisely known 238U and 235U decay constants, as well as on the crucial 238U/235U ratio. Yet there are still uncertainties in the measured U decay constants, and discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks, and the 238U/235U ratio in meteorites. These discrepancies and variations remain unexplained. This only serves to highlight that if the Re-Os dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then it cannot be absolute.
In any case, the half-life of 187Re has also been shown to be dependent on environmental conditions. Fluctuations in nuclear decay rates have been observed to correlate with fluctuations in solar activity, and the degree of ionization of 187Re atoms can result in a change of nine orders of magnitude in the measured decay rate. Furthermore, there is evidence that nuclear decay rates have not been constant in the past. Thus without an accurately known 187Re decay constant and half-life, accurate Re-Os radioisotope ages cannot be determined. Therefore, Re-Os dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Acknowledgments
The invaluable help of my research assistant in compiling and plotting the data in the color-coded age diagrams is acknowledged. The three reviewers are also acknowledged for their helpful comments and input, though the final content of this paper is solely my responsibility. Our production assistant Laurel Hemmings is also especially thanked for her painstaking work in preparing this paper for publication.
References
Alessandrello, A., J. W. Beeman, C. Brofferio , O. Cremonesi, E. Fiorini, A. Giuliani, E. E. Haller, et al. 1999. Bolometric measurements of beta decay spectra of 187Re with crystals of silver perrhenate. Physics Letters B 457, no. 1–3:253–260.
Arnaboldi, C., C. Brofferio, O. Cremonesi, E. Fiorini, C. Lo Bianco, L. Martensson, A. Nucciotti, et al. 2003. Bolometric bounds on the antineutrino mass. Physical Review Letters 91:161802.
Ashktorab, K., W. Janecke, F. D. Becchetti, and D. A. Roberts. 1993. Beta decay of 187Re and cosmochronology. Physical Review C 47, no. 6:2954–2959.
Austin, S. A. 2005. Do radioisotope clocks need repair? Testing the assumptions of isochron dating using K-Ar, Rb-Sr, Sm-Nd, and Pb-Pb isotopes. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 325–392. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/do-radioisotope-clocks-need-repair/.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. Call for an improved set of decay constants for geochronological use. Geochimica et Cosmochimica Acta 65, no. 1:111–121.
Birck, J.-L., and C.-J. Allègre. 1988. Manganese-chromium isotope systematics and the development of the early Solar System. Nature 331:579–584.
Birck, J.-L., and C.-J. Allègre. 1998. Rhenium 187-osmium 187 in iron meteorites and the strange origin of the Kodaïkanal meteorite. Meteoritics and Planetary Science 33:647–653.
Bosch, F. 1999. Setting a cosmic clock with highly charged ions. Physica Scripta T80:28–34.
Bosch, F., T. Faestermann, J. Friese, F. Heine, P. Kienle, E. Wefers, K. Zeitelhack, et al. 1996. Observation of bound-state β- decay of fully ionized 187Re: 187Re-187Os cosmochronometry. Physical Review Letters 77, no. 26:5190–5193.
Bowring, S. A., and M. D. Schmitz. 2003. High-precision U-Pb zircon geochronology and the stratigraphic record. In Zircon, ed. J. M. Hanchar and P. W. O. Hoskin. Reviews in Mineralogy and Geochemistry, vol. 53:305–326. Chantilly, Virginia: Mineralogical Society of America.
Brennecka, G. A., and M. Wadhwa. 2012. Uranium isotope compositions of the basaltic angrite meteorites and the chronological implications for the early Solar System. Proceedings of the National Academy of Sciences USA 109, no. 24:9299–9303.
Brodzinski, R. L., and D. C. Conway. 1965. Decay of rhenium-187. Physical Review 138:B1368–B1371.
Bucher, K., and M. Frey. 2002. Petrogenesis of metamorphic rocks. 7th ed. Berlin, Germany: Springer-Verlag.
Chen, J. H., and G. J. Wasserburg. 1981. The isotopic composition of uranium and lead in Allende inclusions and meteoritic phosphates. Earth and Planetary Science Letters 52, no. 1:1–15.
Chen, J. H., and G. J. Wasserburg. 1985. U-Th-Pb isotopic studies of meteorite ALHA 81005 and Ibitira. Lunar and Planetary Science Conference 16:119–120.
Chown, M. 2009. Gravity’s seasons: Does an apple fall faster in spring? New Scientist 202, no. 2704:28–32.
Cox, K. G., J. D. Bell, and R. J. Pankhurst. 1995. The interpretation of igneous rocks. London, United Kingdom: Chapman & Hall.
Curran, S. C. 1952. Measurement of beta particles of low energy and allied phenomena. Physica 18, no. 12:1161–1170.
Dickin, A. P. 2005. Radiogenic isotope geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press.
Dixon, D., and A. McNair. 1954. A search for natural radioactivity in neodymium, rhenium and osmium. Philosophical Magazine 45, no. 370:1099–1108.
Dyson, F. J. 1972. The fundamental constants and their time variation. In Aspects of quantum theory, ed. A. Salam, and E. P. Wigner, 213–236. Cambridge, United Kingdom: Cambridge University Press.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Galeazzi, M., F. Fontanelli, F. Gatti, and S. Vitale. 2001. Endpoint energy and half-life of the 187Re β decay. Physical Review C 63:012302.
Gauthe, B., and J. M. Blum. 1953. Mise en évidence de la radioactive naturelle du rhenium par la méthode des émulsions nucléaires. Comptes Rendus de L’Académie des Sciences 236:1255–1259.
Göpel, C., G. Manhès, and C.-J. Allègre. 1994. U-Pb systematics of phosphates from equilibrated ordinary chondrites. Earth and Planetary Science Letters 121, no. 1–2:153–171.
Heaman, L., and R. R. Parrish. 1991. U-Pb geochronology of accessory minerals. In Applications of radiogenic isotope systems to problems in geology, ed. L. Heaman, and J. N. Ludden, Short Course Handbook, vol. 19, 59–102. Quebec, Canada: Mineralogical Association of Canada.
Herr, W., H. Hintenberger, and H. Voshage. 1954. Half-life of rhenium. Physical Review 95, no. 6:1691.
Herr, W., and E. Merz. 1955. Eine nuene methode zur altersbestimmung von rhenium-haltigen mineralen mittels neutronenaktivierung. Zeitschrift für Naturforschung A 10:613–615.
Herr, W., and E. Merz. 1958. Zur bestimmung der halbwertszeit des 187Re: Weitere datierungen nach der Re/Os-methode. Zeitschrift für Naturforschung A 13:231.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. 238U/235U systematics in terrestrial uranium-bearing minerals. Science 335, no. 6076:1610–1614.
Hintenberger, H., W. Herr, and H. Voshage. 1954. Radiogenic osmium from rhenium-containing molybdenite. Physical Review 95:1690–1691.
Hirt, B., W. Herr, and W. Hoffmeister. 1963. Age determinations by the rhenium-osmium method. In Proceedings of the Symposium on Radioactive Decay, 39–43. Vienna, Austria: International Atomic Energy Agency.
Hirt, B., G. R. Tilton, W. Herr, and W. Hoffmeister. 1963. The half-life of 187Re. In Earth sciences and meteoritics, ed. J. Geiss, and E. D. Goldberg, 273–280. Amsterdam, The Netherlands: North Holland Publishing Co.
Horan, M. F., J. W. Morgan, R. J. Walker, and J. N. Grossman. 1992. Rhenium-osmium isotope constraints on the age of iron meteorites. Science 255, no. 5048:1118–1121.
Hutcheon, I. D., and E. Olsen. 1991. Cr isotopic composition of differentiated meteorites: A search for 53Mn. Lunar and Planetary Science Conference 22:605–606.
Hutcheon, I. D., E. Olsen, J. Zipfel, and G. J. Wasserburg. 1992. Cr isotopic composition of differentiated meteorites: Evidence for 53Mn. Lunar and Planetary Science Conference 23:565–566.
Jaffey, A. H., K. F. Flynn, L. E. Glendenin, W. C. Bentley, and A. M. Essling. 1971. Precision measurement of half-lives and specific activities of 235U and 238U. Physical Review C 4, no. 5:1889–1906.
Jenkins, J. H., D. W. Mundy, and E. Fischbach. 2010. Analysis of environmental influences in nuclear half-life measurements exhibiting time-dependent decay rates. Nuclear Instruments and Methods in Physics Research A 620, no. 2–3:332–342.
Kostlecký, V. A., and J. D. Tasson. 2009. Prospects for large relativity violations in matter-gravity couplings. Physical Review Letters 102, no. 1.010402:1–4.
Lindner, M., D. A. Leich, R. J. Borg, G. P. Russ, J. M. Bazan, D. S. Simons, and A. R. Date. 1986. Direct laboratory determination of the half-life of 187Re. Nature 320:246– 248.
Lindner, M., D. A. Leich, G. P. Russ, J. M. Bazan, and R. J. Borg. 1989. Direct determination of the half-life of 187Re. Geochimica et Cosmochimica Acta 53, no. 7:1597–1606.
Luck, J.-M., J.-L. Birck, and C.-J. Allègre. 1980. 187Re- 187Os systematics in meteorites: Early chronology of the solar system and age of the galaxy. Nature 283:256–259.
Luck, J.-M., and C.-J. Allègre. 1982. The study of molybdenites through the 187Re- 187Os chronometer. Earth and Planetary Science Letters 61, no. 2:291–296.
Luck J.-M., and C.-J. Allègre. 1983. 187Re- 187Os systematics in meteorites and cosmological consequences. Nature 302:130–132.
Lugmair, G. W., and S. J. G. Galer. 1992. Age and isotopic relationships among the angrites Lewis Cliff 86010 and Angra dos Reis. Geochimica et Cosmochimica Acta 56, no. 4:1673–1694.
Ludwig, K. R. 2000. Decay constant errors in U-Pb concordia-intercept ages. Chemical Geology 166, no. 3–4:315–318.
Manhès, G., C. Göpel, and C.-J. Allègre. 1986. Lead isotopes in Allende inclusions: The oldest known solar material. Terra Cógnita 6:173.
Manhès, G., C. Göpel, and C.-J. Allègre. 1988. Systematique U-Pb dans les inclusions réfractaires d’Allende: le plus vieux matériau solaire. Comptes Rendus de l’ATP Planetologie, 323–327.
Miller, J. L. 2012. Time to reset isotopic clocks? Two new studies revise key parameters in radiometric dating. Physics Today 65, no. 6:20–22.
Min K., R. Mundil, P. R. Renne, and K. R. Ludwig. 2000. A test for systematic errors in 40Ar/39Ar geochronology through comparison with U-Pb analysis of a 1.1 Ga rhyolite. Geochimica et Cosmochimica Acta 64, no. 1:73–98.
Morgan, J. W., M. F. Horan, R. J. Walker, and J. N. Grossman. 1995. Rhenium-osmium concentration and isotope systematics in group IIAB iron meteorites. Geochimica et Cosmochimica Acta 59, no. 11:2331–2344.
Naldrett, S. N. 1958. Half-life of rhenium and ages of minerals. Annals of the New York Academy of Sciences 72:217–226.
Naldrett, S. N. 1984. Half-life of rhenium: Geologic and cosmologic ages. Canadian Journal of Physics 62, no. 1:15–20.
Naldrett, S. N., and W. F. Libby. 1948. Natural radioactivity of rhenium. Physical Review 73:487–493.
Olive, K. A., M. Pospelov, Y.-Z. Qian, A. Coc, M. Cassé, and E. Vangioni-Flam. 2002. Constraints on the variations of the fundamental couplings. Physical Review D 66, no. 4.045022:1–13.
Olive, K. A., M. Pospelov, Y.-Z. Qian, G. Manhès, E. Vangioni- Flam, A. Coc, and M. Cassé. 2004. Reexamination of the 187Re bound on the variation of fundamental couplings. Physical Review D 69, no. 2.027701:1–4.
Olive, K. A., and Y.-Z. Qian. 2004. Were fundamental constants different in the past? Physics Today 57, no. 10:40–45.
Payne, J. A., and R. Drever. 1965. “An investigation of the beta decay of rhenium to osmium with high temperature proportional counters.” PhD thesis. University of Glasgow, Scotland, United Kingdom.
Renne, P. R., D. B. Karner, and K. R. Ludwig. 1998. Absolute ages aren’t exactly. Science 282, no. 5395:1840–1841.
Schmitz, M. D. 2012. Radiogenic isotope geochronology. In The geologic time scale 2012, ed. F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 1, chap. 6, 115–126. Amsterdam, The Netherlands: Elsevier.
Schoene, B., J. L Crowley, D. J. Condon, M. D. Schmitz, and S. A. Bowring. 2006. Reassessing the uranium decay constants for geochronology using ID-TIMS U-Pb data. Geochimica et Cosmochimica Acta 70, no. 2:426–445.
Segawa, M., T. Masaki, Y. Nagai, Y. Temma, T. Shima, K. Mishima, M. Igashira, S. Goriely, A. Koning, and S. Hilaire. 2007. Neutron capture cross sections of 186Os, 187Os, and 189Os for Re-Os chronology. Physical Review C 76, no. 2.022802(R):1–5.
Selby, D., R. A. Creaser, H. J. Stein, R. J. Markey, and J. L. Hannah. 2007. Assessment of the 187Re decay constant by cross calibration of Re-Os molybdenite and U-Pb zircon chronometers in magmatic ore systems. Geochimica et Cosmochimica Acta 71, no. 8:1999–2013.
Shen, J. J., D. A. Papanastassiou, and G. J. Wasserburg. 1996. Precise Re-Os determinations and systematics of iron meteorites. Geochimica et Cosmochimica Acta 60, no. 15:2887–2900.
Shen, J. J., D. A. Papanastassiou, and G. J. Wasserburg. 1998. Re-Os systematics in pallasite and mesosiderite metal. Geochimica et Cosmochimica Acta 62, no. 15:2715–2723.
Shirey, S. B., and R. J. Walker. 1998. The Re-Os isotope system in cosmochemistry and high-temperature geochemistry. Annual Review of Earth and Planetary Sciences 26:423–500.
Shukolyukov, A., and G. W. Lugmair. 1997. The 53Mn-53Cr isotope system in the Omolon pallasite and the half-life of 187Re. Lunar and Planetary Science Conference 28:1237.
Smoliar, M. I., R. J. Walker, and J. W. Morgan. 1996. Re-Os ages of group IIA, IIIA, IVA, and IVB iron meteorites. Science 271, no. 5252:1099––1102.
Snelling, A. A. 2005. Isochron discordances and the role of mixing and inheritance of radioisotopes in the mantle and crust. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/isochron-discordances-role-inheritance/.
Snelling, A. A. 2014a. Determination of the radioisotope decay constants and half-lives: Rubidium-87 (87Rb). Answers Research Journal 7:311–322. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, A. A. 2014b. Determination of the radioisotope decay constants and half-lives: Lutetium-176 (176Lu). Answers Research Journal 7:483–497. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Steiger, R. H., and E. Jäger. 1977. Subcommission on geochronology: Convention on the use of decay constants in geo- and cosmochronology. Earth and Planetary Science Letters 36, no. 3:359–362.
Stein, H. J., R. J. Markey, J. W. Morgan, J. L. Hannah, and A. Schersten. 2001. The remarkable Re-Os chronometer in molybdenite: How and why it works. Terra Nova 13, no. 6:479–486.
Sugarman, N., and H. Richter. 1948. Note on the “natural radioactivity of rhenium.” Physical Review 73:1411–1412.
Suttle, A. D., and W. F. Libby. 1954. Natural radioactivity of rhenium. Physical Review 95:866–867.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the age of the earth: A young-earth creationist research initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Walton, J. R. 1957. “Studies in radiochemistry:1. The photoexchange reaction between hydrogen-chloride and chlorine, II. The natural radioactivity of rhenium-187.” PhD thesis. Purdue University, Lafayette, Indiana.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nemov, and C. A. Bauman. 1969. A programmable magnetic field mass spectrometer with on-line data processing. Reviews of Scientific Instruments 40, no. 2:288–295.
Watt, D. E., and R. N. Glover. 1962. A search for radioactivity among the naturally occurring isobaric pairs. Philosophical Magazine 7, no. 73:105–114.
Wolf, C. J., and W. H. Johnston. 1962. Natural radioactivity of rhenium. Physical Review 125:307–310.








