Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Over the last 75 years numerous determinations have been made of the 176Lu half-life and decay constant. However, even though the measurement technology has improved, the determinations over the last 30 years have resulted in unexplained and unresolved discrepancies. Direct physical counting experiments have resulted in two separate groupings of results with different 176Lu mean half-life values. Early determinations based on comparisons of ages of meteorites gave different 176Lu half-life and decay constant values than determinations based on comparisons of ages of terrestrial minerals and rocks. But more recent determinations using meteorites have yielded 176Lu half-life and decay constant values that agree with both determinations based on comparisons of ages of terrestrial minerals and rocks, and with one of the groupings of determinations by direct physical counting experiments. Thus the 176Lu half-life and decay constant values of 37.12 Byr and 1.867 × 10-11 per year respectively have now been generally adopted for standard use by the geological community, based particularly on the determinations using comparisons of ages of terrestrial minerals and rocks. The more recent meteorite determinations used chondrite meteorites rather than the eucrite meteorites used for the earlier determinations, because it was realized the latter have suffered thermal and shock metamorphism that resulted in significant disturbance of the Lu-Hf systematics among mineral phases due to open geochemical system behavior, such as leakage of 176Hf. Yet the discrepancies in the determinations by the direct physical counting experiments remain unexplained and unresolved. Furthermore, all the determinations using age comparisons on terrestrial minerals and rocks and most of the more recent determinations using age comparisons on chondrite meteorites have been calibrated against the U-Pb method, but even this “gold standard” has unresolved uncertainties due to variations measured in terrestrial rocks and minerals and meteorites of the 238U/235U ratio which is so critical to the method. So the U-Pb method should not be used as a standard to determine other decay constants. This only serves to highlight that if the Lu-Hf dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then it cannot be absolute, and therefore it cannot be used to reject the young-earth creationist timescale. Indeed, current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
Keywords: radioisotope dating, decay constant, half-life, lutetium-176, 176Lu, β decay, direct physical counting, γ-rays, geological age comparisons, terrestrial minerals and rocks, meteorites, eucrites, chondrites, discrepancies, U-Pb “gold standard”, 238U/235U ratio.
Introduction
Radioisotope dating of rocks and meteorites is perhaps the most potent claimed proof for the supposed old age of the earth and the solar system. The absolute ages provided by the radioisotope dating methods provide an apparent aura of certainty to the claimed millions and billions of years for formation of the earth’s rocks.
However, accurate radioisotopic age determinations require that the decay constants of the respective parent radionuclides be accurately known. Ideally, the uncertainty of the decay constants should be negligible compared to, or at least be commensurate with, the analytical uncertainties of the mass spectrometer measurements entering the radioisotope age calculations (Begemann et al. 2001). Clearly, based on the ongoing discussion in the conventional literature this is not the case at present. The stunning improvements in the performance of mass spectrometers during the past four or so decades, starting with the landmark paper by Wasserburg et al. (1969), have not been accompanied by any comparable improvement in the accuracy of the decay constants (Begemann et al. 2001; Steiger and Jäger 1977), in spite of ongoing attempts (Miller 2012). The uncertainties associated with direct half-life determinations are, in most cases, still at the percent level at best, which is still significantly better than any radioisotope method for determining the ages of rock formations. The recognition of an urgent need to improve the situation is not new (for example, Min et al. 2000; Renne, Karner, and Ludwig 1998). It continues to be mentioned, at one time or another, by every group active in geo- or cosmochronology (Schmitz 2012).
From a creationist perspective, the 1997–2005 RATE (Radioisotopes and the Age of The Earth) project successfully made progress in documenting some of the pitfalls in the radioisotope dating methods, and especially in demonstrating that radioisotope decay rates may not have always been constant at today’s measured rates (Vardiman, Snelling, and Chaffin 2000, 2005). Yet much research effort remains to be done to make further in-roads into not only uncovering the flaws intrinsic to these long-age dating methods, but towards a thorough understanding of radioisotopes and their decay during the earth’s history within a biblical creationist framework.
One crucial area the RATE project did not touch on was this issue of how accurate and reliable are the determinations of the radioisotope decay rates (decay constants and half-lives), which are so crucial for calibrating these dating “clocks.” The reliability of the other two assumptions these absolute dating methods rely on, that is, the starting conditions and no contamination of closed systems, are unprovable. Yet these can be circumvented somewhat via the isochron technique, because it is independent of the starting conditions and is sensitive to revealing any contamination. This is especially the case when mineral isochrons are used. Data points that do not fit on the isochron are simply ignored because their values are regarded as due to contamination. That this is common practice is illustrated with numerous examples from the relevant literature by Faure and Mensing (2005) and Dickin (2005). On the other hand, it could be argued that this discarding of data points which do not fit the isochron is somewhat arbitrary and therefore is not good science, because it is merely assumed “aberrant” values are due to contamination rather than that being proven to be so.
In order to rectify this deficiency, Snelling (2014) documented the methodology behind and history of determining the decay constant and half-life of the parent radioisotope 87Rb used as the basis for the Rb-Sr long-age dating method. He showed that there is still some uncertainty in what the values for these measures of the 87Rb decay rate should be, and that the determined values differ when Rb-Sr ages are calibrated against the U-Pb ages of either the same terrestrial minerals and rocks or the same meteorites and lunar rocks. Ironically it is the slow decay rates of isotopes such as 87Rb used for deep time dating that makes precise measurements of their decay rates so difficult. Thus it could be argued that direct measurements of their decay rates should be the only acceptable experimental evidence, especially because measurements which are calibrated against other radioisotope systems are already biased by the currently accepted methodology employed by the secular community in their rock dating methods. We thus need to further explore just how accurate these determinations are for other parent radioisotopes, whether there really is consensus on standard values for their half-lives and decay constants, and just how independent and objective their standard values are from one another between the different long-age dating methods. Of course, it is to be expected that every long-lived radioactive isotope is likely to show similar variation and uncertainty in half-life determinations because these are difficult measurements to make. However, even small variations and uncertainties in the half-life values result in large variations and uncertainties in the calculated ages for rocks, and the question remains as to whether the half-life values for each long-lived parent radioisotope are independently determined. Here we continue these investigations by exploring the determinations of the lutetium-176 (176Lu) decay rate, which is the basis for the Lu-Hf method.
Lutetium and Lutetium-176 Decay
With an atomic number of 71, lutetium is therefore element 71, which places it in the sixth period of the periodic table. It is the last of the lanthanide series and thus is the heaviest of the rare earth elements (REEs). It has two naturally occurring isotopes whose abundances are 97.4% 175Lu and 2.6% 176Lu, so that the 175Lu/176Lu ratio is 37.46 (Dickin 2005). There has been some disagreement over this ratio, but the value of 37.701 ± 0.028 experimentally determined by Patchett and Tatsumoto (1980b) has been used exclusively in all subsequent research. However,the differences in the values obtained between that and the few other determinations remain unexplained.
The geochemical properties of Lu are similar to those of the REE Sm (samarium). Lutetium has a valence of 3+ and an ionic radius of 0.93 Å, the latter being similar to that of Ca2+ at 0.99 Å. This causes Lu3+ to be captured by crystals in place of Ca2+. Lutetium is thus present and widely dispersed in all types of rocks, but concentrations rarely exceed 0.5 ppm and so it does not form its own minerals in most geological environments. The average concentrations of Lu in ordinary rock-forming silicate minerals are generally low, so the average Lu concentrations in igneous rocks increase very little with the increasing degree of differentiation from basalt to granite (Faure and Mensing 2005). The most important mineral carriers of Lu in the common rock types are apatite, garnet, and biotite, plus the rarer alkali-rich pyroxene aegirine and amphibole arfvedsonite. Elevated Lu concentrations are present in Zr-bearing minerals such as zircon, baddeleyite and eudialyte, but the highest Lu concentrations are found in rare-earth oxides such as euxenite, carbonates such as bastnaesite, phosphates such as xenotime and monazite, and silicates such as gadolinite and allanite. All such rare-earth minerals are relatively rare and occur primarily in complex pegmatites, alkali-rich intrusives, and carbonatites. Thus these rare-earth minerals are not important for dating by the Lu-Hf method, but their presence as accessory minerals makes their host rocks suitable for such dating.
Lutetium-176 is radioactive and displays branched isobaric decay by beta (β) emission to stable 176Hf and by electron capture to stable 176Yb. The frequency of electron captures is of the order of 3% or less (Dixon, McNair, and Curran 1954; Glover and Watt 1957), so in view of the long half-life of 176Lu and the current estimate of the frequency at only 0.095% (http://www.nucleonica.net/unc.aspx) the slow decay to 176Yb can be usually ignored. Thus current estimates for the decay constant of 176Lu are solely based on its β-decay to 176Hf, ignoring any potential electron capture. 176Hf is left in an excited state after the β-emission, and decays to the ground state by γ-emission. The relevant decay scheme is therefore depicted as:
where β- is a β-particle, ⊽ is an anti-neutrino, and Q is the decay energy.
The first Lu-Hf geochronological measurement was made by Herr et al. (1958), who attempted to determine the 176Lu half-life by analyzing the isotopic composition of Hf in the heavy-REE-rich mineral gadolinite. Boudin and Deutsch (1970) were the first to determine the 176Lu half-life by dating Lu-bearing minerals of “known” age, while Owen and Faure (1974) attempted to use the method to date common rocks and minerals, but had trouble with the isotopic analysis of Hf due to the difficulties of its chemical separation and its poor ionization efficiency during thermal-ionisation mass spectrometry (TIMS). However, these problems were finally overcome by Patchett and Tatsumoto (1980a) with a modified analytical technique, so after this breakthrough the Lu-Hf method became useful in the dating of terrestrial rocks and minerals, and of meteorites.
There are two parameters by which the decay rate is measured and expressed, namely, the decay constant (λ) and the half-life (t½). The decay constant can be defined as the probability per unit time of a particular nucleus decaying, whereas the half-life is the time it takes for half of a given number of the parent radionuclide atoms to decay. The two quantities can be almost used interchangeably, because they are related by the equation:-
Thus here we will simply focus on the determinations of the 176Lu half-life.
Determination Methods
Two approaches have so far been followed to determine the β-decay half-life of the long-lived radioactive 176Lu.
Direct counting
Except for the very first attempts, direct determinations of the half-life of 176Lu have been by β-γ and γ-γ-coincidence counting.
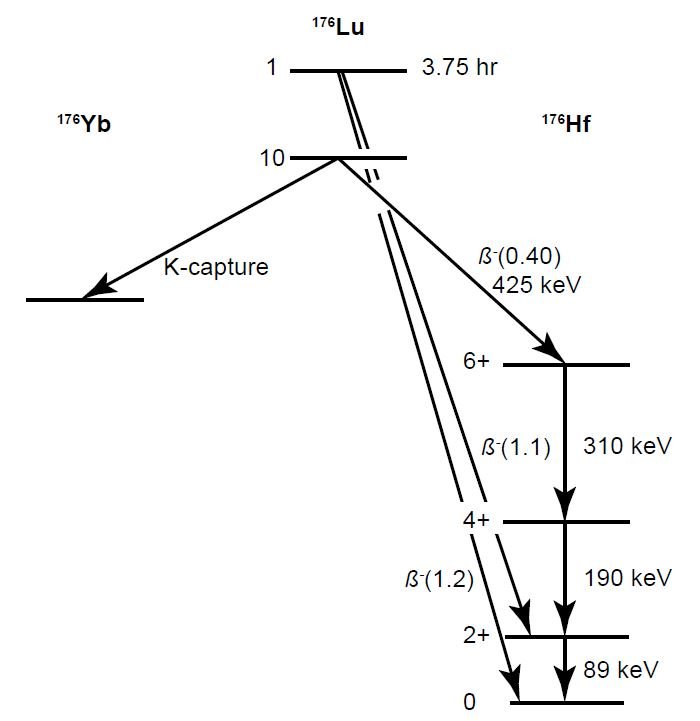
Fig. 1. The decay scheme of 176Lu as initially proposed (after Arnold and Sugihara 1953; Dixon, McNair, and Curran 1954). In this figure there is a “10” next to the ground state of 176Lu, but this is a spin 7, negative parity state.
In the β-γ-coincidence counting technique, the beta (β) activity of 176Lu was counted in a suitable solid Lu2O3 source material using a proportional tube spectrometer/counter (Dixon, McNair, and Curran 1954; Donhoffer 1964; McNair 1961; Prodi, Flynn, and Glendenin 1969), and divided by the total number of radioactive atoms in the known quantity of Lu, based on Avogadro’s number and the isotopic abundance of 176Lu. At the same time a low-level NaI (sodium iodide) scintillation spectrometer/counter doped with Tl was used to detect the γ-ray spectrum and to measure the energy peaks of the γ-rays produced by the energy transitions of the daughter 176Hf as it decays from its excited state to its ground state (Arnold 1954; Brinkman, Aten, and Veenboer 1965; Glover and Watt 1957) (fig. 1). Thus the detection of the number of daughter 176Hf atoms produced can be compared with the number of β-particles counted from the parent 176Lu decay. Among the difficulties of this approach, and with just β-particle counting, are problems with detector efficiencies and geometry factors, the self-shielding or self-absorption of the finite-thickness solid samples, the stopping power of the crystal source and the fraction of pulses appearing in the “photo peak” (typically included in the detection efficiency for scintillation and solid state detection systems). Furthermore, the escape of I (iodine) K electron shell x-rays is an important factor in the size of the lowest γ-ray energy peak, which would only be a secondary check against the two primary γ-rays, that is, the 201 and 306.9 keV γ-rays, for determining the amount of 176Lu present (Arnold 1954; Begemann et al. 2001; Brinkman, Aten, and Veenboer 1965; Dixon, McNair, and Curran 1954; Flammersfeld and Mattauch 1943).
In the γ-γ-coincidence counting technique, one or more Ge detectors or a γ-ray spectrometer is used to simultaneously measure the γ-ray energy peaks corresponding to those produced by the cascading energy states of the daughter 176Hf atom (fig. 2). Since each daughter 176Hf atom produced by β-decay from each parent 176Lu atom cascades down through these energy levels to reach its ground state, measuring each γ-ray energy peak should effectively count the same number of daughter 176Hf atoms produced in the given time of the experiment, which only after correction for the number of decays which produce a given γ-ray, namely the branching ratio for each γ, is equivalent to the 176Lu decay rate. Both Sguigna, Larabee, and Washington (1982) and Grinyer et al. (2003) set out the mathematical principles by which the 176Lu half-life is calculated from the γ-ray counts in each energy peak. In order to increase the counting rate, Sguigna, Larabee, and Washington (1982) used three Ge-Ge detectors placed at 120° to each other around their Lu2O3 sample and shielded from each other to prevent scattered coincidences, whereas Grinyer et al. (2003) used an 8π γ-ray spectrometer consisting of 20 HPGe γ-ray detectors. Because of the better resolution of the solid state detectors, these determinations would tend to be trusted more than those determinations made with the combination of proportional chamber/NaI (Tl doped) detectors (see below in the discussion).
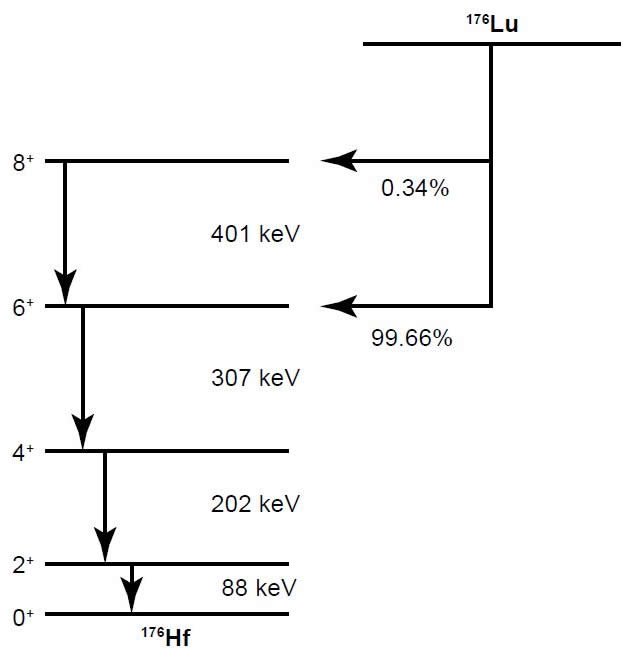
Fig. 2. The decay scheme of 176Lu as currently proposed (after Firestone and Shirley 1996; Grinyer et al. 2003).
Gehrke, Casey, and Murray (1990), Dalmasso, Barci-Funel, and Ardisson (1992), and Nir-El and Lavi (1998) have all highlighted the difficulties in this approach, which has produced a wide range of half-life results. These difficulties include the calibration of the detector efficiencies, variations in response of detectors to different parts of the source sample, and corrections for γ-ray self-attenuation in the Lu solid source material, true-coincidence summing depending on the source sample’s distance from the detector, and internal conversion. However, in their experiment Grinyer et al. (2003) arranged the twenty detectors in the 8π γ-ray spectrometer so each viewed approximately 13% of the solid angle, and so that angular correlation effects were minimized. Furthermore, they introduced to their mathematical treatment of their data a lumped efficiency parameter, which was the probability per decay that a γ-ray photo-peak event was detected, and included the effects of internal conversion, solid angle coverage, photo-peak efficiency, and self-attenuation of the source sample. This lumped efficiency parameter thus appears to have been a model that was applied to the real experimental data. Grinyer et al. (2003) also applied another small correction factor to represent the probability that another γ-ray (or the x-ray following internal conversion) entered the detector at the same time, thus destroying a photopeak event that should have been counted. These are generally termed peak summing corrections.
Nevertheless, judged from the fact that many of the direct counting experiments have yielded results that are not compatible with one another within the stated uncertainties (see below), it would appear that not all the measurement uncertainties are accounted for in whatever correction factors have been used, and therefore the stated uncertainties are unrealistically small and typically are underestimated. It can therefore be argued that many of such experiments are plagued by unrecognized systematic errors (Begemann et al. 2001). As the nature of these errors is obscure, it is not straightforward to decide which of the, often mutually exclusive, results of such direct counting experiments is closest to the true value. Furthermore, the presence of unknown systematic biases makes any averaging dangerous. It is possible that reliable results of careful workers, listing realistic uncertainties, will not be given the Fig. 2. The decay scheme of 176Lu as currently proposed (after Firestone and Shirley 1996; Grinyer et al. 2003). weights they deserve—this aside from the question of whether it makes sense to average numbers that by far do not agree within the stated uncertainties.
Geological comparisons of methods
The second approach to the determination of the 176Lu decay half-life has been to Lu-Hf date geological samples whose ages have also been measured by other methods with presumably more reliable decay constants, particularly the U-Pb and Pb-Pb methods (Dickin 2005; Faure and Mensing 2005). This approach has the disadvantage that it involves geological uncertainties, such as whether all isotopic systems closed at the same time and remained closed. However, it is claimed to still provide a useful check on the direct laboratory determinations. In this respect it is worth noting that Boudin and Deutsch (1970) proposed a 176Lu half-life of 33 Byr on the basis of Lu-Hf dating of two minerals that had also been U-Pb dated, essentially the same as the 176Lu half-life value of 32.7 Byr determined via direct counting at the same time by Prodi, Flynn, and Glendenin (1969).
This approach entails multi-chronometric dating of terrestrial rocks or a mineral (or minerals) from them (for example, Scherer, Münker, and Mezger 2001; Söderlund et al 2004), or meteorites and a mineral from them (for example, Amelin 2005; Patchett et al. 2004), and cross-calibration of different radioisotopic age systems by adjusting the decay constant of one system so as to force agreement with the age obtained via another dating system (Begemann et al. 2001). In essence, because the half-life of 238U is regarded as the most accurately known of all relevant radionuclides, this usually amounts to expressing ages in units of the half-life of 238U. This has increasingly become the preferred method for determining the half-life of 176Lu.
Results of the Lutetium-176 Decay Determinations
During the last 75 years numerous determinations of the 176Lu decay half-life have been made using these two methods. The results are listed with details in Table 1. The year of the determination versus the value of the half-life is plotted in Fig. 3. The data points plotted have been color-coded to differentiate the values as determined by the two approaches that have been used—direct β-γ and γ-γ-coincidence counting, and geological comparisons with other radioisotope dating methods.
Table 1. Determinations of the 176Lu decay rate expressed in terms of the half-life using direct physical counting experiments, and comparisons of radioisotope ages of terrestrial minerals and rocks, and meteorites.
| Determination of the 176Lu Decay Rate | |||||
|---|---|---|---|---|---|
| Date | Half-Life (Byr) | Error | Method | Source | Notes |
| 1938 | 40 | direct counting | Heyden and Wefelmeier 1938 | ||
| 1943 | 24 | direct counting | Flammersfeld and Mattauch 1943 |
||
| 1954 | 21`.5 | ±1 | direct counting | Arnold 1954 | |
| 1954 | 45.6 | ±3 | direct counting (scintillation/spectrometer) | Dixon, McNair, and Curran 1954 | |
| 1957 | 21 | ±2 | direct counting (mass spectrometer) | Glover and Watt 1957 | |
| 1958 | 21.7 | ±3.5 | direct counting | Herr et al. 1958 | |
| 1961 | 36 | ±1 | direct counting (spectrometer) | McNair 1961 | |
| 1964 | 21.8 | ±0.6 | direct counting (liquid scintillation) | Donhoffer 1964 | |
| 1965 | 35 | ±1.4 | direct counting (liquid scintillation) | Brinkman, Aten, and Veenboer 1965 |
|
| 1965 | 35.4 | ±0.5 | direct counting (liquid scintillation) | Brinkman, Aten, and Veenboer 1965 |
|
| 1965 | 36.8 | ±0.6 | direct counting (liquid scintillation) | Brinkman, Aten, and Veenboer 1965 |
|
| 1967 | 50 | ±3 | direct counting (spectrometer) | Sakamoto 1967 | |
| 1969 | 32.7 | ±0.5 | direct counting (liquid scintillation) | Prodi, Flynn, and Glendenin 1969 |
|
| 1970 | 33 | ±5 | comparison of Lu-Hf and U-Pb ages of two minerals |
Boudin and Deutsch 1970 | |
| 1972 | 37.9 | ±0.3 | direct counting | Komura, Sakamoto, and Tanaka 1972 |
|
| 1980 | 40.8 | ±2.4 | direct counting | Norman 1980 | |
| 1980 | 35.3 | ±1.4 | comparison of Lu-Hf isochron of eucrite meteorites with Rb-Sr, U-Pb, and Sm-Nd ages |
Patchett and Tatsumoto 1980b | |
| 1981 | 35.7 | ±1.4 | comparison of Lu-Hf and U-Pb ages of Antarctic meteorites |
Tatsumoto, Unruh, and Patchett 1981 |
|
| 1982 | 35.7 | comparison of Lu-Hf, Rb-Sr, and U-Pb ages of the Amîtsoq Gneisses |
Pettingill and Patchett 1981 | ||
| 1982 | 35.9 | ±0.5 | direct counting | Sguigna, Larabee, and Waddington 1982 |
|
| 1983 | 37.8 | ±0.1 | direct counting | Sato, Ohoka, and Hirose 1983 | |
| 1990 | 40.5 | ±0.9 | direct counting (spectrometer) | Gehrke, Casey, and Murray 1990 |
|
| 1992 | 37.3 | ±0.5 | direct counting | Dalmasso, Barci-Funel, and Ardisson 1992 |
|
| 1998 | 36.9 | ±0.2 | direct counting | Nir-El and Lavi 1998 | |
| 2001 | 35 | comparison of methods (adjusting Tatsumoto et al 1981) |
Begemann et al. 2001 | ||
| 2001 | 37.16 | ±0.46 | comparison of Lu-Hf and U-Pb isochron ages of four minerals |
Scherer, Münker, and Mezger 2001 |
|
| 2002 | 35.9 | ±0.5 | comparison of Lu-Hf and Sm-Nd ages of eucrite meteorites (based on Sguigna, Larabee, and Waddington 1982) |
Blichert-Toft et al. 2002 | |
| 2003 | 34.95 | ±0.21 | comparison of meteorites with Allende Pb-Pb ages |
Bizzarro et al. 2003 | |
| 2003 | 40.8 | ±0.3 | direct counting (spectrometer) | Grinyer et al. 2003 | |
| 2003 | 36.77 | ±0.75 | direct counting (spectrometer) | Nir-El and Haquin 2003 | |
| 2004 | 37.12 | ±0.09 | comparison of Lu-Hf and U-Pb ages of Precambrian mafic intrusions |
Söderlund et al. 2004 | |
| 2004 | 37.12 | ±0.09 | comparison of Lu-Hf and Sm-Nd ages of chondrite meteorites |
Patchett et al. 2004 | |
| 2005 | 37.18 | ±0.43 | comparison of Lu-Hf and U-Pb ages of phosphates from meteorites |
Amelin 2005 | for Richardton (H5) |
| 2005 | 37.83 | ±0.24 | comparison of Lu-Hf and U-Pb ages of phosphates from meteorites |
Amelin 2005 | for Acapulco |
| 2006 | 38.3 | ±0.4 | mean values | Albarède et al. 2006 | for physical counting experiments |
| 2006 | 37.12 | ±0.05 | mean values | Albarède et al. 2006 | for age comparisons of terrestrial minerals |
| 2006 | 35.39 | ±0.16 | mean values | Albarède et al. 2006 | for age comparisons of meteorites |
| 2008 | 36.78 | ±0.12 | comparison of Lu-Hf and U-Pb ages of chondrite meteorites |
Bouvier, Vervoort, and Patchett 2008 |
|
Discussion
Since the early 1960s the reported half-life determinations have scattered around 37 Byr, although there are extreme outliers on the low side at 21.8 Byr (Donhoffer 1964), as well as on the high side at 50 Byr (Sakamoto 1967) (table 1 and fig. 3). However, during the last three decades since 1980 the scatter has been very much reduced. So that the differences and trends in the data can be more easily seen, the relevant section of Fig. 3 has been expanded in Fig. 4. The values of 40.8 ± 2.4 Byr of Norman (1980) and 40.5 ± 0.9 Byr of Gehrke, Casey, and Murray (1990), the latter obtained on a sample enriched in 176Lu to 44%, are more than 3σ above each of the measurements preceding and following this work (table 1). Nir-el and Lavi (1998) suggested the adoption of a half-life of 37.3 ± 0.1 Byr, which is the weighted mean of the half-life determinations of 37.8 ± 0.01 Byr (Sato, Ohoka, and Hirose 1983), 37.3 ± 0.05 Byr (Dalmasso, Barci-Funel, and Ardisson 1992), and their own 36.9 ± 0.02 Byr. Nir-el and Lavi (1998) did not explain their selection criteria, except that the adopted value should be calculated from the grouping of values in the range 37–38 Byr. Taken at face value, this criterion disqualifies their own result of 36.9 Byr, but makes eligible that of Komura, Sakamoto, and Tanaka (1972) of 37.9 Byr which they did not consider. These half-life differences do not at first glance appear to be really significant in view of the value being in excess of 30 billion years. However, even a small difference in the half-life can mean a huge difference when it is used to calculate the age of a rock, on the order of tens of millions of years,
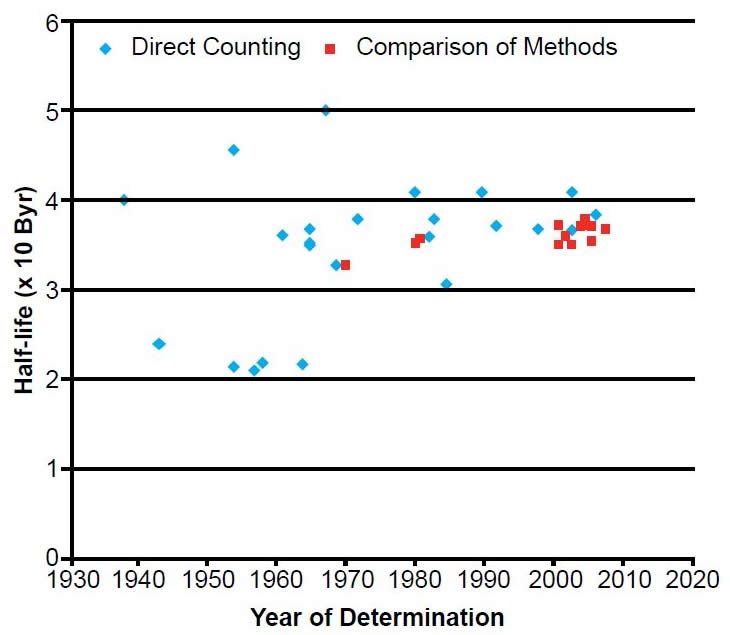
Fig. 3. Plot of each 176Lu half-life determination versus the year of its determination, color-coded according to the method of its determination.
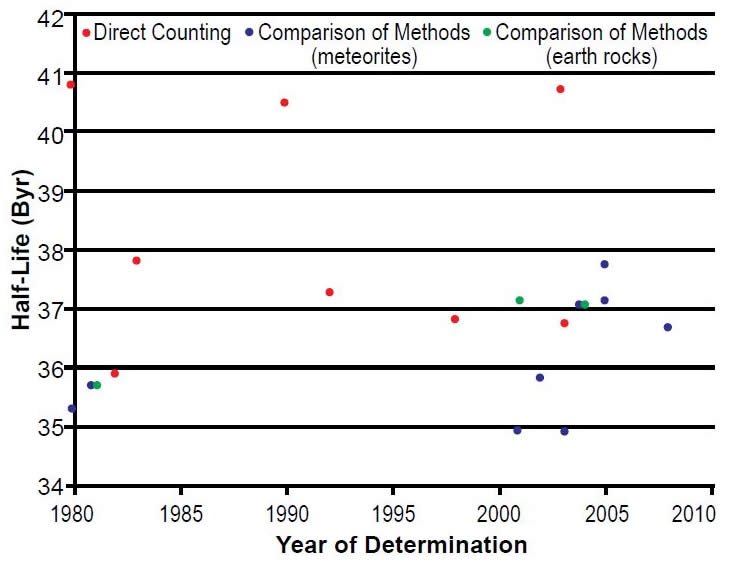
Fig. 4. Enlarged plot of the 176Lu half-life determinations since 1980 versus the year of their determination, color-coded according to the method of their determination.
Patchett and Tatsumoto (1980b) produced a Lu-Hf isochron for eucrite meteorites, which based on several lines of good evidence are regarded to have all come from the same asteroid 4-Vesta that supposedly differentiated at about 4.55 Ga (McSween et al. 2013). Using this “known age,” the Lu-Hf isochron yielded a decay constant of 1.96 ± 0.08 × 10-11 per year, with uncertainty at the 95% confidence level, which is equivalent to a half-life of 35.3 ± 1.4 Byr. This was subsequently updated by Tatsumoto et al. (1981) to 1.94 ± 0.07 × 10-11 per year (a half-life of 35.7 ± 1.4 Byr) by the addition of three more eucrite meteorite analyses to their Lu-Hf isochron. However, Begemann et al. (2001) argued that because some of the eucrites, notably those at the higher end of their Lu-Hf isochron, have been interpreted as having an age of formation that is 0.1 Ga younger than the main population (Mittlefehldt et al. 1998), it could be argued that a 176Lu decay constant of 1.98 × 10-11 per year (a half-life of 35 Byr) is the best value resulting from the Tatsumoto, Unruh, and Patchett (1981) study.
In subsequent cosmochronology, geochronology and corresponding chemical evolutionary studies, the decay constant of 1.94 × 10-11 per year (half-life of 35.7 Byr) from Tatsumoto, Unruh, and Patchett (1981) was used from 1981 to 1997. This half-life of 35.7 Byr is 4% lower than the optimum value of 37.3 ± 0.1 Byr suggested by Nir-el and Lavi (1998). Blichert-Toft and Albarède (1997) analyzed a number of chondritic meteorites for their Lu-Hf isotope systematics, and redefined the meteoritic reference parameters for Hf isotope evolution in rocky planets and asteroids. They used the decay constant of 1.93 × 10-11 per year (a half-life of 35.9 Byr) from Sguigna, Larabee, and Waddington (1982). This value is so similar to that of Tatsumoto, Unruh, and Patchett (1981) that this switch had only a small effect on Hf isotopic studies of the earth and other planetary samples. However, the discrepancy of ~4% between half-lives from physical measurements and from meteorite radioisotope ages remained, as well as the dispersion in all determinations, so this problem still needed to be addressed in future investigations.
Because naturalists postulate the origin of the elements via nucleosynthesis in stars so that they comment on Lu decay in that context, some explanations of terms they use are warranted here. The s-process (or slow-neutron-capture-process) is the nucleosynthesis process that evidently occurs at relatively low neutron density and intermediate temperature conditions in stars. Under these conditions heavier nuclei are “created” by neutron capture, increasing the atomic weight of the nucleus by one. A neutron in the new nucleus then decays by β- decay to a proton, creating a nucleus of higher atomic number. This s-process is thus secondary, meaning that it requires preexisting heavy isotopes as seed nuclei to be converted into other heavy nuclei. The rate of neutron capture by atomic nuclei is slow relative to the rate of radioactive β- decay, hence the name. Although considerable variability exists, it is estimated that the current time between successive neutron captures is about 100 years, whereas the time for β decay is about one minute. Thus if β decay can occur at all, it almost always occurs before another neutron can be captured. On the other hand, the r-process, which differs from the s-process by its faster rate of neutron capture of more than one neutron, entails a succession of rapid neutron captures (hence the name r-process) by heavy seed nuclei, typically 56Fe or other more neutron-rich heavy isotopes, before β decay takes place. The r-process is thus responsible for the “creation” of approximately half of the neutron-rich atomic nuclei heavier than iron, whereas the s-process produces approximately the other half of the isotopes of the elements heavier than iron. Taken together these two processes are claimed to account for a majority of the supposed galactic chemical “evolution” of elements heavier than iron.
In any case, it should be emphasized that any differences in the 176Lu half-life between those values determined by direct counting experiments and those values determined by comparisons of radioisotope ages of the same meteorites and terrestrial materials cannot be accounted for by the branching in the decay of 176Lu because both methods measure only the partial decay to 176Hf (fig. 1), which accounts for >99% of the 176Lu decay. Furthermore, as pointed out by Begemann et al. (2001), 176Lu is also claimed to be important as the only long-lived nuclide that is close to 100% s-process in terms of its supposed stellar origin, being shielded from r-process contributions by stable 176Yb. Thus, according to naturalistic theory, 176Lu could be used to calculate the supposed age of the galactic s-process. However, a consistent level of early interest (for example, Audouze, Fowler, and Schramm 1972; Beer et al. 1981; McCulloch, De Laeter, and Rosman 1976) became tempered by the realization that an excited isomer of 176Lu that decays rapidly to 176Hf would have its abundance enhanced by typical stellar temperatures. This thermal effect would thus prevent any s-process “age” calculation (Beer et al. 1984). In any case, this is not relevant to these problems involving terrestrial, lunar, or meteoritic materials, because at temperatures up to 10 million degrees the 176Lu half-life would apparently be shortened by only a miniscule amount. On the other hand, if the 176Lu atoms were highly ionized or buffeted by the high pressure waves which occur due to cavitation, for example, during the rapid flow of water (as would have been occurring during the Flood), then changes to the decay rate could have been significantly large, even by several orders of magnitude (Cardone, Mignani, and Petrucci 2009). It only stands to reason that any process which reduces the coulomb barrier of the nucleus can significantly affect the decay process, especially a radionuclide which β decays.
The discrepancies between different determinations of the 176Lu half-life became even more apparent when in 2003 two independent results of direct counting experiments were published. Grinyer et al. (2003) measured a half-life of 40.8 ± 0.03 Byr, whereas Nir-El and Haquin (2003) reported a half-life of only 36.77 ± 0.75 Byr from their experiment. Both of these published uncertainties were claimed to be the actual uncertainties from the presumed correct values for the half-life, given the claimed elimination of measurement uncertainties in the methods used in each case. Furthermore, further radioisotope age comparisons had determined the 176Lu half-life as 37.16 ± 0.46 Byr based on the U-Pb and Lu-Hf isochron ages of minerals extracted from four earth rocks (Scherer, Münker, and Mezger 2001), as 35.9 ± 0.09 Byr based on Sm-Nd and Lu-Hf isochron ages of eucrite meteorites (Blichert- Toft et al. 2002), and as 34.95 ± 0.21 Byr based on the Lu-Hf isochron age of a large group of chondrite and eucrite meteorites compared to the Pb-Pb isochron age of 4.56 Ga for the naturalistic formation of chondrites (Amelin et al. 2002; Bizzarro et al. 2003) (table 1). The subtle discrepancies between determinations were thus highlighted by Scherer, Mezger, and Münker (2003) in a diagram which is reproduced here as Fig. 5. They added further 176Lu decay constant determinations based on the U-Pb and Lu-Hf isochron ages of minerals extracted from more earth rocks, plus their own 176Lu decay constant determination based on comparing the radioisotope ages of eucrite meteorites, to their previous study (Scherer, Münker, and Mezger 2001) to show that there are differences in the 176Lu decay rate as determined by physical counting experiments, as determined by age comparisons of terrestrial minerals, and as determined by age comparisons of meteorites.
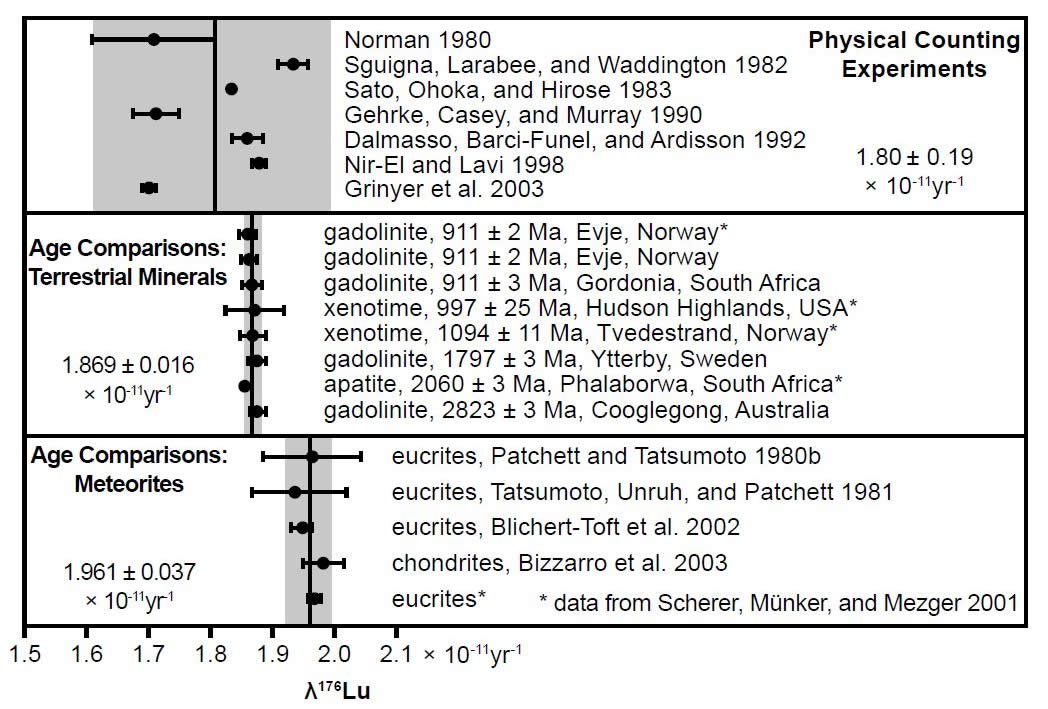
Fig. 5. Comparison of the 176Lu decay constant determinations since 1980, grouped according to the determination method by Scherer, Mezger, and Münker (2003). The vertical shaded areas indicate the two standard deviations (2σ) from the mean values (vertical lines) for each method.
Albarède et al. (2006) continued the recognition and discussion of this same observation. Their diagram plotting the differences in the decay constant between determinations using terrestrial materials and determinations using meteorites, as well determinations resulting from physical counting experiments was based on the Scherer, Mezger, and Münker (2003) diagram, but also included the Nir-El and Haquin (2003) physical counting result and determinations by Söderlund et al. (2004) from comparing the Lu-Hf and U-Pb radioisotope ages of Precambrian mafic intrusions. Their diagram is reproduced here as Fig. 6. Albarède et al. (2006) found that using the earth-based 176Lu decay constant the Lu-Hf ages of chondrites were consistently 4% higher than their U-Pb ages, so the reconciliation of the Lu-Hf and U-Pb ages required using a different meteorite-based 176Lu decay constant. Ironically, but significantly, Albarède et al. (2006) proposed that this discrepancy between the terrestrial and meteoritic decay constants could be because of accelerated 176Lu decay during the first few million years of the supposed existence of the solar nebula due to irradiation of the 176Lu by γ-rays emitted by one or more supernova(e) exploding in the vicinity of the solar nebula.
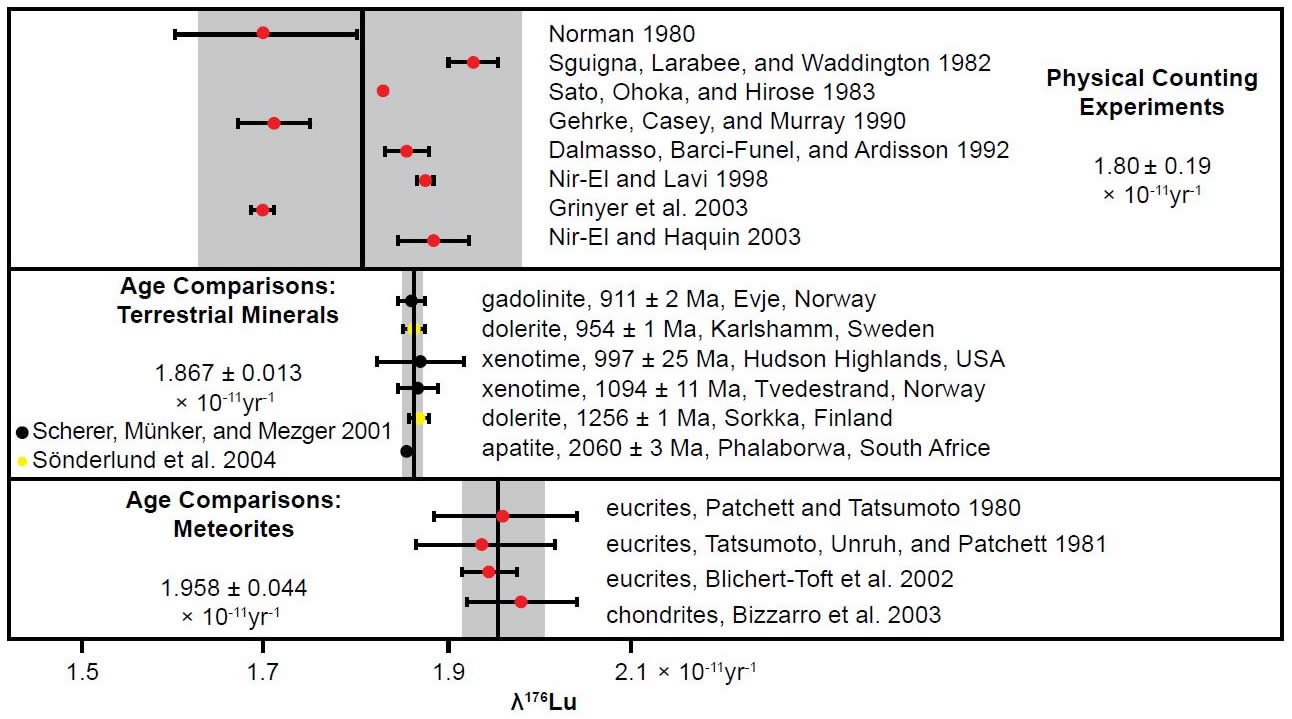
Fig. 6. Comparison of the 176Lu decay constant determinations since 1980, grouped according to the determination method by Albarède et al. (2006). The vertical shaded areas indicate the two standard deviations (2σ) from the mean values (vertical lines) for each method.
However, in the related context of nucleosynthesis of the elements inside stars, Zhao and Käppeler (1990) had found the absorption cross-section to produce 176Lu to be small and hence had found problems explaining their data. On the other hand, 176Lu is produced at rather high rates in high energy accelerators, which of course means relatively high cross-sections at energies above 1 GeV. Nevertheless, they concluded that to reestablish the 176Lu clock for determining the supposed age of the s-process elements would, in any case, require a quantitative description of all processes feeding the ground state as well as a reliable model for the s-process environment, in particular for the temperatures to which 176Lu was exposed during its production and ever since. However, even though these effects of ionization on the nuclear half-lives can be enhanced inside stars due to the extreme ionization prevalent there, such contexts are not relevant in the creationist framework for the history of the earth and the universe. The earth and its rocks, and their contained elements and isotopes, were all created before the stars, the other planets, the moons, and the asteroids from which the meteorites subsequently came. And then in their history since their creation, neither the earth nor the asteroids have been subjected to the intense ionization inside stars.
In any case, Wimpenny, Amelin, and Yin (2013) have pointed out that using the 176Lu decay constant determined from radioisotope age comparisons of terrestrial rocks to calculate the Lu-Hf ages of meteorites supposedly older than ~4.556 Ga results in apparent ages that are older than the claimed age of the solar system. They noted the suggested possible explanation that the 176Lu decay rate had been enhanced (or accelerated) by photo-excitation of 176Lu by γ-rays (Albarède et al. 2006) or by cosmic rays (Thrane et al. 2010) shortly after supposed accretion began in the early solar system. But they then sought to test that explanation by looking for the depleted 175Lu/176Lu ratios and excess 176Hf such irradiation would have produced in meteorites. They found no systematic differences in the Lu isotopic compositions between terrestrial basalts and achondrite meteorites (eucrites and angrites). Furthermore, the Lu-Hf systematics in whole rock and mineral separates from angrite meteorites (Amelin, Wimpenny, and Yin 2011; Sanborn, Carlson, and Wadhwa 2012) produce Lu-Hf ages concordant with their Pb-Pb and Sm-Nd radioisotope ages rather than expected older ages. Thus they concluded that together these data do not support the hypothesis of accelerated decay of 176Lu by γ-ray or cosmic ray irradiation during supposed solar system accretion, which of course is an evolutionary concept that simply does not work.
Now while Albarède et al. (2006) included in their diagram (fig. 6) the latest determinations from physical counting experiments and from the comparison of ages for more earth rocks, they missed including further more recent determinations using the comparison of ages for more meteorites, and for minerals extracted from them. Patchett et al. (2004) analyzed the Lu-Hf and Sm-Nd isotopic systematics for 19 chondrite meteorites and found agreement between the calculated Sm-Nd and Lu-Hf isochron ages by using a 176Lu decay constant of 1.867 × 10-11 per year (a half-life of 37.12 Byr) similar to that obtained by Scherer, Münker, and Mezger (2001) and Söderlund et al. (2004) from comparison of Lu-Hf and U-Pb isochron ages in terrestrial rocks and minerals. Similarly, Amelin (2005) obtained Lu-Hf and U-Pb isotope data for phosphate minerals separated from the Acapulco (primitive achondrite) and Richardton (ordinary chondrite) meteorites and concordant Lu-Hf and Pb-Pb isochron ages yielded 176Lu decay constants of 1.832 × 10-11 per year and 1.864 × 10-11 per year (half-lives of 37.83 Byr and 37.18 Byr) respectively (table 1). Then Bouvier, Vervoort, and Patchett (2008) similarly obtained Lu-Hf isotopic data for another 28 pristine chondrite meteorites and added to them the Lu-Hf data of Bizzarro et al. (2003) and Patchett et al. (2004) to calculate a Lu-Hf isochron age concordant with the presumed Pb-Pb isochron age for the start of the supposed accretion of the solar system (Bouvier et al. 2007), by which they determined a 176Lu decay constant of 1.884 × 10-11 per year (a half-life of 36.78 Byr).
All the 176Lu half-life determinations since 1980 are thus plotted in Fig. 7, color-coded according to the different determination methods. At this expanded scale for the half-life values it is apparent that there are two groupings of values among those obtained by the physical counting experiments, and another two groupings of values among those obtained by age comparisons using meteorites, each with their own mean value and two standard deviation spread. On the other hand, the half-life values obtained by age comparison using terrestrial minerals and rocks cluster very tightly around a mean value of 37.12 Byr (a decay constant of 1.867 × 10-11 per year) with a two standard deviation spread of 0.43 Byr, which would be much less if one sample’s value was ignored. The mean values and two standard deviation spreads for all the groupings depicted in Fig. 7 are listed in Table 2, including the grouping of all the determinations using meteorites for age comparisons (the black vertical line and cross-hatched area in fig. 7). For comparison, the mean (average) half-life value for the 14 direct counting determinations made prior to 1980 (from table 1) is listed in Table 2. At 32.8 Byr it is much lower than the means of both groups of post- 1980 direct counting determinations. This is of course a reflection of the better resolution of the solid state detectors used for the post-1980 determinations, in contrast to the combination of proportional chamber/ NaI (Tl doped) detectors used for the pre-1980 determinations (as already noted above). In any case, what is immediately evident from Fig. 7 and Table 2 is that the mean half-life values for the groupings of shorter half-life physical counting experiments, age comparisons using terrestrial minerals and rocks, and longer half-life age comparisons using meteorites are virtually identical within their two standard deviation spreads. That is why a 176Lu decay constant of 1.867 × 10-11 per year (a half-life of 37.12 Byr), based primarily on the age comparisons using terrestrial minerals and rocks, has now generally been adopted by the geological community as the agreed value for standard use in Lu-Hf age calculations (for example, Amelin, Wimpenny, and Yin 2011; Debaille, Yin, and Amelin 2011; Sanborn, Carlson, and Wadhwa 2012; Thrane et al. 2010).
Table 2.Mean half-life values and two standard deviation spreads for the groupings of determinations by the different methods as plotted in Fig. 7.
| Determination Method | Grouping | Mean Value | Two Standard Deviation |
|---|---|---|---|
| physical counting | shorter half-life | 36.93 Byr |
± 0.41 Byr |
| physical counting | longer half-life | 40.7 Byr |
± 1.2 Byr |
| physical counting | prior to 1980 | 32.8 Byr |
|
| age comparisons (terrestrial minerals and rocks) | 37.12 Byr |
± 0.43 Byr |
|
| age comparisons (meteorites) | shorter half-life | 35.39 Byr |
± 0.88 Byr |
| age comparisons (meteorites) | longer half-life | 37.23 Byr |
± 0.22 Byr |
| age comparisons (meteorites) | all determinations | 36.35 Byr |
± 0.65 Byr |

Fig. 7. Comparison of all the 176Lu half-life determinations since 1980 grouped and color-coded according to the determination method. The vertical color shaded areas indicate the two standard deviations from the mean values (colored vertical lines) for the groupings of determinations in each method. The uncertainties are at the 2σ level.
Three issues stemming from this choice need to be resolved. First, why do a few of the physical counting experiments yield a longer half-life mean value of 40.7 Byr, especially when the most recent of these experiments (Grinyer et al. 2003) was reported at the same time as the most recent determination in the shorter half-life grouping with a half-life mean value of 36.93 Byr in Fig. 7 (Nir-El and Haquin 2003)? There was a difference in the methodology of these two physical counting experiments. Grinyer et al. (2003) used the γ-γ-coincidence method, whereas Nir- El and Haquin (2003) simply used γ-counting. The γ-γ-coincidence method has more potential difficulties if not done correctly, so the direct γ-counting method may give a better result. However, that must not explain this difference in the determined half-life values, because the γ-γ- coincidence method was also used by Sguigna, Larabee, and Waddington (1982), but they obtained a half-life value of only 35.9 Byr, whereas Norman (1980) used the γ-counting method and obtained a half-life value of 40.8 Byr, the same as Grinyer et al. (2003). And the different half-life values obtained cannot be explained by the Lu source material used, because both Grinyer et al. (2003) and Nir- El and Haquin (2003) used Lu2O3 powder, whereas Norman (1980) used Lu metal foil. Of course, the grain size of the powder can make a difference in the effective density of the powder and therefore the absorption correction. So these disparities in the determined half-lives between these physical counting experiments remain unresolved.
Second, why do the earlier determinations using age comparisons of meteorites yield a shorter half-life value than the more recent determinations using age comparisons of meteorites? Bouvier, Vervoort, and Patchett (2008) seem to have the answer when they concluded “that thermal- or shock-metamorphosed meteorites (such as eucrites) cannot be used to reliably determine the 176Lu decay constant” and “this is especially true when multiple meteorites or meteorite groups with distinct thermal and shock metamorphic histories, and parent bodies are included in the regression” to determine the 176Lu decay constant. Patchett and Tatsumoto (1980b), Tatsumoto, Unruh, and Patchett (1981), and Blichert-Toft et al. (2002) all used eucrite meteorites, and Bizzarro et al. (2003) used both eucrite and chondrite meteorites, whereas Patchett et al. (2004) and Bouvier, Vervoort, and Patchett (2008) only used chondrite meteorites, and Amelin (2005) used phosphate minerals from chondrite and primitive achondrite meteorites, not eucrite meteorites. As Amelin, Wimpenny, and Yin (2011) and Sanborn, Carlson, and Wadhwa (2012) found, there is evidence of significant disturbance of the Lu-Hf systematics among the mineral phases in some meteorites after initial closure of the isotopic system due to open geochemical system behavior, such as leakage of 176Hf.
Third, the favored radioisotope method used for age comparisons to most reliably determine the 176Lu decay constant and half-life is the U-Pb method. All the age comparisons on terrestrial rocks and minerals (Scherer, Münker, and Mezger 2001; Scherer, Mezger, and Münker 2003; Söderlund et al. 2004), and the age comparisons on meteorites by Amelin (2005) and Bouvier, Vervoort, and Patchett (2008), used the U-Pb method to determine the 176Lu decay constant and half-life. So the values of 1.867 × 10-11 per year and 37.12 Byr now routinely adopted for Lu-Hf age calculations are firmly calibrated against the U-Pb method. Yet even this U-Pb “gold standard” has come under similar scrutiny in the last decade. The U-Pb method depends on the crucial 238U/235U ratio, but discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites (Brennecka and Wadhwa 2012; Hiess et al. 2012). These discrepancies and variations remain unexplained, so their potential significance from a creationist perspective awaits further study, especially in the context of examination of the determinations of the 238U and 235U decay constants and half-lives. Furthermore, the fact that there are these variations in the crucial 238U/235U ratio in terrestrial minerals and rocks on which the U-Pb dating “gold standard” depends, which has been used to calibrate Lu-Hf isochron ages to determine the 176Lu half-life and decay constant, only underscores that these radioisotope methods cannot provide the absolute invariable “dates” they are so confidently proclaimed to provide. Thus the U-Pb method should not be used as a standard to determine other radioisotope decay constants.
Finally, it would remain prudent to be very careful with these geological comparison methods for two other reasons. First, there are significant flaws in the basic assumptions on which all the radioisotope dating methods depend. Second, the U-Pb method relies primarily on α decay, whereas the Lu-Hf method relies on β decay. As observed by both Austin (2005) and Snelling (2005), these different decay modes seem to yield different ages for some earth rocks using the same samples with essentially the same methodology. Furthermore, as described earlier, the differences in the 176Lu decay constant and half-life values determined by physical γ counting and γ-γ-coincidence counting experiments remain unexplained and unresolved, when these direct counting methods should be expected to yield reliable and consistent 176Lu decay constant and half-life determinations. However, at the low counting rates which are involved even small corrections to the data can easily cause the observed differences. So without an accurately known 176Lu decay constant and half-life, accurate Lu-Hf radioisotope ages cannot be determined. Therefore, Lu-Hf dating cannot be used to reject the young-earth creationist timescale. Indeed, current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos. Nevertheless, although the products from the multi-billion half-life of Lu are a seeming challenge to a young age for the earth, they have been already explained by the evidence for accelerated radioisotope decay during a past catastrophic event, such as the Flood (Vardiman, Snelling, and Chaffin 2000, 2005).
Conclusions
There have been numerous attempts to determine the 176Lu half-life and decay constant in the last 75 years by two methods—direct counting of the γ-rays emitted by the daughter 176Hf as it “falls” from an excited state to its ground state after being derived by the β decay of its parent 176Lu, and comparisons of Lu-Hf ages of terrestrial minerals and rocks, and meteorites, with ages derived by other radioisotope systems, especially U-Pb. The estimates of the 176Lu half-life have not been consistent, even since 1980 as improvements have been made in measurement technologies. Indeed, there are two distinct separate groupings of determinations obtained by physical direct counting experiments with mean half-life values of 36.93 Byr and 40.7 Byr, with these differences apparent in two experiments performed in the same year (2003). This discrepancy has still neither been explained nor resolved.
The initial use of meteorites to determine the 176Lu decay constant (and half-life) via age comparisons also suggested a disparity with the 176Lu decay constant (and half-life) determined by the physical counting experiments and with the 176Lu decay constant (and half-life) determined by age comparisons of terrestrial minerals and rocks. However, more recent determinations using meteorites for age comparisons have produced a distinct separate grouping with 176Lu decay constant and half-life mean values virtually identical to those obtained by age comparisons of terrestrial minerals and rocks, and to those in the shorter half-life grouping of physical counting experiments. It was thus realized that the eucrite meteorites used for not as suitable because of significant disturbance of the Lu-Hf systematics among mineral phases due to open geochemical system behavior, such as leakage of 176Hf. Consequently a 176Lu decay constant of 1.867 × 10-11 per year (a half-life of 37.12 Byr), based primarily on the age comparisons using terrestrial minerals and rocks, has now generally been adopted by the geological community as the agreed value for standard use in Lu-Hf age calculations.
Nevertheless, all the age comparisons on terrestrial rocks and minerals, and the more recent age comparisons on meteorites, used the U-Pb method to determine the 176Lu decay constant of 1.867 × 10-11 per year and half-life of 37.12 Byr, and thus Lu-Hf age calculations are ultimately calibrated against the U-Pb method. However, this U-Pb “gold standard” depends on the crucial 238U/235U ratio, and yet discrepancies and variations have been found between the 238U/235U ratio in U-bearing terrestrial minerals and rocks and the 238U/235U ratio in meteorites. These discrepancies and variations remain unexplained. This only serves to highlight that if the Lu-Hf dating method has been calibrated against the U-Pb “gold standard” with its own uncertainties, then it cannot be absolute, especially as the 176Lu decay rate has also not been accurately determined by physical direct counting experiments. Without an accurately known 176Lu decay constant and half-life, accurate Lu-Hf radioisotope ages cannot be determined. Therefore, Lu-Hf dating cannot be used to reject the young-earth creationist timescale, especially as current radioisotope dating methodologies are at best hypotheses based on extrapolating current measurements and observations back into an assumed deep time history for the cosmos.
References
Albarède, F., E. E. Scherer, J. Blichert-Toft, M. Rosing, A. Simionovici, and M. Bizzarro. 2006. γ-ray irradiation in the early solar system and the conundrum of the 176Lu decay constant. Geochimica et Cosmochimica Acta 70:1261–1270.
Amelin, Y. 2005. Meteorite phosphates show constant 176Lu decay rate since 4557 million years ago. Science 310, no. 5749:839–841.
Amelin, Y., A. N. Krot, I. D. Hutcheon, and A. A. Ulyanov. 2002. Lead isotopic ages of chondrules and calcium-aluminum-rich inclusions. Science 297, no. 5587:1678–1683.
Amelin, Y., J. Wimpenny, and Q.-Z. Yin. 2011. Angrite Lu-Hf whole rock data provide no direct support to accelerated decay of 176Lu by supernova irradiation. Workshop on the Formation of the First Solids in the Solar System #9014.
Arnold, J. R. 1954. Energy levels in Lu176 and Hf176. Physical Review 93, no. 4:743–745.
Arnold, J. R., and T. Sugihara. 1953. The decay scheme of natural lutetium 176. Physical Review 90:332.
Audouze J., W. A. Fowler, and D. N. Schramm. 1972. 176Lu and s-process nucleosynthesis. Nature Physical Science 238:8–11.
Austin, S. A. 2005. Do radioisotope clocks need repair? Testing the assumptions of isochron dating using K-Ar, Rb-Sr, Sm- Nd, and Pb-Pb isotopes. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 325–392. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/do-radioisotope-clocks-need-repair/.
Beer H., F. Käppeler, K. Wisshak, and R. A. Ward. 1981. 176Lu: Cosmic clock or stellar thermometer? Astrophysical Journal Supplement 46:295–317.
Beer, H., G. Walter, R. L. Macklin, and P. J. Patchett. 1984. Neutron capture cross sections and solar abundances of 160,161Dy, 170,171Yb, 175,176Lu, and 176,177Hf for the s-process analysis of the radionuclide 176Lu. Physical Review C 30:464–478.
Begemann, F., K. R. Ludwig, G. W. Lugmair, K. Min, L. E. Nyquist, P. J. Patchett, P. R. Renne, C.-Y. Shih, I. M. Villa, and R. J. Walker. 2001. Call for an improved set of decay constants for geochronological use. Geochimica et Cosmochimica Acta 65, no. 1:111–121.
Bizzarro, M., J. A. Baker, H. Haack, D. Ulfbeck, and M. Rosing. 2003. Early history of earth’s crust-mantle system inferred from hafnium isotopes in chondrites. Nature 421: 931–933.
Blichert-Toft, J., and F. Albarède. 1997. The Lu-Hf isotope geochemistry of chondrites and the evolution of the mantle-crust system. Earth and Planetary Science Letters 148: 243–258.
Blichert-Toft, J., M. Boyet, P. Télouk, and F. Albarède. 2002. 147Sm–143Nd and 176Lu–176Hf in eucrites and the differentiation of the HED parent body. Earth and Planetary Science Letters 204, nos. 1–2:167–181.
Boudin, A., and S. Deutsch. 1970. Geochronology: Recent development in the lutetium-176/hafnium-176 dating method. Science 168, no. 3936:1219–1220.
Bouvier, A., J. Blichert-Toft, F. Moynier, J. D. Vervoort, and F. Albarède. 2007. Pb-Pb dating constraints on the accretion and cooling history of chondrites. Geochimica et Cosmochimica Acta 71, no. 6:1583–1604.
Bouvier, A., J. D. Vervoort, and P. J. Patchett. 2008. The Lu-Hf and Sm-Nd isotopic composition of CHUR: Constraints from unequilibrated chondrites and implications for the bulk composition of terrestrial planets. Earth and Planetary Science Letters 273, nos. 1–2:48–57.
Brennecka, G. A., and M. Wadhwa. 2012. Uranium isotope compositions of the basaltic angrite meteorites and the chronological implications for the early Solar System. Proceedings of the National Academy of Sciences USA 109, no. 24:9299–9303.
Brinkman, G. A., A. H. W. Aten Jr., and J. Th. Veenboer. 1965. Natural radioactivity of K-40, Rb-87 and Lu-176. Physica 31, no. 8:1305–1319.
Cardone, F., R. Mignani, and A. Petrucci. 2009. Piezonuclear decay of thorium. Physics Letters A 373, no. 22:1956–1958.
Dalmasso, J., G. Barci-Funel, and G. J. Ardisson. 1992. Reinvestigation of the decay of the long-lived odd-odd 176Lu nucleus. Applied Radiation and Isotopes 43, no. 1–2:69–76.
Debaille, V., Q.-Z. Yin, and Y. Amelin. 2011. The role of phosphates for the Lu-Hf chronology of meteorites. Workshop on the Formation of the First Solids in the Solar System #9066.
Dickin, A. P. 2005. Radiogenic isotope geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press. Dixon, D., A. McNair, and S. C. Curran. 1954. The natural radioactivity of lutetium. Philosophical Magazine 45, no. 366:683–694.
Donhoffer, D. 1964. Bestimmung der halbwertszeiten der in der natur vorkommenden radioaktiven nuklide Sm147 and Lu176 mittels flüssiger szintillatoren. Nuclear Physics 50:489–496.
Faure, G. and T. M. Mensing. 2005. Isotopes: Principles and applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Firestone, R. B., and V. S. Shirley. 1996. Table of the isotopes. 8th ed. New York, New York: John Wiley & Sons.
Flammersfeld, A., and J. Mattauch. 1943. Die natürliche und künstliche Aktivität des Cassiopeiums ein neuer Fall von Isomerie. Naturwissenschaften 31:66–67.
Gehrke, R., J. C. Casey, and R. K. Murray. 1990. Half-life of 176Lu. Physical Review C 41, no. 6:2878–2882.
Glover, R. N., and D. E. Watt. 1957. A search for electron capture in 176Lu. Philosophical Magazine 2, no. 17:699–702.
Grinyer, G. F., J. C. Waddington, C. E. Svensson, R. A. E. Austin, G. C. Ball, G. Hackman, J. M. O’Meara, C. Osborne, F. Sarazin, H. C. Scraggs, and H. D. H. Stöver. 2003. Half-life of 176Lu. Physical Review C 67:#014302.
Herr, W., E. Merz, P. Eberhardt, and P. Signer. 1958. Zur Bestimmung der β-Halbwertszeit des 176Lu durch den Nachweis von radiogenem 176Hf. Zeitschrift für Naturforschung A 13:268–273.
Heyden, M., and W. Wefelmeier. 1938. Eine natürliche β-Radioaktivität des Cassiopeiums. Naturwissenschaften 26, no. 37:612.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. 238U/235U systematics in terrestrial uranium-bearing minerals. Science 335, no. 6076:1610–1614. Komura, K., K. Sakamoto, and S. Tanaka. 1972. The half-life of long-lived 176Lu. Nuclear Physics A 198, no. 1:73—80.
McCulloch, M. T., J. R. De Laeter, and K. J. R. Rosman. 1976. The isotopic composition and elemental abundance of lutetium in meteorites and terrestrial samples and the 176Lu cosmochronometer. Earth and Planetary Science Letters 28, no. 3:308–322.
McNair, A. 1961. The half-life of long-lived lutetium-176. Philosophical Magazine 6, no. 67:851–856.
McSween, H. Y., R. P. Binzel, M. C. De Sanctis, E. Ammannito, T. H. Prettyman, A. W. Beck, V. Reddy, et al. 2013. Dawn; the Vesta-HED connection; and the geologic context for eucrites, diogenites, and howardites. Meteoritics and Planetary Science 48, no. 11:2090–2104.
Miller, J. L. 2012. Time to reset isotopic clocks? Two new studies revise key parameters in radiometric dating. Physics Today 65, no. 6:20–22.
Min K., R. Mundil, P. R. Renne, and K. R. Ludwig. 2000. A test for systematic errors in 40Ar/39Ar geochronology through comparison with U-Pb analysis of a 1.1 Ga rhyolite. Geochimica et Cosmochimica Acta 64, no. 1:73–98.
Mittlefehldt, D. W., T. J. McCoy, C. A. Goodrich, and A. Kracher. 1998. Non-chondritic meteorites from asteroidal bodies. In Planetary Materials, ed. J. J. Papike, Reviews in Mineralogy, vol. 36, 4-1–4-195. Washington, DC: Mineralogical Society of America.
Nir-El, Y., and N. Lavi. 1998. Measurement of the half-life of 176Lu. Applied Radiation and Isotopes 49, no. 12:1653–1665.
Nir-El, Y., and G. Haquin. 2003. Half-life of 176Lu. Physical Review C 68, no. 6:#067301.
Norman, E. B. 1980. Half-life of 176Lu. Physical Review C 21, no. 3:1109–1110.
Owen, L. B., and G. Faure. 1974. Simultaneous determination of hafnium and zirconium in silicate rocks by isotope dilution. Analytical Chemistry 46, no. 9:1323–1326.
Patchett, P. J., and M. Tatsumoto. 1980a. A routine highprecision method for Lu-Hf isotope geochemistry and chronology. Contributions to Mineralogy and Petrology 75, no. 3:263–268.
Patchett, P. J., and M. Tatsumoto. 1980b. Lu-Hf total-rock isochron for the eucrite meteorites. Nature 288:571–574.
Patchett, P. J., J. D. Vervoort, U. Söderlund, and V. J. M. Salters. 2004. Lu-Hf and Sm-Nd isotopic systematics in chondrites and their constraints on the Lu-Hf properties of the earth. Earth and Planetary Science Letters 222, no. 1:29–41.
Pettingill, H. S., and P. J. Patchett. 1981. Lu-Hf total-rock age for Amîtsoq gneisses, West Greenland. Earth and Planetary Science Letters 55, no. 1:150–156.
Prodi, V., K. F. Flynn, and L. E. Glendenin. 1969. Half-life and β spectrum of 176Lu. Physical Review 188, no. 4:1930–1933.
Renne, P. R., D. B. Karner, and K. R. Ludwig. 1998. Absolute ages aren’t exactly. Science 282, no. 5395:1840–1841.
Sakamoto, K. 1967. The natural half-lives of 176Lu and 180Ta. Nuclear Physics A 103, no. 1:134—144.
Sanborn, M. E., R. W. Carlson, and M. Wadhwa. 2012. Internal Lu-Hf isochrons for the quenched and plutonic angrites and their chronological implications. Lunar and Planetary Science Conference 43:#2039.
Sato, J., Y. Ohoka, and T. Hirose. 1983. La période de 176Lu. Radiochemical and Radioanalytical Letters 58, nos. 5–6:263–270.
Scherer, E., C. Münker, and K. Mezger. 2001. Calibration of the lutetium-hafnium clock. Science 293, no. 5530:683–687.
Scherer, E., K. Mezger, and C. Münker. 2003. The 176Lu decay constant discrepancy: terrestrial samples vs. meteorites. Meteoritics and Planetary Science 38:A136.
Schmitz, M. D. 2012. Radiogenic isotope geochronology. In The Geologic Time Scale 2012, ed. F. M. Gradstein, J. G. Ogg, M. D. Schmitz, and G. M. Ogg, vol. 1, chap. 6, 115–126. Amsterdam, The Netherlands: Elsevier.
Sguigna, A. P., A. J. Larabee, and J. C. Waddington. 1982. The half-life of 176Lu by a γ-γ coincidence measurement. Canadian Journal of Physics 60, no. 3:361–364.
Snelling, A. A. 2005. Isochron discordances and the role of mixing and inheritance of radioisotopes in the mantle and crust. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/isochronal-discordances-role-inheritance/.
Snelling, A. A. 2014. Determination of the radioisotope decay constants and half-lives: Rubidium-87 (87Rb). Answers Research Journal 7:311–322. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Söderlund, U., P. J. Patchett, J. D. Vervoort, and C. E. Isachsen. 2004. The 176Lu decay constant determined by Lu-Hf and U-Pb isotope systematics of Precambrian mafic intrusions. Earth and Planetary Science Letters 219, nos. 3–4:311–324.
Steiger, R. H., and E. Jäger. 1977. Subcommission on geochronology: Convention on the use of decay constants in geo- and cosmochronology. Earth and Planetary Science Letters 36, no. 3:359–362.
Tatsumoto, M., D. M. Unruh, and P. J. Patchett. 1981. U-Pb and Lu-Hf systematics of Antarctic meteorites. In: Proceedings of sixth symposium on the Antarctic meteorites, ed. T. Nagata, 237–249. Tokyo, Japan: National Institute for Polar Research.
Thrane, K., J. N Connelly, M. Bizzarro, B. S. Meyer, and L.-S. The. 2010. Origin of excess 176Hf in meteorites. Astrophysical Journal 717, no. 2:861–867.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2000. Radioisotopes and the age of the earth: A young-earth creationist research initiative. El Cajon, California: Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Wasserburg G. J., D. A. Papanastassiou, E. V. Nemov, and C. A. Bauman. 1969. A programmable magnetic field mass spectrometer with on-line data processing. Review of Scientific Instruments 40, no. 2:288–295.
Wimpenny, J. B., Y. Amelin, and Q.-Z. Yin. 2013. Isotopic composition of Lu in terrestrial samples and achondrites: Implications for the Lu-Hf systematics in the early solar system. 76th Annual Meteoritical Society Meeting, Goldschmidt Conference #5218.
Zhao, W. R., and F. Käppeler. 1990. The 176Lu chronometer in trouble. In Astrophysical ages and dating methods (Proceedings of the Fifth IAP Workshop, June 26–30, 1989, Institut d’Astrophysique de Paris, France), ed. E. Vangioni- Flam, M. Cassé, J. Audouze, and J. Tran Thanh Van, 357–364. Paris, France: Editions Frontières.









