Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Meteorites date the earth with a 4.55 ± 0.07 Ga Pb-Pb isochron called the geochron. They appear to consistently yield 4.55–4.57 Ga radioisotope ages, adding to the uniformitarians’ confidence in the radioisotope dating methods. Many radioisotope dating studies of groups of asteroidal meteorites (chondrites, stony achondrites, pallasites and mesosiderites, and irons) in the last six decades have used the Rb-Sr, Sm-Nd, U-Th-Pb, Lu-Hf, Re-Os, Mn-Cr, and Hf-W methods to yield many isochron ages of groups of these meteorites from whole-rock samples, and mineral and other fractions. Such age data for groups of these meteorites were tabulated and plotted on frequency versus age histogram diagrams. They strongly cluster in the groups of chondrites, stony achondrites, and irons at 4.55–4.57 Ga, dominated by Pb-Pb, U-Pb, and Pb-Pb calibrated isochron ages, testimony to the Pb-Pb technique’s supremacy as the uniformitarians’ ultimate dating tool, which they consider very reliable. These ages are often confirmed by Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isochron ages, but agreement could be due to calibration with the Pb-Pb system. There is also scattering of many Rb-Sr, Lu-Hf, Re-Os, Sm-Nd isochron ages, and a few Pb-Pb isochron ages, in most cases likely due to thermal disturbances resulting from impact cratering of the parent asteroids. No pattern was found in the isochron ages for these groups of meteorites similar to the systematic patterns of isochron ages found in Precambrian rock units during the RATE project, so there is no evidence of past accelerated radioisotope decay having occurred in these meteorites, and therefore on their parent asteroids. This is not as expected, yet it is the same for all meteorites so far studied. Thus it is argued that accelerated radioisotope decay must have only occurred on the earth, and only the 500–600 million years’ worth we have physical evidence for during the Flood. Otherwise, due to their 4.55–4.57 Ga “ages” these meteorites and their parent asteroids are regarded as originally representing “primordial material” that God made on Day One of the Creation Week, from which He made the non-earth portion of the solar system on Day Four, which is compatible with the Hebrew text of Genesis. Thus today’s measured radioisotope compositions of these meteorites could reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes. So if some or most of the measured daughter isotopes were already in these meteorites when they were formed on their parent asteroids, then their 4.55–4.57 Ga “ages” obtained by Pb-Pb, U-Pb, and Pb-Pb–calibrated isochron age dating are likely not their true real-time ages, which according to the biblical paradigm is only about 6000 real-time years. It is anticipated that further investigation of radioisotope ages data for martian and lunar meteorites, for lunar rocks, and for rocks from every level in the earth’s geologic record, should enable these interim ideas to be further confirmed or modified.
Keywords: meteorites, classification, groups of asteroidal meteorites, chondrites, stony achondrites, pallasites, mesosiderites, irons, Rb-Sr, Lu-Hf, Re-Os, Pb-Pb, U-Pb, Sm-Nd, Mn-Cr, Hf-W, isochron ages, agreement of isochron ages, scattering of isochron ages, accelerated radioisotope decay, thermal disturbance, resetting, cosmic-ray exposure ages, fission tracks, “primordial material,” geochemical signature, inheritance, mixing, Day Three Great Upheaval, the Flood.
Introduction
In 1956 Claire Patterson at the California Institute of Technology in Pasadena reported a Pb-Pb isochron age of 4.55 ± 0.07 Ga for three stony and two iron meteorites, which since then has been declared the age of the earth (Patterson 1956). Adding weight to that claim is the fact that many meteorites appear to consistently date to around the same “age” (Dalrymple 1991, 2004), thus bolstering the evolutionary community’s confidence that they have successfully dated the age of the earth and the solar system at around 4.56 Ga. These apparent successes have also strengthened their case for the supposed reliability of the increasingly sophisticated radioisotope dating methods.
Creationists have commented little on the radioisotope dating of meteorites, apart from acknowledging the use of Patterson’s geochron to establish the age of the earth, and that many meteorites give a similar old age. Morris (2007, 59–61) did focus on the Allende carbonaceous chondrite as an example of a well-studied meteorite analyzed by many radioisotope dating methods, but he only discussed the radioisotope dating results from one, older paper (Tatsumoto, Unruh, and Desborough 1976). In order to rectify this lack of engagement by the creationist community with the meteorite radioisotope dating data, Snelling (2014a) obtained as much radioisotope dating data as possible for the Allende CV3 carbonaceous chondrite meteorite (due to its claimed status as the most studied meteorite), displayed the data, and attempted to analyze them. He found that both isochron and model ages for the total rock, separated components, or combinations of these strongly clustered around a Pb-Pb age of 4.56–4.57 Ga, the earliest (Tatsumoto, Unruh, and Desborough 1976) and the latest (Amelin et al. 2010) determined Pb-Pb isochron ages at 4.553 ± 0.004 Ga and 4.56718 ± 0.0002 Ga respectively being essentially the same. Apart from scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar ages, no systematic pattern was found in the Allende isochron and model ages similar to the systematic pattern of isochron ages found in Precambrian rock units during the RATE project that was interpreted as produced by an episode of past accelerated radioisotope decay (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005).
Snelling (2014b) grouped together all the radioisotope ages obtained for ten ordinary (H, L, and LL) and five enstatite (E) chondrites and similarly displayed the data. They generally clustered, strongly in the Richardton (H5), St. Marguerite (H4), Bardwell (L5), Bjurböle (L4), and St. Séverin (LL6) ordinary chondrite meteorites, at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages, but confirmed by Ar-Ar, Rb-Sr, Re-Os, and Sm-Nd isochron ages. There was also scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar model ages, in some cases possibly due to thermal disturbance. Again, no pattern was found in these meteorites’ isochron ages indicative of past accelerated radioisotope decay.
Snelling (2014c) subsequently compiled all the radioisotope ages for 12 eucrite (basaltic) achondrites. The data for many of these meteorites again strongly clustered at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages but confirmed by Rb-Sr, Lu-Hf, and Sm-Nd isochron ages. There was also scatter of the U-Pb, Pb-Pb, Th-Pb, Rb-Sr, K-Ar, and Ar-Ar model ages, in most cases likely due to thermal disturbances resulting from metamorphism or impact cratering of the parent asteroid, identified as 4-Vesta. Again, no pattern was found in these meteorites’ isochron ages similar to the systematic patterns of isochron ages found in Precambrian rock units during the RATE project, so there is no evidence of past accelerated radioisotope decay having occurred in these eucrites, and therefore on their claimed parent asteroid.
Snelling (2015a) tabulated all the radioisotope ages of ten further achondrites that have been repeatedly dated—primitive achondrites, angrites, aubrites, mesosiderites, and irons. The data again strongly clustered at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages, and sometimes confirmed by Ar-Ar, Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isochron and/or model ages. There was also again scattering of many K-Ar, Ar-Ar, Rb-Sr, Re-Os, Sm-Nd, and a few U-Pb, Pb-Pb, Th-Pb ages, in most cases likely due to thermal disturbances resulting from impact cratering of the parent asteroids. And again, no pattern was found in these meteorites’ isochron ages indicative of past accelerated radioisotope decay having occurred in these achondrites, and therefore on their claimed parent asteroids.
Snelling (2014a, b, c, 2015a) then sought to discuss the possible significance of this clustering in terms of various potential creationist models for the history of radioisotopes and their decay. He favored the idea that asteroids and the meteorites derived from them represent residual “primordial material” from the formation of the solar system, which is compatible with the Hebrew text of Genesis that could suggest God made “primordial material” on Day One of the Creation Week, from which He made the non-earth portion of the solar system on Day Four. Thus he argued that today’s measured radioisotope compositions of all these achondrites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes, “inherited” at their creation. So if some (or most) of the daughter isotopes were already in all these meteorites when they were formed, then the 4.55–4.57 Ga “ages” for them obtained by Pb-Pb and U-Pb isochron and model age dating are likely not their true real-time ages, which according to the biblical paradigm is only about 6000 real-time years.
However, Snelling (2014a, b, c, 2015a) suggested that drawing final conclusions from the radioisotope dating data for just these 16 chondrite, 12 eucrite meteorites, and 10 primitive and other achondrites was still premature, and recommended further studies of the radioisotope dating data for groups of the same categories of meteorites, and for martian and lunar meteorites, for lunar rocks, and for rocks from every level in the earth’s geologic record so as to hopefully confirm or modify these initial conclusions. This present contribution is therefore designed to document the radioisotope dating data for groups of the same category of meteorites (chondrites, stony achondrites, pallasites and mesosiderites, and irons), so as to continue the discussion of the potential significance of these data.
The Classification of Meteorites
Meteorites have been classified into distinct groups and subgroups that show similar chemical, isotopic, mineral, and physical relationships. Within the evolutionary community the ultimate goal of such a classification scheme is to group all known specimens that apparently share a common origin on a single, identifiable parent body, or even a body yet to be identified. This could be another planet, moon, asteroid, or other current solar system object, or one that is believed to have existed in the past (for example, a shattered asteroid). However, several meteorite groups classified this way appear to have come from a single, heterogeneous parent body, or even a single group may contain members that may have come from a variety of similar but distinct parent bodies. So any meteorite classification system is not absolute, and is only as valid as the criteria used to develop it.
More than 24,000 meteorites are currently catalogued (Norton 2002), and this number is rapidly growing due to the ongoing discovery of large concentrations of meteorites in the world’s cold and hot deserts (for example, in Antarctica, and Australia and Africa, respectively). Traditionally meteorites have been divided into three overall categories based on whether they are dominantly composed of rocky materials (stones or stony meteorites), metallic material (irons or iron meteorites), or mixtures (stony-irons or stony-iron meteorites). These categories have been in use since at least the early nineteenth century, but they are merely descriptive and do not have any genetic connotations. In reality, the term “stony-iron” is a misnomer, as the meteorites in one group (the CB chondrites) have over 50% metal by volume and were called stony-irons until their affinities with chondrites were recognized. Similarly, some iron meteorites also contain many silicate inclusions but are rarely described as stony-irons.
Nevertheless, these three categories are still part of the most widely used meteorite classification systems. Stony meteorites are traditionally divided into two other categories—chondrites (meteorites that are characterized by containing chondrules and which apparently have undergone little change since their parent bodies originally formed), and achondrites (meteorites that appear to have had a complex origin involving asteroidal or planetary differentiation). Iron meteorites were traditionally divided into objects with similar internal structures (octahedrites, hexahedrites, and ataxites), but these terms are now only used for descriptive purposes and have given way to chemical group names. Stony-iron meteorites have always been divided into pallasites (which now comprise several distinct groups) and mesosiderites (a textural term which is also synonymous with the name of a modern group).
The most recent classification scheme for the meteorites is that of Weisberg, McCoy, and Krot (2006), which is reproduced in Fig. 1. Based on their bulk compositions and textures, Krot et al. (2005) divided meteorites into two major categories, chondrites (meteorites containing chondrules) and achondrites (or non-chondritic meteorites, that is, meteorites not containing chondrules). They further subdivided the achondrites into primitive achondrites and igneously differentiated achondrites. However, Weisberg, McCoy, and Krot (2006) simply subdivided all meteorites into three categories—chondrites, primitive achondrites and achondrites (fig. 1). As in Krot et al.’s (2005) classification scheme, Weisberg, McCoy, and Krot (2006) have included the IAB and IIICD irons in the primitive achondrites because of their silicate inclusions, while the rest of the groups of irons, the stony-irons, the martian and lunar meteorites are included with the other achondrite groups in the achondrites.
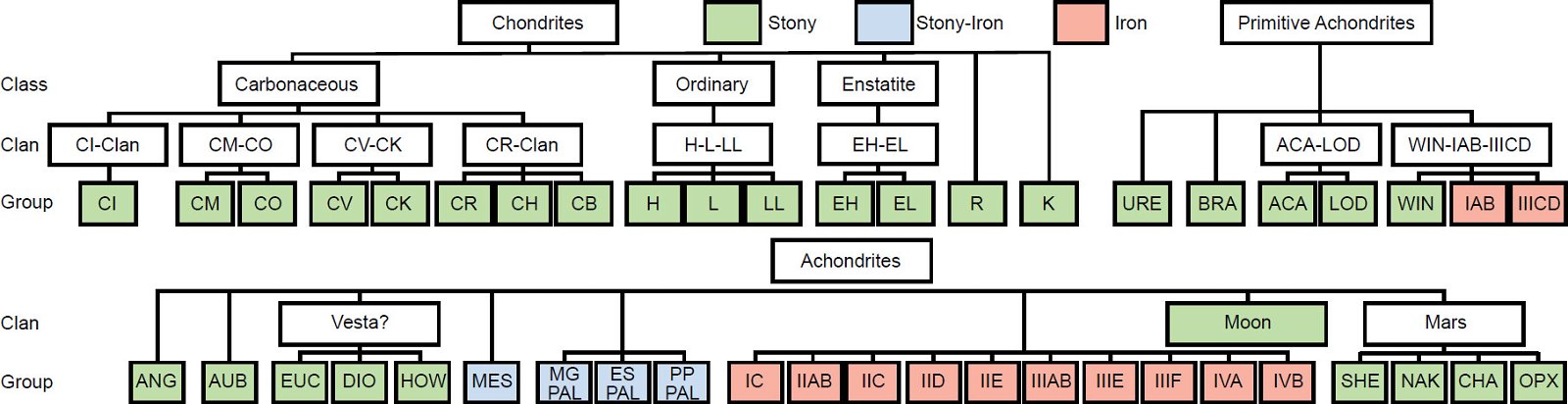
Fig. 1. The classification system for meteorites (after Weisberg, McCoy, and Krot 2006).
About 82% of all meteorite falls are chondrites (Norton 2002). The chondrites derive their name from their interior texture, which is unlike any found in terrestrial rocks. Dispersed more or less uniformly throughout these meteorites are spherical, sub-spherical and sometimes ellipsoidal structures called chondrules. These range in size from about 0.1 to 4 mm (0.0039 to 0.15 in) diameter, with a few reaching centimeter size. Their abundance within a given chondrite can vary enormously from only a few percent of the total volume of the meteorite to as much as 70%, with fine-grained matrix material dispersed between the chondrules. Most chondrules are rich in the silicate minerals olivine and pyroxene. The other major components of chondrites are refractory inclusions—Ca-Al-rich inclusions (CAIs) and amoeboid olivine aggregates (AOAs)—and Fe-Ni metal alloys and sulfides (Brearley and Jones 1998; Scott and Krot 2005).
The chondrites have been subdivided into three classes—carbonaceous (C), ordinary (O), and enstatite (E) chondrites—and 15 groups, including the rare R and K chondrites (fig. 1). The carbonaceous (C) chondrites, representing almost 4% of all chondrites, are so named because their matrix is carbon-rich, containing various amounts of carbon in the form of carbonates and complex organic compounds including amino acids (Cronin, Pizzarello, and Cruikshank 1988). The ordinary (O) chondrites are by far the most common type of meteorite to fall to earth. About 77% of all meteorites and nearly 94% of chondrites are ordinary chondrites. They have been divided into three groups—H, L, and LL chondrites—the letters designating their different bulk iron contents (H for high and L for low) and their different amounts of metal (L for low) (Krot et al. 2005; Norton 2002). The E chondrites comprise only 1.4% of the chondrites, and are named after their primary silicate mineral, enstatite. Enstatite is the Mg-rich end member of the orthopyroxene solid-solution series, and makes up 60–80 vol. % of these meteorites (Krot et al. 2009; Norton 2002). Further details of the classification of the chondrites are provided by Snelling (2014a, b).
The non-chondritic meteorites or achondrites contain virtually none of the components found in chondrites. It is conventionally claimed that they were derived from chondritic materials by planetary melting, and that fractionation caused their bulk compositions to deviate to various degrees from chondritic materials (Krot et al. 2005). The degrees of melting that these rocks experienced are highly variable, and thus, these meteorites have been divided into the two major categories—primitive and differentiated. However, there is no clear cut boundary between these categories.
The differentiated non-chondritic meteorites, or achondrites (fig. 1), are conventionally regarded as having been derived from parent bodies that experienced large-scale partial melting, isotopic homogenization (ureilites are the only exception), and subsequent differentiation. Based on abundance of Fe-Ni metal, these meteorites are commonly divided into three types—achondrites, stony-irons, and irons. Each of these types contains several meteorite groups and ungrouped members (fig. 1). According to uniformitarians, several groups of achondrites and iron meteorites are likely to be genetically related and were possibly derived from single asteroids or planetary bodies.
The achondrites account for about 8% of meteorites overall, and the majority of them (about two-thirds) are HED meteorites (howardites, eucrites, and diogenites), believed to have originated from the crust of asteroid 4-Vesta (Norton 2002) (fig. 1). Other types include the primitive achondrites, angrites, aubrites, martian, lunar, and several types thought to originate from as yet unidentified asteroids, as well as the pallasites, mesosiderites, and various groups of irons. These groups have been determined on the basis of, for example, their bulk Fe/Mn and 17O/18O ratios, which are thought to be characteristic “fingerprints” for each parent body (Mittlefehldt et al. 1998). The achondrites represent the products of classical igneous processes acting on the silicate-oxide system of asteroidal bodies—partial to complete melting, differentiation, and magmatic crystallization (Mittlefehldt 2005). Thus the achondrites consist of materials similar to terrestrial basalts and plutonic rocks, so they exhibit igneous textures, or igneous textures modified by impact and/or thermal metamorphism, and distinctive mineralogies indicative of igneous processes. Iron meteorites represent the complimentary metal-sulfide system products of this process. The structural parameters in irons have been combined with several chemical parameters such as nickel and trace element contents to produce a more definite classification with meaningful distinct genetic groups that could represent different parent bodies. Also, certain trace elements such as gallium (Ga), germanium (Ge), and iridium (Ir) that like Ni are siderophile (or iron-loving) have been used to sub-divide the iron meteorites into distinct chemical groups. Further details about the achondrites and their classification are provided by Snelling (2014c, 2015a)
The Radioisotope Dating of Groups of Meteorites
To thoroughly investigate the radioisotope dating of groups of similar meteorites all the relevant literature was searched. The objective was to find various groups of the same category of meteorites that had been dated by the different radioisotope methods, and a convenient place to start was Dalrymple (1991, 2004), who compiled lists of such data. His radioisotope dating data was tabulated into four categories of meteorites—chondrites, stony achondrites, pallasites and mesosiderites, and irons—which reflected the categories found in the literature. When papers containing radioisotope dating results for groups of meteorites in these four categories were found, the reference lists were also scanned to find further relevant papers. In this way a comprehensive set of papers, articles, and abstracts on radioisotope dating of groups of meteorites in these four categories was collected. While it cannot be claimed that all the papers, articles and abstracts which have ever been published containing radioisotope dating results for groups of meteorites in these four categories have thus been obtained, the cross-checking undertaken between these publications does indicate the data set obtained is very comprehensive.
All the radioisotope dating results for groups of meteorites in these four categories were then compiled and tabulated. For ease of viewing and comparing the radioisotope dating data, the various isochron ages for groups of meteorites in these four categories were tabulated separately—the isochron ages for groups of chondrites in Table 1, the isochron ages for groups of stony achondrites in Table 2, the isochron ages for groups of pallasites and mesosiderites in Table 3, and isochron ages for groups of irons in Table 4. Examples from the literature of a few of the isochrons from which isochron ages were calculated are shown in Fig. 2.
| Samples | Method | Reading | Error +/- | Notes | Source |
|---|---|---|---|---|---|
| β-Decayers | |||||
| Carbonaceous condrites (4, including Orgueil) | Rb-Sr | 4.46 | 0.35 | 5 whole-rock samples (decay constant 1.39) | Murthy and Compston 1965 |
| Carbonaceous condrites (4, including Orgueil) | Rb-Sr | 4.74 | 0.21 | 5 whole-rock samples (assuming Sr mean initial for achondrites) | Murthy and Compston 1965 |
| L chondrites (6, including Pasamonte and Bruderheim) | Rb-Sr | 4.48 | 0.14 | 13 whole-rock samples | Gopalan and Wetherill 1968 |
| LL chondrites (16, including St. Séverin and Olivenza) | Rb-Sr | 4.56 | 0.06 | 26 whole-rock samples | Gopalan and Wetherill 1969 |
| H chondrites (15, including Richardton and Forest Vale) | Rb-Sr | 4.69 | 0.07 | 19 whole-rock samples | Kaushal and Wetherill 1969 |
| Rb-Sr | 4.63 | 0.16 2 | Guarena pyroxene samples plus 18 Olivenza fractions | Sanz and Wasserburg 1969 | |
| E chondrites (8) | Rb-Sr | 4.54 | 0.08 | 14 whole-rock samples | Gopalan and Wetherill 1970 |
| L chondrites (6, including Bruderheim) | Rb-Sr | 4.54 | 0.12 | 16 whole-rock samples | Gopalan and Wetherill 1971 |
| H, L, LL, and E chondrites (50) | Rb-Sr | 4.43 | 0.04 | Whole-rock samples | Wetherill 1975 |
| H chondrites (10, including Allegan, Forest Vale, and Guarena) | Rb-Sr | 4.52 | 0.05 | 18 whole-rock samples | Minster and Allègre 1979 |
| Rb-Sr | 4.508 | 0.37 | 9 whole-rock and density fractions of E chondrites | Minster, Rickard, and Allègre 1979 | |
| E chondrites (6, including Norton County) | Rb-Sr | 4.516 | 0.029 | 10 whole-rock samples | Minster, Rickard, and Allègre 1979 |
| H chondrites | Rb-Sr | 4.64 | 0.11 | (decay constant 1.39) | Mittelfehldt and Wetherill 1979 |
| Rb-Sr | 4.486 | 0.02 | 10 whole-rock samples from 10 LL cohondrites | Minster and Allègre 1981 | |
| LL chondrites (10, including Olivenza and St. Séverin) | Rb-Sr | 4.493 | 0.018 | 26 whole-rock samples | Minster and Alllègre 1981 |
| H chondrites | Rb-Sr | 4.518 | 0.039 | 17 whole-rock samples | Minster, Birck, and Allègre 1982 |
| LL chondrites | Rb-Sr | 4.486 | 0.02 | 13 whole-rock samples | Minster, Birck, and Allègre 1982 E chondrites |
| Rb-Sr | 4.508 | 0.037 | 8 whole-rock samples for 4 E chondrites | Minster, Birck, and Allègre 1982 | |
| H, LL, and E chondrites | Rb-Sr | 4.498 | 0.015 | 38 whole-rock samples (decay constant 1.42) | Minster, Birck, and Allègre 1982 |
| H, LL, and E chondrites | Rb-Sr | 4.555 | 0.01 | 38 whole-rock samples (decay constant 1.402) | Minster, Birck, and Allègre 1982 |
| Rb-Sr | 4.54 | 0.054 | 9 silicate fractions from 3 L chondrites | Rotenburg and Amelin 2002 | |
| Rb-Sr | 4.499 | 0.04 | 9 silicate and 4 phosphate fractions from 3 L chondrites | Rotenburg and Amelin 2002 | |
| Rb-Sr | 4.46 | 0.08 | updated decay constant applied to Goplan and Wetherill 1970 data on 14 whole-rock samples | Dalrymple 1991 | |
| E chondrites (8) | Rb-Sr | 4.51 | 0.04 | Whole rocks | Dalrymple 2004 |
| Chondrites (13, including Allende) | Lu-Hf | 4.56 | 19 samples (Lu decay constant calibrated against U) | Bizzarro et al. 2003 | |
| Chondrites (31, including Allende, Bjurböle, Bruderheim, Allegan, and Richardton) | Lu-Hf | 4.44 | 0.34 | 19 meteorites and 23 analyses (using decay constant of 1.867 of Söderlund et al. 2004) | Patchett et al. 2004 |
| Chondrites (31, including Allende, Bjurböle, Bruderheim, Allegan, and Richardton) | Lu-Hf | 4.51 | 0.24 | 31 meteorites and 42 analyses (using decay constant of 1.867 of Söderlund et al. 2004, and data of Bizzarro et al. 2003) | Patchett et al. 2004 |
| Carbonaceous chondrites (6, including Allende) | Lu-Hf | 4.78 | 0.62 | 8 analyses (using decay constant of 1.867 of Söderlund et al. 2004) | Patchett et al. 2004 |
| H, L, and LL chondrites (10, including St. Séverin and Barwell) | Re-Os | 4.55 | 10 metal fractions plotted with irons, decay constant 1.52 (recalibrated against U-Pb) | Luck and Allègre 1983 | |
| H chondrites (5, including Guarena) | Re-Os | 4.61 | 0.01 | 14 whole rock and metal samples) | Chen, Papanastassiou, and Wasserburg 1998 |
| Carbonaceous chondrites (8, including Allende and Orgueil) | Re-Os | 4.55 | 7 samples, 9 analyses (calibrated to U-Pb, halflife 42.3by) | Walker and Morgan 1989 | |
| α-Decayers | |||||
| H, L chondrites (5) | Pb-Pb | 4.48 | 0.08 | Whole rocks | Murthy and Patterson 1962 |
| Chondrites (with achondrites, 53) | Pb-Pb | 4.5 | 0.03 | Whole rocks | Kanasewich 1968 |
| H, L chondrites (12) | Pb-Pb | 4.49 | 0.05 | Whole rocks | Cumming 1969 |
| Chondrites (16 CC, H, L, and E, including Allende, Richardton, and Bruderheim) | Pb-Pb | 4.505 | 0.008 | 35 whole-rock samples | Huey and Kohman 1973 |
| Chondrites (6, including Allende, Bruderheim, and Richardton) | Pb-Pb | 4.635 | 16 whole-rock samples | Tilton 1973 | |
| Chondrites (8, plus 3 achondrites) | Pb-Pb | 4.555 | 0.005 | 11 whole-rock samples | Tatsumoto, Knight, and Allègre 1973 |
| E chondrites (4) | Pb-Pb | 4.577 | 0.004 | Whole rocks | Manhès and Allègre 1978 |
| Chondrites (13, plus 2 achondrites | Pb-Pb | 4.551 | 0.004 | 13 chondrite fractions plus 2 achondrite fractions | Chen and Wasserburg 1981 |
| L chondrites (7, including Bjurböle, Barwell, and Bruderheim) | Pb-Pb | 4.521 | 0.01 | 18 whole-rock samples | Unruh 1982 |
| Chondrites (4, including Barwell, Richardton, and Allegan) | Pb-Pb | 4.557 | 0.008 | 11 samples of whole rocks, fractions, and chondrules | Unruh, Hutchinson, and Tatsumoto 1979 |
| L and LL chondrites (8, including Barwell) | Pb-Pb | 4.556 | Whole-rock samples using Göpel, Manhes, and Allègre 1994 data | Tera, Carlson, and Boctor 1997 | |
| L and LL chondrites (8, including Barwell) | Pb-Pb | 4.553 | Whole-rock samples using Göpel, Manhes, and Allègre 1994 data | Tera, Carlson, and Boctor 1997 | |
| Pb-Pb | 4.549 | 0.01 | Many whole-rock samples of chondrites plus their phosphates and troilites | Tera and Carlson 1999 | |
| Chondrites (11, including 2 carbonacious [Allende], 4 H [St. Marguerite] and 5 L/LL [St. Séverin; Bjurböle]) | Pb-Pb | 4.566 | 88 analyses of whole rock, olivine, olivine-pyroxene, and chondrule fragments and separates | Bouvier et al. 2007 | |
| Carbonaceous chondrites (3, including Allende) | Pb-Pb | 4.5685 | 0.0005 | ≥34 analyses of Ca-Al inclusions | Bouvier et al. 2007 |
| L chondrites | U-Pb | 4.55 | 7 samples from L meteorites | Unruh and Tatsumoto 1980 | |
| L chondrites (7, including Bjurböle, Barwell, and Bruderheim) | U-Pb | 4.547 | 0.015 | 18 whole-rock samples | Unruh 1982 |
| L chondrites (7, including Bjurböle, Barwell, and Bruderheim) | U-Pb | 4.551 | 0.007 | 15 whole-rock samples and troilite-corrected data | Unruh 1982 |
| Chondrites (8, including St. Séverin, Allende, and Guarena) | Sm-Nd | 4.6 | 11 samples from six meteorites | Jacobsen and Wasserburg 1980 | |
| Sm-Nd | 4.54 | 13 whole-rock samples | Jacobsen and Wasserburg 1984 | ||
| Chondrites (9, including Allende, Richardton, and Bjurböle) | Sm-Nd | 4.182 | 0.51 | 13 phosphate samples from five meteorites | Rotenberg and Amelin 2001 |
| Sm-Nd | 4.588 | 0.1 | 34 analyses of phosphates and chondrules | Amelin and Rotenberg 2004 | |
| Chondrites (9, including Allende, Richardton, and Bjurböle) | Sm-Nd | 4.547 | 0.11 | 89 analyses of phosphates, chondrules, and whole rocks, including earlier data | Amelin and Rotenberg 2004 |
| Chondrites (19, including Allende, Bjurböle, Bruderheim, Allegan, and Richardton) | Sm-Nd | 4.24 | 0.62 | 23 analyses, mean of 22 meteorites plotted with an Allende sample | Patchett et al. 2004 |
| Pb-Pb Calibrated | |||||
| Carbonaceous chondrites (5, including Allende) | Hf-W | 4.568 | 0.0017 | (>17 analyses of Ca-Al inclusions and various fractions; calibrated against St. Marguerite) | Kleine et al. 2005 |
| Carbonaceous chondrites (2, including Allende) | Hf-W | 4.5683 | 0.0007 | 21 analyses of separates from 5 examples (calibrated against Pb-Pb age of D'Orbigny) | Burkhardt et al. 2008 |
| H5 chondrites (2, including Richardton) | Hf-W | 4.5627 | 0.0008 | 15 analyses of various fractions (calibrated against D'Orbigny) | Kleine et al. 2008 |
| H6 chondrites (2) | Hf-W | 4.559 | 0.0009 | 8 analyses of various fractions (calibrated against D'Orbigny) | Kleine et al. 2008 |
| Carbonaceous chondrites (6, including Allende) | Mn-Cr | 4.5681 | 0.001 | 7 whole rock samples (using LEW 86010 Pb-Pb age as the anchor point) | Moynier, Yin, and Jacobsen 2007; Shukolyukov and Lugmair 2006 |
| Carbonaceous, H, L, LL, and E chondrites (including Allende, Orgueil, St. Marguerite, Bjurböle, Olivenza, and St. Séverin) | Mn-Cr | 4.5673 | 0.0019 | Mean values of multiple analyses | Trinquier et al. 2008 |
| Samples | Method | Reading | Error +/- | Notes | Source |
|---|---|---|---|---|---|
| β-Decayers | |||||
| Rb-Sr | 4.411 | 0.088 | whole-rock samples of 6 meteorites | Shields, Pinson, and Hurley 1965 | |
| Rb-Sr | 4.557 | 0.253 | whole-rock samples of 9 meteorites | Cumming 1969 | |
| Basaltic achondrites (7, including Juvinas, Pasamonte, Stannern, and Moore County | Rb-Sr | 4.39 | 0.26 | 7 whole-rock samples (decay constant 1.39) | Papanastassiou and Wasserburg 1969 |
| Basaltic eucrites, plus Angra dos Reis | Rb-Sr | 4.47 | 0.24 | Papanastassiou and Wasserburg 1969 data, plus Angra dos Reis 4 whole-rock and 3 mineral samples | Wasserburg et al. 1977 |
| Basaltic achondritics (10, including Juvinas, Ibitira, Bereba, Sierra de Magé, Stannern, and Pasamonte) | Rb-Sr | 4.33 | 0.49 | 11 whole-rock samples | Birck and Allègre 1978 |
| Basaltic achondritic (10, including Juvinas, Ibitira, Bareba, Sierra de Magé, Stannern, and Pasamonte) | Rb-Sr | 4.57 | 0.13 | 11 whole-rock and 8 mineral samples (Juvinas and Ibitira) | Birck and Allègre 1978 |
| Diogenites and basaltic achondrites (basaltic eucrites; 5 diogenites and 10 eucrites, including Juvinas and Ibitira) | Rb-Sr | 4.47 | 0.1 | 16 whole-rock and 8 mineral samples (Juvinas and Ibitira; decay constant 1.42) | Birck and Allègre 1981 |
| Eucrites (11) | Rb-Sr | 4.44 | 0.3 | whole rocks | Basaltic Volcanism Study Project 1981 |
| Eucrites (polymict, 23) | Rb-Sr | 4.53 | 0.19 | whole rocks | Wooden et al. 1983 |
| Achondrites (8) | Rb-Sr | 4.45 | 0.18 | whole rocks | Dalrymple 2004 |
| Rb-Sr | 4.56 | 3 whole-rock samples of 2 angrites | Hans, Kleine, and Bourdon 2010 | ||
| Basaltic achondrites (basaltic eucrites; 10 meteorites, including Juvinas, Bereba, Pasamonte, Stannern, Sierra de Magé, Moama, and Moore County | Rb-Sr | 4.55 | 0.19 | 10 whole-rock and 3 plagioclase samples (decay constant 1.393) | Hans, Kleine, and Bourdon 2013 |
| Angrites (eucrites; 6, including D'Orbigny, Angra dos Reis) | Rb-Sr | 4.56 | Mix of plag and pyrox fractions plus data from literature | Hans, Kleine, and Bourdon 2013 | |
| Eucrites (basaltic; 10, including Stannern, Bereba, Pasamonte, Juvinas, Serra de Magé, Moore County, and Moama) | Lu-Hf | 4.55 | 12 analyses and 10 whole-rock samples (calibrated against Birck and Allegre 1978 Rb-Sr isochron age) | Patchett and Tatsumoto 1980 | |
| Eucrites (13) | Lu-Hf | 4.57 | 0.19 | whole rocks | Tatsumoto, Unruh, and Patchett 1981 |
| Eucrites (basaltic and cumulates; 21 including Bereba, Cachari, Caldera, Camel Donga, Ibitira, Juvinas, Moama, Moore County, Pasamonte, Serra de Magé, and Stannern | Lu-Hf | 4.47 | 0.022 | 3 samples (Moama, Moore County, and Serra de Mage | Blichert-Toft et al. 2002 |
| Eucrites (basaltic and cumulates; 21 including Bereba, Cachari, Caldera, Camel Donga, Ibitira, Juvinas, Moama, Moore County, Pasamonte, Serra de Mage, and Stannern | Lu-Hf | 4.604 | 0.039 | 21 samples of 15 eucrites | Blichert-Toft et al. 2002 |
| Lu-Hf | 4.576 | 0.049 | Whole-rock samples of 5 angrites | Amelin, Wimpenney, and Yin 2011 | |
| α-Decayers | |||||
| Achondrites (with chondrites, 53) | Pb-Pb | 4.5 | 0.03 | whole rocks | Kanasewich 1968 |
| Eucrites (4) | Pb-Pb | 4.52 | 0.02 | whole rocks | Silver and Duke 1971 |
| Eucrites and howardites (9) plus 2 angrites and an aubrite | Pb-Pb | 4.54 | 0.02 | whole rocks | Basaltic Volcanism Study Project 1981 |
| Pb-Pb | 4.5578 | 0.00042 | 5 mineral separates from 2 angrites | Lugmair and Galer 1992 | |
| Eucrites (3; Moama, Moore County, and Serra de Magé) | Pb-Pb | 4.483 | 0.057 | 3 whole-rock samples | Tera, Carlson, and Boctor 1997 |
| Angrites (4, plus I chondrite) | Pb-Pb | 4.558 | 0.006 | 4 angrite fractions plus St. Séverin phosphates | Tera and Carlson 1999 |
| Basaltic angrites (2) | Pb-Pb | 4.55618 | 0.00014 | 6 whole-rock fragments and 2 pyroxene fractions | Baker et al. 2005 |
| Eucrites (5, including Y75011) | U-Pb | 4.552 | 0.009 | 49 analyses of zircons | Misawa, Yamaguchi, and Kaiden 2005 |
| Eucrites (non-cumulates; 12, including Cachari, Bereba, Caldera, Camel Donga, and Juvinas) | U-Pb | 4.55 | 0.004 | 84 analyses of 32 zircon grains in 5 meteorites, plus data from earlier studies, including Misawa, Yamaguchi, and Kaiden 2005) | Zhou et al. 2013 |
| Eucrites (basaltic and cumulates; 21 including Bereba, Cachari, Caldera, Camel Donga, Ibitira, Juvinas, Moama, Moore County, Pasamonte, Serra de Magé, and Stannern | Sm-Nd | 4.464 | 0.075 | 18 whole-rock samples (did not include Moama, Pasamonte, and Caldera) | Blichert-Toft et al. 2002 |
| Pb-Pb Calibrated | |||||
| Eucrites (5, including Juvinas, Stannern, and Pasamonte) | Hf-W | 4.5632 | 0.0014 | 8 whole-rock samples, plus 8 more previously published analyses (calibrated against Pb-Pb age of St. Marguerite) | Kleine et al. 2004 |
| Angrites (2, including D'Orbigny) | Hf-W | 4.5622 | 0.0013 | 17 anaylses of whole-rock and mineral fractions (calibrated against the Pb-Pb age of Allende CAIs after Amelin, Wadhwa, and Lugmair 2006) | Markowski et al. 2007 |
| Achondrites (14 meteorites, including Caldera, Ibitira, Juvinas, Moore County, Serra de Magé, and Acapulco) | Mn-Cr | 4.5648 | 0.0009 | Whole-rock samples calibrated by Pb-Pb ages |
Lugmair and Shukolyukov 1998, 2001 |
| Angrites (4, including D'Orbigny) | Mn-Cr | 4.5632 | 0.0006 | 4 whole-rock samples, fractionation normalization, calibrated by Pb-Pb age of LEW 86010 | Shukolyukov and Lugmair 2007 |
| Samples | Method | Reading | Error +/- | Notes | Source |
|---|---|---|---|---|---|
| β-Decayer | |||||
| Pallasites and Mesosiderites (10, including Estherville) | Re-Os | 4.6 | 0.05 | 10 metal samples | Shen, Papanastassiou, and Wasserburg 1998 |
| Pallasites and Mesosiderites (10, including Estherville) | Re-Os | 4.528 | 0.05 | Decay constant 1.666 | Dickin 2005; Shen, Papanastassiou, and Wasserburg 1998 |
| α-Decayers | |||||
| Mesosiderites (2 zircons) | U-Pb | 4.563 | 0.015 | Ireland and Wlotzka 1992 | |
| Mesosiderites (2 meteorites, 4 samples) | Sm-Nd | 4.475 | 0.09 | Averaged | Stewart, Papanastassiou, and Wasserburg 1994 |
| Samples | Method | Reading | Error +/- | Notes | Source |
|---|---|---|---|---|---|
| β-Decayers | |||||
| Iron meteorites (4, silicate inclusions) |
Rb-Sr | 4.55 | 11 fractions plotted | Burnett and Wasserburg 1967 |
|
| Iron IIE meteorites (3, including Weekeroo) | Rb-Sr | 4.39 | 0.07 | Including data from previous studies, about 20 silicate fractions | Snyder et al. 2001 |
| Iron meteorites (5 mixed types, plus St. Séverin LL6 chondrite | Re-Os | 4.55 | 0.03 | 8 metal fractions (decay constant 1.62 calibrated against U-Pb) | Luck, Birck, and Allègre 1980 |
| Iron meteorites (5 mixed types, plus St. Séverin LL6 chondrite | Re-Os | 4.58 | 0.21 | 8 metal fractions (decay constant 1.61 measured) | Luck, Birck, and Allègre 1980 |
| Iron meteorites (8 mixed types, plus Estherville mesosiderite and 10 chondrites | Re-Os | 4.55 | 11 samples (decay constant 1.52 calibrated against U-Pb) |
Luck and Allègre 1983 |
|
| Iron IIA meteorites (6, but 7 samples) | Re-Os | 4.596 | 0.031 | Decay constant 1.639 | Horan et al. 1992 |
| Iron IIIA meteorites (3) | Re-Os | 4.554 | 0.105 | Decay constant 1.639 | Horan et al. 1992 |
| Iron IIAB meteorites (8) | Re-Os | 4.522 | 0.029 | Decay constant 1.666 | Dickin 2005; Horan et al. 1992 |
| Iron IIIAB meteorites (3) | Re-Os | 4.48 | 0.1 | Decay constant 1.666 | Dickin 2005; Horan et al. 1992 |
| Iron IIAB meteorites (9) | Re-Os | 4.64 | 0.13 | Decay constant 1.64 | Morgan, Walker, and Grossman 1992 |
| Iron IIIAB meteorites (11) | Re-Os | 4.56 | 0.23 | Decay constant 1.64 | Morgan, Walker, and Grossman 1992 |
| Iron IIAB and IIIAB meteorites (20) | Re-Os | 4.65 | 0.11 | Decay constant 1.64 | Morgan, Walker, and Grossman 1992 |
| Iron IIA meteorites (6) | Re-Os | 4.584 | 0.043 | Decay constant 1.64 (10 analyses of 6 samples) | Morgan et al. 1995 |
| Iron IIAB meteorites (10) | Re-Os | 4.577 | 0.037 | Decay constant 1.64 (21 analyses of 10 samples) | Morgan et al. 1995 |
| Iron meteorites (16, 24 analyses) | Re-Os | 4.62 | 0.02 | Decay constant 1.64 | Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IIAB meteorites (4, 7 analyses) | Re-Os | 4.61 | 0.01 | Decay constant 1.64 | Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IIAB meteorites (4, 7 analyses) | Re-Os | 4.535 | 0.01 | Decay constant 1.666 | Dickin 2005; Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IVA meteorites (4, 7 analyses) | Re-Os | 4.67 | 0.04 | Decay constant 1.64 | Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IVA meteorites (4, 7 analyses) | Re-Os | 4.592 | 0.044 | Decay constant 1.666 | Dickin 2005; Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IVAB meteorites (8, 12 analyses) | Re-Os | 4.65 | 0.01 | Decay constant 1.64 | Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IVAB meteorites (8, 12 analyses) | Re-Os | 4.575 | 0.011 | Decay constant 1.666 | Dickin 2005; Shen, Papanastassiou, and Wasserburg 1996 |
| Iron IIA meteorites (6, 11 analyses) | Re-Os | 4.537 | 0.008 | Decay constant 1.666 | Smoliar, Walker, and Morgan 1996 |
| Iron IIIA meteorites (8, 12 analyses) | Re-Os | 4.558 | 0.012 | Decay constant 1.666 | Smoliar, Walker, and Morgan 1996 |
| Iron IVA meteorites (10) | Re-Os | 4.464 | 0.026 | Decay constant 1.666 | Smoliar, Walker, and Morgan 1996 |
| Iron IVB meteorites (6, 9 analyses) | Re-Os | 4.527 | 0.029 | Decay constant 1.666 | Smoliar, Walker, and Morgan 1996 |
| Iron IA meteorites (7 samples)) | Re-Os | 4.529 | 0.023 | Decay constant 1.666 | Smoliar, Walker, and Morgan 1997 |
| IA, IIA, IIE, IVB iron meteorites (5, 9 analyses; including Kodaïkanal) | Re-Os | 4.624 | 0.017 | Birck and Allègre 1998 | |
| Iron IVA meteorites (3) | Re-Os | 4.61 | 0.01 | Decay constant 1.64 (plotted with Shen, Papanastassiou, and Wasserburg 1996 data; IIAB isochron) | Chen, Papanastassiou, and Wasserburg 1998 |
| Iron IA meteorites (8, 11 analyses; including Canyon Diablo) | Re-Os | 4.537 | 0.021 | Decay constant 1.666 | Horan, Smoliar, and Walker 1998 |
| Iron IIAB High-Os meteorites (4) | Re-Os | 4.558 | 0.039 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIAB Low-Os meteorites (8, 13 analyses) | Re-Os | 4.569 | 0.073 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIAB meteorites (12, 17 analyses) | Re-Os | 4.546 | 0.046 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIAB meteorites (12, 16 analyses) | Re-Os | 4.53 | 0.05 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIIAB High-Os meteorites (10, 13 analyses) | Re-Os | 4.506 | 0.056 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIIAB Low-Os meteorites (8) | Re-Os | 4.529 | 0.046 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IIIAB meteorites (22, 26 analyses) | Re-Os | 4.517 | 0.032 | Decay constant 1.666 | Cook et al. 2004 |
| Irons (Cape York suite) (4, 5 analyses) | Re-Os | 4.579 | 0.13 | Decay constant 1.666 | Cook et al. 2004 |
| Iron IVA meteorites (14, 19 analyses) | Re-Os | 4.54 | 0.017 | Decay constant 1.666 | McCoy et al. 2011 |
| Iron IIAB meteorites (12, 16 analyses) | Pt-Os | 4.323 | 0.08 | Decay constant 1.477 | Cook et al. 2004 |
| Iron IIIAB meteorites (22, 26 analyses) | Pt-Os | 4.325 | 0.026 | Decay constant 1.477 | Cook et al. 2004 |
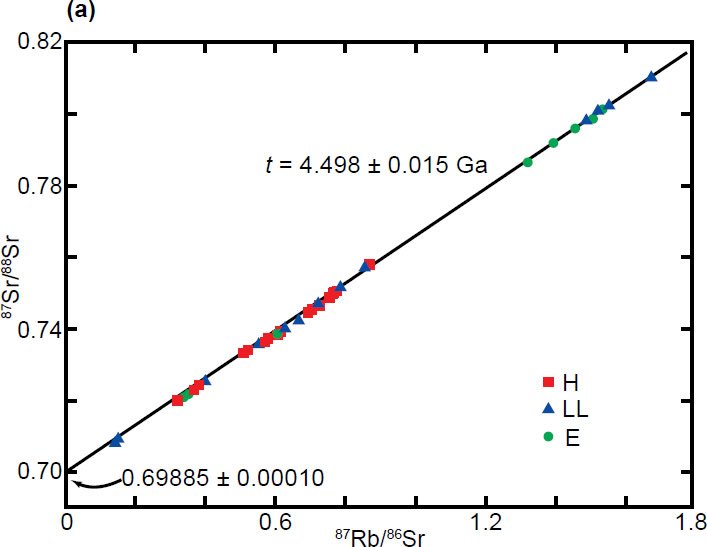
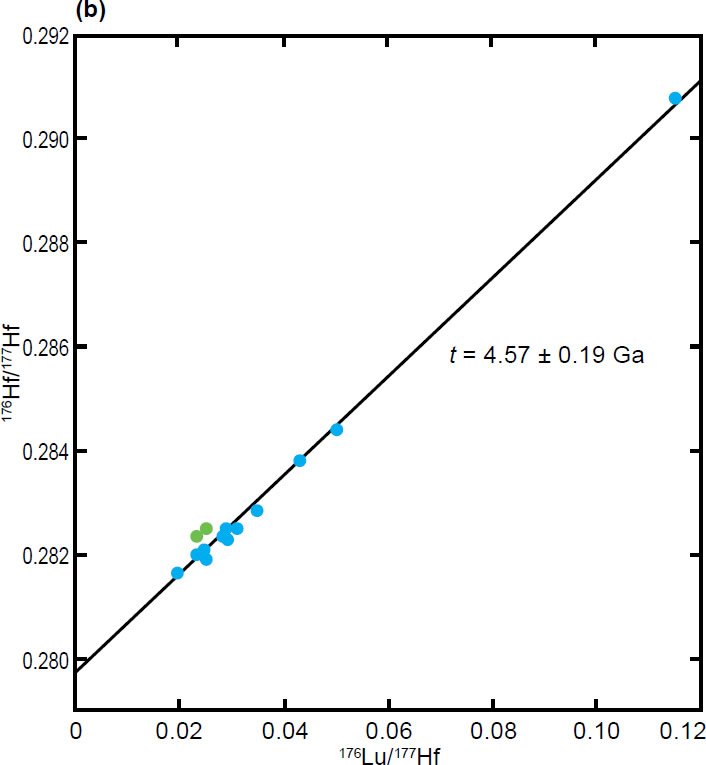
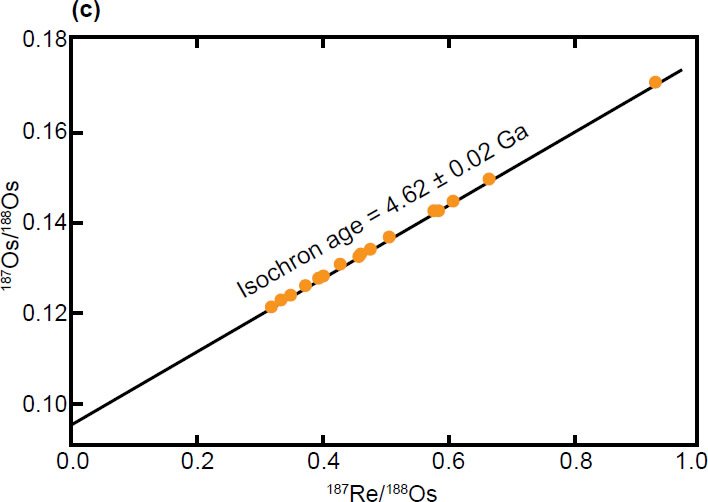
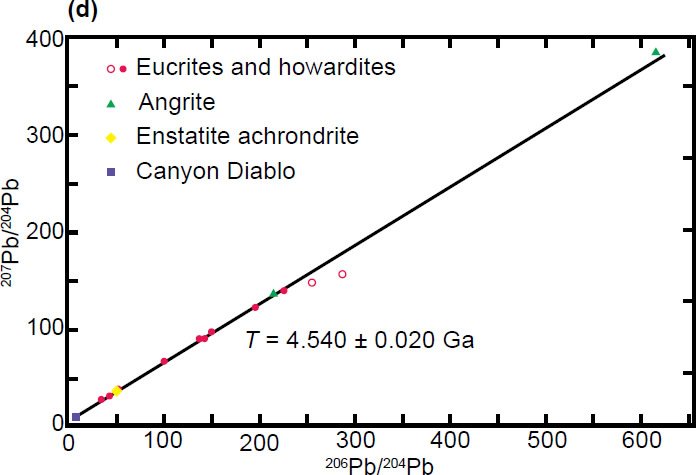
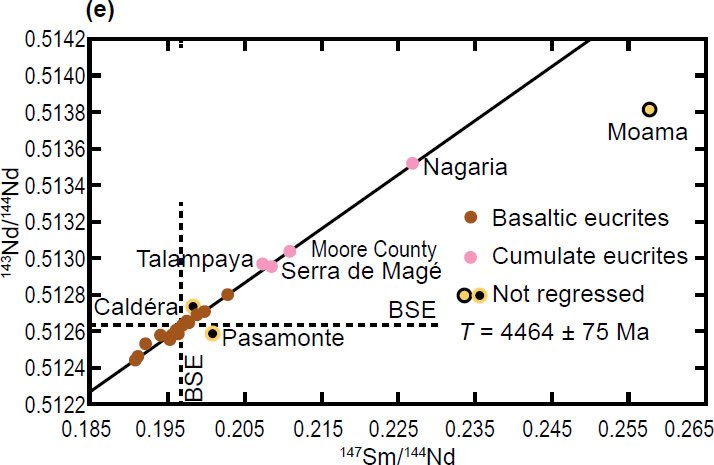
Fig. 2. Examples of published isochrons for groups of meteorites. (a) A Rb-Sr isochron for 38 chondrites (Minster, Birck, and Allègre 1982) (b) A Lu-Hf isochron for 13 eucrites (Patchett and Tatsumoto1980; Tatsumoto, Unruh, and Patchett 1981) (c) A Re-Os isochron for 24 analyses of 16 irons (Shen, Papanastassiou, and Wasserburg 1996) (d) A Pb-Pb isochron for 12 achondrites (Basaltic Volcanism Study Project 1981) (e) A Sm-Nd isochron for 17 eucrites (Blichert-Toft et al. 2002).
In several instances there were a few stony achondrites grouped with many chondrites to derive Rb-Sr and Pb-Pb isochron ages, but these isochron ages were still added to Table 1 and these details were indicated in the notes. Similarly it has been noted in Table 2 that phosphate fractions from the St. Séverin LL6 chondrite had been grouped with fractions from angrites to obtain a Pb-Pb isochron age, while in Table 4 the Fe-Ni metal fraction of the St. Séverin LL6 chondrite had been grouped with irons to derive two Re-Os isochron ages. Furthermore, the isochron ages of the chondrites and stony achondrites in Tables 1 and 2 were obtained from either whole rock samples or various combinations of whole-rock samples and separated fractions (minerals, chondrules, Ca-Al inclusions, or density fractions), so this was also noted in these tables. However, in the literature none of these circumstances were deemed a problem to obtaining meaningful radioisotope ages for those groupings of meteorites, so it was likewise assumed that these circumstances were not an impediment to this study’s objectives.
The data in these tables were then plotted on frequency versus age histogram diagrams, with the same color coding being used to show the isochron ages obtained by the different radioisotope dating methods—the isochron ages for groups of chondrites in Fig. 3, the isochron ages for groups of stony achondrites in Fig. 4, the isochron ages for groups of pallasites and mesosiderites in Fig. 5, and the isochron ages for groups of irons in Fig. 6. Furthermore, for ease of discerning any pattern of differences in the isochron ages among and between the α-decaying and β-decaying parent radioisotopes, the isochron ages of groups of chondrites obtained from the α-decaying and β-decaying parent radioisotopes respectively were plotted on separate histogram diagrams in Fig. 7, while the isochron ages of groups of stony achondrites obtained from the α-decaying and β-decaying parent radioisotopes respectively were plotted on separate histogram diagrams in Fig. 8.
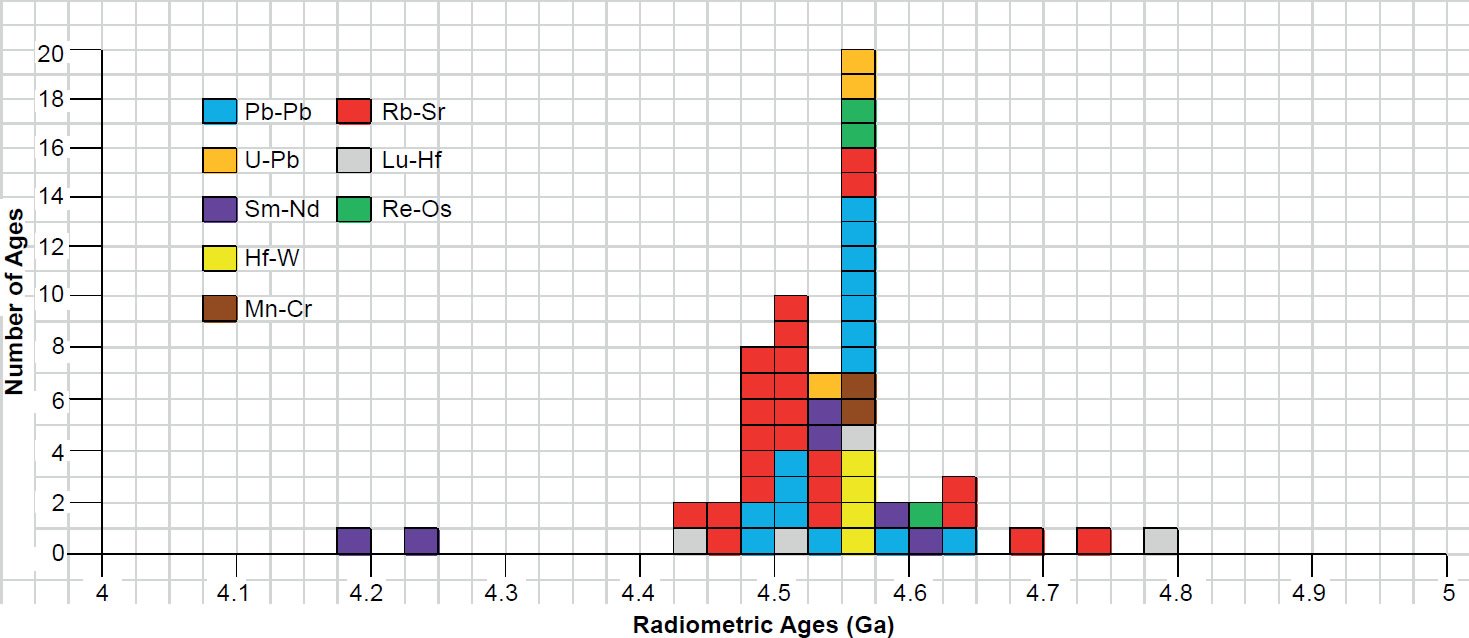
Fig. 3. Frequency versus radioisotope ages histogram diagram for the isochron ages for whole-rock samples and some or all components of groups of chondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
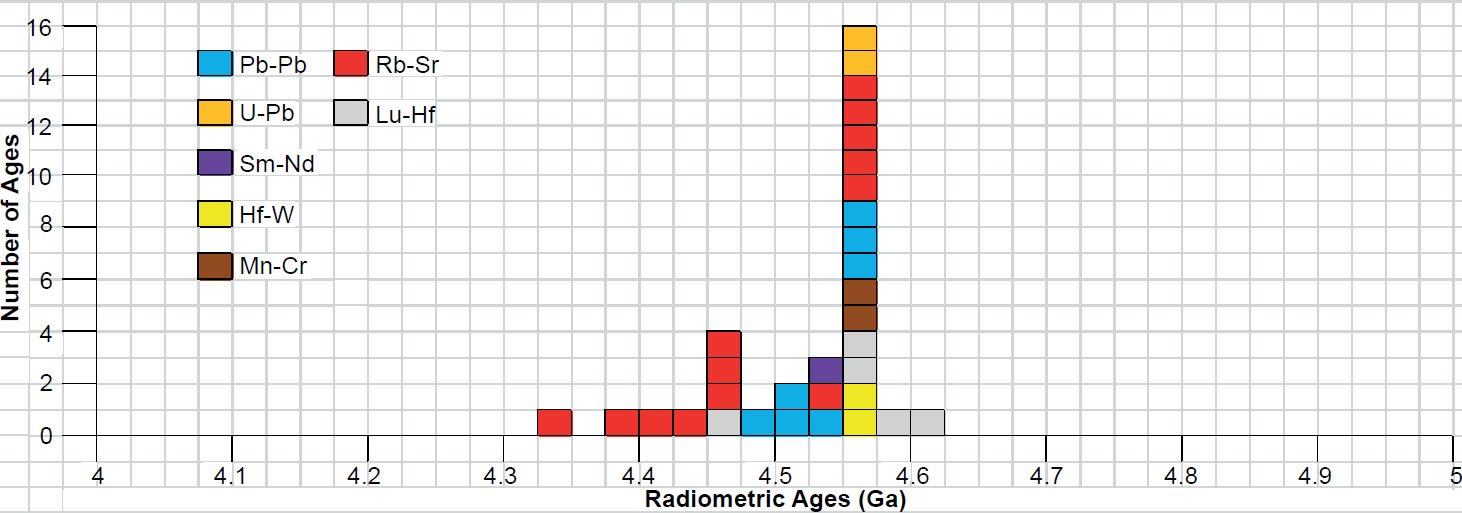
Fig. 4. Frequency versus radioisotope ages histogram diagram for the isochron ages for whole-rock samples and some or all components of groups of achondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
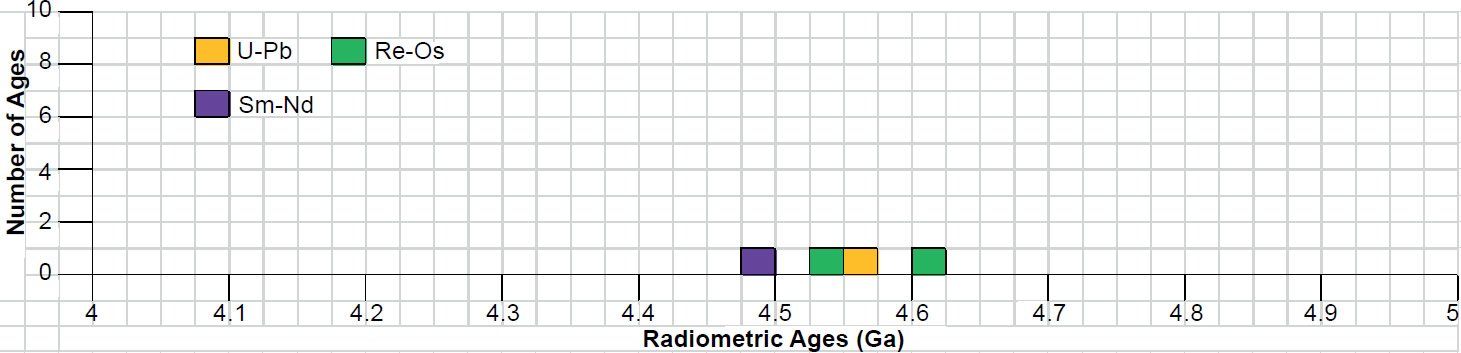
Fig. 5. Frequency versus radioisotope ages histogram diagram for the isochron ages for whole-rock samples and some or all components of groups of pallasites and mesosiderites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
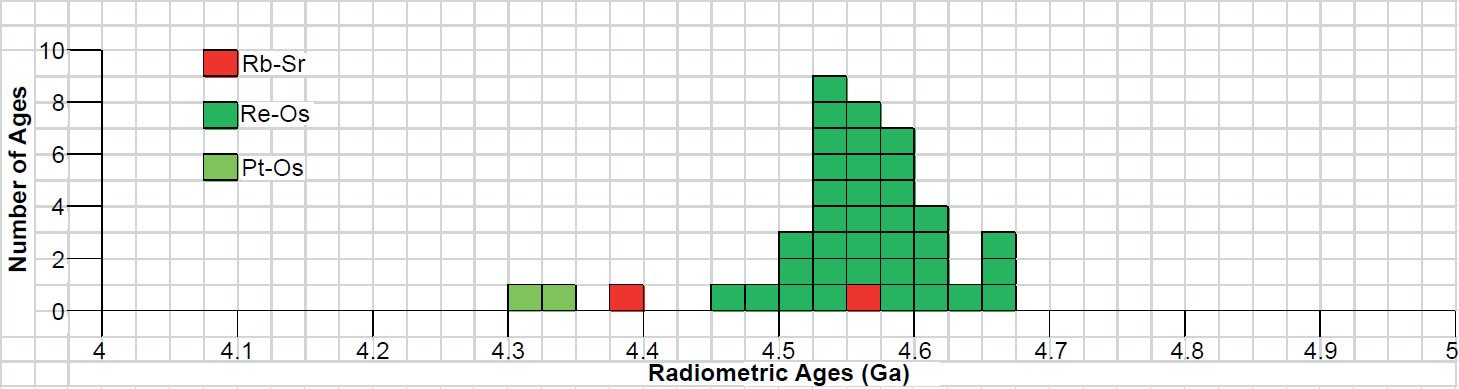
Fig. 6. Frequency versus radioisotope ages histogram diagram for the isochron ages for whole-rock samples and some or all components of groups of irons, with color coding being used to show the ages obtained by the different radioisotope dating methods.
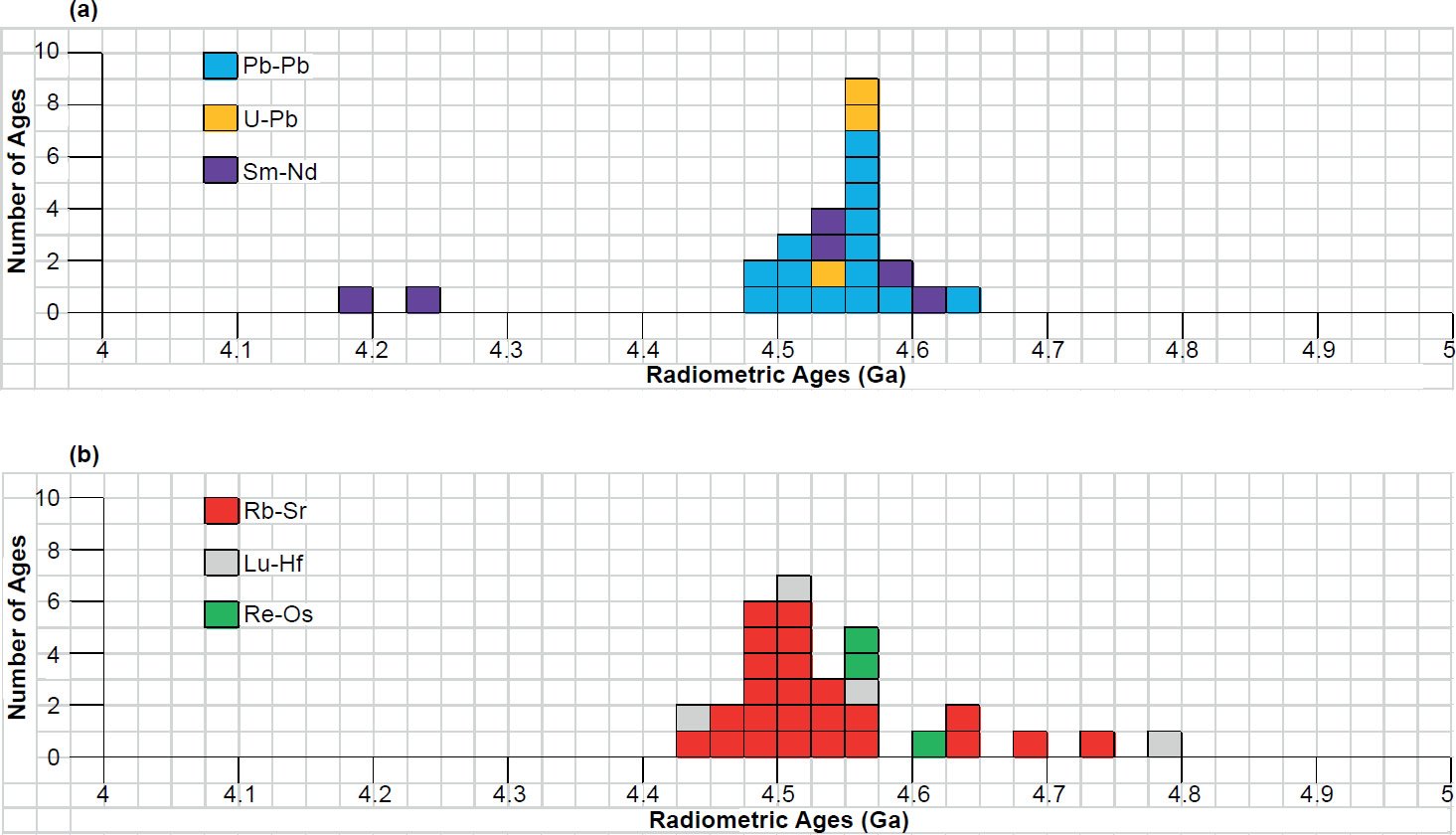
Fig. 7. Frequency versus radioisotope ages histogram diagram for the isochron ages from (a) α-decaying parent radioisotopes, and (b) β-decaying parent radioisotopes for whole-rock samples and some or all components of groups of chondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
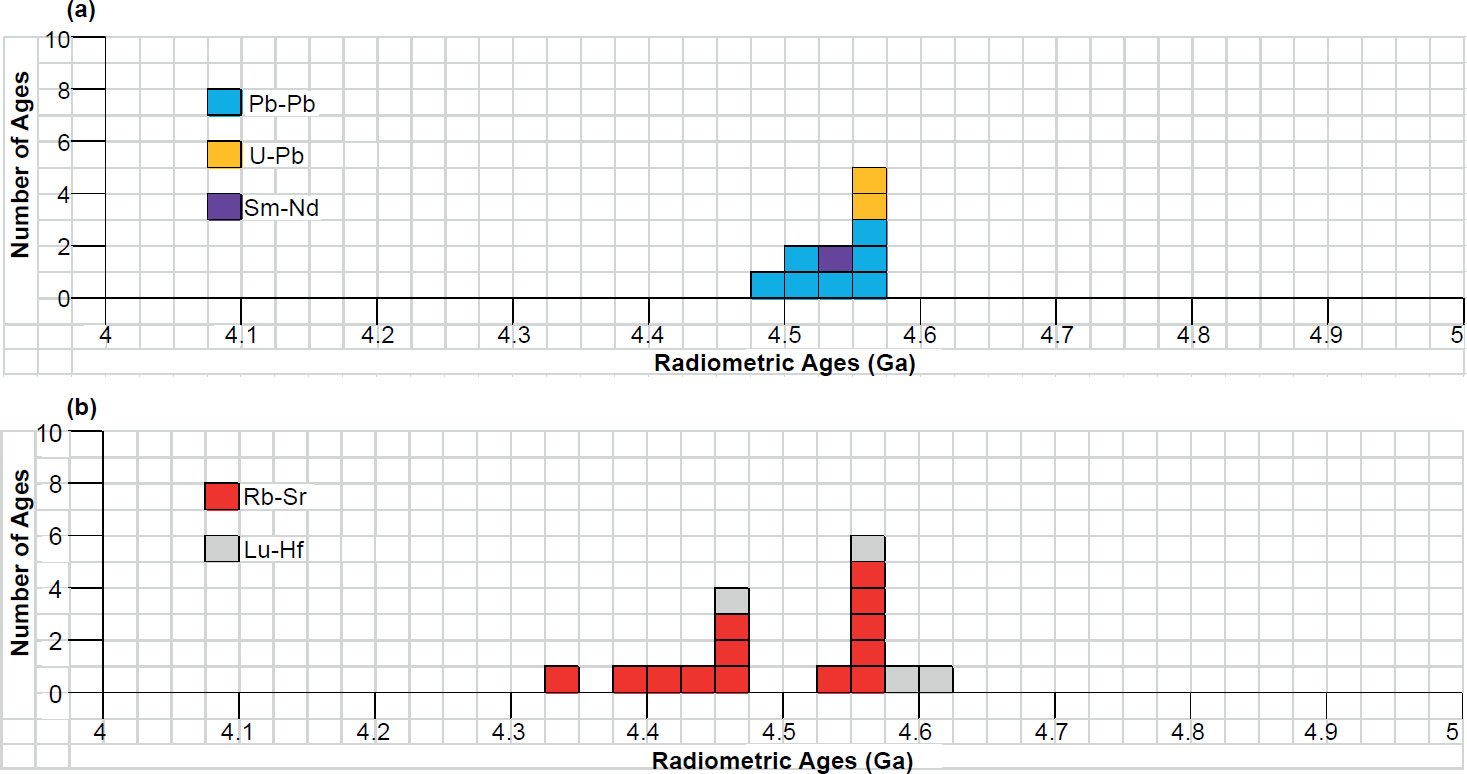
Fig. 8. Frequency versus radioisotope ages histogram diagram for the isochron ages from (a) α-decaying parent radioisotopes, and (b) β-decaying parent radioisotopes for whole-rock samples and some or all components of groups of achondrites, with color coding being used to show the ages obtained by the different radioisotope dating methods.
Discussion
In contrast to the Allende CV3 carbonaceous chondrite meteorite (Snelling 2014a), there have been fewer radioisotope ages obtained for these groups of chondrites, stony achondrites, pallasites and mesosiderites, and irons, because fewer radioisotope determinations have been undertaken on them and fewer radioisotope methods are suited to producing reliable and meaningful isochron ages. For example, the K-Ar and Ar-Ar methods are not routinely used to produce any isochron ages. Yet the outcome is similar to that found for the ordinary and enstatite chondrites (Snelling 2014b), the eucrites (basaltic achondrites) (Snelling 2014c), and the primitive and other achondrites (Snelling 2015a). There are no consistent patterns evident of the α-decay isochron ages being older than the β-decay isochron ages. Furthermore, there are no consistent patterns of the α-decay mode Sm-Nd isochron ages always being younger or older than the U-Th-Pb isochron ages according to the parents’ atomic weights or their decay rates (half-lives) respectively, and simultaneously the β-decay mode Rb-Sr, Lu-Hf, and Re-Os isochron ages increasing or decreasing in that order according to the parents’ atomic weights or their decay rates (half-lives) respectively. Such patterns would be potentially indicative of a past episode of accelerated radioisotope decay, as suggested by Snelling (2005c) and Vardiman, Snelling, and Chaffin (2005) from their radioisotope investigations of earth rocks and minerals. Thus it could be concluded from these data that no accelerated radioisotope decay event has occurred on the asteroids which parented all these meteorites.
The Chondrites
The isochron ages for the groups of chondrites listed in Table 1 and plotted in Fig. 3 are spread across a range from 4.182 ± 0.51 Ga (an Sm-Nd isochron age) to 4.78 ± 0.62 Ga (a Lu-Hf isochron age). However, even those isochron ages within their error ranges overlap with the clustering of all the isochron ages around the peak at 4.55–4.575 Ga, coinciding with the claimed age of the earth. This peak in Fig. 3 is dominated by seven Pb-Pb and two U-Pb isochron ages, plus as to be expected the two Mn-Cr and four Hf-W isochron ages also coincide with this peak because they are calibrated against meteorite Pb-Pb model and isochron ages. But this peak is also supported by two Rb-Sr, two Re-Os, and one Lu-Hf isochron ages. The isochron ages obtained by all but the Pb-Pb calibrated methods are spread around this peak, with the biggest spreads to either side of the peak being the Sm-Nd and Lu-Hf isochron ages. There is also a clustering of Rb-Sr isochron ages around 4.475–4.525 Ga, which overlaps with a small secondary clustering of Pb-Pb isochron ages at 4.50–4.525 Ga. Two Sm-Nd isochron ages cluster at 4.525–4.55 Ga.
In Fig. 7 the isochron ages of the α-decaying and β-decaying parent radioisotopes are plotted on separate histogram diagrams for ease of discerning any patterns of differences. Comparing these histogram diagrams, the α-decay isochron ages are not systematically older than the β-decay isochron ages, as found for the isochron ages of Precambrian rock units during the RATE project (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005). These plots also confirm that there are no discernible patterns of differences in the isochron ages according to the parents’ atomic weights or decay half-lives.
Among the α-decaying parent radioisotopes three of the five Sm-Nd isochron ages overlap the clustering of the Pb-Pb and U-Pb isochron ages centered on the 4.55–4.575 Ga peak (fig. 7a). The other two Sm-Nd isochron ages are distinctly younger, but no significance can be attached to that minority grouping, except perhaps to suggest the Sm-Nd radioisotope system in the samples of those two groups of meteorites (one set of samples was of phosphates) had been disturbed and/or reset.
Among the β-decaying parent radioisotopes, the plot in Fig. 7b is dominated by the strong clustering of Rb-Sr isochron ages around 4.475–4.525 Ga. If any pattern of differences were according to the atomic weights of the parent radioisotopes, then the Re-Os isochron ages should be the oldest (187Re has the heaviest atomic weight) and the Rb-Sr isochron ages the youngest (87Rb has the lightest atomic weight), but here there are both Rb-Sr and Lu-Hf isochron ages older than the Re-Os isochron ages. However, in general the strong clustering of Rb-Sr isochron ages are the youngest ages (apart from one Lu-Hf isochron age), and most of the Lu-Hf isochron ages are younger than the Re-Os isochron ages. So maybe there is a hint of a pattern here among the β-decaying parent radioisotopes according to atomic weights, similar to that suggested by Snelling (2005c) and Vardiman, Snelling, and Chaffin (2005) from their radioisotope investigations of earth rocks and minerals. But if this were indicative of an episode of accelerated radioisotope decay, then the same pattern according to atomic weights should also be evident in the α-decaying parent radioisotopes, which it is not (fig. 7a). On the other hand, if any pattern of differences were according to the decay half-lives of the parent radioisotopes, then the Rb-Sr isochron ages should be the oldest because 87Rb has the longest half-life at 48.8 Ga, whereas the Lu-Hf isochron ages should be the youngest as 176Lu has the shortest half-life at 35.7 Ga. No such pattern is evident in Fig. 7b.
In any case, the patterns of differences in isochron ages documented by Snelling (2005c) and Vardiman, Snelling, and Chaffin (2005) resulted from radioisotope dating analyses by the different methods on the same samples, whereas in this study the isochron ages were obtained by the different radioisotope methods on different groups of samples. Yet these groups of meteorites are claimed to be from similar asteroids, so potentially they represent the same original rock units and thus the comparison here of radioisotope ages seems warranted.
The Stony Achondrites
The groups of stony achondrites whose isochron ages are listed in Table 2 and plotted in Fig. 4 are mostly basaltic achondrites or eucrites, which are claimed to have all come from the crust of the asteroid 4-Vesta and thus represent the same rock unit (McSween et al. 2013, 2014; Snelling 2014c), so comparing their isochron ages to look for patterns is justified. In Fig. 4 the isochron ages are spread across a range from 4.33 ± 0.49 Ga (a Rb-Sr isochron age) to 4.604 ± 0.039 Ga (a Lu-Hf isochron age). However, even those isochron ages within their error ranges overlap with the clustering of all the isochron ages around the large peak at 4.55–4.575 Ga, coinciding with the claimed age of the earth. This peak in Fig. 4 is dominated by three Pb-Pb and two U-Pb isochron ages, plus as to be expected the two Mn-Cr and two Hf-W isochron ages also coincide with this peak because they are calibrated against meteorite Pb-Pb model and isochron ages. But this peak is also supported by five Rb-Sr and two Lu-Hf isochron ages. The isochron ages obtained by all but the Pb-Pb calibrated methods are spread around this peak, with the biggest spreads to either side of the peak being the Rb-Sr and Lu-Hf isochron ages. There is also a small clustering of Rb-Sr isochron ages around 4.45–4.475 Ga, and the only Sm-Nd isochron age is 4.464 ± 0.075 Ga.
In Fig. 8 the isochron ages of the α-decaying and β-decaying parent radioisotopes are plotted on separate histogram diagrams for ease of discerning any patterns of differences. Comparing these histogram diagrams, the α-decay isochron ages are not systematically older than the β-decay isochron ages, as found for the isochron ages of Precambrian rock units during the RATE project (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005).
Among the α-decaying parent radioisotopes there are no discernible patterns of differences in the isochron ages according to the parents’ atomic weights or decay half-lives. The only Sm-Nd isochron age overlaps the spread of the Pb-Pb isochron ages (fig. 7a). And whereas the Pb-Pb and U-Pb isochron ages form a peak at 4.55–4.575 Ga, the Pb-Pb isochron ages are spread from 4.483 ± 0.057 Ga to 4.5578 ± 0.00042 Ga, perhaps suggesting the samples of some of these meteorites may have been slightly disturbed and/or reset.
Among the β-decaying parent radioisotopes, the plot in Fig. 8b is dominated by the two clusterings of the Rb-Sr isochron ages around 4.45–4.475 Ga and 4.55–4.575 Ga, each clustering supported by a single Lu-Hf isochron age. If any pattern of differences were according to the atomic weights of the parent radioisotopes, then the Lu-Hf isochron ages should be the oldest (176Lu has heaviest atomic weight) and the Rb-Sr isochron ages the youngest (87Rb has the lightest atomic weight). If the youngest Lu-Hf isochron age which plots with the younger clustering of Rb-Sr isochron ages is ignored, then in a general way the Lu-Hf isochron ages overall (or the average of them) would be older than the Rb-Sr isochron ages (or the average of them). So maybe there is a hint of a pattern here among the β-decaying parent radioisotopes according to atomic weights, similar to that suggested by Snelling (2005c) and Vardiman, Snelling, and Chaffin (2005) from their radioisotope investigations of earth rocks and minerals. But if this were indicative of an episode of accelerated radioisotope decay, then the same pattern according to atomic weights should also be evident in the α-decaying parent radioisotopes, which it is not (fig. 8a). On the other hand, if any pattern of differences were according to the decay half-lives of the parent radioisotopes, then the Rb-Sr isochron ages should be the oldest because 87Rb has the longest half-life at 48.8 Ga, whereas the Lu-Hf isochron ages should be the youngest as 176Lu has the shortest half-life at 35.7 Ga. No such pattern is evident in Fig. 8b. In fact, as observed in a general way the opposite is true, namely, the Rb-Sr isochron ages overall are younger than the Lu-Hf isochron ages.
The Pallasites and Mesosiderites
There are so few isochron ages for groups of pallasites and mesosiderites listed in Table 3 and plotted in Fig. 5 that discerning any patterns is simply not feasible. There is no peak in the isochron ages, which instead are spread from 4.475 ± 0.09 Ga (a Sm-Nd isochron age) to 4.6 ± 0.05 Ga (a Re-Os isochron age), although within their error ranges all four reported isochron ages overlap. Among the α-decaying parent radioisotopes the sole Sm-Nd isochron age is younger than the sole U-Pb isochron age, which follows the order of atomic weights (147Sm is lighter than 238U and 235U), but does not follow the order of decay half-lives (147Sm has a much longer half-life than both 238U and 235U). Any simultaneous trend among the β-decaying parent radioisotopes is simply not available because there are only two reported Re-Os isochron ages.
The Irons
The isochron ages for groups of iron meteorites listed in Table 4 and plotted in Fig. 6 are dominated by Re-Os isochron ages. Both Re and Os are strongly siderophile (iron-loving) elements and thus are present in high trace amounts in the dominant Fe-Ni metal alloy component of these meteorites. This makes the Re-Os method the major technique for radioisotope dating iron meteorites. In contrast, the two Rb-Sr isochron ages listed in Table 4 and plotted in Fig. 6 were obtained using silicate inclusions within iron meteorites, particularly IIE irons.
The Re-Os isochron ages are spread from 4.464 ± 0.026 Ga to 4.67 ± 0.04 Ga at the limits of a broad clustering from 4.5 Ga to 4.625 Ga, with a broad 4.525–4.6 Ga peak within it. This peak thus includes the 4.55–4.57 Ga “target” age consistent with the peaks for the groups of chondrites and stony achondrites. One Rb-Sr isochron age plots right in the middle of that peak at 4.55–4.575 Ga, the claimed age of the earth, while the other Rb-Sr isochron age at 4.39 ± 0.037 Ga falls well below outside the broad clustering of Re-Os isochron ages. The two α-decay Pt-Os isochron ages are even younger, but there is uncertainty about the accuracy of this method because of the poorly-measured long half-life of 190Pt (c. 470 Ga) coupled with its miniscule isotopic abundance (Cook et al. 2004). No real pattern of differences in the isochron ages is discernible between the β-decaying parent radioisotopes 87Rb and 187Re. 187Re has the heavier atomic weight and thus might be expected to yield older ages, while 87Rb has a slightly longer half-life and thus might be expected to yield older ages. Yet of the only two Rb-Sr isochron ages, one is much younger and the other is the same as the broad 4.525–4.6 Ga peak in the Re-Os isochron ages.
Explanation for the Agreement of Ages
As noted previously by Snelling (2014a, b, c, 2015a), for individual chondrites, eucrites, and primitive and other stony achondrites there was generally a strong agreement among most of the Pb-Pb isochron and model ages for most of the individual meteorites in these different categories for a common 4.55–4.57 Ga age. Many of the Pb-Pb and U-Pb isochron ages for the groups of chondrites and stony achondrites plotted in Figs. 3 and 4 are also in strong agreement with this common 4.55–4.57 Ga age. Often, where used, some Rb-Sr, Lu-Hf, and Re-Os isochron ages also match this common 4.55–4.57 Ga age. This is to be expected, since the Rb, Lu, Re, Sm, and K decay constants are all ultimately calibrated against the U-Pb method and thus the U decay constants (Dickin 2005, 70–71; Lugmair, Scheinin, and Marti 1975; Nebel, Scherer, and Mezger 2011; Renne et al. 2010; Selby et al. 2007; Söderlund et al. 2004). This ultimately means that all meteorite ages are dependent on the reliability of determinations of the 238U and 235U decay constants, and the critical 238U/235U ratio. However, such calibrations are dependent on assuming the crucial 238U/235U ratio is constant in all rocks and minerals, but recently significant variations in this ratio have been measured in both terrestrial minerals and meteorites (Brennecka and Wadhwa 2012; Hiess et al. 2012). It also may be significant that the estimated half-life of 238U is 4.468 Ga, which is almost identical to the claimed 4.55–4.57 Ga age of the earth, the asteroids, and the meteorites derived from them.
Additionally, whenever Hf-W and Mn-Cr isochron ages were determined they always matched the “target” 4.55–4.57 Ga age defined by the Pb-Pb isochron ages. This is because these methods are calibrated against the 4.55–4.57 Ga Pb-Pb isochron and model ages of other meteorites and their components. The Hf-W method is calibrated by an Hf-W isochron obtained on the H5 chondrite St. Marguerite being calibrated by the Pb-Pb model ages of whole-rock fragments and phosphates from St. Marguerite (Göpel, Manhès, and Allègre 1994; Kleine et al. 2002, 2004, 2005; Markowski et al. 2006), and also by calibrating the Hf-W isochron obtained on the angrite D’Orbigny against its Pb-Pb isochron age corrected for U isotopic variations (Amelin 2008; Brennecka and Wadhwa 2011; Kleine et al. 2012). The Mn-Cr method is calibrated by an Mn-Cr isochron obtained on the H5 chondrite St. Marguerite being calibrated against its Pb-Pb model age and the Pb-Pb isochron age of the angrite LEW 86010, or calibrated by the Mn-Cr isochrons of measured meteorites being calibrated against the Mn-Cr isochron for the angrite LEW 86010, which is in turn calibrated against its Pb-Pb isochron age (Göpel, Manhès, and Allègre 1994; Lugmair and Galer 1992; Lugmair and Shukolyukov 1998; Polnau and Lugmair 2001).
Explanation for the Scattering of Ages
To explain the scattering of ages either side of the 4.55–4.57 Ga “target” age appeal is usually made to the effects of thermal disturbance of the radioisotope systems, either during the supposed cooling of the parent asteroid body from its formation in the aftermath of the supposed solar nebula, or during subsequent fragmentation and reassembly of the parent asteroid, and/or as a result of impact cratering of the parent asteroids (Bogard 2011; Bogard, Dixon, and Garrison 2010; Bogard et al. 1990, 1993; Bogard and Garrison 1998, 2009; Bogard, Garrison, and McCoy 2000; Bogard, Garrison, and Takeda 2005; Lewis 1997). This must be especially the case where among the groups of meteorites studied here the scattering of ages is common in the Rb-Sr, Lu-Hf, Re-Os, Sm-Nd, and U-Th-Pb systems. He being a gas is readily mobile within and between minerals, and metamorphism is known to reset all these radioisotope systems (Faure and Mensing 2005; Snelling 2000).
Another potential cause of scattering of ages is the exposure of meteorites to cosmic-rays during the time they travelled through space before landing on the earth’s surface. Cosmic-ray exposure ages are based on measuring pairs of radioactive-stable nuclides, primarily those involving the noble gases He, Ne, Ar, and Kr (Eugster 2003), so such cosmic-ray bombardment will have affected potentially only the K-Ar and U-Th-Pb radioisotope ages. Reported cosmic-ray exposure ages for stony meteorites suggest that their travel times in space from their parent asteroids to the earth’s surface has been up to 120 Ma, whereas those for iron meteorites have travelled for up to 1500 Ma, probably due to a stronger resistance against crushing in space compared to silicate material. Furthermore, the significance of cosmic-rays producing scattering of U-Th-Pb system ages has been highlighted by Carver and Anders (1976b) who found that cosmic-ray tracks were almost indistinguishable from fission tracks in two stony meteorites and thus cosmic-rays impacting these meteorites would explain the excess He in them which produced unrealistic larger U-He ages than their radioisotope ages.
Thermal disturbances tend to reset the radioisotope systems so that the resultant ages are usually lower than their original ages (Lewis 1997), which is very evident for the Rb-Sr, Lu-Hf, and Sm-Nd systems in the groups of chondrites and stony achondrites. On the other hand, for many of these groups of meteorites, including the irons, the Pb-Pb, Sm-Nd, Rb-Sr, Lu-Hf, and Re-Os isochron ages are both younger and older than the believed formation age of the parent bodies, determined as 4.55–4.57 Ga from the clustering of all the radioisotope systems at that age. Birck and Allègre (1998) noted that the older Re-Os age for the Kodaïkanal iron IIE meteorite could be reconciled by simply adjusting the 187Re decay constant to thus force the older Re-Os age to agree with the expected 4.55–4.57 Ga age. Indeed, Snelling (2014d, e, 2015b, c) has documented how decay constants have repeatedly been adjusted so as to bring Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isochron ages into agreement with Pb-Pb and U-Pb isochron and model ages, including for meteorites. It should also be noted that in some instances the isochron ages listed in the tables and plotted in the corresponding figures have been calculated using different decay constants. Thus some of the scattering of ages of these meteorites is due to the decay constants used to calculate the respective isochron ages. Nevertheless, the few older ages in the U-Th-Pb isotopic system, and perhaps even those in the Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isotopic systems, could be due to parent radioisotope migration out of, or daughter isotope migration into, minerals and meteorites during thermal disturbances.
Is There Physical Evidence of Radioisotope Decay?
One of the key questions investigated during the RATE project was whether there is physical evidence that radioisotope decay has occurred. Because radioisotope ages are calculated from measurements of isotope ratios, which essentially are chemical analyses, it could thus be argued that the isotope ratios may simply be the product of the chemistry of the rocks and minerals, rather than due to physical radioactive decay. Therefore, Snelling (2005b) investigated whether there were tracks produced by nuclear decay via fission of 238U in zircon grains in volcanic tuffs at three levels in the geologic record of the Flood in the Colorado Plateau area of the USA. He found that there were fission tracks in sufficient numbers to provide fission track ages for the zircon grains. Furthermore, those fission track ages essentially agreed with the U-Pb radioisotope ages for the same zircons. Thus it was confirmed that there is physical evidence for at least 600 millions’ worth of nuclear decay (at today’s decay rate) in those rocks formed during the Flood year, so their radioisotope ages really are due to radioisotope decay.
The next logical question to explore is whether there is similar physical evidence for nuclear decay in meteorites? And if so, is the quantity of nuclear decay commensurate with the 4.55–4.57 Ga radioisotope ages of meteorites?
Fleischer et al. (1965) reported that they had found fossil tracks of charged particles in minerals, including zircon grains, separated from the Vaca Muerta mesosiderite. In the zircon grains the track densities were so high (more than 108 per cm2) that the tracks could not be easily resolved. However, their further investigation of a pyroxene grain with more easily resolved and counted tracks revealed that assuming an age of ~4.5 Ga for the meteorite about a third of this pyroxene grain’s tracks had resulted from spontaneous fission of U impurities in it. So based on the meteorite’s assumed age at least two-thirds of the tracks were of a different origin, most likely due to cosmic-rays and spontaneous fission of 244Pu. Subsequently, Fleischer, Price, and Walker (1965) sought to demonstrate that 98–99% of the fossil tracks in two minerals from two other meteorites were due to 244Pu fission. However, Fleischer et al. (1967a) then determined experimentally that the fossil tracks in meteorites would be produced by charged particles with a large rate of ionization loss, in particular, slowed down, very heavy cosmic-ray nuclei (Z ≥ 20), spontaneous fission of 238U and 244Pu, fission of heavy element impurities induced by cosmic-rays, and spallation recoils. Furthermore, Fleischer et al. (1967b) examined some 42 meteorites and identified tracks of primary cosmic rays in 23 of them, which equated to cosmic-ray exposure ages of 5–500 million years. Although fission tracks from 238U and 244Pu were often also present, they concluded that the majority of fossil particle tracks in meteorites are due to heavy primary cosmic rays.
Nevertheless, Carver and Anders (1970) claimed to have fission-track dated the unbrecciated Serra de Magé basaltic achondrite (eucrite) at 540 ± 90 Ma. This is of course grossly short of its supposed Pb-Pb radioisotope (isochron) age of 4.4 Ga (Tera, Carlson, and Boctor 1997), and is difficult to reconcile with any specific past event having triggered the beginning of U fission in this meteorite. Subsequently, Carver and Anders (1976a) developed a method for selective annealing of cosmic-ray tracks so that fission-track ages could be determined potentially on four other meteorites. However, they obtained mixed results. Of the two mesosiderites studied, one yielded a fission-track age of 140 ± 40 Ma identical to its cosmic-ray exposure age of 150 Ma, and the other yielded a fission-track age of 1500 ± 400 Ma, which is equivalent to the cosmic-ray exposure age of iron meteorites (Eugster 2003). In the other two meteorites studied the fission tracks were found to be primarily due to 244Pu, similar to what Shirck (1974) had found in an inclusion within the Allende carbonaceous chondrite. Consequently, Carver and Anders (1976b) investigated the charged particle tracks in two other stony meteorites, and after resolving the fission tracks from the cosmic-ray tracks found that the fission-track densities in these two meteorites were 10–100 times higher than expected from 238U, that is, assuming these two meteorites are ~4.5 Ga old. So they simply concluded the excess must be due to fission of extinct 244Pu.
These studies are sufficient to demonstrate that at best any physical evidence in meteorites of nuclear decay due to 238U fission is very equivocal, because the estimated fission-track ages involved first assuming the ~4.5 Ga radioisotope age of the meteorites. However, this physical evidence is more likely totally unreliable due to confusion over the identification of the copious tracks produced by cosmic rays and other fissionable isotopes such as perhaps 244Pu. Indeed, it is rather telling that the few claimed fission-track ages are equivalent to claimed cosmic-ray exposure ages (Eugster 2003). Those are based often on measurements of noble gases that could well be extraneous to the original state of the meteorites and thus not reliable age indicators. It is noteworthy here that Carver and Anders (1976b) also reported that a search for radiohalos in the two stony meteorites they studied produced negative results. That is significant, as radiohalos are the other physical evidence in earth rocks that radioisotope decay has occurred (Snelling 2005a). So from all these considerations we have to conclude there is not good clear physical evidence that a lot of nuclear decay has occurred in meteorites, certainly not ~4.5 Ga worth, and thus not in their parent asteroids either. Furthermore, even cosmic-ray exposure ages are based on assumptions about past cosmic-ray fluxes through the solar system and thus are not a reliable true age indicator.
A Biblical Perspective
Any postulated naturalistic or uniformitarian history for the formation of the parent asteroids of these meteorites, and of course for the solar system itself, is completely invalidated by the divinely provided biblical account of the six normal days of God creating supernaturally during the Creation Week. On Day One God ex nihilo created the earth (Genesis 1:1), and only on Day Four did He make the sun and the moon to provide light on the earth during the day and night respectively (Genesis 1:14–16). We are not specifically told that the rest of the solar system was also created on Day Four, but He did make the stars also on that day, and all the lights were placed in the expanse of the heavens to be for signs and seasons. From this description it is not unreasonable to conclude that the rest of the solar system was made on Day Four, including the other planets and the asteroids. Furthermore, each entity God created and made during these six normal days of the Creation Week was formed exceedingly rapidly within the time and space of each normal day, so by the end of Day Four planets and asteroids were completely formed entities, including those with iron cores, ultramafic mantles, and basaltic crusts, all the necessary supposed silicate-metal fractionation and crust-mantle differentiation happening exceedingly rapidly within hours, and thus not requiring the millions of years postulated by uniformitarians.
Given the general consensus that the asteroids and the other planets consist of residual material from the formation of the solar system, Snelling (2014a, b, c, 2015a) proposed that the accepted coincident 4.55–4.57 Ga ages for the earth and many meteorites could be due to the earth and the parent asteroids having been created by God from the same primordial material, which He had created on Day One, as already proposed by Faulkner (1999, 2013). His proposal is based on the usages in Genesis 1 of the Hebrew words āśâ (meaning to do or to make) and bārā’ (meaning to create). Because it is indisputably evident that āśâ is commonly used to refer to the act of fashioning something out of already-existing material (for example, the creation of man in Genesis 1:26; cf. 2:7), Faulkner (2013) contends that, apart from any contextual clues to suggest that it must bear the sense of creation out of nothing, there is a distinct possibility that the making of the astronomical bodies was instead a matter of fashioning them from material previously created on Day One. Just as the description of the earth in Genesis 1:2 is of something unfinished that God returned to over the next several days to shape and prepare, perhaps the matter that would become the astronomical bodies was created on Day One but was shaped on Day Four, whereupon God brought forth their light to the earth.
Thus the simplest unifying assumption would therefore be that all such primordial material may have had the same created isotopic endowment. This assumption seems to be borne out by the earth apparently having the same time-integrated Pb isotopic endowment and thus being the same Pb-Pb “age” as the meteorites plotted on the geochron (Patterson 1956). The earth’s current Pb isotopic endowment was represented on that geochron by the Pb isotopic composition of a modern oceanic sediment sample, which would appear to contain the time-integrated Pb isotopic endowment from the earth’s beginning which was then processed through the earth’s subsequent rock cycle (Tyler 1990). However, while the possibility could be considered that the created initial ratios of parent to daughter elements were different for the earth compared to those created for other solar system objects, that possibility seems unwarranted if God made all the solar system objects (planets, moons, and asteroids) from the same primordial material He had created on Day One, which is consistent with them all having a common Designer. Nevertheless, if there were created differences in the initial isotopic ratios, then it would not have been possible to plot the meteorites and the earth on the same Pb-Pb geochron, or groups of meteorites would not have yielded the same Pb-Pb, U-Pb, Rb-Sr, Sm-Nd, Lu-Hf, and Re-Os isochron ages as shown in this study.
It would also seem reasonable to propose that God created some of all the isotopes of each element at the beginning in the primordial material, including those isotopes that subsequently also formed by radioisotope decay as daughter isotopes from parent isotopes, regardless of when radioisotope decay started. In other words, when God made the primordial material He included in it 206Pb, 207Pb, and 208Pb atoms along with 238U, 235U, and 232Th atoms. It is reasonable to posit that He did, given that when He created the “primordial material” it likely had to have some initial isotopic ratios. Whether it will be possible to develop a model for initial isotope ratios that will explain the current data must be the goal of future research. In any case, initial ratios in the primordial material need not be required to be in secular equilibrium, because these initial ratios are solely the ratios in the daughter Pb isotopes, without any of the other isotopes in the 238U, 235U, and 232Th decay “chains” being relevant. Indeed, even the conventional scientific community has assumed the initial material of the solar system had the “primeval” Pb isotopic ratios as measured in the troilite (iron sulfide) in the Canyon Diablo iron meteorite, without reference to any of the intermediate daughters (Faure and Mensing 2005). This is consistent with God creating a fully-functioning universe, as typified by Him creating fruit trees already bearing fruit in fully-functioning soil on prepared land, all during Day Three, and the sun, moon, asteroids, and stars fully-functioning in their ordained positions and roles on Day Four. Thus when by the end of Day Four the asteroids had been formed, all the supposed silicate-metal fractionation and crust-mantle differentiation of that primordial material necessary to produce their internal layering had happened exceedingly rapidly within hours. That silicate-metal fractionation and crust-mantle differentiation may have also resulted in some redistribution or mixing of parent and daughter atoms, the latter having been originally created rather than derived via radioactive decay. These processes may also explain some of the scattering in the radioisotope ages for these groups of meteorites, especially those older than the 4.55–4.57 Ga clusterings.
At what point in time radioactive decay began is unclear from Scripture, and is still a matter of debate among creationists. The RATE project considered the possibility of a large amount of accelerated radioisotope decay occurring during the Creation Week, as radioisotope decay was not regarded as decay in the sense of deterioration of matter (Vardiman, Snelling, and Chaffin 2005). It is instead a transmutation process, by which one element is changed into another. The daughter element is certainly not inferior to the parent element. However, it is the radiation given off which is harmful that causes concern as to whether the radioisotope decay processes meet the standard of God’s declaration of His completed creation being “very good” (Genesis 1:31).
In the context of the decay evident today due to the operation of the second law of thermodynamics, Anderson (2103) contended that there is no real biblical evidence to suggest that the second law was inoperable prior to the curse, and so argued that rather the second law was in effect from the beginning of creation. He thus also suggested that the tendency toward entropy implicit in the second law was never of a kind that conflicted with God’s declaration that the creation was “very good,” or that eventuated in the death of any sentient creature. On the other hand, it could be argued that radioisotope decay is more than the operation of the second law of thermodynamics; the additional outcome being the radiation produced which is harmful to life’s biological and chemical makeup. Indeed, if billions of years of accelerated radioisotope decay had occurred mainly during the early part of the Creation Week, as considered a possibility by the RATE team (Vardiman, Snelling, and Chaffin 2005), the enormous burst of radiation would surely have been detrimental to all life on the earth, for example, the plants of Day Three. It is for this reason that many creationists are not comfortable with postulating that accelerated radioisotope decay happened during the Creation Week, so maybe there was no radioisotope decay at all until it was started as part of the curse.
There is a lack of any definitive evidence of patterns of different isochron ages yielded by the different radioisotope systems in the groups of chondrite, stony achondrite, pallasite and mesosiderite, and iron meteorites in this study, as well as in the 38 chondrite, basaltic achondrite (eucrite), and primitive and other achondrite meteorites previously studied (Snelling 2014a, b, c, 2015a), that matches the pattern found during the RATE project (Snelling 2005c; Vardiman, Snelling, and Chaffin 2005). This would therefore strongly suggest that all these meteorites and their parent asteroids have not experienced any episode of accelerated radioisotope decay, either at the time of the creation of the primordial material on Day One or at the time of their formation on Day Four, or since. This could then be taken to infer that no accelerated radioisotope decay occurred anywhere in the solar system during the Creation Week, including on the earth during Days One–Three. Such a conclusion is based on the assumption that the mechanism of small changes to the binding forces in the nuclei of the parent radioisotopes proposed as the cause of a past episode of accelerated radioisotope decay (Vardiman, Snelling, and Chaffin 2005) would thus have affected every atom making up the earth, and by logical extension every atom of the universe at the same time, because God appears to have created the physical laws governing the universe to operate consistently through time and space.
On the other hand, if this assumption is true, and it is consistent with God’s work of providentially maintaining the universe after He created it, then why is there evidence of an episode of accelerated radioisotope decay in the earth, but not in these parent asteroids and their meteorite fragments? Indeed, the meteorites do not have unequivocal physical evidence in them that they have experienced ~4.5 Ga worth of nuclear decay commensurate with their radioisotope ages. The answer would seem to be that the accelerated radioisotope decay only occurred subsequent to the end of the Creation Week during the catastrophic global Flood event on the earth, and that the parent asteroids of these meteorites were not similarly affected. However, if the earth’s atoms were affected by accelerated radioisotope decay during the Flood, then surely every other atom in the universe would have been similarly affected. However, God is not bound by the physical laws He put in place at creation, as He can change them at any time anywhere or everywhere. After all, when Jesus Christ the Creator locally suspended the law of gravity as He walked on the surface of the stormy waters of the Sea of Galilee, the law of gravity was still operating at the same time to keep the disciples in their boat, their boat on the water, and the earth in space in orbit around the sun. Thus God could have made small changes to the binding forces of the nuclei of only the earth’s atoms during the Flood to cause accelerated radioisotope decay only on the earth, while leaving the atoms making up the rest of the solar system and universe untouched. Perhaps the reason God initiated accelerated radioisotope decay only on the earth was to generate the heat necessary to initiate and drive the catastrophic plate tectonics which reshaped the earth’s surface during the Flood (Baumgardner 2003).
Another reason for arguing that accelerated radioisotope decay occurred in earth’s rocks only during the Flood is that the earth’s rocks contain the physical evidence of only 500–600 million years’ worth of radioisotope decay (as calculated using today’s measured decay rates), which equates to approximately the same time period postulated by uniformitarians during which the geologic record of the Flood accumulated (Snelling 2009). This physical evidence of radioisotope decay in earth’s rocks is provided by radiohalos and fission tracks (Snelling 2005a, b). Each fully-formed U radiohalo, no matter where in the geologic record it occurs or the supposed age of its host rock, only represents up to 100 million or so years’ worth of U decay. So even if U radiohalos are in a Precambrian (pre-Flood or Creation Week) granite they still only record up to 100 million or so years’ worth of U decay that occurred during the Flood. At the same time during the Flood new granites containing U radiohalos were forming in plutons which had intruded into fossil-bearing (and therefore Flood-deposited) sedimentary strata. On the other hand, up to 600 or so million years’ worth of fission tracks are found in zircon grains in tuff beds near the base of the strata record of the Flood matching the U-Pb radioisotope ages of those same zircon grains (Snelling 2005b).
This still does not fully explain why there is such a spread of radioisotope “ages” from 4.03 Ga to the present in the earth’s rocks, or why the radioisotope “ages” of the oldest earth rock (the Acasta Gneiss, Canada) (Bowring, Williams, and Compston 1989; Stern and Bleeker 1998) and the oldest mineral in an earth rock (a zircon grain in the Jack Hills sandstone, Western Australia) (Valley et al. 2014; Wilde at al. 2001) are 4.03 Ga and 4.4 Ga respectively rather than 4.56 Ga, the supposed age of the earth. The answer might be that the earth’s rocks, subsequent to their creation on Day One, first suffered from the processes of mixing of isotopes and resetting of radioisotope “clocks” in the mantle and crust during the Day Three “Great Upheaval” when God formed the dry land, and then further suffered from mixing of isotopes and resetting of radioisotope “clocks” in the mantle and crust as a consequence of the catastrophic plate tectonics during the Flood, as well as the concurrent accelerated radioisotope decay during the Flood (Snelling 2000, 2005c). These mixing processes would not just have affected isochron ages. The mixing and adding or removing of parent and/or daughter isotopes produces mixing lines that are then interpreted as isochrons, but the same mixing, adding and/or subtracting of parent and/or daughter isotopes would also have reset the radioisotope model ages. In these ways the radioisotope “clocks” would have been reset during both the “Great Upheaval” and the Flood, just as they were when pre-Flood crustal rocks (with older radioisotope ages) were melted to form granite magmas, which when they crystallized had their radioisotope “clocks” reset to record the younger granite formation ages.
By comparison, the Day Three “Great Upheaval” which the Scriptures describe as occurring on the earth would not have affected other bodies in the solar system, including the asteroids which were the source of the groups of meteorites in this study, because these other bodies were not created until Day Four. Thus we can be dogmatic that this event was earth-specific, as it was designed to produce the continental crust and the dry land on the earth in readiness for the subsequent creation of plants, birds, animals, and man. In any case, so far our observations of the surfaces of asteroids do not indicate any continental crust on them akin to that which formed on the earth on Day Three. Instead their crusts are basaltic, equivalent to earth’s oceanic crust, which is evident from the basaltic achondrites (eucrites) that are believed to have come from the large, differentiated asteroid 4-Vesta. However, when the asteroids were formed on Day Four their formation would have included incredibly rapid silicate-metal fractionation and mantle-crust differentiation with accompanying redistribution of the previously created parent and (what uniformitarians now interpret as) daughter isotopes.
The scatter in the radioisotope ages of the 38 individual asteroidal meteorites reported in previous studies (Snelling 2014a, b, c, 2015a), and for the groups of asteroidal meteorites in this study, would then be due to processes subsequent to the initial creation of the parent asteroids from the primordial material on Day Four of the Creation Week which have reset the radioisotope “clocks” at various times. Such processes would include the initial fractionation and differentiation, heating due to impact cratering, impact disintegration and re-coalescing of the asteroids, space weathering, and heating on passage of the meteorites through the earth’s atmosphere (Bogard and Garrison 2009; Cloutis, Binzel, and Gaffey 2014; Michel 2014; Norton 2002).
Where to From Here?
As concluded by Snelling (2014a, b, c, 2015a) from his studies of 16 chondrite meteorites, 12 basaltic achondrites (eucrites), and 10 primitive and other achondrites, based on the assumptions made the 4.55–4.57 Ga radioisotope “ages” for the groups of chondrites, stony achondrites, pallasites and mesosiderites, and irons obtained in this study are likely not their true real-time ages. These 4.55–4.57 Ga radioisotope “ages” were obtained primarily by Pb-Pb, U-Pb, and Re-Os isochron dating, supported by some Rb-Sr and Lu-Hf isochron dating, of whole-rock samples of these meteorites and some various constituent minerals and fractions, but also by the Mn-Cr and Hf-W radioisotope methods directly calibrated against Pb-Pb meteorite ages. The assumptions on which the radioisotope dating methods are based are simply unprovable, and in the light of the possibility of an inherited primordial geochemical signature, subsequent resetting of radioisotope “clocks” due to impact cratering of asteroids, and the evidence in earth rocks for past accelerated radioisotope decay, mixing of isotopes and resetting of radioisotope “clocks,” these assumptions are unreasonable.
However, we still need to develop a coherent and comprehensive explanation of what these radioisotope compositions in both meteorites and earth rocks really represent and mean within our biblical young-age creation-Flood framework for earth and universe history. We have some possible clues already, as discussed here, and a clearer picture may yet emerge from continued investigations. Examination of the radioisotope dating data for groups of meteorites here was necessary to essentially complete our understanding of what the meteorite radioisotope “ages” might mean. If only the earth was affected by accelerated radioisotope decay during the Flood, then it is also necessary to examine the radioisotope dating data for martian meteorites, and lunar meteorites and rocks to determine whether Mars and the Moon were affected by that aspect of the Flood catastrophe or not. Additionally, the radioisotope dating data for many more earth rocks from all levels of the geologic record need to be collated and examined. If accelerated radioisotope decay only occurred during the Flood, then it might be expected that the radioisotope “ages” of pre-Flood (mostly Precambrian) strata determined by the different methods would be noticeably discordant (Snelling 2005c), whereas the radioisotope “ages” of the strata formed during the Flood (mostly Phanerozoic) would be mostly concordant (Snelling 2005b). This difference might be expected due to the pre-Flood rocks having already been formed and their radioisotope “clocks” started before the onset of the accelerated radioisotope decay during the Flood, when their radioisotope “clocks” would have been speeded up by different amounts according to the atomic weights or decay constants (half-lives) of the parent radioisotopes for the full duration of the Flood event. In contrast, the Flood rocks would have had their radioisotopes mixed and then reset when those rocks formed. Thus their radioisotope “clocks” only started at different times during the accelerated radioisotope decay of the Flood event, and consequently progressively formed Flood rocks experienced progressively less accelerated radioisotope decay than pre-Flood rocks. It may take the collation and examination of the huge radioisotope dating data sets of as many different earth rocks as possible from all levels of the geologic record to enable any firm conclusions to be made.
Whatever the radioisotope dating data for the earth’s rocks may reveal, it is already well-established that there are so many problems with the radioisotope dating methods which render them totally unreliable in providing time markers for the different stages in the earth’s history (Dickin 2005; Faure and Mensing 2005; Snelling 2000). Indeed, the investigations of determinations of the decay constants of each of the parent radioisotopes (Snelling 2014d, e, 2015b, c) needs to be completed to provide further documentation of the numerous uncertainties in that crucial time assumption. Therefore, even though most of these groups of meteorites yield a consistent Pb-Pb, U-Pb, and Pb-Pb-calibrated isochron age of 4.55–4.57 Ga, that cannot be their true real-time age, which according to the biblical paradigm is only about 6000 real-time years.
Conclusions
After six decades of numerous careful radioisotope dating investigations of groups of these asteroidal meteorites (chondrites, stony achondrites, pallasites and mesosiderites, and irons) their Pb-Pb, U-Pb, and Pb-Pb calibrated isochron age of 4.55–4.57 Ga has been well established. This date for these groups of meteorites is supported for most of them by a strong clustering of their Pb-Pb, U-Pb, and Pb-Pb calibrated isochron ages in the 4.55–4.57 Ga range, as well as often being confirmed by isochron age results via the Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd methods. The Hf-W and Mn-Cr methods are all calibrated against the Pb-Pb method, so their results are not objectively independent. Thus the Pb-Pb dating method stands supreme in the conventional evolutionary uniformitarian community as the ultimate, most precise tool for determining the ages of these groups of meteorites.
There are no discernible patterns in the isochron ages for these groups of meteorites, apart from scattering of many Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isochron ages, and a few Pb-Pb and U-Pb isochron ages. The radioisotope ages for these groups of meteorites do not follow the systematic patterns found in Precambrian rock units during the RATE project. The α-decay isochron ages are not always older than the β-decay isochron ages for particular groups of meteorites, and among the α-decayers and among the β-decayers the isochron ages are not always older according to the increasing heaviness of the atomic weights of the parent radioisotopes, or the increasing lengths of their half-lives. Thus there appears to be no consistent evidence of past accelerated radioisotope decay in these groups of meteorites similar to that found in earth rocks, nor unequivocal physical evidence in them that they have experienced a lot of nuclear decay. Therefore it could be concluded from these data that no accelerated radioisotope decay event has occurred on the asteroids which parented these groups of meteorites.
Any explanation for the 4.55–4.57 Ga age for these groups of meteorites needs to consider their origin. These groups of meteorites are regarded as fragments of asteroids, debris derived from disintegration of parent asteroids, or from impact cratering of their surfaces and collisions with other asteroids. Even in the naturalistic paradigm the asteroids, and thus the meteorites, are regarded as “primordial material” left over from the formation of the solar system. Similarly, it has been suggested the Hebrew of the Genesis text allows for God to have made “primordial material” on Day One of the Creation Week from which He made the earth on Day One and the non-earth portion of the solar system on Day Four. Thus today’s measured radioisotope compositions of these groups of meteorites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes created by God. Therefore some, or perhaps most, of the daughter isotopes measured today in these groups of meteorites were thus “inherited” by them when they were formed from that “primordial material,” and the parent isotopes in these meteorites have only been subjected to some subsequent radioisotope decay (and none at accelerated rates). Thus the 4.55–4.57 Ga Pb-Pb, U-Pb, and Pb-Pb calibrated isochron “age” for these groups of meteorites, and their supporting Rb-Sr, Lu-Hf, Re-Os, and Sm-Nd isochron “ages,” cannot be their true real-time age, which according to the biblical paradigm is only about 6000 real-time years.
However, even though these suggested explanations and conclusions as discussed here are still somewhat tentative, they are supported by the previous studies of the isochron and model ages of 38 individual meteorites from these same groups of meteorites. Yet the confirmation or adjustment of these suggested explanations and conclusions await the examination of more radioisotope dating data for martian and lunar meteorites, as well as further extensive studies of the radioisotope dating of lunar rocks, and rocks from all levels of the earth’s geologic record. Such further studies are required to attempt to systematize what proportions of the isotopes in each radioisotope dating system measured today are due to inheritance from the “primordial material,” to accelerated radioisotope decay during the Flood, and mixing, additions and subtractions in the earth’s mantle and crust through earth history, particularly during the Day Three Great Upheaval and then subsequently during the Flood.
Acknowledgments
The invaluable help of my research assistant in compiling these radioisotope dating data into the tables and then plotting the data in the color coded age versus frequency histogram diagrams is acknowledged. Also, our production assistant Laurel Hemmings is especially thanked for her painstaking work in preparing these papers for publication.
References
Amelin, Y. 2008. “U–Pb Ages of Angrites.” Geochimica et Cosmochimica Acta 72 (1): 221–32.
Amelin, Y., A. Kaltenbach, T. Iizuka, C. H. Stirling, T. R. Ireland, M. Petaev, and S. B. Jacobsen. 2010. “U-Pb Chronology of the Solar System’s Oldest Solids with Variable 238U/235U.” Earth and Planetary Science Letters 300 (3–4): 343–50.
Amelin, Y., and E. Rotenberg. 2004. “Sm-Nd Systematics of Chondrites.” Earth and Planetary Science Letters 223 (3–4): 267–82.
Amelin, Y., M. Wadhwa, and G. Lugmair. 2006. “Pb-Isotopic Dating of Meteorites Using 202Pb-205Pb Double-Spike: Comparison with Other High-Resolution Chronometers.” Lunar and Planetary Science Conference 37: #1970.
Amelin, Y., J. Wimpenny, and Q.-Z. Yin. 2011. “Angrite Lu-Hf Whole Rock Data Provide No Direct Support to Accelerated Decay of 176Lu by Supernova Irradiation.” Workshop on the Formation of the First Solids in the Solar System #9014.
Anderson, L. A. Jr. 2013. “Thoughts on the Goodness of Creation: In What Sense was Creation ‘Perfect’?” Answers Research Journal 6: 391–97. https://answersingenesis.org/physics/thoughts-on-the-goodness-of-creation-in-whatsense-was-creation-perfect/.
Baker, J., M. Bizzarro, N. Wittig, J. Connelly, and H. Haack. 2005. “Early Planetesimal Melting from an Age of 4.5662 Gyr for Differentiated Meteorites.” Nature 436 (7054): 1127–131.
Basaltic Volcanism Study Project. 1981. Basaltic Volcanism on the Terrestrial Planets. New York, New York: Pergamon Press, Inc.
Baumgardner, J. R. 2003. “Catastrophic Plate Tectonics: The Physics Behind the Flood.” In Proceedings of the Fifth International Conference on Creationism. Edited by R. L. Ivey Jr., 113–26. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Birck, J. L., and C. J. Allègre. 1978. “Chronology and Chemical History of the Parent Body of Basaltic Achondrites Studied by the 87Rb-87Sr Method.” Earth and Planetary Science Letters 39 (1): 37–51.
Birck, J. L., and C. J. Allègre. 1981. “87Rb/87Sr Study of Diogenites.” Earth and Planetary Science Letters 55 (1): 116–22.
Birck, J. L., and C. J. Allègre. 1998. “Rhenium-187–Osmium-187 in Iron Meteorites and the Strange Origin of the Kodaïkanal Meteorite.” Meteoritics and Planetary Science 33 (4): 647–53.
Bizzarro, M., J. A. Baker, H. Haack, D. Ulfbeck, and M. Rosing. 2003. “Early History of Earth’s Mantle-Crust System Inferred from Hafnium Isotopes in Chondrites.” Nature 421 (6926): 931–33.
Blichert-Toft, J., M. Boyet, P. Télouk, and F. Albarède. 2002. “147Sm-143Nd and 176Lu-176Hf in Eucrites and the Differentiation of the HED Parent Body.” Earth and Planetary Science Letters 204 (1–2): 167–81.
Bogard, D. D. 2011. “K-Ar Ages of Meteorites: Clues to Parent-Body Thermal Histories.” Chemie der Erde 71 (3): 207–26.
Bogard, D. D., E. T. Dixon, and D. H. Garrison. 2010. “Ar-Ar Ages and Thermal Histories of Enstatite Meteorites.” Meteoritics and Planetary Science 45 (5): 723–42.
Bogard, D. D., and D. H. Garrison. 1998. “39Ar-40Ar Ages and Thermal History of Mesosiderites.” Geochimica et Cosmochimica Acta 62 (8): 1459–68.
Bogard, D. D., and D. H. Garrison. 2009. “Ar-Ar Impact Heating Ages of Eucrites and Timing of the LHB.” Lunar and Planetary Science Conference 40: #1131.
Bogard, D. D., D. H. Garrison, J. L. Jordan, and D. Mittlefehldt. 1990. “39Ar-40Ar Dating of Mesosiderites: Evidence for Major Parent Body Disruption < 4 Ga Ago.” Geochimica et Cosmochimica Acta 54 (9): 2549–64.
Bogard, D. D., D. H. Garrison, T. J. McCoy, and K. Keil. 1993. “39Ar-40Ar Ages of Acapulcoites and Lodranites: Evidence for Early Parent Body Heating.” Lunar and Planetary Science Conference 24: 141–42.
Bogard, D. D., D. H. Garrison, and T. J. McCoy. 2000. “Chronology and Petrology of Silicates from IIE Iron Meteorites: Evidence of a Complex Parent Body Evolution.” Geochimica et Cosmochimica Acta 64 (12): 2133–54.
Bogard, D. D., D. H. Garrison, and H. Takeda. 2005. “Ar-Ar and I-Xe Ages and the Thermal History of IAB Meteorites.” Meteoritics and Planetary Science 40 (2): 207–24.
Bouvier, A., J. Blichert-Toft, F. Moynier, J. D. Vervoort, and F. Albarède. 2007. “Pb–Pb Dating Constraints on the Accretion and Cooling History of Chondrites.” Geochimica et Cosmochimica Acta 71 (6): 1583–604.
Bowring S. A., I. S. Williams, and W. Compston. 1989. “3.96 Ga Gneisses from the Slave Province, Northwest Territories, Canada.” Geology 17 (11): 971–75.
Brearley, A. J., and R. H. Jones. 1998. “Chondritic Meteorites.” In Planetary Materials. Edited by J. J. Papike. Reviews in Mineralogy, vol. 36, 3-1–3-398. Washington DC: Mineralogical Society of America.
Brennecka, G. A., and M. Wadhwa. 2011. “238U/235U Ratios of Angrites: Adjusting Absolute Ages of Anchors.” Mineralogical Magazine 75 (3): 579.
Brennecka, G. A., and M. Wadhwa. 2012. “Uranium Isotope Compositions of the Basaltic Angrite Meteorites and the Chronological Implications for the Early Solar System.” Proceedings of the National Academy of Sciences USA 109 (24): 9299–303.
Burkhardt, C., T. Kleine, B. Bourdon, H. Palme, J. Zipfel, J. M. Friedrich, and D. S. Ebel. 2008. “Hf-W Mineral Isochron for Ca,Al-Rich Inclusions: Age of the Solar System and the Timing of Core Formation in Planetesimals.” Geochimica et Cosmochimica Acta 72 (24): 6177–97.
Burnett, D. S., and G. J. Wasserburg. 1967. “87Rb-87Sr Ages of Silicate Inclusions in Iron Meteorites.” Earth and Planetary Science Letters 2 (5): 397–408.
Carver, E. A., and E. Anders. 1970. “Serra de Magé: A Meteorite with an Unusual History.” Earth and Planetary Science Letters 8 (3): 214–20.
Carver, E. A., and E. Anders. 1976a. “Fission-Track Ages of Four Meteorites.” Geochimica et Cosmochimica Acta 40 (4): 467–77.
Carver, E. A., and E. Anders. 1976b. “Nuclear Tracks in the Angra dos Reis and Moore County Meteorites.” Geochimica et Cosmochimica Acta 40 (8): 935–44.
Chen, J. H., D. A. Papanastassiou, and G. J. Wasserburg. 1998. “Re-Os Systematics in Chondrites and the Fractionation of the Platinum Group Elements in the Early Solar System.” Geochimica et Cosmochimica Acta 62 (19–20): 3379–92.
Chen, J. H., and G. J. Wasserburg. 1981. “The Isotopic Composition of Uranium and Lead in Allende Inclusions and Meteoritic Phosphates.” Earth and Planetary Science Letters 52 (1): 1–15.
Cloutis, E. A., R. P. Binzel, and M. J. Gaffey. 2014. “Establishing Asteroid–Meteorite Links.” Elements 10 (1): 25–30. Cook, D. L., R. J. Walker, M. F. Horan, J. T. Wasson, and J. W. Morgan. 2004. “Pt-Re-Os Systematics of Group IIAB and IIIAB Iron Meteorites.” Geochimica et Cosmochimica Acta 68 (6): 1413–31.
Cronin, J. R., S. Pizzarello, and D. P. Cruikshank. 1988. “Organic Matter in Carbonaceous Chondrites, Planetary Satellites, Asteroids and Comets.” In Meteorites and the Early Solar System. Edited by J. F. Kerridge and M. S. Matthews, 819–57. Tucson, Arizona: University of Arizona Press.
Cumming, G. L. 1969. “A Recalculation of the Age of the Solar System.” Canadian Journal of Earth Sciences 6 (4): 719–35.
Dalrymple, G. B. 1991. The Age of the Earth. Stanford, California: Stanford University Press.
Dalrymple, G. B. 2004. Ancient Earth, Ancient Skies. Stanford, California: Stanford University Press.
Dickin, A. P. 2005. Radiogenic Isotope Geology. 2nd ed. Cambridge, United Kingdom: Cambridge University Press. Eugster, O. 2003. “Cosmic-Ray Exposure Ages of Meteorites and Lunar Rocks and Their Significance.” Chemie der Erde 63 (1): 3–30.
Faulkner, D. R. 1999. “A Biblically-Based Cratering Theory.” Creation Ex Nihilo Technical Journal 13 (1): 100–04.
Faulkner, D. R. 2013. “A Proposal for a New Solution to the Light Travel Time Problem.” Answers Research Journal 6: 295–300. https://answersingenesis.org/astronomy/starlight/a-proposal-for-a-new-solution-to-the-light-traveltime-problem/.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and Applications. 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Fleischer, R. L., C. W. Naeser, P. B. Price, R. M. Walker, and U. B. Marvin. 1965. “Fossil Particle Tracks and Uranium Distributions in Minerals of the Vaca Muerta Meteorite.” Science 148 (3670): 629–32.
Fleischer, R. L., P. B. Price, and R. M. Walker. 1965. “Spontaneous Fission Tracks from Extinct Pu244 in Meteorites and the Early History of the Solar System.” Journal of Geophysical Research 70 (11): 2703–07.
Fleischer, R. L., P. B. Price, R. M. Walker, and M. Maurette. 1967a. “Origins of Fossil Charged-Particle Tracks in Meteorites.” Journal of Geophysical Research 72 (1): 331–53.
Fleischer, R. L., P. B. Price, R. M. Walker, M. Maurette, and G. Morgan. 1967b. “Tracks of Heavy Primary Cosmic Rays in Meteorites.” Journal of Geophysical Research 72 (1): 355–66.
Gopalan, K., and G. W. Wetherill. 1968. “Rubidium-Strontium Age of Hypersthene (L) Chondrites.” Journal of Geophysical Research 73 (22): 7133–36.
Gopalan, K., and G. W. Wetherill. 1969. “Rubidium-Strontium Age of Amphoterite (LL) Chondrites.” Journal of Geophysical Research 74 (17): 4349–58.
Gopalan, K., and G. W. Wetherill. 1970. “Rubidium-Strontium Studies on Enstatite Chondrites: Whole Meteorite and Mineral Isochrons.” Journal of Geophysical Research 75 (17): 3457–67.
Gopalan, K., and G. W. Wetherill. 1971. “Rubidium-Strontium Studies on Black Hypersthene Chondrites: Effects of Shock and Reheating.” Journal of Geophysical Research 76 (35): 8484–92.
Göpel, C., G. Manhès, and C. J. Allègre. 1994. “U-Pb Systematics of Phosphates from Equilibrated Ordinary Chondrites.” Earth and Planetary Science Letters 121 (1–2): 153–71.
Hans, U., T. Kleine, and B. Bourdon. 2010. “Rb-Sr Chronology of Volatile Depletion of the Angrite and Eucrite Parent Bodies.” Lunar and Planetary Science Conference 41: #2680.
Hans, U., T. Kleine, and B. Bourdon. 2013. “Rb-Sr Chronology of Volatile Depletion in Differentiated Protoplanets: BABI, ADOR and ALL Revisited.” Earth and Planetary Science Letters 374: 204–14.
Hiess, J., D. J. Condon, N. McLean, and S. R. Noble. 2012. “238U/235U Systematics in Terrestrial Uranium-Bearing Minerals.” Science 335 (6076): 1610–14.
Horan, M. F., J. W. Morgan, R. J. Walker, and J. N. Grossman. 1992. “Rhenium-Osmium Isotope Constraints on the Age of Iron Meteorites.” Science 255 (5048): 1118–21.
Horan, M. F., M. I. Smoliar, and R. J. Walker. 1998. “182W and 187Re-187Os Systematics of Iron Meteorites: Chronology for Melting, Differentiation, and Crystallization in Asteroids.” Geochimica et Cosmochimica Acta 62 (3): 545–54.
Huey, J. M., and T. P. Kohman. 1973. “207Pb-206Pb Isochron and Age of Chondrites.” Journal of Geophysical Research 78 (17): 3227–44.
Ireland, T. R., and F. Wlotzka. 1992. “The Oldest Zircons in the Solar System.” Earth and Planetary Science Letters 109 (1–2): 1–10.
Jacobsen, S. B., and G. J. Wasserburg. 1980. “Sm-Nd Isotopic Evolution of Chondrites.” Earth and Planetary Science Letters 50 (1): 139–55.
Jacobsen, S. B., and G. J. Wasserburg. 1984. “Sm-Nd Isotopic Evolution of Chondrites and Achondrites, II.” Earth and Planetary Science Letters 67 (2): 137–50.
Kanasewich, E. R. 1968. “The Interpretation of Lead Isotopes and Their Geological Significance.” In Radiometric Dating for Geologists. Edited by E. I. Hamilton and R. M. Farquhar, 147–70. New York, New York: Interscience.
Kaushal, S. K., and G. W. Wetherill. 1969. “Rb87-Sr87 Age of Bronzite (H Group) Chondrites.” Journal of Geophysical Research 74 (10): 2717–26.
Kleine, T., U. Hans, A. J. Irving, and B. Bourdon. 2012. “Chronology of the Angrite Parent Body and Implications for Core Formation in Protoplanets.” Geochimica et Cosmochimica Acta 84: 186–203.
Kleine, T., K. Mezger, C. Münker, H. Palme, and A. Bischoff. 2004. “182Hf-182W Isotope Systematics of Chondrites, Eucrites, and Martian Meteorites: Chronology of Core Formation and Early Mantle Differentiation in Vesta and Mars.” Geochimica et Cosmochimica Acta 68 (13): 2935–46.
Kleine, T., K. Mezger, H. Palme, E. Scherer, and C. Münker. 2005. “Early Core Formation in Asteroids and Late Accretion of Chondrite Parent Bodies: Evidence from 182Hf-182W in CAIs, Metal-Rich Chondrites, and Iron Meteorites.” Geochimica et Cosmochimica Acta 69 (24): 5805–18.
Kleine, T., C. Münker, K. Mezger, and H. Palme. 2002. “Rapid Accretion and Early Core Formation on Asteroids and the Terrestrial Planets from Hf-W Chronometry.” Nature 418 (6901): 952–55.
Kleine, T., M. Touboul, J. A. Van Orman, B. Bourdon, C. Maden, K. Mezger, and A. N. Halliday. 2008. “Hf-W Thermochronometry: Closure Temperature and Constraints on the Accretion and Cooling History of the H Chondrite Parent Body.” Earth and Planetary Science Letters 270 (1–2): 106–18.
Krot, A. N., Y. Amelin, P. Bland, F. J. Ciesla, J. N. Connelly, A. M. Davis, G. R. Huss, et al. 2009. “Origin and Chronology of Chondritic Components: A Review.” Geochimica et Cosmochimica Acta 73 (17): 4963–97.
Krot, A. N., K. Keil, C. A. Goodrich, E. R. D. Scott, and M. K. Weisberg. 2005. “Classification of Meteorites.” In Meteorites, Comets, and Planets. Edited by A. M. Davis. Treatise on Geochemistry, vol. 1, 83–128. Amsterdam, The Netherlands: Elsevier.
Lewis, J. S. 1997. Physics and Chemistry of the Solar System. Rev. ed. London, England: Academic Press. Luck, J.-M., and C.-J. Allègre. 1983. “187Re-187Os Systematics in Meteorites and Cosmological Consequences.” Nature 302 (5904): 130–32.
Luck, J.-M., J.-L. Birck, and C.-J. Allègre. 1980. “187Re-187Os Systematics in Meteorites: Early Chronology of the Solar System and Age of the Galaxy.” Nature 283 (5744): 256–59.
Lugmair, G. W., and S. J. G. Galer. 1992. “Age and Isotopic Relationships Among the Angrites Lewis Cliff 86010 and Angra dos Reis.” Geochimica et Cosmochimica Acta 56 (4):1673–94.
Lugmair, G. W., N. B. Scheinin, and K. Marti. 1975. “Search of Extinct 146Sm, 1. The Isotopic Abundance of 142Nd in the Juvinas Meteorite.” Earth and Planetary Science Letters 27 (1): 79–84.
Lugmair, G. W., and A. Shukolyukov. 1998. “Early Solar System Timescales According to 53Mn-53Cr Systematics.” Geochimica et Cosmochimica Acta 62 (16): 2863–86.
Lugmair, G. W., and A. Shukolyukov. 2001. “Early Solar System Events and Timescales.” Meteoritics and Planetary Science 36 (8): 1017–26.
Manhès, G., and C. J. Allègre. 1978. “Time Differences as Determined from the Ratio of Lead 207 to Lead 206 in Concordant Meteorites.” Meteoritics 13 (4): 543–48.
Markowski, A., G. Quitté, A. N. Halliday, and T. Kleine. 2006. “Tungsten Isotopic Composition of Iron Meteorites: Chronological Constraints vs. Cosmogenic Effects.” Earth and Planetary Science Letters 242 (1–2): 1–15.
Markowski, A., G. Quitté, T. Kleine, A. N. Halliday, M. Bizzarro, and A. J. Irving. 2007. “Hafnium–Tungsten Chronometry of Angrites and the Earliest Evolution of Planetary Objects.” Earth and Planetary Science Letters 262 (1–2): 214–29.
McCoy, T. J., R. J. Walker, J. I Goldstein, J. Yang, W. F. McDonough, D. Rumble, N. L. Chabot, et al. 2011. “Group IVA Irons: New Constraints on the Crystallization and Cooling History of an Asteroidal Core with a Complex History.” Geochimica et Cosmochimica Acta 75 (22): 6821–43.
McSween, H. Y. Jr., R. P. Binzel, M. C. De Sanctis, E. Ammannito, T. H. Prettyman, A. W. Beck, V. Reddy, et al. 2013. “Dawn; the Vesta-HED Connection; and the Geologic Context for Eucrites, Diogenites, and Howardites.” Meteoritics and Planetary Science 48 (11): 2090–104.
McSween, H. Y., M. C. De Sanctis, T. H. Prettyman, and the Dawn Science Team. 2014. “Unique, Antique Vesta.” Elements 10 (1): 39–44.
Michel, P. 2014. “Formation and Physical Properties of Asteroids.” Elements 10 (1): 19–24.
Minster, J.-F., and C.-J. Allègre. 1979. “87Rb-87Sr Chronology of H Chondrites: Constraint and Speculations on the Early Evolution of their Parent Body.” Earth and Planetary Science Letters 42 (3): 333–47.
Minster, J.-F., and C.-J. Allègre. 1981. “87Rb-87Sr Dating of LL Chondrites.” Earth and Planetary Science Letters 56: 89–106.
Minster, J.-F., J.-L. Birck, and C. J. Allègre. 1982. “Absolute Age of Formation of Chondrites Studied by the 87Rb-87Sr Method.” Nature 300 (5891): 414–19.
Minster, J.-F., L.-P. Rickard, and C.-J. Allègre. 1979. “87Rb-87Sr Chronology of Enstatite Meteorites.” Earth and Planetary Science Letters 44 (3): 420–40.
Misawa, K., A. Yamaguchi, and H. Kaiden. 2005. “U-Pb and 207Pb-206Pb Ages of Zircons from Basaltic Eucrites: Implications for Early Basaltic Volcanism on the Eucrite Parent Body.” Geochimica et Cosmochimica Acta 69 (24): 5847–61.
Mittlefehldt, D. W. 2005. “Achondrites.” In Meteorites, Comets, and Planets. Edited by A. M. Davis. Treatise on Geochemistry, vol. 1, 291–324. Amsterdam, The Netherlands: Elsevier.
Mittlefehldt, D. W., T. J. McCoy, C. A. Goodrich, and A. Kracher. 1998. “Non-Chondritic Meteorites from Asteroidal Bodies.” In Planetary Materials. Edited by J. J. Papike, Reviews in Mineralogy, vol. 36, 4-1–4-195. Washington, DC: Mineralogical Society of America.
Mittlefehldt, D. W., and G. W. Wetherill. 1979. “Rb-Sr Studies of CI and CM Chondrites.” Geochimica et Cosmochimica Acta 43 (2): 201–06.
Morgan, J. W., M. F. Horan, R. J. Walker, and J. N. Grossman. 1995. “Rhenium-Osmium Concentration and Isotope Systematics in Group IIAB Iron Meteorites.” Geochimica et Cosmochimica Acta 59 (11): 2331–44.
Morgan, J. W., R. J. Walker, and J. N. Grossman. 1992. “Rhenium-Osmium Isotope Systematics in Meteorites I: Magmatic Iron Meteorite Groups IIAB and IIIAB.” Earth and Planetary Science Letters 108 (4): 191–202.
Morris, J. D. 2007. The Young Earth. Rev. ed. Green Forest, Arkansas: Master Books.
Moynier, F., Q.-Z. Yin, and B. Jacobsen. 2007. “Dating the First Stage of Planet Formation.” The Astrophysical Journal 671: L181–L183.
Murthy, V. R., and W. Compston. 1965. “Rb-Sr Ages of Chondrules and Carbonaceous Chondrites.” Journal of Geophysical Research 70 (20): 5297–307.
Murthy, V. R., and C. C. Patterson. 1962. “Primary Isochron of Zero Age for Meteorites and the Earth.” Journal of Geophysical Research 67 (3): 1161–67.
Nebel, O., E. E. Scherer, and K. Mezger. 2011. “Evaluation of the 87Rb Decay Constant by Age Comparison Against the U–Pb System.” Earth and Planetary Science Letters 301 (1–2): 1–8.
Norton, O. R. 2002. The Cambridge Encyclopedia of Meteorites. Cambridge, United Kingdom: Cambridge University Press. Papanastassiou, D. A., and G. J. Wasserburg. 1969. “Initial Strontium Isotopic Abundances and the Resolution of Small Time Differences in the Formation of Planetary Objects.” Earth and Planetary Science Letters 5: 361–76.
Patchett, P. J., and M. Tatsumoto. 1980. “Lu-Hf Total-Rock Isochron for the Eucrite Meteorites.” Nature 288 (5791): 571–74.
Patchett, P. J., J. D. Vervoort, U. Söderlund, and V. J. M. Salters. 2004. “Lu–Hf and Sm–Nd Isotopic Systematics in Chondrites and Their Constraints on the Lu–Hf Properties of the Earth.” Earth and Planetary Science Letters 222 (1): 29–41.
Patterson, C. 1956. “Age of Meteorites and the Earth.” Geochimica et Cosmochimica Acta 10 (4): 230–37.
Polnau, E., and G. W. Lugmair. 2001. “Mn-Cr Isotope Systematics in the Two Ordinary Chondrites Richardton (H5) and Ste. Marguerite (H4).” Lunar and Planetary Science Conference 32: #1527.
Renne, P. R., R. Mundil, G. Balco, K. Min, and K. R. Ludwig. 2010. “Joint Determination of 40K Decay Constants and 40Ar*/40K for the Fish Canyon Sanidine Standard, and Improved Accuracy for 40Ar/39Ar Geochronology.” Geochimica et Cosmochimica Acta 74 (18): 5349–67.
Rotenburg, E., and Y. Amelin. 2001. “Combined Initial Sr, Sm-Nd, and U-Pb Systematics of Chondritic Phosphates: How Reliable are the Ages?” Lunar and Planetary Science Conference 32: #1675.
Rotenburg, E., and Y. Amelin. 2002. “Rb-Sr Chronology of Chondrules from Ordinary Chondrites.” Lunar and Planetary Science Conference 33: #1605.
Sanz, H. G., and G. J. Wasserburg. 1969. “Determination of an Internal 87Rb-87Sr Isochron for the Olivenza Chondrite.” Earth and Planetary Science Letters 6 (5): 335–45.
Scott, E. R. D., and A. N. Krot. 2005. “Chondrites and Their Components.” In Meteorites, Comets, and Planets. Edited by A. M. Davis. Treatise on Geochemistry, vol. 1, 143–200. Amsterdam, The Netherlands: Elsevier.
Selby, D., R. A. Creaser, H. J. Stein, R. J. Markey, and J. L. Hannah. 2007. “Assessment of the 187Re Decay Constant by Cross Calibration of Re-Os Molybdenite and U-Pb Zircon Chronometers in Magmatic Ore Systems.” Geochimica et Cosmochimica Acta 71 (8): 1999–2013.
Shen, J. J., D. A. Papanastassiou, and G. J. Wasserburg. 1996. “Precise Re-Os Determinations and Systematics of Iron Meteorites.” Geochimica et Cosmochimica Acta 60 (15): 2887–900.
Shen, J. J., D. A. Papanastassiou, and G. J. Wasserburg. 1998. “Re-Os Systematics in Pallasite and Mesosiderite Metal.” Geochimica et Cosmochimica Acta 62 (15): 2715–23.
Shields, R. M., W. H. Pinson, and P. M. Hurley. 1965. “The Rb87-Sr87 Age of Stony Meteorites.” Massachusetts Institute of Technology 13th Annual Program Report, 121–44.
Shirck, J. 1974. “Fission Tracks in a White Inclusion of the Allende Chondrite—Evidence for 244Pu.” Earth and Planetary Science Letters 23 (3): 308–12.
Shukolyukov, A., and G. W. Lugmair 2006. “Manganese–Chromium Isotope Systematics of Carbonaceous Chondrites.” Earth and Planetary Science Letters 250 (1–2): 200–13.
Shukolyukov, A., and G. W. Lugmair. 2007. “The Mn-Cr Isotope Systematics of Bulk Angrites.” Lunar and Planetary Science Conference 38: #1423.
Silver, L. T., and M. B. Duke. 1971. “U-Th-Pb Isotope Relations in Some Basaltic Achondrites.” EOS Transactions of the American Geophysical Union 52 (4): 289.
Smoliar, M. I., R. J. Walker, and J. W. Morgan. 1996. “Re-Os Ages of Group IIA, IIIA, IVA, and IVB Iron Meteorites.” Science 271 (5252): 1099–102.
Smoliar, M. I., R. J. Walker, and J. W. Morgan. 1997. “Rhenium-Osmium Isochron for IA Meteorites: Further Refinement of the Rhenium-187 Decay Constant.” Meteoritics and Planetary Science 32 (4): A122–A123.
Snelling, A. A. 2000. “Geochemical Processes in the Mantle and Crust.” In Radioisotopes and the Age of the Earth: A Young-earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 123–304. El Cajon, California : Institute for Creation Research, and St. Joseph, Missouri: Creation Research Society. http://www.icr.org/rate/.
Snelling, A. A. 2005a. “Radiohalos in Granites: Evidence of Accelerated Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 101–207. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/radiohalos-granites-evidence-for-accelerated/.
Snelling, A. A. 2005b. “Fission Tracks in Zircons: Evidence for Abundant Nuclear Decay.” In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 209–324. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/fission-tracks-zircons-evidence-for/.
Snelling, A. A. 2005c. “Isochron discordances and the role of inheritance and mixing of radioisotopes in the mantle and crust. In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Edited by L. Vardiman, A. A. Snelling, and E. F. Chaffin, 393–524. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/article/isochron-discordances-role-inheritance/.
Snelling, A. A. 2009. Earth’s Catastrophic Past: Geology, Creation and the Flood. Green Forest, Arkansas: Master Books and Petersburg, Kentucky: Answers in Genesis. Snelling, A. A. 2014a. “Radioisotope Dating of Meteorites: I. The Allende CV3 Carbonaceous Chondrite.” Answers Research Journal 7: 103–45. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-i-allende-cv3-carbonaceous-chrondrite/.
Snelling, A. A. 2014b. “Radioisotope Dating of Meteorites: II. The Ordinary and Enstatite Chondrites.” Answers Research Journal 7: 239–96. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-ii-ordinary-and-enstatite-chondrites/.
Snelling, A. A. 2014c. “Radioisotope Dating of Meteorites: III. The Eucrites (Basaltic Achondrites).” Answers Research Journal 7: 533–85. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-meteorites-iii/.
Snelling, A. A. 2014d. “Determination of the Radioisotope Decay Constants and Half-Lives: Rubidium-87 (87Rb).” Answers Research Journal 7: 311–22. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rubidium-87-87rb/.
Snelling, A. A. 2014e. “Determination of the Radioisotope Decay Constants and Half-Lives: Lutetium-176 (176Lu).” Answers Research Journal 7: 483–97. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-lutetium-176/.
Snelling, A. A. 2015a. “Radioisotope Dating of Meteorites: IV. The Primitive and Other Achondrites.” Answers Research Journal 8: 209–52. https://answersingenesis.org/astronomy/age-of-the-universe/radioisotope-dating-of-meteorites-primitive-and-other-achondrites/.
Snelling, A. A. 2015b. “Determination of the Radioisotope Decay Constants and Half-Lives: Rhenium-187 (187Re).” Answers Research Journal 8: 93–111. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-rhenium-187/.
Snelling, A. A. 2015c. “Determination of the Radioisotope Decay Constants and Half-Lives: Samarium-147 (147Sm).” Answers Research Journal 8: 305–21. https://answersingenesis.org/geology/radiometric-dating/determination-radioisotope-decay-constants-and-half-lives-samarium-147/.
Snyder, G. A., D.-C. Lee, A. M. Ruzicka, M. Prinz, L. A. Taylor, and A. N. Halliday. 2001. “Hf-W, Sm-Nd, and Rb-Sr Isotopic Evidence of Late Impact Fractionation and Mixing of Silicates on Iron Meteorite Parent Bodies.” Earth and Planetary Science Letters 186 (2): 311–24.
Söderlund, U., P. J. Patchett, J. D. Vervoort, and C. E. Isachsen. 2004. “The 176Lu Decay Constant Determined by Lu-Hf and U-Pb Isotope Systematics of Precambrian Mafic Intrusions.” Earth and Planetary Science Letters 219 (3–4): 311–24.
Stern, R. A., and W. Bleeker. 1998. “Age of the World’s Oldest Rocks Refined Using Canada’s SHRIMP: The Acasta Gneiss Complex, Northwest Territories, Canada.” Geoscience Canada 25 (1): 27–31.
Stewart, B. W., D. A. Papanastassiou, and G. J. Wasserburg. 1994. “Sm-Nd Chronology and Petrogenesis of Mesosiderites.” Geochimica et Cosmochimica Acta 58 (16): 3487–509.
Tatsumoto, M., R. J. Knight, and C. J. Allègre. 1973. “Time Differences in the Formation of Meteorites as Determined from the Ratio of Lead-207 to Lead-206.” Science 180 (4092): 1279–83.
Tatsumoto, M., D. M. Unruh, and G. A. Desborough. 1976. “U-Th-Pb and Rb-Sr Systematics of Allende and U-Th-Pb Systematics of Orgueil.” Geochimica et Cosmochimica Acta 40 (6): 617–34.
Tatsumoto, M., D. M. Unruh, and P. J. Patchett. 1981. “U-Pb and Lu-Hf Systematics of Antarctic Meteorites.” Proceedings of the Sixth Symposium on Antarctic Meteorites. Edited by T. Nagata, 237–49. Tokyo, Japan: National Institute of Polar Research.
Tera, F., and R. W. Carlson. 1999. “Assessment of the Pb-Pb and U-Pb Chronometry of the Early Solar System.” Geochimica et Cosmochimica Acta 63 (11–12): 1877–89.
Tera, F., R. W. Carlson, and N. Z. Boctor. 1997. “Radiometric Ages of Basaltic Achondrites and Their Relation to the Early History of the Solar System.” Geochimica et Cosmochimica Acta 61 (8): 1713–31.
Tilton, G. R. 1973. “Isotopic Lead Ages of Chondritic Meteorites.” Earth and Planetary Science Letters 19 (3): 321–29.
Trinquier, A., J.-L. Birck, C. J. Allègre, C. Göpel, and D. Ulfbeck. 2008. “53Mn–53Cr Systematics of the Early Solar System Revisited.” Geochimica et Cosmochimica Acta 72 (20): 5146–63.
Tyler, D. J. 1990. “The tectonically-controlled rock cycle.” In Proceedings of the Second International Conference on Creationism. Edited by R. E. Walsh and C. L Brooks, vol. 2, 293–301. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Unruh, D. M. 1982. “The U-Th-Pb Age of Equilibrated L Chondrites and a Solution to the Excess Radiogenic Pb Problem in Chondrites.” Earth and Planetary Science Letters 58 (1): 75–94.
Unruh, D. M., R. Hutchinson, and M. Tatsumoto. 1979. “U-Th-Pb Systematics and Uranium Isotopic Composition of Chondrites.” Lunar and Planetary Science Conference 10: 1256–58.
Unruh, D. M., and M. Tatsumoto. 1980. “Excess Pb in L-chondrites: Is It Terrestrial?” Lunar and Planetary Science Conference 11: 1184–86.
Valley, J. W., A. J. Cavosie, T. Ushikubo, D. A. Reinhard, D. F. Lawrence, D. J. Larson, P. H. Clifton, et al. 2014. “Hadean Age for a Post-Magma-Ocean Zircon Confirmed by Atom-Probe Tomography.” Nature Geoscience 7 (3): 219–23.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. El Cajon, California: Institute for Creation Research, and Chino Valley, Arizona: Creation Research Society. http://www.icr.org/rate2/.
Walker, R. J., and J. W. Morgan. 1989. “Rhenium-Osmium Isotope Systematics of Carbonaceous Chondrites.” Science 243 (4890): 519–22.
Wasserburg, G. J., F. Tera, D. A. Papanastassiou, and J. C. Huneke. 1977. “Isotopic and Chemical Investigations on Angra dos Reis.” Earth and Planetary Science Letters 35 (2): 294–316.
Weisberg, M. K., T. J. McCoy, and A. N. Krot. 2006. “Systematics and Evaluation of Meteorite Classification.” In Meteorites and the Early Solar System II. Edited by D. S. Lauretta and H. Y. McSween, 19–52. Tucson, Arizona: University of Arizona Press.
Wetherill, G. W. 1975. “Radiometric Chronology of the Early Solar System.” Annual Review of Nuclear Science 25: 283–328. Wilde, S. A., J. W. Valley, W. H. Peck, and C. M. Graham. 2001. “Evidence from Detrital Zircons for the Existence of Continental Crust and Oceans on the Earth 4.4 Gyr Ago.” Nature 409 (6817): 175–78.
Wooden, J. L., H. Takeda, L. E. Nyquist, H. Wiesmann, and B. Bansal. 1983. “A Sr and Nd Isotopic Study of Five Yamato Polymict Eucrites and a Comparison to Other Antarctic and Ordinary Eucrites.” Memoirs of the National Institute of Polar Research, Special Issue no. 30: 315–22.
Zhou, Q., Q.-Z. Yin, E. D. Young, X.-H. Li, F.-Y. Wu, Q.-L. Li, Y. Liu, and G.-Q. Tang. 2013. “SIMS Pb-Pb and U-Pb Age Determination of Eucrite Zircons at <5 μm Scale and the First 50 Ma of the Thermal History of Vesta.” Geochimica et Cosmochimica Acta 110: 152–75.













