Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Meteorites date the earth with a 4.55 ± 0.07 Ga Pb-Pb isochron called the geochron. They appear to consistently yield 4.55-4.57 Ga radioisotope ages, adding to the uniformitarians’ confidence in the radioisotope dating methods. About 82% of all meteorite falls are chondrites, stony meteorites containing chondrules. Nearly 94% of chondrites are ordinary (O) chondrites, which are subdivided into H, L, and LL chondrites based on their iron contents. Enstatite (E) chondrites comprise only 1.4% of the chondrites. Many radioisotope dating studies in the last 45 years have used the K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, U-Th-Pb, Re-Os, U-Th/He, Mn-Cr, Hf-W, and I-Xe methods to yield an abundance of isochron and model ages for these meteorites from whole-rock samples, and mineral and other fractions. Such age data for fifteen O and E chondrites were tabulated and plotted on frequency versus age histogram diagrams. They generally cluster, strongly in some of these chondrites, at 4.55–4.57 Ga, dominated by Pb-Pb and U-Pb isochron and model ages, testimony to that technique’s supremacy as the uniformitarians’ ultimate, most reliable dating tool. These ages are confirmed by Ar-Ar, Rb-Sr, Re-Os, and Sm-Nd isochron ages, but there is also scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar model ages, in some cases possibly due to thermal disturbance. No pattern was found in these meteorites’ isochron ages similar to the systematic patterns of isochron ages found in Precambrian rock units during the RATE project, so there is no evidence of past accelerated radioisotope decay having occurred in these chondrites. This is not as expected, because if accelerated radioisotope decay did occur on the earth, then it could be argued every atom in the universe would be similarly affected at the same time. Otherwise, asteroids and the meteorites derived from them are regarded as “primordial material” left over from the formation of the solar system, which is compatible with the Hebrew text of Genesis that could suggest God made “primordial material” on Day One of the Creation Week, from which He made the non-earth portion of the solar system on Day Four. Thus today’s measured radioisotope compositions of these O and E chondrites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes. So if some of the daughter isotopes were already in these O and E chondrites when they were formed, then the 4.55-4.57 Ga “ages” for the Richardton (H5), St. Marguerite (H4), Bardwell (L5), Bjurbole (L4), and St. Séverin (LL6) ordinary chondrite meteorites obtained by Pb-Pb and U-Pb isochron and model age dating are likely not their true real-time ages, which according to the biblical paradigm is only about 6,000 real-time years. The results of further studies of more radioisotope ages data for many more other meteorites should further elucidate these interim suggestions.
Keywords: meteorites, classification, ordinary (O) chondrites, H chondrites, L and LL chondrites, enstatite (E) chondrites, radioisotope dating, Allegan, Forest Vale, Guarena, Richardton, St. Marguerite, Barwell, Bjurbole, Bruderheim, Olivenza, St. Séverin, Abee, Hvittis, Indarch, St. Marks, St. Sauveur, K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, U-Th-Pb, U-Th/He, Re-Os, Mn-Cr, Hf-W, I-Xe, isochron ages, model ages, discordant radioisotope ages, accelerated radioactive decay, asteroids, “primordial material,” geochemical signature, inheritance and mixing
Introduction
Ever since 1956 when Claire Patterson at the California Institute of Technology in Pasadena reported a Pb-Pb isochron age of 4.55 ± 0.07 Ga for three stony and two iron meteorites, this has been declared the age of the earth (Patterson 1956). Furthermore, many meteorites appear to have consistently dated around the same “age” (Dalrymple 1991, 2004), bolstering the evolutionary community’s confidence that they have successfully dated the age of the earth and the solar system at around 4.57 Ga. It has also strengthened their case for the supposed reliability of the increasingly sophisticated radioisotope dating methods.
Creationists have commented little on the radioisotope dating of meteorites, apart from acknowledging the use of Patterson’s geochron to establish the age of the earth, and that many meteorites give a similar old age. Morris (2007) did focus on the Allende carbonaceous chondrite as an example of a well-studied meteorite analysed by many radioisotope dating methods, but he only discussed the radioisotope dating results from one, older (1976) paper. Furthermore, he only focused on the U-Th-Pb model ages published in that paper, apparently ignoring the excellent Pb-Pb isochron age of 4.553 ± 0.004 Ga based on some twenty isotopic analyses of the matrix, magnetic separates, aggregates and chondrules reported in that same paper, as well as the U-Pb concordia isochron age of 4.548 ± 0.025 Ga based on those same samples.
In order to rectify this lack of engagement by the creationist community with the meteorite radioisotope dating data, Snelling (2014) obtained as much radioisotope dating data as possible for the Allende CV3 carbonaceous chondrite meteorite (due to its claimed status as the most studied meteorite), displayed the data, and attempted to analyse it. He found that both isochron and model ages for the total rock, separated components, or combinations of these strongly clustered around a Pb-Pb age of 4.56–4.57 Ga. However, while he then sought to discuss the possible significance of this clustering in terms of various potential creationist models for the history of radioisotopes and their decay, drawing firm conclusions from the radioisotope dating data for just this one meteorite was premature. This present contribution is therefore designed to document the radioisotope dating data for more meteorites, the ordinary and enstatite chondrites, so as to continue the discussion of the significance of these data.
The Classification of Meteorites
Meteorites have been classified into distinct groups and subgroups that show similar chemical, isotopic, mineral, and physical relationships. Within the evolutionary community the ultimate goal of such a classification scheme is to group all known specimens that apparently share a common origin on a single, identifiable parent body, or even a body yet to be identified. This could be another planet, moon, asteroid, or other current solar system object, or one that is believed to have existed in the past (for example, a shattered asteroid). However, several meteorite groups classified this way appear to have come from a single, heterogeneous parent body, or even a single group may contain members that may have come from a variety of similar but distinct parent bodies. So any meteorite classification system is not absolute, and is only as valid as the criteria used to develop it.
More than 24,000 meteorites are currently catalogued (Norton 2002), and this number is rapidly growing due to the ongoing discovery of large concentrations of meteorites in the world’s cold and hot deserts (for example, in Antarctica, and Australia and Africa, respectively). Traditionally meteorites have been divided into three overall categories based on whether they are dominantly composed of rocky materials (stones or stony meteorites), metallic material (irons or iron meteorites), or mixtures (stony-irons or stony-iron meteorites). These categories have been in use since at least the early nineteenth century, but they are merely descriptive and do not have any genetic connotations. In reality, the term “stony-iron” is a misnomer, as the meteorites in one group (the CB chondrites) have over 50% metal by volume and were called stony-irons until their affinities with chondrites were recognized. Similarly, some iron meteorites also contain many silicate inclusions but are rarely described as stony-irons.
Nevertheless, these three categories are still part of the most widely used meteorite classification system. Stony meteorites are traditionally divided into two other categories—chondrites (meteorites that are characterized by containing chondrules and which apparently have undergone little change since their parent bodies originally formed), and achondrites (meteorites that appear to have had a complex origin involving asteroidal or planetary differentiation). Iron meteorites were traditionally divided into objects with similar internal structures (octahedrites, hexahedrites, and ataxites), but these terms are now only used for descriptive purposes and have given way to chemical group names. Stony-iron meteorites have always been divided into pallasites (which now comprise several distinct groups) and mesosiderites (a textural term which is also synonymous with the name of a modern group).
Based on their bulk compositions and textures, meteorites have been more recently divided by Krot et al. (2005) into two major categories—chondrites and non-chondritic meteorites. They also further subdivided the non-chondritic meteorites into the primitive achondrites and igneously differentiated meteorites, the latter including the achondrites, stony-irons (pallasites and mesosiderites), and the irons. Within all these categories the meteorites are grouped on the basis of their oxygen isotopes, chemistry, mineralogy, and petrography.
Weisberg, McCoy and Krot (2006) made only minor changes to this classification scheme, which is illustrated in Fig. 1. Note that the three main categories have now been reduced just to chondrites, primitive achondrites and achondrites, the main change being to simply rename the igneously differentiated meteorites the achondrites. As in Krot et al.’s (2005) classification scheme, the IAB and IIICD irons are included in the primitive achondrites because of their silicate inclusions, while the rest of the groups of irons, the stony-irons, the martian and lunar meteorites are included with the other achondrite groups in the achondrites.
The Chondrites
About 82% of all meteorite falls are chondrites (Norton 2002). As already noted, the chondrites derive their name from their interior texture, which is unlike any found in terrestrial rocks. Dispersed more or less uniformly throughout these meteorites are spherical, sub-spherical and sometimes ellipsoidal structures called chondrules. These range in size from about 0.1 to 4 mm (0,0039 to 0,15 in) diameter, with a few reaching centimeter size. Their abundance within a given chondrite can vary enormously from only a few per cent of the total volume of the meteorite to as much as 70%, with fine-grained matrix material dispersed between the chondrules. Most chondrules are rich in the silicate minerals olivine and pyroxene. The other major components of chondrites are refractory inclusions—Ca-Al-rich inclusions (CAIs) and amoeboid olivine aggregates (AOAs)—and Fe-Ni metal alloys and sulfides (Brearley and Jones 1998; Scott and Krot 2005; Snelling 2014).
The chondrites have been subdivided into three classes—carbonaceous (C), ordinary (O), and enstatite (E) chondrites—and fifteen groups, including the rare R and K chondrites (fig. 1). The carbonaceous (C) chondrites, representing almost 4% of all chondrites, are so named because their matrix is carbon-rich, containing various amounts of carbon in the form of carbonates and complex organic compounds including amino acids (Cronin, Pizzarello, and Cruikshank 1988). Further classification involves typing according to where the first meteorite or prototype in the category was found and whose characteristics are used to define the group—for example, CI where I denotes Ivuna, a town in Tanzania, CM where M stands for Mighei in Ukraine, CV where V designates Vigarano in Italy, CO where the O stands for the town of Ornans in France, CR where R denotes Renazzo in Italy, and CK where K designates Karoonda, a town in South Australia (Krot et al. 2009; Norton 2002).
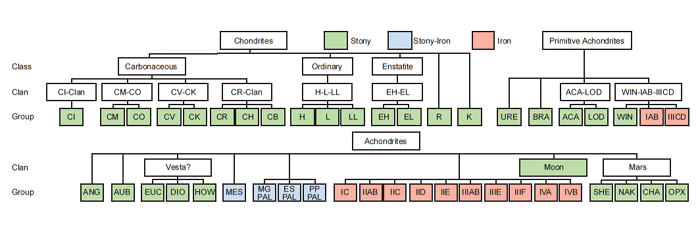
Fig. 1. The classification system for meteorites (after Weisberg, McCoy, and Krot 2006). Click image for larger view.
Ordinary (O) chondrites are by far the most common type of meteorite to fall to earth. About 77% of all meteorites and nearly 94% of chondrites are ordinary chondrites. They have been divided into three groups—H, L and LL chondrites—the letters designating their different bulk iron contents and different amounts of metal (Krot et al. 2005; Norton 2002):
- H chondrites have High total iron contents and high metallic Fe (15–20% Fe-Ni alloys by mass) and smaller chondrules than L and LL chondrites. About 42% of ordinary chondrite falls belong to this group.
- L chondrites have Low total iron contents (including 7–11% Fe-Ni alloys by mass). About 46% of ordinary chondrite falls belong to this group, which makes them the most common type of meteorite to fall to earth.
- LL chondrites have Low total iron and Low metal contents (3–5% Fe-Ni alloys by mass, of which 2% is metallic Fe). About 10–12% of ordinary chondrite falls belong to this group.
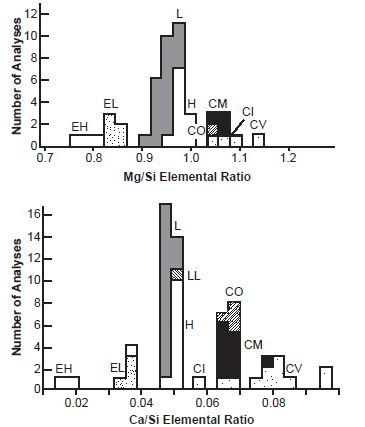
Fig. 2. Two histograms showing the Mg/Si and Ca/Si compositions of chondrites (after Norton 2002; Von Michaelis, Ahrens, and Willis 1969; Van Schmus and Hayes 1974). These atomic ratios differ significantly so that three divisions or classes of chondrites are evident—the enstatite (E) chondrites, ordinary (O) chondrites, and carbonaceous (C) chondrites. The data even allows each class to be resolved into groups—enstatite chondrites into EH and EL; ordinary chondrites into H, L, and LL; and carbonaceous chondrites into CI, CM, CV, and CO.
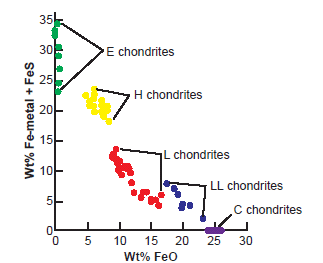
Fig. 3. Plot of the weight percent oxidized iron (in minerals) versus the weight percent iron metal plus FeS (unoxidized iron) in chondrites observed to fall and recovered shortly thereafter (after Mason 1962). A clear division of the three classes of chondrites is obvious, along with the three groups in the ordinary chondrites—H, L, and LL.
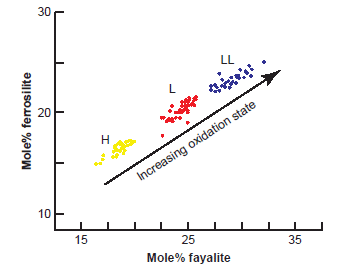
Fig. 4. Plot of the fayalite (Fa) content of olivine versus the ferrosilite (Fs) content of orthopyroxene in equilibrated ordinary chondrites clearly reveals the existence of the three oxidation groups—H, L, and LL (after Keil and Fredriksson 1964; Norton 2002).
The E chondrites comprise only 1.4% of the chondrites, and are obviously named after their primary silicate mineral, enstatite. Enstatite is the Mg-rich end member of the orthopyroxene solid-solution series and makes up 60–80 vol. % of these meteorites (Krot et al. 2009; Norton 2002). E chondrites contain more metal phases than any other stony meteorite class, with total iron contents varying between 22 and 33 wt %. Virtually all of their iron is in metal phases (13–28 vol. %) or as sulfides (5–17 vol. %). So like the ordinary (O) chondrites, the E chondrites are divided into two groups, EH and EL, according to whether they have relatively High or Low total iron and metal contents. EH chondrites average about 30 vol. % total iron of which about 5 vol. % is sulfides, whereas EL chondrites have about 25 vol. % total iron with 3.5 vol. % sulfides.
Of all the meteorites, the chondrites show the greatest similarities in composition, so there are only subtle chemical differences between them. The lithophile elements (those with a strong affinity for oxygen that tend to concentrate in silicate phases) Mg and Ca show the most distinct divisions among the chondrites. Fig. 2 provides histogram plots of Mg/Si and Ca/Si abundances in the chondrite groups (Von Michaelis, Ahrens, and Willis 1969; Van Schmus and Hayes 1974), and shows an obvious distinction between the chondrite groups. The E chondrites exhibit the lowest element/Si ratios, while the C chondrites cluster among the highest ratios, and the ordinary chondrites fall in a tight cluster between the two.
An even more striking distinction among the chondrites is evident when oxidized Fe is plotted against Fe in the metal phase and FeS (Mason 1962). Fig. 3 shows a clear distinction between the three classes of chondrites. The E chondrites form a tight cluster exhibiting little oxidation, while the C chondrites display the greatest oxidation of their Fe. Again, the O chondrites fall in between, with separate clusters for each of their constituent H, L and LL groups reflecting their respective Fe metal contents, the H chondrites having the highest Fe metal content.
The O chondrites can thus also be classified according to their range of FeO/(FeO + MgO) molecular percentages in their two most common ferromagnesian minerals, olivine and pyroxene. For meteorites in general the fayalite (Fe2SiO4) composition of olivine most commonly lies between 15 and 30% (Fa15-30), with the olivine in a typical O chondrite in the H group having an Fa18 composition. Like olivine, the orthopyroxene composition in meteorites is measured as the mole percent of the Fe-bearing end member, ferrosilite (FeSiO3). A typical pyroxene composition for an L group O chondrite would be Fs22.
The enstatite and three groups of ordinary chondrites are distinguished by their total iron content, both oxidized iron (combined in minerals) and metal (unoxidized iron), with the normal variations found in the metal phase, total iron, fayalite (in olivine) and ferrosilite (in pyroxene) contents listed in Table 1. The H, L, and LL designations are as defined above, and are applied to both the O and E chondrites. From these data in Table 1 it is evident that the more oxidized iron in minerals such as fayalite and ferrosilite, the less unoxidized iron there is as metal in the bulk composition of these chondrite meteorites. Furthermore, as the oxidized iron increases in minerals so their oxygen content also increases. So if the mole percent fayalite (Fa) in the olivine and the mole percent ferrosilite (Fs) in the pyroxene are plotted against each other the three ordinary chondrite groups are clearly distinguished, because the H chondrites are the least oxidized and the LL chondrites are the most oxidized of the ordinary chondrites (fig. 4).
The classification of chondrites based on chemical and mineralogical criteria is considered a primary classification because the bulk chemistry of meteorites is a primary characteristic. However, meteorites within a particular chemical group, such as the three groups within the ordinary (O) chondrite class, have remarkably similar bulk compositions, but under a hand lens and microscope there are striking petrographic differences. Thus a classification system needs to take into account these petrographic differences so that meteorites can be at least roughly classified by visual inspection. This requires secondary properties be considered, that is, properties that formed from processes which modified the original primary petrographic characteristics. Consequently, an effective classification of chondrites takes into account both their petrographic properties and their chemical differences, using the petrographic differences to subdivide and further refine the chemical groups.
Table 1. The classification of the enstatite (E) chondrites (H, L) and ordinary (O) chondrites (H, L, LL) according to their total iron content (after Norton 2002).The symbols H, L, and LL designate the chemical abundance of iron found in each, both as metal (unoxidized) and iron combined in minerals (oxidized)—H (High total iron), L (Low total iron), and LL (Low total iron and Low iron). The fayalite content of olivine and the ferrosilite content of pyroxene are both distinguishing indicators of each group.
| Class | Group | Metal (wt %) |
Total Iron (wt %) |
Fayalite (Fa mole %) |
Ferrosilite (Fs mole %) |
| Enstatite | EH & EL | 17–23 | 22–33 | 1 | 0 |
| Ordinary | H | 15–19 | 25–30 | 16–20 | 14–20 |
| L | 1–10 | 20–23 | 21–25 | 20–30 | |
| LL | 1–3 | 19–22 | 26–32 | 32–40 |
Fig. 5 is a comprehensive classification chart giving ten criteria proposed by Van Schmus and Wood (1967) that with some modification is still being used to determine the petrographic type of each chondrite group. Of the ten, most involve precise chemical and mineral analyses. However, fortunately, among the criteria (numbers 3, 4, 7, and 8) there are well-defined properties that are readily observable through microscope study of thin sections so that the petrographic type can be visually estimated with some confidence without chemical analyses. Criteria numbers 7 and 8 are discussed here because they establish the features needed to understand the classification of the petrographic types to which the remaining criteria refer.
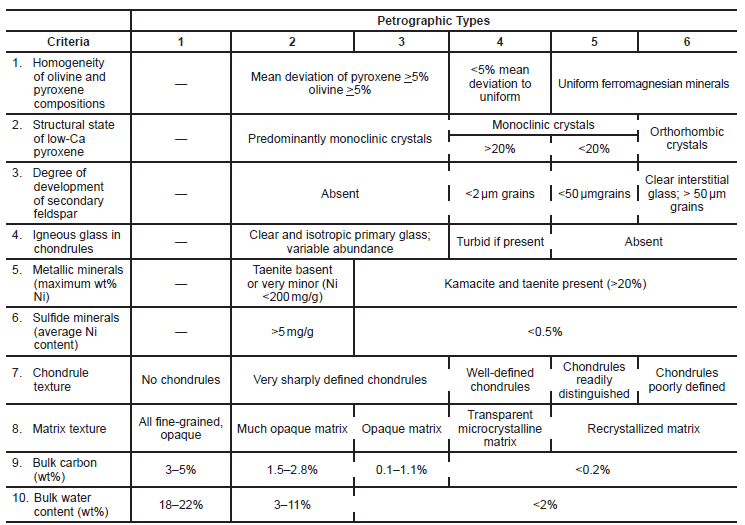
Fig. 5. Chart showing the criteria for distinguishing petrographic types in chondrites (after Brearley and Jones 1998; Norton 2002; Sears and Dodd 1988; Van Schmus and Wood 1967). The ten criteria used in this scheme as they were originally devised are displayed with the details that define each type for each criterion. The broken lines are intended to reflect the lack of sharpness of the boundaries between two petrographic types.
Of the ten criteria, the chondrule texture and density (criterion number 7) is the most easily observed. Petrographic types range from 1 to 6. In Type 1 chondrites chondrules are absent. Type 2 chondrites contain distinct chondrules but they are sparsely distributed within a matrix that constitutes nearly 50% of the meteorite by volume. Types 3–6 show progressive stages of thermal metamorphism. The chondrule boundaries became progressively indistinct as solid state recrystallization occurred. This caused alteration of the original chondrule boundaries due to intergrowth of chondrules and the matrix. This recrystallization does not represent heating to the point of fusion, but only sufficient heating to allow migration and recombination of the mineral elements into new minerals. This solid state recrystallization occurred between 400 and 950°C.
Ordinary chondrites show petrographic types from 3 to 6 (fig. 5). Often Types 5 and 6 O chondrites show brecciated textures, composed of light clasts set against a dark matrix. It is not unusual to see more than one petrographic type in these breccias. Typically the clasts show Type 5 or 6, while the matrix shows Type 3 or 4. In that case the entire petrographic range is designated Type 3–6. Matrix texture (criterion number 8) is easily observed in thin sections.
Matrix textures in Type 1 and 2 chondrites are opaque (black) and very fine-grained with scattered recognizable crystal fragments. Type 2 chondrites show small chondrules, enclosing only about 12% of the meteorites by volume. Type 3 chondrites are still unequilibrated and their matrix is still dark but chondrules are increased in number and take up 30% or more of the volume. From Type 4 to 6, increasing thermal metamorphism in ordinary chondrites produced recrystallization of the matrix in which the crystals grew from cryptocrystalline to near naked-eye visibility. This turned the matrix transparent, giving the interior of the chondrite a white appearance.
In examining the homogeneity of olivine and pyroxene compositions (criterion number 1) (fig. 5), from the textures of the ordinary chondrites it is assumed they all began in a relatively unmetamorphosed state designated Type 3. The parent chondritic body from which the meteorite came is said to have been chemically unequilibrated; that is, its mineral composition was heterogeneous, showing wide variations in chemical composition within each mineral. In particular, the two most common minerals in chondrites, olivine and pyroxene, show wide variations in their Mg/Fe compositions (table 1 and fig. 4). The minerals in unequilibrated Type 3 O chondrites were therefore not in equilibrium with their surroundings, the iron composition in olivine and orthopyroxene varying from grain to grain by more than 5%. This variation was progressively reduced through Type 4 until it reached nearly a singular composition at Type 5 where both have become more ferrous. All the olivine and orthopyroxene then have similar iron compositions. Types 5 and 6 chondrites are both homogeneous and equilibrated.
The other criteria are listed in Fig. 5 and the characteristics for each criterion are provided for each petrographic type. Most are self-evident and require thin section examinations, whereas others require mineral or bulk chemical analyses. The defining of these petrographic types adds to the classification of chondrite meteorites. The known petrographic types for the chondrite groups are summarized in Fig. 6. Thus chemical types H, L, and LL ordinary (O) chondrites can have a petrographic type between 3 and 6, labelled as H3–H6, L3–L6, and LL3–LL6, respectively. Taken together, the carbonaceous (C) chondrites vary from C1–6 and the enstatite (E) chondrites EH and EL 1–6.
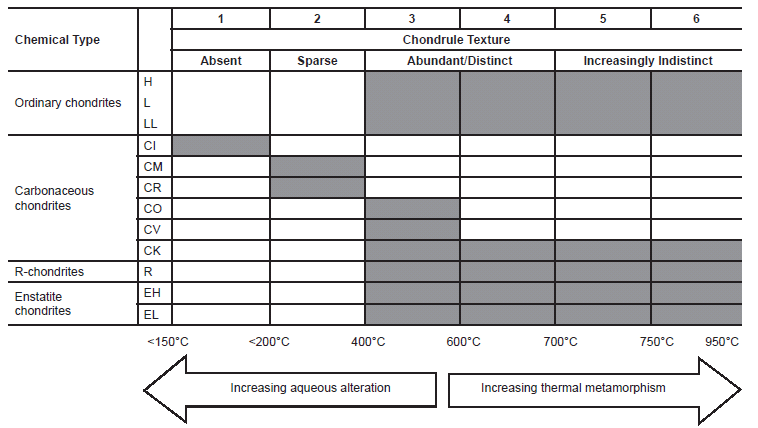
Fig. 6. Chart summarizing the grouping of all chondrites into chemical and petrographic types (after Norton 2002). The chemical types are claimed to represent different asteroid parent bodies, while the petrographic types refer to various states of thermal metamorphism or aqueous alteration occurring on or within the parent bodies. The ordinary chondrites show thermal metamorphism, while the carbonaceous chondrites can be divided into those that show aqueous alteration and those that show thermal metamorphism. The blank boxes indicate the combinations that either do not exist or have yet to be found.
However, the exceptions are the Type 3 ordinary and carbonaceous chondrites, which have been sub-typed from 3.0 to 3.9 using a different set of criteria. This was found necessary because Type 3 ordinary chondrites appear to have gone through an unusually large range of thermal metamorphism, more so than other types. Among the new criteria are thermoluminesence sensitivity (tendency to emit light or infrared energy upon heating), percent matrix recrystallization, variation of cobalt in the low nickel kamacite, variations of the fayalite in olivine, and the FeO/(FeO + MgO) ratio in the matrix.
While these details are all background information, their presentation is necessary for an understanding of the identifications and designations of the meteorites investigated in this study. It is important to establish what the different designations mean so that one can have confidence that within the groupings of the meteorites chosen for comparing their radioisotope dates the meteorites are essentially the same chemically and mineralogically. This hopefully eliminates any differences in radioisotope ages being due to chemical and/or mineralogical differences.
The Radioisotope Dating of the Ordinary and Enstatite Chondrites

Fig. 7. Hand specimen of the L4 chondrite Bjurbole (after Norton 2002). Its extreme friability makes it subject to crumbling, so that the chondrules (the high relief, ovoid shapes) frequently fall out of the surrounding matrix leaving cavities. The specimen is 5.3 cm (2 in) in the largest dimension.
To thoroughly investigate the radioisotope dating of the ordinary (O) and enstatite (E) chondrite meteorites all the relevant literature was searched. The objective was to find chondrites that have been dated by more than one radioisotope method, and a convenient place to start was Dalrymple (1991, 2004), who compiled lists of such data. Ordinary (O) chondrite meteorites that were found to have been dated multiple times by more than one radioisotope method included five H chondrites—Allegan (H5), Forest Vale (H4), Guarena (H6), Richardton (H5), and St. Marguerite (H4); three L chondrites—Bardwell (L5), Bjurbole (L4) (fig. 7), and Bruderheim (L6) (fig. 8); and two LL chondrites—Olivenza (LL5) and St. Séverin (LL6). Five E chondrite meteorites were found to have been dated multiple times by more than one radioisotope method—Abee (EH4), Hvittis (EL6), Indarch (EH4), St. Marks (EH5), and St. Sauveur (EH5). So this study focused on all fifteen of these meteorites. When papers containing radioisotope dating results for these chondrites were found, the reference lists were also scanned to find further relevant papers. In this way a comprehensive set of papers, articles and abstracts on radioisotope dating of these chondrite meteorites was collected. While it cannot be claimed that all the papers, articles and abstracts which have ever been published containing radioisotope dating results for these chondrites have thus been obtained, the cross-checking undertaken between these publications does indicate the data set obtained is very comprehensive.
All the radioisotope dating results from these papers, articles and abstracts were then compiled and tabulated. For ease of viewing and comparing the radioisotope dating data, the isochron and model ages for some or all components of each meteorite were tabulated separately—the H chondrites in Tables 2 (isochron ages) and 3 (model ages), the L chondrites (tables 4 and 5 respectively), the LL chondrites (tables 6 and 7 respectively), and the E chondrites (tables 8 and 9 respectively).

Fig. 8. Photomicrograph of a cut surface of the L6 chondrite Bruderheim, which fell in Alberta, Canada, in 1960 (after Norton 2002). The limonite (yellow-brown hydrated iron oxides) staining of the matrix around the included metallic iron-nickel grains demonstrates the effect of chemical weathering after meteorites fall to earth due to the reactions with water and atmospheric oxygen. The horizontal field of view is 35 mm (1.3 in).
The data in these tables were then plotted on frequency versus age histogram diagrams, with the same color coding being used to show the ages obtained by the different radioisotope dating methods—the isochron and model ages for some or all components of the H chondrites (figs. 9 and 10 respectively), of the L chondrites (figs. 11 and 12 respectively), of the LL chondrites (figs. 13 and 14 respectively), and of the E chondrites (figs. 15 and 16 respectively).
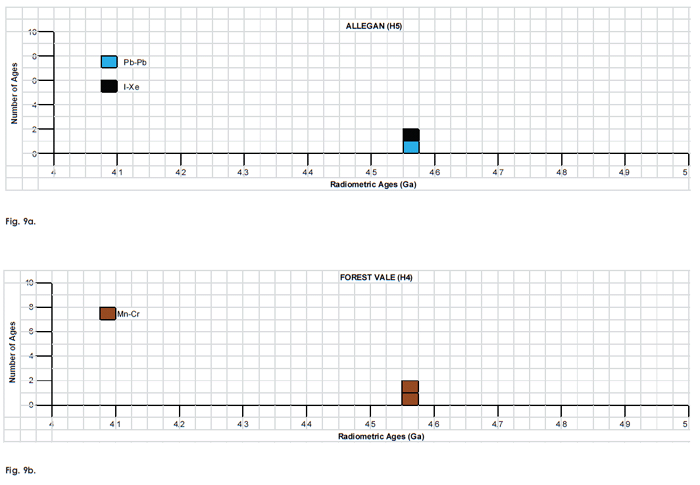
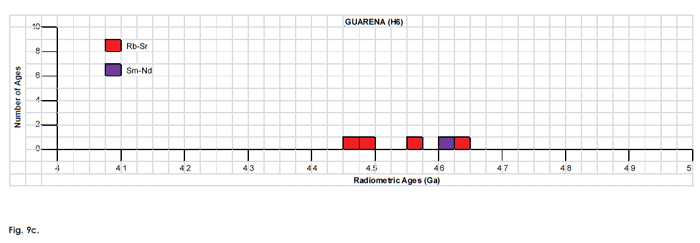
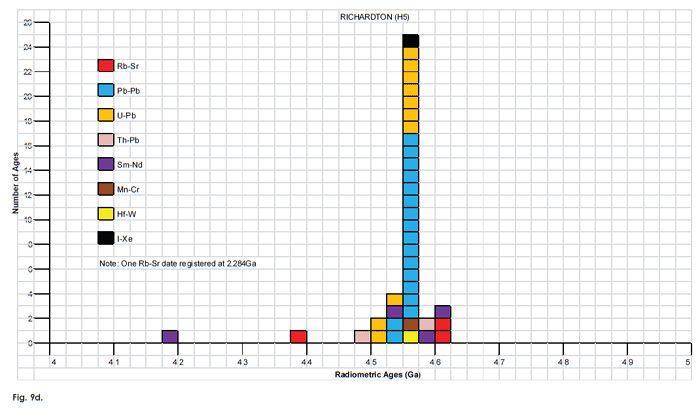
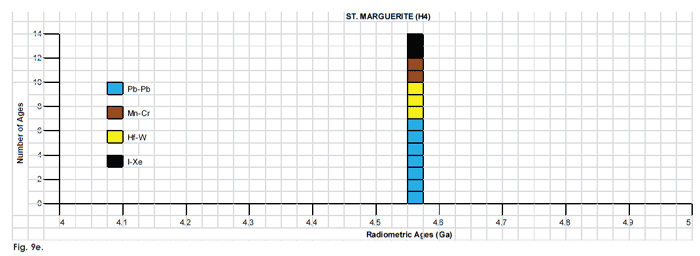
Fig. 9. Frequency versus radioisotope ages histogram diagram for the isochron ages for some or all components of the H chondrite meteorites (a) Allegan (H5), (b) Forest Vale (H4), (c) Guarena (H6), (d) Richardton (H5), and (e) St. Marguerite (H4), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.

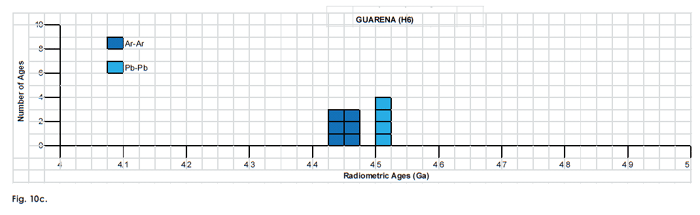
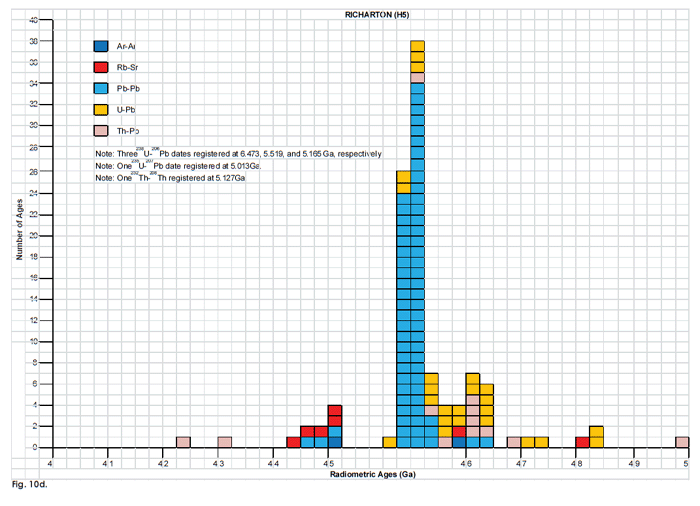
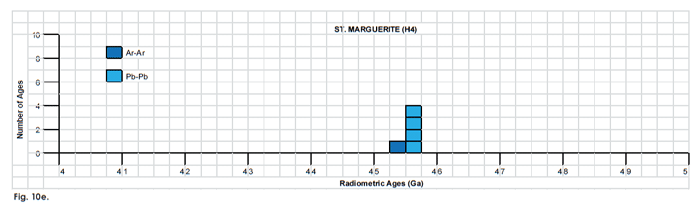
Fig. 10. Frequency versus radioisotope ages histogram diagram for the model ages for some or all components of the H chondrite meteorites (a) Allegan (H5), (b) Forest Vale (H4), (c) Guarena (H6), (d) Richardton (H5), and (e) St. Marguerite (H4), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
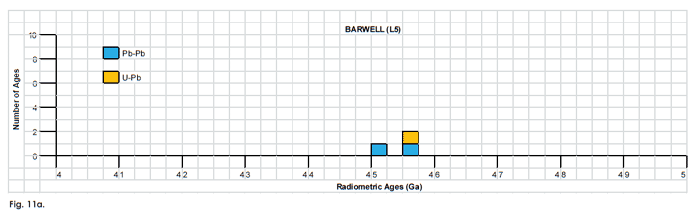
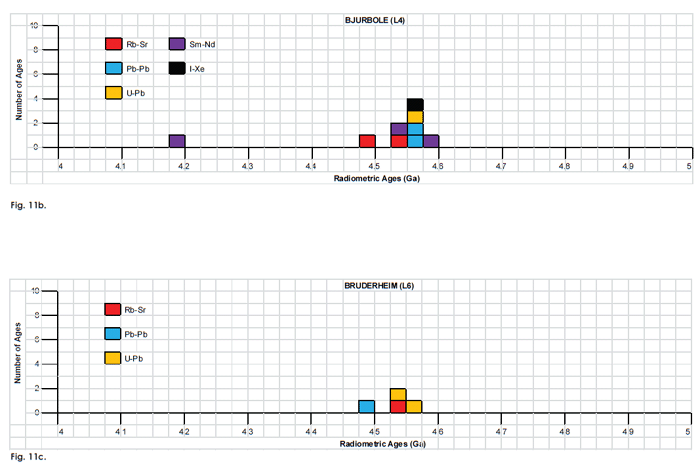
Fig. 11. Frequency versus radioisotope ages histogram diagram for the isochron ages for some or all components of the L chondrite meteorites (a) Bardwell (L5), (b) Bjurbole (L4), and (c) Bruderheim (L6), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
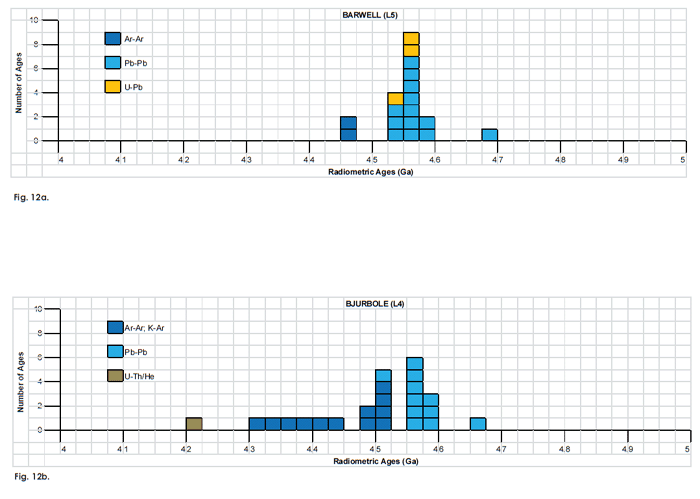
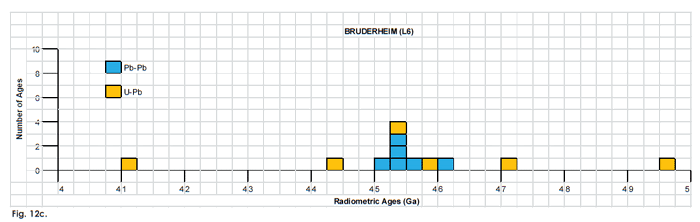
Fig. 12. Frequency versus radioisotope ages histogram diagram for the model ages for some or all components of the L chondrite meteorites (a) Bardwell (L5), (b) Bjurbole (L4), and (c) Bruderheim (L6), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
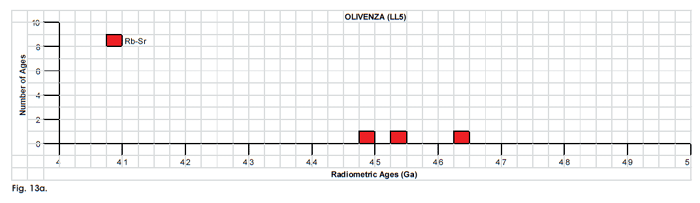
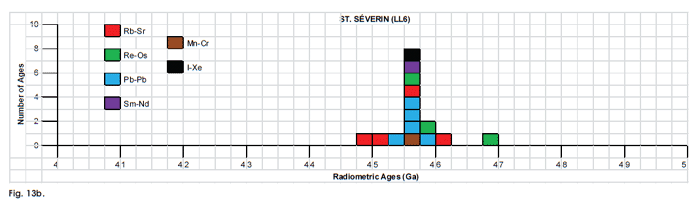
Fig. 13. Frequency versus radioisotope ages histogram diagram for the isochron ages for some or all components of the LL chondrite meteorites (a) Olivenza (LL5) and (b) St. Séverin (LL6), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
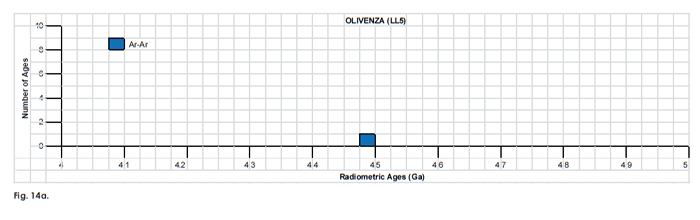
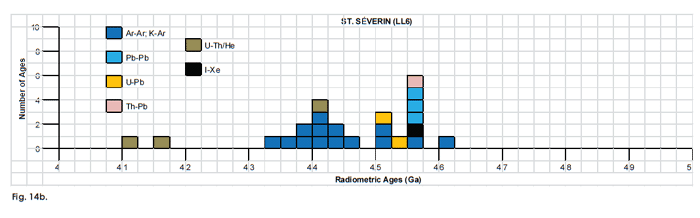
Fig. 14. Frequency versus radioisotope ages histogram diagram for the model ages for some or all components of the LL chondrite meteorites (a) Olivenza (LL5) and (b) St. Séverin (LL6), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
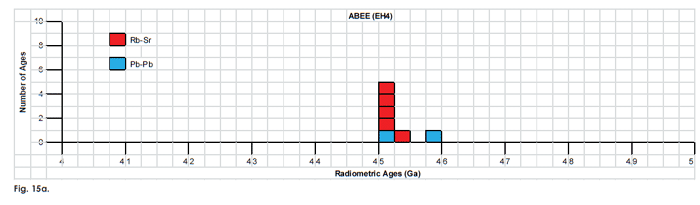
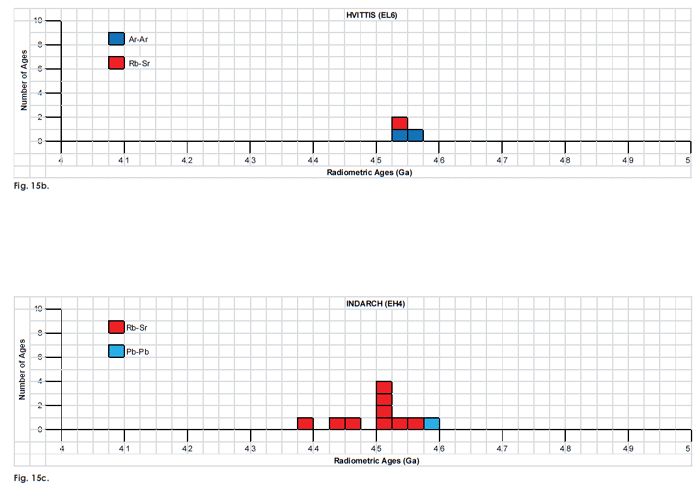
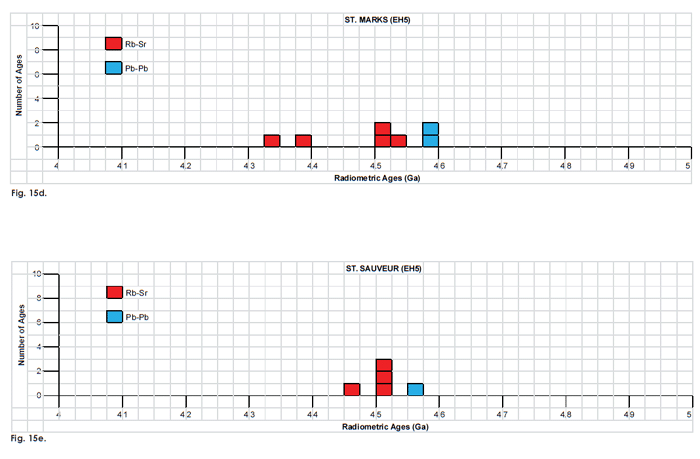
Fig. 15. Frequency versus radioisotope ages histogram diagram for the isochron ages for some or all components of the E chondrite meteorites (a) Abee (EH4), (b) Hvittis (EL6), (c) Indarch (EH4), (d) St. Marks (EH5), and (e) St. Sauveur (EH5), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
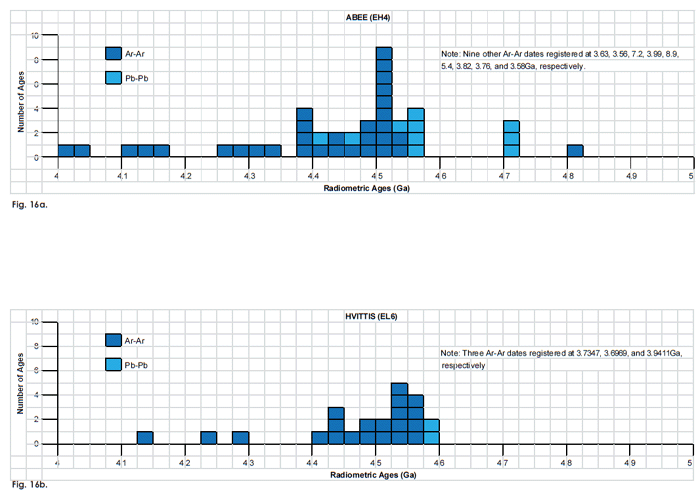
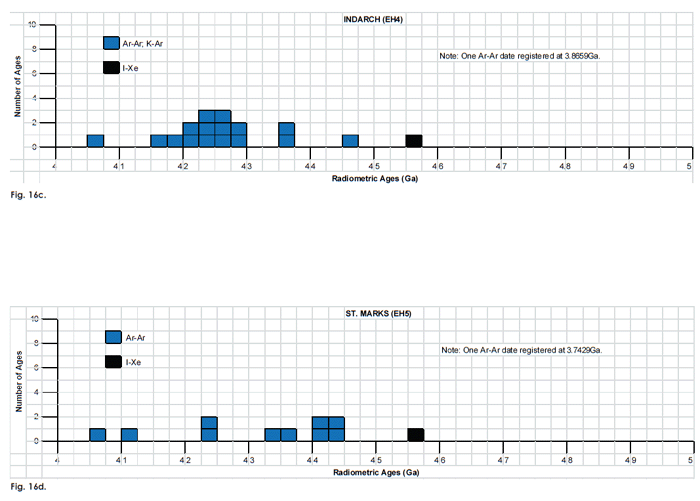
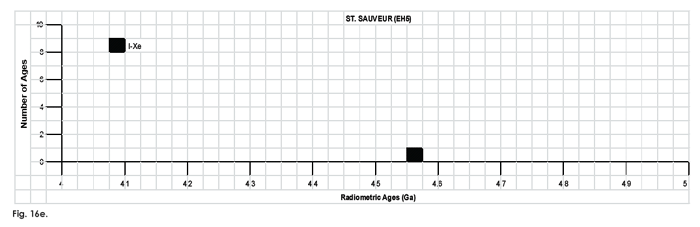
Fig. 16. Frequency versus radioisotope ages histogram diagram for the model ages for some or all components of the E chondrite meteorites (a) Abee (EH4), (b) Hvittis (EL6), (c) Indarch (EH4), (d) St. Marks (EH5), and (e) St. Sauveur (EH5), with color coding being used to show the ages obtained by the different radioisotope dating methods. Click images for larger view.
Table 2. Isochron ages for some or all components of the H chondrite meteorites Allegan (H5), Forest Vale (H4), Guarena (H6), Richardton (H5) and St. Marguerite (H4), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Allegan (H5) | ||||||
| whole rock samples plotted with five Barwell samples (1 each) from three other chondrite meteorites | 206Pb-207Pb | 4.557 | 0.008 | Unruh, Hutchison, and Tatsumoto 1982 | isochron age | |
| feldspar, temperature extractions (800–1800°C) | I-Xe | 4.573 | 0.003 | Brazzle et al. 1999 | isochron age | |
| Forest Vale (H4) | ||||||
| Mn-Cr | 4.5613 | 0.0008 | Polnau and Lugmair 2000 | isochron age | ||
| Mn-Cr | 4.5609 | 0.0008 | Polnau and Lugmair 2001 | isochron age | ||
| Guarena (H6) | ||||||
| two pyroxene samples plotted with eighteen fractions of the Olivenza chondrite | Rb-Sr | 4.63 | 0.16 | Sanz and Wasserburg 1969 | isochron age | |
| thirteen fractions plotted—whole meteorite (3), phosphate (1) and density splits (9) | Rb-Sr | 4.56 | 0.08 | Wasserburg, Papanastassiou, and Sanz 1969 | isochron age | |
| Rb-Sr | 4.46 | 0.08 | Dalrymple 2004 | isochron age | ||
| Rb-Sr | 4.48 | 0.08 | Minster, Birck, and Allègre 1982 | isochron age | ||
| one sample plotted with ten analyses from five other meteorites | Sm-Nd | 4.6 | Jacobsen and Wasserburg 1980 | isochron age | ||
| Richardton (H5) | ||||||
| seven chondrules | Rb-Sr | 4.39 | 0.03 | Evensen et al 1979 | isochron age | |
| six silicate chondrules combined with phosphates (4) | Rb-Sr | 4.611 | 0.11 | Rotenberg and Amelin 2002 | isochron age | |
| only phosphates (4) | Rb-Sr | 2.284 | 0.88 | Rotenberg and Amelin 2002 | isochron age | |
| only silicates (6) | Rb-Sr | 4.62 | 0.14 | Rotenberg and Amelin 2002 | isochron age | |
| chondrules and fragments | Pb-Pb | 4.5627 | 0.0017 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| phosphate fractions | Pb-Pb | 4.5507 | 0.0026 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| nine meteorite fragments | 207Pb-206Pb | 4.545 | 0.01 | Abranches, Arden, and Gale 1980 | isochron age | |
| six mineral fractions | 207Pb-206Pb | 4.5622 | 0.0012 | Amelin 2001 | isochron age | |
| all fractions | 204Pb/206Pb-207Pb/206Pb | 4.5512 | 0.0032 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| #2 excluded | 204Pb/206Pb-207Pb/206Pb | 4.5505 | 0.0008 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| radiogenic (206Pb-204Pb > 200) | 204Pb/206Pb-207Pb/206Pb | 4.551 | 0.001 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions plus troilite | 204Pb/206Pb-207Pb/206Pb | 4.5583 | 0.0077 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions plus primordial Pb | 204Pb/206Pb-207Pb/206Pb | 4.5546 | 0.0036 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions plus Göpel, Manhès, and Allègre 1994 analyses | 204Pb/206Pb-207Pb/206Pb | 4.5507 | 0.0026 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions | 204Pb/206Pb-207Pb/206Pb | 4.5629 | 0.0016 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions plus troilite | 204Pb/206Pb-207Pb/206Pb | 4.5621 | 0.0042 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| all fractions plus primordial Pb | 204Pb/206/Pb-207Pb/206Pb | 4.5626 | 0.0014 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| chondrules | 204Pb/206Pb-207Pb/206Pb | 4.5627 | 0.0017 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| chondrules plus troilite | 204Pb/206Pb-207Pb/206Pb | 4.5631 | 0.0007 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| chondrules plus primordial Pb | 204Pb/206Pb-207Pb/206Pb | 4.562 | 0.0008 | silicates | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| phosphates (5) | 206Pb/238U-207Pb/238U | 4.5523 | 0.0031 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| silicates (8) | 206Pb/238U-207Pb/238U | 4.5624 | 0.0022 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| nine meteorite fragments | U-Pb | 4.549 | 0.007 | Abranches, Arden, and Gale 1980 | isochron age | |
| five phosphate fractions | U-Pb | 4.551 | 0.0035 | Amelin 2000 | isochron age | |
| six mineral fractions | U-Pb | 4.5623 | 0.0013 | 3D linear regression | Amelin 2001 | isochron age |
| phosphates (5) | U-Pb | 4.5513 | 0.0029 | 3D linear regression | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| silicates (8) | U-Pb | 4.563 | 0.001 | 3D linear regression | Amelin, Ghosh, and Rotenberg 2005 | isochron age |
| phosphates (5) | 235U-207Pb | 4.538 | 0.004 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| silicates (8) | 235U-207Pb | 4.562 | 0.026 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| phosphates (5) | 232Th-208Pb | 4.486 | 0.14 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| silicates (8) | 232Th-208Pb | 4.594 | 0.15 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| four phosphate samples plotted with nine other samples of four other chondrite meteorites | Sm-Nd | 4.182 | 0.51 | Rotenberg and Amelin 2001 | isochron age | |
| twelve chondrules and phosphates plotted with twenty-two other samples with seven other meteorites | Sm-Nd | 4.588 | 0.1 | Amelin and Rotenberg 2004 | isochron age | |
| twelve chondrules and phosphates plotted with seventy-seven other samples of other chondrite meteorites | Sm-Nd | 4.547 | 0.11 | Amelin and Rotenberg 2004 | isochron age | |
| five phosphates and seven chondrule fractions | Sm-Nd | 4.624 | 0.12 | Amelin and Rotenberg 2004 | isochron age | |
| eleven fractions | Hf-W | 4.5628 | 0.001 | Kleine et al 2008 | isochron age | |
| whole rock, silicates, and chondrite fractions | Mn-Cr | 4.5563 | 0.0016 | Polnau and Lugmair 2001 | isochron age | |
| feldspar, temperature extractions (800-1800°C) | I-Xe | 4.588 | 0.002 | Brazzle et al. 1999 | isochron age | |
| St. Marguerite (H4) | ||||||
| whole rock residue—CDT | 206Pb-207Pb | 4.5624 | 0.0011 | Bouvier et al 2007 | isochron age | |
| chondrule residue—CDT | 206Pb-207Pb | 4.5655 | 0.0012 | Bouvier et al 2007 | isochron age | |
| pyroxene-olivine residue—leachate | 206Pb-207Pb | 4.5633 | 0.0011 | Bouvier et al 2007 | isochron age | |
| pyroxene-olivine residue—CDT | 206Pb-207Pb | 4.5643 | 0.0008 | Bouvier et al 2007 | isochron age | |
| chondrule—pyroxene—olivine residue | 206Pb-207Pb | 4.5617 | 0.0012 | Bouvier et al 2007 | isochron age | |
| whole rock, chondrules, phosphates, olivene leachates—ten point plotted | 207Pb-204Pb | 4.5627 | 0.0006 | Bouvier et al 2007 | isochron age | |
| Radioisotope Dating of Meteorites II: The Ordinary and Enstatite Chondrites 267 mean of a whole rock and chondrule ages of Göpel, Manhès, and Allègre (1994) and Bouvier et al (2007) | Pb-Pb | 4.5644 | 0.0034 | Kleine et al 2008 | isochron age | |
| one magnetic and three non-magnetic fractions | Hf-W | 4.5653 | 0.0006 | Kleine et al 2002 | isochron age | |
| four non-magnetic fractions and the mean of three analyses of a metal fraction | Hf-W | 4.5669 | 0.0005 | Kleine et al 2008 | isochron age | |
| internal isochron recalculated | Hf-W | 4.5665 | 0.0005 | Kleine et al 2008 | isochron age | |
| whole rock, silicate and chromite fractions | Mn-Cr | 4.5649 | 0.0007 | Polnau and Lugmair 2001 | isochron age | |
| seven fractions of minerals and chondrules | Mn-Cr | 4.5629 | 0.001 | Trinquier et al 2008 | isochron age | |
| phosphate, temperature extractions (800–1800°C) | I-Xe | 4.565 | 0.006 | Brazzle et al 1999 | isochron age | |
| feldspar, temperature extractions (800–1800°C) | I-Xe | 4.567 | 0.002 | Brazzle et al 1999 | isochron age | |
Table 3. Model ages for some or all components of the H chondrite meteorites Allegan (H5), Forest Vale (H4), Guarena (H6), Richardton (H5), and St. Marguerite (H4), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Allegan (H5) | ||||||
| whole rock (with 100%, 24 out of 26 extractions) | Ar-Ar | 4.511 | 0.011 | Trieloff et al 2003 | plateau age | |
| fragments of the meteorite | 206Pb-207Pb | 4.5477 | 0.0019 | Göpel, Manhès, and Allègre 1994 | model age | |
| fragments of the meteorite | 206Pb-207Pb | 4.5359 | 0.0019 | Göpel, Manhès, and Allègre 1994 | model age | |
| fragments of the meteorite | 206Pb-207Pb | 4.5385 | 0.0015 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphate separates | 206Pb-207Pb | 4.5502 | 0.0007 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphate separates | 206Pb-207Pb | 4.5563 | 0.0008 | Göpel, Manhès, and Allègre 1994 | model age | |
| Forest Vale (H4) whole rock (width 40%, 19 out of 42 extractions) | Ar-Ar | 4.522 | 0.008 | Trieloff et al 2003 | plateau age | |
| whole rock | Ar-Ar | 4.52 | 0.03 | Turner, Enright, and Hennessey 1978 | plateau age | |
| fragment of meteorite | 206Pb-207Pb | 4.6142 | 0.0042 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphate separate | 206Pb-207Pb | 0.0007 | Göpel, Manhès, and Allègre 1994 | model age | ||
| Guarena (H6) | ||||||
| Ar-Ar | 4.44 | 0.03 | Turner, Enright, and Hennessey 1978 | plateau age | ||
| whole rock (10/24 extractions, 80% Ar) | Ar-Ar | 4.445 | 0.008 | Trieloff et al 2003 | plateau age | |
| feldspar separate (9/14 extractions, 90% Ar) | Ar-Ar | 4.472 | 0.013 | Trieloff et al 2003 | plateau age | |
| pyroxene separate (9/14 extractions, 80% Ar) | Ar-Ar | 4.46 | 0.013 | Trieloff et al 2003 | plateau age | |
| mean of the whole rock, feldspar and pyroxene ages | Ar-Ar | 4.454 | 0.006 | Trieloff et al 2003 | plateau age | |
| Ar-Ar | 4.44 | 0.06 | Dalrymple 2004 | plateau age | ||
| two phosphate separates | 206Pb-207Pb | 4.5044 | 0.0005 | Göpel, Manhès, and Allègre 1994 | model age | |
| two phosphate separates | 206Pb-207Pb | 4.5044 | 0.0005 | Göpel, Manhès, and Allègre 1994 | model age | |
| two phosphate separates | 206Pb-207Pb | 4.5056 | 0.0005 | Göpel, Manhès, and Allègre 1994 | model age | |
| fragment of meteorite | 206Pb-207Pb | 4.5172 | 0.0018 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphates (5) | 235U-207Pb | 4.538 | 0.004 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| silicates (8) | 235U-207Pb | 4.562 | 0.026 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| phosphates (5) | 232Th-208Pb | 4.486 | 0.14 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| silicates (8) | 232Th-208Pb | 4.594 | 0.15 | Amelin, Ghosh, and Rotenberg 2005 | isochron age | |
| Richardton (H5) | ||||||
| whole rock (width 100%, 32 out of 32 extractions) | Ar-Ar | 4.595 | 0.011 | Trieloff et al 2003 | plateau age | |
| whole rock | Ar-Ar | 4.5 | 0.03 | Turner, Enright, and Hennessey 1978 | plateau age | |
| chondrules (6) plus matrix | Rb-Sr | 4.5 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.44 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.48 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.59 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.5 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.46 | Evensen et al 1979 | model age | ||
| chondrules (6) plus matrix | Rb-Sr | 4.8 | Evensen et al 1979 | model age | ||
| mean of five phosphate fractions | Pb-Pb | 4.5539 | 0.0028 | Amelin 2000 | model age | |
| whole rock | 207Pb-206Pb | 4.633 | Tilton 1973 | model age | ||
| whole rock | 207Pb-206Pb | 4.604 | Tilton 1973 | model age | ||
| whole rock | 207Pb-206Pb | 4.478 | 0.008 | Huey and Kohman 1973 | model age | |
| whole rock | 207Pb-206Pb | 4.519 | 0.015 | Tatsumoto, Knight, and Allègre 1973 | model age | |
| phosphates | 207Pb-206Pb | 4.5514 | 0.0006 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphates | 207Pb-206Pb | 4.5534 | 0.0006 | Göpel, Manhès, and Allègre 1994 | model age | |
| plagioclase | 207Pb-206Pb | 4.5644 | 0.0064 | Amelin 2001 | model age | |
| olivine | 207Pb-206Pb | 4.5646 | 0.0037 | Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5621 | 0.0009 | Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5627 | 0.001 | Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5649 | 0.0023 | Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5623 | 0.0007 | Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.554 | 0.001 | Rotenberg and Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.555 | 0.001 | Rotenberg and Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.56 | 0.002 | Rotenberg and Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.552 | 0.001 | Rotenberg and Amelin 2001 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.572 | 0.001 | Rotenberg and Amelin 2002 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.559 | 0.003 | Rotenberg and Amelin 2002 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.562 | 0.001 | Rotenberg and Amelin 2002 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.561 | 0.001 | Rotenberg and Amelin 2002 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.563 | 0.002 | Rotenberg and Amelin 2002 | model age | |
| silicate chondrules | 207Pb-206Pb | 4.56 | 0.001 | Rotenberg and Amelin 2002 | model age | |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.554 | 0.0013 | Phosphate 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5554 | 0.0007 | Phosphate 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5531 | 0.0008 | Phosphate 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5597 | 0.0016 | Phosphate 4 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5519 | 0.0007 | Phosphate 5 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.4593 | 0.005 | Troilite | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5666 | 0.0065 | Low-density fraction 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5638 | 0.0045 | Low-density fraction 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5608 | 0.0261 | Olivine | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5621 | 0.0008 | Chondrule fragment 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5627 | 0.0008 | Chondrule fragment 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5623 | 0.0007 | Chondrule Fragment 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5626 | 0.0007 | Chondrule 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5613 | 0.0008 | Chondrule 4 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5608 | 0.001 | Chondrule 8 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Tatsumoto, Knight, and Allègre 1973 | 207Pb-206Pb | 4.5608 | 0.001 | Chondrule 8 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5574 | 0.0014 | Phosphate 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5581 | 0.0008 | Phosphate 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5566 | 0.0008 | Phosphate 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5705 | 0.0018 | Phosphate 4 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.553 | 0.0008 | Phosphate 5 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5674 | 0.0052 | Low-density fraction 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5674 | 0.0037 | Low-density fraction 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5864 | 0.0249 | Olivine | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5629 | 0.0008 | Chondrule fragment 1 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5635 | 0.0008 | Chondrule fragment 2 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5629 | 0.0007 | Chondrule Fragment 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5641 | 0.0007 | Chondrule 3 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5623 | 0.0008 | Chondrule 4 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| meteorite fractions and fragments using primodial Pb of Richardson troilite | 207Pb-206Pb | 4.5632 | 0.0011 | Chondrule 8 | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (all fractions) | 207Pb-206Pb | 4.553 | 0.0028 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (#2 excluded) | 207Pb-206Pb | 4.5533 | 0.0039 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (radiogenic [206Pb-204Pb > 200]) | 207Pb-206Pb | 4.5535 | 0.0026 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (all fractions plus Göpel, Manhès, and Allègre 1994 analyses) | 207Pb-206Pb | 4.5531 | 0.0023 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (all fractions) | 207Pb-206Pb | 4.5621 | 0.0005 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using primodial Pb (chondrules) | 207Pb-206Pb | 4.562 | 0.0007 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (all fractions) | 207Pb-206Pb | 4.5568 | 0.0053 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (#2 excluded) | 207Pb-206Pb | 4.5562 | 0.0081 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (radiogenic [206Pb-204Pb >200]) | 207Pb-206Pb | 4.556 | 0.0039 | phosphates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (all fractions plus Göpel, Manhès, and Allègre 1994 analyses) | 207Pb-206Pb | 4.556 | 0.004 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (all fractions) | 207Pb-206Pb | 4.5632 | 0.0007 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| fractions, weighted averages, corrected using Richardton troilite Pb (chondrules) | 207Pb-206Pb | 4.5631 | 0.0028 | silicates | Amelin, Ghosh, and Rotenberg 2005 | model age |
| Phosphate 1 | 206Pb-238U | 4.628 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 2 | 206Pb-238U | 4.596 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 3 | 206Pb-238U | 4.647 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 4 | 206Pb-238U | 4.845 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 5 | 206Pb-238U | 4.548 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Troilite | 206Pb-238U | 6.473 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 1 | 206Pb-238U | 5.165 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 2 | 206Pb-238U | 4.724 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Olivine | 206Pb-238U | 5.519 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 1 | 206Pb-238U | 4.576 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 2 | 206Pb-238U | 4.593 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule Fragment 3 | 206Pb-238U | 4.554 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 3 | 206Pb-238U | 4.643 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 8 | 206Pb-238U | 4.625 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 1 | 207Pb-235U | 4.577 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 2 | 207Pb-235U | 4.568 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 3 | 207Pb-235U | 4.582 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 4 | 207Pb-235U | 4.646 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 5 | 207Pb-235U | 4.551 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Troilite | 207Pb-235U | 5.013 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 1 | 207Pb-235U | 4.743 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 2 | 207Pb-235U | 4.612 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Olivine | 207Pb-235U | 4.837 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 1 | 207Pb-235U | 4.566 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 2 | 207Pb-235U | 4.572 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule Fragment 3 | 207Pb-235U | 4.56 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 3 | 207Pb-235U | 4.587 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 8 | 207Pb-235U | 4.58 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 1 | 208Pb-232Th | 4.607 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 2 | 208Pb-232Th | 4.619 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 3 | 208Pb-232Th | 4.683 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 4 | 208Pb-232Th | 4.98 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Phosphate 5 | 208Pb-232Th | 4.604 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 1 | 208Pb-232Th | 4.6 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Low-density fraction 2 | 208Pb-232Th | 4.626 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Olivine | 208Pb-232Th | 5.127 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 1 | 208Pb-232Th | 4.582 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 2 | 208Pb-232Th | 4.57 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule fragment 3 | 208Pb-232Th | 4.565 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 3 | 208Pb-232Th | 4.32 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| Chondrule 8 | 208Pb-232Th | 4.249 | Amelin, Ghosh, and Rotenberg 2005 | model age | ||
| St. Marguerite (H4) | ||||||
| whole rock (30/38 extractions, 93% Ar) | Ar-Ar | 4.532 | 0.016 | Trieloff et al 2003 | plateau age | |
| two phosphate fractions | 206Pb-207Pb | 4.563 | 0.0006 | Göpel, Manhès, and Allègre 1994 | model age | |
| two phosphate fractions | 206Pb-207Pb | 4.5627 | 0.0007 | Göpel, Manhès, and Allègre 1994 | model age | |
| two phosphate fractions | 206Pb-207Pb | 4.5627 | 0.0006 | Göpel, Manhès, and Allègre 1994 | model age | |
| fragment of meteorite | 206Pb-207Pb | 4.5667 | 0.0016 | Göpel, Manhès, and Allègre 1994 | model age | |
Table 4. Isochron ages for some or all components of the L chondrite meteorites Bardwell (L5), Bjurböle (L4), and Bruderheim (L6), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Barwell (L5) | ||||||
| two samples plotted with 16 other points from six other meteorites | 207Pb-206Pb | 4.521 | 0.01 | Unruh 1982 | isochron age | |
| two whole rocks, chondrules and troilie fractions, plus -150 mesh fraction | 207Pb-206Pb | 4.557 | 0.008 | Unruh, Hutchison, and Tatsumoto 1982 | isochron age | |
| whole rock and troilite plotted with other L chondrites | U-Pb | 4.55 | Unruh and Tatsumoto 1980 | isochron age | ||
| Bjurböle (L4) | ||||||
| two silicate fractions with seven other samples of two other L chondrites | Rb-Sr | 4.54 | 0.054 | Rotenberg and Amelin 2002 | isochron age | |
| silicate (2) and phosphate (3) fractions plotted with silicate (7) and phosphate (4) fractions of two other L chrondrites | Rb-Sr | 4.499 | 0.04 | Rotenberg and Amelin 2002 | isochron age | |
| two pyroxene fractions | Pb-Pb | 4.5542 | 0.0046 | Amelin 2001 | isochron age | |
| pyroxenes | Pb-Pb | 4.5543 | 0.0033 | Rotenberg and Amelin 2001 | isochron age | |
| triolite sample plotted with seven other L chondrites | U-Pb | 4.55 | Unruh and Tatsumoto 1980 | isochron age | ||
| three phosphate fractions plotted with ten other samples of four other chondrite meteorites | Sm-Nd | 4.182 | 0.51 | Rotenberg and Amelin 2001 | isochron age | |
| four chondrules and three phosphates plotted with 27 other samples of seven other chondrite meteorites | Sm-Nd | 4.588 | 0.1 | Amelin and Rotenberg 2004 | isochron age | |
| four chondrules and three phosphates plotted with 82 other samples of seven other chondrite meteorites | Sm-Nd | 4.547 | 0.11 | Amelin and Rotenberg 2004 | isochron age | |
| whole rock | I-Xe | 4.566 | 0.22 | Hohenberg and Kennedy 1981; Brazzle et al. 1999 | isochron age | |
| Bruderheim (L6) | ||||||
| whole rock and fractions (eight total) | Rb-Sr | 4.54 | Shima and Honda 1967 | isochron age | ||
| 15 whole rock samples | 207Pb-206Pb | 4.482 | 0.017 | Gale. Arden, and Abranches 1980 | isochron age | |
| 15 whole rock samples | U-Pb | 4.536 | 0.006 | Gale. Arden, and Abranches 1980 | isochron age | |
| triolite and whole rock plotted with seven other L-chrondrites | U-Pb | 4.55 | Unruh and Tatsumoto 1980 | isochron age | ||
Table 5. Model ages for some or all components of the L chondrite meteorites Bardwell (L5), Bjurböle (L4), and Bruderheim (L6), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Barwell (L5) | ||||||
| Ar-Ar | 4.45 | 0.06 | Turner, Enright, and Hennessey 1978 | plateau age | ||
| Ar-Ar | 4.45 | 0.03 | Turner, Enright, and Cardogan, 1979 | plateau age | ||
| whole rock sample | 207Pb-206Pb | 4.68 | Gale, Arden, and Hutchinson 1972 | model age | ||
| troilite sample | 207Pb-206Pb | 4.548 | 0.004 | Unruh and Tatsumoto 1980 | model age | |
| whole rock sample | 207Pb-206Pb | 4.561 | Unruh and Tatsumoto 1980 | model age | ||
| silicate fractions of two whole rock samples | 207Pb-206Pb | 4.549 | 0.004 | Unruh 1982 | model age | |
| silicate fractions of two whole rock samples | 207Pb-206Pb | 4.545 | 0.003 | Unruh 1982 | model age | |
| “contaminant-corrected” concordant model ages for two silicate fractions of whole-rock samples | 207Pb-206Pb | 4.56 | 0.005 | Unruh 1982 | model age | |
| 207Pb-206Pb | 4.56 | 0.005 | model age | |||
| meteorite fragments | 207Pb-206Pb | 4.5577 | 0.0018 | Göpel, Manhès, and Allègre 1994 | model age | |
| meteorite fragments | 207Pb-206Pb | 4.5522 | 0.001 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphate separates | 207Pb-206Pb | 4.5382 | 0.0007 | Göpel, Manhès, and Allègre 1994 | model age | |
| phosphate separates | 207Pb-206Pb | 4.5384 | 0.0008 | Göpel, Manhès, and Allègre 1994 | model age | |
| silicate fractions of two whole rock samples | 207Pb-208Pb | 4.583 | 0.025 | Unruh 1982 | model age | |
| “contaminant-corrected” concordant model ages for two silicate fractions of whole rock samples | 207Pb-208Pb | 4.578 | 0.025 | Unruh 1982 | model age | |
| two samples plotted with 16 other points from six other meteorites | U-Pb | 4.547 | 0.015 | Unruh 1982 | concordia age | |
| triolite-corrected data for two samples plotted with 16 other data points from six other meteorites | U-Pb | 4.551 | 0.007 | Unruh 1982 | concordia age | |
| U-Pb | 4.564 | 0.005 | Unruh 1982 | concordia age | ||
| Bjurböle (L4) | ||||||
| whole rock | K-Ar | 4.32 | Geiss and Hess 1958; Wood 1967 | model age | ||
| whole rock | K-Ar | 4.394 | 0.016 | 630°C extraction | Podosek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.369 | 0.005 | 745°C extraction | Podesek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.413 | 0.009 | 850°C extraction | Podosek & Huneke 1973b | step model age |
| whole rock | K-Ar | 4.438 | 0.015 | 935°C extraction | Podesek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.334 | 0.029 | 1040°C extraction | Podosek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.518 | 0.005 | 1125°C extraction | Podesek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.496 | 0.004 | 1195°C extraction | Podosek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.486 | 0.002 | 1370°C extraction | Podesek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.513 | 0.005 | 1515°C extraction | Podesek and Huneke 1973b | step model age |
| whole rock | K-Ar | 4.51 | high temperature | Podesek and Huneke 1973b | plateau age | |
| whole rock | Ar-Ar | 4.51 | 0.08 | Turner 1969 | plateau age | |
| triolite | 207Pb-206Pb | 4.556 | 0.01 | Unruh and Tatsumoto 1980 | model age | |
| whole rock | 207Pb-206Pb | 4.583 | Unruh and Tatsumoto 1980 | model age | ||
| whole rock | 207Pb-206Pb | 4.59 | 0.006 | Unruh 1982 | model age | |
| 207Pb-206Pb | 4.5543 | 0.0033 | Rotenberg and Amelin 2001 | model age | ||
| silicate fractions | 207Pb-206Pb | 4.556 | 0.004 | Rotenberg and Amelin 2001 | model age | |
| silicate fractions | 207Pb-206Pb | 4.552 | 0.003 | Rotenberg and Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.59 | 0.011 | Rotenberg and Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.661 | 0.011 | Rotenberg & Amelin 2001 | model age | |
| phosphate fractions | 207Pb-206Pb | 4.519 | 0.002 | Rotenberg & Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5545 | 0.0012 | Amelin 2001 | model age | |
| pyroxene | 207Pb-206Pb | 4.5546 | 0.0018 | Amelin 2001 | model age | |
| whole rock | U-Th/He | 4.2 | Eberhardt and Hess 1960; Wood 1967 | model age | ||
| Bruderheim (L6) | ||||||
| whole rock | 207Pb-206Pb | 4.53 | Gale, Arden, and Hutchinson 1972 | model age | ||
| whole rock | 207Pb-206Pb | 4.518 | 0.003 | Huey and Kohman 1973 | model age | |
| whole rock sample | 207Pb-206Pb | 4.605 | Tilton 1973 | model age | ||
| triolite | 207Pb-206Pb | 4.537 | 0.004 | Unruh and Tatsumoto 1980 | model age | |
| whole rock | 207Pb-206Pb | 4.55 | Unruh and Tatsumoto 1980 | model age | ||
| whole rock | 207Pb-206Pb | 4.535 | 0.004 | Unruh 1982 | model age | |
| whole rock sample | 206Pb-238U | 4.126 | Tilton 1973 | model age | ||
| whole rock sample | 206Pb-238U | 4.542 | Tilton 1973 | model age | ||
| whole rock sample | 206Pb-238U | 4.959 | Tilton 1973 | model age | ||
| whole rock sample | 207Pb-235U | 4.447 | Tilton 1973 | model age | ||
| whole rock sample | 207Pb-235U | 4.592 | Tilton 1973 | model age | ||
| whole rock sample | 207Pb-235U | 4.703 | Tilton 1973 | model age | ||
Table 6. Isochron ages for some or all components of the LL chondrite meteorites Olivenza (LL5) and St. Séverin (LL6), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Olivenza (LL5) | ||||||
| 18 fractions—whole rock, chondrules, pyroxene, olivene, density splits and leachates | Rb-Sr | 4.63 | 0.16 | Sanz and Wasserburg 1969 | isochron age | |
| Rb-Sr | 4.53 | 0.16 | Dalrymple 1991 | isochron age | ||
| one whole rock plotted with ten other meteorites | Rb-Sr | 4.486 | 0.02 | Minster and Allègre 1981 | isochron age | |
| St. Séverin (LL6) | ||||||
| four fractions ploted with other meteorites | Rb-Sr | 4.56 | 0.15 | These four on isochron Gopalan and Wetherill 1969 | isochron age | |
| whole rock + heavy liquid separates + whitlockite | Rb-Sr | 4.61 | 0.15 | Manhès, Minster, and Allègre 1978 | isochron age | |
| two whole rock samples with ten other meteorites | Rb-Sr | 4.486 | 0.02 | Minster and Allègre 1981 | isochron age | |
| recalculated | Rb-Sr | 4.51 | 0.15 | Minster and Allègre 1981 | isochron age | |
| one sample plotted with five iron meteorites | Re-Os | 4.58 | 0.21 | Luck, Birck, and Allègre 1980 | isochron age | |
| one sample plotted with 21 other meteorites | Re-Os | 4.55 | Luck and Allègre 1983 | isochron age | ||
| five whole rock, two metal, one FeS analyses | Re-Os | 4.68 | 0.15 | Chen, Papanastassiou, and Wasserburg 1998 | isochron age | |
| whole rock, px + ol, ap + met, 3 leachates | Pb-Pb | 4.5759 | 0.009 | Bouvier et al 2007 | isochron age | |
| phosphates | Pb-Pb | 4.5549 | 0.0002 | Bouvier et al 2007 | isochron age | |
| whole rock + plagioclase + whitlockite | 206Pb-207Pb | 4.543 | 0.019 | Manhès, Minster, and Allègre 1978 | isochron age | |
| whole rock + plagioclase + Canyon Diablo triolite | 208Pb-206Pb | 4.55 | Manhès, Minster, and Allègre 1978 | isochron age | ||
| phosphates (Manhès, Minster, and Allègre1978; Chen and Wasserburg 1981; Göpel, Manhès, and Allègre 1994) | 207Pb-204Pb | 4.558 | 0.006 | Tera and Carlson 1999 | isochron age | |
| whole rock, whitlockite, light and dark fractions | Sm-Nd | 4.55 | 0.33 | Jacobson and Wasserburg 1984 | isochron age | |
| whole rock, silicates, and chromite-spinel fractions | Mn-Cr | 4.5546 | 0.0014 | Glavin and Lugmair 2003 | isochron age | |
| feldspar, temperature extractions (800–1800°C) | I-Xe | 4.558 | 0.004 | Brazzle et al 1999 | isochron age | |
Table 7. Model ages for some or all components of the LL chondrite meteorites Olivenza (LL5) and St. Séverin (LL6), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Olivenza (LL5) | ||||||
| Ar-Ar | 4.49 | 0.06 | Turner, Enright, and Hennessey 1978 | plateau age | ||
| St. Séverin (LL6) | ||||||
| one sample | K-Ar | 4.38 | 0.06 | Funkhouser, Kirsten, and Schaeffer 1967 | model age | |
| whole rock sample | K-Ar | 4.6 | 0.05 | used Ar-Ar measurements | Podosek 1971 | plateau age |
| 14 samples from drill core | K-Ar | 4.4 | 0.45 | used Ar-Ar measurements | Schultz and Signer 1976 | plateau age |
| used as monitor, irradiated, stepwise-heating | Ar-Ar | 4.56 | 0.05 | Alexander, Davis, and Lewis 1972 | plateau age | |
| Ar-Ar | 4.5 | 0.03 | Podosek and Huneke 1973a | model age | ||
| weighted average calculated from three standards irradiated | Ar-Ar | 4.504 | 0.02 | Alexander and Davis 1974 | model age | |
| light and dark fractions | Ar-Ar | 4.383 | 0.03 | Hohenberg et al 1981 | plateau age | |
| Ar-Ar | 4.42 | 0.03 | plateau age | |||
| Ar-Ar | 4.333 | 0.03 | total age | |||
| Ar-Ar | 4.359 | 0.03 | total age | |||
| light fraction (Hohenberg et al 1981) | Ar-Ar | 4.4313 | using revised decay constants | Min, Reiners, and Shuster 2013 | plateau age | |
| Ar-Ar | 4.4053 | plateau age | ||||
| dark fraction (Hohenberg et al 1981) | Ar-Ar | 4.4688 | using revised decay constants | Min, Reiners, and Shuster 2013 | plateau age | |
| Ar-Ar | 4.4424 | plateau age | ||||
| single phosphate separate | 206Pb-207Pb | 4.5536 | 0.0007 | Göpel, Manhès, and Allègre 1994 | model age | |
| 206Pb-207Pb | 4.5571 | 0.0015 | model age | |||
| one whitlockite analysis only | 206Pb-207Pb | 4.55 | 0.01 | Manhès, Minster, and Allègre 1978 | model age | |
| one whitlockite analysis only | 208Pb-232Th | 4.57 | 0.05 | Manhès, Minster, and Allègre 1978 | model age | |
| one whitlockite analysis only | 238U-206Pb | 4.52 | 0.04 | Manhès, Minster, and Allègre 1978 | concordia age | |
| 235U-207Pb | 4.54 | 0.02 | concordia age | |||
| five phosphates (merrillite) grains | U-Th/He | 4.412 | 0.075 | weighted mean of five oldest grains out of fourteen analyzed | Min, Reiners, and Shuster 2013 | model age |
| four phosphates (merrillite) grains | U-Th/He | 4.152 | 0.07 | weighted mean of four oldest grains out of five analyzed | Min, Reiners, and Shuster 2013 | model age |
| interior whole rock sample | U-Th/He | 4.1 | 0.15 | Eugster 1988 | model age | |
| revised, anchored to ADOR | I-Xe | 4.556 | 0.04 | Glavin and Lugmair 2003 | model age | |
Table 8. Isochron ages for some or all components of the E chondrite meteorites Abee (EH4), Hvittis (EL6), Indarch (EH4), St. Marks (EH5), and St. Sauveur (EH5), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Abee (EH4) | ||||||
| whole rock and three fractions | Rb-Sr | 4.52 | Shima and Honda 1967 | isochron age | ||
| two whole rock samples plotted with 12 whole rock samples from seven other meteorites | Rb-Sr | 4.54 | 0.13 | Goplan and Wetherill 1970 | isochron age | |
| nine whole rock and density fractions | Rb-Sr | 4.51 | 0.1 | Minster, Rickard, and Allègre 1979 | isochron age | |
| one whole rock samples plotted with seven other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.516 | 0.029 | Minster, Rickard, and Allègre 1979 | isochron age | |
| one whole rock samples plotted with seven other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.508 | 0.037 | Minster, Birck, and Allègre 1982 | isochron age | |
| one whole rock sample plotted with 16 other meteorites | 207Pb-206Pb | 4.505 | 0.008 | Huey and Kohman 1973 | isochron age | |
| 10 fractions from three clasts plotted with Manhès and Allègre, 1978 analyses of four meteorites | 207Pb-206Pb | 4.578 | 0.007 | Bogard, Unruh, and Tatsumoto 1983 | isochron age | |
| Hvittis (EL6) 7–95% heating steps | Ar-Ar | 4.547 | 0.006 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| 7–95% heating steps | Ar-Ar | 4.569 | 0.008 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| one whole rock sample plotted with 13 whole rock samples from other meterorites | Rb-Sr | 4.54 | 0.13 | Gopalan and Wetherill 1970 | isochron age | |
| Indarch (EH4) three whole rock samples plotted with five other whole rock samples from three other meteorites | Rb-Sr | 4.516 | 0.029 | Minster, Rickard, and Allègre 1979 | isochron age | |
| three whole rock E-chondrite samples plotted with five other E-chondrite samples | Rb-Sr | 4.508 | 0.037 | Minster, Birck, and Allègre 1982 | isochron age | |
| updated decay constant applied to Gopalan and Wetherill 1970 | Rb-Sr | 4.46 | 0.08 | Dalrymple 1991 | isochron age | |
| updated with newer decay constant | Rb-Sr | 4.52 | 0.15 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| updated with newer decay constant | Rb-Sr | 4.449 | 0.043 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| updated with newer decay constant | Rb-Sr | 4.5 | 0.13 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| St. Marks (EH5) two whole rock samples plotted with 12 other whole rock samples of seven other meteorites | Rb-Sr | 4.54 | 0.13 | Goplan and Wetherill 1970 | isochron age | |
| three whole rock samples plotted with five other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.516 | 0.029 | Minster, Rickard,and Allègre 1979 | isochron age | |
| nine fractions of whole rock | Rb-Sr | 4.335 | 0.05 | Minster, Rickard, and Allègre 1979 | isochron age | |
| three whole rock samples plotted with five other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.508 | 0.037 | Minster, Birck, and Allègre 1982 | isochron age | |
| updated with newer decay constant | Rb-Sr | 4.391 | 0.05 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| St. Sauveur (EH5) | ||||||
| one whole rock sample plotted with seven other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.516 | 0.029 | Minster, Rickard, and Allègre 1979 | isochron age | |
| nine fractions of whole rock | Rb-Sr | 4.457 | 0.047 | Minster, Rickard, and Allègre 1979 | isochron age | |
| one whole rock sample plotted with seven other whole rock samples from three other E-chondrite meteorites | Rb-Sr | 4.508 | 0.037 | Minster et al 1982 | isochron age | |
| updated with newer decay constant | Rb-Sr | 4.514 | 0.047 | Bogard, Dixon, and Garrison 2010 | isochron age | |
| one whole rock sample plotted with three other E-chondrite meteorites | 207Pb-206Pb | 4.577 | 0.004 | Manhès and Allègre 1978 | isochron age | |
Table 9. Model ages for some or all components of the E chondrite meteorites Abee (EH4), Hvittis (EL6), Indarch (EH4), St. Marks (EH5), and St. Sauveur (EH5), with the details and literature sources.
| Sample | Method | Reading | Err +/- | Note | Source | Type |
| Abee (EH4) | ||||||
| Clast 1, 1, 04 | Ar-Ar | 4.5 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | plateau age | |
| Clast 2, 2, 05 | Ar-Ar | 4.52 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | plateau age | |
| Clast 3, 3, 06 | Ar-Ar | 4.49 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | plateau age | |
| Clast 1, 1, 04 (350°C) | Ar-Ar | 4.1 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (450°C) | Ar-Ar | 4.43 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (525°C) | Ar-Ar | 4.5 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (600°C) | Ar-Ar | 4.38 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (650°C) | Ar-Ar | 4.41 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (725°C) | Ar-Ar | 4.52 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (800°C) | Ar-Ar | 4.5 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (875°C) | Ar-Ar | 4.53 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (975°C) | Ar-Ar | 4.48 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (1090°C) | Ar-Ar | 4.39 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (1250°C) | Ar-Ar | 4.13 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (1400°C) | Ar-Ar | 3.63 | 0.06 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 04 (1500°C) | Ar-Ar | 3.56 | 0.06 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (300°C) | Ar-Ar | 7.2 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | ||
| Clast 2, 2, 05 (400°C) | Ar-Ar | 4.8 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | ||
| Clast 2, 2, 05 (500°C) | Ar-Ar | 4.33 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (600°C) | Ar-Ar | 4.5 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (675°C) | Ar-Ar | 4.52 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (750°C) | Ar-Ar | 4.52 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (800°C) | Ar-Ar | 4.54 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (900°C) | Ar-Ar | 4.5 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (1000°C) | Ar-Ar | 4.43 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (1150°C) | Ar-Ar | 4.27 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (1300°C) | Ar-Ar | 4.03 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 2, 2, 05 (1550°C) | Ar-Ar | 3.99 | 0.09 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (300°C) | Ar-Ar | 8.9 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | ||
| Clast 3, 3, 06 (400°C) | Ar-Ar | 5.4 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | ||
| Clast 3, 3, 06 (500°C) | Ar-Ar | 3.82 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (600°C) | Ar-Ar | 4.15 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (675°C) | Ar-Ar | 4.31 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (725°C) | Ar-Ar | 4.38 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (775°C) | Ar-Ar | 4.47 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (850°C) | Ar-Ar | 4.49 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (950°C) | Ar-Ar | 4.39 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (1050°C) | Ar-Ar | 4.29 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (1175°C) | Ar-Ar | 4 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (1325°C) | Ar-Ar | 3.76 | 0.02 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 3, 3, 06 (1500°C) | Ar-Ar | 3.58 | 0.09 | Bogard, Unruh, and Tatsumoto 1983 | step-heating age | |
| Clast 1, 1, 01; fraction 1, 1, I | 207Pb-208Pb | 4.56 | 0.15 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 1, 1, 01; fraction 1, 1, E1 | 207Pb-208Pb | 4.72 | 0.05 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 1, 1, 01; fraction 1, 1, E2 | 207Pb-208Pb | 4.56 | 0.1 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 1, 1, 01; fraction 1, 1, E2 (H2O-L) | 207Pb-208Pb | 4.45 | 0.07 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 2, 2, 02; fraction 2, 2, I | 207Pb-208Pb | 4.7 | 0.1 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 2, 2, 02; fraction 2, 2, E | 207Pb-208Pb | 4.54 | 0.13 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 2, 2, 02; fraction 2, 2, E (H2O-L) | 207Pb-208Pb | 4.41 | 0.03 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 3, 3, 07; fraction 3, 3, I | 207Pb-208Pb | 4.56 | 0.1 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 3, 3, 07; fraction 3, 3, E | 207Pb-208Pb | 4.7 | 0.06 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Clast 3, 3, 07; fraction 3, 3, E (H2O-L) | 207Pb-208Pb | 4.55 | 0.05 | Bogard, Unruh, and Tatsumoto 1983 | model age | |
| Hvittis (EL6) | ||||||
| clast (whole rock) | Ar-Ar | 4.47 | Kinsey et al 1995 | plateau age | ||
| Ar-Ar | 4.544 | 0.018 | Bogard, Dixon, and Garrison 2010 | plateau age | ||
| 7-95% heating steps | Ar-Ar | 4.494 | 0.046 | Bogard, Dixon, and Garrison 2010 | plateau age | |
| 250°C | Ar-Ar | 4.2276 | 0.0131 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 300°C | Ar-Ar | 3.7347 | 0.0078 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 350°C | Ar-Ar | 3.6969 | 0.0054 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 400°C | Ar-Ar | 3.9411 | 0.0057 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 475°C | Ar-Ar | 4.2912 | 0.0049 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 550°C | Ar-Ar | 4.5024 | 0.0049 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 600°C | Ar-Ar | 4.5285 | 0.0048 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 650°C | Ar-Ar | 4.5295 | 0.0047 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 700°C | Ar-Ar | 4.5457 | 0.0044 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 725°C | Ar-Ar | 4.5535 | 0.0045 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 750°C | Ar-Ar | 4.5606 | 0.0044 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 775°C | Ar-Ar | 4.56 | 0.0046 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 825°C | Ar-Ar | 4.5557 | 0.0045 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 875°C | Ar-Ar | 4.5393 | 0.0046 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 925°C | Ar-Ar | 4.5112 | 0.0046 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 975°C | Ar-Ar | 4.4783 | 0.0052 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1025°C | Ar-Ar | 4.4222 | 0.005 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1100°C | Ar-Ar | 4.4498 | 0.0045 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1200°C | Ar-Ar | 4.4444 | 0.0043 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1300°C | Ar-Ar | 4.1384 | 0.0047 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1400°C | Ar-Ar | 4.4291 | 0.0283 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| Indarch (EH4) | ||||||
| 29-83% five extractions | Ar-Ar | 4.249 | 0.013 | Bogard, Dixon, and Garrison 2010 | model (plateau) age | |
| 83–99% extractions | Ar-Ar | 4.351 | 0.008 | Bogard, Dixon, and Garrison 2010 | model (plateau) age | |
| 525°C | Ar-Ar | 3.8659 | 0.0059 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 625°C | Ar-Ar | 4.0582 | 0.005 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 700°C | Ar-Ar | 4.1812 | 0.0044 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 775°C | Ar-Ar | 4.2169 | 0.0036 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 825°C | Ar-Ar | 4.255 | 0.004 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 875°C | Ar-Ar | 4.2538 | 0.0048 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 925°C | Ar-Ar | 4.2492 | 0.0038 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 975°C | Ar-Ar | 4.2275 | 0.0038 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1075°C | Ar-Ar | 4.2525 | 0.0035 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1125°C | Ar-Ar | 4.2977 | 0.0037 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1225°C | Ar-Ar | 4.2958 | 0.0048 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1325°C | Ar-Ar | 4.3511 | 0.0073 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1450°C | Ar-Ar | 4.1725 | 0.0149 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| whole rock | K-Ar | 4.2 | 0.1 | Schaeffer and Stoenner 1965 | model age | |
| enstatite | K-Ar | 4.45 | 0.16 | Schaeffer and Stoenner 1965 | model age | |
| relative to Shallowater | I-Xe | 4.56 | Busfield, Turner, and Gilmour 2008 | model age | ||
| St. Marks (EH5) 71–91% extraction | Ar-Ar | 4.433 | 0.004 | Bogard, Dixon, and Garrison 2010 | model (maximum) age | |
| 59–71% extraction | Ar-Ar | 4.411 | 0.005 | Bogard, Dixon, and Garrison 2010 | model (maximum) age | |
| 950°C | Ar-Ar | 3.7429 | 0.0103 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1050°C | Ar-Ar | 4.0609 | 0.0051 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1125°C | Ar-Ar | 4.2363 | 0.004 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1200°C | Ar-Ar | 4.236 | 0.0058 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1275°C | Ar-Ar | 4.3382 | 0.0039 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1325°C | Ar-Ar | 4.4107 | 0.004 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1375°C | Ar-Ar | 4.4329 | 0.0031 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1450°C | Ar-Ar | 4.3504 | 0.0066 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| 1600°C | Ar-Ar | 4.1247 | 0.0666 | Bogard, Dixon, and Garrison 2010 | model (step heating) age | |
| relative to Shallowater | I-Xe | 4.56 | Busfield, Turner, and Gilmour 2008 | model age | ||
| St. Sauveur (EH5) | ||||||
| relative to Shallowater | I-Xe | 4.56 | Busfield, Turner, and Gilmour 2008 | model age | ||
Discussion
In contrast to the Allende CV3 carbonaceous chondrite meteorite (Snelling 2014), there have been fewer radioisotope methods used on these meteorites and therefore fewer radioisotope ages obtained. However, even a cursory examination of Figs. 9–16 reveals that there is still a clustering of radioisotope ages, both isochron and model ages, around 4.55–4.57 Ga. And where there are larger numbers of radioisotope ages available the clustering around 4.55–4.57 Ga is very pronounced, similar to the pattern found for Allende CV3 carbonaceous chondrite by Snelling (2014). Again this clustering is dominated by Pb-Pb isochron and model ages, and Pb-Pb calibrated Mn-Cr, Hf-W, and I-Xe ages, but it is also supported by some U-Pb, Th-Pb, Rb-Sr, Sm-Nd, Ar-Ar, and Re-Os ages. There is also much scattering of K-Ar, Ar-Ar, Rb-Sr, Sm-Nd, U-Pb, Th- Pb, Re-Os, and U-Th/He ages, though the pattern varies from meteorite to meteorite and depends on which methods were applied to them.
The H Chondrites
The Richardton (H5) meteorite has been the most radioisotope dated of the H chondrites, and the clustering of both its Pb-Pb isochron and model ages at 4.55–4.57 Ga is very strong (figs 9 and 10). St. Marguerite (H4) has only Pb-Pb isochron ages that are around 4.56–4.57 Ga. As to be expected, by definition the Mn-Cr and Hf-W isochron ages coincide with the St. Marguerite’s Pb-Pb isochron ages because they have been calibrated against the St. Marguerite meteorite’s Pb-Pb isochron and model ages (figs. 9 and 10) (Göpel, Manhès, and Allègre 1994; Polnau and Lugmair 2001; Kleine et al. 2002, 2008; Trinquier et al. 2008), and the I-Xe isochron ages similarly coincide with the Pb-Pb isochron ages (fig. 9), because they are calibrated against the I-Xe isochron age of the Shallowater achondrite, which in turn is calibrated against the Pb-Pb ages of several other meteorites (Brazzle et al. 1999; Gilmour et al. 2006, 2009). Thus the Richardton (H5) meteorite’s Mn-Cr, Hf-W, and I-Xe isochron ages also coincide with its Pb-Pb isochron ages at 4.56–4.57 Ga for the same reasons. But Richardton’s Pb-Pb isochron and model 4.56–4.57 Ga ages are both supported by U-Pb isochron and model ages and a Th-Pb model age (figs. 9 and 10). Nevertheless, there is also some scatter of U-Pb, Th-Pb, Sm-Nd, and Rb-Sr isochron ages for Richardton (H5) either side of this strong 4.56–4.57 Ga clustering, plus two outlying Rb-Sr isochron ages and one outlying Sm-Nd isochron age (table 2 and fig. 9). In contrast, there is considerable wide scatter of U-Pb, Th-Pb, Ar-Ar, and Rb-Sr model ages for Richardton (H5) (table 3 and fig. 10). And there is no real pattern to this scatter. For both isochron and model ages there are U-Pb, Th-Pb, Rb-Sr, Sm-Nd, and Ar-Ar ages respectively either side of the strong 4.56–4.57 Ga clustering, although the U-Pb isochron ages are all lower (younger) than the clustering, while the U-Pb model ages are nearly all above (older) than the clustering. Furthermore, when the U-Pb and Th-Pb model ages for the same sample fractions in the same study are compared [for example, the Amelin, Ghosh, and Rotenberg (2005) data in table 3], the U-Pb model ages are for some sample fractions older than the Th-Pb model ages, and for other sample fractions younger than the Th-Pb model ages.
The other three H chondrites in tables 2 and 3, and figs. 9 and 10, have only a few radioisotope age data for them. Allegan (H5) has one Pb-Pb 4.56 Ga isochron age, one I-Xe isochron age (which via calibration agrees with the Pb-Pb isochron age) and two Pb-Pb 4.56 Ga model ages. Forest Vale (H4) has only two Mn-Cr isochron ages that are calibrated by St. Marguerite’s Pb-Pb isochron age (Polnau and Lugmair 2000, 2001), so by definition there is agreement. In contrast, the Guarena (H6) meteorite only has one Sm-Nd isochron age which is older than 4.56–4.57 Ga, whereas the four Rb-Sr isochron ages are scattered, with one at 4.56 Ga, one above 4.56 Ga, and two below 4.50 Ga. Among the model ages for these three H chondrites, the Ar-Ar model ages are all younger than their corresponding Pb-Pb-Pb model ages (fig. 10). However, whereas one Pb-Pb model age for Forest Vale (H4) is older than the other 4.56 Ga Pb-Pb model age, all four Pb-Pb model ages for Guarena (H6) are younger than the 4.56–4.57 Ga “target,” and all six Ar-Ar model ages are much younger. This could well be related to the classification of these meteorites on a scale of increasing thermal metamorphism from H4 through to H6 (fig. 6) based on the observable and measurable criteria listed in fig. 5 (Norton 2002; Van Schmus and Wood 1967). It is thus logical that the U-Pb and K-Ar systems in the more thermally metamorphosed (to higher temperatures) Guarena (H6) meteorite have been disturbed, some of the daughter Ar gas particularly having been lost and thus resulting in younger Ar-Ar measured ages.
The L Chondrites
All three meteorites investigated have only a few isochron and model ages via only a few radioisotope dating methods (tables 4 and 5, and figs. 11 and 12). However, the clustering of the radioisotope ages is again around the 4.55–4.57 Ga mark. This “target” date was achieved by both Pb-Pb and U-Pb isochron ages for Bardwell (L5) and Bjurböle (L4), and by both Pb-Pb and U-Pb model ages for Bardwell (L5), but only by Pb-Pb model ages for Bjurböle (L4). One Rb-Sr, one I-Xe, and two Sm-Nd isochron ages also cluster around the 4.55–4.57 Ga mark for Bjurböle (L4), but one Rb-Sr isochron age is slightly younger and one Sm-Nd isochron age is very much younger. The I-Xe isochron age, though initially designated as the I-Xe standard (Hohenberg and Kennedy 1981), by definition agrees with Bjurböle’s Pb-Pb isochron age, because its I-Xe isochron age has also been calibrated against the I-Xe isochron age of the Shallowater achondrite, which in turn is calibrated against the Pb-Pb ages of several other meteorites (Brazzle et al. 1999; Gilmour et al. 2006, 2009). The other patterns are that for both Bardwell (L5) and Bjurböle (L4) the K-Ar and Ar-Ar model ages are consistently younger than the “target” age, while one Pb-Pb model age for each meteorite is well above (much older) than the 4.55–4.57 Ga cluster.
The sole U-Th/He model age for Bjurböle (L4), similar to its K-Ar and Ar-Ar model ages, is much younger than the 4.55–4.57 Ga mark (fig. 12), probably because these methods depend on daughter isotopes He and Ar that are noble (inert) gases of light atomic weights and small sizes which therefore are prone to diffusing away from their parent radioisotopes and escaping completely from the host mineral lattices. Indeed, it has been suggested that severe heating after meteorite formation may cause total loss of both gases, which results in the He and Ar ages being younger and concordant, with both clocks reset to zero at the time of the heating event after the meteorites formed (Lewis 1997). Furthermore, where U-Th/He ages are younger than K-Ar and Ar-Ar ages, as here for the Bjurböle (L4) chondrite (fig. 12), it has been suggested that even moderate heating of the meteorites would have caused He to diffuse out of the mineral grains in a time too short for major loss of the more slowly diffusing Ar.
As a more thermally metamorphosed meteorite, Bruderheim (L6) displays a slightly different pattern, consistent with disturbance of the radioisotope systems. Among the few isochron ages it is the two U-Pb and single Rb-Sr isochron ages that cluster around the 4.55–4.57 Ga mark, while the single Pb-Pb isochron age is less than 4.50 Ga (fig. 11). However, among the model ages it is the Pb-Pb model ages that cluster close to and just below the 4.55–4.57 Ga mark, while the U-Pb model ages are widely scattered both well above (older) and well below (younger), and around the 4.55–4.57 Ga mark.
The LL Chondrites
Only two LL chondrites have been radioisotope dated multiple times. For the Olivenza (LL5) meteorite only Rb-Sr isochron and Ar-Ar model ages have been obtained (figs. 13 and 14), and these are somewhat scattered with respect to the 4.55–4.57 Ga mark, with one Rb-Sr isochron age above and the other ages below. In contrast, the St. Séverin (LL6) meteorite’s age has been well constrained by one Rb-Sr, one Re-Os, three Pb-Pb, and one Sm-Nd 4.56–4.57 Ga isochron ages (fig. 13), and by three Pb-Pb, one Th-Pb, and one Ar-Ar 4.56–4.57 Ga model ages (fig. 14). These 4.56–4.57 Ga ages are also supported by Mn-Cr isochron and I-Xe isochron and model ages, as is to be expected because of these methods being calibrated against Pb-Pb isochron and model ages for other meteorites (Brazzle et al. 1999; Gilmour et al. 2006, 2009; Kleine et al. 2008; Polnau and Lugmair 2001; Trinquier et al. 2008). Again there is also scatter, with Re-Os, Rb-Sr, and Pb-Pb isochron ages above the 4.56–4.57 Ga mark, and Rb-Sr and Pb-Pb isochron ages below. In contrast, apart from one K-Ar model age above the 4.56–4.57 Ga mark (table 7), all the other K-Ar and Ar-Ar (bar one) model ages, and the U-Pb and U-Th/He model ages, are below the 4.56–4.57 Ga mark. In fact, many of the Ar-Ar, K-Ar, and U-Th/He model ages are well below the 4.56–4.57 Ga mark (table 7), with a clustering of such model ages centred around the 4.00–4.20 Ga mark. Two U-Th/He ages are lower outliers. The probable explanation for this pattern would seem to be that these methods depend on daughter isotopes that are noble (inert) gases of light atomic weights and small sizes which therefore are prone to diffusing away from their parent radioisotopes and escaping completely from the host mineral lattices, especially due to a heating event subsequent to meteorite formation (Lewis 1997). Conventionally this 4.00–4.20 Ga age clustering would be identified as the age of such a re-heating event that reset the K-Ar, Ar-Ar, and U-Th/He model ages due to the loss of Ar and He gases (Bogard 2011; Min, Reiners, and Shuster 2013; Trieloff et al. 2003).
The E Chondrites
Five E chondrites have been dated by more than one radioisotope method—four by the Rb-Sr and Pb-Pb isochron methods and one by the Ar-Ar and Rb-Sr isochron methods (fig. 15); two by the Ar-Ar and Pb-Pb model age methods, two by the K-Ar, Ar-Ar, and I-Xe model age methods, and one just by the I-Xe model age method (fig. 16). None of the methods produced results on these meteorites that clustered at the 4.56–4.57 Ga mark, except for the I-Xe model ages for Indarch (EH4), St. Marks (EH5), and St. Sauveur (EH5). These are by definition in agreement with this 4.56–4.57 age, because I-Xe ages are always calibrated against the I-Xe age of the Shallowater achondrite (Busfield, Turner, and Gilmour 2008), which in turn is calibrated against the Pb-Pb ages of several other meteorites that date at the 4.56–4.57 Ga mark (Brazzle et al. 1999; Gilmour et al. 2006, 2009). However, some individual age determinations did produce results in the 4.56–4.57 Ga range—one Ar-Ar isochron age for Hvittis (EL6), one Rb-Sr isochron age for Indarch (EH4), and one Pb-Pb isochron age for St. Sauveur (EH5) (fig.15); four Pb-Pb model ages for Abee (EH4), and four Ar-Ar model ages for Hvittis (EL6) (fig.16).
Otherwise, in general the Rb-Sr isochron ages for these meteorites are younger than the 4.56–4.57 Ga “target” age (except for the one Rb-Sr isochron age for Indarch that is in that range), and younger than or equal to all of both the Pb-Pb and Ar-Ar isochron ages, the one exception being an Abee (EH4) Pb-Pb isochron age (fig. 15). This pattern of isochron ages for these two β-decaying radioisotope systems is not consistent with that reported by the RATE project, which found that K-Ar and Ar-Ar isochron ages were always younger than Rb-Sr isochron ages (Snelling 2005; Vardiman, Snelling and Chaffin 2005). Among the model ages the Ar-Ar (and the two K-Ar) model ages are widely scattered and invariably are younger than both the 4.55–4.57 Ga target age and the Pb-Pb model ages, except for the four Hvittis (EL6) Ar-Ar ages in the 4.55–4.57 Ga range, and the four Abee (EH4) Ar-Ar model ages greater than 4.8 Ga (fig. 16). Both the K-Ar and Pb-Pb systems seem to have been affected in the Abee (EH4) meteorite, as the Pb-Pb model ages are scattered between 4.42 and 4.72 Ga (table 9), which is much less that the scatter in the Ar-Ar model ages between 3.56 and 8.9 Ga. The usual explanation for disturbance of the K-Ar (and Ar-Ar) system is a heating event sometime after formation of the meteorite’s parent body (Bogard 2011; Min, Reiners, and Shuster 2013; Trieloff et al. 2003), so that might explain this pattern in these E chondrites. The U-Pb system if usually perturbed by earth surface weathering, so perhaps the Abee (EH4) chondrite was affected by water on the earth’s surface before it was recovered for study.
Comparisons to the RATE Study
One of the issues Snelling (2014) discussed in relation to the radioisotope ages that have been obtained for the Allende CV3 carbonaceous chondrite is whether the meteorite yielded a pattern of isochron ages similar to that found for earth rocks by the 1997–2005 RATE (radioisotopes and the age of the earth) project (Vardiman, Snelling, and Chaffin 2005). The major conclusion of the RATE project was that radioisotope decay rates have not necessarily been constant throughout earth history, because there is evidence that there have been one or more episodes of accelerated rates of radioisotope decay, particularly during the Flood only about 4350 years ago (Vardiman, Snelling, and Chaffin 2005). While there were several lines of documented evidence that confirmed this conclusion, the principal evidence was different isochron ages obtained from the same samples from the same rock units by the different radioisotope dating methods (Snelling 2005; Vardiman, Snelling, and Chaffin 2005). Furthermore, there was a consistent pattern to the isochron ages from the different methods that indicated that there was an underlying systematic cause of these age differences, namely, an episode (or episodes) of accelerated radioisotope decay (Snelling 2005; Vardiman, Snelling, and Chaffin 2005). For example, it was found that the α-decaying radioisotopes U and Sm always gave older ages than the β-decaying K and Rb. And then between the β-decayers, K with the shorter half-life (more rapid decay today) and the lighter atomic weight, always yielded younger ages than the slower decaying and heavier Rb. While exactly the same pattern was not confirmed among the α-decaying U and Sm radioisotopes, both their half-lives and atomic weights were still believed to be the factors at work.
The mechanism proposed for this past episode (or episodes) of accelerated radioisotope decay was small changes to the binding forces in the nuclei of the parent radioisotopes (Vardiman, Snelling, and Chaffin 2005). These changes would thus have to have affected every atom making up the earth, and by logical extension every atom of the universe at the same time, because God appears to have created the physical laws governing the universe to operate consistently through time and space, though of course He Himself is not bound by those physical laws which He can change at any time anywhere or everywhere. Therefore, we should expect that this past episode(s) of accelerated radioisotope decay had affected the asteroids from where many meteorites have come, and that the meteorites may thus today yield the same pattern of different radioisotope ages from the different radioisotope dating methods.
Snelling (2014) found no pattern of isochron ages similar to the patterns found in the RATE study was yielded by the Allende CV3 carbonaceous chondrite, and the same is true of the isochron ages for the fifteen H, L, LL, and E chondrites reported in this study, as already discussed above. In fact, the β-decay isochron ages (Rb-Sr, Re-Os) are sometimes older than the α-decay (U, Sm) isochron ages. Furthermore, the E chondrites yielded Rb-Sr isochron ages generally younger than or equal to their Ar-Ar isochron ages (table 8 and fig. 15), when the pattern in the RATE study’s rocks was the opposite because Rb has a longer half-life and a heavier atomic weight. In contrast, the Re-Os isochron ages yielded by the St. Séverin (LL6) chondrite were greater than or equal to its Rb-Sr isochron ages (table 6 and fig. 13). While the RATE study didn’t deal with Re-Os isochron ages, this pattern is arguably somewhat predictable from the conclusions of the RATE study, because while the β-decaying Re has a slightly shorter half-life (at 42.7 billion years) than the β-decaying Rb (at 48.8 billion years), it has a heavier atomic weight (187 for Re compared to 87 for Rb) (Faure and Mensing 2005). So if the atomic weight is the dominant factor in the amount of accelerated radioisotope decay which occurred, then the Re-Os isochron ages should be older than the Rb-Sr isochron ages, though the effect of the half-lives may result in the occasional equality of their isochron ages.
Extending this argument further, if the atomic weight is the dominant factor in the amount of accelerated radioisotope decay which occurred, then among the α-decaying parent radioisotopes the Pb-Pb isochron ages should be older than the Sm-Nd isochron ages, because the parent U radioisotopes have atomic weights of 238 and 235, whereas the parent Sm radioisotope’s atomic weight is only 147. But again the heavier atomic weight U radioisotopes have shorter half-lives (at 4.47 billion years and 0.704 billion years respectively) than Sm (at 106 billion years) (Faure and Mensing 2005). So the Pb-Pb isochron ages are mostly older (or equal to) the Sm-Nd isochron age of the St Séverin (LL6) chondrite (table 6 and fig. 13), but this is not the case with the Bjurböle (L4) chondrite (table 4 and fig. 11) and the Richardton (H5) chondrite (table 2 and fig. 9), where some Sm-Nd isochron ages are older than the Pb-Pb isochron ages. So again the effect of the half-lives may result in the occasional equality or reversal in the pattern of their isochron ages.
It is therefore fairly obvious that there are no clear and consistent patterns in these meteorite isochron ages comparable to the patterns of isochron ages obtained in the RATE study. However, there is a major difference between the RATE study and these studies on meteorites, in that the RATE study investigated earth rocks that yielded isochron ages of less than 3 Ga, whereas these meteorites come from elsewhere in the solar system and generally yield 4–5 Ga ages. So the origin of these meteorites could well have a major bearing on the radioisotope ages they yield, as initially discussed by Snelling (2014).
The Origin of Meteorites from Asteroids
There is unanimity among astronomers and planetary geologists that most meteorites come from asteroids, which are primarily orbiting the Sun in the asteroid belt between Mars and Jupiter (Libourel and Corrigan 2014). There is also unanimity among conventional scientists that the asteroids represent leftover precursors to the terrestrial planets (Mercury-Mars) (Michel 2014). They postulate that about 4.56 billion years ago the early solar system consisted of a rotating disk of gas and dust, called the protoplanetary disk, revolving around the sun. Planets then supposedly formed from that disk, and different populations of small bodies, in particular the main belt asteroids between the orbits of Mars and Jupiter, survived as remnants of that era.
According to current conventional models, the asteroid belt that remained at the end of the planet-forming processes was probably very different from the current main belt, perhaps containing an earth mass or more of material in planetary embryos with masses similar to the Moon or Mars, as well as tens, hundreds, or thousands of times more bodies like the asteroid 4 Vesta and the dwarf planet 1 Ceres than are present in the main belt today (Michel 2014). Throughout its history the asteroid belt appears to have been shaped by collisional processes, such as cratering, disruption, and the generation of new asteroids as collisional fragments. The net result is that the total mass of the main asteroid belt today is only about 4% of the Moon’s mass, or less than 1/1000th of the Earth’s mass (Libourel and Corrigan 2014). So it would appear that the asteroid belt has been significantly depleted of asteroids since its early history.
Orbital resonances, when two bodies have orbital periods that are a simple integer ratio of each other, may lead to destabilization of the orbits of small bodies (Libourel and Corrigan 2014). Within the main asteroid belt, objects that have orbital periods in resonance with the orbital period of Jupiter are gradually ejected into different, random orbits, leading to the removal of asteroids from regions within the main asteroid belt that are now empty. Another important resonance is that between asteroids and Saturn, which has formed the inner boundary of the main asteroid belt, and which is responsible for delivering asteroids into planet-crossing orbits. Once asteroids become Mars-crossers they are usually ejected from the main asteroid belt due to close encounters with Mars’ gravitational field. If Mars-crossing asteroids fail to interact with Mars, then their orbital semi-major axes are gradually reduced and they become Near Earth Asteroids (NEAs).
Asteroids that are nudged by the gravitational attraction of nearby planets or have significant inclination and eccentricity may collide with other bodies traveling along different orbits (Libourel and Corrigan 2014). Even if the current impact probability appears low, collisions between asteroids are not rare, and do not appear to have been rare in the past. Depending on the relative impact velocity between the bodies and on their sizes, collisions result in 1) fragmentation of a parent asteroid into several large pieces, and/or 2) the formation of fine, micron-sized asteroidal dust. A collision between large asteroids brings into play both fragmentation and gravitation (Michel 2014). The asteroids are partially to totally shattered, and subsequent gravitational attraction between fragments leads to reaccumulation, which finally forms an entire family of large and small objects (new asteroids). Accordingly, most of the smaller asteroids are thought to be piles of rubble held together loosely by gravity (Michel and Richardson 2013; Tsuchiyama 2014). The largest asteroids, those larger than 125 km (200 mi) in diameter, however, are probably primordial objects that have never been disrupted (Asphaug 2009; Michel 2014). Asteroids are therefore currently thought to have been quite mobile within the main belt. Due to asteroid collisions and other effects, main belt asteroids migrate, passing through the orbital resonances to end up crossing the orbits of Mars, Earth, Venus, and even Mercury (Libourel and Corrigan 2014). NEAs do not have stable orbits, so they have relatively short lifetimes. Once the orbits of asteroids whose diameters exceed 100–150 m (330–490 ft) are within 7.5 million km (4.7 million mi) of the earth’s orbit, there is a greater possibility of them colliding with the earth and impacting its surface. By definition, meteors are asteroids that enter the earth’s atmosphere. Due to their high entry velocity (several kilometers per second) they are heated to high temperatures as they are slowed by the atmosphere. This produces visible paths, and the meteors are then known as fireballs or shooting stars. If the meteors survive their plunge through the atmosphere and land on the earth’s surface, they are classified as meteorites.
From these orbital and dynamical arguments, it is believed that most meteorites have indeed come from the asteroid belt and therefore are samples of asteroidal materials (Cloutis, Binzel, and Gaffey 2014; Libourel and Corrigan 2014). However, linking meteorites to their parent asteroids is a complicated issue. There is a photographic technique that has been used to get estimates of the orbital parameters (approximately) of meteors before they make contact with earth’s atmosphere. Two cameras have to have synchronized shutters and photograph the object before it makes contact with the atmosphere. This has been done for a few cases of meteors and the orbital elements suggest the objects did come from the asteroid region. So there are some cases where this has been done and then fragments of the photographed objects were found, which has established good indications of meteorites coming from asteroids. Furthermore, there have been a multitude of methods used to investigate asteroids, such as earth-based radar imaging, optical and radar polarimetry, thermal-infrared observations, reflectance spectroscopy, and thermal emission spectroscopy, but only the availability of meteorites of known provenance has enabled additional confirmation of asteroid-meteorite links. Two recent examples confirming the asteroid-meteorite link are relevant to the H, L, LL, and E chondrites in this study.
On October 6, 2008, the small, ~4 m (13 ft) wide asteroid 2008 TC3 was discovered and predicted to hit the earth within ~19 hours (Goodrich, Bischoff, and O’Brien 2014). Early morning, October 7, 2008, eyewitnesses saw the fireball that resulted when the asteroid hit the earth’s atmosphere above the Nubian Desert of northern Sudan, Africa. A few seconds later, at ~37 km (23 mi) above the earth, the asteroid was shattered in the atmosphere by dynamic ram pressures in a series of explosions into fragments. Approximately 700 cm-sized (275 in-sized) fragments were subsequently recovered and constitute what became known as the Almahata Sitta meteorite. Study of their physical, chemical, and mineralogical properties has revealed that the fragments are remarkably heterogeneous. The most abundant samples are ureilitic lithologies (see fig. 1— URE among the Primitive Achondrites) with various olivine/pyroxene ratios, mineral compositions and grain sizes (Bischoff et al. 2010; Goodrich, Bischoff, and O’Brien 2014). Among the chondritic samples, enstatite (E) chondrites are the most abundant, including both E chondrite subgroups (EL and EH), though the EL subgroup dominates, with representatives of the various petrologic types (EL3, EL4, EL5, and EL6), which are indistinguishable from previously known E chondrites. So far, several L and H group ordinary (O) chondrites have also been analysed. It has been concluded that the 2008 TC3 asteroid was not solid rock, but consisted mostly of fine-grained, highly porous matrix material, weakly cementing a small fraction of isolated, centimeter-sized fragments of denser rocks that became the fallen meteorite.
In June 2010 the Japanese spacecraft Hayabusa successfully returned to earth with fine particles collected in September 2005 from the surface of Near Earth Asteroid 25143 Itokawa (Nakamura et al. 2011; Tsuchiyama 2014). Measuring 30–180 μm (0.0011–0.007 in) in diameter, initial analyses of the mineralogy, micropetrology, and elemental and isotopic compositions of the returned regolith particles from asteroid Itokawa indicate that these dust particles are identical to thermally metamorphosed LL chondrites, particularly the LL5 and LL6 ordinary chondrites, such as Olivenza and St. Séverin (respectively) in this study.
A Biblical Perspective
Faulkner (1999) suggested that when God created the other planets and satellites on Day Four of the Creation Week He may have formed them from material He had already created in His creative act of Genesis 1:1. In further developing this proposal, Faulkner (2013) pointed out that the Hebrew word ‘āśâ meaning “to do” and “to make” is used specifically of the creation of the astronomical bodies in Genesis 1:16, rather than the Hebrew word bārā’ meaning “to create” as used in Genesis 1:1 in reference to the creation of the universe generally. Indeed, the Hebrew word bārā’ appears only with God as its agent (cf. Koehler and Baumgartner 2001, p. 153). Similarly, the Hebrew word ‘āśâ is used in Genesis 1:26 when God took already-existing material, which in Genesis 2:7 we are told was “the dust of the ground”, to make man’s body, before breathing “into his nostrils the breath of life” to make man “a living soul” (Genesis 2:7). Faulkner (2013) goes on to say:
Granted, such is not always the intended meaning, even with respect to the astronomical bodies (for example, compare Genesis 1:1 with 2 Kings 19:15; Isaiah 37:16, 66:22; Jeremiah 32:17). However, the use of ‘āśâ in the Day Four creation record apart from any contextual clues to suggest that it must bear the sense of creation out of nothing suggests that there is a distinct possibility that the making of the astronomical bodies was instead a matter of fashioning them from material previously created on Day One. Just as the description of the earth in Genesis 1:2 is of something unfinished that God returned (to) over the next several days to shape and prepare, perhaps the matter that would become the astronomical bodies was created on Day One but was shaped on Day Four. (p. 298, emphasis his)
Furthermore, as Snelling (2014) pointed out, though Jesus took already-existing water to make it into wine at the wedding feast in Cana (John 2:1–11), it was nonetheless a similar act of creation, because He was taking water molecules and adding to them carbon atoms as He instantaneously fashioned it all into the complex organic molecules of wine.
Therefore, it seems entirely possible to read Genesis 1:16 as saying God used already-existing “primordial material” which He had created out of nothing at the beginning of Day One of the Creation Week (Genesis 1:1) to then fashion it on Day Four into the other planets, their satellites and the stars. Snelling (2014) thus argued that the asteroids could similarly be regarded as Day One primordial material left over from the making of the other planets and their satellites in the solar system on Day Four. Since most meteorites are believed to have been derived from asteroids via collisions between them breaking off fragments that then hurtled towards the earth, and this asteroid-meteorite link has now been confirmed by observational examples, then this would imply the meteorites could represent samples of this same Day One “primordial material.”
Similarly, this would have to also mean that at the beginning of Day One the earth was also fashioned out of the same “primordial material.” Thus Snelling (2014) suggested that the 4.56–4.57 Ga Pb isotopic composition of the well-studied Allende CV3 carbonaceous chondrite meteorite and the bulk earth, as plotted on the age of the earth isochron known as the geochron (Patterson 1956), may represent a geochemical signature from this “primordial material” created by God “in the beginning.” The results of this study add to that possibility, since several of the well-studied meteorites reported here—Richardton (H5), St. Marguerite (H4), Bardwell (L4), Bjurböle (L5), and St. Séverin (LL6) in particular—clearly also have a 4.56–4.57 Ga Pb isotopic composition, supported by some other isotope systems. This same geochemical signature would be expected if the asteroids from which these meteorites came also represent the same Day One “primordial material” out of which the earth, the other planets, their satellites and the asteroids were all made.
This raises the obvious question about another aspect of the radioisotope dating technique, also discussed by Snelling (2014). The evidence of past accelerated radioisotope decay (non-constant radioisotope decay rates), that is, the inconsistent radioisotope age data in some Precambrian earth rocks (Vardiman, Snelling, and Chaffin 2005), would appear to negate the assumption of constant decay rates that enables the radioisotope “clocks” to be “reading” 4.56–4.57 Ga for the supposed elapsed real time since the formation of the asteroids, the meteorites derived from them, and the earth. However, another assumption necessary for these radioisotope “clocks” to work is that all the daughter isotopes were only derived by radioisotope decay from the parent isotopes. But what if God made all the isotopes at the beginning in the “primordial material,” including isotopes that subsequently also formed by radioisotope decay as daughter isotopes from parent isotopes? In other words, when God made the “primordial material” did He include in it 206Pb, 207Pb, and 208Pb atoms along with 238U, 235U, and 232Th atoms? It may be reasonable to posit that He did, given that when created the “primordial material” likely had to have some initial isotopic ratios. Even the conventional scientific community has assumed the initial material of the solar system had the “primeval” Pb isotopic ratios as measured in the troilite (iron sulfide) in the Canyon Diablo iron meteorite (Faure and Mensing 2005). So if He did, then the Pb isotopes we measure today are not all the product of radioisotope decay, due to some being created in place in the beginning, and they therefore cannot be measuring the elapsed real time since God created the earth and the universe at the beginning only about 6000 real-time years ago.
Following from this is another consideration. How many atoms of each of the Pb isotopes did God create in the “primordial material”? And if the 4.56–4.57 Ga “age” for these meteorites is a geochemical signature of the “primordial material” God created with some of each of the Pb isotopes we measure today already in it, then how many of the atoms of the measured-today Pb isotopes are due to past accelerated radioisotope decay? Is it most of them, or only some of them? So far we don’t know. What we do know is that here on the earth we don’t find rocks that still have the 4.56–4.57 Ga Pb isotopic signature in them, though most rocks that date back to the continental foundations laid down during Creation Week, the lower Precambrian rocks, still contain various large amounts of Pb isotopes in them and therefore yield an array of multi-Ga “ages”. Significantly, the earth sample that plotted on the geochron (Patterson 1956) was a modern ocean sediment sample whose Pb isotopic signature had been acquired by mixing and integration from many earth rocks over much of the time of the earth’s history. This may point to a possible third additional process responsible for the Pb isotopic compositions in earth rocks, namely, inheritance of the primordial geochemical signature and then mixing of it with the isotopes generated by subsequent radioactive decay in the earth’s mantle and crust since the creation of the original earth on Day One of the Creation Week. This has been previously proposed by Snelling (2000, 2005) as primarily occurring during the catastrophic geologic processes of the Day Three Upheaval when the dry land was formed, and then again during the Flood (Snelling 2009). And as part of this mixing process the primordial geochemical signature could also have been diluted by the addition of parent isotope atoms, thus making the resultant rocks appear to progressively “date” younger.
As Snelling (2014) also observed, the Pb-Pb radioisotope dating technique has proven precise in measuring the apparent age of meteorites such as the Allende CV3 carbonaceous chondrites and several of the ordinary (O) chondrites (H, L, and LL) reported in this study. The other radioisotope dating techniques are more variable in their reliability, most of those isotopic systems (K-Ar, Rb-Sr, U-Pb, Th-Pb, Sm-Nd, and Re-Os) being apparently subject to disturbance by processes and conditions subsequent to the formation of the asteroids from the Day One “primordial material.” Such processes meteorites were subjected to after the asteroids were formed on Day Four include space weathering (Cloutis, Binzel, and Gaffey 2014), fragmentation and reassembly of their parent asteroids (Michel 2014), reheating and pressure during passage through the earth’s atmosphere, pressures from disintegration into fragments in the earth’s atmosphere and then from impacting the earth’s surface, and weathering while lying on the earth’s surface before collection for study. However, such post Day One creation disturbances of the radioisotope systems were largely within the closed confines of the parent asteroids or the resultant meteorites. In contrast, there were greater opportunities for much larger disturbances, additions and subtractions in earth rocks, because they have been subjected to the cataclysmic geologic processes of the Day Three Upheaval and then the Flood. For example, the melting of large batches of rocks both in the mantle and crust formed magmas in which the isotopes were mixed, homogenized, and the radioisotope “clocks” reset before crystallization and cooling formed new rocks with new isotope ratios distinct from those in the original rocks. It will thus take a lot more research on many earth rocks to unravel and elucidate the proportions of isotopes from each of these major contributing factors and processes—inheritance of the primordial geochemical signature, accelerated radioisotope decay, and mixing in the mantle and crust—to the “dates” measured today by using these radioisotope systems.
The resultant conclusion from all these considerations, based on the assumptions made, is that the 4.56–4.57 Ga “ages” for the Richardton (H5), St. Marguerite (H4), Bardwell (L5), Bjurböle (L4), and St. Séverin (LL6) ordinary chondrite meteorites obtained by Pb-Pb radioisotope isochron and model age dating of various constituent minerals and fractions (for example, Amelin, Ghosh, and Rotenberg 2005; Bouvier et al. 2007; Göpel, Manhès, and Allègre 1994; Kleine et al. 2008; Rotenberg and Amelin 2001 respectively) are likely not their true real-time ages. The assumptions on which the radioisotope dating methods are based are simply unprovable, and in the light of the possibility of an inherited primordial geochemical signature, and the evidence for both possible past accelerated radioisotope decay and mixing of isotopes in earth rocks, these assumptions are unreasonable. However, we are still left without a coherent explanation of what these radioisotope compositions in both meteorites and earth rocks really represent and mean within our biblical young-age creation-Flood framework for earth and universe history. We have some possible clues already, and a clearer picture may yet emerge from continued investigations now in progress, for example, of the radioisotope dating of more meteorites, and also of many more earth rocks from all levels of the geologic record.
Conclusions
After decades of numerous careful radioisotope dating investigations of ordinary (O) chondrite meteorites (H, L, and LL groups) and enstatite (E) chondrite meteorites their Pb-Pb isochron age of 4.55–4.57 Ga has been well established. This date for these chondrite meteorites is supported for some of them by a strong clustering of their Pb-Pb isochron and model ages in the 4.55–4.57 Ga range, as well as being confirmed by both isochron and model age results via the U-Pb method, and to a lesser extent, by the Ar-Ar, Rb-Sr, Re-Os, and Sm-Nd methods. The Hf-W, Mn-Cr, and I-Xe methods are all calibrated against the Pb-Pb isochron method, so their results are not objectively independent. Thus the Pb-Pb isochron dating method stands supreme as the ultimate, most precise tool for determining the ages of the chondrite meteorites.
There are only two other discernible patterns in the isochron and model ages for these O and E chondrites, apart from scatter of the U-Pb, Th-Pb, Rb-Sr, and Ar-Ar model ages particularly. These chondrite ages do not follow the systematic pattern found in Grand Canyon Precambrian rock units during the RATE project. The α-decay ages are not always older than the β-decay ages for particular meteorites, and among the β-decayers the ages are not always older according to the increasing heaviness of the atomic weights of the parent radioisotopes, but may have also been modified according to the lengths of their half-lives. Thus there appears to be no consistent evidence in these O and E chondrite meteorites similar to the evidence found in earth rocks of past accelerated radioisotope decay.
Any explanation for the 4.55–4.57 Ga age for these O and E chondrite meteorites needs to consider the origin of meteorites. Most meteorites appear to be fragments derived from asteroids via collisions, but even in the naturalistic paradigm the asteroids, and thus the meteorites, are regarded as “primordial material” left over from the formation of the solar system. Similarly, the Hebrew text of Genesis could suggest God made “primordial material” on Day One of the Creation Week from which He made the earth on Day One and the non-earth portion of the solar system on Day Four, so today’s measured radioisotope compositions of these O and E chondrite meteorites may reflect a geochemical signature of that “primordial material,” which included atoms of all elemental isotopes created by God. Therefore if some of the daughter isotopes were thus “inherited” by these O and E chondrite meteorites when they were formed from that “primordial material,” and the parent isotopes in the meteorite were also subject to some subsequent accelerated radioisotope decay, then the 4.55–4.57 Ga Pb-Pb isochron “age” for these O and E chondrite meteorites cannot be their true real-time age, which according to the biblical paradigm is only about 6000 real-time years.
However, these conclusions and the suggested explanation can at best be regarded as tentative and interim while their confirmation or adjustment awaits the examination of more radioisotope dating data from many more meteorites. Furthermore, further extensive studies of the radioisotope dating of many more earth rocks from all levels within the whole geologic record are required to attempt to systematize the proportions of isotopes in each radioisotope dating system measured today that are due to inheritance from the “primordial material,” past accelerated radioisotope decay, and mixing, additions and subtractions in the earth’s mantle and crust through earth history, particularly during the Day Three Upheaval and then subsequently during the Flood. Such studies are already in progress.
References
Abranches, M. C. B., J. W. Arden, and N. H. Gale. 1980. Uranium-lead abundances and isotopic studies in the chondrites Richardton and Farmington. Earth and Planetary Science Letters 46, no. 3:311–322.
Alexander, E. C. Jr., P. K. Davis, and R. S. Lewis. 1972. Argon-40–argon-39 dating of Apollo sample 15555. Science 175, no. 4020:417–419.
Alexander, E. C. Jr., and P. K. Davis. 1974. 40Ar-39Ar ages and trace element contents of Apollo 14 breccias: An interlaboratory cross-calibration of 40Ar-39Ar standards. Geochimica et Cosmochimica Acta 38, no. 6:911–928.
Amelin, Y. 2000. U-Th-Pb systematics of chondritic phosphates: Implications for chronology and origin of excess Pb. Lunar and Planetary Science Conference 31: #1201.
Amelin, Y. 2001. U-Pb chronology of chondritic pyroxenes. Lunar and Planetary Science Conference 32: #1389.
Amelin, Y., and E. Rotenberg. 2004. Sm-Nd systematics of chondrites. Earth and Planetary Science Letters 223, no. 3–4:267–282.
Amelin, Y., A. Ghosh, and E. Rotenberg. 2005. Unraveling the evolution of chondrite parent asteroids by precise U-Pb dating and thermal modeling. Geochimica et Cosmochimica Acta 69, no. 2:505–518.
Asphaug, E. 2009. Growth and evolution of asteroids. Annual Review of Earth and Planetary Sciences 37:413–448.
Bischoff, A., M. Horstmann, A. Pack, M. Laubenstein, and S. Haberer. 2010. Asteroid 2008 TC3—Almahata Sitta: A spectacular breccia containing many different ureilitic and chondritic lithologies. Meteoritics and Planetary Science 45, no. 10–11:1638–1656.
Bogard, D. D., D. M. Unruh, and M. Tatsumoto. 1983. 40Ar/39Ar and U-Th-Pb dating of separated clasts from the Abee E4 chondrite. Earth and Planetary Science Letters 62, no. 1:132–146.
Bogard, D. D., E. T. Dixon, and D. H. Garrison. 2010. Ar-Ar ages and thermal histories of enstatite meteorites. Meteoritics and Planetary Science 45, no. 5:723–742.
Bogard, D. D. 2011. K-Ar ages of meteorites: Clues to parent-body thermal histories. Chemie der Erde—Geochemistry 71, no. 3:207–226.
Bouvier, A., J. Blichert-Toft, F. Moynier, J. D. Vervoort, and F. Albarède. 2007. Pb–Pb dating constraints on the accretion and cooling history of chondrites. Geochimica et Cosmochimica Acta 71, no. 6:1583–1604.
Brazzle, R. H., O. V. Pravdivtseva, A. P. Meshik, and C. M. Hohenberg. 1999. Verification and interpretation of the I-Xe chronometer. Geochimica et Cosmochimica Acta 63, no. 5:739–760.
Brearley, A. J., and R. H. Jones. 1998. Chondritic meteorites. In Planetary Materials, ed. J. J. Papike, Reviews in Mineralogy, vol. 36, pp. 3–1, 3–398. Washington DC: Mineralogical Society of America.
Busfield, A., G. Turner, and J. D. Gilmour. 2008. Testing an integrated chronology: I-Xe analysis of enstatite meteorites and a eucrite. Meteoritics and Planetary Science 43, no. 5:883–897.
Chen, J. H., D. A. Papanastassiou, and G. J. Wasserburg. 1998. Re-Os systematics in chondrites and the fractionation of the platinum group elements in the early solar system. Geochimica et Cosmochimica Acta 62, no. 19–20:3379–3392.
Cloutis, E. A., R. P. Binzel, and M. J. Gaffey. 2014. Establishing asteroid-meteorite links. Elements 10, no. 1:25–30.
Cronin, J. R., S. Pizzarello, and D. P. Cruikshank. 1988. Organic matter in carbonaceous chondrites, planetary satellites, asteroids and comets. In Meteorites and the early solar system, ed. J. F. Kerridge and M. S. Matthews, pp. 819–857. Tucson, Arizona: University of Arizona Press.
Dalrymple, G. B. 1991. The age of the earth. Stanford, California: Stanford University Press.
Dalrymple, G. B. 2004. Ancient earth, ancient skies. Stanford, California: Stanford University Press.
Eberhardt, P., and D. C. Hess. 1960. Helium in stone meteorites. Astrophysical Journal 131:38–46.
Eugster, O. 1988. Cosmic-ray production rates for 3He, 21Ne, 38Ar, 83Kr, and 126Xe in chondrites based on 81Kr-Kr exposure ages. Geochimica et Cosmochimica Acta 52, no. 6:1649–1662.
Evensen, N. M., S. R. Carter, P. J. Hamilton, R. K. O’Nions, and W. I. Ridley. 1979. A combined chemical-petrological study of separated chondrules from the Richardton chondrite. Earth and Planetary Science Letters 42:223–236.
Faulkner, D. R. 1999. A biblically-based cratering theory. Creation Ex Nihilo Technical Journal 13, no. 1:100–104.
Faulkner, D. R. 2013. A proposal for a new solution to the light travel time problem. Answers Research Journal 6:295–300.
Faure, G., and T. M. Mensing. 2005. Isotopes: Principles and applications, 3rd ed. Hoboken, New Jersey: John Wiley & Sons.
Funkhouser, J., T. Kirsten, and O. A. Schaeffer. 1967. Light and heavy rare earth gases in four fragments of the St. Séverin meteorite. Earth and Planetary Science Letters 2, no. 3:185–190.
Gale, N. H., J. W. Arden, and R. Hutchison. 1972. Uranium-lead chronology of chondritic meteorites. Nature 240:56–57.
Gale, N. H., J. W. Arden, and M. C. B. Abranches. 1980. Uranium-lead age of the Bruderheim L6 chondrite and the 500-Ma shock event in the L-group parent body. Earth and Planetary Science Letters 48, no. 2:311–324.
Geiss, J., and D. C. Hess. 1958. Argon-potassium ages and the isotopic composition of argon from meteorites. Astrophysical Journal 127, no. 1:224–236.
Gilmour, J. D., O. V. Pravdivtseva, A. Busfield, and C. M. Hohenberg. 2006. The I-Xe chronometer and the early solar system. Meteoritics and Planetary Science 41, no. 1:19–31.
Gilmour, J. D., S. A. Crouther, A. Busfield, G. Holland, and J. A. Whitby. 2009. An early I-Xe age for CB chondrite chondrule formation, and a re-evaluation of the closure age of Shallowater enstatite. Meteoritics and Planetary Science 44, no. 4:573–579.
Glavin, D. P., and G. W. Lugmair. 2003. Mn-Cr isotope systematics in the LL type ordinary chondrite St. Séverin. Lunar and Planetary Science Conference 34:#1276.
Goodrich, C., A. Bischoff, and D. P. O’Brien. 2014. Asteroid 2008 TC3 and the fall of Almahata Sitta, a unique meteorite breccia. Elements 10, no. 3:31–37.
Göpel, C., G. Manhès, and C.-J. Allègre. 1994. U-Pb systematics of phosphates from equilibrated ordinary chondrites. Earth and Planetary Science Letters 121, no. 1–2:153–171.
Gopalan, K., and G. W. Wetherill. 1969. Rubidium-strontium age of hypersthene (L) chondrites. Journal of Geophysical Research 73, no. 22:7133–7136.
Gopalan, K., and G. W. Wetherill. 1970. Rubidium-strontium studies on enstatite chondrites: Whole meteorite and mineral isochrons. Journal of Geophysical Research 75, no. 17:3457–3467.
Hohenberg, C. M., and B. M. Kennedy. 1981. I-Xe dating: Intercomparisons of neutron irradiations and reproducibility of the Bjurböle standard. Geochimica et Cosmochimica Acta 45, no. 2:251–256.
Hohenberg, C. M., B. Hudson, B. M. Kennedy, and F. A. Podosek. 1981. Noble gas retention chronologies for the St. Séverin meteorite. Geochimica et Cosmochimica Acta 45, no. 4:535–546.
Huey, J. M. and T. P. Kohman. 1973. 207Pb-206Pb isochron and age of chondrites. Journal of Geophysical Research 78, no. 17:3227–3244.
Jacobsen, S. B., and G. J. Wasserburg. 1980. Sm-Nd isotopic evolution of chondrites. Earth and Planetary Science Letters 50, no. 1:139–155.
Keil, K. and K. Fredriksson. 1964. The iron, magnesium, and calcium distribution in coexisting olivine and rhombic pyroxenes of chondrites. Journal of Geophysical Research 69: 3487–3515.
Kinsey, L. K., T. J. McCoy, K. Keil, D. D. Bogard, D. H. Garrison, K. Kehm, R. H. Brazzle, C. M. Hohenberg, D. W. Mittlefehldt, and I. Casanova. 1995. Petrology, chemistry and chronology of an impact-melt clast in the Hvittis EL6 chondrite. Lunar and Planetary Science Conference 26:753–754.
Kleine, T., C. Münker, K. Mezger, and H. Palme. 2002. Rapid accretion and early core formation on asteroids and the terrestrial planets from Hf-W chronometry. Nature 418:952–955.
Kleine, T., M. Touboul, J.A. Van Orman, B. Bourdon, C. Maden, K. Mezger, and A. N. Halliday. 2008. Hf-W thermochronometry: Closure temperature and constraints on the accretion and cooling history of the H chondrite parent body. Earth and Planetary Science Letters 270, no. 1–2:106–118.
Koehler, L., and W. Baumgartner. 2001. The Hebrew and Aramaic lexicon of the Old Testament, vol. 1. Rev. ed. Trans. and ed. M. E. J. Richardson. Leiden, The Netherlands: Brill.
Krot, A.N., K. Keil, C. A. Goodrich, E. R. D. Scott, and M.K. Weisberg. 2005. Classification of meteorites. In Meteorites, comets, and planets, ed. A. M. Davis, Treatise on geochemistry, vol. 1, pp. 83–128. Amsterdam, The Netherlands: Elsevier.
Krot, A. N., Y. Amelin, P. Bland, F. J. Ciesla, J. N. Connelly, A. M. Davis, G. R. Huss, I. D. Hutcheon, K. Makide, K. Nagashima, L. E. Nyquist, S. S. Russell, E. R. D. Scott, K. Thrane, H. Yurimoto, and Q.-Z. Yin. 2009. Origin and chronology of chondritic components: A review. Geochimica et Cosmochimica Acta 73, no. 17:4963–4997.
Lewis, J. S. 1997. Physics and chemistry of the solar system, rev. ed. London, England: Academic Press.
Libourel, G., and C. M. Corrigan. 2014. Asteroids: New challenges, new targets. Elements 10, no. 1:11–17.
Luck, J.-M., and C.-J. Allègre. 1983. 187Re-187Os systematics in meteorites and cosmological consequences. Nature 302:130–132.
Luck, J.-M., J.-L. Birck, and C.-J. Allègre. 1980. 187Re-187Os systematics in meteorites: Early chronology of the solar system and age of the galaxy. Nature 283:256–259.
Manhès, G., and C. J. Allègre. 1978. Time differences as determined from the raio of lead-207 and lead-206 in concordant meteorites. Meteoritics 13:543–548.
Manhès, G., J. F. Minster, and C. J. Allègre. 1978. Comparative uranium-thorium-lead and rubidium-strontium study of the Saint Séverin amphoterite: Consequences for early solar system chronology. Earth and Planetary Science Letters 39, no. 1:14–24.
Mason, B. 1962. Meteoritics. New York, New York: John Wiley and Sons Inc.
Michel, P. 2014. Formation and physical properties of asteroids. Elements 10, no. 1:19–24.
Michel, P., and D. C. Richardson. 2013. Collision and gravitational reaccumulation: Possible formation mechanism of the asteroid Itokawa. Astronomy and Astrophysics 554:L1.
Min, K., P. W. Reiners, and D. L. Shuster. 2013. (U-Th)/He ages of phosphates from St. Séverin LL6 chondrite. Geochimica et Cosmochimica Acta 100, no. 1:282–296.
Minster, J.-F., L.-P. Rickard, and C. J. Allègre. 1979. 87Rb-87Sr chronology of enstatite meteorites. Earth and Planetary Science Letters 44, no. 3:420–440.
Minster, J.-F. and C.-J. Allègre. 1981. 87Rb-87Sr dating of LL chondrites. Earth and Planetary Science Letters 56:89–106.
Minster, J.-F., J.-L. Birck, and C. J. Allègre. 1982. Absolute age of formation of chondrites studied by the 87Rb-87Sr method. Nature 300:414–419.
Morris, J. D. 2007. The young earth, rev. ed., pp. 59–61. Green Forest, Arkansas: Master Books.
Nakamura, T. et al. 2011. Itokawa dust particles: A direct link between S-type asteroids and ordinary chondrites. Science 333, no. 6046:1113–1116.
Norton, O. R. 2002. The Cambridge encyclopedia of meteorites. Cambridge, United Kingdom: Cambridge University Press.
Patterson, C. 1956. Age of meteorites and the earth. Geochimica et Cosmochimica Acta 10:230–237.
Podosek, F. A. 1971. Neutron-activation potassium-argon dating of meteorites. Geochimica et Cosmochimica Acta 35, no. 2:157–173.
Podosek, F. A., and J. C. Huneke. 1973a. Noble gas chronology of meteorites. Meteoritics 8:64.
Podosek, F. A., and J. C. Huneke. 1973b. Argon 40-argon 39 chronology of four calcium-rich achondrites. Geochimica et Cosmochimica Acta 37, no. 3:667–684.
Polnau, E. and G. W. Lugmair. 2000. Manganese-chromium isotopic systematics in the ordinary chondrite Forest Vale (H4). Meteoritics and Planetary Science 35:A128.
Polnau, E. and G. W. Lugmair. 2001. Mn-Cr isotope systematics in the two ordinary chondrites Richardton (H5) and St. Marguerite (H4). Lunar and Planetary Science Conference 32: #1527.
Rotenberg, E., and Y. Amelin 2001. Combined initial Sr, Sm-Nd, and U-Pb systematics of chondritic phosphates: How reliable are the ages? Lunar and Planetary Science Conference 32: #1675.
Rotenberg, E. and Y. Amelin 2002. Rb-Sr chronology of chondrules from ordinary chondrites. Lunar and Planetary Science Conference 33: #1605.
Sanz, H. G. and G. J. Wasserburg. 1969. Determination of an internal 87Rb-87Sr isochron for the Olivenza chondrite. Earth and Planetary Science Letters 6, no. 5:335–345.
Scott, E. R. D., and A. N. Krot. 2005. Chondrites and their components. In Meteorites, comets, and planets, ed. A. M. Davis, Treatise on geochemistry, vol. 1, pp. 143–200. Amsterdam, The Netherlands: Elsevier.
Sears, D. W. G., and R. T. Dodd. 1988. Overview and classification of meteorites. In Meteorites and the early solar system, eds. J. F. Kerridge and M. S. Matthews, pp. 3–31. Tucson, Arizona: University of Arizona Press.
Schaeffer, O. A., and R. W. Stoenner. 1965. Rare gas isotope contents and K-Ar ages of mineral concentrates from the Indarch meteorite. Journal of Geophysical Research 70, no. 1:209–213.
Schultz, L., and P. Signer. 1976. Depth dependence of spallogenic helium, neon and argon in the St. Séverin meteorite. Earth and Planetary Science Letters 30, no. 2:191–199.
Shima, M., and M. Honda. 1967. Determination of rubidium-strontium age of chondrites using their separated components. Earth and Planetary Science Letters 2, no. 4:337–343.
Snelling, A. A. 2000. Geochemical processes in the mantle and crust. In Radioisotopes and the age of the earth: A young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, pp. 123–304. El Cajon, California: Institute for Creation Research; St. Joseph, Missouri: Creation Research Society.
Snelling, A. A. 2005. Isochron discordances and the role of inheritance and mixing of radioisotopes in the mantle and crust. In Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative, ed. L. Vardiman, A. A. Snelling, and E. F. Chaffin, pp. 393–524. El Cajon, California: Institute for Creation Research; Chino Valley, Arizona: Creation Research Society.
Snelling, A. A. 2009. Earth’s catastrophic past: Geology, creation and the Flood. Dallas, Texas: Institute for Creation Research.
Snelling, A. A. 2014. Radioisotope dating of meteorites: I. The Allende CV3 carbonaceous chondrite. Answers Research Journal 7:103–145.
Tatsumoto, M., R. J. Knight, and C. J. Allègre. 1973. Time differences in the formation of meteorites as determined from the ratio of lead-207 to lead-206. Science 180, no. 4092:1279–1283.
Tera, F. and R. W. Carlson. 1999. Assessment of the Pb-Pb and U-Pb chronometry of the early solar system. Geochimica et Cosmochimica Acta 63, no. 11–12:1877–1889
Tilton, G. R. 1973. Isotopic lead ages of chondritic meteorites. Earth and Planetary Science Letters 19, no. 3:321–329.
Trieloff, M., E. K. Jessberger, I. Herrwerth, J. Hopp, C. Fiérl, M. Ghélls, M. Bourot-Denise, and P. Pellas. 2003. Structure and thermal history of the H-chondrite parent asteroid revealed by thermochronometry. Nature 422:502–506.
Trinquier, A., J.-L. Birck, C. J. Allègre, C. Göpel, and D. Ulfbeck. 2008. 53Mn-53Cr systematics of the early solar system revisited. Geochimica et Cosmochimica Acta 72, no. 20:5146–5163.
Tsuchiyama, A. 2014. Asteroid Itokawa: A source of ordinary chondrites and a laboratory for surface processes. Elements 10, no. 1:45–50.
Turner, G. 1969. Thermal histories of meteorites by the 39Ar-40Ar method. In Meteorite research, ed. P. M. Millman, pp. 407–417. Dordrecht, The Netherlands: D. Reidel.
Turner, G., M. C. Enright, and J. Hennessey. 1978. Argon ages: From primitive planetesimals to differentiated moon. Lunar and Planetary Science Conference 9:1178–1179.
Turner, G., M. C. Enright, and P. H. Cardogan. 1979. The earliest history of chondrite parent bodies inferred from 40Ar-39Ar ages. Proceedings of the 9th Lunar and Planetary Science Conference, pp. 989–1025.
Unruh, D. M. and M. Tatsumoto. 1980. Excess Pb in L-chondrites: Is it terrestrial? Lunar and Planetary Science Conference 11:1184–1186.
Unruh, D. M. 1982. The U-Th-Pb age of equilibrated L chondrites and a solution to the excess radiogenic Pb problem in chondrites. Earth and Planetary Science Letters 58:75–94.
Unruh, D. M., R. Hutchison, and M. Tatsumoto. 1982. U-Th-Pb systematics and uranium isotopic composition of chondrites. Lunar and Planetary Science Conference 10:1256–1258.
Van Schmus, W. R., and J. A. Wood. 1967. A chemical-petrologic classification for the chondritic meteorites. Geochimica et Cosmochimica Acta 31, no. 5:747–765.
Van Schmus, W. R., and J. M. Hayes. 1974. Chemical and petrographic correlations among carbonaceous chondrites. Geochimica et Cosmochimica Acta 38, no. 1:47–64.
Von Michaelis, H., L. H. Ahrens, and J. P. Willis. 1969. The compositions of the stony meteorites—II. The analytical data and an assessment of their quality. Earth and Planetary Science Letters 5:387–394.
Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the age of the earth: Results of a young-earth creationist research initiative. El Cajon, California: Institute for Creation Research; Chino Valley, Arizona: Creation Research Society.
Wasserburg, G. J., D. A. Papanastassiou, and H. G. Sanz. 1969. Initial strontium for a chondrite and the determination of a metamorphism or formation interval. Earth and Planetary Science Letters 7, no. 1:33–43.
Weisberg, M. K., T. J. McCoy, and A. N. Krot. 2006. Systematics and evaluation of meteorite classification. In Meteorites and the early solar system II, ed. D. S. Loretta and H. Y. McSween, pp. 19–52. Tucson, Arizona: University of Arizona Press.
Wood, J. A. 1967. Chondrites: Their metallic minerals, thermal histories, and parent planets. Icarus 6, no. 1–3:1–49.










