The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.
Abstract
Jason Lisle in his self-published refutation of Dennis (2024) fails to refute. His refutation is yet another rehearsal of his special relativistic thesis built on Reichenbach’s conventionalism and an unshakeable faith in the reality of the block universe called spacetime. Lisle also betrays his limited knowledge of the mathematics of relativity by his terminology and by the concepts he entertains in his self-published Physics of Einstein that run afoul of the mathematics of special relativity. These are telltale shibboleths. He betrays his limited knowledge of the philosophical literature regarding eternalism and presentism and shockingly accepts Einstein’s metaphysics of the block universe of eternalism with its heretical implications. Lisle’s philosophy appears to be driven by his reverential attitude towards Einstein’s philosophy of eternalism and his infatuation with time travel that would only be possible in the block universe of four dimensional spacetime. This leads him to interpret the Bible in terms of the authority of Einstein rather than the authority of the Bible which should have led him to reject Einstein’s anti-theistic eternalist worldview. I point out that relativity is compatible with presentism which is not heretical. Christians should reject the eternalist spacetime metaphysics of Einstein as adopted by Lisle and embrace the presentist interpretation of relativity.
Keywords: ASC, synchrony conventions, conventionality thesis, one-way speed of light, light travel time, anisotropic, simultaneity, special relativity, general relativity, empirical observations, eternalism, presentism, time travel
Introduction
In writing this reply to Jason Lisle there certainly is no joy in exposing his misconceptions and mathematical errors in both his refutation and in his self-published book The Physics of Einstein (Lisle 2018), a blend of mathematical errors, time travel science fiction, an apologetic for eternalism, and lastly a platform to expound his ASC (Anisotropic Synchrony Convention) model. However, there is joy in the hope that this reply will enlighten those who have been misled by his mistaken theory. I will clearly show via multiple arguments that the model is flawed. This is based on empirical evidence, mathematics, philosophical misconceptions, and—most seriously—the theological implications of Lisle’s adherence to the eternalist philosophy of time. A philosophy, as we will see, which runs afoul of the biblical revelation and, if knowingly held, is a serious heresy.
Let me begin by pointing out that I am a young earth creationist who is thoroughly committed to a literal seven days of an actual Creation Week. In my 2018 ICC paper (Dennis 2018) I published a general relativity (GR) solution to the LTTP (light travel time problem) consistent with a literal seven days of creation. In that paper I also gave an exposition of the presentist philosophy of time, a philosophy that is that of the Bible and fully consistent with the mathematics of GR. Presentism asserts that there is an actual present (now), and that time is not an illusion as Jason Lisle’s adherence to Einstein’s eternalism requires. Many creationists have informed me that the discussions of eternalism and presentism in my ICC paper were the most important portions for them and that they were made aware that there are two views of time: that presentism is compatible with the mathematics of special and general relativity (contrary to Lisle’s incorrect dogmatic claim) and the importance of presentism to the orthodox Christian worldview. We will get to that a little bit later when we explain that presentism is a consistent interpretation of the mathematics of special relativity (SR), but first let’s deal with some empirical facts of God’s Creation that have been verified by scientists and engineers. Hopefully you will see that Jason Lisle has not kept up with the latest in technology, and that he lives in the past when there was nothing but low precision clocks, a time of ancient technology compared to today’s high precision lasers and ultra stable clocks, among other advances. We shall begin with the perpetuated myth that it is impossible to measure a one-way speed of light. If this supposed unassailable assumption is destroyed, the whole ASC program crashes to the ground.
The Supposed Inability to Measure a One-Way Speed of Light
A Stacked Deck Argument
Lisle rests his case on a stacked deck argument that all one-way experiments require two clocks to be synchronized (2C proposition). The second assertion is that apparently the only way to synchronize remote clocks is via a one-way light signal (LS proposition). This obviously leads to a circular argument regarding interpreting the results. Simply, according to the stacked deck, one must know the speed of light to set the clocks and thus you only measure what you assumed. This is inescapable logic that follows from the propositions 2C and LS. The problem is that both are false. At this point, the reader needs to note that the position of the conventionalists is that it is impossible to measure any one-way speed of light. They go so far to state, like logical positivists, that there is no objective one-way speed of light. As Lisle, in his reverential attitude toward Einstein, states, “Einstein pointed out, the one-way speed of light is not a property of nature.” Thanks to Reichenbach (1956), it can be set, by the ignorance of man, to any value between c/2 and infinite. We will see that is not the case by examining two indisputable empirical cases.
The Femtosecond Photography of Extremely Short Laser Pulses
There have been amazing advances in physics and technology since the days of the antiquated methods available to physicists 100 years ago in the days of Einstein (1920) and Reichenbach (1956). At that time even the atomic clock was merely a theory. Experiments at that time were limited to continuous beams of light. Today we can chop a light beam into tiny packets (light bullets) that was impossible in the 1920s. That means we can visually track the centroid of a light pulse with widths of several picoseconds (ps) or less and film the travel of the light bullet using a single clock and camera (and thus the 2C proposition is invalid). Amazingly, pulse widths of 43 attoseconds (as = 10−18 sec) were achieved in 2017. The femtosecond photography used 7ps pulse widths which resulted in a wave packet length of 2 mm.
The films1 published by Caltech researchers can be analyzed to compute the one-way speed of light. Using frame extraction software, I assembled a sequence of still frames of the femtosecond camera showing the trajectory of the light bullet for a time interval of 10 ps. These are shown in fig. 1. The centroid of the bullet was then computed and plotted (red circles) as a function of time as shown in fig. 2. A linear least squares fit calculation yields the value of c = 2.264 × 108 m/s. Note that the light in the experiment was traveling in water. Thus, the computation yielded a value equal to the speed of light in water. This is a very precise value measurement of a one-way speed of light.

Fig 1. Sequence of images of light bullet trajectory in water (10 ps sequence).
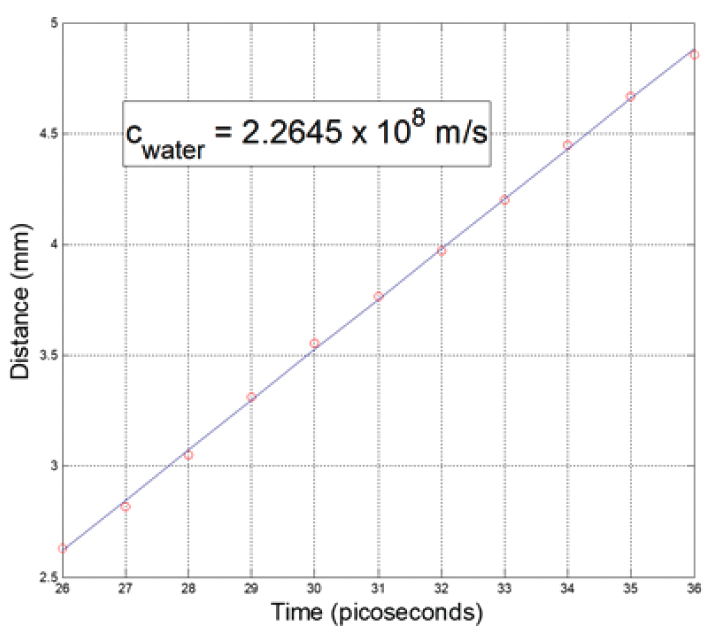
Fig 2. Linear least squares fit to fig. 1 yielding a oneway speed of light in water.
At this point, it is important to note that the orientation of the imaged trajectory is in an arbitrary direction. If the experiment is repeated by rotating the orientation the same result will be obtained. For example, if the above observation was light traveling west to east, then rotating the apparatus by 90° would yield a one-way speed along the north-south axis. Thus, the Caltech experiment empirically establishes the isotropy of the one-way speed-of-light.
Gao et al. (2014) also published calculations of light speeds in air and in resin. The values were (3.1 ± 0.5) × 108 m/s and (2.0 ± 0.2) × 108 m/s, respectively, consistent with the theoretical values 3.0 × 108 m/s and 2.0 × 108 m/s. Also, fig. 3 in Gao et al. (2014) has examples of
- the camera capturing the one-way trajectory of light;
- the image of light refracting at an air to resin surface, thus dramatically confirming Snell’s law; and
- a race between two light bullets, one in air and the other in resin.
One other point is that the formula for the ASC pseudo speed of light (to be examined later) logically requires that the transverse speed of light is exactly c in every transverse direction to the two-way single clock experiments. This means a necessary theoretical deduction of the ASC theory is that the transverse speed of light is isotropic. It doesn’t take much imagination to realize that the orientation of the Reichenbach single clock two-way experiments (for example, is the clock-mirror baseline in the north-south direction, or the east-west direction) establishes isotropy of the one-way speed of light for all transverse directions. We will revisit this later when we examine the ASC anisotropic pseudo-speed formula in the section “Reichenbach ‘magic’ light rays.”
For additional information and analysis performed at Caltech see Gao et al. (2014).
Slow Clock Transport and NASA Deep Space Missions
A second example of one-way speed of light measurements is available in NASA deep space probes, such as the MESSENGER mission to the planet Mercury and the New Horizons mission to Pluto and beyond. These missions provide a remarkable example of real-world slow clock transport of onboard spacecraft clocks.
Undeniably, there has been controversy regarding the slow clock transport method of synchronizing clocks. I am not going to enter that controversy at this point because it is not essential. But what I will bring to evidence is that slowly transported clocks, even if no longer synchronized due to time dilation, disprove the infinite speed claim of Lisle. If the time dilation is miniscule compared to the one-way light time, a very accurate speed of light can be measured. In short, ignoring the small amount of time dilation can be considered an experimental error. The case at hand is timekeeping during NASA deep space missions. One mission of particular interest to astronomers, both professionals and amateurs, is the New Horizons mission to Pluto and beyond.
One may wonder about time dilation. First, it is important to remember that time dilation is an objective property that depends on the invariant spacetime interval along the spacecraft trajectory. We cannot make distant clocks run faster or slower by changing a conceptual coordinate label. We can estimate the actual amount of time dilation of the New Horizons’ clock using the interval between the launch event and the event of encounter at Pluto. The encounter with Pluto required ∆t = 9.5 years for New Horizons to reach orbit at Pluto at a distance D ≈ 4.7 × 109 km from the earth. For the vast majority of time the spacecraft was inertial so we will estimate the time elapsed on the spacecraft ∆τ (New Horizon’s proper time) by computing the spacetime interval between the launch event and the encounter event with Pluto via:
For ∆t = 9.5 years and ∆r = 4.7 × 109 km we obtain
This estimate, based on the average speed of the spacecraft during its nine-year flight to encounter Pluto, yields a miniscule time loss of the onboard clock at time of downlink of less than 0.5 seconds in the 9.5 year journey. This is clearly a case of slow clock transport.
The New Horizons spacecraft has on board an ultra-stable oscillator (USO) for timekeeping of time elapsed on the spacecraft. The onboard time counter was set to zero at time of launch and the UTC (earth time) of launch is known. As the spacecraft flew toward its encounter with Pluto, the time counter on board measured what is denoted MET (mission elapsed time). All telemetry data downloaded to earth contained the value of MET, that is, the spacecraft clock reading. This time field allowed the ground systems to compute the time it took the message to reach earth. It is simply:
Light travel time = the recorded UTC of reception by the Deep Space Network – (UTC of Launch + MET)
Sample data available on the NASA website states that the distance of New Horizons spacecraft at the encounter with Pluto was D = ~4.7 × 109 km, and the computed time of flight (difference of earth clock at reception at the DSN and New Horizons’ downlinked clock reading) during the encounter was ~4 hours 25 minutes. Using this to compute the speed of light gives:
This is not infinite, and even with rough estimates of D and T, the computation is within 1.4% of the expected value. Thus, this is an example of slow transport. Such a small difference does not affect the uncompensated 4.5 hours used in the speed computation. This empirical observation is a direct refutation of the Reichenbach prescription and Lisle’s thesis. If we had a large telescope and a clock on the exterior of New Horizons, the image would show a clock reading 4.5 hours in the past. But of course, that is what the downlinks show in the digital frames. We do see an image of the past as it was, and which is no longer. To maintain ASC in the light of the evidence of these two empirical cases places one into the denialist camp.
Eternalism and “Spacetime”—Einstein and Lisle, a Strange Alliance
A shocking revelation in Lisle’s refutation is his adherence to the reality of Minkowski’s four-dimensional spacetime and a repudiation of presentism. Lisle states:
I do hold that spacetime is non-abstract—no misrepresentation there.
I reject such a philosophy [presentism] as mere rhetoric at best and inconsistent with physics and the Bible at worst.
Lisle’s philosophy and metaphysics, that the creation is Minkowski’s block universe and the repudiation of presentism along with the acceptance of philosophical eternalism, lands him in heretical territory as we will later show.
It appears that Lisle is not familiar with the term eternalism. Several times in his refutation Lisle uses the word eternalism. At one point he even conflates eternal life with eternalism. Lisle states, “all believers will enjoy eternal life: biblical eternalism.” This is not what the term eternalism means.
Lisle’s comment reveals a stunning lack of awareness of the philosophical literature on the nature of time. This is indicated when Lisle said: “Apparently, eternalism exists in contradistinction with Dennis’s view . . . [presentism]. At best, this is a distinction without a difference.” Not apparently, but actually. Eternalism is in contradistinction to presentism and there is a radical difference between the two views: heretical implications of the former and biblical orthodoxy of the latter.
So, contrary to Lisle, the term eternalism is a philosophical term that pertains to one interpretation of time in SR; it has nothing to do with the redeemed enjoying eternal life. Biblical eternalism is an example of a word salad. Lisle is engaging in fanciful rhetoric. And displays his limited philosophical knowledge.
So, what exactly is eternalism in SR? It is the philosophical belief in a real block universe (now called spacetime) in which there is no passage or flow of time. There is no present. All events past and future exist timelessly and statically in a four-dimensional Minkowski space. Nothing happens. The fact that Lisle admits his full throated belief in a concrete Minkowski spacetime and that time travel to the past is hypothetically possible is an explicit presupposition that the past is still there, even now. We will examine Lisle’s views on time travel (along with egregious mathematical errors that lead him to false conclusions and interpretation of relativity in The Physics of Einstein [Lisle 2018]) in detail later.
That the past is still there and indeed also that the future is already here (or should that be there too?) may be a bit difficult to digest so let’s begin with an imaginary conversation in the four-dimensional block universe of spacetime.
A Short Conversation in Spacetime
What are you doing now? I believe you will say that you are reading this reply to Jason Lisle. But is there a now? Eternalists, such as Lisle, say no. What you are doing now is in the future as I now compose this reply. And that is now in the past as you now read it. But to an eternalist, these are just relational. I am still writing this paper, and you were reading the paper even as I wrote it. This is the essence of the block universe of Minkowski spacetime. You think there is passing of time, but you are mistaken. Time is an illusion according to Einstein’s interpretation of relativity. On the death of his friend Besso, Einstein wrote a letter to Besso’s grieving family. Einstein wrote:
Now he has departed from this strange world a little ahead of me. That signifies nothing. For those of us who believe in physics, the distinction between past, present and future is only a stubbornly persistent illusion.
This philosophy is scarily close to the Hindu philosophy of maya—“that which is not” or an illusion. For the eternalist, time is maya.
We close with some questions for the eternalists. First, we might ask, “How did the universe “arrive” at “now”? This is a meaningless question for the eternalist. There is no now according to the eternalist interpretation of SR. Or we might ask, “When did the future begin to exist?” Or “When did the past cease to exist?” A creationist eternalist answer to the first must be “in the beginning” and the answer to second must be “never” as long as spacetime exists. At any rate, this is to say Genesis 1:1 means, “In the beginning God created spacetime.” We will explore the heretical implications of this anti-biblical philosophy of time below.
The Biblical View of Time and Theological Objections to Eternalism
From a theological perspective, the unreality of time is incompatible with biblical revelation. First, and most important, the reality of time is presented in the Bible in the opening verses of Genesis that describe the miraculous Creation Week and the occurrence of the first day.
Eternalism and the Creation Week
So according to Lisle and Einstein the implication for the account of the Creation Week in Genesis 1 is that the days did not pass, they are an illusion. It should be mentioned that one does not need to believe that the block universe is coeternal with God. A theist might say God created spacetime—the entirety of creation history. It came into existence sometime in an instant. But to say God created Minkowski spacetime as a concrete entity is to say past, present, and future, the entire history came directly from the hand of God in that instant, “in the beginning.” In fact, the entire temporal extent (which is all there is in the block universe), the entire history of the Creation was created at once, directly from the hand of God.
An eternalist cannot say the universe is young. Since the future already exists, God created a universe with a temporal extent equal to the geometric distance from the first Creation events to a hypothetical final destruction of spacetime and some unknown future boundary. Or we might ask “When did the future come to pass?” In eternalism, it came to pass in the beginning.
Since to an eternalist time is an illusion, this means that the Creation Week is still there. When the Bible therefore speaks of Day One, Day Two, Day Three, etc. it is not referring to an actual progression of time. Rather, it is merely making a static geometric statement about the block universe. Within the eternalist block universe the relationship between the first day and the second day is that they are geometrically a temporal extent, they are static events separated by an interval of one day; likewise, the second day and third day are geometrically separated by the interval of one day; and so shall they be forever in the static universe of Lisle and Einstein, unless, of course, the Lord decides to annihilate spacetime. All the eternalist can say is Day One is earlier than Day Two, etc. This is the eternalist view of relativity espoused by Einstein.
However, this eternalist interpretation of SR is not a necessary deduction from the mathematics of SR. It is only based upon a metaphysical presupposition that the time labels that we, as temporal finite creatures, apply to past observed events have ontological significance. Contra Lisle we do see an image of the past, and that is the very essence of the LTTP.
Eternalism is bad news for Christian theism; it is heresy. Let’s explore some of the consequences of life in the static block universe of spacetime. Reading Lisle’s refutation, he appears to be a bit confused about spacetime. He claims we owe our existence to spacetime. He engages in some fanciful word play. We exist in space, and we exist in time; therefore, space plus time equals spacetime. This is another word salad, a feeble assertion with no attendant philosophical argumentation. Lisle asserts that without spacetime we could not be. This is merely rhetoric. As a presentist I too claim that without space we could not be, and without time we could not be. After all, we are spatial creatures, and we change as time actually passes. But the ontology of presentism is that three-dimensional space exists, and that time is real—but is not an actual fourth dimension. We live in space, and we persist as time passes. We are born, grow, and ultimately die as time passes. This is space and time, not an objectified static block called spacetime in which nothing happens. Amazingly, Lisle seems not to understand what “persisting through time” means.2 To refute presentism, he ironically compares the passage of time to spatial dimensions.
Lisle states:
What is a “three-dimensional spatial universe that persists through time” if not a four-dimensional spacetime? It would be like a person arguing, “there are only two real dimensions of space: length and width, but these lengths and widths persist over height.
Lisle defends his ontological spacetime by a word salad, a mere linguistic twist, viz. that “3 + 1 = 4”. The fact that creaturely existence requires four coordinates to designate events (place and time) is not a proof of ontological spacetime. I can also say as a presentist that Minkowski spacetime is four-dimensional, it just isn’t real; it is a mathematical abstraction. Lisle’s counterargument in which he presents an analogy comparing a spatial object, which has no temporal attributes (or causal connections between parts), with something that does have temporal attributes is philosophically and logically absurd. Lisle seems to have forgotten that the geometry of Minkowski is pseudo-Riemannian. Minkowski spacetime has a distinction between time and space as embodied in the signature of the metric. Time is distinguished from space in the metric by its opposite sign. So, comparing the time with the spatial directions ignores a fundamental feature of the Minkowski mathematical model of relativity. Of course, there is no causation among spatial dimensions, and similarly in the static block universe called spacetime there is no causation. This is the notion that time is a place or the spatialization of time. Of course, this is precisely the metaphysics of eternalism that Lisle embraces. Lisle has just admitted that he believes in the spatialization of time when he introduces a 3D cube to try to elucidate the unreality of time. Jason Lisle believes time is a place in a Humean universe of eternal conjunctions. A universe where there is no human free agency. Just as there is no causation in the spatial dimensions, there is no causation in the time dimension. Just as spatial objects do not flow, time also does not flow.
Some may not realize that Lisle believes such, but he does. Just as you can travel through the three dimensions of space, Lisle believes it would be possible (with some unspecified technology) to travel through time (an actual path through the fourth dimension), even into the past, and revisit past happenings, that is, those unchangeable events that are points in spacetime. Lisle does present some bad news as to why it might not be possible technologically due to some materialistic reasoning. But the inability to achieve actual time travel does not invalidate his presupposition that the past is still there (you just may not be able to get there). To theoretically travel to some place, the place must exist and there must be a path through that fourth dimension. For Lisle, as a full-throated eternalist and shockingly a repudiator of presentism, the past exists. Lisle, in an astounding (and mathematically false) quote, claims:
Nonetheless, hypothetically if faster than light travel was possible, then time travel into the past would also be possible. This is provable from the Lorentz transformation . . . (Lisle 2018, 101, emphasis added)
We will examine this claim in more detail later when we discuss the errors in The Physics of Einstein (Lisle 2018).
Fortunately, there is some good news. The eternalist philosophy of time is not a necessary deduction from relativity no matter how much the eternalists insist. The presentist view of relativity is that there is an ontological now and time is real. All SR implies is that now is not detectable in an empty universe via human agency. In Christian theism it is the cosmic clock that was started on Day One of the Creation Week. As Christian creationists, we must say the creation is on the order of ~7,000 years old. General relativity supports this biblical view. We will discuss that later.
Heretical Aspects of Eternalism—You Are Your Worldline3
We’ve already mentioned the implications of eternalism for the biblical account of Creation. But we need to expand on the implications of a completed static concrete object of spacetime extended in a spatialized time dimension (including all of history, past, and future) directly in an instant from the hand of God in the beginning. The first implication is that men have no free agency, their worldlines were completed and engraved in the immutable structure of spacetime. This is unalloyed fatalism. That means their sins were engraved by God in the finished structure of spacetime. Thus, sin and evil were created directly from the hand of God. Yet, God declared it good. This is an utterly repugnant implication. Let’s look at a spacetime diagram of the worldline of a hypothetical person, Albert—a four-dimensional spacetime worm (fig. 3). Albert both body and soul is a temporally extended worldline in eternalist reality. The worm Albert exists as a totality in a timeless reality. His soul has an unsaved part and a saved part. His body has a living part and a dead part. The entity Albert is a born, lost, saved, dead, resurrected thing (a spacetime worm to stress the metaphysics) extended in spacetime. This is not Christian. In presentism you are not a worldline. You are not spread through time. You are three-dimensional and your entire being—body, soul, and spirit—persists within a 3D space as time passes. Shockingly, what applies to our fictional Albert, pertains to Christ incarnate. Christ is still on the cross suffering for sinners again and again and uttering “It is finished” (as potential time-travelers journey back in time to witness the event). Christ is still talking with the disciples (which Lisle would like to do also after he jumps in his time machine). Of course, there are so many more abhorrent theological consequences of eternalism that Lisle may want to work through.
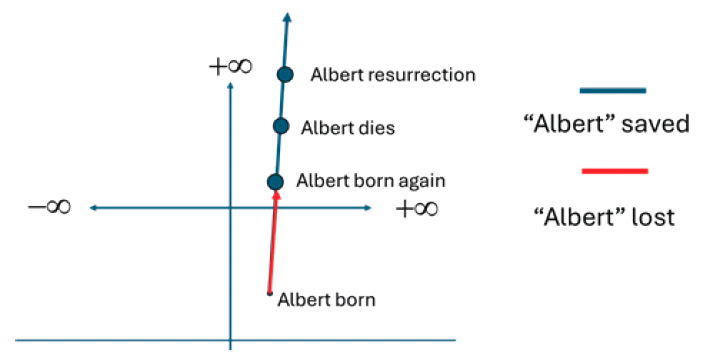
Fig 3. Spacetime diagram of the worldline of Albert, a born, lost, saved, dead, resurrected temporally extended geometric entity in spacetime.
We leave off the heresies of eternalism to now discuss presentism, which is consistent with SR and is a view that is attested by many physicists, Christians and philosophers.
The Presentists
Presentism stands in stark contrast to the eternalist philosophy. Presentism is the view that the present is real; that there is an actual real moment called now throughout the Creation. A present moment that continually passes. The past is forever gone, the future will be. Reality is a three-dimensional universe that exists at each moment of time. That such a view is consistent with the Bible should be readily apparent.
Before I proceed, let me address a possible misconception, and a very important one. I have encountered a small number who think that presentism compels one to embrace the heresy of open theism—the view that God is subject to time. Open theists, obviously and unsurprisingly, embrace presentism. But in their version of presentism God is trapped in time as something outside of God, independent of God and uncreated. That is not the God of Scripture.
On the other hand, theistic presentism is built on the fact that both space and time (but not spacetime) are creations of God. If one would want to say God can only exist in time according to presentism, then would they say that God can only exist in created space? Such is not sound reasoning. God is not subject to any aspect of His Creation.
God is immanent within the Creation (omnipresence). He is present within the spatial creation at each moment of time. He is also transcendent and exists independently of the Creation in every respect.
Presentists deny that the mathematics of relativity theory compels one to an eternalist view. Originally among these are Eddington and Reichenbach. More recent advocates of the reality of time and the flow of time are Bohm (1965),4 Ellis (2012) and Unger and Smolin (2015).
Also, there is a return to the presentist position among Christian physicists and philosophers that Christians need to recognize. Among these are Crisp (2008), Craig (2001), Pitts (2004) and myself, Dennis (2018) (and as I argue herein) to name a few.
For instance, Craig (2008) points out three competing metaphysical interpretations of SR; and that in particular, Lorentzian and neo-Lorentzian interpretations have the same theoretical structure, and yet assert an actual present. That is a significant push back on the notion that SR compels eternalism. It doesn’t. I personally am not a Lorentzian of either stripe. I will point out later that SR does not have sufficient theoretical resources to describe God’s Creation. Special Relativity of any interpretational variety is too impoverished. Instead, my claim regarding the present is based on a Machian interpretation of GR. That is that the gravitational field of all matter in the universe provides the universal reference frame. In this regard the cosmic gravitational field provides the metaphysical foundation for Mach’s fixed stars (see Dennis 2022).
Whitrow (1980, 348) in his comments regarding the flow of time quotes the eternalist Weyl (1949, 116): “the objective world simply is, it does not happen. Only to the gaze of my consciousness, crawling upward along the lifeline of my body, does a section of the world come to life as a fleeting image in space which continually changes in time.” The reader will detect that Weyl smuggles in time after saying it does not happen.
Whitrow continues summarizing Eddington’s and Reichenbach’s criticism of the eternalist philosophy:
Nevertheless, as has been stressed by Eddington (1935) and Reichenbach (1956 passim) the theory of relativity does not provide a complete account of time. Despite what Weyl has said, the theory is not incompatible with the happening of events but is neutral in this respect . . . The theory is compatible with either point of view and does not invalidate the concept of temporal transition. (Emphasis added)
To recap, the spacetime interval of special relativity only describes a causal structure of spacetime, and the causal relations are determined by the null cones as shown in fig. 4.
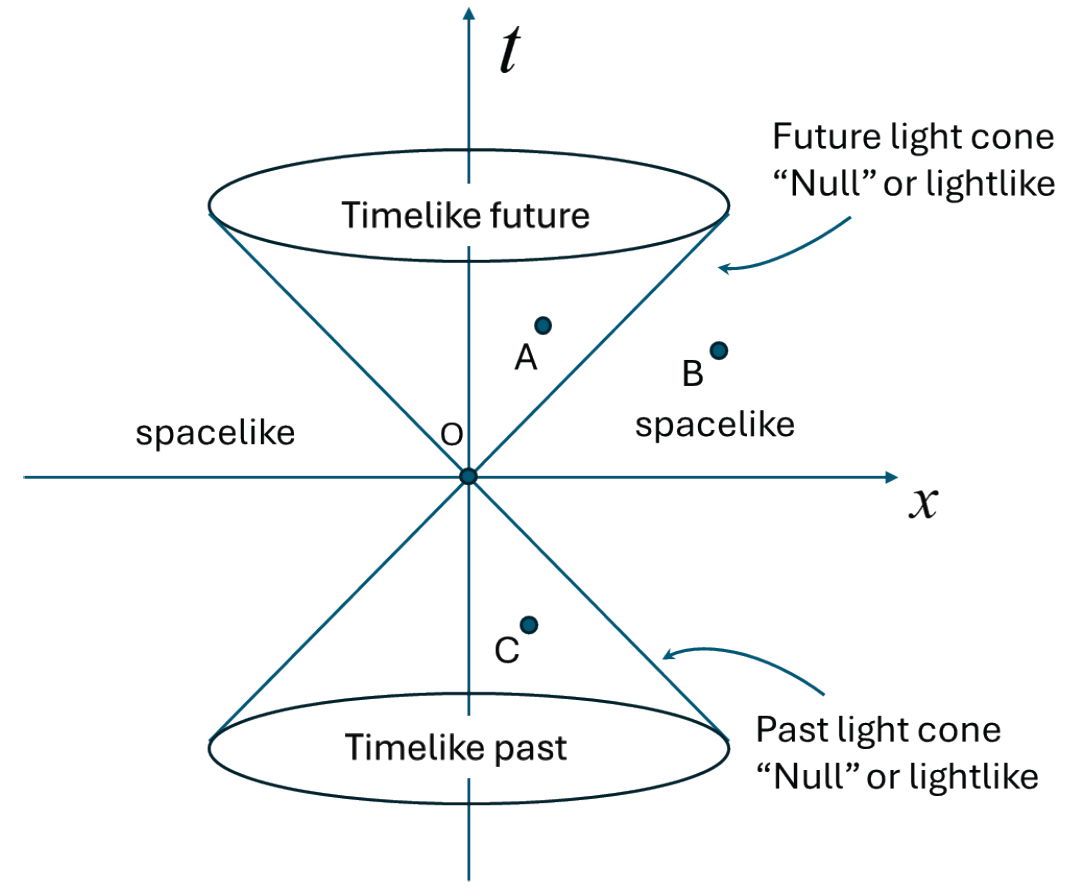
Fig 4. Causal geometry of Minkowski spacetime.
The null cones represent the surface of the motion of light, which are the surfaces of fastest causal signals, and thereby separate spacetime into regions which can causally influence each other. Within the interior of the forward null cone are future events that can be influenced by event O; and within the interior of the backward null cone are the events that can influence O. The remainder of spacetime, consisting of all events outside the null cone at O (and called spacelike relative to O), can have no causal connection with O. No observer at O can see any of the spacelike events that might be considered in the present. All spacelike events can only be seen at some time in the future when they are then in the past. Further, all causal connections are preserved, and the history of the past can be reconstructed. That history does not depend on which now might be considered as a present by way of the Lorentz coordinates. So, it cannot preclude the existence of an actual now—a real ontological present. When we consider that the Lorentzian and neo-Lorentzian models of the mathematics of special relativity are based on an actual (but unobservable) present, as mentioned previously, we can easily see that the eternalist argument based on a coordinate transform of the Lorentz transformation has no force. Eternalism is just a dogmatic article of faith, a philosophical metaphysical interpretation imposed on the mathematics. In short, an unknown and operationally indeterminable now (an epistemological judgement) does not imply the nonexistence of “now” (an ontology).
Does the Bible Use ASC?
Lisle makes this claim repeatedly. He does so without proof. Lisle states in his “refutation”:
ASC was the only convention in use until very modern times. It is therefore my position that the Bible likewise uses ASC. And in that system, there is no starlight problem.
Several incredible problems appear in that remark. First, it is “his position.” It is an opinion, and it is not a position revealed in the Bible. Second, he says there is no starlight problem. That is elliptical for the “light travel TIME problem.” ASC is not needed to solve the travel time problem in Lisle’s eternalist spacetime, as there is no such thing as the flow of time. Spacetime just is. It was created with all light paths already here and there. The ancients had no notion of ASC, it is a modern idea. He seems to think it took the likes of Einstein, Reichenbach, and their ilk to discover relativity, then add a conventionalist parameter, devised by the logical-positivist Han’s Reichenbach, which represents ignorance that followed from the technological limitations of the early twentieth century to rescue the Word of God! The ancient Hebrews had no need of such, and the Word gives not a single hint of such. In the end all of Lisle’s theorizing ends up being nothing more than an empty support to claim that light traversed (if I can use that term) billions of light years, by definition. As John Byl (2024) points out, “Therefore, Lisle’s proposal is not so much a solution to the distant starlight problem but more a dismissal of the question as physically meaningless.” And elsewhere Byl states,
Thus, the Anisotropic Synchrony Convention model does not really solve the distant starlight problem. It merely dismisses it as physically meaningless. It relies on a positivist interpretation of Special Relativity, leading to a phenomenalist interpretation of Genesis 1 that contradicts the plain reading of the biblical text.
It would also be remarkable that the God-breathed words of Bible, which obviously uses tensed verbs5 describing events in the past and the future, and thus a flow of time, would need to be rescued by an eternalist interpretation of special relativity that denies the reality of time.
Are Conventionalism and Special Relativity the Same Thing?
Lisle at one-point claims that conventionalism is “the physics of Einstein,” that is, special relativity. This is an assertion without proof, and flies in the face of a body of philosophical publications. If philosophers take positions with respect to conventionalism (that is, the conventionality of simultaneity) versus non-conventionalism (that is, the relativity of simultaneity) then there is broad consensus that Lisle’s assertion is false. I’ll give one example from the philosopher of science John D. Norton (though an eternalist), who states:
In balance, my view is more sympathetic to the non-conventionalist view. I incline towards the realist view of Minkowski geometry.6
Readers can easily search the literature to find the debate on the two points of view. If the two views are equivalent according to Lisle, it certainly is remarkable that there is a continuing debate. Lisle’s continued assertion that the conventionality of simultaneity is relativity is simply false.
Another key point is that the conventionality thesis is only valid within the context of the empty universe of special relativity. For our universe filled with gravitational bodies the argument fails. As John Norton remarks, regarding spacetime solutions in GR:
These spacetimes have an absolute relation of simultaneity and a distinguished motion, the expanding motion of the cosmic fluid formed by the galaxies, viewed on the largest scale. In sum, whatever fundamental moral we may have drawn about the conventionality of simultaneity, it is limited specifically to the special theory of relativity. It has no general applicability. There is no such convention in later theories of space and time and, in particular, in the spacetime structure that we think better represents our universe. (Emphasis added, cf. footnote 6)
We will say more later, but cosmological solutions in GR do comport with presentism, as evidenced in the Friedmann-Lemaître-Robertson-Walker (FLRW) solutions which reinstated a global present equal to the cosmic time or age of the universe. Lisle bases his repudiation of presentism via elevating special relativity over general relativity. Special relativity has no physical mechanisms to model a realistic creation. Special relativity (a sub theory of general relativity) is a theory of light travel in an empty universe. Interestingly, special relativity still holds locally in the cosmological solutions with absolute global cosmic time and a global preferred reference frame given by the Hubble flow. This is not a contradiction. More on that later.
Misconceptions in the Refutation
Unique Reflection Events, Euclidean Geometry Constraint and Lisle’s Light Cone Morph
We can begin with my initial claim regarding the properties of Minkowski spacetime. Before I proceed though, it is important to emphasize that Minkowski spacetime is a geometric space with intrinsic symmetries. These symmetries are absolute and independent of coordinates. They can be hidden by bad choices in coordinates or revealed with coordinates adapted to the symmetries. More on this later.
Fig. 5 shows my original figure illustrating anisotropic speeds. To recap, my statement regarding the diagram is that as shown it presupposes two properties. That 1) the spatial geometry was Euclidean and 2) that there was no assumption that the speed of light was isotropic. We will say more on Euclidean geometry and the non-Euclidean spatial geometry of the ASC “surfaces of simultaneity” later. (It is important to note that those surfaces have different geometries than that of the Minkowski spacetime in which they are embedded. This is an important point that amazingly Lisle fails to notice when he claims I am contradicting myself regarding coordinates.) Fig. 5, as drawn, is taking seriously one way of viewing Reichenbach’s conventionality thesis. The reflection is shown occurring at a time not equal to the halfway time of ESC and that the distance to the reflector is indeed R equal to the coordinate x1. By only drawing one such possible time of reflection, I may have inadvertently not given enough argumentation. To rectify this, we can look at Fig. 6 which, true to the Reichenbach proposal, shows several different times of reflection. According to Reichenbach (1956) each conventional reflection time is potentially (?) consistent with reality. Another way of looking at the diagram is to compute the time of reflection assuming a variable outgoing speed-of-light which we will denote as c+. Under the Euclidean constraint, the distance from the origin to A and B, etc. is fixed and equal to R (which ironically is the ESC distance). By standard kinematics we then have for the arrival time (tR) at the reflector:
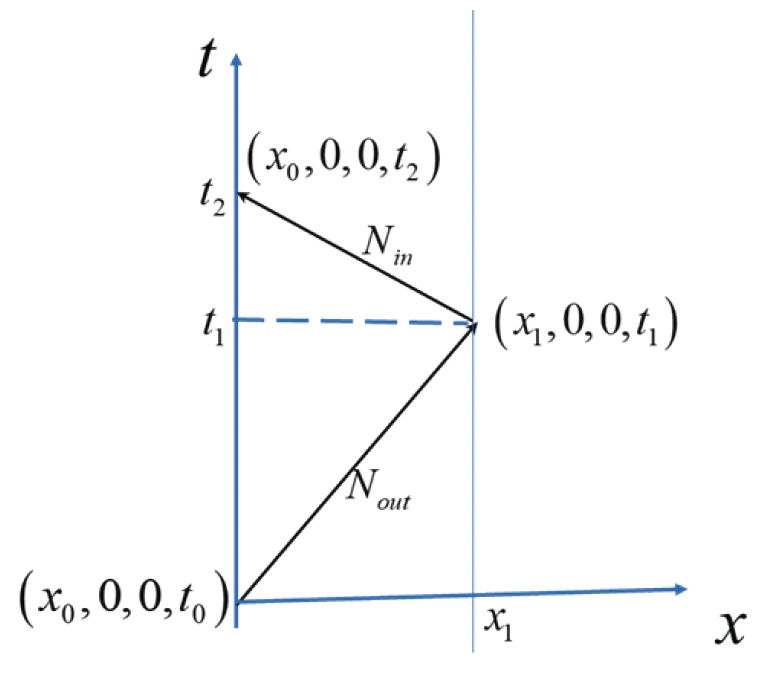
Fig 5. Geometry of two-way light travel in Minkowski space assuming anisotropic light speeds.
So, under the specifications of the experimental arrangement, we have:
Clearly, if we assign different values to c+, the time of reflection will change; it will move upward as in fig. 6 if we allow c+ to approach c/2. Of course, there is only a single actual reflection event, and it is not conventional. That implies there must be a one-way speed of light that is a fact of nature. According to the conventionalists we just don’t know what it is. How else did the light get from the origin to the mirror? Now, we cannot cause there to be a different reflection event by change of Reichenbach’s ε parameter of ignorance. The notion that an epistemological and operational limitation due to the technology of the day (resulting in an unknown value for the one-way speed of light) implies an ontological fact that the one-way speed of light is not a fact of nature is a major philosophical faux pas. In fact, such an assertion flies in the face of equation (1). If there is a unique reflection event, then there must be a speed-of-light that is a fact of nature. There must be a one-way speed of light; the technology of the 1920s only implied they didn’t empirically know its value. Today we know its value empirically from experiments such as the Caltech femtosecond camera, among others.
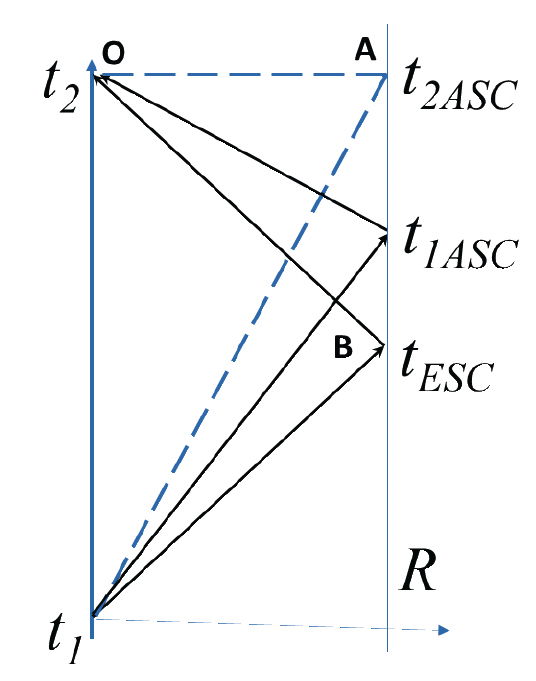
Fig 6. Three “conventional” reflection events using a “conventional” time in a spatially Euclidean geometry.
Returning to the figure, we note that it is a spacetime diagram for which the intrinsic geometric model assumed is Minkowski spacetime. This means that OB for instance is a lightlike interval. The same would hold for each of the intervals from O to the ASC reflections—if they are the actual events of reflection. These all cannot be lightlike; only one can be so. We agree that there is only one actual event at which the photon was reflected. This implies that what we are viewing under the Euclidean constraint, is a morphing of the light cone.
The attentive reader who attended Jason Lisle’s presentation at the 2018 ICC may notice, upon consideration, that fig. 6 is in fact a version of Lisle’s light cone morphing shown in fig. 7 (it was an animation at the ICC).
We can view the alternative reflection events as a morphing of the light cone, such that the Euclidean distance is maintained and such that the speed of light becomes truly anisotropic. In other words, the coordinate R maintains its meaning as a distance. Those who watched Lisle’s ICC presentation in which he morphed the null cone to illustrate ASC will notice that the movement of the reflection times upward in my figure is identical to Lisle’s null cone morphing shown in fig. 7. In that figure we denote a point B on the incoming null cone being displaced upward at constant x = R.
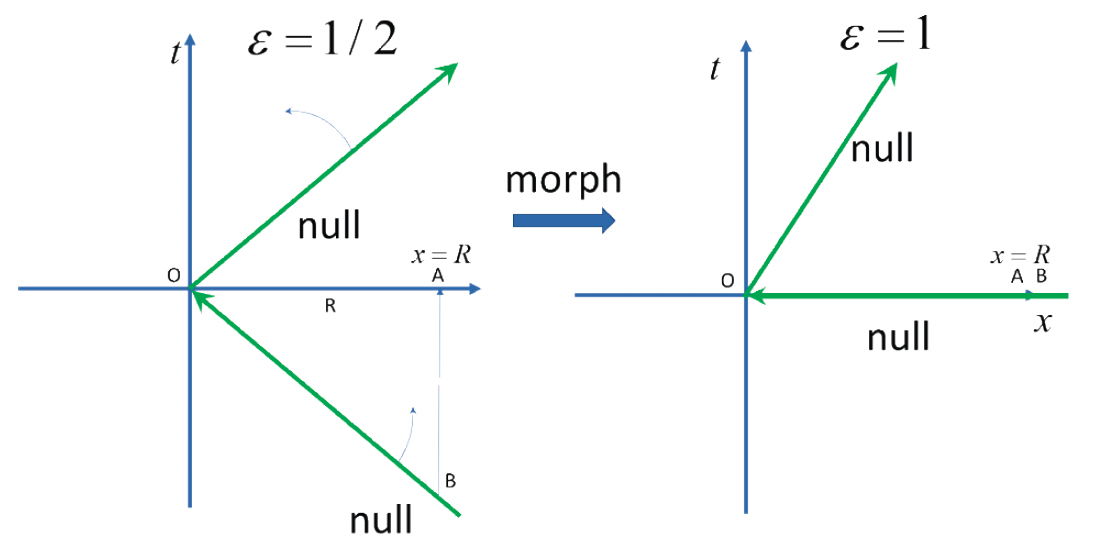
Fig 7. Lisle’s 2018 ICC light cone morphing.
This figure has several misleading aspects. First, the light cone deformation is displayed as an active distortion of the light cones. This would affect an actual physical change in the one-way speed, if it were real, since if x is constant and maintains its meaning as a distance, we would have.
To repeat, the time and spatial axes are displayed as unaltered, implying that the underlying geometry is still Euclidean and preserved during the morphism. This aspect will be lost on laymen and apparently Lisle, too.
But we note the following. In the final configuration on the right, the null interval is congruent to , that is, the final state has the light ray aligned with the x-axis. But for null rays the spacetime interval is zero. So, the x coordinate is now null and thus the distance along the x-axis is zero. It is no longer the original distance R. In fact, as the morph evolves according to the change in epsilon from ½ to 1, the distance represented by the x coordinate changes from R to 0 continuously.
But the false impression given to the lay audience is that the light is traversing actual distances (x interpreted as the original distances) in zero time (hence infinite speed of light). This is a deception (though I am not imputing intention to Lisle in that regard).
This is an example of Lisle’s mistaken notion that the ASC coordinate change does not alter distance. The morphing cannot lay claim to maintaining the coordinate value of x (= R) as the physical distance and stay true to the geometry of Minkowski spacetime. We will say more about this in detail when we address Lisle’s mistaken notion that the ASC space of simultaneity is Euclidean; it seems he has forgotten some basics of calculus and does not have a full understanding of how to read a metric.
Before we leave Lisle’s misleading morphing diagram, we should note that as drawn it omits key physical features of spacetime. It only shows a 2D cross section of the right most portion of the null cones. A more complete illustration is shown in fig. 8. We have shown the final state of the null cones. The striking point is, that in Minkowski space, light rays are straight lines, yet the Reichenbach convention as portrayed by Lisle would require that light rays are no longer straight lines, but rather bent. The green light ray represents a single light ray, and similarly for the red. At the ASC origin, both rays encounter an instantaneous impulse7 that changes the “speed” from infinite to c/2. This is clearly not what the Reichenbach coordinate change implies. A coordinate change cannot alter the geometry of the geometric object known as Minkowski space nor can it impose symmetries on spacetime (more on this later when we examine further errors in Lisle’s self-published The Physics of Einstein [Lisle 2018]). Thus, a different diagram is needed to represent the ASC convention which is just a relabeling of the spacetime. We have more to say later.
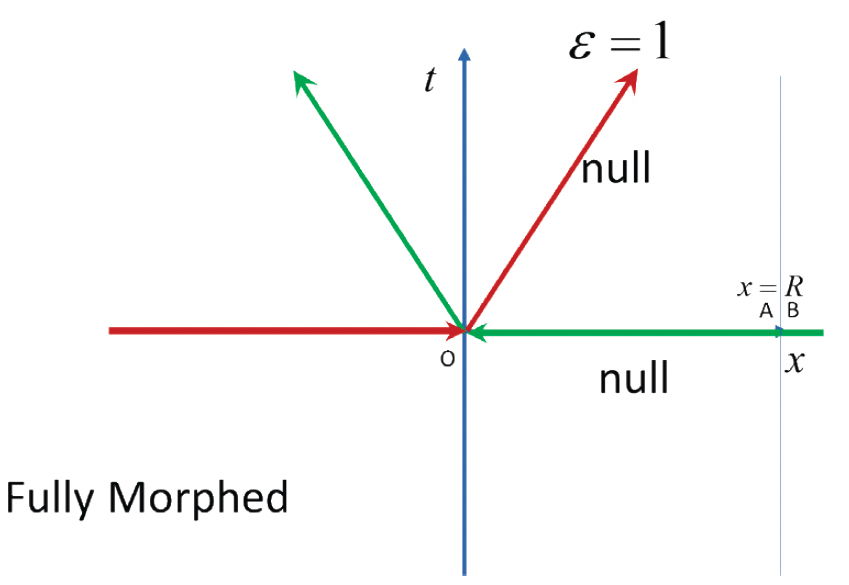
Fig 8. Distortion of the full null cones in cross section.
Reichenbach Magic Light Rays
Lisle elaborates on the details of ASC by presenting the derivation of the general anisotropic (pseudo) “speed” formula. The most general formula in polar coordinates (for ε = 1, Lisle’s favorite value) is:8
In this formula θ is the angle between the light’s velocity vector and the spherical coordinate radial direction. This formula as usually presented hides some detail. The speed is independent of the azimuthal angle, thus indicating that the speed is independent of that angle. Thus, the surfaces of constant ν are cones about the radial direction (of course, θ = π/2 it is not a cone but the transverse plane).9 This means that in the plane transverse to the anisotropy axis the light is fully isotropic. This will have important repercussions on the viability of the Reichenbach’s conjecture, as we now analyze.
The genesis of Reichenbach’s conjecture dealt with the issue of experiments to measure a one-way speed of light, all of which were restricted to two-way one-clock configurations. In the days of Reichenbach, technology was primitive compared to today. The notion that one could produce light bullets of 2 mm (7 ps durations) and less in width was unheard of. We have already disposed of those antiquated restrictions of the Reichenbach operationalism above.
However, let’s explore Reichenbach’s model and the necessary theoretical deductions that ASC advocates must accept (unless they are willing to reject special relativity and search for an alternative theory). Let us examine a fictional Hans Reichenbach performing his two-way experiments at various locations and orientations relative to a reflector. According to the equations of the ASC convention, light knows how to respond to Reichenbach’s experimental clock and light source; he must have had an attractive personality!
This is shown in the fig. 9.
But there is more to explore. The pseudo-speed formula above constructed from special relativity (Minkowski space) necessarily implies that when we perform any two-way speed measurement we must conclude that the speed of light transverse to two-way light path is isotropic. So, in fig. 9, in which ASC center 1 is aligned roughly northwest to southeast, a measurement of a two-way speed of c means we have also measured a southwest to northeast (and northeast to southwest) one-way speed = c by necessary logic of the theory.10 Likewise, when using ASC center 2 aligned roughly southwest to northeast, a measurement of a two-way speed of c means we have also measured a northwest to southeast (and southeast to northwest) one-way speed = c by necessary logic of the theory. By imagining the experiment being repeated at multiple locations around the mirror, we can easily conclude that ASC is not a speed of light, and in fact, ASC must conclude that the one-way speed of light is indeed isotropic. What would be remarkable would be a two-way speed of light that was angle dependent. But such has never been observed.
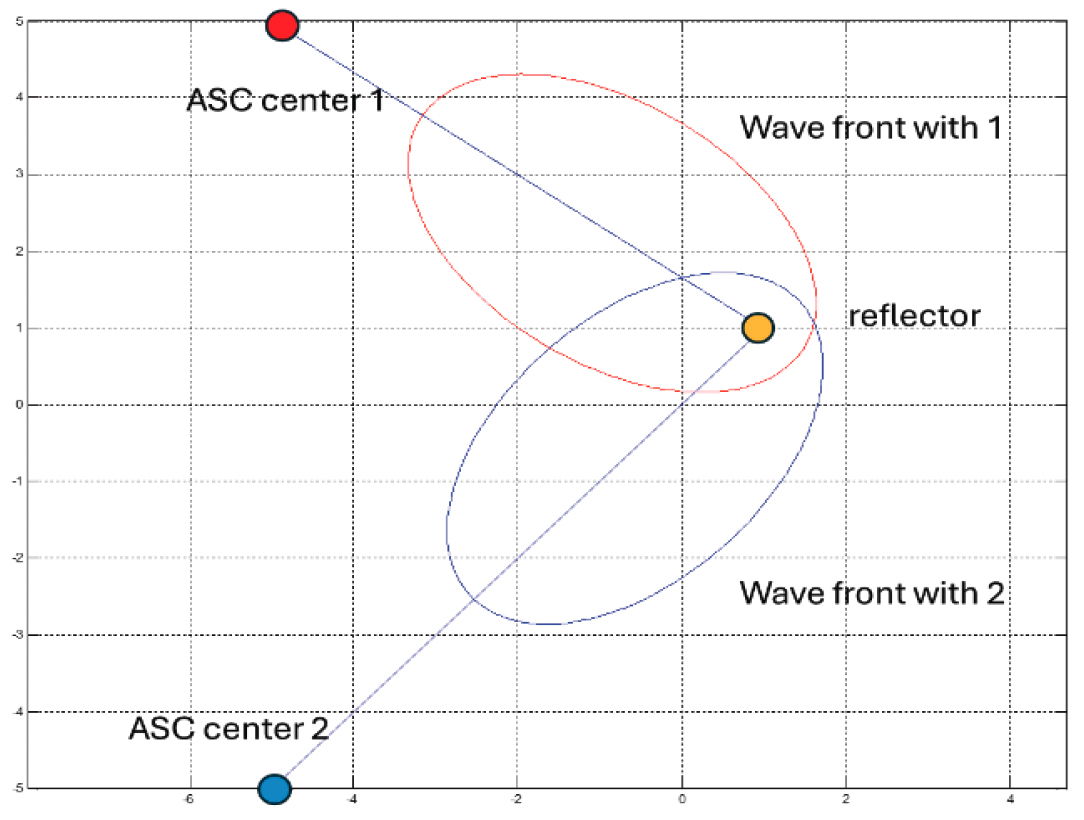
Fig 9. Magic ASC pseudo-speeds depending on where Reichenbach decides to measure a 2-way speed of light.
So much for the magic pseudo-speed-of-light formula.
The Jet Airliner Analogy
It is always a danger when using an analogy that an opponent will seize on aspects that are not part of the analogy to dismiss it. This is what Lisle does when he appeals to the aspect that a human on the plane would feel tired from the trip. The presence of a sentient being on the plane is not relevant. In my attempt to relate to laymen the purely artificial kinematical aspect of the ASC coordinate transformation I used a familiar example. Let’s rephrase the analogy using an unmanned aircraft. The experience of a person versus the experience of a photon (whatever that means, photons do not experience anything) is not a point of contact. The point of contact is the purely kinematical correspondence of the desynchronization process used for the jet airliner and the similar desynchronization of the clocks for the photons to result in a purely kinematical relabeling of events. We display the equations as shown in Table 1.
Table 1. Comparison of kinematic formulas.
| Jet Airliner Analogy | ASC and Eddington Finkelstein Coordinates |
|---|---|
| t = t'−r/vjet | t = t'−r/c1way |
| r(t) = vjet(t'−t) | r(t) = c1way(t'−t) |
The first line expresses the trajectories in terms of time. The second line shows that the equations are the familiar kinematic formula for uniform motion, expressed in terms of time of arrival t′. None of the equations expressly indicate a time of departure—though it can be deduced if the distance at departure is known. The analogy lies in the kinematical (algebraic) correspondence between the jet and ASC, which is exact. The second line for the jet is the trajectory of the jet and the second line for light is the trajectory of the light. Both cases require knowledge of the one-way speed to achieve infinite speed by eliminating the one-way speed time.
Lisle bites hard and calls this absurd. It obviously is absurd, which is precisely the point of the mathematical analogy. It is also absurd to claim that the ASC desynchronization of clocks can change the speed of a photon. This is a theoretical result and is independent of the supposed empirical limitation of not being able to measure the one-way speed of light. To repeat, the theoretical content of the above two equations is that both the jet speed and the light speed are one-way kinematical equations. Inverting them as equations for time and declaring them a synchronization convention is mere rhetoric. Lisle saying Eddington-Finklestein coordinates (identical to ASC in SR) is also a synchrony convention is a result of his seeing all kinematic relations as susceptible to a synchrony convention interpretation. This is just another case of Lisle making unsubstantiated interpretational claims. To claim the ASC equations can only be a two-way average is a philosophical error and a misinterpretation of mathematics. Lisle’s repeated claims that the symbol c in theoretical equations can only be a two-way speed is to confuse and import an empirical claim into a mathematical expression in which the symbol c does not represent a two-way speed of light. Of course, none of this is relevant today since we have seen that we do empirically know the value of the one-way speed of light; and second that the ASC model thereby also necessarily predicts an isotropic one-way speed of light. To make it clearer, one cannot subtract out (that is, eliminate) a one-way travel time unless one uses a one-way speed to desynch theoretical clocks. That is precisely what the ASC equation says, and what the jet analogy says. ASC has zero physical content, being able to make any object travel at a kinematic infinite pseudo-speed by merely claiming it arrives at the same time it departed.
Imposing Symmetries on Spacetime” and the “Simplicity” Red Herring
A major misconception of Lisle’s occurs in The Physics of Einstein. Lisle (2018, 241) states:
Of the infinite possible choices of Epsilon, two stand out as particularly useful. We already know that epsilon equal 1/2 is especially nice because it makes the mathematical equations less cumbersome. Furthermore, this choice imposes a symmetry on spacetime by insisting that the one-way speed of light is isotropic. This means that we do not need to know the direction in which light travels to know its speed. This is very convenient. There is a third advantage to using this convention which we will discuss below. (Emphasis added)
This is another major conceptual faux pas. Here Lisle makes the astounding and strange claim that a coordinate system can impose a symmetry on spacetime! That is a shibboleth and is not a statement that a well-informed student of relativistic physics would make. We note that Lisle admits in his refutation the contradictory (but true) claim that coordinate changes cannot alter the geometry. Coordinates cannot impose symmetry on Minkowski spacetime. Symmetries of a geometric space are intrinsic and cannot be created or destroyed. It may be that Lisle has advanced in his study of relativity since 2018, and he will now agree that the above quote was a gross misunderstanding.
So, what is the symmetry that Lisle thinks is imposed on spacetime by ESC coordinates? It is clearly the formal simplicity of the algebraic representation of the metric components. But the form of the metric in local coordinates is irrelevant to discovering the symmetries (isometries) of a geometric space. Some coordinates can hide the symmetries and others can reveal the symmetries more transparently. The latter is the deeper understanding of what the simplicity means. In short, the brute simplicity remark of ASC advocates (or Lisle’s less cumbersome), that stops short of asking “Why are some coordinates simpler?”, reveals a lack of that deeper understanding. Let’s explore the isometries of Minkowski spacetime in terms of ESC and ASC coordinates.
Let’s begin with those simpler ESC coordinates. Here again is the Minkowski metric in ESC coordinates (in the spacelike convention):
Can we immediately recognize the isometries of this geometric space? The answer is yes.
Minkowski spacetime is an example of a maximally symmetric space. A maximally symmetric space of dimension n is one for which the group of isometries is composed of n(n + 1)/2 generators. It is also homogeneous and isotropic.
The dimension of Minkowski spacetime is n = 4, so if Minkowski spacetime is maximally symmetric then the isometry group must have 4(4 + 1)/2 = 10 generators. Looking at equation (2), we see that since the metric is independent of position there are four translations in each of the four directions t, x, y, and z. This means that Minkowski spacetime is homogeneous. Also, we can see that the spatial components (with dt = 0), are symmetric with respect to the three rotations about the x, y, and z axes. The final three transformations are the Lorentz boosts corresponding to constant speed motion in the x, y, and z directions. These are perhaps not easy to see for some, but they correspond to the three hyperbolic rotations in the (t, x), (t, y), and (t, z) planes. Counting all these isometries, we arrive at a 10 dimensional group of isometries. That group is the Poincaré group. Thus, Minkowski spacetime is maximally symmetric and thereby homogeneous and isotropic. The deep meaning of the simplicity of ESC coordinates is that they transparently reveal the isometries of Minkowski spacetime. This aspect seems to be lost to all those who declare that ESC is merely simpler as if by some strange accident.
The remark in The Physics of Einstein is also markedly at odds with Lisle’s true statement in his refutation that coordinate transforms cannot change the geometry. Yet Lisle claims they can impose symmetries on spacetime (that is, the geometric object). So, to use Lisle’s words, doesn’t Lisle both affirm and deny that coordinate transforms cannot change the geometry?
So, if ESC imposes a symmetry on spacetime, does ASC annihilate symmetries of spacetime? Of course not. Can we easily see the symmetries of Minkowski spacetime in ASC coordinates? Not so much. Here is the ASC version of Minkowski spacetime:
We can easily see the time translation isometry (since the metric is independent of the time). And we can easily recognize rotations (three dimensions) about the origin (spherical symmetry). These account for four of the ten isometries. The homogeneity of space is not so transparent, nor are the Lorentz boosts—which are the other six isometries. Given the metric form above is there a way to discover all the isometries? The technical answer is, yes. Given the metric of a space in an arbitrary coordinate system, the isometries can be found by solving the Killing equations. The solutions are the Killing vector fields that generate the isometries. The Killing equations are partial differential equations, which in local coordinate index notation are:11
Note that there is a maximum of 10 such vector fields since the symmetric tensor equation (3) has ten independent components. We won’t solve those here in ASC. The solution in terms of ESC is not surprisingly hard since there are no pseudo forces (the connection coefficients are all zero). In ASC there are non-zero connection coefficients complicating the partial differential equations.
At any rate, Lisle’s symmetry imposition claim is another symptom of his incomplete understanding of how to interpret the metric.12 In fact, Lisle’s claim opens him to the charge of contradictions that he injudiciously hurls at me. Lisle both affirms “(ESC imposes a symmetry on spacetime) and denies that coordinates alter the “underlying geometry.” These point to deficiencies in Lisle’s education and understanding that might be explained by the sources used in his studies of relativity.
Lisle’s Lack of Understanding of Coordinate Representations of the Metric
How to Interpret a Coordinate Representation of a Metric
Lisle several times challenges my interpretation of the coordinates in ASC. These all stem from his calculus gaff that the ASC transform does not alter distances and apparently conjoined with his ignoring my challenge to analyze coordinates using the geometry as represented by ds.
So how do we interpret the coordinate labels in terms of the geometry of various geometric objects in a space? We must look at how the labels contribute to the metric of the space. In relativistic parlance, this geometry is encapsulated by the invariant metric as expressed in the formula for ds which gives the actual distances in the space, whether they be distances along a 1D curve, 2D, or 3D surfaces, etc. within the space.
In an early and famous exchange between the French mathematician Paul Painlevé and Albert Einstein, concerning coordinates and invariants, Painlevé mistakenly said: “It is pure imagination to claim to draw consequences of this nature from ds2” Einstein, in reply, correctly stated: “only conclusions reached after the elimination of coordinates may pretend to an objective significance . . . the metrical interpretation of the quantity ds2 is not ‘pure imagination’ but the deep core of the theory itself.” (Emphasis added)
We will now show using several examples from relativistic physics how this procedure works.
First, we examine Minkowski spacetime. In ESC coordinates the invariant is:
How do we know what the coordinates represent physically? Do we just construct an arbitrary set of labels and presuppose their physical meaning? No. We must interpret the coordinates in terms of the geometry embodied in ds.
The formula above is a sum of terms involving coordinate differences. But we can consider, one by one, the one-dimensional paths in the space. For example, suppose we move along the x-direction alone, maintaining the other coordinates constant. We then get for the interval:
This shows that the coordinate x directly measures distance ds, it is not merely an arbitrary label. It is ds that imparts the physical content to the label dx, not the reverse. It is at once obvious that the same considerations apply to the other coordinates. For the case of the time coordinate a minor technical detail is that the interval is not given by ds2 but its negative. (This is one unfortunate accident that historically the spacetime interval was written as ds2 in concession to the traditional notation employed in differential geometry of Riemannian spaces). Thus, for someone situated at constant x, y, and z, we have:
This shows that the tcoordinate is not an arbitrary label but is the physical time elapsed on an ideal clock. If a Lorentz transformation is applied to the coordinates, we find that:
Thus, the same analysis shows that t′, x′, y′, z′ also directly represent and measure physical quantities but in a different inertial frame.
We next turn to an example that has caused much pain, consternation, and confusion among those who were not attuned to the developments within the GR community in the late 50s and early 60s. Such pain and confusion continued among the uninformed and self-educated students of GR well into the 1990s. This is the dreaded Schwarzschild black hole solution. This was one of the early exact solutions of the Einstein equations of GR. The famous (or infamous) equation for the metric in “Schwarzschild coordinates” is:
Before we proceed, note that the metric above can be used to describe many geometric objects within the solution. Of course, all four terms describe the geometry of the 4D Schwarzschild geometry overall. Within that geometry there is a family of 1D worldlines, that is, those spanned by each coordinate line (t, r, θ, φ). For example, if only the coordinate t varies, we have a 1D worldline of an object at rest at a fixed radius from the origin. We will show below that the 1D metric indicates that the coordinate t does not measure physical time. We must use ds. The last three terms describe a 3D space at a fixed moment of time, and finally it should be obvious that the last two terms describe the metric of a 2D sphere of radius r. As can be seen if r → ∞ the metric reduces to Minkowski metric in spherical coordinates:
We see that for an object at rest, following the line of reasoning given above, that the t coordinate measures the time elapsed on the local clocks far removed from the gravitational source. While we are here though, consider an arc with t, r, φ constant. In this case we have a 1D curve that lies within the 2D sphere, and the metric of that curve (a geometric object) is:
From which we readily see that the angle theta does not measure distance, but rdθ, being equal to ds, is the distance, as recognizable by the formula for arc-lengths of a circle. We are using ds to interpret the coordinates.
You will note we are precisely following Einstein’s correct prescription for interpreting the content of the theory by looking at ds.
Returning to the Schwarzschild black hole solution, we ask what is the t for someone stationed at constant r, r, θ, φ?
We get for the time component of the spacetime interval a value of
This shows that the coordinate dt does not measure (proper) time at the radial coordinate r. The metric coefficient must be employed to produce the physical proper time registered by the ideal clock in terms of t (the time registered by clocks at infinity). Now the fly in the ointment is: What does the coordinate t mean physically if
The quantity rs delineates what is called the event horizon of the black hole. We should notice that values of
are not in the domain of the equation for dτ. This should alert us to the fact that dt is not time in that region! We need to go back to equation (4) to properly interpret the time label. Just because it is lexically a t should not cause us to jump to a false conclusion that it is time. That is not the way the geometrical principles of relativity work. We change the signs of the coefficients of t and r so that they are applicable for the region r < rs this gives:
We now note that dr has the negative sign in the metric and dt now has the positive sign. This means that dr is the time coordinate and dt is the spatial coordinate. Another point is that since r is now time, the solution inside the horizon is time dependent. This is because objects inside the horizon can no longer stop their fall to the singularity. Repeating the analysis for the proper time of an object falling past the horizon we get:
So, the coordinate interval dr is not physical time, rather dτ is the proper time and dr is not a distance but a time interval. Quite a surprise for those who might be dabblers in coordinates.
At the risk of multiplying examples, I adduce the FLRW (big bang) cosmological solutions. The use of the full big bang is not an endorsement thereof but is an example of how to correctly interpret a metric and the coordinate labels that are used to specify events. We will also use this metric later when we continue a discussion on GR’s overthrow of conventionalist philosophy.
The big bang cosmology (without affecting the main point, I am using the flat space version) in terms of comoving coordinates x, y, and z is:
The function a(t) is the expansion factor. The coordinates dx etc. are the comoving coordinates. They are attached to the matter in the universe, and they follow each elemental particle of matter as the universe expands, so they are constants. To simplify the analysis, consider a particle positioned along the x-direction with x = x0 and y = z = 0. For this case, we ask: Is the distance from the origin? If so, that would mean the distance is constant and we have a static universe? But clearly the FLRW model is not a static universe, it is an expanding ball of matter, so the comoving coordinates x, y, and z are not distances.
So yet again, and consistently, we need to look at the invariant geometric interval ds.
Rather, the distance from the origin in x-direction for a particle with coordinate x = X at cosmic time t is:
The distance from the origin changes due to the time dependent scale factor a(t) in the metric which, when combined with dx, gives the correct interpretation of the geometric distance.
From the above we get the Hubble law from the distance R(t)
To summarize these examples, if we are moving along an x direction in a general metric, with all other coordinates constant we have:
From this we can immediately deduce that the coordinate dx would represent a physical distance only if gxx = 1.
The main take away that should be noticed is that if the coefficient of a coordinate label is 1 then the coordinate directly measures physical intervals as one moves along the curves in that direction while all other coordinates are held constant. We see that dx is a physical distance in this case by seeing that it is equal to the invariant ds. Otherwise, the coordinates are merely labels to identify points.
The above are examples of analyzing the geometry by way of the combination of the metric components and the coordinate differentials, both must be combined to extract the geometric/physical content and to ascertain the meaning of the coordinates employed.13 We have followed Einstein’s correct prescription. To only make statements about coordinates (as Paul Painlevé believed) is inadequate and can lead to egregious errors in interpretation. One of the most famous being that time flows backwards inside black holes.
We will use the above later when we analyze the geometry of ASC’s 3D spaces of simultaneity and Lisle’s misapprehension of my comments and references to different geometric structures involved in ASC and ESC and what they represent physically (and philosophically). Not all the geometric structures to which I refer are Minkowski spacetime as a whole, some are 3D subspaces (or hypersurface) embedded within Minkowski spacetime and thus have different intrinsic geometries because they have different shapes.
Coordinates in Themselves are not Geometric Objects
Lisle states:
It appears that Dennis both affirms and denies that coordinate transformations affect the underlying geometry. To be clear, they do not. A sphere is still a sphere regardless of what coordinate system one uses to express it. Some coordinate systems may be more useful than others in a given scenario. But they are merely ways of assigning numbers to represent the position and time of an event.
First, Lisle claims I have affirmed contradictory views regarding coordinates. This is not true. Lisle appeals vaguely to underlying geometries. To what does he think underlying geometry refers? The point he is missing is that there is a distinction between the geometry of spacetime and the intrinsic geometry of embedded hypersurfaces. I will explain later that Lisle is not carefully reading and comprehending that I am referring to different geometric objects within abstract Minkowski space.
But Lisle is correct that coordinates cannot alter physical reality. They are merely labels that identify points in a geometric space, be it an abstract n-dimensional Euclidean space or 4-dimensional abstract Minkowski space. I’ve said this repeatedly in my writings. In fact, even a cursory introduction to the mathematical foundations of differential geometry shows that the coordinate functions that assign labels in Rn to points p in an n-dimensional manifold only preserve topology.14 They do not (necessarily) preserve distances. I refer the reader to Dennis (2022, footnote 23). This footnote was added since one anonymous reviewer of the paper made the claim that I had predetermined the solution in a cavity devoid of matter. The reviewer asserted I had neglected a different solution, namely the Milne model, and that presumably, that would lead to a different conclusion. The reviewer had thus confused a coordinate system with a geometry. Much like Lisle mistakenly saying that ESC imposes a symmetry on spacetime. Here is a portion of the footnote: “Different functional forms of the metric tensor can represent the same geometry. Stated in geometric terms the invariant spacetime interval along a geodesic between two points is independent of the coordinates. An analogy can be made with cartography, map projections, and the geometry of the earth’s surface (as an idealized sphere). Different map projections provide different mathematical representations of the surface of the earth. For example, the expression for ds2 in the coordinates of a Mercator projection look different from the expression in a polar stereographic projection. But map projections cannot alter the earth’s intrinsic geometry. The mistaken claim that different looking expressions for ds2 (of the same underlying space) are different geometries is to conflate coordinates (map projections) with the intrinsic geometry of the space (surface of the earth). Claiming that the Milne model is a different geometry than Minkowski space is incorrect.”
More not Understanding the Metric Tensor
I quote Lisle in extenso to show his limited knowledge of how to read metric tensors. Lisle states:
Strangely, Dennis then states, “This shows that the x-axis and y-axis are no longer orthogonal.” But that is not the case, and it is not clear why he thinks it is. I suspect Dennis has again confused a distance with the invariant spacetime interval. All the above equation demonstrates is that the product of x and y contribute to the spacetime interval in ASC coordinates. This does not mean that the spatial axes are no longer orthogonal. By construction, the x and y axes are orthogonal, which is to say that changing the x coordinate alone has no effect on the y coordinate, and vice versa. We demonstrated above that synchrony conventions have no effect on spatial geometry since x′ = x, y′ = y, and z′ = z. Even Dennis himself admitted earlier that “this coordinate transform has not altered the intrinsic geometry of Minkowski space.” So, again we see that Dennis both affirms and denies that coordinate transformations affect geometric realities.
We will treat the several wrong statements and misinterpretations of my remarks regarding coordinates in order.
Strangely Strange
A telling remark of Lisle that reveals his confusion and a lack of depth in understanding the mathematics of relativistic physics and spacetime is when he says:
Strangely, Dennis then states, “This shows that the x-axis and y-axis are no longer orthogonal.” But that is not the case, and it is not clear why he thinks it is. I suspect Dennis has again confused a distance with the invariant spacetime interval.”
My claim is not so strange! And, no, I have not confused a distance with the spacetime interval. (Actually, every interval in spacetime is a spacetime interval. On the other hand, it is Lisle who has confused a coordinate interval with a spacetime interval.) Lisle’s admission that “it is not clear (to him)” indicates a major hole in Lisle’s mathematical knowledge. In fact, Lisle’s comment is the one that would be extremely strange for an expert in relativistic physics. This is another shibboleth. This is further indicated in his next incredible claim regarding cross terms in a metric, viz. “All the above equation demonstrates is that the product of x and y contribute to the spacetime interval in ASC coordinates.” This is incredibly unbelievable. Another bald statement of ignorance. The metric does not merely represent the spacetime interval alone. The value of the metric tensor at a point is the inner product (2-form) in the tangent space of vectors at that point. This is also manifest in the tensor operation of contraction. For example, if Xa and Yb are contravariant tensors (vector fields in this case), then the contraction of the tensor Zab = XaYb is Zaa = XagabYb. The latter being the inner product of the vector Xa and the vector Yb. These are basic facts of differential geometry that obviously Lisle is not aware of. Though Lisle should know it. How else can we account for such a gaff? And why did Lisle claim “But that is not the case” regarding the non-orthogonality claim? We will see that he gets lost in spacetime and uses the ESC metric to show orthogonality. A major blunder. We know they are orthogonal in the ESC 3D plane because that 3D ESC plane is Euclidean.
The x and y axes in Lisle’s ASC surface of simultaneity are indeed not orthogonal. They are tangent to the null cone not the ESC plane. Let me make this clear.
The Proof that the x and y Axes in Non-Euclidean Cone World are not Orthogonal
In a general coordinate system, the metric can be represented at a single point p by a 4 × 4 matrix thus:
The metric provides the inner product at the tangent space at p. The tangent space is a vector space at the point, and we determine angles using the metric tensor components. The dimensionality of the tangent space is the same as the dimensions of the space under discussion. Note that at a given point, the metric components are constants. Let’s see how this works by way of an elementary calculation in the tangent space.
Consider the vectors (in matrix notation) in the x and y directions at a point p:
The inner product in matrix notation is:
Thus, proving that if gxy is not zero, then the inner product X•Y ≠ 0 and that X and Y are not orthogonal. Thus, the only strange thing is that Lisle thought my statement was strange.
This brings us to the analysis of the ASC cone worlds in terms of cartesian coordinates. We will find that Lisle cannot keep the objects of discussion in focus. To refute my claim that the ASC cones, that is, ASC spaces of simultaneity are not Euclidean, Lisle gets lost and transforms back to ESC to refute my true statement regarding the geometry of the one parameter family of space of simultaneity specified by the parameter ε. We will show this as we continue.
To begin, here are my equations for the ASC cones expanded in full detail. The ASC time coordinate change is:
In equation (5) t is the ESC time coordinate and t′ is the ASC time coordinate equal to the time of arrival of the photon. This transformation yields the spacetime interval for all synchrony values in polar coordinates:
It is important to note that this formula displays all the synchrony convention coordinate representations for any value of Remembering what I outlined above concerning interpreting coordinates in terms of the metrics, the reader will note that the coefficient of dr is not 1. This means that the coordinate dr (at constant time t′) is not a distance unless ε = 1/2. It must be multiplied by to obtain the physical distance.
As in Dennis (2024), we can also illustrate the non-Euclidean features of the ASC 3D hypersurfaces in Cartesian coordinates. Starting with the Minkowski spacetime interval in infinitesimal Cartesian form:
and taking the differential of equation (5) with gives:
Thus, the spacetime interval in Cartesian ASC coordinates is:
To find the components of the metric we expand all terms to obtain:
From this we can display the metric tensor in ASC cartesian coordinates:
This equation displays every synchrony convention metric in terms of cartesian coordinates. We will refer to this more when we investigate Lisle’s claim that my deductions from that metric are incorrect. We can directly read off the inner product of the x and y axes in cone world. It is:15
Note that if ε = 1/2 the axes are orthogonal, that is, gxy = 0 and we have a Euclidean three-dimensional space. The ESC space is Euclidean, cone world of ASC is not. For ε = 1/2 the metric of course reduces to the Minkowski form:
Thus, ESC and Euclidean 3D geometry are logically equivalent. Lisle could have saved himself some mistaken labor by merely setting ε = 1/2 in the general epsilon dependent expression I computed. That might have alerted him that he had just inadvertently transformed back to ESC.
At this point, I mention two other shibboleths in Lisle’s refutation.
First, Lisle states at the end of his Appendix B analysis:
So, when the computations are done correctly and without assuming any particular synchrony convention, we see that the spatial coordinates of both ESC and ASC are Euclidean, contrary to Dennis’s claim.
That statement is false. My equations (6) and (9) do not assume any synchrony convention. It is the formula for the entire family of synchrony dependent metrics as a function of the ε parameter. Simple substitution of ε = 1/2 yields a Euclidean 3D space for dt′ = 0 and a non-Euclidean 3D space if ε ≠ 1/2. My equations are done correctly and did not assume any synchrony convention. In case this is not sufficient, in the section below titled, “The direct mathematical coup de grâce,” I compute the Ricci curvature scalar for every space of simultaneity as a function of ε. It shows that only ε = 1/2 yields a Euclidean 3D space for dt′ = 0.
Second, we have a case of proof by pictures. At the end of his Appendix B analysis, Lisle states:
Likewise, when viewing the x and t axes of ASC using ESC coordinates, they will not appear orthogonal. However, the reverse is also true! That is, when viewing the x and t axes of ESC using ASC coordinates, they too will not appear orthogonal. The geometrical interpretation imposed upon the coordinates will depend on what synchrony convention the author has in mind.
All in all, when determining if directions are orthogonal, one does not look at pictures in R4 (or rather R2 for Lisle’s example). These are merely graphs in a number space. It is not a space with a Euclidean metric. Lisle’s remarks about an appearance of orthogonality have no meaning and are irrelevant. One must use the metric as in equation (10) above. Thus, in Lisle’s quote above, he reverts to a fallacious understanding of differential geometry. The geometrical interpretation imposed is not dependent on what synchrony convention one has in mind, rather it is imposed by the metric of the space as discussed in section “How to interpret a coordinate representation of a metric” above. Sadly, Lisle has apparently forgotten how to do inner products using the metric and reverts to a false pictorial account. This hand waving is not rigorous mathematics.
We can find which axes are orthogonal by simply looking at the metric in ESC and ASC. The metric determines the geometry, not coordinate labels in a topological Cartesian space. Looking at equation (8) above we can see that the ASC axes are not orthogonal due to the gx′t′ term in the metric. This is true regardless of which coordinate system we decide to use. Likewise, we can see that the ESC axes are orthogonal since equation (7) above shows there is no gxt term in the metric. The same conclusion follows from Lisle’s metric in footnote 36 on page 255 in The Physics of Einstein (Lisle 2018). There is a component of the metric:
For ESC we have ε = 1/2. Thus gxt = 0 and the x and t axes are orthogonal. For ASC and Lisle’s choice ε = 1. Thus gxt = c and the x and t axes are not orthogonal.
Lisle in his appearance argument above has abandoned sound differential geometry and has forgotten that the inner product of two vectors is an invariant. This means of course, that we get the same number for the inner product regardless of the coordinate system used. That number is a property of the Minkowskian geometry and cannot be imposed or altered by using a false graph in a Cartesian space representation. The manifestly invariant inner product of two vectors X and Y is:
This means that the inner product of the ASC x and t axes is:
That inner product is independent of the coordinate system. The ASC coordinate axes, as specified, are not orthogonal and their inner product cannot be changed via any coordinate transformation.
Likewise, the inner product of the ESC x and t axes is:
That inner product is independent of the coordinate system. The ESC coordinate axes are orthogonal, and their inner product cannot be changed via any coordinate transformation. These properties can be properly graphed as will be shown in fig. 11 later.
We note that Einstein (1920) discussed general Gaussian coordinates in chapter 25, “Gaussian Co-ordinates.” I provide a brief illustration of non-orthogonal coordinates in an Appendix developed from an application of the law of cosines which shows that cross terms in the metric indicate axes that are not orthogonal. The cross term is directly related to the cosine of the angle between the coordinate axes.
A Major Mathematical Mistake—Another Distance faux pas.
A major gaffe of Lisle is that he makes the astounding claim that the ASC time transformation does not alter distances since it leaves the spatial coordinates unchanged. Here is his fallacious claim. Since x′ = x, y′ = y, z′ = z it is the case that
This is certainly trivially true algebraically. It would be true for any arbitrary functions f(x, y, z). But here Lisle is merely assuming the Euclidean ESC Pythagorean formula applies. This is short-sighted hand waving and a major gaffe. (Lisle’s statements about distances are devoid of geometric analysis. As we have shown above in his light cone morph, the distance—yes, a spacetime interval—represented by the algebraic coordinate value R, necessarily changes even though R does not. This is one direct counter example to Lisle’s mistaken claim that distances do not change. And it is an example provided by Lisle himself.)
The Pythagorean theorem would apply if the ASC transformation preserved the geometry of the surface of simultaneity specified by t′. But the ASC space of simultaneity given by dt′ = 0 selects a different slicing of spacetime. It selects a different 3D geometry. So, the Pythagorean theorem does not apply in the ASC cone world. This gaffe is related to Lisle’s failure to distinguish my statements that coordinates cannot change the geometry of Minkowski spacetime itself, as opposed to ASC (and, yes, ESC) time slices selecting different 3D hypersurfaces in abstract 4D spacetime. My comments are referring to different geometric objects. So, in one case the geometry is not altered, in the second case the geometry is different. A fact that Lisle failed to discern. I did not contradict myself.
We now give an example from elementary calculus that shows constancy in coordinates does not imply constancy in distance. We can represent a level surface in three-dimensional Euclidean space via a function z = f(x, y). In this mapping, the x and y coordinates do not change. Shall we conclude that the distance in the surface between two coordinates point is No, of course not. But that is what has been done when it is claimed that the ASC cone world is Euclidean and assumes the Pythagorean theorem.
Let us look at the geometry of the case and show that the Pythagorean theorem formula is not valid in level surfaces.
We can illustrate Lisle’s gaffe concerning unchanging distances directly using introductory calculus.
Let’s consider different coordinates in Euclidean three-space of the form:
z = z'+ƒ(x, y) = z' + g(r)
x = x'
y = y'
The equation for z specifies a family of 2D surfaces in 3D Euclidean space. Since g is a function of r only, it specifies a surface of revolution around the z-axis. Since x and y are unaltered, we cannot claim that the geometry of a surface specified by z′ = constant is Euclidean—which is Lisle’s gaffe. In the above example, z corresponds to time in the ASC spacetime case. Consider a specific case, a family of paraboloids of revolution, parameterized by location of the minimum z′:
What is the length of intervals between points separated by the unchanged coordinates dx = dx′ and dy = dy′?
As usual we must use the intrinsic geometry of the space in which the surface is embedded, that is,
A straightforward substitution for a surface specified by z′ = constant, that is, gives:
For the example given above, evaluating the partial derivatives yields:
This expression is the intrinsic geometry of each paraboloid of revolution. It is immediately apparent that each value of z′ = constant specifies a surface with non-Euclidean geometry. This is manifest since the coefficients of dx and dy are not equal to one. Thus, the coordinates dx and dy do not measure distance within the paraboloid. Further, we see that the x and y axes (vectors tangent to the paraboloid) are not orthogonal due to the cross term in metric. This example is sufficient to show that a coordinate representation of surfaces within an embedding space do not preserve distances even though the coordinate labels did not change. Lisle’s claim is a major mathematical mistake. And again, it is based on his not distinguishing the difference between the hypersurfaces that are chosen by definition to be simultaneous events.
As we will see Lisle’s attempt to claim ASC cone world is Euclidean makes a startling transformation back to ESC (which is Euclidean) to claim my general formula valid for all values of ε is incorrect while the ESC formula is correct. Well, it is correct for ESC, for ASC not so much.
As I mentioned above, contra Lisle, I have not assumed a particular synchrony parameter in my equations, so Lisle could have saved himself from getting lost in the math by just noting that the only value of ε in my general convention dependent family of spaces of simultaneity that reduces to Euclidean geometry is ε = 1/2. A fact we already know, but Lisle seems oblivious to the same.
The fact that Lisle makes such an error shows he is not paying attention to my remarks, and substitutes verbal proofs based on a strawman—but such is not rigorous mathematics.
Do I Both Affirm and Deny that Transformations Affect Geometric Realities?
Returning to Lisle’s extended quote above, he says:
Even Dennis himself admitted earlier that ‘this coordinate transform has not altered the intrinsic geometry of Minkowski space.’ So, again we see that Dennis both affirms and denies that coordinate transformations affect geometric realities.
Lisle is Lost in Spacetime—Going Around in Circles
Here we look at Lisle’s mistaken algebraic merry go round proof that ASC cone worlds are Euclidean. Lisle wants to claim that the ASC spaces of simultaneity are in fact Euclidean. But they aren’t. We showed that above regarding the ASC time transformation singling out a non-Euclidean space of simultaneity. In his attempt to show that my general expressions for the non-Euclidean (excluding ε = 1/2) geometry of the ε dependent 3D geometries (as given by the non-Euclidean formulas for the geometry of circles and spheres) is incorrect, he uses his mistaken notion regarding distance, described above, to transform from his ASC cone back into the ESC Euclidean space! He is confused regarding which geometric surface he is talking about. See fig. 10 which displays the Euclidean ESC plane of simultaneity (t = constant) and two examples of ASC cones of simultaneity (labeled by t′ = constant and t″ = constant), that is, events all at the same “time.” We will be contrasting the intrinsic geometry of the ESC plane (ε = 1/2) with the intrinsic geometry of the cones.
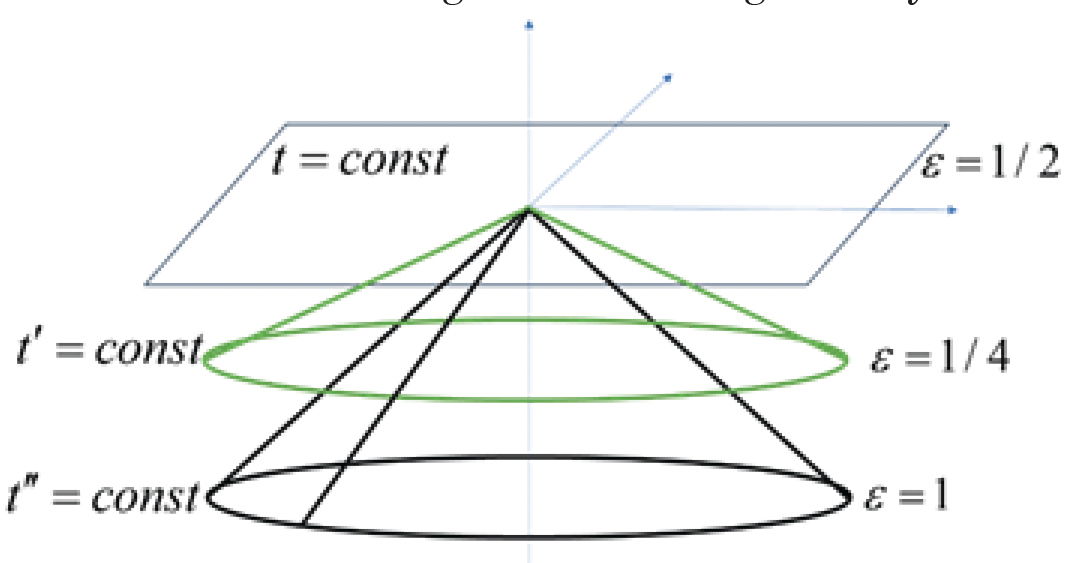
Fig 10. Illustration of three-dimensional spaces of simultaneity for three choices of epsilon.
Lisle Is Not Paying Attention
We now get back to Lisle’s remark:
Even Dennis himself admitted earlier that ‘this coordinate transform has not altered the intrinsic geometry of Minkowski space.’ So, again we see that Dennis both affirms and denies that coordinate transformations affect geometric realities.
One wonders what Lisle considers to be geometric realities. The technically correct phrase in the discipline of differential geometry, is geometric objects.16 In my article I dealt with different geometric objects. Examples of which are Minkowski space and then (abstract) geometric objects within Minkowski space, such as planes and cones (known as hypersurfaces). I said coordinate transformations on the entire Minkowski space do not alter the geometry of Minkowski space. So, Lisle’s paraphrase of my remark is an egregious misunderstanding. Lisle has not seen again, rather he is confused due to not carefully reading my words. My remark regarding geometry being altered was in regard to what is considered to be a spatial geometry in a 3D space of simultaneity, that is, the events happening at the same time. These hypersurfaces of simultaneity can be specified by way of different (coordinate) functions on spacetime. Different functions such as ESC or ASC specify different geometric objects, as in fig. 11. It does not take much imagination to see that the geometry of the 3D ASC cone (which is the set of incoming light rays) and the 3D ESC Euclidean plane shown in fig. 11 are distinct geometric objects with distinct geometries. The ASC transform specifies different hypersurfaces than ESC hypersurfaces. Apples and oranges, different geometric objects, but Lisle does not see the difference.
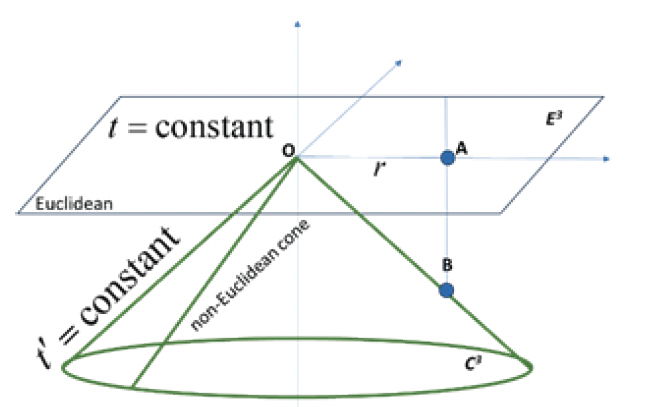
Fig 11. Illustration of the three-dimensional cone world C3and the ESC Euclidean space E3 along with the coordinate r and the points A and B associated via the ASC time coordinate transformation. The cordinate r does not change under the map, but the distances do. The Euclidean distance in ESC is r. It measures the distance OA in the 3D space E3. OB is the distance in the cone C3, and it is not equal to r.
In a remarkable statement regarding his equation (34) (correcting a typographical error):
Lisle explicitly states this is the interval for events simultaneous according to ASC, that is, dt′ = 0. Two important points:
- In fact, Lisle is following my admonition to analyze geometrically rather than just doing algebra on coordinate labels. In other words, we must use ds to determine distances and angles. The metric on Minkowski space induces the metric on all embedded submanifolds, including worldlines, hypersurface, such as cones and planes, etc.
- The equation is supposed to represent a 3D space. But amazingly the metric in equation (12) is singular since there is no term with dr; so, intervals within Lisle’s singular cone of simultaneity are only a function of the spherical angular coordinates. Is the subspace specified by dt′ = 0 three-dimensional or two-dimensional? Actually, it is the three-dimensional past null cone (and that null cone is obviously non-Euclidean). This means that for two distinct points at radial coordinates r1 and r2 the interval ds = 0. Thus, the “distance” between any two points along a radial line at the same time is zero. I place the word “distance” in quotes, since technically setting ε = 1 is an abuse of the geometric structure of abstract spacetime. It means that the surfaces characterized by constant t′ (that is, dt′ = 0) is the past null cone. The null cone is neither timelike nor spacelike. In the past Lisle apparently was sensitive to setting ε = 1 (cf. Lisle 2001). For this reason, it is best to use the form:
Equation (13) makes it evident that the value ε = 1 results in a degenerate three-dimensional space since the determinant of the metric is zero. That also means that for ε = 1 the metric has no inverse. Note for ε = 1 equation(13) reduces to Lisle’s equation (34) [reproduced in equation (12) above]. It should be remarked that Lisle writes equation (12) [his (34)] and then makes no attempt to explicate the implications by mathematical analysis. He just hurries by. If he had paused and analyzed the equation which is the induced intrinsic 3D metric of his claimed (conical) space of simultaneity, maybe he would detect the holes in his understanding of differential geometry. At least he might have noticed his contradictory principles of when to use ds and when to conveniently ignore it when it suits his argument and impute a contradiction to me. For example, in analyzing equation (12) above [his (34)] would he be tempted to say that the coordinate labels dφ are a distance by ignoring the coefficient of dφ? I hope not. Yet, as we will see below, that is exactly what he claims when it comes to the coordinate label dr′ (incidentally trivially equal to dr); he ignores the coefficient of dr′. So, referring again to the section “how to interpret a metric” above, we determine that dφ is not a distance but rather rsinθdφ is the distance along a small circular arc of extent dφ at polar angle θ, which incidentally is ds. But not for Lisle, according to him I have just confused a distance dφ with a spacetime interval ds. This clearly is not the case. The arc along the circle is a spacetime interval. To find the length (yes, the length) of an arc of extent φ=2π at polar angle θ we integrate along the (need I say it?) spacetime arc via:
The arc described above, via ds, is a circle lying in the plane of constant (co)latitude. That circle has radius rsinθ, and the circumference shrinks to zero as θ → 0. Moral of the story: the coordinate interval dφ is not a distance, in the spatial geometry, rather ds is the distance. This is all rather elementary differential geometry, which Lisle seems to have forgotten. The equations for ds and dr must be consistently analyzed in the same way as ds and dφ were analyzed. Contra Lisle, this is the physics of Einstein. We will see that Lisle abandons that analysis when it comes to the expressions ds and dr.
Let us examine the implications of the rest of Lisle’s statement: “setting dt′ = 0 [ASC] does determine intervals that are simultaneous, but it is not the same as distance unless ε = ½...” (Emphasis added). We addressed the ASC case above. But then Lisle admits that ESC selects the hypersurface in which dr (= dr′ since the radial coordinate labels are identical) measures the distance. That is exactly my point. For ASC (ε = 1) dr = dr′ is not the distance (cf. equations (9) and (10) above). Note that equation with ε = ½ (ESC) becomes:
Clearly that is the metric for 3D Euclidean space in spherical coordinates.
To summarize, Lisle is mixing two hypersurfaces again. He agrees that cone world is specified via dt′ = 0 which are simultaneous but then says distance must be measured according to dt = 0 (that is, ESC). He wants to have his cake and eat it too. Again, refer to fig. 11 above. As before the coordinate r locates both the event A in E3 and the distinct event B in C3. These distinct events differ only in their time labels which specify their locations in the plane or the cone. On one hand Lisle wants to use the obvious ESC Euclidean hyperplane (equation [14]) for distance between simultaneous ESC (dt = 0) events O and A and, on the other hand, use the ASC non-Euclidean cone for time between ASC (dt′ = 0) events O and B. But this is illegitimate; A and B are different events! One might ask: “Did the light originate from A or B?” It can’t originate from both! It originated from B in the past and arrived at O.
Next, in a series of strange comments, Lisle explicitly demonstrates that contrary to Einstein he places coordinates above the metric which is what specifies the geometry.
For example, Lisle states,
That is, assuming that ds = dr′ tacitly assumes ESC. Dennis then claims, “This shows that the distance from the origin of a point along a constant ray (dθ = 0 and dφ = 0) is not measured by r, but rather by: (35).”
But this is the spacetime interval ds, not the distance dr′. Dennis has assumed that dr′ = ds; this is the same error he made in equation 22. Only when using ESC does the spacetime interval conveniently reduce to distance when dt = 0. Dennis has again confused a distance with a spacetime interval. And since the rest of his derivation incorporates this error, it too is incorrect.
I have made no errors, and I am not confused. It is Lisle who has confused a coordinate with a distance and who is incorrect. Lisle conveniently decides to ignore the metric coefficient of dr = dr′. In fact, my equation clearly indicates that ds ≠ dr′. The claim above shows that he is still stuck in his light cone morphing. Lisle has failed to follow Einstein’s admonition to eliminate coordinates to determine the physical content of a model—which is exactly what equation (35) in the above quote illustrates. Lisle demonstrates he does not know how to interpret the metric and to what geometric object (among the several under discussion) the metric applies. Equation (35) in Lisle’s quote is precisely the distance (indeed the invariant interval ds) between events within the surface of simultaneity t′ = constant, which (for ε = 1) is the past null cone in which light travels inwardly at the one-way speed c. In fact, note that with ε = 1 in equation (35), (which represents a radial line for which dθ = 0 and dφ = 0), we get ds = 0. So, yet again dr is not a distance—it has a non-zero value for the coordinate difference between any two distinct points but geometrically represents a null spacetime interval.
Lisle continues:
In reality dr′ = dr. For that matter, dθ′ = dθ, and dφ′ = dφ. This is necessarily the case because synchrony conventions only differ in their time coordinate dt. Thus, an infinitesimal distance for any given observer is unaffected by his choice of synchrony conventions. We demonstrated this in Appendix A (showing that R′ = R).
Lisle states the obvious that the spatial coordinate values do not change and only the time coordinate does. That is just algebra. Here Lisle repeats his calculus gaff, discussed above, based on his conceptual shortcoming that the ASC coordinate transform does not change distances in the spaces of simultaneity. Lisle has it backwards. Only in the flat Euclidean plane of ESC does dr represent distance, since in the Euclidean hyperspace ds = dr allowing us to interpret the meaning of dr. On the other hand, within the ASC surface of simultaneity (which is a different geometric object, that is, a cone, the surface of the incoming distant light), the coordinate interval dr (same label, same numerical value as for ESC) is not a distance. It is merely a coordinate interval marking the ends of an infinitesimal within the cone, not the Euclidean ESC plane. Referring to fig. 11 above we can see that the vector displacement measuring a difference in the coordinate r lies in the cone for ASC (OB). But for ESC it lies in the plane (OA).
The Direct Mathematical Coup de Grâce
In Dennis (2024) and herein I have shown repeated demonstrations that the ASC space of things at the same time would result in non-Euclidean configurations of things at the same time. I showed this by the non-orthogonality of the spatial axes in the cones, the non-Euclidean formulas for those configurations in the cone among others. There is, however, one direct proof for those familiar with differential geometry. We take the general formula for the metrics of the family of hypersurfaces of simultaneity in equation (13) above (which includes Lisle’s metric in equation [12] as special case) and compute the invariant Ricci scalar curvature, R as a function of ε. This computation yields:
We see that the curvature of the 3D spaces depends on distance from the origin. The 3D cones are asymptotically flat as r → ∞ and are infinitely curved at the apex r = 0 unless ε = ½. This infinity indicates a pathology at the origin.
We immediately see that R becomes infinite everywhere if ε = 1. This result shows that Lisle’s choice of ε = 1 is mathematically inadmissible. Even choosing a value slightly smaller than 1 results in a space with a huge curvature.
However, note that for ESC, ε = ½ and we get R = 0, that is, manifestly a flat Euclidean space.
Of course, fig. 11 above makes it clear that the ESC space is Euclidean, and the ASC cone is not. But this is the mathematical proof.
General Relativity and the Overthrow of Conventional Simultaneity
In closing, we will look at why GR is the theory that must be used to construct a biblically and physically realistic solution to the LTTP. Special relativity is simply put, too impoverished to describe the Creation. We live in a universe which, at large, is dominated by gravitational fields. Massive fields that bend and deflect light and which can also impede the approach of light between separated bodies.
Previously, I mentioned the big bang cosmology (FLRW models) when we discussed how to interpret a metric. Here we look at its properties and show how it is a certain fact that renders a conventionalist philosophy as an unnecessary adjunct of relativistic physics. Lisle asserts that conventionalism is a necessary adjunct to the physics of Einstein—but saying it is so does not make it so. Lisle on this count is engaged in a falsehood. He may believe it but that is an opinion. Of course, the physics of Einstein which Lisle most quotes is the empty universe of SR. And as I have said, SR is an inadequate theory for describing light transit in a huge and non-empty universe. However, GR is also the the physics of Einstein that replaces SR. In fact, we will show below that SR still holds in a limited way within a universe with absolute cosmic time.
We have already mentioned that there is no consensus on Lisle’s assertion of conventionality. In particular, the philosopher John D. Norton states his leaning toward the non-conventionalist side of the continuing debate.
So let us consider the big bang cosmologies. Recall the big bang cosmology can be written in terms of comoving coordinates as follows (without loss of generality I am using the flat space version):
The spatial coordinates are comoving, they are permanently attached to the infinitesimal element of matter and specify the locations of matter in the cosmos at a specific epoch of cosmic time t = t0. The expansion factor at the epoch is taken to be a(t0) = 1. Typically, the epoch is taken to be the current age (according to big bang timeline) so that the coordinates specify the distance D to where the matter is now, that is, now, according to:
All the matter moves along worldlines for which their coordinates are constant, consequently the clocks for each element of matter record the same cosmic time:
This is the global absolute cosmic time. Each value of t specifies a 3D space of simultaneous events. Thus, this solution has a global time and is a GR counterexample to the conventionalist’s claim that there is no such thing as global time or a metaphysical present. All it takes to disprove a theory is one small certain fact. Of course, GR supersedes SR and so undermines the basis of the conventionalist arguments that takes place in the arena of Minkowski spacetime. The solution above is clearly not Minkowski spacetime. Our universe is not described by Minkowski spacetime. The solution above also has a preferred frame of reference contra special relativity. Thus, GR reestablishes a global time, and therefore, absolute simultaneity. The FLRW solutions also have a preferred frame of reference. The latter is the Hubble flow which is in line with the Machian view of GR as I discussed in Dennis (2022). The matter distribution in freefall in the universe along with its attendant gravitational field constitutes the unique global inertial reference frame. This was Mach’s equivalent of the fixed stars of classical mechanics.
Another interesting aspect of GR is that cosmological solutions exhibit faster than light (= c of special relativity) velocities between distant objects, cf. Dennis (2022). This faster than c feature of GR does not result in time travel to the past since such motion also results in the light also traveling faster than c via the dragging of light by the gravitational field. Matter with mass always travels within the future null cone.
One might wonder how special relativity connects with the general relativistic universe described above with absolute simultaneity. The answer is that SR is only valid in limited domains in space and time. The simplest way to see this is by considering equation (15). The scale factor is independent of position and changes very slowly with time. Therefore, for short timescales we can treat it as a constant. In fact, as mentioned above, at epoch a(t0) = 1, therefore equation becomes:
This is the Minkowski metric. The implication is that for small regions of the universe, local observers cannot detect local deviations from the global cosmic time, and of course, for short times, they cannot perceive their position within, or their (peculiar) motion with respect to the global flow. The cosmic effects are minuscule on the local scale. From this one cannot argue that eternalism is true and time does not flow and that there is no universal now. In fact, there is such, since the little patch of the universe is embedded in the global creation and its global time, its absolute simultaneity and its global reference frame.
So, in summary, Lisle’s adamant adherence to conventionalism and the eternalist interpretation of special relativity is without merit. First, special relativity is not relevant to the Creation on the whole, so Lisle’s ASC solution is irrelevant. Special relativity and ASC with the Reichenbach amendment are not up to the task of solving the LTTP. Especially so since, in the end, it is a vacuous coordinate transformation.
Mathematical and Conceptual Errors in The Physics of Einstein
Lisle makes several egregious mathematical and conceptual errors in his self-published The Physics of Einstein (Lisle 2018). These errors are telltale shibboleths that expose holes in Lisle’s knowledge of relativistic physics. Many of these constitute internally inconsistent claims. In addition to those described previously, the ones described here are among the most egregious.
We mentioned previously that Lisle thinks a Lorentz transformation proves time travel if we could attain to faster than light travel. Here we analyze the mathematical blunders involved in that argument.
Lisle Claims that Time Travel into the Past would be Possible if . . .
One of the most striking of his errors is his belief in the possibility of time travel. The most serious part of this belief is not only his major mathematical errors, but the heretical belief in spacetime as an actual entity and that the past is still there. We discussed this previously. Lisle bases his false belief not only on the reality of the past (which is a necessary presupposition of the possibility of time travel) but also on egregious statements regarding the Lorentz transformation (LT) and an appeal to superluminal speeds. It is well known that superluminal speeds are a violation of the mathematics of SR, and thus it is amazing that Lisle appeals to such. Here is his claim:
Nonetheless, hypothetically if faster than light travel were possible, then time travel into the past would also be possible. This is provable from the Lorentz transformation . . . (Lisle 2018, 101, emphasis added).
Lisle is badly mistaken that the LT proves the possibility of time travel via faster than light speeds. That is not something one learns in an undergraduate course in modern physics.
Is it true that if v > c a supposed modified Lorentz transform would allow time travel? The answer is no. For v > c the resulting transformation is not a legitimate transformation of spacetime. We show this as follows.
To begin, first we note that the abstract mathematical model of spacetime as a four-dimensional continuum means that it is a collection of points in a real space (R4). The coordinates of the points are all real numbers. For example, for an event E, the coordinates (t, x, y, z) are an ordered 4-tuple whose values are real numbers. Those numbers are used to identify physical events that occur at a place (x, y, z) measured by real numbers (tick marks along a ruler for example) and at a time (t) measured by real numbers (such as the hands on a clock pointing to real numbers on the clock face or any other timekeeping instrument).
Now consider the basic coordinate equations of a Lorentz transformation:
For ν > c we obtain:
Thus, the transformed coordinates (labels) are imaginary. Who has heard of an imaginary frame of reference? This is illegitimate. Imaginary coordinates are not allowed in the mathematical structure of the model of Minkowski spacetime. Coordinates on a manifold are necessarily real numbers.17
Again, we measure time and distance with clocks and rulers, not with imaginary units of √−1. The stipulation that coordinates are measured by real numbers necessitates from equation (16) the constraint that −c < v < c.
This is a concept every high school student knows. When dealing with real valued functions of real numbers, the domain of a function is necessarily restricted. Looking at equation (16) such students will recognize that the domain of t′ and x′ as real valued functions of v is −c < v < c.
Furthermore, values with │v│>c violate the group structure of the Lorentz group. That means that the transformation in equation (17) does not give an element of the Lorentz group. That is a contradiction of the mathematics of special relativity and constitutes a refutation of Lisle’s statement quoted above. Time travel into the past is not provable from the Lorentz transformation.
So much for Lisle’s time travel claim and the power of a false LT. Lisle, via an egregious mathematical blunder that violates the mathematics of special relativity, claims that special relativity proves the possibility of traveling to the past.
Later in support of time travel, Lisle claims that if the speed of light is exceeded, then based on the spacetime interval, time becomes space and vice versa. This is another egregious error regarding the Lorentz transformation.
Lisle states,
This is also illustrated in a Minkowski diagram. As we consider objects and increasing velocity, the angle (θ) increases. The x′ axis rotates counterclockwise and the t′ axis rotates clockwise. As the velocity passes c, the x′ and t′ axis cross! At superluminal speeds the x′ (space) axis becomes timelike, and the t′ (time) axis becomes spacelike. (Lisle 2018, 102, footnote 12)
This is another case of descriptive hand waving, not rigorous mathematics. As mentioned, the Minkowski spacetime diagram in the (x, t) plane consists of ordered pairs of real numbers. The axes would not continue to rotate into the superluminal region, but rather, would disappear, since as shown above, the (x′, t′) coordinates would be an ordered pair of imaginary numbers! We already mentioned this above. Ordered pairs of imaginary numbers do not exist in a Minkowski diagram.
Lisle then says that as v increases, the time and space axes rotate and approach the null cone. That is true, but then, continuing, he erroneously claims that if v exceeds c, the axes continue to rotate through the null cone and the new t axis becomes spacelike and the new x axis becomes timelike. However, according to the spacetime picture he is appealing to, the new t axis would still be labeled by real numbers, and the same for the x axis. So, his claim of rotation past the light cone with resulting imaginary coordinates is an egregious error, as I said above. In fact, he seems to be putting a Euclidean notion of angles on top of a Minkowski diagram! That is a major conceptual mistake. Let’s analyze the correct mathematics.
Within the mathematical framework of special relativity and the Lorentz (isometry) group, how is increasing velocity v abstractly accomplished? One cannot just on a whim let v become algebraically greater than c. Velocity is increased (or rotated) by applying successive Lorentz transforms of speeds v less than c. The resultant frames of reference thereby achieved never have a time axis that rotates past the light cone. Instead, the time axis converges on the light cone. This is because the rotation angles (θ in Lisle’s quote) are not Euclidean rotations as Lisle seems to think, rather they are hyperbolic rotations. Lisle’s quote is all the stranger, given that he elsewhere correctly points out that it would take an infinite amount of energy to accelerate to a speed approaching the speed of light (let alone surpassing it). Of course, infinity is not an actual quantity, so one cannot reach the speed of light, let alone cross the light cone.
So, is it the case that the time axis and the space axis rotate past the null cone? It is not.
We can see this yet another way. Mathematically a Lorentz transform preserves the norm of a 4-vector.18 For a material system, such as our physical bodies, the 4-vector v is timelike.
This means that (for the timelike metric convention) the norm is given by (the superscript T denote the matrix transpose):
For a LT matrix L which by construction satisfies the isometry condition:
And the transformed (or boosted) timelike vector is ν′ = Lν, so we find that:
This shows that the transformed vector is also timelike. Thus, a LT cannot transform a timelike vector into a spacelike or a null vector.
We can illustrate the above abstract matrix algebra geometrically by looking at a Minkowski space graph. Equation (18) above is the equation of a pseudo-sphere. It describes a hyperboloid with constant spacetime radius equal to one. If we expand equation (18) for the special case of a two-dimensional section in the (x, t) plane, we have the hyperbolic equation:19
We illustrate the geometry in fig. 12. Equation (19) above shows that under a LT points in the pseudo sphere H are mapped to another point in H. This means the orbit of a point under a continuous LT is H. Since the pseudo sphere H is asymptotic to the null cone as shown in fig. 12 this means the timelike vectors in H never cross the null cone. This analysis also shows that a LT is an isometry of the pseudo sphere H which is a maximally symmetric three-dimensional spacelike hypersurface within Minkowski space.
Fig 12. Geometry of the pseudo sphere H and image points under successive hyperbolic rotations.
A LT in the (x, t) plane (corresponding to a boost in speed) can be conveniently represented as a hyperbolic rotation in terms of a hyperbolic angle ρ, thus:
Straightforward matrix algebra shows that
indicating that the composition of successive rotations through rotation angles is additive. After five successive rotations by the angle ρ the point P is rotated to point Q at an angular distance of 5ρ. Using the LT
the spacetime point Q has coordinates:
Obviously, the coordinates of Q trivially satisfy equation (18).
The result of the above is that the phrase traveling faster than light is meaningless nonsense within the mathematical theory of SR. In fact, fig. 12 is a graphic illustration of the special relativistic velocity addition formula. Addition of two relative speeds ν1 of frame S1 (relative to a rest frame S) and a speed of ν2, of frame S2 (relative to S1) does not yield a speed of ν1 + ν2 relative to S. Instead, the speed relative to S is:
Someone traveling faster than light would not be timelike, but spacelike. This is indisputable since a displacement between two events with the spatial separation Δx greater than cΔt yields c2 Δt2 − Δx2 < 0 which is the indication of a spatial separation not a timelike separation; therefore, the LT is not able to imply time travel.
Summary and Conclusion
In summary we have demonstrated that Lisle’s ASC program is fatally flawed on many counts. It fails empirically, mathematically, and most seriously biblically since it is founded on the heretical notion that spacetime is a real entity. Many of Lisle’s mistaken beliefs are based on his mathematical mistakes in his idiosyncratic notions of special relativity. In particular Lisle’s abuse of the mathematics of special relativity involved in the Lorentz transformation is a major failing.
In summary:
- Empirically, the foundational premise of the Reichenbach conventionality thesis is disproven by the measurement of the speed of light at Caltech.
- Mathematically (and logically) it is proven to be internally incoherent since geometrically the Reichenbach model implies that a measurement of the two-way speed of light in arbitrary directions, logically requires from the theoretical model that we have deduced a transverse isotropic speed of light in every transverse direction.
- It has been shown that Lisle’s characterizations of my statements are incorrect and based on his misunderstanding or lack of careful reading.
- It is hermeneutically unsound. Asserting that ancient cultures believed that light arrived at their eyes instantaneously when it had departed from distant stars and galaxies (and the Scripture does not tell us the distance to the stars) is an attempt to shoehorn his pet theory into the sacred text. It is the dismissal of the LTTP not the solution thereof.
- Lisle falsely claims that conventionalism necessarily follows from special relativity. That is refuted by the continuing debate between conventionalists and the non-conventionalists.
- He falsely believes that eternalism is the necessary interpretation of SR when there are other presentist interpretations of SR. Furthermore, since SR is superseded by GR, arguments for eternalism from SR are rendered invalid. The cosmological solutions of GR describe universes with absolute cosmic time. Such are imminently suitable for creationist solutions of the LTTP.
- Attempting to solve the LTTP within special relativity with its impoverished theoretical resources is naïve. First, special relativity is not a realistic model of the cosmos that we see through our observational instruments. A realistic model requires the use of GR and solving the Einstein field equations for a cosmological solution that models the mass-energy distributions in the creation, along with the resulting gravitational fields and their effects on the propagation of light. Second, general relativistic cosmologies have preferred frames of reference and global absolute cosmic time. Such features of general relativistic solutions vitiate the eternalist’s claims made within the limited confines of special relativity. We explained that special relativity still holds in the small even within the global cosmological solutions. The very fact that it only holds in the small means it can have no say on the large-scale structure of God’s creation. I have pointed out in Dennis (2018) that the 3+1 formalism of GR is inherently compatible with presentism and is the natural formalism for generating presentist cosmologies.
- Lisle thinks time travel to the past might be possible, but to claim that he must embrace the eternalist block universe in which the past, present and future exist as a timeless entity. The past must still be there for it to be revisited. Despite entertaining doubt that time travel is technologically possible or his questioning of its compatibility with divine constraints, he does not repudiate eternalism (with its many heretical implications). He is nevertheless left with his basic presupposition that the past is still there, and the future is already here.
- Finally, the worst aspect is that Lisle’s philosophically incomplete understanding of the literature on the philosophy of time leads him to a naïve philosophical and anti-biblical adherence to the heretical philosophy of eternalism. He is apparently unaware of the literature debating the two philosophies of time. He ignores the other interpretations of the mathematics of special relativity that are not eternalist interpretations, such as the 3+1 Lorentzian and neo-Lorentzian views.
In this reply I have included many technical mathematical details required to explicate many of the errors in Lisle’s mathematics and false concepts. Only those equipped with the necessary mathematical knowledge will be able to follow many of those. For those who cannot, I hope that the discussions of the empirical evidence against conventionalism, the mistaken notion that special relativity requires eternalism and most importantly the obvious heretical theological ramifications of eternalism will be sufficient to convince them of the serious defects of Lisle’s philosophy and a rejection thereof.
In conclusion, Lisle’s refutation reveals serious errors in his thought. Creationists need to stay clear of Lisle’s worldview which is based more on his uncritical reverence of Einstein’s antichristian interpretation and philosophy of relativity. His shockingly obstinate belief in eternalism and a block spacetime and a defiant repudiation of presentism is even more unfathomable since the latter is a readily available biblical interpretation of special relativity and the natural philosophy of time that follows from GR. Lisle should seek out the physics of God and abandon the eternalist metaphysics of Einstein.
References
Bohm, David. 1965. The Special Theory of Relativity. New York, New York: W. A. Benjamin, Inc.
Byl, John. 2024. God and Cosmos: A Christian View of Time, Space, and the Universe. https://bylogos.blogspot.com/2024/03/my-three-e-books.html.
Craig, William Lane. 2001. Time and the Metaphysics of Relativity. Dordrecht, Netherlands: Kluwer Academic.
Craig, William L. 2008. “The Metaphysics of Special Relativity: Three Views.” In Einstein, Relativity and Absolute Simultaneity. Edited by William L. Craig and Quentin Smith, 11. New York, New York: Routledge.
Crisp, Thomas M. 2008. “Presentism, Eternalism and Relativity Physics.” In Einstein, Relativity and Absolute Simultaneity. Edited by William Lane Craig and Quentin Smith. New York, New York: Routledge.
Dennis, Phillip W. 2018. “Consistent Young Earth Relativistic Cosmology”. In Proceedings of the Eighth International Conference on Creationism. Edited by J. H. Whitmore, 14–35. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Dennis, Phillip W. 2022. “Mach’s Principle in General Relativity and Reduced Light Travel Times in Cavitated Cosmologies.” Answers Research Journal 15 (October 26): 339–357. https://answersresearchjournal.org/machs-principle-in-general-relativity-and-reduced-light-travel-times-in-cavitated-cosmologies/.
Dennis, Phillip W. 2024. “An Internal Contradiction of Lisle’s Anisotropic Synchrony Convention (ASC) Model.” Answers Research Journal 17 (July 10): 427–433. https://answersresearchjournal.org/astrophysics/asc-model-contradiction/.
Eddington, Arthur S. 1935. The Nature of the Physical World. London, United Kingdom: Dent.
Ellis, George F. R. 2012. Space Time and the Passage of Time. https://arxiv.org/abs/1208.2611.
Einstein, Albert. 1920. Relativity: The Special and General Theory. New York, New York: Henry Holt and Company.
Gao, Liang, Jinyang Liang, Chivye Li, and Lihong V. Wang. 2014. “Single-Shot Compressed Ultrafast Photography at One Hundred Billion Frames per Second.” Nature 516, no. 7529 (3 December): 74–77.
Liang, Jinyang, Liren Zhu, and Lihong V. Wang. 2018. “Single-Shot Real-Time Femtosecond Imaging of Temporal Focusing. Light Science and Applications 7, no. 1 (August): 42.
Lisle, Jason [published as R. Newton]. 2001. “Distant Starlight and Genesis: Conventions of Time Measurement.” TJ 15, no. 1 April): 80–85.
Lisle, Jason. 2018. The Physics of Einstein: Black Holes, Time Travel, Distant Starlight. Dallas, Texas: Bible Science Institute.
Matsushima, Yozo. 1972. Differentiable Manifolds. New York, New York: Dekker.
Misner, Charles W., Kip S. Thorne, and John Archibald Wheeler. 1973. Gravitation. San Francisco, California: W. H. Freeman.
Pitts, J. Brian. 2004. “Some Thoughts on Relativity and the Flow of Time: Einstein’s Equations Given Absolute Simultaneity.” The Annual Proceedings of the Philosophy of Time Society 6. https://philsci-archive.pitt.edu/id/eprint/2760.
Reichenbach, Hans. 1956. The Direction of Time. Berkeley, California: University of California Press.
Unger, Roberto Mangabeira, and Lee Smolin. 2015. The Singular Universe and the Reality of Time. Cambridge, England: Cambridge University Press.
Weinberg, Steven. 1972. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. Hoboken, New Jersey: John Wiley and Sons.
Weyl, Hermann. 1949. Philosophy of Mathematics and Natural Science. Princeton, New Jersey: Princeton University Press.
Whitrow, Gerald James. 1980. The Natural Philosophy of Time. 2nd ed. Oxford, United Kingdom: Oxford University Press.
Appendix—Gaussian Coordinates
In fig. 13 we show a curvilinear coordinate mesh drawn over the Euclidean plane. The Pythagorean form for the distance c of the line between P and Q expressed in terms of u and v is not valid.
Fig 13. Gaussian coordinates in the Euclidean plane.
The line segment is a geometric object. Its length is invariant and cannot be altered via overlaid coordinates.
The distance c is not . Also, the lengths a and b are not equal to the differences of the coordinates. The labels in the figure are arbitrary and do not reflect geometric lengths. They do locate points: P = (2,3) and Q = (3,2). If the coordinates are called u and ν then in general a = αu, b = βν.
Note that since the mesh is not orthogonal, we must also use the cosine law: c2 = a2 + b2 − 2ab cos φ. Finally, writing a and b in terms of u and v gives the distance c: c2 =α2u2 + β2ν2 − 2αβ cos φuν.
In the infinitesimal limit (by considering very small increments in the coordinates, denoted by du, dv) this is written according to standard notation as:
Comparison gives the metric components used to convert from coordinate quantities du, dv to physical distance ds.
Note that α, β, and φ are not constants, they vary as the curved lines show. For example, the angle at (2,1) is not the same as φ at (2,2). Also note, this derivation shows the explicit relation between the angle φ between coordinate lines and the off diagonal cross terms in the metric components. A feature of the metric that Lisle considered strange, but is a result of the law of cosines.
Electronic Supplementary Material
Supplementary Movie S6 available for download and can be viewed at https://streaming.answersingenesis.org/vid/arj/supplementary-movie-s6.mp4





