An Internal Contradiction of Lisle’s Anisotropic Synchrony Convention (ASC) Model

by Dr. Phillip W. Dennis Published on July 10, 2024

Answers Research Journal 17 (2024): 427–433.

PDF Download Cite This

The views expressed in this paper are those of the writer(s) and are not necessarily those of the ARJ Editor or Answers in Genesis.

Abstract

Jason Lisle has formulated a model that purports to solve the light travel time problem (LTTP). The model is based on the Reichenbach ε formalism of specifying remote simultaneity by a coordinate convention (Reichenbach 1958, 127). The convention is directly based on the assumption that the one-way speed of light cannot be measured, since remote clocks cannot be synchronized. This conventionalist approach apparently allows one to alter the one-way speed of light such that incoming light to an observer can be made arbitrarily large by a suitable choice of the ε parameter. We show herein that such is not the case. The ASC model explicitly assumes the mathematical structure of Minkowski space and the foundations of special relativity (SR). Minkowski space presupposes an isotropic physical speed of light. The assumption of Minkowski space, as correctly embraced by Lisle, is incompatible with the conclusions of ASC which purports that the incoming speed of light can be made arbitrarily large.

Keywords: light travel time problem, anisotropic synchrony convention, special relativity, Minkowski spacetime, coordinate transformation, invariant quantities, one-way speed of light, physical speed

Introduction

In 2001 Jason Lisle published under the pseudonym R. Newton, a proposed solution to the LTTP (Newton 2001). Lisle (2010) subsequently published another exposition of the solution in 2010. In 2018, Lisle published a book The Physics of Einstein in which he provides an exposition of the special theory of relativity (SR). That exposition, written for an audience with basic high school mathematics, correctly states a central, key feature of the theory, which is the invariance of the spacetime interval. Lisle also discusses his ASC solution in his book (Lisle 2018). However, the ASC solution was developed based on Einstein’s theory of special relativity. Thus, the ASC model explicitly assumes the mathematical structure of Minkowski space and the foundations of special relativity, in particular, invariance of the spacetime interval. Minkowski space presupposes an isotropic physical speed of light. The assumption of Minkowski space, as embraced by Lisle, is incompatible with the conclusions of ASC which purports that the incoming speed of light can be made arbitrarily large. Thus, ASC is internally inconsistent. In fact, we will discuss how the ASC time transformations (mathematical synchronization) cannot even be derived without the assumption of an actual one-way speed of light. We will demonstrate this logical inconsistency of the invariance of the spacetime interval with an anisotropic speed of light in the following section.

The Contradiction

Here we show the contradiction between ASC and Lisle’s correct statements of the basics of SR. The arena of special relativity is Minkowski spacetime.1 It is characterized as a four-dimensional space in which points, called “events” are labeled by where and when they occurred. The coordinates of an event E in standard Euclidean spatial coordinates measured by rigid rods and the time of the event measured by ideal clocks is then:

$E : (x, y, z, t)$

We follow Lisle’s (2018) notation. The geometry of Minkowski spacetime is specified by the invariant interval between two events as follows2:

$S^{2} = Δ x^{2} + Δ y^{2} + Δ z^{2} - c^{2} Δ t^{2}$

Equation 1

To show the contradiction let N_out and N_in be vectors in Minkowski space that represent the paths of outgoing and incoming light rays respectively (with respect to a stationary observer at the origin). The vector N_out is the light ray from (x₀, 0, 0, t₀) to (x₁, 0, 0, t₁). The vector N_in is the light ray from (x₁, 0, 0, t₁) to (x₀, 0, 0, t₂). This is illustrated in fig. 1.

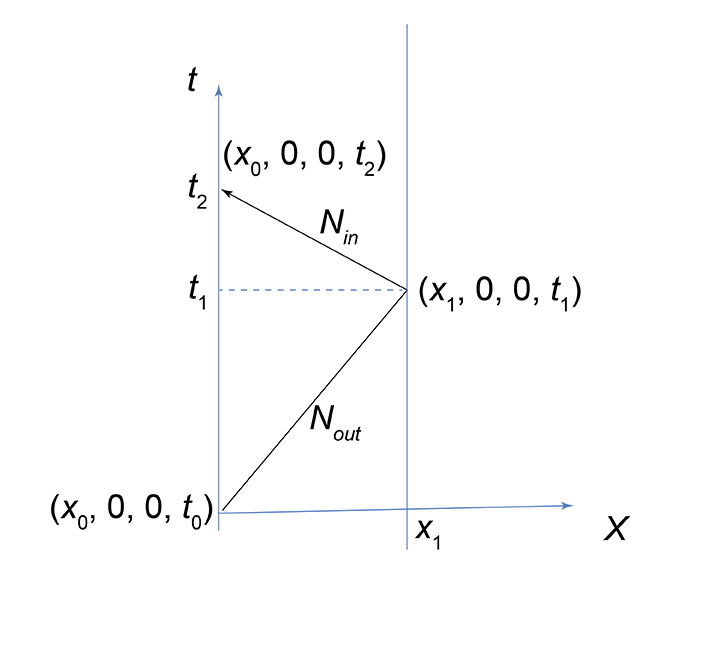
Fig 1. Geometry of two-way light travel in Minkowski space

It is important to note two assumptions implied by the figure. First, the figure does not presuppose equality of incoming and outgoing light speeds. This is indicated by the slope of the incoming and outgoing light paths; so that the travel times are different:
t₁−t₀ ≠ t₂−t₁. Second, the figure presupposes Euclidean spatial geometry. This is required so that R is the distance to the reflection and so that the round-trip speed of light is c = 2R/(t₂−t₀). Finally, even though the diagram is drawn for a light ray moving in the x-direction, the argument applies for a light ray traveling in the y-direction, z-direction or any direction from the origin. This is due to the invariance of the spacetime interval under spatial rotations about the origin.

Any vector that represents a light path in special relativity satisfies the “null interval” (or lightlike) property, viz:

$S^{2} = Δ x^{2} + Δ y^{2} + Δ z^{2} - c^{2} Δ t^{2} = 0$

Equation 2

Note that the definition of physical speed is distance, D, traveled in a time of T:

$v = \frac{D}{T}$

Assuming Euclidean distance in 3D space3, the distance measured using rods along orthogonal directions (x, y, z) is:

$D = \sqrt{Δ x^{2} + Δ y^{2} + Δ z^{2}}$

Thus, we have for the one-way physical speed of light:

$c = \frac{\sqrt{Δ x^{2} + Δ y^{2} + Δ z^{2}}}{Δ t}$

This equation implies:

$Δ x^{2} + Δ y^{2} Δ z^{2} - c^{2} Δ t^{2} = 0$

thus, verifying the null interval property for the spacetime separation given in equation(2).

Supposedly, according to ASC, the speed of the light represented by N_out is different than the speed of N_in. However, the above null interval condition for light rays is an invariant property of the vectors. This means that the value is independent of which coordinate system one uses to compute its value. Lisle (2018) correctly agrees with this and asserts this in his book The Physics of Einstein. Lisle writes4:

The spacetime interval is invariant under the Lorentz transformation. This means that whatever one inertial observer calculates the space time interval to be between any two events, all other inertial observers will calculate exactly the same value. You can verify this for yourself using the Lorentz transformations from the previous chapter. Pick two points in spacetime with any values you like (x₀, y₀, z₀, t₀) and (x₁, y₁, z₁, t₁). Then calculate the spacetime interval (s). Now calculate the position of the same two points in the Ο´ frame selecting a velocity of your choice (ν) using the Lorentz transformation to find (x′, y′, z′, t′,) and (x′, y′, z′, t′,). If you again compute the spacetime interval (s) using the primed coordinates you will find it is always exactly the same as the value computed from the unprimed coordinates.

So Michael and Sarah may disagree on the times and positions of any events in the universe. But they will always agree on the spacetime interval between any two events. This tells us something quite profound about the universe. The spacetime interval is the “real” absolute quantity. (Emphasis added). (Lisle 2018, 90)

And what is lightlike for one observer will be lightlike for all . . . . (Lisle 2018, 92)

Lisle’s ASC thesis is that the speed of light is a convention and can be made infinitely fast in one arbitrary direction and slower in the opposite arbitrary direction. But is that so? Does Lisle truly believe it? There is another telling remark of Lisle. In Lisle (2018, 91), he correctly states:

Relativity does have absolutes, such as the speed of light in vacuum and the spacetime interval. These are invariant absolute quantities.

This raises the question that if the speed of light is invariant and absolute (and it is), then how can ASC claim otherwise? Simply put, it can’t. We will see later that the ASC coordinate transformation relies on an equivocation of the word “speed.”

We now show that the invariance of the spacetime interval yields (as it must) isotropic speed of light, contrary to the assertion of ASC. This isotropic speed is in accordance with Lisle’s remark above.

To this end we write the vectors N_out and N_out as representing light receding and approaching along the x-axis. The vectors are then an interval from the emission event to the reflection, and from the reflection to the reception event, respectively. For N_out we take a path from (x₀, 0, 0, t₀) to (x₁, 0, 0, t₁). So that

$N_{out} = (x_{1} - x_{0}, 0, 0, t_{1} - t_{0})$

From this we compute the invariant interval:

$s^{2} = {(x_{1} - x_{0})}^{2} - c^{2} {(t_{1} - t_{0})}^{2} = 0$

The solution of this equation for x₁>x₀ (outgoing rays), is:

$x_{1} - x_{0} = c (t_{1} - t_{0})$

This demonstrates that the outgoing speed of light is c.5

For the incoming light ray from the reflection at event (x₁, 0, 0, t₁) to reception at the event (x₀, 0, 0, t₂) we obtain, as anticipated, the same result:

$s^{2} = {(x_{0} - x_{1})}^{2} - c^{2} {(t_{2} - t_{1})}^{2} = 0$

The solution of this equation for x₀<x₁ (incoming ray), is:

$x_{1} - x_{0} = - c (t_{2} - t_{1})$

This demonstrates that the incoming speed of light is also c.

This conclusion could be reached quickly with the realization that ASC is based on the presupposition of the geometry of Minkowski space. The speed of light (physical distance divided by physical time) in Minkowski space is isotropic and it is an invariant property of Minkowski space (since s² = 0 is obtained by all observers for a light ray interval).

Thus, we conclude that ASC’s purported conclusion is logically inconsistent with the basis of special relativity which Lisle has presupposed. The conclusion that the speed of light in ASC is anisotropic is incorrect; this is because the purported speed of light is not a physical speed. The anisotropic speed of ASC is a coordinate rate not a physical speed and the word speed in ASC is used in an equivocation. We demonstrate this in Appendix A.

Conclusion

We have shown that the purported anisotropic speed of light contradicts the intrinsic and invariant speed of light in Minkowski space on which ASC is based. The ASC convention is merely a coordinate transform that cannot alter physical quantities. The conclusion is that ASC does not alter the invariant speed of light or the time that it takes light to reach the earth and therefore does not solve the LTTP.

Acknowledgements

I thank John Byl, Danny Faulkner, Tim Lewis, Robert Walsh, and an anonymous reviewer for their comments.

References

Dennis, Phillip W. 2018. “Consistent Young Earth Relativistic Cosmology.” In Proceedings of the Eighth International Conference on Creationism. Edited by J. H. Whitmore, 14–35. Pittsburgh, Pennsylvania: Creation Science Fellowship.

Lisle, Jason. 2010. “Anisotropic Synchrony Convention—A Solution to the Distant Starlight Problem.” Answers Research Journal 3 (September 22): 191–207. https://answersresearchjournal.org/anisotropic-synchrony-distant-starlight/.

Lisle, Jason. 2018. The Physics of Einstein: Black Holes, Time Travel, Distant Starlight, E-mc². Aledo, Texas: Biblical Science Institute.

Misner, Charles W., Kip S. Thorne, and John Archibald Wheeler. 1973. Gravitation. San Francisco, California: W. H. Freeman.

Newton, Robert, 2001. “Distant Starlight and Genesis: Conventions of Time Measurement.” TJ 15, no. 1 (April): 80–85.

Reichenbach, Hans, 1958. The Philosophy of Space and Time. Translated by Maria Reichenbach and John Freund. New York, New York: Dover Publications.

Appendix A

Proof that ASC speeds are not physical speeds.

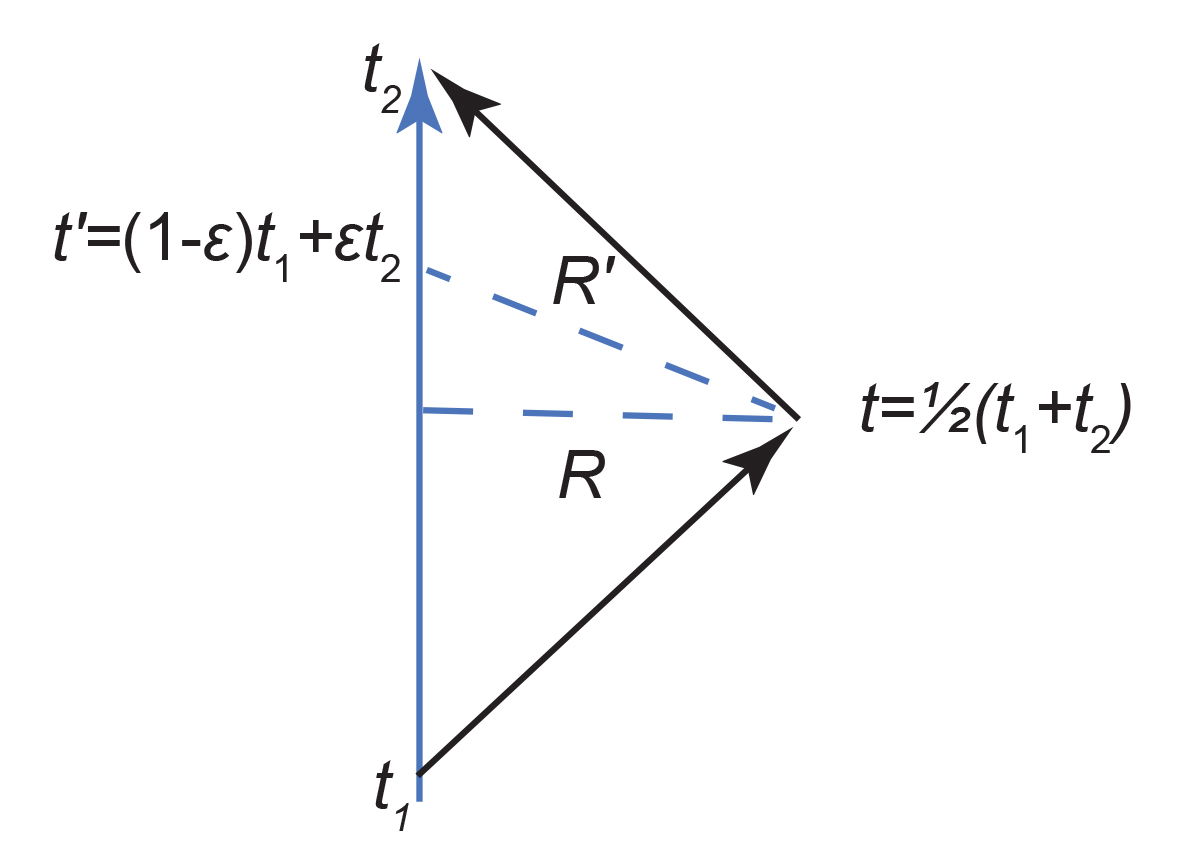
Fig 2. Geometry of Reichenbach’s simultaneity convention.

From fig. 2 we note that the interval denoted R′ lies in the ASC space of simultaneity. Every point along the ray is at the same time according to the ASC assumptions. Presumably such a spatial interval is measured by laying out rigid rods along the ray all at the same time. That is how we understand the concept of physical distance. The question is what is the distance R′? The answer is that R′ is given by the invariant interval specified by the Minkowski geometry, viz:

$R^{' 2} = Δ x^{2} + Δ y^{2} + Δ z^{2} - c^{2} Δ t^{2}$

Equation 3

The coordinates of the events denoted by the point labeled t′ at x = 0, and $t = \frac{1}{2} (t_{1} + t_{2})$ at x = R are, (0, 0, 0, t′) and $(R, 0, 0, \frac{1}{2} (t_{1} + t_{2}))$ , respectively.

Substitution into equation (3) yields:

$\begin{aligned} R^{' 2} & = Δ x^{2} + Δ y^{2} + Δ z^{2} - c^{2} Δ t^{2} \\ = (R - 0)^{2} - c^{2} {[t^{'} - \frac{1}{2} (t_{1} + t_{2})]}^{2} \\ = R^{2} - c^{2} {[(1 - ε) t_{1} + ε t_{2} - \frac{1}{2} (t_{1} + t_{2})]}^{2} \\ = R^{2} - \frac{c^{2}}{4} {[2 (1 - ε) t_{1} + 2 ε t_{2} - t_{1} - t_{2}]}^{2} \\ = R^{2} - \frac{c^{2}}{4} {[(2 ε - 1) (t_{2} - t_{1})]}^{2} \end{aligned}$

Equation 4

We now note that the stipulation that the two-way speed of light is c requires:

$t_{2} - t_{1} = \frac{2 R}{c}$

Substitution in the last line of equation yields:

$\begin{matrix} R^{' 2} & = R^{2} - \frac{c^{2}}{4} {[(2 ε - 1) \frac{2 R}{c}]}^{2} \\ = R^{2} [1 - (2 ε - 1)^{2}] \\ = 4 R^{2} ε (1 - ε) \end{matrix}$

And finally:

$R^{'} = 2 \sqrt{ε (1 - ε)} R$

Equation 5

This shows that the distance R′ to the light reflection in ASC is not the same as the distance R used to calculate the two-way speed of light. What this means in principle is that the ASC synchrony convention does not maintain the geometric meaning of the spatial coordinate x. Using the value R in ASC calculations of the speed of light is the reason that there is an apparent alteration of the speed of light. If ASC takes seriously that the interval R′ lies in a simultaneous space, then R′ should be used in calculating distances, rather than R.6

This can be seen by computing the incoming speed of light using the ε convention. From fig. 2, and incorrectly using R as the distance to the reflection, we obtain:

$\begin{aligned} c_{-} & = \frac{R}{t_{2} - t^{'}} \\ = \frac{R}{t_{2} - (1 - ε) t_{1} - ε t_{2}} \\ = \frac{R}{(1 - ε) (t_{2} - t_{1})} \\ = \frac{c}{2 (1 - ε)} \end{aligned}$

The last equality is the supposed ASC incoming speed of light, but it was erroneously derived using the Minkowski isotropic geometry—assuming R is still the distance to the reflection after adopting a different time coordinate! That calculation is inconsistent with ASC as follows.

Referring to fig. 2 we see that R is the Einstein synchrony convention (ESC) distance (computed from the reflection at the half-way point); while R′ is the ASC distance. One cannot use both the ESC distance and the ASC distances and times within a derivation and expect a valid calculation. It uses two different spatial coordinates from two different coordinate systems. That dual use is illegitimate and leads to an apparent change in the speed of light. One must use a single coordinate system when extracting physical quantities from a theory. We remark that using both distances is an eternalist notion—that both distances exist. This shows that in eternalism, on which ASC is based, there is no objective distance to the reflection just as there is no objective time of reflection.

Ignoring this distinction between the apparent speed based on coordinates (instead of invariants) and the true physical speed embodied in the geometry of Minkowski space is the source of the mistaken claim of an anisotropic “speed of light.” As such, it is an example of incorrectly interpreting and dealing with coordinates rather than using the invariants of the geometry of Minkowski space which is independent of coordinates (by using the correct transformed metric). In short, the speed of light cannot be both isotropic and anisotropic, except by equivocation on the word “speed of light.” Such is the logical lapse of ASC. ASC is not consistent with its presupposition of the Minkowskian geometry of SR.

Appendix B

Mathematics of ASC

We begin with the invariant spacetime interval for Minkowski space in its infinitesimal or differential form in polar coordinates:

$d s^{2} = - c^{2} d t^{2} + d r^{2} + r^{2} (d θ^{2} + \sin^{2} θ d φ^{2})$

Equation 6

In the above r is the physical distance from the origin. It can be seen that when t, θ and φ are constants that ds = ±dr thus showing that intervals of dr are invariant and measure physical distances.

The ASC transformation is given by:

$t = t^{'} - (2 ε - 1) r / c$

Equation 7

In the above t is the ESC time and t′ is the ASC time. It is the putative time measured by a clock at r = 0. The intent of this transformation is to produce a nearly infinite incoming speed of light, that is, a light ray that arrives at the earth nearly instantaneously after it was emitted. How is this theoretically achieved?

First we note that equation (7) says that the ESC time is slow relative to the ASC time coordinate. Equivalently, the ASC transformation sets the ASC clocks fast. We note that equation (7), on which ASC equations are based, actually concedes the one-way speed of light. This should be clear, since equation (7) must use the one-way speed of light c to set the ASC clock fast. To make the point clear, let us set ε = 1 in the equation which corresponds to the desired limit of the ASC model to obtain light arriving at earth, supposedly instantaneously. This gives:

$t = t^{'} - r / c$

Equation 8

This shows that the amount an ASC clock is advanced is precisely the amount of time it takes the light to travel from a distance r to the origin.7

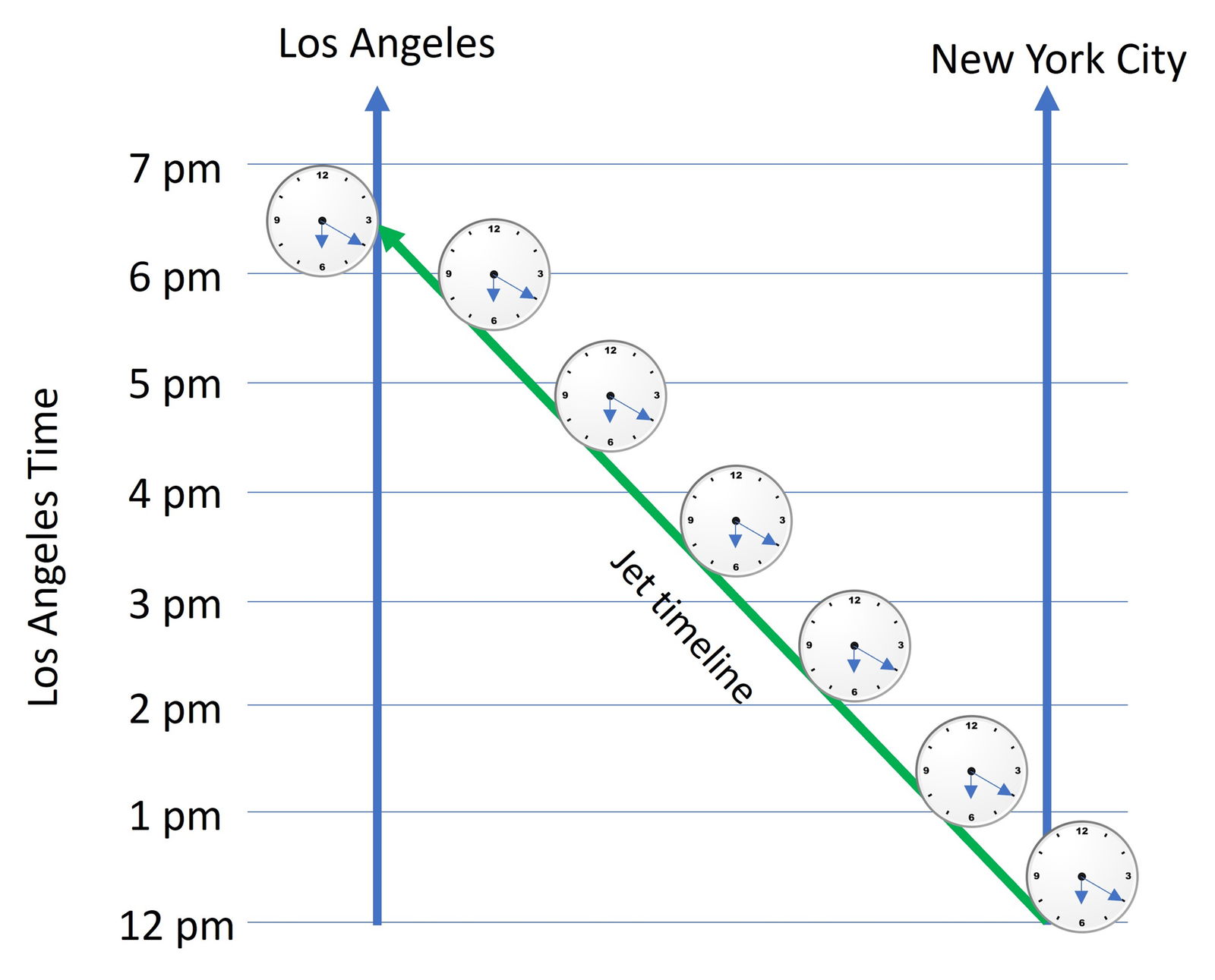
Fig 3. Clock synchronization for airliners. Illustration of the ASC transformation in equation(8). Local clocks along the flight path are set to the arrival time in LA. Equivalently clocks are set fast according to time needed to arrive at LA.

We note that equation (8) also describes an ingoing light ray traveling at a one-way speed of light (= c) arriving at the earth (r = 0) at time t = t′.8

To summarize, the ASC transformation must use the isotropic Minkowski space to derive the ASC transformation which disguises the isotropy. Another way of stating this is that the ASC transformation, equation (7), requires use of the one-way physical speed of light c to perform the mathematics. As such, ASC commits a serious logical lapse. It presupposes the Minkowskian spacetime and a one-way isotropic physical speed of light to derive the ASC formulae (cf. equation [7] ), then denies it. This is a presuppositional defeat of ASC. One cannot have one’s presupposed ontology and eat it too.

Proceeding, the differential form of (7) is:

$d t = d t^{'} - (2 ε - 1) d r / c$

If we substitute this into equation (6), we get:

$\begin{aligned} d s^{2} & = c^{2} d t^{' 2} \\ + 2 (2 ε - 1) c d r d t^{'} \\ + 4 ε (1 - ε) d r^{2} \\ + r^{2} (d θ + \sin^{2} θ d φ^{2}) \end{aligned}$

Equation 9

This is the ASC coordinate form of the invariant Minkowski interval. This coordinate transform has not altered the intrinsic geometry of Minkowski space. (Just as transforming to polar coordinates in the Euclidean plane does not alter the geometry of the Euclidean plane; or representing the globe in terms of polar stereographic coordinates alters the spherical geometry of the globe.)

It should be mentioned here that ASC commits an abuse of coordinates when one performs the transformation in equation (7) and then only analyzes equations algebraically (coordinate symbols) while ignoring the geometry as embodied in equation (9).9 Remarkably, ASC performs a coordinate transformation, then forgetfully ignores the metric tensor in the new coordinates or just throws it away. Such is not the method of rigorous differential geometry and analysis.10

From equation (9) we can obtain the interval of the 3D spatial surfaces of ASC by setting dt′ = 0.11 This specifies the space for which t′ is constant, that is, all events occurring at the same ASC time, or a putative set of simultaneous events. This gives:

$d s^{2} = 4 ε (1 - ε) d r^{2} + r^{2} (d θ + \sin^{2} θ d φ^{2})$

Equation 10

This shows that the distance from the origin of a point along a constant ray (dθ = 0 and dφ = 0) is not measured by r, but rather by:

$d s = 2 \sqrt{ε (1 - ε)} d r$

as was given in equation (5) above.

We can now recast equation (10) in terms of the distance coordinate ρ:

$\begin{matrix} d ρ = 2 \sqrt{ε (1 - ε)} d r, yielding \\ d s^{2} = d ρ^{2} + \frac{ρ^{2}}{4 ε (1 - ε)} (d θ^{2} + \sin^{2} θ d φ^{2}) \end{matrix}$

Equation 11

Equation (11) manifests the global conical non-Euclidean geometry of the ASC spatial geometry.

Considering a circle of constant radius about the origin we obtain the circumference:

$C = \int d s = \frac{ρ}{2 \sqrt{ε (1 - ε)}} \int_{0}^{2 π} d θ = \frac{π ρ}{\sqrt{ε (1 - ε)}}$

as in footnote 6.

Similar integrations yield the surface area of a sphere:

$A = \frac{ρ^{2}}{4 ε (1 - ε)} \int \sin θ d θ φ = \frac{π ρ^{2}}{ε (1 - ε)}$

and the volume of sphere:

$V = \frac{1}{4 ε (1 - ε} \int ρ^{2} \sin θ d θ d φ ρ = \frac{π ρ^{3}}{3 ε (1 - ε)}$

These non-Euclidean properties would hold for circles and spheres of arbitrarily small radius about the ASC origin, and in fact, for all spheres and circles regardless of radius. Thus, the ASC time convention is incompatible with the presuppositions of Euclidean spatial geometry and presentism12.

The reader can verify that these reduce to the Euclidean formulae for ε = ½, reinforcing the fact that ESC implies a global Euclidean spatial geometry.

We can also illustrate the non-Euclidean features of ASC in Cartesian coordinates. Starting with the Minkowski spacetime interval in infinitesimal Cartesian form:

$d s^{2} = - c^{2} d t + d x^{2} + d y^{2} + d z^{2}$

and taking the differential of equation (8), with $r = \sqrt{x^{2} + y^{2} + z^{2}}$ gives:

$d t = d t^{'} - \frac{(2 ε - 1)}{c} (\frac{x d x + y d y + z d z}{r})$

Thus, the spacetime interval in “Cartesian ASC” coordinates is:

$\begin{aligned} d s^{2} = c^{2} d t^{' 2} \\ + 2 (2 ε - 1) c (\frac{x d x + y d y_{-} z d z}{r}) d t^{'} \\ - (2 ε - 1)^{2} {(\frac{x d x + y d y_z d z}{r})}^{2} \\ + d x^{2} + d y^{2} + d z^{2} . \end{aligned}$

This can be expanded to identify the metric components for the x, y, and z coordinates. For example, the inner product of a vector in the x-direction and the y-direction is given by the term:

$g_{x y} = - (2 ε - 1)^{2} \frac{x y}{r^{2}}$

This shows that the x-axis and the y-axis are no longer orthogonal. Thus, the ASC coordinates are not Cartesian. The error in many derivations in ASC papers is that only algebra is performed without noting that the geometric meaning of the new coordinates has changed even if they have the same numerical values.13 This error leads to mistaken interpretations of the ASC formulas.

Footnotes

When I use the term “spacetime,” I am referring to the abstract mathematical structure developed by Minkowski. Spacetime does not exist. Unfortunately, ASC presumes that spacetime exists as an actual non-abstract and static indivisible four-dimensional reality (eternalism) in which time and space cannot be objectively resolved, rather than reality being a three-dimensional spatial universe that persists through time (presentism). The implication of eternalism is that there are no such things as three-dimensional spatial entities; all entities are four-dimensional with both spatial and temporal extents. In presentism, there are three-dimensional entities that persist through time. This important distinction is not directly invoked in this paper—though it has profound theological consequences that Christians should not ignore.
This is equation (9.5) in Lisle (2018). It gives the interval between two events $E_{1} : (x_{1}, y_{1}, z_{1}, t_{1})$ and $E_{2} : (x_{2}, y_{2}, z_{2}, t_{2})$ in terms of coordinate differences $Δ x = x_{2} - x_{1}$ , etc. Presumably the value of c in equation (9.5) is the round-trip speed of light. We will allow this for argument’s sake but will show herein that it is also the one-way speed of light.
In Appendix B it is shown that the spatial geometry of ASC is non-Euclidean.
In the following quote Lisle correctly states that the spacetime interval (essentially the length of a line segment) is invariant under a Lorentz transformation. However, that characterization is unduly restrictive. The Lorentz transformation is just one example of a coordinate transformation. The length of a line segment in Minkowski space is invariant under any coordinate transformation. In particular, the length is invariant under the ASC conventional change of synchrony. A moment’s reflection should make this obvious. The straight-line segment in Minkowski space is a geometric object and its length is an intrinsic property of the line segment independent of the set of coordinates used to describe the segment. This is true in any geometric space, including the familiar Euclidean plane.
If one takes c to be the two-way speed of light in the spacetime interval, this result shows that the one-way outgoing speed of light is equal to the two-way speed. Thus, there is an invariant one-way speed of light, and it is not conventional. This is contrary to the assertions of ASC advocates.
Several remarks are in order. If the ASC advocate embraces eternalism then he can claim there is no such thing as simultaneity. That answer provides no solace to ASC, since the ability to select any time of reflection and maintaining the claim that the distance R is the real distance means there is no unique reflection event. On the other hand, abandoning the uniqueness of R means that there is no objective spatial distance to the reflection. This last conclusion is a basic feature of eternalism. Objects have no actual 3D properties, only static 4D spacetime properties. There is no instant (now) in the creation and there are no objective spatial relations between objects—only spacetime relations. There are also no objective relative speeds. If the ASC advocate resorts to presentism, and claims there is a unique value for ε other than ½, then we obtain a 3D space with a pathology at the origin with a global non-Euclidean geometry. Resorting to presentism means accepting that the distance to the reflection is uniquely R′. As a result, it can be shown that the circumference of a circle about the origin would be $c = π R^{'} / \sqrt{ε (1 - ε)}$ , which is not a Euclidean geometry even for any radius unless ε = ½. Similar results can be obtained for the surface area and volume of spheres centered at the origin. We give the mathematical details in Appendix B.
Here is a more down to earth example to elucidate the method of equation (8). I am taking a flight from New York City to Los Angeles at noon LA time. The flight duration is 6:20 hours. I “synchronize” the local NY clock by setting it forward to 6:20 p.m. (synchronizing it with LA time). I land at Los Angeles and check the times. I departed at 6:20 p.m. (according to the ASC synchrony) and land at LA at 6:20 p.m., so I compute my speed as infinite! Of course, artificially setting the departure time forward cannot alter aircraft speeds, and neither can the ASC transform in equation (8) alter light speeds. Cf. fig. 3.
Equation (8) is also used as the definition of Eddington-Finklestein ingoing coordinates (EFC) used in the analysis of black holes. That coordinate system is based on ingoing light rays. It labels events by the time of their arrival at the origin, the location on the celestial sphere and a radial coordinate from the origin. The coordinates are useful in the analysis of black holes since the EFC describe the trajectory of photons falling into a black hole. It is important to note that use of EFC does not imply that the time of arrival of a light ray is also the actual time of all events along the light ray. They merely identify events along a light ray. See Misner, Thorne, and Wheeler 1973, 28–31.
It bears repeating that coordinates, per se, are amorphous and devoid of geometric or physical meaning. Their physical meaning is derived via the coordinate independent invariant interval ds.
For those familiar with tensor calculus, this entire paper can be summarized as follows. ASC utilizes a coordinate transformation, $d x^{a^{'}} = \frac{\partial x^{a}}{\partial x^{b}} d x^{b}$ , then only uses the new coordinates x^ta without transforming the metric to its representation in ASC coordinates, viz. $g_{a b}^{'} = \frac{\partial x^{c}}{\partial x^{' a}} \frac{\partial x^{d}}{\partial x^{' b}} g_{c d}$ , given in equation(9), to analyze the intrinsic geometry and physics. This is tantamount to ignoring the intrinsic geometry of Minkowski spacetime.
The reader should note that the procedure of setting a time coordinate to zero, thereby indicating a space of “simultaneity,” is precisely how the Lorentz contraction formula is derived, viz: $\begin{aligned} t^{'} = γ (t - x v / c^{2}) \\ x^{'} = γ (x - v t) \end{aligned}$ For t′=0 we get t=xv/c² which when substituted into the equation for x′ yields the Lorentz contraction: $x^{'} = γ^{- 1} x = x \sqrt{1 - v^{2} / c^{2}}$
Adhering to presentism we would require a smooth geometry at every point and a locally Euclidean geometry in a neighborhood of the earth. This can be achieved by selecting an objective 3D hyperbolic geometry representing space at objective cosmic time (“age of the creation”) as I presented in Dennis (2018).
The new axes are no longer perpendicular since the vectors in those directions have changed due to the change in the time coordinate. For example, the modern notation for the tangent vector in the x-direction in ESC is ${(\frac{\partial}{\partial x})}_{t}$ and for ASC is ${(\frac{\partial}{\partial x})}_{t^{'}}$ These are not the same vectors and illustrates why the geometric interpretation of the coordinates has changed. Ignoring which coordinates are held constant by simply writing $\frac{\partial}{\partial x}$ for the vector in the x-direction is a serious conceptual lapse—a lapse that is frequently made by students in introductory thermodynamics course work.

Cite this Article

An Internal Contradiction of Lisle’s Anisotropic Synchrony Convention (ASC) Model

Abstract

Introduction

The Contradiction

Conclusion

Acknowledgements

References

Appendix A

Proof that ASC speeds are not physical speeds.

Appendix B

Mathematics of ASC

Featured Topics

Astronomy

Astrophysics

Cosmology

Physics

You May Also Like

Astronomical Distance Determination Methods and the Light Travel Time Problem

Footnotes