A Review of Stellar Formation Theory

Introduction

Recent creationists appear to be divided on the question of whether stars form today. For instance, Thomas (2015) has argued that stars cannot form today because God made all the stars on day four of the creation Week. On the other hand, Faulkner (2014) has argued that God’s creation of stars on day four does not necessarily preclude the possibility that at least a few stars could from today any more than the creation of land animals on Day 6 prevents new animals from being born today. Besides possible biblical objections to star formation today, recent creationists are divided over physical reasons for doubting star formation. Mulfinger (1970), Williams (2000, 2001), and Henry (2002) argued that stars forming from gas clouds would violate the second law of thermodynamics while Faulkner (2001, 2002) disagreed.

Why do astronomers generally think that stars form today? Since stars radiate energy, they must possess energy sources. All energy sources are finite, so the lifetime of any star may be estimated by dividing its energy supply by its observed luminosity (power). The energy source of stars is generally understood to be nuclear fusion of hydrogen into helium in their cores. This energy source is very large, but it is not unlimited. The estimated lifetimes of the least massive stars greatly exceed that of the current 13.8-billion-year age for the big bang, so low mass stars could be primordial. However, the lifetimes of the most massive stars are computed to be on the order of a few million years. Therefore, in a big bang universe, the most massive stars must have formed very recently. Even a midrange star like the sun cannot be primordial. The sun’s maximum lifetime is nearly 10 billion years, only about 70% of 13.8 billion years (the sun is believed to be approximately 4.55 billion years, about half its maximum lifetime and approximately one-third the age of the big bang universe). Therefore, in the current evolutionary model, there is need for ongoing star formation.

Where might stars form? The space between stars is not empty. The interstellar medium (ISM) contains a very rarefied, yet significant, amount of matter. The ISM is not uniform. Rather, the ISM is very clumpy, with wide variations in density. While the typical ISM may have an average number density of less than one particle (atom, ion, or molecule) per cubic centimeter, there are clouds in the ISM with number density more than 1,000 particles per cubic centimeter. The composition of the ISM closely matches that of the observed composition of stars, mostly hydrogen and helium with at most a few percent being the heavier elements. The masses of large clouds in the ISM can be many thousands of solar masses. Given that gas clouds have composition similar to stars and sufficient mass, astronomers generally conclude that under the right conditions, gas clouds can collapse to form stars.

How gas clouds may collapse to form stars is not entirely understood. One can find frank admissions of the physical problems with star formation in the astronomical literature, often in advanced textbooks on stellar structure and evolution. However, simply quoting such sources falls far short of an effective response to the theory of star formation. There are many examples of physical processes that are not fully understood. For instance, there is much that we don’t understand about formation of storm-related phenomena, such as lightning, tornados, and hurricanes, but gaps in our knowledge of such things hardly are good arguments against the reality of these things. Since a detailed discussion of star formation does not exist in the creationary literature, this review of the theory of star formation is warranted.

The naturalistic theory for the formation of stars usually traces back to a suggestion by Emanuel Swedenborg in 1734. This was embellished by Immanuel Kant in 1755. However, this concept is best associated with Pierre-Simon Laplace and his 1796 treatment of what has come to be called the nebular hypothesis. The nebular hypothesis was more concerned with the formation of a disk around the young sun from which the planets supposedly formed. Therefore, it is best to trace the lineage of this idea to modern theories of planet formation in the solar system rather than star formation per se. William Herschel, a contemporary of Laplace, was among the first to suggest that stars formed from gravitational collapse of nebulae, what astronomers call large clouds of gas in the ISM. This idea was debated throughout the nineteenth century before finally being widely accepted by the end of that century.

The Jeans Criterion

The name of Sir James Jeans is associated with this theory of star formation more than any other single individual. Jeans (1902) was the first to derive a physical description of what the process of star formation from a gas cloud might entail. Gas clouds have considerable mass, so they possess gravity that operates inward, toward their centers of mass. If left unopposed, this self-gravity would tend to contract gas clouds into smaller volumes, inevitably resulting in star formation. However, gas clouds also possess pressure, which tends to oppose the inward force of gravity. This balance is called hydrostatic equilibrium, and it can be expressed as:

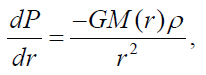
where P is pressure, G is the gravitational constant, M(r) is the mass enclosed by radius r, and ρ is density. Due to their large size, the self-gravity of gas clouds is very feeble, and because of the extremely low density of gas clouds, gas pressure also is very feeble. If these are the only two forces at work, then even a slight imbalance in favor of gravity ought to overcome the constraint of hydrostatic equilibrium and lead to gradual collapse of a gas cloud into a star.

To obtain the Jeans Criterion for the collapse of a gas cloud, one must make several simplifying assumptions about the cloud. Assume a very large cloud with the gas initially at rest and having uniform density, pressure, and temperature, T, and having gravitational potential, Φ. There are two fluid dynamics equations that apply. The first is the continuity equation:

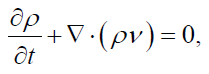
where v is the velocity of the gas as a function of time. The second fluid dynamic equation is the Euler equation, coming from conservation of momentum:

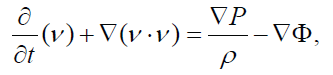
Additionally, Poisson’s equation applies:

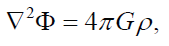
where G is the gravitational constant. Finally, the gas can be described as an ideal gas:

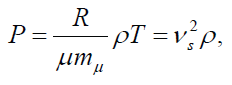
where R is the ideal gas constant, μ is the mean molecular weight, m_u is the atomic mass constant, and v_s² is the speed of sound.

Let the cloud be perturbed so that ρ = ρ₀ + ρ₁, P = P₀ + P₁, and Φ = Φ₀ + Φ₁. Since the gas is initially at rest, v₀ = 0, and so let v₁ = v. Keep in mind that due to the assumption that the cloud is isothermal with uniform density, ρ₀ and T are functions of time but are not functions of position. Substituting the perturbation terms into the equation of continuity, Euler’s equation, and Poisson’s equation results in

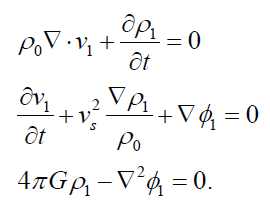
This is a linear homogeneous system of differential equations in v₁, ρ₁, and Φ₁. A solution exists in the form e^{i(kx + ωt)}, where k is the wave number and ω is the angular frequency, with ∂ / ∂x = ik, ∂ / ∂y = ∂ / ∂z = 0, and ∂ / ∂t = iω. With appropriate substitution, the equations reduce to

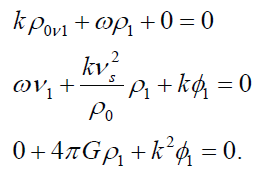
The solution to this homogeneous linear set of three equations for v₁, ρ₁, and Φ₁ is found by setting the determinant of the matrix

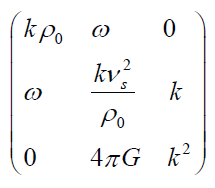
to zero. Assuming that k ≠ 0, the solution is

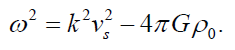
If k²v_s² 4πGρ₀, then ω is real, and the perturbation varies periodically in time and equilibrium is stable. As k → ∞, then ω → k²v_s², which corresponds to isothermal sound waves. This means that for very short wavelengths, gravity is not important, compression is restored by increased pressure, and perturbations travel with the speed of sound. However, if k²v_s² 4πGρ₀, then ω is not real, and the eigenvalue ω has the form iζt, where ζ is a real number. Perturbations of this type grow exponentially with time, rendering the equilibrium unstable.

The critical wavenumber, k_J, between these two regimes is

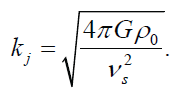
The Jeans length is the corresponding critical wavelength,

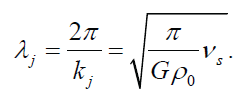
A perturbation with wavelength λ > λ_J will produce instability.

Taking the Jeans length as a length scale, we can define the critical mass (Jeans mass) as

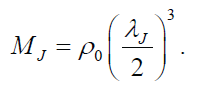
The speed of sound is

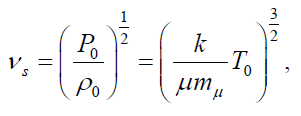
where k is the Boltzmann constant, μ is the mean molecular weight, and m_u is the atomic mass unit. Combining the last three equations arrives at

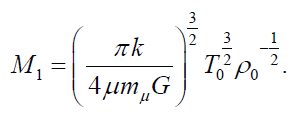
If the mass of a gas cloud having temperature T₀ and density ρ₀ exceeds the Jeans mass, then it is unstable and ought to collapse due to its own gravity.

Before proceeding, I must address concerns about the simplifying assumptions. Gas clouds are not isothermal, nor do they have uniform density. Furthermore, though I didn’t state it, the mathematical assumption is that the cloud is infinite, not merely large. As long at the density and temperature within a cloud do not vary over a wide range (which is what we observe), then the assumption of uniform density and temperature is not a great departure from the true state of clouds. The departure of a very large, but finite, cloud does not radically depart from an infinite cloud.

This derivation assumed that the cloud was a cube having sides of length λ_J/2. It would be more realistic to assume a spherical gas cloud. This would cause the result to differ from what I found by a factor of 4π/3, a factor of approximately four. The point of this calculation is that there is a threshold mass above which a cloud will collapse. The calculation only gives an order of magnitude for that threshold. The exact mass threshold depends upon the details of a gas cloud, such as shape and variations in temperature and density. Therefore, there is confidence that the Jean’s mass is well within an order of magnitude of being realistic.

A reviewer recommended including a simpler, less rigorous derivation of the Jean’s criterion. The virial theorem states that for a stable, gravitationally bound system such as a gas cloud,

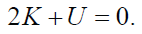
where K is the total internal energy of the cloud, and U is the gravitational potential energy of the cloud. If twice the internal energy of a cloud exceeds the absolute value of the gravitational potential energy, then gas pressure dominates over gravity, and the cloud expands. However, if the absolute value of the cloud’s gravitational potential energy exceeds twice its internal energy, then gravity dominates, and the cloud will collapse. Therefore, the Jean’s criterion can be stated as

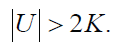
The gravitational potential energy of a uniform cloud of density ρ having radius R is

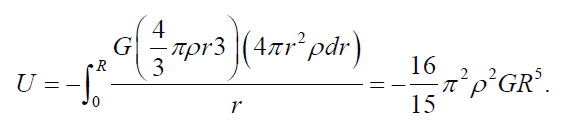
Noting that

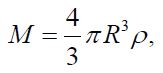
This simplifies to

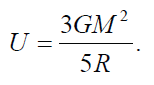
If the cloud has initial density ρ₀, then

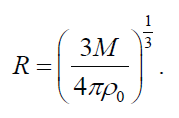
Therefore, the gravitational potential energy can be written as

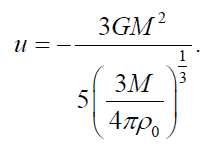
The internal energy is

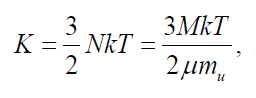
where N is the number of particles.

Substituting these last two equations into the inequality above, we find the Jean’s criterion to be

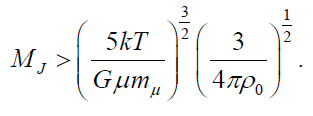
Note that this derivation results in the same functional T^3/2 and ρ₀^-1/2 dependence of the more detailed calculation above. The only difference is the constant, but the constant of this inequality differs from the earlier corrected calculation for a spherical cloud by a factor of two. The Jean’s criterion is an estimate, so agreement within a factor of two using two different approaches demonstrates the soundness of the approximation.

Computation of the Jean’s criterion for Two Examples

For purpose of comparison, I shall use this equation for computing the Jean’s criterion:

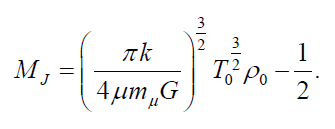
Factoring out μ, this equation becomes

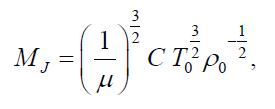
where

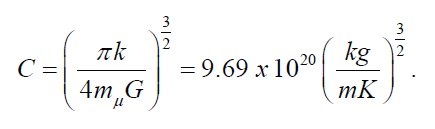
Over the past century, the interstellar medium (ISM) has been extensively studied. Spectroscopy has allowed measurement of the properties of the ISM. The ISM is very clumpy, and it has several components, in terms of both composition and temperature. However, one may focus on different clouds of the ISM for which a few simplifying yet accurate assumptions may be made. For instance, most of the mass of the ISM is in the form of hydrogen. Probably half the mass of the ISM is in molecular clouds, which, as the name implies, are clouds composed mostly of molecules. The most common molecules in molecular clouds are H2 and CO. Due to ionizing radiation in space, molecules are relatively rare in the ISM. Only in the protective environments of the densest clouds can molecules exist. Consequently, it is not coincidental that molecular clouds are the densest parts of the ISM, with number densities typically a few hundred particles per cm³ (the number density in the solar neighborhood is about 1 particle per cm³). What molecular clouds lack in density, they more than make up in volume. Spanning tens to hundreds of parsecs, giant molecular clouds can have masses many thousands to millions of times greater than the sun. Even more modest molecular clouds typically have masses of a few hundred solar masses. Most of the remaining ISM is in HI regions, dominated by neutral hydrogen atoms.1 What is the Jean’s criterion for these two distinct major components of the ISM? For the computation, I took values from Mathis (2000, 524)

First, consider HI regions. The number density of HI regions is between 10 cm^-3 and 1,000 cm^-3. I will assume a typical number density of 100 cm^-3 = 10⁸ m^-3.2 HI regions generally have temperature of 80 K. Since the hydrogen is in atomic form, μ = 1. This results in a Jean’s criterion of 1.7 × 10³³ kg. This is about a thousand solar masses. With the assumed average density, a spherical cloud having this mass would require a radius of 4.3 light years. HI regions are very clumpy and have irregular shapes. While some HI regions or portions of HI regions may achieve this size and hence achieve the Jean’s criterion, remember that collapse requires exceeding the Jean’s criterion, so it is unlikely that many, if any, HI regions are capable of star formation. Indeed, astronomers don’t think HI regions are places where stars form.

What about molecular clouds? The temperatures of molecular clouds are between 10 and 20 K. For ease of computation, I will assume T = 10 K. Number densities of molecular clouds exceed 100 cm^-3. However, the number densities of the cores of giant molecular clouds typically are 10⁴–10⁶ cm^-3. Since the densest regions (the cores) of molecular clouds are the most likely regions of star formation, I will assume an average of 10⁵ cm^-3 = 10¹¹ m^-3. Since the hydrogen is diatomic, μ = 2. The resulting Jean’s mass is 5.9 × 10²⁹ kg. This is one-quarter the sun’s mass. The corresponding radius required to contain this much mass is 7.5 × 10¹⁴ m = 5.0 astronomical units (AU). This size is orders of magnitude less than the radii of cores of giant molecular clouds, so the cores of giant molecular clouds greatly exceed the Jean’s criterion. Hence, it appears unavoidable that these cores will eventually collapse. Consequently, astronomers generally believe that the cores of giant molecular clouds are stellar nurseries.

The key factors in these computations are density and temperature. Gravitational collapse is facilitated by high density and low temperature. While HI regions certainly are cool, they lack sufficient density to overwhelmingly exceed the Jean’s criterion as giant molecular clouds do. Most other components of the ISM lack either higher density and low temperature, or both. The only exception is HII regions (fig. 1), regions of hydrogen gas ionized by embedded hot, bright stars. The number densities of HII regions are similar to those of HI regions (this is no surprise since if HII regions were un-ionized, they would HI regions). However, HII regions are about 100 times hotter, with temperatures typically 8,000 K. This results in a Jean’s mass of 1.7 × 10³⁵ kg, approximately 10⁵ solar masses. While the masses of some HII regions are comparable to this, remember that assurance of collapse only exists for clouds that greatly exceed the Jean’s criterion. Indeed, HII regions generally are associated with star-forming areas. HII regions are powered by bright, hot stars that are thought to be recently formed. The radiation from these stars make collapse of HII regions highly unlikely.

Fig. 1. The Rosette Nebula. This is an HII region powered by the star cluster NGC 2244 at the center. The cluster’s hot, bright stars have short lifetimes, so astronomers think they recently formed. Photograph courtesy of Jim Bonser.

What Causes Instability?

The collapse of a cloud to form a star takes more than a few thousand years. For most stars, the process requires millions of years, far less than the supposed 10+ billion-year age of the universe. If the cores of molecular clouds are prone to collapse, it is obvious that they could not have existed in their current state very long (only for a few tens of millions of years at most). In a recent creation model, this is not a difficulty—God could have created gas clouds in the process of collapse. However, if the universe is billions of years old, how did molecular clouds form? Since much of the ISM outside of molecular clouds is not prone to collapse, star formation needs some mechanism to initiate the process. There have been several suggested triggers of star formation. The most popular mechanism is supernovae explosions. Supernovae eject considerable matter at very high speeds, as great as 10% the speed of light. These speeds are hypersonic, so the expanding matter overtakes the ISM along a shock front that compresses and heats the ISM. This interaction slows the shock front, but the expanding front of material can travel tens of parsecs before ceasing to be hypersonic. Since the restoring force of pressure acts at the speed of sound, a shock front easily overwhelms the force acting to resist the compression of gas. Astronomers believe this compression acts to produce clouds that meet the Jeans criterion for gravitational contraction, leading to star formation.

Another proposed trigger for star formation is dust. The ISM has two primary components: gas and dust. Gas consists of atoms, ions, and molecules. Dust is made of solid particles encompassing many molecules, so dust particles are much larger than gas particles. The composition of dust is silicates, ices, and even elemental iron. Due to collisions with gas particles, dust particles are in thermal equilibrium with the surrounding gas. However, unlike gas, dust readily loses heat via emission of infrared radiation. Cool gas clouds are transparent to infrared, so heat radiated by dust particles is lost. As the dust particles become slightly cooler than the ambient gas, collisions transfer heat from the gas particles to the dust, which is further radiated. Since collisions act to maintain thermal equilibrium between the dust and gas particles, this process acts as a refrigerator, gradually cooling the gas. Cooler gas produces less pressure, so the cloud contracts due to hydrostatic equilibrium. As this process continues, the density of the gas slowly increases. However, due to loss of internal energy via thermal emission, the temperature of the gas does not change appreciably. Therefore, according to the last equation, the Jeans mass will decrease as the density increases. Consequently, this mechanism can shrink a cloud until the inward force of gravity exceeds the outward force of pressure, and the gravity becomes the primary factor driving contraction.

A third proposed trigger of star formation is spiral density waves. In the 1960s, Frank Shu and C. C. Lin proposed spiral density wave theory as the solution to the problem of windup of spiral arms of galaxies. According to this model, spiral arms are maintained by a density enhancement, a sound wave, that travels through a spiral galaxy’s disk. Being a mechanical wave, the density enhancement travels at a velocity entirely independent of orbital velocity due to gravity. However, gravity does modify the wave, as does the varying density of the ISM. As the sound wave passes through the ISM, gas clouds are compressed to reach the Jeans criterion whereupon self-gravity continues the process of star formation. One should not think of this process as entirely independent of the other two triggers of star formation mentioned here. Spiral arms are density enhancements in the ISM of disks of galaxies. Shock fronts created by supernova explosions probably alter and merge with the spiral density wave and might even be the ultimate source of the spiral density wave. Furthermore, both gas and dust density are greater in spiral arms than between spiral arms, providing the material (gas) and an additional mechanism (dust) of star formation in spiral arms. Consequently, astronomers consider spiral arms to be locations of ongoing star formation. Is there supporting evidence for this? Yes. Massive blue stars are fond along spiral arms. These stars have very short lifetimes, so they could not have traveled far since their formation, which explains (in the evolutionary model) why massive blue stars are found along spiral arms, sites of ongoing star formation.

Before moving on to other topics, it is important that I emphasize that most, if not all, proposed triggers for star formation require that stars first exist. For instance, supernovae are explosions of stars, so one must ask where the stars that exploded came from. Saying that those stars formed from shock fronts from previous supernova explosions may work for a few generations of stars, but it doesn’t tell us where the first stars came from. A similar, but more subtle reasoning, also applies to the triggering mechanism of cooling by dust particles. Where did the dust particles come from? According to the big bang model, the universe began with hydrogen, helium, and a trifling amount of lithium. Dust particles require heavier elements, such as oxygen and silicon. Those elements hypothetically were produced by thermonuclear reactions in the first generations of stars and then were returned to the ISM via stellar winds and/or supernovae explosions, and later generations of stars incorporated those heavier elements. It was in the atmospheres of some of these later generations of stars that dust particles were produced and then spewed back into the ISM by stellar winds. Therefore, the cooling dust trigger requires at least two generations of stars first exist. Consequently, theories of triggers of star formation may explain how stars may form today, but they don’t reveal where the primordial stars came from. This is particularly problematic in that most astronomers now think star formation was extremely intense in the early universe (only 1–2 billion years after the big bang). For instance, Faisst et al. (2017) discussed dust in galaxies at redshift z > 5 (with an age only 1 Gyr after the big bang). How did this copious dust get produced in so little time? The mechanism that drove this burst of star formation is unknown. Therefore, the ultimate cause of star formation remains a mystery.

Protostars

As previously pointed out, astronomers consider molecular clouds to be the likely sites of star formation. With such large masses, astronomers do not think that molecular clouds collapse to form single stars. Rather, astronomers think the densest inner parts collapse first, with infall of surrounding material upon them. Thus, large clouds typically would sub-fragment to produce many stars. The physical reason for this is that as density rises, the Jean’s mass decreases, so individual sub-clouds become super- Jeans and start their own collapse. This is believed to be the mechanism whereby star clusters form. The cores of collapsing stars are thought to be denser than average, having number densities of many thousands of particles per cm3. Because included dust scatters visible light, the collapsing cores ought to appear dark when not totally embedded in molecular clouds. When silhouetted against bright backgrounds, these cores would stand out. In the 1940s, Bart Bok was the first astronomer to make note of small dark nebulae in front of emission nebulae (HII regions), and he suggested that they may be stellar cocoons, where star formation is taking place. Most astronomers today concur with this assessment, with supporting data being infrared sources inside Bok Globules, as these objects are called (fig. 2). These infrared sources are presumed to be collapsing protostars.

Fig. 2. A portion of the Eagle Nebula (M16). The Eagle Nebula lies on the edge of a giant molecular cloud, believed to be the site of star formation. Some of the small dark knots are Bok globules. Photograph courtesy of Glen Fountain.

Once the Jeans criterion is met and a gas cloud begins to contract under its own gravity, it is called a protostar. Unlike mature stars that are powered by thermonuclear reactions in and around their cores, protostars derive most of their energy from liberating gravitational potential energy (the Kelvin-Helmholtz mechanism).

Astronomers consider the Hertzsprung-Russell (H-R) diagram the key to understanding stellar evolution. The H-R diagram is a plot of stellar luminosity as a function of temperature, with temperature increasing right to left for historical reasons. On the H-R diagram, most stars fall on the main sequence, a roughly diagonal band from upper left to lower right. For a discussion of the H-R diagram in the creation literature, see Faulkner and DeYoung (1991). Because of the enshrouding molecular clouds in which stars presumably form, it would be difficult to observe the very earliest stages of star formation. Since the surface temperatures of protostars in their earliest stages would be quite low, they would not be visible to our eyes. However, they would be quite luminous in the infrared. With such low surface temperature, protostars would begin far off to the right of the H-R diagram. Gravity is the dominant force in the earliest stages of a protostar, so the earliest phases last on the order of the free-fall time. For solar-mass protostars, the free-fall time is on the order of a few hundred thousand years.

By the time the surface temperature of a protostar reaches a few thousand K, it has moved to the upper right of the lower end of the main sequence on the H-R diagram and continues to evolve to the left at nearly constant luminosity. However, this change soon comes to a halt and changes direction. This is the beginning of the pre-main sequence phase. Much of the theory of the pre-main sequence phase of stars having less than three solar masses was worked out by Hayashi (1966) in the early 1960s, who concluded that protostars follow paths in the H-R diagram down toward the main sequence. The exact locations of these Hayashi tracks depend upon the masses of the forming stars.

An important factor in stellar structure and any consequent change, or evolution, in gross properties of a star as expressed on the H-R diagram is the method of energy transfer from the star’s interior to its surface. In most stars, conduction is a relatively minor method of energy transfer. That leaves radiation and convection as the primary means of energy transfer. The most significant factor in determining which of these two methods of energy transport is predominant is opacity, the measure of how impenetrable to radiation a star’s interior is. Opacity is a function of composition, density, and temperature. If the temperature gradient and opacity of a stellar envelope (the region of a star’s interior between its core and surface) will permit effective radiative transfer of heat, then the envelope is said to be radiative. Otherwise, the envelope is convective. The envelopes of massive stars are fully radiative, but the envelopes of lower mass stars tend to be dominated by convection. Mid-range stars, such as the sun, have radiative lower envelopes but convective outer envelopes.

The Hayashi track is nearly vertical on the H-R diagram, with protostars evolving downward toward the main sequence. Stars on the Hayashi track are fully convective, with opacity dominated by hydrogen ions. Stars with mass lower than about 0.5 solar mass remain convective all the way down to the main sequence. As nuclear fusion in the core sets in as the energy source (rather than gravitational contraction), the contraction ceases and the low mass stars become stable on the main sequence. Stars more massive than 0.5 solar mass develop a radiative zone part way down the Hayashi track. This causes those stars to turn off the Hayashi track and travel nearly horizontal path toward the main sequence. This is the Henyey track, named for the first author of a study that elucidate it (Henyey, Lelevier, and Levée 1955). Protostars with more than three solar masses are thought to skip the Hayashi track and evolve nearly horizontally on the Heyey track to the main sequence.

Interestingly, low and intermediate mass stars are thought to evolve away from the main sequence at the end of their main sequence lifetimes to become red giants along paths that are similar to the Hayashi track, except in reverse. Therefore, West (1981) raised the question in the creation literature whether one can tell if a star is pre-main sequence or post-main sequence. Astronomers generally believe that they can tell the difference between pre-main sequence and post-main sequence stars from the environments that stars above the main sequence are found. For instance, West discussed binary stars in which one member was on the main sequence and the other star was above the main sequence, and he suggested that the stars of these systems might be very young pre-main sequence stars. Without mentioning them by name, West discussed Algol-type binary stars. There are good reasons to think that the members of Algol-type binaries are not pre-main sequence stars (Faulkner 2019).

On the other hand, astronomers are confident that T Tauri stars (Bertout 1989) are protostars on the Hayashi track. T Tauri stars are variable stars that are over luminous for their spectral types, F, G, K, and M. Thus, their location on the H-R diagram fits the expectation for Hayashi track protostars. T Tauri stars have irregular periods. They are highly active across all wavelengths, indicating intense chromospheric activity. Forming stars are expected to be chaotic. Some periodicities may be coincident with heavy spotting that rotate into and out of view. The rotation periods of T Tauri stars are a few days. Due to angular momentum loss through magnetic fields, young stars are expected to rotate very quickly and then slow down due to age. For instance, the sun, as a mature star, rotates about once per month. T Tauri stars are found in and around molecular clouds and have much dust. These are the environments where most astronomers think stars are born.

Angular Momentum Loss

A major problem with star formation is conservation of angular momentum. Virtually all astronomical bodies possess angular momentum. In the case of gas clouds that might collapse to form stars, the angular momentum could originate from slight differential orbital motion around the galaxy. As a rotating body contracts in size with no external torque acting, angular momentum must be conserved. Considering the very large change in size a contracting gas cloud must undergo to form a star, angular momentum conservation presents a difficulty. The protostar eventually reaches a point where it is spinning so quickly that further contraction is not possible. Therefore, if stars form this way, there must be a torque acting to remove angular momentum. Astronomers think that magnetic interaction provides this torque. Stars, including the sun, have magnetic fields. For that matter, the Galaxy has a magnetic field that threads through the ISM, including any collapsing gas clouds. With rising temperatures with a collapsing cloud, its material begins to behave as a plasma. This leads to an interaction that can transfer angular momentum from forming stars.

Even mature stars have angular momentum loss. The sun takes about a month to rotate on its axis. The solar wind is a tenuous outrush of charged particles from the sun. As these charged particles move outward, they are subject to the sun’s gravity, but they are much more affected by the sun’s magnetic field. Solar wind particles leave the sun with rotational motion that they had on the solar surface. As the particles move outward, their rotational velocity slows due to conservation of angular momentum. Meanwhile, the sun’s magnetic field extends far from the sun, but the field must rotate approximately with the sun’s monthly rotation. This results in the sun’s magnetic field rotating much faster than the wind particles do. Since the wind particles are charged, the sun’s rapidly rotating magnetic field exerts a force (a torque) onto the wind particles, accelerating them. Newton’s third law of motion dictates that the wind particles exert an equal and opposite force (a torque) on the sun, slowing the sun’s rotation.

Do other stars have winds? Winds from stars of similar magnitude to the solar wind would be too feeble to detect. However, some stars are observed to be exceedingly windy. For instance, some stars thought to be post main sequence have winds that eject a few ten-thousandths of a solar mass per year. Obviously, such large winds cannot be sustained for more than a few thousand years. Presumably, all stars have stellar winds. The interaction between stellar wind particles and stellar magnetic fields described above is expected to slow stars’ rotation throughout their main sequence lifetimes. As an example, the sun’s rotation presumably was a few days when it was very young but has now lengthened to a month. Rotation periods of many stars can be measured via the Doppler effect. Stars that are deemed to be young rotate more quickly than stars that are thought to be old. This process of magnetic braking appears to be very important in the evolution of close binary stars. Samec et al. (2020) have shown that the rate of magnetic braking in close binaries is much faster than generally thought and may have implications in developing a young-universe cosmology.

T Tauri stars typically have intense winds too. In addition, T Tauri stars often have bipolar outflows (Bacciotti et al. 2002; Launhardt et al. 2009). Bipolar outflows are encountered quite a bit in astronomy, from supermassive black holes at the centers of quasars and galaxies, to stellar black holes and neutron stars, which are considered to be highly evolved and hence old stars, to protostars. Bipolar outflows are driven by a complex magnetic interaction of infalling matter in equatorial accretion disks that produces opposing jets that are parallel to magnetic poles that are roughly perpendicular to the accretion disks. The prototype of T Tauri stars is worthy of mention. T Tauri has observed strong winds and a bipolar outflow. Burnham (1890) was the first to notice a faint, small nebulosity next to T Tauri. Burnham’s Nebula, as this object came to be called, attracted little attention for many years. In the late 1940s, George Herbig and Guillermo Haro independently discovered several other small nebulosities that resembled Burnham’s Nebula. Their unusual spectra, variability, and proximity to what were thought to be protostars began to attract attention. Herbig-Haro objects, as these small nebulae are now called, are thought to be a result of shocks caused by bipolar jets from forming stars as they interact with the surrounding ISM. Herbig- Haro objects are associated with T Tauri stars and other protostars.

The End of the Star Formation Process

Eventually, the temperature in the core of a protostar rises to the point that thermonuclear reactions begin. This is not a dramatic switch from all power coming from conversion of gravitational potential energy to a thermonuclear source. Rather, the transition takes time. For lower mass stars, this causes a change in opacity sufficient to drive the forming stars nearly horizontally in the H-R diagram along a Henyey track to reach the main sequence. Stars with more than 3 solar masses skip the Hayashi track altogether, while stars with less than 0.5 solar masses never follow the Henyey track, following the Hayashi track all the way to the main sequence of the H-R diagram. Once on the main sequence, contraction ceases, and astronomers say that a star is born. Often one hears in the news an account of astronomers witnessing the birth of a star. Given the long timescales expected for star formation, such reports are misleading. Rather than directly observing star formation, these news stories refer to astronomers that either observed a star that in their estimation very recently formed (in the past million years or so) or is a protostar still undergoing the process. These amount to snapshots that are arranged to fit the theory of how stars form.

Conclusion

It is not the intent of this review to promote mainstream theories of star formation. Nor is this review necessarily intended as a critique of those theories. Rather, the purpose of this review is to inform creationists on some of the details of the theory of star formation, something that has been lacking in the creationary literature for a very long time. The calculation based upon the measured conditions within giant molecular clouds indicate that they are unstable against collapse. Therefore, the conclusion that star formation is possible at least in some situations seems unavoidable. I hope that this review can stimulate discussion, perhaps resulting in some consensus of how much, if any, of this theory recent creationists may accept. If all of it is rejected, it is important that we develop alternate explanations of the observed objects that are interpreted as protostars or even young stars.

References

Bacciotti, Francesca, Thomas P. Ray, Reinhard Mundt, Jochen Eislöffel and Josef Solf. 2002. “Hubble Space Telescope/ STIS Spectroscopy of the Optical Outflow from DG Tauri: Indications for the Rotation in the Initial Jet Channel.” Astrophysical Journal 576, no. 1 (September): 222–231.

Bertout, Claude. 1989. “T Tauri Stars: Wild as Dust.” In Annual Review of Astronomy and Astrophysics. Vol. 27. Edited by Geoffrey Burbidge, David Layzer and John G. Phillips, 351–395. Palo Alto, California: Annual Review Inc.

Burnham, S. W. 1890. “Note on Hind’s Variable Nebula in Taurus. Monthly Notices of the Royal Astronomical Society 51 (December): 94–95.

Faisst, Andreas L., et al. 2017. “Are High-Redshift Galaxies Hot? Temperature of z > 5 Galaxies and Implications for Their Dust Properties.” The Astrophysical Journal 847, no. 1 (September 20): 21–48.

Faulkner, Danny. 2001. “Does the Collapse of a Gas Cloud to Form a Star Violate the Second Law of Thermodynamics?” Creation Research Society Quarterly 38, no. 1 (June): 40–44.

Faulkner, Danny. 2002 “Star formation: Natural or Supernatural—Reply” Creation Research Society Quarterly 39, no. 1 (June): 60–62.

Faulkner, Danny R. 2014. “Are Stars Still Forming Today?” Answers 9, no. 2 (April/June): 48–49.

Faulkner, Danny R. 2019. “An Evaluation of Astronomical Young-Age Determination Methods 2: Solar, Stellar, Galactic, and Extragalactic.” Answers Research Journal 12 (October 30): 329–349. https://answersresearchjournal.org/astronomical-age-galactic/.

Faulkner, Danny R., and DeYoung, Don B. 1991. “Toward a Creationist Astronomy.” Creation Research Society Quarterly 28, no. 3 (December): 87–92.

Hayashi, Chushiro. 1966. “The Evolution of Protostars.” In Annual Review of Astronomy and Astrophysics. Vol. 4. Edited by Leo Goldberg, David Layzer, and John G. Phillips, 171–192. Palo Alto, California: Annual Review Inc.

Henry, Jonathan. 2002. “Star Formation: Natural or Supernatural?” Creation Research Society Quarterly 38, no. 4 (June): 217–220.

Henyey, L. G., Robert LeLevier, and R. D. Levée. 1955. “The Early Phases of Stellar Evolution.” Publications of the Astronomical Society of the Pacific 67 (396): 154–160.

Jeans, J. H. 1902. “The Stability of a Spherical Nebula.” Philosophical Transactions of the Royal Society A 199, no. 312 (January): 1–53.

Launhardt, R., Ya Pavlyuchenkov, F. Gueth, X. Chen, A. Dutrey, S. Giulloteau, Th. Henning, et al. 2009. “Rotating Molecular Outflows: The Young T Tauri Star in CB 26.” Astronomy and Astrophysics 494, no. 1 (January): 147–156.

Mathis, John S. 2000. “Circumstellar and Interstellar Material” in Allen’s Astrophysical Quantities. 4th ed, edited by Arthur N. Cox, 523–544. New York: Springer-Verlag.

Mulfinger, George. 1970. “Critique of Stellar Evolution.” Creation Research Society Quarterly 7, no. 1 (June): 7–24.

Samec, Ronald G., Amber Olsen, Christopher Gray, Ropafadzo Nyaude, James Kring, Jeremy Clark, T. Shebs, et al. 2020. “Magnetic Orbital Decay of Solar-Type Binaries and Creation Implications.” Creation Research Society Quarterly 57, no. 1 (Summer): 4–19.

Thomas, Brian. 2015. “Do Stars Still Form Today?” Acts & Facts 44, no. 5 (June): 15.

West, Jon K. 1981. “A Pre-Main Sequence Stellar Model Applied to Close Binary Star Systems” Creation Research Society Quarterly 18, no. 1 (June): 15–20.

Williams, Emmett L. 2000. “Star Formation According to Faulkner and Mulfinger: Some Observations.” Creation Research Society Quarterly 37, no. 1 (June): 47–49.

Williams, Emmett L. 2001. “Star Formation: Faulkner and Mulfinger—II?” Creation Research Society Quarterly 38, no. 1 (June): 46–49.