Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Tidal braking (sometimes called tidal friction) has long been used as an argument for recent creation, and it remains so. However, this argument often is accompanied by the claim that the addition of leap seconds to bring Universal Time into synchronization with time measured in Greenwich is direct evidence of tidal braking. But this overlooks two important points. First, there are far more factors than tidal braking involved in the earth’s changing rotation period. In this paper, I discuss the other factors showing that the picture is far more complicated than many recent creationists realize. The other factors are periodic sometimes slowing the earth’s rotation and sometimes increasing the earth’s rotation. However, the secular (non-periodic) change due to tidal braking always slows the earth’s rotation. Second, the true reason that leap seconds occasionally have been inserted over the past half century has little to do with tidal braking. More important is that the definition of the second adopted and modified since the early twentieth century is based upon the earth’s motion in 1900, which subtly incorporates a time when the earth’s rotation was near its fastest rate over the past two centuries. Therefore, it is best that recent creationists cease citing the addition of leap seconds as evidence of the earth’s slowing rotation.
Keywords: tidal braking, Universal Time, Ephemeris Time, leap seconds
Introduction
What time is it? We take that question for granted, with very few people considering what the measurement of time involves. For practical purposes, answering that question is related to the sun’s position in the sky. When the sun is highest in the sky it is noon. A day later it will be noon again with midnight halfway in between. For time between one noon to the next, we express time as a fraction of a day in terms of hours, minutes, and seconds of time with one hour being 1/24 of a day. Prior to modern rapid communication and transportation, each community observed its own local time. By the 1880s railroad networks made continued use of local time impractical, so standard time was born. Standard time established well-defined boundaries of time zones around the world where everyone within each time zone observes the same time with the difference between adjacent time zones usually being one hour (though there are exceptions, such as Adelaide, Australia).
Expression of time this way relies upon the rotation of the earth, and at least since the time of Isaac Newton, scientists assumed that the earth’s rotation was constant. But by the nineteenth century, it became obvious that the earth’s rotation was not constant after all. The first clue came from the ability to precisely predict solar eclipses. The method accurately predicted eclipses then happening, but when compared with historically recorded eclipses, there was a systematic shift in longitude between observed and calculated eclipses that increased farther back in time. It was obvious that the earth’s rotation was slowing. Astronomers soon figured out the reason—a complex tidal interaction between the moon and earth gradually slows the earth’s rotation. We call this effect tidal braking (or friction). We now know that tidal braking is just one process that affects the earth’s rotation. The March 2025 issue of Physics Today had an excellent brief review of changes in the earth’s rotation (Agnew 2025), and I learned much from it. There are many factors that affect the earth’s rotation over timescales of weeks, years, and centuries. The article featured three stacked plots that illustrated all these factors. These plots are included here as fig. 1.
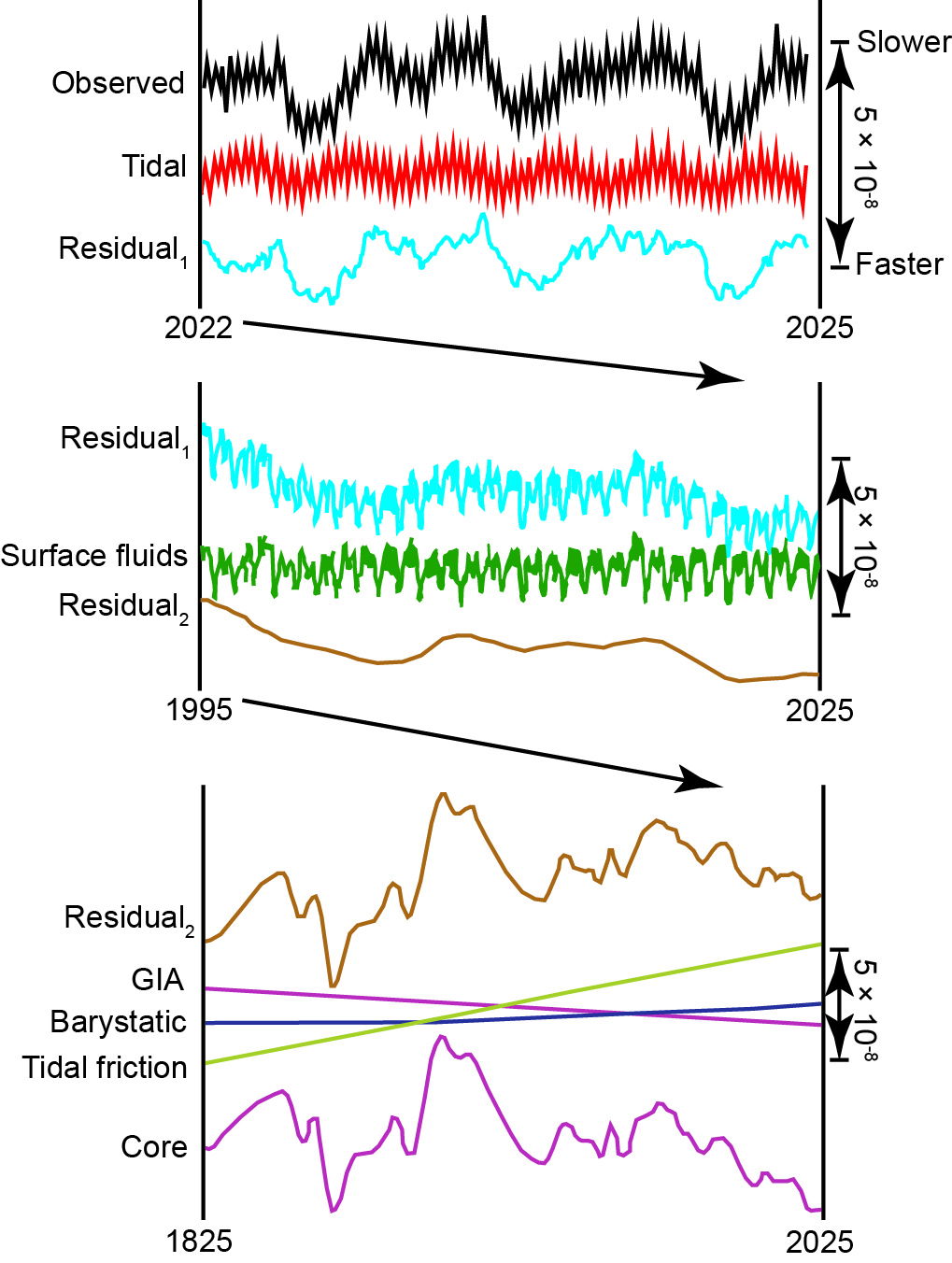
Fig. 1. Figure 3 from Agnew (2025). See the text for explanation of these curves.
Short-Term, Mid-Term, and Long-Term Changes in the Earth’s Rotation
The largest effect on the earth’s rotation is due to daily tides raised on the earth by the sun and moon (not tidal braking). The first plot in the Agnew paper showed changes in the earth’s rotation over the three-year period between the beginning of 2022 to the beginning of 2025. Monthly variations due to tides of the moon and sun raised on the earth show up well in this plot. These are the observed changes in the earth’s rotation during the three years considered. What about the calculated changes? According to Agnew (2025), the effect of daily solar and lunar tides is well understood. Along with the observed plot of the variation in the earth’s rotation is a plot of the calculated changes. The match was very good as illustrated by the plotted residual as a function of time showing the difference between observed and calculated differences (an O-C plot). The text of the article explained that the residual was due to seasonal effects.
This residual plot was compressed slightly in the vertical direction and was displayed in the second plot expanded in time to encompass the 30 years since the beginning of 1995. The seasonal effects affect the surface fluids on the earth, the oceans and the atmosphere. As Agnew (2025) once again explained, from weather data those effects are well understood too, so the calculated seasonal effects were plotted, and a residual plot was displayed.
This second residual was also compressed vertically and displayed in the third plot with the time now expanded to two centuries, back to 1825. There are four long-term factors at play here, three of which are relatively well understood and hence are shown in the third plot with all four effects briefly described by Agnew (2025). One factor is glacial isostatic adjustment (GIA), which is land slowly rebounding from when it was depressed during the ice age. A second factor is barystatic caused by water being redistributed on the earth’s surface primarily from melting ice sheets since the late nineteenth century. These two effects are in the opposite sense, one slowing the earth’s rotation, and the other speeding the earth’s rotation. Coincidentally, they nearly cancel one another, so they have little net effect. The third effect is tidal friction which slows the earth’s rotation. The tidal effect is of interest to recent creationists.
Since the moon is much closer to the earth than the sun is, the tides raised on the earth dominate over the sun’s tides on the earth. Many textbooks incorrectly teach what causes the tides. Most textbooks say that the moon’s gravity lifts water from the earth’s surface, but that explanation leaves students without any understanding of why there is a tidal bulge on either side of the earth. The moon and earth orbit one another each month due to their mutual gravity. But the tides are caused by a differential gravity force. What this means is a difference in the moon’s gravity acting upon the earth. Gravity goes as the inverse square of the distance. That is, the moon’s gravity on the side of the earth facing the moon is greater than the moon’s gravity on the side of the earth opposite the moon with varying amounts of gravity in between. This difference in force causes the moon to stretch the earth along a line connecting the earth and moon.
This stretching deforms the entire earth. But much of the earth is solid, which prohibits the earth from deforming as much as it should. Therefore, any leftover stretching is done upon the fluid parts of the earth’s surface, the oceans and the atmosphere (yes, there are atmospheric tides, but they are very small). At the same time, the earth raises tides on the moon producing a permanent slightly elongated shape in the earth-moon direction. The moon rotates at the same rate that it revolves, so this tidal stretching is always in the same direction on the moon. The moon’s tides on the earth, while weaker, attempt to stretch the earth along a line—that is what ocean tides are. However, since the earth rapidly rotates, the tidal bulge on the earth rotates ahead of the earth-moon axis (fig. 2). The earth is the larger green circle while the moon is the smaller yellow circle. Notice that the earth is slightly stretched along the axis A-B, and that that axis is not aligned with the earth-moon line. Note that the distances are not to scale, and the earth’s oblong shape is exaggerated.
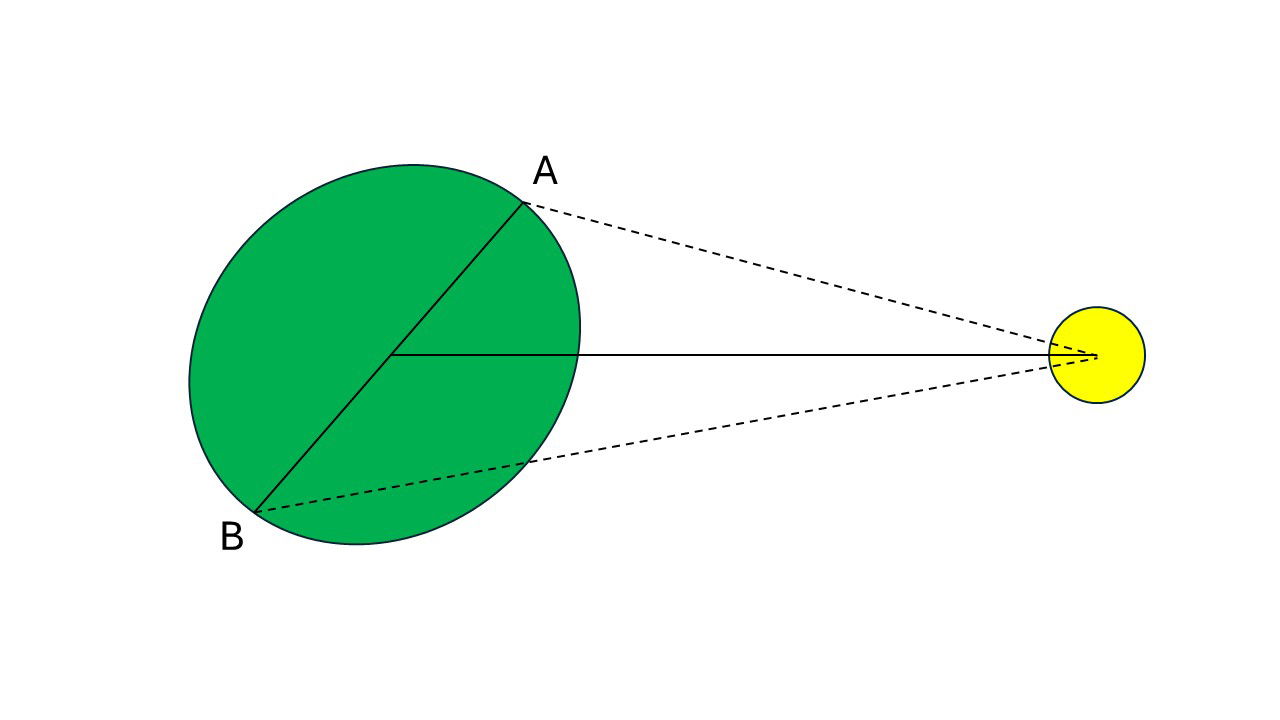
Fig. 2. Illustration of the tidal bulge of the earth not aligning with the earth-moon axis due to the earth’s rapid rotation. Note that the distances are not to scale and the earth’s tidal bulge is exaggerated.
As seen from the moon, this displaced tidal bulge produces a sort of pair of handles on the earth. Note that one handle is closer to the moon indicated by the letter A. The moon’s gravity pulls on that closer handle to pull it toward the moon. The moon also pulls on the other handle (indicated by B) to pull it toward the moon too. Since gravity decreases with increasing distance, the force on the nearer handle is greater than the force on the farther handle. The earth is rotating counterclockwise as shown in fig. 2. Note that the force on the nearer handle will be in the opposite direction of the earth’s rotation, so that force will tend to slow the earth’s rotation. But the farther handle will pull on the earth in the same direction speeding the earth’s rotation. Since we are dealing with circular motion, it is best to describe this with torques. A torque is a force applied over a lever distance. When torques are applied to a spinning body, the torque will cause the rate of rotation to change. A torque in the same direction of rotation will speed up the rotation, but a torque in the direction opposite to the rotation will slow the rotation. The lever arms of the two torques are nearly equal, but the forces involved are not. Since the force applied at point A is greater than the force applied at point B, then the torque acting at point A is greater than the torque acting at point B, and the result is that the earth’s rotation is slowed. This is tidal braking.
There are too many unknowns to model tidal braking, so it cannot be calculated directly, but it can be computed indirectly. Newton’s third law of motion applied to rotating bodies such as this means that for every torque there is an equal and opposite torque. As the moon pulls on the tidal bulge of the earth, the earth pulls back on the moon. The “opposite” in Newton’s third law of motion means that the directions of the torques acting on the moon are opposite of the directions of the torques acting on the earth. The torques acting on the earth are opposite the earth’s rotation causing the earth’s rotation to slow. But the torques acting on the moon are in the same direction of the moon’s orbital motion around the earth. This causes the moon to accelerate in its orbit around the earth resulting in the moon’s distance from the earth increasing. Some of the Apollo moon missions left special reflectors on the lunar surface. Periodically, telescopes on earth send very powerful and short laser pulses to these reflectors with the time delay between the sent and received signals revealing the distance between the earth and moon very precisely. The current rate of lunar recession has been accurately measured to be about 4 cm per year (DeYoung 2008). The change in angular momentum of the moon must be equal and opposite to the change in the angular momentum of the earth. The change in the moon’s angular momentum can be found knowing the moon’s mass, distance, and orbital speed. Knowing the earth’s moment of inertia, we can calculate the current rate at which the earth’s rotation is slowing. This rate matches the rate at which the earth is slowing that is inferred from records of past solar eclipses giving us confidence that we know the rate at which the earth’s rotation is slowing due to tidal braking.
Returning to Agnew’s plots, the three long-term effects (GIA, barystatic, and tidal braking) are subtracted from the second residual, resulting in a third residual, which is plotted in the third plot in fig. 1. As Agnew (2025) explained, this third residual must be due to the lone remaining factor, motion of material in the earth’s molten core. Currents in the molten part of the core produce the earth’s magnetic field. Furthermore, the earth’s magnetic poles are moving indicating that the earth’s molten core is a very dynamic place. The earth’s magnetic poles move, but less than a decade ago, they began to move at an unprecedented rate (Weisberger 2025). What is going on in the earth’s core is not understood very well, so data provided by the third residual in the plot is vital information in probing and modeling the processes in the earth’s molten core. I shall return to this shortly.
Why Creationists Are Interested in Tidal Braking
Why are recent creationists interested in tidal braking? Over thousands of years, tidal braking is of no consequence. However, over the supposed 4.5 billion years that the earth and moon have existed as most scientists believe, there is a problem. Quoting from the Agnew (2025) paper:
Extrapolating the recession rate backward in time implies that the Moon must be 1.5 Gyr old. Its age is known to be much greater, approximately 4.5 Gyr, which means that over most of geological time, tidal friction must have been smaller.
The first sentence of this quote could have come from a creationist source because creationists have been saying much the same thing for decades (DeYoung 1990, 2008; Faulkner 1998; Henry 2006; Psarris 2009, 2017). But notice in the second sentence how quickly Agnew dismissed the implication appealing instead to a change in the past for which there is no evidence. This is the nature of those who believe the world is billions of years old when confronted with evidence that contradicts billions of years—minimize the evidence and dismiss it with the wave of a hand.
If one were to extrapolate the current rate of lunar recession linearly into the past, then there is no difficulty for the earth-moon system being 4.5 billion years old. However, I must point out that the rate of lunar recession, and hence tidal braking, is not linear. Rather, they are proportional to the inverse sixth power of the distance between the earth and the moon (DeYoung 1990). This is a very steep function of distance which means that tidal braking was much more efficient in the past when the earth and the moon were closer to one another. Over thousands of years the rate does not change appreciably. From the plot of lunar recession in DeYoung (1990), it is easy to see that even over millions of years into the past from the present that the rate of lunar recession is nearly linear. However, extrapolating the correct functional dependence into the past, the separation between the earth and the moon would have been nearly linear back almost a billion years ago, but it would have been very steep prior to that. This means that a 1.5-billion-year age for the moon is a maximum age and not the true age of the moon. The best discussion of the tidal evolution1 of the earth-moon system in the creation literature is that of DeYoung (2008).
Digging Deeper into Time Measurement
When the measurement of time was not as precise as it is today, the earth’s rotation was a good standard for measuring time. However, by the end of the nineteenth century, astronomers were aware that use of time defined by the earth’s rotation was out of step from dynamic time, the time which governs the rate of physical mechanisms such as orbits. The discrepancy between the two was small, but our ability to measure the positions of astronomical objects accurately required a new time standard. Hence, a century ago astronomers introduced ephemeris time as the basis of precise orbital motions. Very important in tracking this dynamic time was the observations of when the moon occulted or passed in front of stars and planets. As the ability to measure time and positions more accurately increased, the standard for dynamic time has changed several times. For instance, dynamic time originally was based upon Newtonian mechanics, but now it is based upon general relativity. In 1972, atomic clocks which are believed to measure absolute time became the standard for time keeping.
But much of the world still uses time as defined by the sun’s position in the sky referenced to the local solar time at Greenwich, England. Universal Time is intended to closely match Greenwich time, but since 1972 Universal Time is defined by atomic clocks and is known to accurately reflect the sought-after dynamic and ephemeris time. The earth’s rotation is continually changing due to the factors discussed above. Therefore, the 1972 definition of Universal Time causes Universal Time to eventually get out of synchronization with time as defined by the sun. The solution to this problem since 1972 has been to insert a leap second whenever necessary to keep the discrepancy between the two time standards to less than a second. Since changes in the earth’s rotation cannot be predicted, leap seconds are announced when necessary. The leap seconds are added to Universal Time either at the end of June or the end of December. For the first 25 years, this required addition of a leap second on average about every 18 months. However, over the past 25 years the need for leap seconds has declined so that over the past half century the average time between leap seconds has grown to 21 months. If this trend continues, then soon we may need to subtract a second for the first time. There is discussion of scrapping the use of leap seconds by the year 2035. If this is done, then Universal Time will gradually depart from solar time.
Many creationists seem to believe that the addition of leap seconds is due entirely to tidal braking. I thought this for a while myself, but now I know that this is incorrect. Years ago, I compared the rate at which leap seconds were occurring and found that leap seconds were happening too often for them to be solely due to tidal braking. Therefore, I assumed that the dominant factor (motions in the earth’s liquid core) was slowing the earth’s rotation more quickly than tidal braking is. However, the one thing that leapt out at me in the Agnew article was the trend in the core shown it the article’s third plot—it was in the opposite direction of tidal braking, making the earth spin faster, not slower, as tidal braking is.
Before discussing what is going on in the earth’s core, let me better describe how we know what correction to apply. Comparing time between two different time standards can be confusing often resulting in the incorrect sign on the conversion between the two. Assume that we have two clocks, clock A and clock B. Further assume that we know clock B keeps the correct time, so any discrepancy between the two clocks is due to clock A not keeping accurate time. Let us further assume that clock A is running slightly faster than clock B. Eventually we will see that the time recorded on clock A is later than the time recorded on clock B. Remember that clock B records the correct time, so if we make any corrections to bring the two clocks back into synchronization, we must subtract time from clock A.
Now let’s apply this logic to the earth’s rotation going back to 1972 when solar time measured at Greenwich was set equal to Universal Time as defined by atomic clocks. More than one atomic clock is used, and the times on the atomic clocks are frequently measured to make sure that they agree on a time standard. Presumably atomic clocks keep perfect time, so the atomic clocks collectively will be clock B. This correct standard of time can be equated to ephemeris time which does not vary. Therefore, clock A will record time as told by observing the sun’s position. Technically not only is the passage of time told by the sun’s motion, but by the motions of many stars. The results are averaged and with so many time measurements Universal Time can be determined with much better precision than with solar measurements alone.
Suppose that the earth’s rotation speeds up. That is, each day the earth completes a rotation a little sooner than it did before. Therefore, like clock A in the discussion above, time as told by the earth’s rotation (clock A in this example) will run faster than clock B (the atomic clocks in this example). The time defined by the earth’s rotation will be later than the time defined by atomic clocks. Therefore, bringing the two time standards back into synchronization requires subtracting time from Universal Time. But if the earth’s rotation is slowing, then the correction is to add time to Universal Time. As I previously stated, this convention has been in force since 1972, and all corrections thus far have been to subtract time from Universal Time. These corrections are applied at the end of June 30 or December 31 when the discrepancy amounts to more than one-half second. These corrections have come to be called leap seconds (DeYoung 2017).
A Needed Correction
As I’ve expressed several times, in the creation literature it is commonly stated that leap seconds are evidence of the slowing of the earth’s rotation due to tidal evolution of the earth-moon system (I have stated so myself). However, as I prepared this article, I became aware that leap seconds are primarily due to an entirely different issue. There have been reports recently that we may soon delete a second rather than add a second to Universal Time (Faulkner 2025). Most people would think that is because the earth’s rotation is speeding up due to some of the periodic changes changing sign. However, from the third plot of Agnew (2025), it is obvious that the earth’s rotation rate has been speeding up for the past half century when we were adding leap seconds. How can that be?
Until the nineteenth century, astronomers had assumed that the earth’s rotation was constant, so the earth’s rotation was deemed a good standard for time definition. But once astronomers realized that the earth’s rotation changes, a better standard for ephemeris time was desired. In 1895, Simon Newcomb provided a standard for ephemeris time by extrapolating a century and a half of observations of the sun’s motion through the stars to establish the length of the year in 1900. This was the unofficial standard until the International Astronomical Union officially adopted it in 1952. Over the years, scientists have modified this definition of the second most notably in terms of atomic processes in 1967 and the modifications continue today. However, these are tweaks to the already defined definition of the second, not an entirely new standard. Consequently, these tweaks are subtly based upon the definition of the second based on the earth’s motion early in the twentieth century. As it turns out, the earth was rotating rather quickly at that time though the earth’s rotation slowed after that.
In deciphering the true cause of leap seconds, it is important to realize that the earth’s actual rotation (not a constant clock) was still the standard for defining Universal Time from which everyday time that people use (not ephemeris time) is derived. This changed in 1972 when the earth’s rotation was replaced by atomic clocks to define Universal Time. But it is still desirable to keep Universal Time so that it closely matches time as defined by the sun’s position which is why we having been adding leap seconds since 1972. If these occasional corrections are not made then the time we use every day (standard time, such as Eastern Standard Time, which is defined in terms of Universal Time), would get out of sync with the astronomical world (imagine noon happening hours before or after noon). This fix of adding leap seconds from time to time was not because the earth’s rotation was slowing (it wasn’t!). The true reason for leap seconds was that in 1972 the earth’s rotation was slightly slower than it was earlier in the twentieth century when the modern and fixed definition of the second was imposed. This meant that leap seconds were added some years even though the earth’s rotation was speeding up. This regime will continue until the earth’s rotation matches the rotation rate when the second was given its modern definition. The rate at which leap seconds have been added in recent years has decreased because the earth’s rotation rate is now decreased nearly to what it was at that earlier epoch. If the earth’s rotation continues to speed up until it is shorter than it was at the earlier epoch then we will need to delete seconds occasionally to keep Universal Time in sync with where the sun appears in the sky. That is, leap seconds have virtually nothing to do with the earth’s slowing rotation due to tidal evolution. Therefore, I suggest that recent creationists cease claiming leap seconds as evidence of tidal evolution.
What Is Going on in the Earth’s Core?
There have been recent news reports (Prisco 2025) about the possibility of subtracting a second rather than adding a leap second (a first). For those who think that leap seconds are entirely due to the earth’s rotation slowing, this must cause some confusion. Look again at the lower two plots of fig. 1. They both show the Residual2 plot albeit at different scales. They both show a decreasing trend over the past five decades. The reason that we haven’t subtracted seconds before is that the second was defined in terms of the earth’s rotation more than a century ago. When the Residual2 remained above the definition of the second of time, the residual was still high, so leap seconds were necessary. However, if the earth’s rotation continues to decrease, we will soon pass the threshold of the modern definition of the second. Therefore, we may be in for a period when seconds are subtracted rather than added. The culprit is that astronomers chose a modern standard for the second when the earth happened to be rotating faster than normal over the past two centuries but that appears to be about to change.
And what caused this change? As Agnew (2025) explained, the only factor remaining is changes in the motion of the core, and our knowledge of the earth’s core is meager at best. But suppose that the motion on the liquid part of the core slows. Conservation of momentum dictates that as the core slows it must impart a faster rotation for the rest of the earth. The core contribution of the lowest curve in fig. 1 was not calculated using a model. Rather, its contribution was inferred by subtracting the GIA, barystatic, and tidal friction components from the Residual2 plot.
Conclusion
Tidal braking has long been an argument that the earth-moon system is far younger than 4.5 billion years. It is still a good argument though recent creationists need to be more careful in their pronouncements about this. For instance, leap seconds are a bit of a red herring in this argument. They are necessitated by the fact that Universal Time (which is not a dynamic time) has been defined in terms of dynamic time since 1972. We must emphasize that there are far more factors involved: some that increase the earth’s rotation rate, but others that decrease the earth’s rotation rate. Fortunately, most of these factors are well understood, and so they can be calculated. Even though the tidal evolution of the earth-moon system cannot be directly modeled, we can easily model lunar recession using the measured current rate of lunar recession giving us confidence that we know its effect on the earth’s rotation. The rate of lunar recession implies that the earth-moon system is far younger than 4.5 billion years old.
References
Agnew, Duncan C. 2025. “As the World Turns—Irregularly.” Physics Today 78, no. 3 (1 March): 54–55.
DeYoung, Don. 2017. “Do you have a second” Creation Matters 22, no. 1 (January/February): 2.
DeYoung, Don B. 1990. “The Earth-Moon System.” In Proceedings of the Second International Conference on Creationism. Edited by R. E. Walsh, 79–84. Pittsburgh, Pennsylvania: Creation Science Fellowship.
DeYoung, Don B. 2008. “Tides and the Creation Worldview.” Creation Research Society Quarterly 45, no. 2 (Fall): 100–108.
Faulkner, Danny R. 1998. “The Current State of Creation Astronomy.” In Proceedings of the Fourth International Conference on Creationism. Edited by R. E. Walsh, 201–216. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Faulkner, Danny R. 2025. “Is the Earth’s Rotation Speeding Up?” Answers in Genesis, August 5. https://answersingenesis.org/blogs/danny-faulkner/2025/08/05/is-earths-rotation-speeding-up/.
Henry, Jonathan. 2006. “The Moon’s Recession and Age.” Journal of Creation 20, no. 2 (August): 65–70.
Prisco, Jacopo. 2025. “Earth is Spinning Faster, Leading Timekeepers to Consider an Unprecedented Move.” CNN Science, July 21. https://www.cnn.com/2025/07/21/science/earth-spinning-faster-shorter-days.
Psarris, Spike. 2009. “The Moon’s Recession from the earth: Still a Valid Young-Age Indicator.” Creation Research Society Quarterly 46, no. 3: 230.
Psarris, Spike. 2017. “Moon Inching Away from an Old Earth.” Answers 12, no. 2 (March 1): 34–35.
Weisberger, Mindy. 2025. “Earth’s Magnetic North Pole is on the Move, and Scientists Just Updated its Position.” CNN Science, January 21. https://www.cnn.com/2025/01/21/science/magnetic-north-pole-new-position/index.html.










