Thermodynamics and its Relation to Creation/Evolution: An Introduction

Introduction

“Entropy isn’t what it used to be.”—Anonymous.

Creationists have long used thermodynamics as an argument against the naturalistic origin and evolution of life. Indeed, if properly handled, thermodynamics can be effectively used to show complex and ordered systems do not arise naturally. However, I have been frustrated with some of the treatments of thermodynamics in the creationary literature—many of these arguments could have been better formulated, and there have been some misapplications of thermodynamics. Furthermore, there has been a lack of a good discussion of thermodynamics in its own right that could be used as a foundation for establishing better thermodynamic arguments against naturalistic origins.

To remedy this situation, I offer this introduction to thermodynamics. I begin with a brief survey of the history of thermodynamics, which naturally leads to some mathematical relationships, or laws, encountered in thermodynamics. I follow that discussion with a macroscopic description of basic thermodynamics, followed by a microscopic description of thermodynamics, in which I will show the two converge into a single theory. While this theory can be found in many general physics textbooks and certainly in textbooks on thermodynamics, this discussion is mostly absent in the creation literature, which is why I have included it here. This is followed by the development of the equivalence of work and energy, leading to the second law of thermodynamics, again with a macroscopic description and a microscopic description that are complementary. I conclude with a brief discussion of the relevance this has to the question of origins, along with a criticism of a common belief among creationists about the origin of the second law of thermodynamics.

What Is Thermodynamics?

The word thermodynamics comes from two Greek words, therme, meaning heat, and dynamis, meaning power, or strength. We have generalized dynamis to refer to motion, so thermodynamics literally means “heat motion.” The word thermodynamics was coined in the early nineteenth century for the study of how heat moves and interacts with the environment. The development of thermodynamics as a subdiscipline of physics was motivated by the desire to improve the efficiencies of steam engines. Thomas Newcomen invented the first practical steam engine in 1712. However, his design, which relied upon the condensation of steam to drive a piston in a cylinder, was of limited use as a pump to remove water from mines. A half century later, James Watt gradually improved upon Newcomen’s invention. One innovation, using steam pressure to drive the piston rather than relying upon the condensation of steam, doubled the engine’s efficiency. In 1781, Watt patented a steam engine that provided rotary motion, unlike his earlier designs, based upon Newcomen’s up-and-down reciprocation. This design closely resembles piston steam engines of today, and it provided the possibility of use in industry. Soon, steam engines began to appear in factories, ships, and finally in steam locomotives. Early steam engines were very inefficient, so further improvements in efficiency would have profound economic implications. The best route to improving efficiency was to have a good understanding of how steam engines worked. Hence, the birth of thermodynamics. For more detailed discussions of the history of thermodynamics, please see the recent surveys by Müller (2007), Girolami (2020), and Saslow (2020).

The generation and use of heat obviously lies at the foundation of a steam engine. But what is heat? Today, we understand that heat is a form of energy. But how did that understanding come about? It was a very long process. The ancient Greeks thought that there were four basic elements, earth, air, water, and fire. Clearly, the ancient Greeks thought that fire was a basic component of most material objects, and they thought this fire was related to heat. This understanding had not changed much by the seventeenth century, when scientists proposed that most substances contained a substance called phlogiston, from the Greek word meaning “burning up.” Phlogiston theory postulated that this fire-like substance was released during combustion. Eventually, the theory was expanded to include the release of phlogiston during rusting and other oxidation processes. Since many substances lose mass when they burn, it follows that phlogiston had mass, mass that was released during combustion. However, it was soon found that some substances gained mass in combustion. This led some to conclude that phlogiston had negative mass. A synthesis of these ideas led to the conclusion that phlogiston had positive mass, but that it was lighter than air, and hence could produce buoyancy. A century later, in the 1770s, Antoine Lavoisier showed combustion required oxygen, a newly discovered gas at the time. In carefully controlled experiments in closed containers, Lavoisier measured the masses of both the fuel and byproducts of combustion, as well as the oxygen involved. This disproved the phlogiston theory, which led to the modern oxygen theory of combustion.

Still, Lavoisier did not have an explanation for heat, so he also proposed that heat was a fluid that he called caloric, from the Latin word calor, meaning heat. Hotter objects presumably had more caloric than cooler objects. The caloric theory dictated that, as with any fluid, caloric flowed from regions of excess to regions of deficiency, eventually resulting in equal distribution of caloric. Since the weight of an object did not change as its temperature cooled, caloric must not have had mass. All substances supposedly had caloric locked inside them, and certain processes, such as combustion, could release caloric. Observation demonstrated that sawing or boring substances also released heat. The explanation was that the sawing or boring released the caloric stored inside the substances. This phenomenon provided a prediction of the caloric theory that could be tested. If the theory were correct, then the amount of material removed by sawing or boring would determine how much heat was generated. A sharp blade or auger would remove more material than a dull blade or auger. Hence, if the caloric theory were true, a sharp blade or auger should release more caloric, and thus more heat, than a dull blade or auger. In 1798, Sir Benjamin Thompson, Count Rumford, published a paper on his studies of the matter. He experimented with machines used to bore the barrels of cannons at the Holy Roman Empire arsenal in Bavaria. He found that a dull instrument removed very little material, but it produced a tremendous amount of heat. On the other hand, a sharp instrument removed much metal while releasing much less heat. Count Rumford reasoned that the caloric theory was false. Rumford further reasoned, as we would today, that friction had generated the heat.

Today, this single experimental result is viewed as the end of the caloric theory. However, at the time that was not the case. The caloric theory had many adherents, and they thought that the caloric theory could be adapted to meet this new challenge. For instance, the dominant theory of electricity of the time was that electricity was a fluid. Experiments showed that friction could produce an unlimited amount of electrical charge, so why could not heat be similarly generated? The major problem with this proposition is that it violates the conservation of energy, that energy can neither be created nor destroyed. Since heat is a form of energy, it cannot spontaneously appear, as the modified caloric theory implied. However, the principle of conservation of energy had not yet been discovered. In fact, caloric theory was a major impediment to recognition of the conservation of energy. The development of thermodynamics in the nineteenth century played a key role in unlocking this important conservation law.

Rejection of a dominant theory usually necessitates adoption of another theory to replace it. Kinetic theory eventually replaced caloric theory. Like the caloric theory, kinetic theory has its roots among the ancient Greeks. In the fifth century B.C., Democritus suggested that matter was composed of indivisible microscopic particles that he called atoms (from the Greek word atomos, meaning “indivisible”). In the first century B.C., Lucretius proposed that the atoms that make up even stationary matter rapidly move, and bounce off each other. These ideas were popular in the Epicurean school, but Aristotelian thinking came to dominate in the late ancient period and throughout the Middle Ages, so atomic ideas had few adherents for two millennia. The atomic theory idea was revived and embellished by Daniel Bernoulli in 1738. Bernoulli’s theory primarily was concerned with gases. His idea was that gases consisted of atoms moving in random directions. The impacts of the atoms between themselves and on surfaces produce pressure, and heat of the gas is the kinetic energy of the moving atoms. Physicists universally accept these concepts today, but Bernoulli’s kinetic theory was not widely received at the time. However, by the end of the eighteenth century, other scientists began to consider kinetic theory. There were attempts to wed the kinetic and fluid theories into a single theory. In some respects, that is the case today. While we accept the kinetic theory as being correct, it is a microscopic description, while caloric theory can be viewed as a macroscopic theory. Many experimental results can be interpreted in terms of heat being a fluid that flows from hotter to cooler. As we shall see, modern thermodynamics can be expressed in terms of heat flow, preserving the terminology of the caloric theory. However, at the same time we realize that this is not what is happening on the microscopic level.

The work of James Prescott Joule in the early 1840s was key in the development of thermodynamics. In a series of experiments, Joule showed that energy could be transformed into different types. More specifically, he demonstrated the mechanical equivalent of heat. One of Joule’s experiments used an apparatus consisting of an insulated container of water with spinning paddles inside, similar to a home ice cream maker. The paddles were connected to weights on a wire suspended by a pulley outside the container. The falling weights stirred the paddles. Joule carefully measured the temperature of the water prior to releasing the weights and after the weights had fallen and come to rest and any visible motion in the water had ceased. He found that the water was slightly warmer after the experiment than before. Joule reasoned that the motion of the water had become randomized, thus heating the water. Joule’s work generalized Bernoulli’s kinetic theory from gases to liquids. It was not too difficult to conceive that it could be applied to solids as well. Joule’s work was not immediately accepted. The caloric theory still was believed by many scientists, and the atomic theory, upon which the kinetic theory was based, would not be embraced by most scientists for many decades yet. However, by the end of the nineteenth century, kinetic theory was widely accepted.

A Macroscopic Description of Thermodynamics

This historical discussion thus far has been concerned with a microscopic description of matter. However, at the same time much progress had been made in the macroscopic description of matter. The seventeenth century saw the development of Boyle’s law, usually attributed to Robert Boyle alone, but it was first formulated by Richard Towneley and Henry Power. Boyle’s law states that if the temperature of a gas is held constant, the pressure and volume of the gas are inversely proportional:

or,

where P and V are the pressure and volume, and k is a constant. It often is more useful to consider the pressure and volume at two different times. If P₁ and V₁ are the pressure and volume at one time, and P₂ and V₂ be the pressure and volume at another time, then

This formulation of Boyle’s law removes the arbitrary constant k.

A little more than a century later, Jacques Charles studied what happens when the pressure of a gas remained constant while the volume and temperature, T, changed. He found that the volume and temperature are directly proportional:

or,

Note that the constant k here is not the same as in Boyle’s law. As with Boyle’s law, it often is helpful to express Charles’ Law as the relationship between volume and temperature at two different times:

Again, this removes the arbitrary constant.

Shortly after Charles’ law was discovered, Joseph Louis Gay-Lussac considered what happens when the volume of a gas remains constant. He found that the pressure and temperature are directly proportional:

or,

Where, as before, this is a different constant k. And, as before, this can be expressed in terms of pressure and temperature at two different times:

again, removing the constant.

Finally, in 1811 Amedeo Avogadro idealized gases by hypothesizing that all gases at a given pressure, temperature, and volume would have an equal number of atoms. Note that today we would say “molecules” rather than “atoms” in most cases. Even better, we ought to generalize and just call them “particles.” If the temperature and pressure are held constant, then the volume would be directly proportional to the number of particles, n:

or, as before:

Where, as before, the constant k is a different constant. Again, we can remove the constant by expressing this as the volume and number of particles at two different times:

The number of particles, n, is expressed in moles, with a mole containing Avogadro’s number of particles, 6.02214076 × 10²³. A mole is abbreviated as mol, and Avogadro’s number is abbreviated N_A.

Note that in these four laws we have used the constant k, but keep in mind the value of k in each equation will be different. The exact value of k depends upon the units used. Inspection of the four relationships shows that we can combine the four into a single equation:

This expression is the ideal gas law. Note that the constant k has been replaced with R, the ideal gas constant. The value of the ideal gas constant depends upon the units one chooses for pressure, volume, and temperature. For instance, the standard SI units are Pascals (Pa = N/m²) for pressure, cubic meters for volume, and Kelvin for temperature, resulting in R being equal to 8.31 J/K^-1mol^-1. The other four relationships discussed above derive directly from the ideal gas law by holding one of the respective variables constant.

A Microscopic Description of Thermodynamics

The macroscopic theory, such as the ideal gas law, is directly observable. But how can we be sure of the microscopic kinetic theory? When developed, microscopic theory makes predictions that agree with the directly observable macroscopic theory. To see this, let us consider a few assumptions of the kinetic theory. Assume that a gas is contained within some volume V. The shape of the container does not matter, but for ease of computation, let us assume that the container is a cube having length l, so that V = l³. Assume that the gas consists of N >> 0 identical particles with each particle having mass m. We may index the particles with the letter i, with the index going from one to N. We further assume the particles are very small, so that their total volume is negligible compared to the volume of the container. Furthermore, the particles are so far apart compared to their sizes that collisions between the particles are relatively rare. That is, far more significant than inter-particle collisions are the collisions the particles have with the walls of the container. Furthermore, assume that the collisions between particles and the container walls are elastic (kinetic energy is conserved during the collisions). Choose a coordinate system with x, y, and z axes parallel to the edges of the cube containing the gas. Let v_i be the vector velocity of the i^th particle. We can express this velocity as the sum of three component vectors in x, y, and z directions:

Consider just the x-component of the velocity of the i^th particle. The particle will bounce back and forth between the two parallel walls perpendicular to the x-axis. The time between successive impacts with one wall will be

If the collisions with the wall are elastic, with each collision the i^th particle and the wall will undergo an equal and opposite change in momentum of

If the duration of the collision is Δt, then by Newton’s second law of motion, both the wall and particle will experience a force equal to

If we identify the duration of the collision as the time between collisions, then we find the average force of the i^th particle on the wall will be

The pressure on the wall due to the i^th particle will be

where A is the area of one side of the cube and V is the volume of the cube. The total pressure will be the sum of the pressure due to each particle:

If the motions of the particles are random, then

By the Pythagorean Theorem,

or,

Substituting into the equation for pressure above,

If is the average of the squared velocities of the particles, then

The average kinetic energy per particle is ½m. Therefore, the total kinetic energy of the gas, KE, is N½m, and the pressure can be written

Notice that this has the form of Boyle’s law. We can rewrite this as

Comparing with the general macroscopic version of the ideal gas law,

we see that temperature is proportional to the total kinetic energy of the gas. That is, the microscopic kinetic theory of gases has led to a macroscopic law determined empirically. This is strong confirmation of this approach. This also leads us to the conclusion that when a gas is heated, the motion of particles making up the gas move faster. We all learned this principle in elementary school science class, though perhaps seeing this derivation for the first time, you can understand why we didn’t learn the physics behind this principle back in elementary school.

Can we quantify this a bit? Yes. We can define a new constant, k_B (the Boltzmann constant), or simply k (not the same as any of the constants above) as the ratio of the ideal gas constant, R, to Avogadro’s number, N_A:

The number of moles, n, is related to the number of particles N by

leading to

Therefore,

or,

In this simple model, the kinetic energy of the gas is the internal energy of the gas. Note that the internal energy and the temperature of the gas are directly proportional. This will be an important bit of information when we consider the most efficient possible heat engines in the next chapter.

Since this formulation has only two variables, temperature, and the average squared velocity, we can compute an average velocity of particles in a gas as a function of temperature. We define the square root of the average squared velocity as the root mean squared velocity, v_rms:

The particles making up the gas will have a wide range of velocities. Note that there are at least three other average velocities, the arithmetic mean, the median, and the mode. However, the root mean squared velocity is the only one of the averages that is so readily computed. In the nineteenth century, James Clerk Maxwell and Ludwig Boltzmann worked out a detailed expression for the probability distribution function of velocity as a function of temperature. The Maxwell-Boltzmann distribution is beyond the intended level of this work. However, we can give some of the results. As temperature increases, the spread in the distribution increases. But the relationship between the averages remain the same—the most probable speed, or mode, v_p, is 81.6% of the v_rms, and the arithmetic mean, v is 92.1% of the v_rms. As particles within a sample of gas undergo elastic collisions with one another, they exchange energy. Individual particles increase and decrease speed, but the distribution remains the same, as long as the temperature remains the same.

It is important to point out that temperature and heat are not the same thing. Temperature is a measure of the average kinetic energy of the particles of a system. Heat is the sum of the kinetic energy of the particles. However, rather than calling this heat, it is more proper to call the sum of the kinetic energy the internal energy of a system. In our everyday experience, the things that we encounter have a staggering number of particles, so it is easy to sloppily confuse temperature and internal energy. But what if a system has relatively few particles? An example would be the highest levels of the earth’s atmosphere, where the pressure and the density of particles both are very low compared to the things that we normally experience. The particles in the gas there can move very fast, and hence have high temperature. Yet, at the same time there are so few particles that there is not much kinetic energy contained in the gas. Examples in space can be even more extreme. Spacecraft typically orbit the earth in a very thin gas having a temperature that may exceed the melting point of the metal that the spacecraft is made of. However, the gas is so thin that very little heat is transferred to the spacecraft. What little heat is transferred to the spacecraft is radiated away very efficiently so that the temperature of the spacecraft may be very cool.

Besides the above microscopic description of a gas that resulted in a relation that is identical to the macroscopically determined Boyle’s law, is there any other evidence that the kinetic theory of gases is correct? Yes. For instance, this theory can be extended to predict the molar specific heats of gases, the amount of heat required to raise a mole of the gas a degree Kelvin. The predicted value of specific heat matches the macroscopically measured values of monatomic gases, those gases composed of molecules consisting of one atom each. The situation is more complicated with diatomic gases (gases with two atoms per molecule) and polyatomic gases (gases with three or more atoms per molecule). A monatomic gas has only three ways to add energy—kinetic energy due to motion in each of the three directions, x, y, and z. We say that a monotonic gas has three degrees of freedom. However, when molecules with more than one atom are considered, energy can be added into rotation of the molecules. This gives additional degrees of freedom, two more for a diatomic gas, and three more for a polyatomic gas in the simple model. Consideration of these effects predicts the molar specific heats of diatomic and polyatomic gases that agree quite well with measured values. Finally, one can even apply this to solids, assuming that in a crystal state there are six degrees of freedom. In a solid, particles are bound in a crystal lattice in three dimensions. The addition of heat results in either vibrational motion in each of those three dimensions, as well as displacement in each of those three dimensions (the displacement is a form of potential energy, as one encounters in a compressed or stretched spring). In many cases, the predicted molar specific heats are very close to the measured values. It is remarkable that a theory developed to describe gases can be generalized to solids so easily. All these considerations give us tremendous confidence in the kinetic theory of gases.

The First Law of Thermodynamics

The brief discussion of the history of thermodynamics of the previous section finished with a short treatment of kinetic theory. However, this got ahead of the development of thermodynamics in the nineteenth century. Let us return to classical thermodynamics. Improving the efficiencies of steam engines (which was the point of thermodynamics in the first place) required generalizing and simplifying the situation inside the engines. However, before doing that, it may be helpful to describe in a non-thermodynamic sense how steam engines and internal combustion engines work.

With a reciprocating steam engine, combustion of fuel heats water in a boiler to produce steam. An intake valve at the top of a cylinder allows the steam to enter the cylinder. There is a piston near the top of the cylinder, and the high pressure of the steam pushes the piston toward the other end of the cylinder. As the piston moves, the intake valve closes. The steam continues to push the piston, but the work done by the gas is at the expense of decreasing pressure and temperature of the steam, diminishing the force on the piston. When the piston reaches the end of the cylinder, an exhaust valve opens. Attached to the piston is a rod connecting the piston to a crankshaft. The piston turns the crankshaft via the connecting rod. The momentum of the crankshaft reverses the direction of the piston, moving it back up the cylinder, and the piston forces the lower temperature steam out the exhaust valve. When the piston arrives back at its original position, the exhaust valve closes, the intake valve opens, and the process begins anew. A more efficient arrangement is the use of a turbine. The steam continually pushes against the turbine blades, turning the turbine shaft. As the steam pushes the turbine, it transfers energy to the turbine, so the steam loses energy (heat). One advantage of a steam turbine is that none of the parts reverse direction, as the piston does in a conventional steam engine. This is more efficient.

An internal combustion engine, such as a four-stroke gasoline engine, works a bit differently. On the intake stroke, an intake valve at the top of the cylinder opens, and the vacuum created by the piston moving down the cylinder draws a mixture of fuel and air into the cylinder. At the end of the intake stroke, the intake valve closes, and the momentum of the crankshaft forces the piston back up the cylinder, compressing and heating the air/fuel mixture. When the piston reaches the top of the cylinder, a spark plug ignites the fuel, producing a hot, high-pressure gas. This gas pushes the piston back down the cylinder during the power stroke, transferring energy to the cylinder the entire way. At the end of the power stroke, an exhaust valve opens at the top of the cylinder, beginning the exhaust stroke. The momentum of the crankshaft carries the piston back up the cylinder, pushing the exhaust gas out of the cylinder. The exhaust valve closes, the intake valve opens, and the cycle repeats. A two-stroke gasoline engine modifies this process, and a diesel engine is another variation on this theme, but there is no need to discuss the details of these engines.

To describe how engines work in terms of thermodynamics, we first must define a few terms. A thermodynamic system is a macroscopic volume of space which can be described by state variables, such as temperature, pressure, and volume. There are three types of thermodynamic systems: open, closed, and isolated. Both matter and energy may enter or leave an open system. Energy may enter or leave a closed system, but matter may not. Neither energy nor heat may enter or leave an isolated system. It is important to point out that truly isolated systems do not exist. However, real systems can closely approximate them, so that for practical purposes, we can say that isolated systems exist. Physicists frequently make this sort of approximation. For instance, we often assume that friction does not exist or at least its effect is small enough that we can ignore it. In many dynamic cases, this is effectively the case with highly lubricated surfaces or the use of wheels with good bearings. Another example is in hydrodynamics, where restricting consideration to low speeds greatly reduces the effect of friction.

What is energy? Energy often is defined as the ability to do work. What is work then? Unfortunately, work often is defined as the expending of energy. If this sounds circular, it is. However, in any philosophical, mathematical, or scientific system, one must start somewhere with certain undefinable or nearly undefinable concepts. Energy clearly is one of those concepts in physics. On the other hand, physicists often define work more precisely as the use of force over some distance, defined differentially as:

where dW is the differential work, F is the force, and dx is the displacement. Notice that work is a scalar, while force and displacement are vectors. In the SI system, the unit of force is the newton, while the unit of distance is the meter. Hence, unit of work is the Newton-meter, defined to be the joule, named in honor of James Prescott Joule. As discussed in an earlier section, Joule was the first to demonstrate that work and energy are equivalent things. In the English, or engineering, system, the unit of force is the pound, and the unit of distance is the foot, so the unit of work is the foot-pound.

There is a result in mechanics, the branch of physics that deals with forces and accelerations, called the work-energy principle. In its basic form, the work-energy principle means that work, ΔW, performed on an object results in a change in the object’s kinetic energy, ΔK. This result can be generalized to include changes in other forms of energy, such as a change in potential energy, ΔU. We can express the work-energy principle as

Conversely, an object’s kinetic energy can be tapped to perform work on other bodies. Note in these interactions that kinetic energy does not spontaneously appear or disappear. Rather, different forms of energy transform into other forms of energy. Work, being a form of energy, changes the kinetic or potential energies of objects. During these transformations, the total energy does not change. Hence energy is conserved. This is the first law of thermodynamics, the law of conservation of energy.

Physicists also noticed that matter is conserved. That is, like energy, matter is neither created nor destroyed. These two principles, the conservation of energy and the conservation of mass, are foundational to physics. However, a little more than a century ago, Albert Einstein saw that energy and matter were equivalent entities. The conversion of one to the other (usually via nuclear reactions) is given by Einstein’s famous equation,

where E is the energy, m is the mass, and c is the speed of light. Since c is a very large number, which in turn is squared in this equation, a little bit of matter converts into a tremendous amount of energy. This is why nuclear weapons have such devastating yields and nuclear plants produce so much energy while consuming very little fuel. With this insight of the equivalence of matter and energy, the law of conservation of energy and the law of conservation of matter have been unified into one law. However, for most situations (those not involving nuclear reactions), mass and energy do not convert to one another, so for our purposes we can treat these as two separate conservation principles.

How does this relate to thermodynamics? Recall from the last chapter that the temperature of a gas is directly proportional to the kinetic energy of the particles in the gas. We know from the work-energy principle that an increase in the kinetic energy of particles can come only from work performed on the particles. Macroscopically, we know that adding heat to a gas usually results in higher temperature. Hence, heat must be a form of energy. Physicists normally use the letter Q to designate heat. We refer to the kinetic energy of a gas as its internal energy. We use the letter U to refer to the internal energy. However, the addition of heat to a gas may not go entirely into heating the gas. For instance, a heated gas can perform work, indicated by the letter W.

We can consider the gas inside an engine as a thermodynamic system. Let the heat flow be ΔQ. ΔQ is positive if heat is added to the system, and negative if heat is extracted from the system. Changes in internal energy, ΔU, will be positive if the internal energy increases, and negative if the internal energy decreases. Historically, since those who developed thermodynamics were concerned with the work that an engine could perform, they considered the work performed by the system, ΔW, to be positive. We shall follow that practice. However, note that very formal thermodynamics textbooks sometimes treat work performed by an engine as negative. This is because any work performed by the engine is done as the expense of energy that the system possesses and/or heat flow into the system. We can state the first law of thermodynamics the following way: heat flow into the system can either go into changing the internal energy of the system, or the performance of work, or both. In equation form,

The first law of thermodynamics is a statement of the conservation of energy principle.

There are several important idealized processes that we can consider. Suppose that no heat enters or leaves the system. Any resulting process is called an adiabatic process. Since in an adiabatic process ΔQ = 0, the first law of thermodynamic reduces to

That is, in an adiabatic process, work is done entirely at the expense of the internal energy of the system. As noted above, we have defined work as work done by the system. Work can be done on the system, in which case the work is negative, and the internal energy increases. Incidentally, the assumption of an adiabatic process of raising a parcel of air in the earth’s atmosphere is a key part of explaining why air temperature generally decreases with increasing elevation.1 That is why this phenomenon is usually expressed as the adiabatic lapse rate.

What if no work is done by or on a system? Then ΔW is zero and the first law of thermodynamics reduces to

That is, any heat flow into or out of the system goes entirely into changing the system’s internal energy.

What if there is no change in internal energy? Then ΔU is zero, and the second law of thermodynamics becomes:

Thus, any heat flow goes entirely into work.

Mechanical engines are cyclical. That is, the engine goes through several steps before returning to an initial state. This is key, because through any cyclical process the change in internal energy is zero. Thus, any work accomplished is equal to the net energy flow:

During the cyclical process, the engine will have heat flow into it and heat flow out of it. Let ΔQ₂ be the heat flowing into the engine and let ΔQ₁ be the heat flow out of the engine. The total heat flow, ΔQ, will be

The action of a cyclical engine can be illustrated by fig. 1. The engine is represented by a box, with a higher temperature (T₂) heat reservoir above, and a lower temperature (T₁) reservoir below. A heat reservoir is a place to store heat that is so large that any addition or removal of heat will not change its temperature. Heat flow is represented by large arrows. ΔQ₂ flows from the higher temperature reservoir, while ΔQ₁ flows from the engine to the lower temperature reservoir. Work, ΔW, flows out from the engine.2 If the net heat flow, ΔQ, is positive, then the work is positive. Under this circumstance, ΔQ₂ > ΔQ₁. The widths of the arrows in fig. 1 are suggestive of this relationship. Heat flows into the engine from above. The engine operates to split the input heat into work and exhaust heat. The sizes of the arrows representing the work and exhaust heat are smaller than the arrow representing the input heat to suggest that the former two sum to the latter.

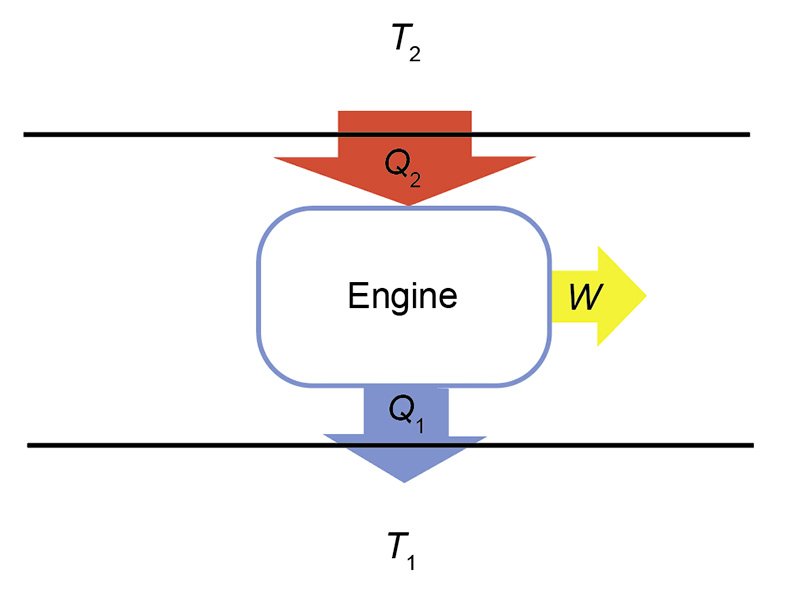
Fig. 1. Schematic of an engine. Heat, Q₂, is input from the high temperature reservoir having temperature T₂, and heat, Q₁, is output to the lower temperature reservoir having temperature T₁. The difference in the heat flows goes into producing work, W.

The Second Law of Thermodynamics

“Time flies like an arrow. Fruit flies like a banana.”—Groucho Marx

Efficiency can be defined as “what you get, divided by what you pay for.” With an engine, what we get is the work, and what we pay for is the input heat. Therefore, efficiency, e, is defined as

Examining this equation, it is easy to see that one maximizes efficiency by minimizing the exhaust heat. If the exhaust heat were zero, the efficiency would be 100%. Such efficiency is not possible, for an engine must always exhaust some heat. This is a consequence of the second law of thermodynamics, soon to be discussed.

However, within the limits of the second law, there is maximum theoretical efficiency. Physicists in the nineteenth century spent much effort to learn what that maximum theoretical efficiency was. In 1824, the French physicist Sadi Carnot first proposed the maximum possible mechanism for an engine, what we call the Carnot cycle. I will not discuss the derivation of the Carnot cycle. Thermodynamically, it consists of four steps, two adiabatic processes, and two isothermal processes. Fig. 2 illustrates this process. During the first adiabatic process, the gas in the engine is compressed, raising the temperature of the gas. This is followed by an isothermal expansion, in which higher temperature heat enters the engine. A subsequent adiabatic compression brings the gas inside the engine to a lower temperature. During a final isothermal compression, heat at lower temperature is exhausted, whereupon the engine returns to its original starting point, and the cycle continues.

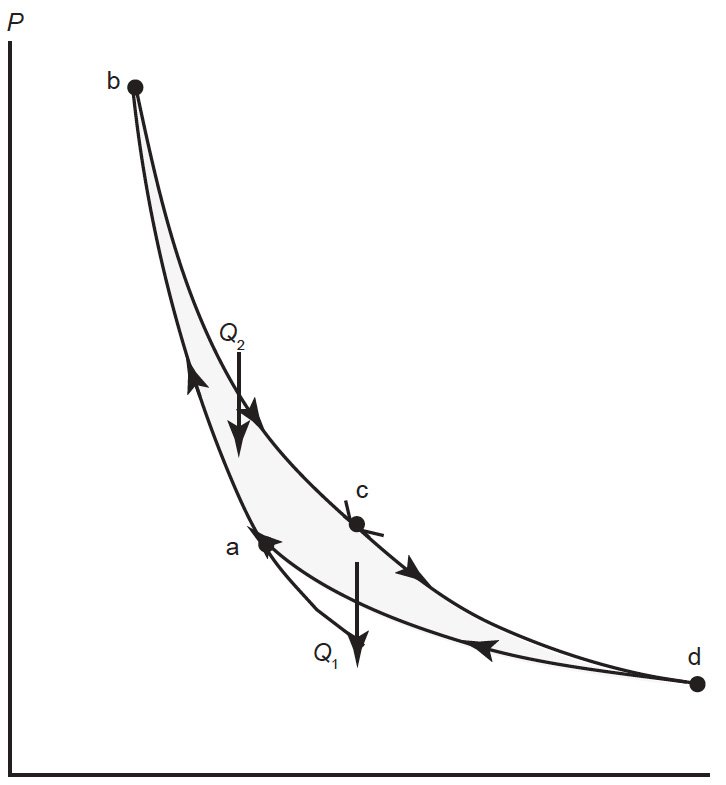
Fig. 2. Diagram of a Carnot cycle in P-V space. In the process from a to b, the gas in the engine is compressed adiabatically raising the temperature of the gas. During the process from b to c, the gas expands isothermally as heat Q₂ enters the system. In the process from c to d, the gas expands adiabatically. The final process from d to a returns the system to its original state via an isothermal compression in which Q₁ leaves the system.

In an earlier section, we saw that the internal energy of a gas is proportional to the temperature of the gas. Since in the Carnot cycle heat flows during isothermal processes, heat flows during the isothermal processes are proportional to the temperatures:

Therefore, the efficiency of a Carnot cycle can be rewritten as:

Physicists often use this equation to compute the maximum highest efficiencies of engines operating between heat reservoirs at different temperatures. From the above equation, you can see that the highest efficiencies occur when the higher temperature is greatest, and the lower temperature is least. We cannot do much about the lower temperature, but we can control the higher temperature. Therefore, power plants typically use input steam that is much hotter than it needs to be to run the steam engine because the higher the input temperature, the greater the efficiency. Furthermore, internal combustion engines have higher efficiencies if the temperature of the gas resulting from combustion of the fuel is as high as possible. On the other hand, higher temperatures promote physical effects that can compromise the ability of the engines to function. Overcoming these difficulties is a matter of engineering. The efficiencies of real engines fall far below those of Carnot engines, so there always remain ways of making improvements.

Why are engines limited in their maximum efficiency? Why can’t engines work with 100% efficiency, transforming all their input energies into work? In answering that question, nineteenth century physicists came to understand the second law of thermodynamics. What is the second law of thermodynamics? Unlike the straightforward nature of the first law of thermodynamics, the second law of thermodynamics has many different statements. One statement is that no engine can have 100% efficiency. But the second law of thermodynamics can be expressed in many other ways. While the first law of thermodynamics ensures that energy is conserved, it does allow that energy can be converted into different forms, such as work. We observe that in these changes, energy becomes less useful to us. To quantify this observation, physicists define a term, entropy, to describe how unuseful energy is. More specifically, we define entropy change as energy (heat flow) divided by temperature, expressed on an absolute scale. The variable S is used for entropy. Treating the change in entropy as a differential, ΔS, and heat flow as ΔQ, we define an entropy change as

The SI unit of energy is the Joule (J), and the preferred absolute temperature scale is Kelvin (K), so entropy is properly expressed in J/K. The second law of thermodynamics can be stated that in isolated systems, entropy never decreases. Therefore, we may state the second law of thermodynamics as

for isolated systems.

This expression shows that, while entropy can be created, it cannot be destroyed. This peculiarity introduces an asymmetry that makes the second law of thermodynamics fundamentally different from the first law of thermodynamics, and from many other laws of physics. While other physical laws permit changes that can go either way in time, the second law works only one way. Any process that follows other physical laws is permitted, provided entropy does not decrease. Thus, the second law of thermodynamics imposes a direction to time, so some physicists and philosophers refer to the second law of thermodynamics as time’s arrow.

Since the universe appears to be an isolated system, it would seem the second law of thermodynamics applies to the universe. The entropy of the universe cannot decrease, though it may increase, and it often does. Thus, the universe has an ever-increasing entropy burden. If the universe were eternal, the universe would have had more than ample time to have reached a state of maximum entropy. We observe that the universe is far from a state of maximum entropy, so the universe cannot be eternal. This point is significant, because until the mid-1960s, many scientists thought that the universe was eternal, despite this clear indication by the second law of thermodynamics to the contrary. Even today there are a few people who hold out for an eternal universe. Their answer to the entropy problem typically is to hypothesize that the second law does not universally apply, that we happen to live in a portion of the universe where entropy increases, but there may be other portions of the universe where entropy decreases. Alternately, they hypothesize that even in our region of the universe, entropy has not always increased.

While the second law of thermodynamics applies to the universe, we can apply the second law to subsystems of the universe. We usually call a subsystem of the universe a thermodynamic system. However, we must be careful that we consider only isolated systems, because the second law of thermodynamics applies only to isolated systems. To see this, consider two thermodynamic systems that are in contact with one another so that heat flows from one system to the other. If no other process occurs, then the heat-donating system has a negative heat flow and the heat-gaining system has a positive heat flow. Since no negative temperatures are possible on an absolute temperature scale, the donating system experiences negative entropy change while the absorbing system experiences a positive entropy change. Does this violate the second law of thermodynamics? No, because there is no isolated system involved, and the second law applies only to isolated systems. A thermodynamic system can absorb energy from other parts of the universe so that its entropy decreases. How is this possible? The entropy changes of surrounding systems that absorb the energy to the system in question have corresponding increases in entropy that more than offset the entropy decrease.

Let me give a more concrete example. Consider two objects that have different temperatures. Bring these two objects into thermal contact and isolate and insulate the two so that no heat escapes or enters the system consisting of the two objects, forming an isolated system. When we do this, we will observe that heat flows from the hotter object to the cooler object until the two objects are at the same temperature. At this point, heat flow ceases. The object that was initially cooler absorbs energy, so it experiences a positive heat flow. Let its heat flow be ΔQ. Since the two objects form an isolated system, the heat gained by the object that was initially cooler is at the expense of the heat of the object that was initially warmer. Therefore, the object that was initially hotter experiences a –ΔQ heat flow. That is, the heat flows of the two objects are opposite and equal so that the total heat flow of the two objects combined is zero. This is a consequence of the first law of thermodynamics.

Since entropy change is proportional to heat flow, and the heat flows of the two objects are opposite in sign, then their entropy changes are opposite in sign. But unlike heat flow, the entropy changes of the two objects will not be equal in magnitude. Let T_H be the temperature of the initially hotter object and T_C be the temperature of the initially cooler object. Both T_H and T_C continually change in a complex way until both are equal. Entropy is the heat flow divided by temperature, so at each moment the entropy change of the hotter object will be ΔS_H = –ΔQ/T_H, while the entropy change of the cooler object will be ΔS_C = ΔQ/T_C. These two quantities are complex functions of time, but the numerators will be the same at each instant. Note that ΔS_H always will be negative, while ΔS_C always will be positive. Furthermore, until the temperatures equalize, T_H always will be greater than T_C, so |ΔS_H| always will be less than |ΔS_C|. Therefore, the sum of the entropy change of the two objects will be positive. Always. This is why we observe that heat flows from hotter to cooler and not the other way around. If heat were to flow from cooler to hotter, that would produce a decrease in entropy, a violation of the second law of thermodynamics.

Note that both objects are examples of a closed thermodynamic system, but that together they form an isolated system. As such, the entropy of one of the closed systems may decrease, but the entropy of the combined isolated system increases. This is an important distinction because people sometimes appeal to open or even closed systems to argue that entropy can decrease, but this overlooks the necessity of considering the entire isolated system that a supposedly second law of thermodynamics law violating system is part of.

A Microscopic Description of The Second Law of Thermodynamics

As mentioned earlier, the second law of thermodynamics can be expressed in many ways. We do not have time to discuss most of these, but it is important to discuss one. An important manifestation of entropy is that it measures the amount of disorder. Since entropy continually increases, or at least cannot decrease, it follows that disorder must increase, or at least not decrease. If disorder cannot decrease, then order cannot increase. How did this understanding of entropy come about? As previously discussed, we have two approaches to thermodynamics, macroscopic theory, and microscopic theory. Macroscopic theory uses state variables, properties of a thermodynamic system that we can measure macroscopically, such as pressure, volume, and temperature. On the other hand, microscopic theory considers properties of a system that we can’t directly observe, such as the speeds of individual particles. The expression and discussion of the second law of thermodynamics above is a macroscopic theory; let us now turn to a microscopic theory.

Consider once again a gas consisting of N particles that we can number with the index i running from 1 to N. At any given moment, each particle will have its unique position, r_i, and velocity, v_i. These variables are written in boldface, indicating they are vectors, quantities with both magnitude (amount) and direction. Both the position and velocity vectors may be broken into three components each—one component in each in the x, y, and z directions. Therefore, we can describe the gas microscopically in a six-dimensional space. Due to their velocities, the particles continually change position, so the first three dimensions of each particle continually change. However, the particles also undergo collisions with one another as well as with the walls of any container present, exchanging kinetic energy in the process. Hence, the velocity components, the other three dimensions of each particle, continually change as well. At any given moment, one hypothetically could stipulate the position and velocity vectors of each particle. Each such description of the six dimensions of every particle is called a microstate. At the same time, one could give a macroscopic description of the volume, pressure, and temperature of the gas. This is called a macrostate. Each macrostate has many corresponding microstates, so there are far more microstates than macrostates. For instance, a container of gas with N particles at some given T, P, and V represents a single macrostate. However, the particles making up the gas could have a huge number of possible position and velocity vectors.

A good way to illustrate the relationship between macrostates and microstates is with poker hands. A poker hand consists of five cards. Relative value is associated with various combinations of cards, depending upon the probability of getting each combination. For instance, a royal flush consists of the cards 10–J–Q–K–A in one suit. Since there are four suits, there are only four ways of having a royal flush. Since a ten is the highest numbered card, with the three face cards being valued higher, and the ace given the highest value, a royal flush is deemed the most powerful hand possible, better than all other possible hands.

Another possible poker hand is four of a kind. How probable is it to have four cards of a kind? Since there are 13 types of cards in a standard deck, there are 13 ways of having just four cards of the same kind, but since a poker hand consists of five cards, we must consider that fifth card. Once four cards out of 52 are stipulated, there remains 48 possible combinations for that fifth card. Therefore, there are

ways to have four of a kind. This is 624/4 = 156 times more probable than having a royal flush. While this combination is 156 times more likely than a royal flush, out of many millions of possible combinations, four of a kind still is a relatively low probability, and hence it is a powerful hand, though not as powerful as a royal flush. The lowest value poker hand is a high card, where none of the five cards match, the five cards are not in the same suit, and the five cards do not form a continual sequence (a straight). Obviously, there are many millions of ways to get this combination. Each of these poker hands, a royal flush, four of a kind, and a high card, is analogous to a macrostate. Note that there are four microstates that correspond to the macrostate of a royal flush, 624 microstates that correspond to the macrostate of four of a kind, and millions of microstates that correspond to the macrostate of a high card. Poker hands (macrostates) with the fewest number of microstates are less probable and hence are deemed the highest hands. The value of poker hands, in decreasing order are:

1. Royal flush
2. Straight flush
3. Four of a kind
4. Full house
5. Flush
6. Straight
7. Three of a kind
8. Two pairs
9. Pair
10. High card

Again, the relative strength of poker hands is determined by the number of microstates corresponding to each macrostate—the fewer the microstates a macrostate has, the more powerful a macrostate is. How many microstates are possible in poker? The stipulation of five specific cards is a unique microstate. Since a standard deck of playing cards has 52 cards, there are

ways of doing this. Hence there are more than 310 million microstates, but only ten macrostates. For instance, of the more than 310 million microstates, only four correspond to a royal flush, while 156 microstates correspond to four of a kind.

There is a fine point of probability that is not obvious to many people. Suppose that two players compare their cards at the end of a hand, and that one player has a royal flush in spades, while the other player has in his hand the king of diamonds, nine of spades, eight of hearts, four of clubs, and three of spades. Since the first player has the highest possible hand, and the second player has the lowest possible hand, many people erroneously think that the first hand is highly improbable, while the second hand is very probable. However, both hands are equally probable—less than one chance in over 310 million. This is because we are comparing microstates, and each microstate is equally probable (or improbable). However, if I had stated that the first player had a royal flush, and the second player had a high card, that would be a different proposition. I would be comparing macrostates. The royal flush macrostate is far less probable than the high card macrostate.

Or consider an unopened deck of cards. A newly manufactured deck of cards is in a highly ordered state—the cards are in order within each suit. Once the deck is shuffled, the cards are no longer so ordered. After the first shuffle, there remains some elements of that order, but with each succeeding shuffle, that order quickly disappears. It is generally agreed that seven good shuffles so randomizes the deck that any order instituted in the deck, say, from the previously played hand in any game, that no further shuffling is required. How many possible ways may the cards in a full deck be arranged? There are 52 possibilities for the first card, followed by 51 possibilities for the second card, 50 for the third, and so forth. Hence, the number of possible ordering of cards in a full deck is the multiplication of the first 52 integers, 52! = 8.07 × 10⁶⁷. That is a staggering number. For comparison, there are only about 10⁵⁰ atoms on the earth; that is, there are nearly a quintillion times more ways that the cards in a deck can be ordered than there are atoms on the earth. Once a deck of cards is well shuffled, it is unlikely that any realistic amount of further shuffling would ever produce the same order of cards again. Furthermore, it is unlikely that any well shuffled decks of cards have ever come to be in the same order through reshuffling. The only way that two decks of cards could arrive in the same order is if someone were to arrange them that way. Consequently, if you were to witness someone shuffling a deck of cards several times and then turning the cards over to reveal a special sequence, such as the sequence a new deck has, you would immediately know that the person had performed a card trick, probably by switching decks between shuffling and revealing the cards.

What does this have to do with thermodynamics? The second law of thermodynamics can be expressed in terms of microstates. According to this approach to the second law of thermodynamics, a system proceeds from one microstate to another, consecutively assuming the macrostate associated with each microstate that the system passes through. Each microstate is equally probable. However, most microstates correspond to no significant macrostates. Consequently, systems naturally proceed toward macrostates that have the greatest number of microstates and hence are most probable. As a system randomly changes (for instance, the particles making up a gas collide with one another and the walls of the container holding the gas), it undergoes changes in microstates. This is similar to what happens each time a full deck of cards is shuffled—once the deck is shuffled, it is virtually impossible that shuffling ever could result in the same microstate it began with. Or for that matter, the macrostate the deck began with; there are 24 = 4 × 3 × 2 × 1 ways that a deck of cards arranged in order within a suit can be arranged. As I suggested above, anyone handed a used deck of cards that was so arranged in number order within suits immediately would realize that someone had arranged the deck that way.

This can be expressed in terms of a gas the following way. Suppose that a gas is confined to a closed container. The gas particles continually collide with one another and the walls of the container, and consequently the six variables of each particle continually change. It would be extremely unlikely that this shuffling of the positions and velocities of the particles this way would result in most of the particles moving in the same direction or that most of the particles would end up on one side of the container. One could give the particles either of these properties initially, but the random collisions of the particles would cause the particles to rapidly depart from such highly ordered states, never to return.

To quantify this approach to the second law of thermodynamics, we can define entropy for a macrostate to be

where k is the Boltzmann constant, and w is the number of microstates that correspond to the macrostate (Sears and Salinger 1975). Note that the units of the Boltzmann constant are J/K, so the units of this microscopic definition of entropy match the units of the macroscopic definition of entropy. Natural logarithm is always positive or zero, so entropy defined this way can never be negative. A macrostate must have at least one microstate, so the minimum value of w is one, with the entropy of such a macrostate being zero. In most situations it is not practical to compute w, so this definition is not useful in an absolute sense. However, this definition is very useful in determining differences, or changes, in entropy. Since the second law of thermodynamics is about changes in entropy, this definition is very useful. Suppose that a system proceeds from a macrostate having w₁ microstates to a macrostate having w₂ microstates. Then the change in entropy will be

Therefore, the change in entropy is proportional to the natural logarithm of the ratio of the number of microstates corresponding to the final and initial macrostates.

To see that entropy defined this way can be equated with a measure of disorder, consider once again a deck of playing cards. As mentioned before, newly manufactured card decks come in sequence within suits. There are two jokers at the top and two advertisement cards at the bottom, which are usually removed before shuffling, so we will ignore them. A standard deck out of the package is arranged A–K Spade, A–K Diamonds, A–K Clubs, and A–K Hearts. Notice that this is a very ordered state, more ordered than simply stipulating that the cards are arranged in order within suits, for the latter could be arranged four different ways. That is, there is only one microstate that corresponds to the standard ordering of a new deck of cards, while there are four microstates that correspond to arranging the cards in order within suits with no specification of the ordering of the suits.

Since there is only one way that a standard deck of cards is arranged at manufacture, then the macrostate of initial manufacture has only one microstate. Since w = 1, then by the definition of entropy given above, the initial entropy of a new deck of cards is zero. When the deck is shuffled once, the number of possible microstates greatly increases. Since the cards are specially arranged when the deck is opened, there are limitations on how randomized the cards can become after the first shuffle, so the number of possible microstates after the first shuffle is far less than the more than 8.07 × 10⁶⁷ ways a deck may be arranged. However, with each shuffle, more microstates become available. Therefore, with each succeeding shuffle, the value of w increases, asymptotically approaching the maximum value. At some point, the value of w is close enough to the maximum number of microstates that further shuffling will not “further randomize” the deck. As mentioned before, seven good shuffles are generally considered to be sufficiently randomized.

Would continual shuffling ever return the deck back to its initial state of A–K Spade, A–K Diamonds, A–K Clubs, and A–K Hearts? Technically, it could. But how probable is that? Remember that there are more than 8.07 × 10⁶⁷ ways for the cards in a deck to be arranged. Suppose that a person shuffled a deck once per second, 24 hours per day, 365 days per year. Most evolutionists think the earth is 4.5 billion years old. In that time, you would have shuffled the deck only 1.4 × 10¹⁷ times. With 8.07 × 10⁶⁷ ways to arrange a deck, it is extremely unlikely that over 4.5 billion years of shuffling the original arrangement of cards would have ever been achieved. That is a profound reality. That is why if anyone showed you a deck of cards in that order and told you they had shuffled the deck, you would not believe them.

It is not that shuffling will not produce any order within a deck of cards. As a deck is shuffled, occasionally a few cards will be found in some sort of order, such as a pair, three of a kind, four of a kind, or even a straight, five cards in sequential order. However, the rarer a sequence is (the fewer the number of microstates correspond to the sequence), the less often it will occur. Can further shuffling build upon that order? Hardly—the next shuffle may add a card or two to a sequence, but the shuffling will break up the original sequence in the process. A truly meaningful, large sequence of cards, such as all the cards of one suit in order, would never realistically arise by random shuffling no longer how many times the deck is shuffled. On the other hand, a person can arrange a deck of cards back to the original order or any order he chooses rather quickly. But this arrangement process requires effort under the direction of intelligence. If either element, effort, or intelligence, is missing, the arrangement cannot be achieved. That is, order must be manufactured. For instance, poker hands usually must be built by discarding some cards and drawing new ones, but occasionally a poker player is dealt a very good hand, such as a full house. Such arrangements are expected to arise occasionally within a deck of cards, but what about the other 47 cards in the deck? They likely will not display anything that we might perceive as anything special.

Keep in mind that a deck of cards is a relatively simple system—it only has 52 parts. Consider a container of gas having some volume, pressure, and temperature (a macrostate). The number of particles involved is staggering, perhaps 10²⁰ even in a small container. And each particle will be described by a six-dimensional system discussed earlier. The number of microstates dwarfs that of the microstates of a deck of cards. As the gas particles interact, they will continually assume new microstates, but all will correspond to a very probable macrostate. It would be remarkable if all the particles were to migrate to one side of the container (a very rare macrostate). The probability of this happening is many orders of magnitude lower than the probability shuffling a deck of cards would return the deck to its initial state. We have already seen that is extremely unlikely that even over billions of years a deck of cards could be shuffled to produce a highly ordered arrangement. It is far less likely that the gas in a container could segregate itself so that all the gas is on one side of the container with a vacuum on the other side. Statistical mechanics does not forbid such a thing from happening, but it makes the probability so low that it almost certainly would never occur.

Following the reasoning applied to a deck of cards, if we could arrange a system of particles so that only one microstate is available, then its entropy would be zero. This would be a very ordered state because each particle would be uniquely specified. If more energy states were made available to the system, then the system would have more microstates available to it, and the entropy would increase. However, the system would not be so ordered as before because the particles have more possible states to occupy. We would say the system is more disordered than before. Ergo, entropy is a measure of disorder.

Two Other Laws of Thermodynamics

Before moving on, for completeness I ought to briefly mention that there are two other laws of thermodynamics. In the early twentieth century, there was much research into achieving temperatures close to absolute zero (–273.15 K). In his research on this topic, Walther Nernst formulated the third law of thermodynamics: as the temperature of a system approaches zero, the change in entropy approaches zero. A consequence of the third law is that it is impossible to attain absolute zero with a finite number of steps.

After the three laws of thermodynamics had been formulated, it was realized that there was a yet another, more fundamental, law of thermodynamics: if two thermodynamic systems are in equilibrium with a third system, then the two systems are in equilibrium with one another. Since this law is more basic than the other three laws, it made no sense to call it the fourth law of thermodynamics. Hence, it has become known as the zeroth law of thermodynamics. Recognition of the zeroth law of thermodynamics is credited to Ralph H. Fowler in the 1930s. You may recognize that the zeroth law of thermodynamics is similar to the transitive law in mathematics.

Application of Entropy to Evolution

It is the microscopic version of the second law of thermodynamics that leads to discussion of the naturalistic origin of life and biological evolution. Living organisms obviously are highly ordered systems, far more ordered than non-living things, such as a deck of cards or a container of gas. Consequently, the number of microstates involved in living systems is far larger than with these two non-living examples. Meanwhile, the number of macrostates sufficient to permit life is incredibly small. For instance, consider a very simple protein, consisting of 50 amino acids, all assembled in proper order to provide a useful function. Since there are about 20 amino acids to choose from, then there are 20⁵⁰ = 1.13 × 10⁶⁵ ways that a 50-amino acid protein may be assembled by random chance. Assembling the correct order of amino acids in a protein to produce the desired function is the reciprocal of this number. Hence, a specified protein is about 700 times more probable than a specified ordering of a deck of cards is to result from a random shuffle. Of course, longer proteins that are much more common are more improbable to assemble randomly.

However, there is far more to it. Proteins are not just long chains of amino acids. The long chains are folded and bonded to themselves many times. This folding can either expose or cover locations where their function can occur—the wrong fold results in the desired function of the protein not occurring. Since this folding is in three dimensions and has many possibilities, the probability of a usable protein coming about by random chance is many orders of magnitude smaller than the simple computation of the linear chain of amino acids.

And if random chance were to produce the correct chain of amino acids folded in the proper way to produce a desired protein molecule, what good would a single protein molecule be? The chemical reactions and structure necessary in living cells would require far more than just a single molecule of the desired protein. Furthermore, living cells generally require hundreds, if not thousands, of different proteins, all assembled properly to cause the functions or create the structures necessary for the cell to thrive. Multiplying the very small probabilities of all the proteins required for even the simplest living cells along with the probabilities of the structures required for the simplest of life forms results in a vanishingly small probability that the first cells could have arisen by chance.

Suppose the first living cell spontaneously arose despite the long odds against it, what then? Living things are not static—they are continually synthesizing material to run the machinery necessary for life. How do cells do this? Biochemical processes in living things are directed by DNA. Hence the first cells not only required the structures of cells and the biochemistry be present, but also the DNA to direct the processes necessary for life.

How complex is DNA? DNA consists of a double strand of base pairs assembled helically. There are four base pairs, adenine, cytosine, guanine, and thymine. Adenine pairs with thymine, and cytosine pairs with guanine, so specifying one of the four nucleobases on one strand of DNA will automatically code for its pair on the other strand. Therefore, for each base pair there are only two choices, not four choices. Candidatus Carsonella ruddii is a bacterium with one of the shortest strands of DNA, just 160,000 base pairs. Therefore, there are 2^160,000 = 6.3 × 10^48,164 ways that its DNA could be assembled randomly, making random assembly of this very short genome impossible. Candidatus Carsonella ruddii exists in a symbiotic relationship with other organisms, so its genome likely is too short to support an organism not in a symbiotic relationship. Most living things have genomes orders of magnitude greater than that of Candidatus Carsonella ruddii. For instance, the human genome has 3.2 billion base pairs. The probability of such an ordered system arising by chance is vanishingly small.

It is commonly believed that many portions of DNA do not code for anything, so some may argue that the probability of randomly assembling the appropriate DNA is not nearly as remote as simply calculated here. It is likely that we have not yet determined the function of so-called junk DNA. However, even if one grants the reality of junk DNA, the improbability of useful DNA assembling randomly still is vanishingly small.

All three parts, cell structure, the biochemistry of life, and DNA must exist simultaneously for life to be possible. How did these three things come into existence? The naturalistic origin of life would require that non-living things gave rise to living things, which would amount to a tremendous increase in order and thus would appear to violate the second law of thermodynamics. Furthermore, biological evolution would be the development of life over time, which involves increasing order, which also appears to violate the second law of thermodynamics.

Evolutionists have offered various theories of how the naturalistic origin and the development of life might not violate the second law of thermodynamics. One approach is to note that the second law of thermodynamics applies only to isolated systems. An isolated system exchanges neither matter nor energy with its surroundings. Living things are continually exchanging both energy and matter with their surroundings, so they clearly are open systems, not isolated systems. Does this mean that living systems are not subject to the second law of thermodynamics? Keep in mind that no isolated systems exist (except for the universe). We may effectively seal systems so that matter cannot pass into or out them, but it is impossible to insulate systems to prevent all heat flow into or out of them. Therefore, in the real world only open and closed systems exist. If all that is necessary to circumvent the second law of thermodynamics is to consider systems that are not isolated, then the second law of thermodynamics is of no effect in the real world since isolated systems do not exist. Clearly, that is not true—the second law of thermodynamics describes very well many thermodynamic processes, even though no truly isolated systems exist. Therefore, there must be much more to this than merely appealing to an open system.

Earlier I illustrated the second law of thermodynamics by considering heat flowing from a warmer object to a cooler object. Indeed, heat flow from warmer to cooler temperature is one of the best examples of increasing entropy. We conclude that the second law of thermodynamics prohibits heat flowing “uphill” from cooler to warmer temperatures. However, heat can be driven from cooler to warmer temperatures by using an appropriately designed engine, such as a refrigerator, freezer, or air conditioner. Such engines work by using a substance, such as freon, that has an evaporation point near room temperature. An electric motor drives a compressor, and the compressor pressurizes freon gas, causing it to condense. This process yields latent heat of vaporization, heating the compressor. That heat must be carried away, usually by a fan. The liquid freon is transported to where it is needed to cool, whereupon a nozzle permits the pressurized liquid to pass to lower pressure, and the freon evaporates. Evaporation requires heat, the same amount as the latent heat of vaporization liberated when the freon gas was condensed. The heat required to evaporate the liquid freon comes from the environment being cooled, causing the temperature of that environment to decrease.

This is a cyclical process that removes heat from a lower temperature reservoir and delivers it to a higher temperature reservoir. Does this process violate the second law of thermodynamics? Hardly. We can see how this works schematically by reversing the three arrows in fig. 2. Instead of work being a product of the engine, work is an input to the engine. That is, the engine consumes energy rather than produces it. Rather than exhausting less heat than the input heat, the exhaust heat is the sum of the heat being removed (the input heat of the engine) and the work input to the engine. Since heat flows out of the lower temperature reservoir, its heat flow is negative, and its entropy change is negative. Meanwhile, the heat flow into the higher temperature reservoir is positive, so its entropy change is positive. The magnitude of the positive heat flow of the higher temperature reservoir is greater than the negative heat flow of the lower temperature reservoir. Even though the entropy calculations require dividing the heat flows by the temperatures of the two reservoirs, the higher temperature of the positive entropy is not enough to offset the larger positive heat flow. Therefore, the magnitude of the positive heat flow is greater than the magnitude of the negative heat flow, and the total entropy change is still positive.

It is very important to notice that this flow of heat from higher temperature to lower temperature is not spontaneous. It requires input of energy, which at best makes this a closed system, not an isolated system. But even as a closed system, the entropy of the system increased because of the second law of thermodynamics. It is true that a portion of the system had a decrease in entropy, but that decrease was more than offset by the increase in entropy of the rest of the system. Furthermore, this process was driven by machinery designed to produce the desired result. Absent the machinery, the process of driving heat from a warmer to cooler place would not happen. If one wishes to overcome the problem of decreasing entropy of a process, one must first address the origin of the machinery required to accomplish that process. Such machinery does not arise spontaneously. Machinery must be designed and then manufactured. Even manufacture of the machinery is subject to the second law of thermodynamics. But a more important factor is the question of where and how the intangible design came about. Design implies a designer. Design is readily seen in physical devices, such as clocks, but many people seem to have difficulty recognizing design in living things.

Life depends upon a huge number of complex biochemical reactions continually operating. These biochemical reactions operate opposite to the direction that they would naturally proceed. That is, living things synthesize simpler molecules into more complex ones. The inputs are matter (the less complex molecules) and energy (required to bond the more complex molecules), which is why living things are open systems. However, these inputs are insufficient in themselves to circumvent the second law of thermodynamics. The direction of the chemical reactions normally is decay from the more complex to simpler molecules, the opposite of what living things require to exist. How do they do this? Living things have complex machinery in the form of organelles (within cells) and structures such as tissue, organs, and systems (in the case of multi-celled organisms). Ultimately, the construction and operation of these machines is regulated by DNA, also included within cells. Both the physical machinery and the coded instructions represented a tremendous amount of order within living things. Some people call this order information. How could this order or information come about naturally?

Some people have proposed that the natural rise of order in complex organic systems is similar to the growth of crystals. Crystals certainly appear ordered. In fact, a crystal lattice is often defined as an orderly array of units, with units being either molecules, atoms, or ions. That is, crystals have a repeating pattern of the units in three dimensions that give crystals their distinctive appearance. But is this truly order? Crystal growth occurs because of the few simple rules of how the constituent units can be arranged. Following this simple pattern, row upon row and column upon column construction yields an ordered arrangement of units, but it is not very complex. In fact, the ordered array is downright simple. Perhaps there is a problem with equivocation here. We often say something is ordered when perhaps we ought to say that is complex. A crystal is ordered in that it has a repeated pattern that could not occur via random processes. Indeed, a crystal forms following a specific pattern, but the pattern is not very complex. On the other hand, a hurricane is very complex—ask any meteorologist who attempts to model hurricanes. But hurricanes do not appear ordered; hurricanes seem to be the embodiment of chaos. But life appears both complex and ordered. The complexity and order of living things fulfill function, which implies design. Such complexity and order while fulfilling design do not appear to be things that arise randomly. If such systems cannot arise randomly, then they must have come about through a process of creation. However, creation is anathema to the thinking of many scientists today, so in their commitment to naturalism (no Creator allowed), scientists cast about for alternate explanations for how the complexity, order, and apparent design of life could have come about naturally.

The most celebrated person to do this was the physical chemist Ilya Prigogine (1917–2003). Prigogine wrote extensively on dissipative structures as a mechanism that he thought would bring about self-organization. Dissipative structures (a term coined by Prigogine) refers to structures that can come about when an environment is far from thermodynamic equilibrium. Any simple structures that might occasionally form small, ordered regions fall many orders of magnitude short of the complexity required for any form of life. Even open systems generally follow the second law of thermodynamics, meaning that even if a piece of chemistry essential for life came about naturally, the second law of thermodynamics would dictate a very high probability that the chemistry would revert back to its simpler constituents. Given this inclination of chemistry to go in the opposite direction to increasing complexity, how could enough of the chemicals of life have developed naturally this way accumulate and morph into even the simplest of living organisms? Evolutionists argue that selective effects, such as those that supposedly drive evolution, could preserve, and accumulate this order until finally life came about. To expect that life somehow developed from this is a gross extrapolation. Despite this, Prigogine received the 1977 Nobel Prize in chemistry for his work.

In similar manner, evolutionists propose that once enough order arose to allow for DNA and the machinery of cells, further random changes led to increased order. Again, the appeal is made to the magic of open systems. But merely being an open system is not sufficient to contradict the second law of thermodynamics. The moment after a living thing dies, the machinery and coded instructions remain. Furthermore, a just-deceased organism is capable of exchanging matter and energy with its surroundings, making it still an open system. However, the indescribable spark of life is absent, and the machinery no longer works. The chemical reactions go in the direction that will reestablish thermodynamic equilibrium, and the molecules become less complex, not more complex. Given this, the appeal to an open system to rescue the day for evolution is not demonstrated and amounts to hand-waving and gross extrapolation.

Growth and development of creatures from embryos to maturity are sometimes used as examples of living things defying the second law of thermodynamics. However, this tack overlooks at least two realities. First, this growth and development are time limited. Once an organism reaches maturity, growth and development cease, followed by gradual decline and eventually death. It is as if this cycle was programmed into living things. Living things have maintenance and repair mechanisms that prolong life and fix the damage due to injury, disease, and even everyday wear and tear, so why don’t these maintenance and repair mechanisms continue indefinitely? Apparently, even the maintenance and repair mechanisms have a shelf life, after which they decay as well. That is, there is no maintenance and repair for the maintenance and repair mechanisms. Creation scientists often attribute this deficiency to an effect of the fall of Genesis 3. Second, as evolutionists frequently point out, living things are open systems, free to import material and energy to grow and develop. It is this aspect that permits living things to grow and develop. For a while. While being an open system is a necessary condition for operating against the second law of thermodynamics, it is not a sufficient condition to do so. Growth and development are dictated by instructions encoded in DNA. The real battle is over how DNA arose in the first place. Such highly ordered information does not rise spontaneously. It requires intelligence.

Furthermore, it is important to point out that even with an open system, there is a net increase in entropy (the system plus the environment). To appeal to an open system is to simply assert that entropy increase is somehow avoided without specifying the mechanism by which it is avoided. One proposed way to get around this problem is to appeal to an open system, coupled with free energy. There are several thermodynamical definitions of free energy, but free energy is simply a measure of the amount of work that a system can perform at constant temperature. Sometimes this work is called the useful energy of a system. If the change in free energy of a process is positive, then that process is possible, but if the change in free energy is negative, the process is forbidden. McIntosh (2009, 2013, 2023) has shown that free energy devices either storing free energy or passing energy down very specific pathways do not occur naturally. This argument that no free energy device where the change in free energy is positive can emerge on its own is a fundamental finding that applies universally.

What about the origin of information, as in DNA? Claude Shannon (1916–2001) is the father of information theory, the study of the coding and transmission of information. More properly, information theory also ought to include the creation of information. Information does not arise naturally. Rather, information must be created, and the creation of information requires intelligence. If intelligence does not exist first, then information cannot exist. To the naturalist, this presents a problem because naturalism posits that there is no God. If there is no God, then what was the intelligence that created the information in DNA? Without DNA, there can be no life, but without life, there can be no DNA. To avoid this chicken or egg dilemma, naturalists assume that DNA and living things developed spontaneously apart from a creator, even though that would violate the second law of thermodynamics. Only divine creation is consistent with the second law of thermodynamics.

Teleology is a concept most identified with William Paley’s 1802 book, Natural Theology or Evidences of the Existence and Attributes of the Deity. However, John Ray’s 1691 work, The Wisdom of God Manifested in the Works of Creation, preceded Paley’s book by more than a century. In between, William Derham published Physico-Theology, Or A Demonstration of the Being and Attributes of God in 1713, followed by Astro-Theology: Or A Demonstration of the Being and Attributes of God, from a Survey of the Heavens the following year. All three of these works influenced Paley. Paley created the watchmaker analogy, that if one found a watch lying on the ground, one would readily see the design in the watch, even if one did not understand the purpose of the watch. One would further conclude that the watch required a designer and a maker. With the rise of Darwinism a few decades after Paley’s book was published, many scientists and philosophers dismissed Paley’s argument with the mere wave of a hand. The most famous dismissal was that of Richard Dawkins (1986). It is ironic that thermodynamics, and especially the second law of thermodynamics, was developed after publication of Paley’s book, during the time that naturalists began to dismiss teleology as a valid argument. The second law of thermodynamics permits a quantitative assessment of the design argument that was not possible in Paley’s time.

The First and Second Law of Thermodynamics Applied to the Universe

The universe represents the ultimate isolated thermodynamic system. The universe is often defined as the totality of physical existence. This definition precludes matter or energy from entering or leaving the universe, so by definition the universe is an isolated system (any subset of the universe cannot strictly be an isolated system but merely approximates an isolated system). Indeed, sometimes the second law of thermodynamics is stated as “the entropy of the universe increases.” The first two laws of thermodynamics operate hand in glove to describe how the universe operates now: the amount of matter/energy in the universe does not change, but the energy of the universe becomes progressively less useful. There is no reason why this situation would change in the future. Extrapolation of these two laws into the distant future paints a bleak picture for the fate of the universe. The universe will one day suffer what is called “heat death,” when all energy available for work will be exhausted. This will happen when the all the universe is at a very low, nearly equal temperature so that there is no temperature gradient available to do any work. Such a universe will be very cold and also very dark (stars will no longer shine because they have exhausted all sources of energy). The good news is that this will happen many trillions of years in the future, much too far into the future for us to worry about.

What about the operation of the first two laws of thermodynamics in the past? There is no reason why they haven’t operated in the past. However, extrapolation of the first two laws of thermodynamics into the distant past results in a contradiction. The sudden appearance of matter and energy would violate the first law of thermodynamics, so this would preclude an origin for the universe. Therefore, the universe could not have a beginning. Indeed, until well into the second half of the twentieth century, an eternal universe was the dominant cosmogony. But if the universe is eternal, then there was more than enough time for the universe to have already reached a heat death today, but this is not what we observe in the world. Therefore, the universe could not have existed forever and hence must have had a beginning. Consequently, if one believes that the universe had a beginning, then one must ultimately deny the first law of thermodynamics, but if one believes the universe is eternal then one must deny the second law of thermodynamics. But which of these two laws will scientists abandon, and why?

The big bang model became the dominant cosmogony by the 1970s, so now it is largely believed that the universe had a beginning 13.8 billion years ago. How does one explain away the first law of thermodynamics? There is no satisfactory answer to that problem. The most common response is to posit that the energy of the universe is exactly zero, so the universe came about as a quantum fluctuation without violating the conservation of energy. It’s not that the universe came about as a quantum fluctuation in a preexisting universe, though some people believe that. Rather, quantum fluctuation is invoked as a way for the universe to come into existence in a manner that is consistent with the laws that govern the universe, such as the laws of thermodynamics. For more discussion of the problems with this approach, please see Faulkner (2015).

There is a better way. Rather than try to rationalize the contradiction of the first two laws of thermodynamics when extrapolated into the distant past, why not acknowledge that this contradiction indicates a limitation of physical explanations? This may indicate that the origin of the universe has no physical explanation. If a phenomenon has no physical explanation, then the only other possible conclusion is that the phenomenon has a metaphysical explanation. That is, the contradiction resulting from application of the first two laws of thermodynamics to the distant past may be evidence of creation.

When Did the Second Law Come into Existence?

The second law of thermodynamics has long been a topic of discussion in the evolution/creation debate (for example, Humphreys 1978; Kauffman, 1983). Henry M. Morris, one of the cofounders of the modern creation science movement, discussed thermodynamics at length (Morris 1963, 1964, 1970a, 1970b, 1985; Morris and Parker 1987). In turn, Morris’ beliefs about thermodynamics heavily influenced other creationists. Morris made two salient points about thermodynamics:

1. Evolution violates the second law of thermodynamics (as well as the first law of thermodynamics).
2. The second law of thermodynamics was imposed on the world after man’s fall in the Garden of Eden.

I will examine the second of these two teachings first.

In his ground-breaking book, The Twilight of Evolution, Morris (1963) argued that the second law of thermodynamics leads to death, decay, and degeneration. Since Morris saw in death, decay, and degeneration a parallel to the curses as result of Adam’s sin (Genesis 3:14–19), he reasoned that the second law of thermodynamics was not in effect until after the Fall. Morris later expounded upon this thesis at length (Morris 1964, 1970a, 1970b, 1985; Morris and Parker 1987). Other creationists, such as Williams (1966, 1967, 1969), furthered the initial work of Morris on thermodynamics.

However, dissident voices among creationists soon arose on the question of whether the second law of thermodynamics was at work in the universe prior to the fall. For instance, Kofahl (1973) argued that entropy increased prior to the Fall, that is, that the second law of thermodynamics was operating in the world immediately after the Creation and not a consequence of the Fall. The primary basis for Kofahl’s argument was that the essential chemical processes of life are dependent upon relationships involved in the second law of thermodynamics. Kofahl proposed a three-part formulation:

1. The second law of thermodynamics was in operation from the completion of creation.
2. Prior to the fall, disruptive effects of random processes on living things were prevented by divine constraints.
3. Those constraints were removed as one aspect of the curse.

In immediate responses to Kofahl, Williams (1973b) and Morris (1973) strongly disagreed. Both accused Kofahl of assuming uniformitarianism. Williams allowed that in the original creation, heat could have flowed from hotter to cooler objects but with 100% efficiency. Apparently, Williams thought heat could flow this way while entropy did not increase, though he gave no physical or mathematical justification for this conclusion. In response to the criticisms of Williams and Morris, Kofahl (1974) showed from the basic definition of entropy that the heat flow that Williams allowed prior to the Fall would have unavoidably resulted in increased entropy. Thus, the second law of thermodynamics was operating prior to the Fall. In response to the controversy, Jansma (1974) proposed a sort of compromise, with the second law of thermodynamics operating on plants and animals prior to the fall, but not on man—that change supposedly occurred at the fall. Williams (1975) responded to the two letters by Kofahl and Jansma. In the same issue of the Creation Research Society Quarterly with Williams’ response, Armstrong (1975) published an article reemphasizing the usefulness of the second law of thermodynamics as an argument against evolution, effectively closing this early discussion on the question of when the second law of thermodynamics began to operate.

Ironically, shortly before Kofahl’s objection, Williams (1973a) wrote, “Frankly I am not willing to speculate about what existed before the Fall,” but that is exactly what Williams did in his response to Kofahl, as well as in his previous writings on thermodynamics. While most creation scientists and creation organizations have abandoned the belief that the second law came into effect at the Fall, the older position lingers among many creationists who are not scientists. When I have engaged such people in discussion, pointing out the physical problems that such a belief causes, their response has been similar to that of Williams. They argued that we don’t know how the physical world operated before the fall, which was preceded by their explanation of how the world worked before the Fall.

Before moving on, I ought to mention that Thomas Barnes, one of the founders of the Creation Research Society (as was Morris), may have disagreed with Morris on when the second law came into operation in the universe. Barnes (1966) wrote,

The Second Law of Thermodynamics began after the existence of a fully wound-up system with Living Maturity.

That statement is a bit vague—with no explicit mention of the Fall, that statement could be read as belief the second law of thermodynamics was ordained by the conclusion of the Creation week and prior to the Fall. That is how Williams (1973a) interpreted Barnes’ statement. If Barnes disagreed with Morris and Williams on the question of when the second law of thermodynamics came into operation, he apparently did not engage in public discussion of the matter. More recently, Lee Anderson (2013) and Faulkner (2013) readdressed the question of whether the second law of thermodynamics was invoked at the time of the Fall, though those papers have stimulated no response in the creationary literature.

Williams eventually collected his thoughts about thermodynamics and how it relates to creation/evolution into a book (Williams 1981). Two decades later, Carl Wieland published a brief introductory book on the second law of thermodynamics and how it relates to origins (Wieland 2013). It differed from Williams’ treatment in that it was more aimed at a popular audience. Williams intended his book to be a definitive treatment of the subject. Over the past four decades little discussion of thermodynamics in the creation literature appeared. Consequently, Williams’ book amounted to the de facto definitive treatment. However, over the years I have had private conversations with creation scientists about the inadequacies of Williams’ treatment of thermodynamics, though none of those discussions led to publication of criticisms in the creation literature.

Two decades after publication of Williams’ book, Hill (2001) briefly rekindled discussion over the question of when the second law of thermodynamics came into effect. He noted that the luminaries God made and placed in the sky on day four of the creation week were visible via an energy flow, and classical thermodynamics was developed to describe energy flow. Consequently, some form of the second law of thermodynamics must have prevailed between the completion of the Creation week and the Fall. In a sort of compromise, Hill proposed that perhaps the second law of thermodynamics was subtly changed at the time of the fall. In a response, Kofahl (2002) disagreed, saying that he thought he had settled the question of whether the second law of thermodynamics came into operation at the Fall in his previous two papers. Kofahl reiterated his previous writings on the subject, suggesting that the apparent palliative effect of the tree of life (Genesis 3:22–24) may have canceled any degeneration in the human body due to entropy change that may have existed prior to the Fall, which subtly implies the second law of thermodynamics operated from the initial Creation. About the same time, Faulkner (2001) engaged in a discussion with Williams (2000, 2001) about whether the formation of stars from gas clouds would violate the second law of thermodynamics, an argument originally advanced by Mulfinger (1970).

It is worth noting that Gitt (2006) published a book on information theory that relates to the origin of living things. Information entropy appears to be related to thermodynamic entropy, though Gitt only briefly mentioned this connection (Gitt 2006, 41, 230–235).

Did the second law of thermodynamics come into existence at the time of the Fall, or was the principle of increasing entropy around since conclusion of the Creation week? Unless at the Fall someone changed the probability of being dealt a royal flush, the second law of thermodynamics existed from the beginning. The manifestations of the second law surround us, from biological processes, to heat transmitting from warmer to cooler. The initial creation obviously exhibited these processes too. Animals and the first people were directed to what food they should eat (Genesis 1:29–30), and presumably digest. God ordained that the sun, moon, and stars He made on Day Four provide light upon the earth (Genesis 1:15, 17). There is nothing in the biblical text (Genesis 3:14–19) to suggest that the curse upended all of physics. It was most unfortunate that this incorrect notion entered into creation studies.

Conclusion

We call the natural tendency for systems to progress from lower entropy to higher entropy, from order to disorder, the second law of thermodynamics. Living creatures are highly ordered systems, and hence have relatively low entropy. Like all things in physical existence, living systems are subject to the second law of thermodynamics. Consequently, the naturalistic origin of life from non-living things and development of life from simple to complex violates the second law of thermodynamics. Evolutionists generally have overplayed their hands in arguing that the second law of thermodynamics does not apply to living things because they are open systems. If one were to randomly add cards to a deck of cards as one continually shuffles the deck, the deck would constitute an open system, but no one would realistically expect that adding cards from time to time would produce order in the deck. Unfortunately, not all discussions of the second law of thermodynamics and biological evolution from a creation perspective have been as well thought out and presented as they ought to have been. I hope that my modest contribution here will advance the discussion.

In some of my presentations, I hand a small rock to people and ask them to identify it. Most people quickly identify it as an arrowhead. When I ask them how they know this, the response always appeals to the shape of the arrowhead. The distinctive shape indicates purpose and function. It also implies that someone intentionally shaped the stone by flaking off parts of it, sculpting the stone into the shape desired to fulfill a purpose. When I ask people if the stone could have naturally weathered into its distinctive shape, none of them agree. When asked to defend that conclusion, the response always is an appeal to the improbability of that a stone would weather this way. Indeed, to argue so would entirely undermine the science of archaeology. The foundation of this conclusion is the recognition of design in what people are looking at. I then ask people to probe deeper to see if they truly are seeing design, and people invariably double down with their conclusion. I then ask them if they see any other design. I ask them this while they are holding the arrowhead in their hands. Some people eventually get what I am driving at, but most people need prompting. I’m not harsh with people who need prompting because I did get them focused on one thing, which prevented them from seeing the truly big thing. We readily see the design imposed on the rock, but we take for granted the infinitely more designed hand that holds the rock.

Creationists readily see the wisdom in the lesson, but naturalistic evolutionists are conflicted. On the one hand they see the much greater design of their hands that can be found in the rock, but on the other hand they don’t want to see the design in their hands that hold the rock. To do so would acknowledge that something is wrong with their worldview. It is not rational to readily see design, and hence a designer, in a relatively simple rock while simultaneously rejecting the design, and hence a Designer, in the much more complex hands that hold the rock. But rationality has little to do with the discussion, for it is not a head problem—it is a heart problem. If we recognize that we are created, then it follows that the Creator likely has a claim upon our lives, that He can expect certain things from us. It is this accountability before God that makes it impossible for man in his natural state to reach the rational conclusion.

References

Anderson, Lee Jr. 2013. “Thoughts on the Goodness of Creation: In What Sense was Creation ‘Perfect’?” Answers Research Journal 6 (November 13): 391–397. https://answersresearchjournal.org/in-what-sense-was-creation-perfect/.

Armstrong, H. L. 1975. “Use of the Second Law of Thermodynamics in Macroscopic Form in Creation Studies.” Creation Research Society Quarterly 12, no. 2 (September): 103–106.

Barnes, Thomas G. 1966. “A Scientific Alternative to Evolution.” Creation Research Society Quarterly 2, no. 4 (January): 5–8.

Dawkins, Richard. 1986. The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design. New York, New York: W. W. Norton & Company.

Faulkner, Danny R. 2001. “Does the Collapse of a Gas Cloud to Form a Star Violate the Second Law of Thermodynamics?” Creation Research Society Quarterly 38, no. 1 (June): 40–44.

Faulkner, Danny R. 2013. “The Second Law of Thermodynamics and the Curse.” Answers Research Journal 6 (November 13): 399–407. https://answersresearchjournal.org/second-law-thermodynamics-curse/.

Faulkner, Danny R. 2015. “Quantum Fluctuations May Kill Big Bang Evangelism.” Answers in Depth 10. https://answersingenesis.org/big-bang/quantum-fluctuations-may-kill-big-bang-evangelism/.

Girolami, Gregory S. 2020. “A Brief History of Thermodynamics, As Illustrated by Books and People. Journal of Chemical and Engineering Data 65, no. 2 (September 12): 298–311.

Gitt, Werner. 2006. In the Beginning Was Information: A Scientist Explains the Incredible Design in Nature. Green Forest, Arkansas: Master Books.

Hill, Robert. 2001. “Did Entropy Change Before the Curse?” Creation Matters 6, no. 5 (September/October): 6–7.

Humphreys, D. Russ. 1978. “Using the Second Law More Effectively.” Creation Research Society Quarterly 14, no. 4 (March): 209–210.

Jansma, S. J. 1974. “Comments on Thermodynamics Before and After the Fall.” Creation Research Society Quarterly 11, no. 3 (December): 177–179.

Kauffman, David A. 1983. “Human Growth and Development, and Thermo II.” Creation Research Society Quarterly 20, no. 1 June: 24–28.

Kofahl, Robert E. 1973. “Entropy Prior to the Fall.” Creation Research Society Quarterly 10, no. 3 (December): 154–156.

Kofahl, Robert E. 1974. “Reply Concerning Entropy Prior to the Fall.” Creation Research Society Quarterly 11, no. 3 (December): 175–177.

Kofahl, Robert E. 2002. “More on Entropy before the Curse.” Creation Matters 7, no. 1: 7.

McIntosh, A. C. 2009 “Information and Entropy—Top-Down or Bottom-Up Development in Living Systems?” International Journal of Design and Nature and Ecodynamics 4, no. 4: 351–385.

McIntosh, Andy C. 2013. “Information and Thermodynamics in Living Systems.” In Biological Information—New Perspectives. Edited by Robert J. Marks, Michael J. Behe, William A. Dembski, Bruce L. Gordon, and John C. Sanford, 179–201. Singapore, Singapore: World Scientific.

McIntosh, Andy. 2023. “The Fingerprint of Intelligence: Thermodynamics and Information.” Biblical Creation on Solid Ground. Edited by Ola Hössjer and Samuel Lampa, 117–144. Denmark: STH Förlag.

Morris, Henry M. 1963. The Twilight of Evolution, 32–46, 58–59, 72. Grand Rapids, Michigan: Baker.

Morris, Henry M. 1964. “The Power of Energy.” Creation Research Society Quarterly Annual 1: 18–23.

Morris, Henry M. 1970a. Biblical Cosmology and Modern Science, 111–139. Grand Rapids, Michigan: Baker. See also footnote 4 on page 19.

Morris, Henry M. 1970b. “Evolution Theory and Thermodynamics.” Creation Research Society Quarterly 6, no. 4 (March): 199–200.

Morris, Henry M. 1973. “Another Reply to Robert Kofahl.” Creation Research Society Quarterly 10, no. 3 (December): 157.

Morris, Henry M. 1985. Scientific Creationism. 2nd ed, 37–46. El Cajon, California: Creation-Life Publishers.

Morris, Henry M., and Gary E. Parker. 1987. What is Creation Science? 2nd ed, 198–220. El Cajon, California, Master Books.

Mulfinger, George. 1970. Critique of Stellar Evolution. Creation Research Society Quarterly 7, no. 1 (June): 7–24.

Müller, Ingo. 2007. A History of Thermodynamics. Heidelberg, Germany, Springer.

Saslow, Wayne M. 2020. “A History of Thermodynamics: The Missing Manual.” Entropy 22, no. 1 (January): 77.

Sears, Frances W., and Gerhard L. Salinger. 1975. Thermodynamics, Kinetic Theory, and Statistical Mechanics. 323–325. Reading, Massachusetts: Addison-Wesley.

Wieland, Carl. 2013 World Winding Down: Understanding the “Law of Disorder” and How it Demands a Creator. Powder Springs, Georgia: Creation Book Publishers.

Williams, Emmett L. 1966. “Entropy and the Solid State.” Creation Research Society Quarterly 3, no. 3 (October): 18–24.

Williams, Emmett L. 1967. “The Evolution of Complex Organic Compounds from Simpler Chemical Compounds: Is it Thermodynamically and Kinetically Possible?” Creation Research Society Quarterly Annual 4, no. 1 (June): 30–35.

Williams, Emmett L. 1969. “A Simplified Explanation of the First and Second Laws of Thermodynamics: Their Relationship to Scripture and the Theory of Evolution.” Creation Research Society Quarterly 5, no. 4 (March): 138–147.

Williams, Emmett L. 1973a. “Thermodynamics: A Tool for Creationists (Review of Recent Literature).” Creation Research Society Quarterly 10, no. 1 (June): 38–44.

Williams, Emmett L. 1973b. “Response to Robert Kofahl.” Creation Research Society Quarterly 10, no. 3 (December): 156–157.

Williams, Emmett L. 1975. “The Fall and Degeneration.” Creation Research Society Quarterly 12, no. 2 (September): 124–126.

Williams, Emmett L. ed. 1981. Thermodynamics and the Development of Order. Creation Research Society Books.

Williams, Emmett L. 2000. “Star Formation According to Faulkner and Mulfinger: Some Observations.” Creation Research Society Quarterly 37, no. 1 (June): 47–49.

Williams, Emmett L. 2001. “Star Formation: Faulkner and Mulfinger—II. Creation Research Society Quarterly 38, no. 1 (June): 45–48.