Sizes of Galaxies in JWST Data Suggest New Cosmology

Introduction

The James Webb Space Telescope (JWST) has been able to detect galaxies at previously unattainable distances. These galaxies have many properties that are contrary to the predictions made by advocates of the big bang, but which match the predictions made by creation scientists (Lisle 2022). In particular, the galaxies are more abundant, more massive, more mature, more structured, have higher metallicity, and exist at greater distances than standard secular cosmologists had predicted (Boylan-Kolchin 2023; Ferreira et al. 2022; Labbé et al. 2023; Rhoads et al. 2023). Most advocates of the big bang have simply readjusted their models of galaxy evolution to accommodate these new discoveries, pushing back galaxy formation to an earlier time. But there are several specific aspects of these distant galaxies that strongly resist any realistic interpretation within the standard cosmological model. The brightnesses, surface brightnesses, and especially the angular diameters of distant galaxies observed by the JWST suggest an entirely different cosmology.

Astronomers have long noted that if we understood the way galaxies change over time, then observations of distant galaxies (assumed to be much younger when their light was emitted) in comparison with nearby ones could be used to test cosmological models (Boylin-Kolchin 2023; Lovyagin et al. 2022; Lubin and Sandage 2001; Tolman 1930; Wilson 1939). This is because different models make different predictions regarding the observed angular size and apparent brightness of a given galaxy at a given distance. Furthermore, they also make different distance estimates based on a galaxy’s redshift.

These differences arise from different assumptions about what is causing redshifts in galaxies—the stretching of their light to longer wavelengths. Until recently, it has been difficult to discern which model best fits the data because the predictions of all models are very similar for nearby galaxies. But the JWST has unveiled the properties of galaxies at unprecedented distances where the predictions of various models radically diverge. These observations are not favorable to the big bang model nor the metric on which it is based. They do, however, fit nicely into a model in which galaxies recede through space without expansion of space itself. We will see that this interpretation of the data suggests that distant galaxies are very similar to nearby ones. This implies that billions of years of galaxy evolution have not taken place, which is favorable to our expectations based on a straightforward reading of Genesis. Thus, this new interpretation of the data may form the basis for a biblically-compatible “young universe” cosmology.1

The wavelength of light we observe is not always the same as the wavelength observed by the source at the time of its creation. The difference may be due to any number of processes, such as the Doppler effect or time dilation. Redshift (z) is defined as the shift of the observed wavelength (λ₀) relative to the emitted wavelength (λ_E) by the following:

In the 1920s, Edwin Hubble discovered a relationship between the distance to a given galaxy, and its redshift. Namely, galaxies that are farther from us tend to have a higher redshift than those nearby. The relationship is nearly linear for nearby galaxies and is called the Hubble Law. It has the following form:

The constant of proportionality, H₀, is called the Hubble constant, c is the round-trip speed of light, r is the distance to the galaxy, and z is the redshift. The subscript 0 in the Hubble constant denotes that this is the current value of this number and may not have always been this value over cosmological time.

In the 1920s, many astronomers interpreted the shifts in wavelength of the spectrum of galaxies as being due to the Doppler effect. Most galaxies are apparently moving away from ours and the larger the distance to the galaxy, the faster its recession velocity. For low redshifts, z ≈ v/c, and the Hubble law can be written as:

Logically, if our galaxy observes neighboring galaxies receding in a way that is linearly proportional to their distance, then each of these other galaxies should also see other galaxies receding away from them according to the same Hubble law. Thus, the Hubble law implies that the entire universe is expanding in the sense that the average distance between galaxies is increasing—if the redshifts are interpreted as a Doppler effect.

Also in the 1920s, four physicists (Alexander Friedmann, George Lemaître, Howard P. Robertson, and Arthur Geoffrey Walker) independently discovered a non-static solution to Einstein’s field equations as applied to the entire universe. Many physicists were convinced that this solution showed that space itself could expand. With the publication of the Hubble law in 1929, Lemaitre argued that the observed redshift-distance relation of galaxies supported his solution. In 1931 Lemaitre conjectured that if the universe is expanding today, it must have been as small as an atom in the distant past. This was the first version of what would later be called the big bang theory. The solution to Einstein’s equations which describes an isotropic, homogeneous, expanding universe is called the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric after the four scientists who discovered it. It is often shortened to the Robertson-Walker metric.

The FLRW metric is assumed by the majority of astronomers today because it naturally explains the Hubble law and why the law is linear for low redshifts. And it is required for the big bang origins story to be plausible. But the FLRW metric does not automatically imply a big bang. An expanding universe does not require that the universe started from a size of zero. Hence, most creation astronomers have largely embraced this metric while rejecting Lemaitre’s conjecture of how and when the universe began.

The FLRW metric is a fundamentally different explanation for galactic redshifts from the Doppler effect. The Doppler effect is the shifting of light wavelengths due to relative motion of the source through space. Such motion causes a redshift or blueshift due to the decompression or compression of the wave fronts relative to the observer. On the other hand, the FLRW metric treats the galaxies as essentially stationary points on an expanding balloon. The points become increasingly separated from each other, not because they are moving through space, but because the space between them is constantly expanding. Since the light is travelling through expanding space, its wavelength is stretched as it travels: the greater the distance, the greater the redshift.

It is impossible to discern the cause of a redshift from the light itself. A galaxy that is moving away from us through space produces the same kind of redshift as a galaxy that is “stationary” at some distance in an expanding space. However, the FLRW metric implies that spacetime is curved in such a way that distant galaxies will appear somewhat different at a given redshift than they would if the redshifts are entirely due to the Doppler effect. For example, the angular diameter of a galaxy at a given redshift will be different between a model that assumes redshifts are caused by expansion and one that assumes that redshifts are caused entirely by the Doppler effect. The apparent brightness will differ as well. Data from the JWST now make it possible to distinguish between these models. (Note that neither a Doppler interpretation nor the FLRW metric imply any central position for the earth. If the rate of galaxy recession increases with distance—the Hubble law—then all other galaxies should observe a similar relation relative to their location regardless of the cause of that recession.)

The FLRW metric permits galaxies to have genuine motion through space in addition to being carried along by expansion of the intervening space. Thus, the Doppler effect either adds to or subtracts from (depending on the direction of motion) the redshift that is due to expansion of space assuming the FLRW metric. The increasing distance between galaxies due to expansion of space is called the Hubble flow, and the individual velocities of galaxies as they move through space are called peculiar velocities. For distant galaxies, the Hubble flow is so large that it overwhelms any peculiar velocity; hence all distant galaxies are redshifted. However, for very nearby galaxies, the Hubble flow is quite small and peculiar velocities dominate. This is why a few very nearby galaxies are actually slightly blue-shifted, such as M31. Peculiar velocities simply add a bit of scatter to the Hubble law. Statistically, the peculiar velocities are essentially random and will therefore tend to cancel out on average in large data sets.

Other explanations for the Hubble law in a non-expanding space have also been suggested (Dennis 2022; de Sitter 1917; Hartnett 2015; Zwicky 1929). The tired light hypothesis was proposed by Fritz Zwicky in 1929. He postulated that galaxies are nearly stationary (except for their small peculiar velocities) in a non-expanding universe and that redshifts are merely a natural result of light traveling vast distances. That is, he thought that light gradually loses energy as it travels. Several mechanisms have been suggested, but most of them predicted a visual blurring of the most distant galaxies—a blurring that is not observed. The theory was not widely accepted, but is now being revisited by some astronomers in light of recent JWST observations (Gupta 2023; Lovyagin et al. 2022).

Distances in the FLRW Metric

In an expanding space, the perceived brightness of a distant standard candle is no longer simply inversely proportional to the square of the distance. And the angular diameter is no longer inversely proportional to distance. Both of these are good approximations for nearby objects, but fail for objects with significant redshifts due to the curvature of spacetime. Moreover, how do we even describe the distance between two objects in a continually expanding universe? To deal with these general relativistic effects, astronomers use several different definitions of distance, and convert between them as needed. The comoving distance uses coordinates that expand with space, maintaining number density within a comoving volume. Luminosity distance is the distance an object would be at if its brightness diminished as the inverse square of distance. So, by definition, an object’s apparent brightness diminishes as the inverse square of its luminosity distance. Finally, the angular diameter distance is the distance at which an object would be for its angular diameter to be inversely proportional to distance. So, an object’s angular diameter (θ) is simply its true diameter (s) divided by its angular diameter distance (D_A).

These three functions of redshift each depend on three cosmological parameters: the Hubble constant (H₀), matter density of the universe relative to critical density (Ω_M), and dark energy density relative to critical density (Ω_Λ). We will here assume the standard “flat” universe in which the sum of matter density and dark energy density equals one: Ω_M + Ω_Λ = 1. And going forward we will assume the standard values of the cosmological parameters: Ω_M = 0.3; Ω_Λ = 0.7; H₀ = 70 km/s/Mpc. Only these values are consistent with observations of the nearby universe under the assumption of the FLRW metric and homogeneity (Choudhury and Padmanabhan 2005: Lisle 2016). This is called the Lambda-Cold-Dark-Matter (ΛCDM) model, or simply the standard model. In a “flat” universe, the comoving distance (D_C), luminosity distance (D_L), and angular distance (D_A) are related to redshift (z) by the following (Hogg 2000):

Fig. 1 shows these distances as a function of redshift under the standard cosmological parameters. Notice that all these distances converge at low z. This is because the spatial geometry of a ΛCDM universe is nearly Euclidian for very short distances. At higher distances, the luminosity distance is always larger than the comoving distance, indicating that objects will appear fainter than they would if stationary in a non-expanding universe at that distance. The angular diameter distance is particularly interesting because it reaches a maximum at z ≈ 1.6. Since the angular diameter distance is the inverse of the angular diameter of an object at redshift z, this means that an object will continue to look smaller with increasing distance until it reaches redshift 1.6. Beyond that distance, the object will start to look larger as its distance increases.

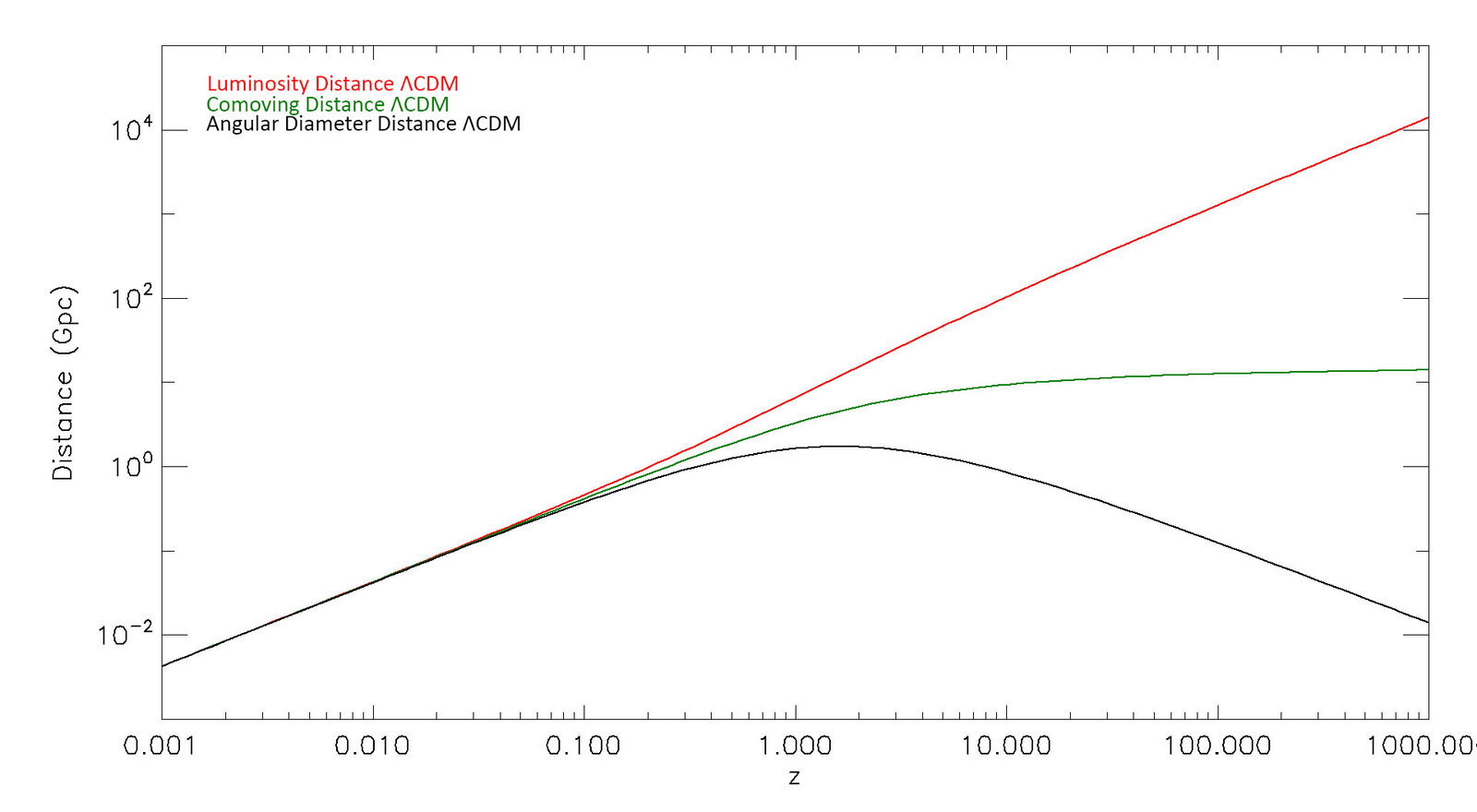
Fig. 1. Comparison of the different definitions of distance used in the standard model of cosmology as a function of redshift (z) under the standard assumptions (H₀ = 70 km/s/Mpc, Ω_M = 0.3, Ω_Λ = 0.7).

Thus, all other things being equal, galaxies should appear smallest at a distance corresponding to redshift 1.6 according to the standard model. Beyond that distance, galaxies should appear larger as their redshift increases. However, this effect is simply not seen in any Hubble Space Telescope (HST) or JWST images. Indeed, galaxies continue to appear smaller with increasing distance as if the large-scale spatial geometry of the universe were purely Euclidian as will be shown below. This is what we would expect if the Hubble law were due to Doppler shifts of galaxies moving through a non-expanding space.

So, we now consider the possibility that galactic redshifts are caused purely by the Doppler effect due to their motion through non-expanding space. Furthermore, let’s assume for the sake of hypothesis that the Hubble law is truly linear with respect to velocity even at high redshifts as shown in equation (3). In this case, the Hubble flow is not due to expansion of space itself, but merely reflects the average recessional velocity of galaxies at a given distance. Then, neglecting peculiar velocities, the distance to any galaxy is simply its velocity (as derived from redshift) divided by the Hubble constant which we take to be 70 km/s/Mpc. We will call this the Doppler model.

The recessional velocity (v) of an object with a Doppler induced redshift (z) is given by the following formula (Lisle 2018)2:

By substitution into equation (3) (and ignoring peculiar velocities) we can compute the distance for any galaxy if we know its redshift:

This “Doppler distance” (D_D) is shown in blue in fig. 2. It corresponds to the true distance to a galaxy when the light was emitted assuming redshifts are entirely due to the Doppler effect. The Doppler distance is nearly identical to the comoving distance (shown in green) for redshifts significantly below unity, and is smaller than the comoving distance for higher redshifts. In the Doppler model, the angular diameter distance is identical to the Doppler distance since motion along the line of sight does not affect lengths in orthogonal directions. Thus, the angular size (θ) of a galaxy of diameter (s) diminishes inversely as the Doppler distance.

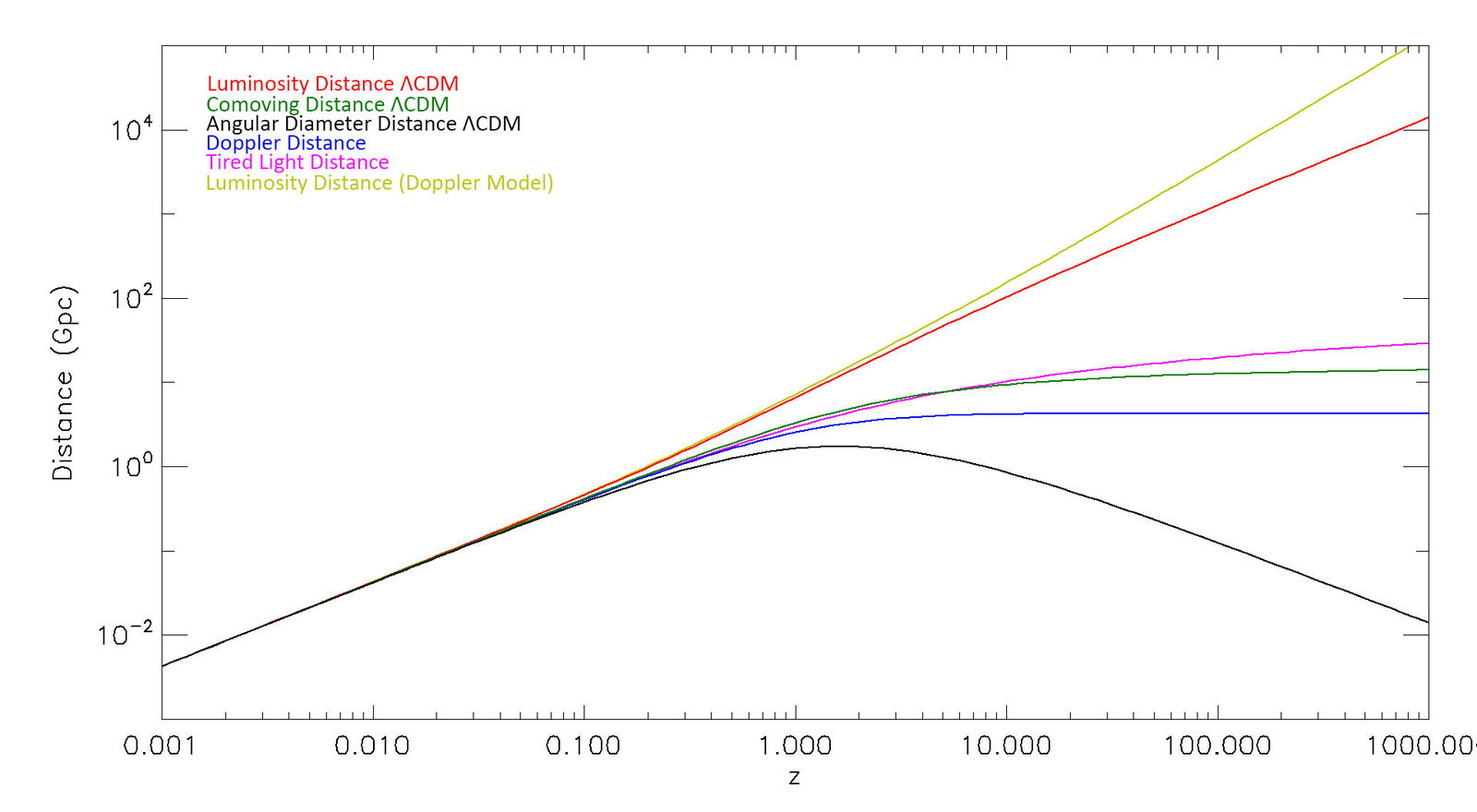
Fig. 2. Comparison of the different definitions of distance used in the standard model of cosmology (ΛCDM), compared with the those of the Doppler and Tired Light models. The Doppler distance (blue) is the distance assuming galactic redshifts are entirely due to the Doppler effect in a non-expanding space. The Luminosity distance in the Doppler model (yellow) is that which increases as the inverse square root of apparent luminosity.

The Doppler model therefore does not predict the magnification effect that is required in the ΛCDM model at redshifts greater than 1.6. We have also plotted the distance predicted by the tired light model in pink (Lovyagin et al. 2022). This would also be the angular diameter distance in the tired light model, since it presupposes that galaxies are essentially stationary (aside from their small peculiar velocities) in a non-expanding space.

In the Doppler model, luminosities do not diminish as 1/r². This is due to relativistic beaming. Beaming is caused by Lorentz aberration (isotropic radiation in the rest frame will not be isotropic in a moving frame), and the time dilation. The formula for luminosity reduction (L_R) by beaming at velocity (v) for an object moving directly away from the observer is (Rybicki and Lightman 1979):

This can also be expressed in terms of redshift by substitution of v from equation (8):

Thus, we can compute the luminosity distance according to the Doppler model:

This is shown in the yellow curve in fig. 2. Since this curve is higher than the luminosity distance for ΛCDM, the Doppler model predicts that galaxies will appear slightly fainter at a given redshift than the prediction of the standard model.

Comparing the Predictions

With these equations, if we know the true size and luminosity of a galaxy, we can compute its angular diameter and apparent brightness at any given redshift for each model. Unfortunately, we don’t know a priori the true size or luminosity of a distant galaxy. However, we can consider the typical size and luminosity of a nearby galaxy, compute its angular diameter and apparent brightness at a high redshift, and see if distant galaxies at that redshift have comparable angular diameters and brightnesses. This assumes that distant galaxies are comparable to nearby ones—a complication we will deal with below. But what is a typical diameter and luminosity of a galaxy?

Let us start by considering a typical diameter. Of the ~30 main, confirmed members of the local group of galaxies, the average diameter is around 5,000 parsecs. The median is only 1,350 parsecs due to the fact that small, dwarf galaxies vastly outnumber the larger ones. Since these smaller galaxies tend to be fainter, they will be under-represented in magnitude-limited surveys like the JWST deep fields. Therefore, it makes sense to use a value closer to the mean as an example of a typical galaxy. We will use 4,500 parsecs as a typical galaxy diameter. The exact value is not important since the different models predict different slopes in angular diameter as a function of redshift.

In fig. 3, we see the angular diameter of a 4.5 kpc galaxy at various redshifts for the three models. The red curve is the angular diameter predicted by the ΛCDM model. Notice that the angular diameter reaches a minimum of about 0.5 arcseconds at a redshift of around 1.6, and is larger for greater redshifts. This magnification effect exists only in expanding-space cosmological models. The predicted angular diameter of the tired light model is shown in green (Lovyagin et al. 2022). The angular diameter predicted by the Doppler model is shown in black. When we examine the angular sizes of images in JWST data, we expect considerable scatter since galaxies come in a range of sizes. But the median should be approximately centered on the curve of the correct model.

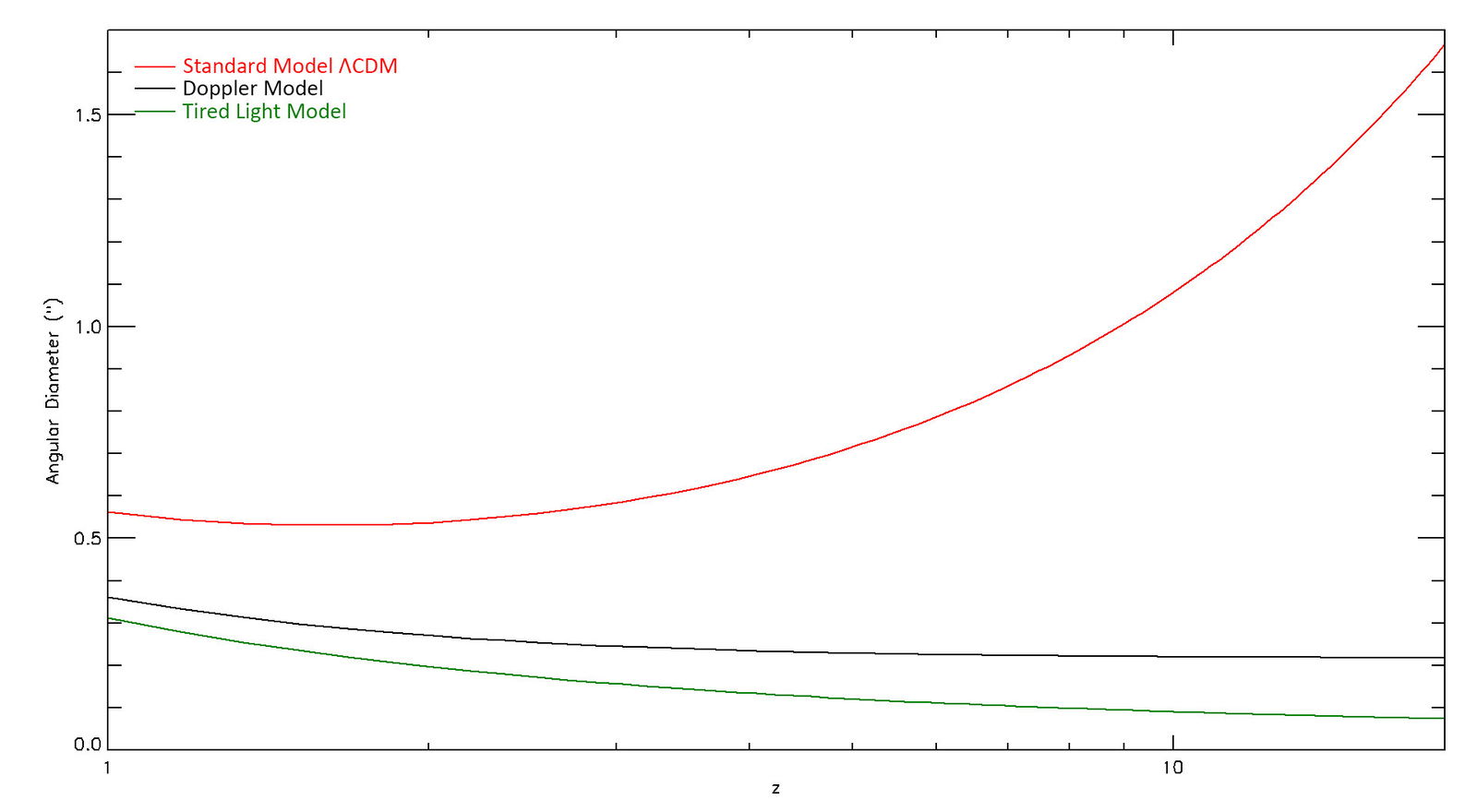
Fig. 3. The angular diameter in arcseconds of a 4.5 kpc diameter galaxy as a function of redshift (z) assuming the standard model (red), the Tired Light model (green), and the Doppler model (black).

JWST Data and Results

Several JWST deep field data sets are now available. Astronomers have published their analyses of the redshifts, angular sizes, and/or brightnesses of galaxies from JWST deep fields. Most of the redshifts were estimated by photometry and are reported in the publications with 1σ random error generally less than 0.5. The uncertainty of size estimates is typically around 15%. In cases where the researchers published only their estimated linear radius of galaxies in kiloparsecs, we converted this back to angular diameter using the cosmological parameters assumed in that study, thereby recovering their original observed angular sizes. For completeness, we also included HST data on lower-redshifted galaxies by Trujillo et al. (2004). The results of all these studies are plotted in fig. 4.

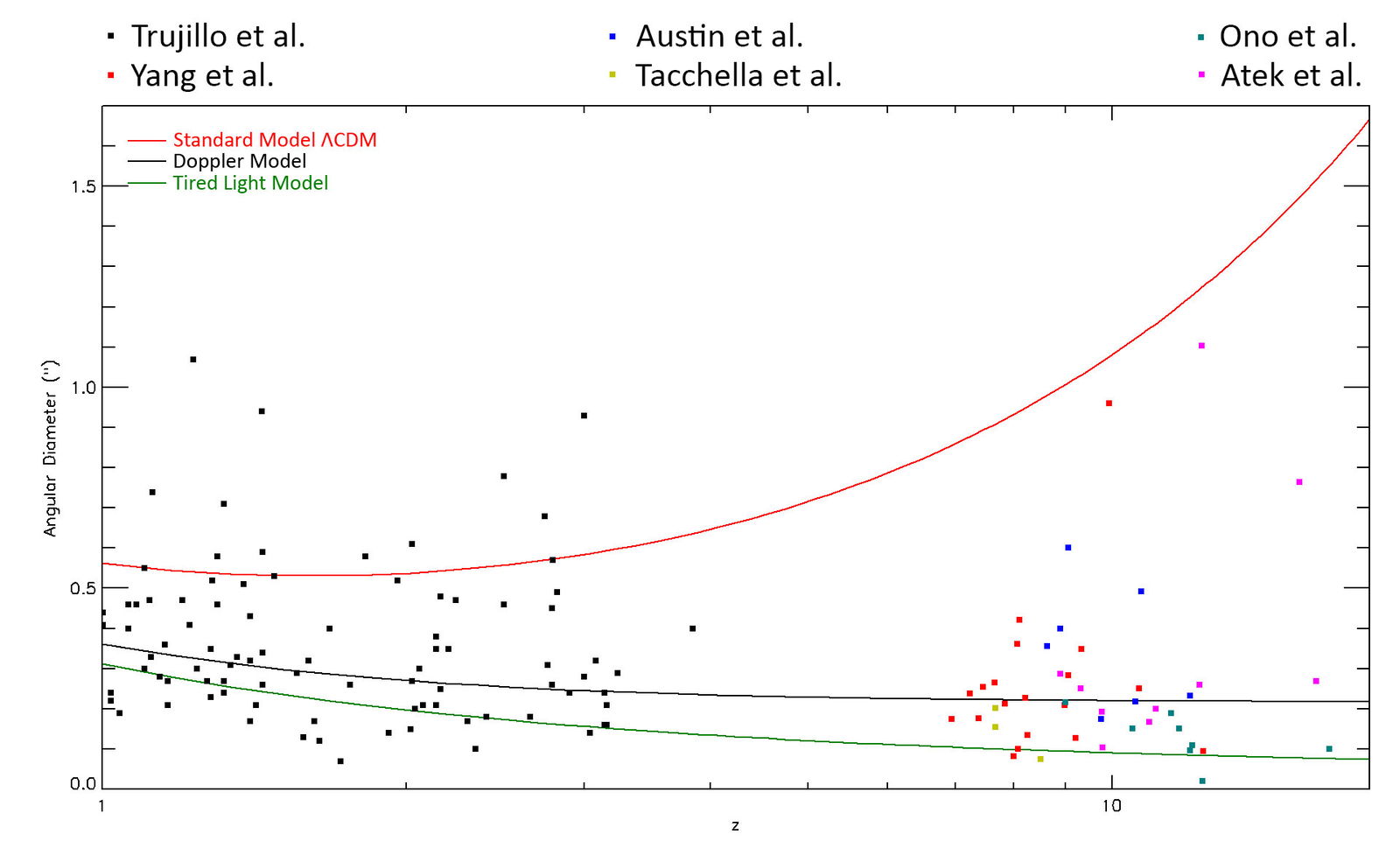
Fig. 4. The measured angular diameters of galaxies at various redshifts from various studies are shown in black. The curves show the angular diameter in arcseconds of a 4.5 kpc diameter galaxy as a function of redshift (z) assuming the standard model (red), the Tired Light model (green), and the Doppler model (black).

The curve reflecting the correct cosmology should bisect these values. We can already see that the ΛCDM curve does not remotely match the data at high redshifts. To see which curve best fits the data, it is useful to bin the data into groups by redshift (z), taking the median value of z and angular size (θ) for each bin in these magnitude-limited surveys. Using the median reduces the influence of galaxies whose redshift or size has been incorrectly estimated. The result is plotted in fig. 5. The median values for each bin are indicated by the square, and the standard deviation is shown by the vertical lines.

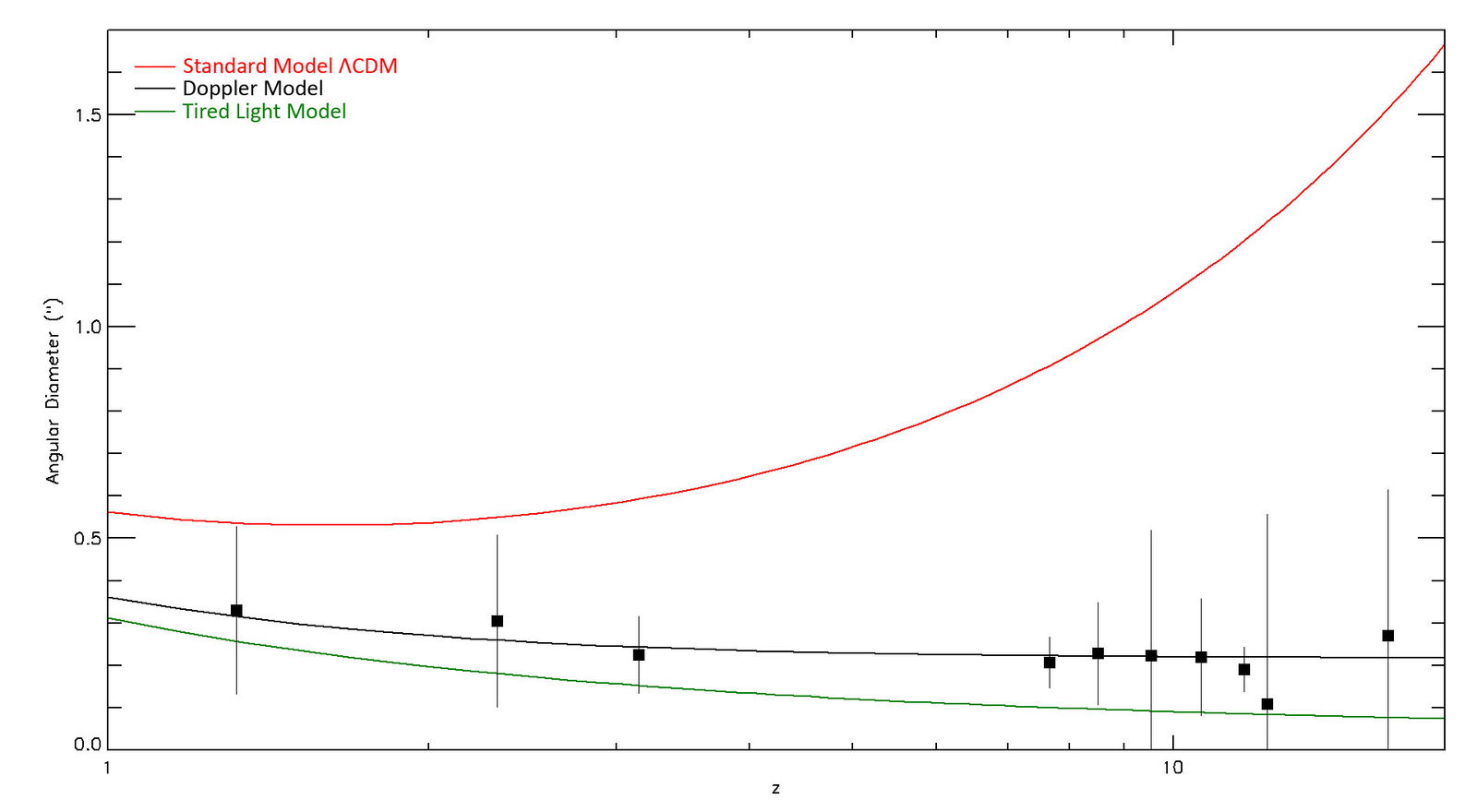
Fig. 5. The measured median angular diameters of galaxies within various redshift bins are shown as squares with the standard deviation indicated by the vertical line. These are compared with the predicted angular size of a typical 4.5 kpc galaxy under the three models.

Clearly the data are remarkably consistent with the Doppler model; all the median values are within one standard deviation, and several are nearly centered on the predicted curve itself. None of the data are within one standard deviation of the ΛCDM curve. Given the scatter in the data and the uncertainty of the median size of a typical galaxy in magnitude-limited surveys, the tired light model cannot be eliminated on the basis of these observations.

These angular diameter observations are particularly useful because of the drastic difference between the predicted sizes based on ΛCDM expansion versus Doppler motion. And these differences grow wider with increasing redshift. At a redshift of 15, the angular size prediction of the Doppler model is 6.6 times smaller than that of the ΛCDM model. At a redshift of 20, the ratio goes up to 8.3. This is mainly due to the increase of the angular size predicted by ΛCDM model; in the Doppler model, the angular size at high redshifts drops only slightly with increasing distance. We therefore predict that future JWST observations of higher redshift galaxies will have a typical angular diameter of approximately 0.2 arcseconds. Astronomers who assume the ΛCDM model must assume that distant galaxies are genuinely 5–10 times smaller than nearby ones.

We can also compare the apparent brightnesses of galaxies as a function of redshift since the ΛCDM model makes different predictions than the Doppler model. This is less determinative than the angular diameter test because (1) luminosity surveys are highly sensitive to selection biases, filters, and k-corrections, and (2) the predictions between the two models are not as disparate as with angular size predictions. As an example of the latter point, at a redshift of 13, the ratio of angular size predictions between the two models is 5.9, but the ratio of luminosity predictions is only 2.5. Galaxy brightnesses are often reported in the magnitude system in which an increase of 1 magnitude corresponds to a drop in luminosity by a factor of the fifth root of 100 (~2.51188). Thus, a galaxy at a redshift of 13 will appear one magnitude higher (thus fainter) under the Doppler model than under the ΛCDM model. This effect is small given the scatter in the data, but it is potentially detectable.

Most surveys of distant galaxies in JWST deep fields report the estimated absolute magnitude (indicative of its actual brightness as if it were a point source only 10 parsecs away) of the galaxy, based on the ΛCDM luminosity distance. If the Doppler model is correct, then these estimates are too faint by about one magnitude as they approach a redshift of 13. Therefore, assuming distant galaxies are truly comparable to nearby ones, we should see a slight drop in their estimated absolute magnitudes with increasing redshifts as reported in studies that assume the ΛCDM model.

Consider an extremely bright galaxy with absolute magnitude –23. If the ΛCDM model is correct, and if distant galaxies are like nearby ones, then the brightest galaxies at all redshifts should also have an estimated magnitude of around –23 as indicated by the red line in fig. 6. On the other hand, if the Doppler model is correct, then when the absolute magnitude of high redshift galaxies is computed by astronomers who assume the ΛCDM model, the estimates should be 2.5 times fainter (1 magnitude) for redshifts of 13. This is indicated by the black curve in fig. 6. The estimated absolute magnitudes of galaxies from several studies are plotted in fig. 6 as squares. All these studies assumed the ΛCDM model, and indeed there seems to be an overall downward trend with increasing redshift.

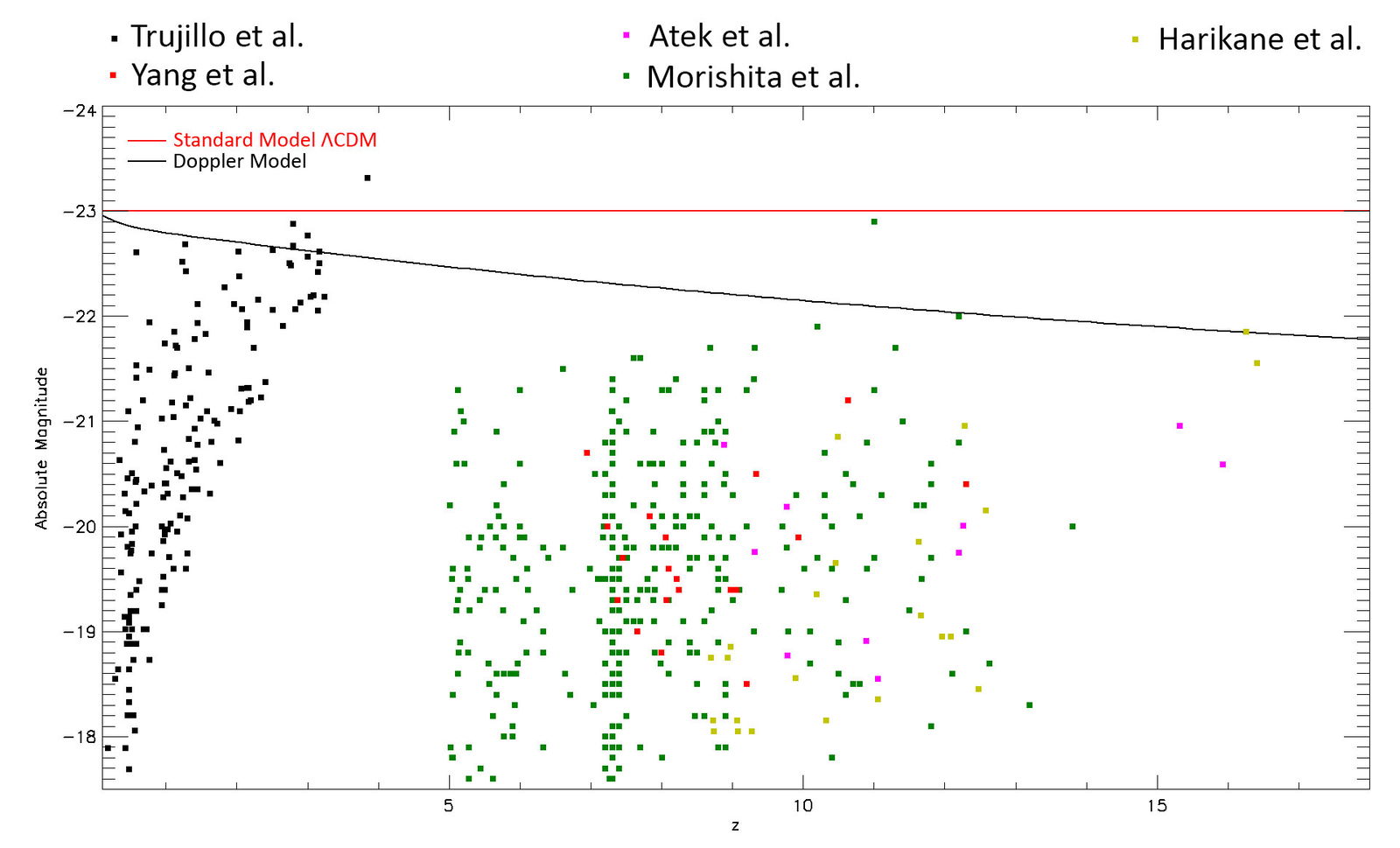
Fig. 6. Estimated absolute magnitudes of galaxies at various redshifts (z) assuming the standard model are shown in the squares for five studies. The expected trend for the brightest galaxies (assuming no galaxy evolution) according to the standard model is indicated by the red line. The Doppler model predicts a downward trend in galaxy brightnesses estimated by the standard model, as shown by the black curve.

When we examine the estimates by Trujillo et al. on the left, we see a clear example of the Malmquist bias. The faintest galaxies (absolute magnitude ~–18) are only detected at very low redshift/distance. By a redshift of 2, only galaxies brighter than absolute magnitude –20 are detected. The fainter galaxies are missing in the plot—not because they are not present but because they are not easy to detect at that distance. The brightest galaxies in that study tend to be found at the highest distances because larger distances sample a greater volume in space, increasing the probability of detecting a rare, ultra-bright galaxy, and because only bright galaxies could be seen at such a distance. Thus, within any given magnitude-limited survey, we expect to see a trend of increasing brightness with distance due to these selection biases. But between surveys we expect to see a downward trend if the Doppler model is correct and no trend at all if the ΛCDM model is correct. We again bin the data, this time selecting the brightest galaxy in each redshift bin to reduce selection effects. The result is plotted in fig. 7.

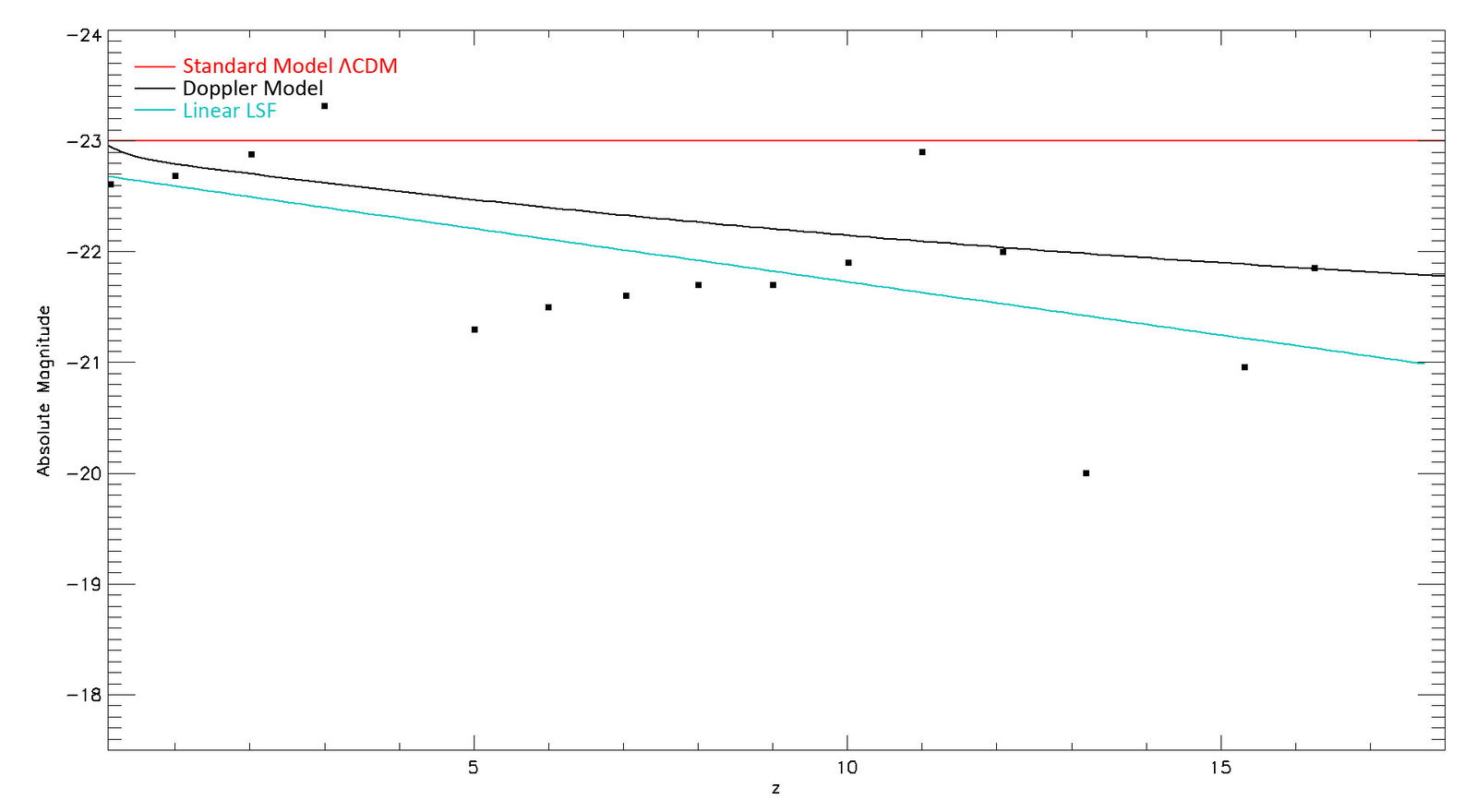
Fig. 7. The brightest galaxy in each redshift bin is shown by the black squares. These are compared with the expected trend for the standard model (red line) and the Doppler model (black curve). The linear least squares fit to the data is shown in light blue.

In fig. 7, we still see some evidence of selection bias and thus an upward trend within a given survey. But between surveys there is a downward trend with increasing redshift. A linear least-squares fit to these data points (shown in light blue) confirms a downward trend with a slope (0.096 ± 0.038) comparable to what is expected by the Doppler model (~0.067). Thus, galaxies at high redshift do indeed appear fainter than predicted by the ΛCDM model, and by approximately the difference the Doppler model predicts.

Analysis

Luminosity and angular diameter data from both the HST and the JWST are consistent with the Doppler model in which galaxy redshifts are produced entirely from the Doppler effect due to motion through a non-expanding space and in which no galaxy evolution has occurred. However, there is degeneracy between cosmological tests and galaxy evolution. How do we really know that galaxies at high redshifts are anything like nearby galaxies? The data above could also be interpreted as being consistent with the ΛCDM model if galaxies at high redshift are actually 5–10 smaller than nearby galaxies and approximately one magnitude intrinsically fainter. Using the standard Einstein synchrony convention (ESC), we are seeing distant galaxies not as they are today, but as they were billions of years ago when the light left. Could galaxy evolution over deep time explain the angular diameter and luminosity trends in a ΛCDM model?

There are several reasons to reject such an explanation. First, theoretical studies of galaxy formation under the assumptions of the standard model did not predict such a size growth without substantial mass growth. Rather, it was the mass of such galaxies that was supposed to increase with time; yet these high redshift galaxies already have high mass (estimated from their luminosity). So, there are theoretical problems with such a claim.

Second, and more importantly, even if we grant that galaxies somehow grow in diameter with time, should we expect that such growth curves would precisely match what the Doppler model predicts without such growth? It is not simply that the observed angular diameters match the Doppler model predictions at high z. Rather, they appear to match at all values of z. Should we expect that galaxies grow in size and in brightness in exactly such a way as to eliminate any evidence of the FLRW metric in favor of simple Doppler shifts? Only by rejecting parsimony could we entertain such a possibility.

Third, there are several observable characteristics of galaxies that are relatively independent of the cause of their redshifts. Astronomers have already noted that the metallicity range in high-redshift JWST surveys is comparable to nearby galaxies—suggesting no strong evolution (Rhoads et al. 2023). Moreover, the structures of such galaxies are mature, with many disk galaxies (Ferreira et al. 2022). There is even evidence of high redshift barred spirals which were previously thought to be a much more recent (nearby) phenomenon (Costantin et al. 2023). The ratios of spiral galaxies to ellipticals or to irregulars is approximately constant out to a redshift of 10 suggesting little, if any, evolution (Lee at al. 2023). Beyond a redshift of 10, the ratio of spiral galaxies to ellipticals appears to drop somewhat, but this may be due to selection effects; typical galaxies at such distances have an average angular diameter of around 0.2 arcseconds and are faint, making morphology classification difficult. In all tests that are relatively independent of cosmological assumptions, high redshift galaxies appear to be very similar to local galaxies. This suggests that no significant evolution has occurred.

The Tolman Test

The Tolman surface brightness test has long been regarded as a way of evaluating various proposed cosmological models (Tolman 1930). This test involves measuring the surface brightness of galaxies at various redshifts. Surface brightness is the brightness per (angular) unit area of a galaxy. In Euclidian geometry for stationary objects, the surface brightness of a given galaxy should be independent of its distance. This is because both apparent brightness and angular area diminish with the square of the distance, so their ratio is constant. But in an expanding universe, this is no longer the case.

Apparent brightness is inversely proportional to the square of the luminosity distance. And the surface area is inversely proportional to the square of the angular diameter distance. Therefore, surface brightness is proportional to D_A²/D_L². From equations (6) and (7), we can see that D_L = D_A(1+z)² for any given value of z. Therefore, in the FLRW metric assumed by the standard model, the surface brightness of a galaxy goes inversely as (1 + z)⁴. Incidentally, the tired light model predicts that surface brightness should decrease as 1 + z.

In the Doppler model, the angular diameter distance is equal to the Doppler distance as given by equation (9). And the luminosity distance is given by equation (13). So, surface brightness is proportional to D_D²/D_LDop². Also from equation 13, we see that D_LDop = D_D(1 + z)^3/2. Therefore, if galaxy redshifts are due to the Doppler effect in a non-expanding metric, then their surface brightness should diminish as (1 + z)³. We can compare the median surface brightnesses of galaxies from JWST data at various redshifts to see if they drop according to (1 + z)⁴ as predicted by the ΛCDM model, or by (1 + z)³ as predicted by the Doppler model. The ratio of these two predictions is 1 + z, which becomes quite large at high redshifts. The observations confirm that the surface brightness of galaxies in JWST data are indeed brighter than the standard model predicts and by a factor of 1 + z.

For example, at a redshift of 13 the Doppler model predicts that the surface brightness of a galaxy should be 14 times greater than that predicted by the ΛCDM model. And indeed, JWST data confirm this. We have already seen that galaxies at redshift 13 are about 1 magnitude (2.5 times) fainter than the ΛCDM model predicts, and 5.95 times smaller in diameter, and so their surface area is 35.4 times smaller. Thus, their surface brightness is 14 times greater than that predicted by the standard model—a factor of 1 + z. At this redshift, the tired light model predicts surface brightnesses nearly 200 times greater than those observed in these JWST data sets.

The Doppler model therefore passes the Tolman test while the standard ΛCDM model and the tired light model do not. Interestingly, this was known to be the case even before these latest JWST results. But why didn’t anyone seem to notice this? In 2001, Lubin and Sandage published their analysis of the Tolman test on galaxies imaged by the HST and argued that the results favor a universe in which space is expanding. They did this for two different wavelength filters and found that the surface brightness diminishes by (1 + z)^2.59±0.17 in the R band and by (1 + z)^3.37±0.13 in the I band (Lubin and Sandage 2001). The average of these two exponents is 2.98 ± 0.55, consistent with the Doppler model prediction of 3, but well below the standard model’s prediction of 4. How then do these authors account for the discrepancy? They conclude that the additional value of 1.02 is due to evolution of the galaxies over time.

So, galaxy evolution can always be used to explain discrepancies between predictions and data. But we now see that galaxies would have to evolve in precisely the right way to eliminate any evidence of the FLRW metric at all redshifts and in such a way as to precisely mimic the predictions of the Doppler model. But in the Doppler model, such auxiliary hypotheses are unnecessary. Moreover, observations that are relatively independent of cosmological model (such as morphology, metallicity, and mass estimates) show no evidence of significant evolution between high redshift and low redshift galaxies.

Given that the Doppler model correctly predicts both the median angular diameter and brightness of galaxies, it would have to pass the Tolman test since surface brightness is entirely determined by these two effects. But it is interesting that the Doppler model predicts angular sizes and brightnesses for all redshifts without invoking any galaxy evolution at all. Furthermore, the Doppler model has only one adjustable parameter—the Hubble constant (H₀). Yet, it fits the data better than the standard model which has three adjustable parameters (H₀, Ω_M, and Ω_Λ), and which must also invoke substantial galaxy evolution in order to accommodate the observations. How many “epicycles” must be added before we reconsider the underlying paradigm?

Conclusions and Predictions

The most straightforward interpretation of the data seems to suggest that the redshifts of galaxies are entirely the result of a relativistic Doppler effect in non-expanding space such that their recessional velocity is linearly proportional to their distance even at high redshifts. Under this cosmology, the high redshift galaxies observed in JWST deep fields are nearly identical to nearby galaxies in linear diameter, brightness, and mass. Independent of cosmology, we have already observed that high redshift galaxies have similar morphologies and a similar range of metallicities to nearby galaxies. Thus, there is no evidence of substantial galaxy evolution as a function of redshift.

In order to salvage the ΛCDM model, one would have to assume that high redshift galaxies are actually 5–10 times smaller than nearby galaxies (though with comparable mass) and somehow expand over time in precisely the right way so as to eliminate any evidence of the FLRW metric. Likewise, the intrinsic brightness would have to gradually increase by one magnitude over a redshift range of 13. The two effects would have to combine in just the right way so that the intrinsic surface brightness is inversely proportional to z + 1, the difference between the standard model and the Doppler model. The Doppler model doesn’t require any such fine tuning because galaxies are as large and as bright at all redshifts as nearby galaxies.

An additional important implication of the Doppler model is that there was no big bang. The big bang requires an expanding space: a scaling factor that changes over time. But the evidence is consistent with a metric that is (approximately) static. The galaxies are receding, but are moving through a non-expanding space. Thus, the universe is indeed expanding in the sense that the average distance between galaxies is increasing. But the fabric of space does not expand. Nor should we conclude that the Hubble law in a non-expanding space implies that galaxies sprang from a common point. Galaxies have tangential motions in addition to their radial motions. Consequently, their negative velocity vectors do not converge to a common point. This is particularly obvious for those nearby galaxies that are blue-shifted.

The big bang model has always had its problems. But until now, we have not had a creation-based alternative that makes specific quantitative cosmological predictions. If indeed the Hubble law remains a linear relationship between distance and recessional velocity at high redshift, then this suggests a very interesting, new cosmology. The implications of this model go well beyond this study. Our purpose here is to show that the Doppler model matches existing data, and to make predictions about the nature of galaxies at as yet undiscovered redshifts.

The Doppler model predicts that the median galaxy angular diameter should be just over 0.2 arcseconds for galaxies at redshifts beyond 15. This is in contrast to the ΛCDM model which predicts an increasing angular diameter for higher redshifts. The Doppler model predicts a fainter apparent brightness for galaxies at a given redshift than the standard model. Thus, absolute magnitudes estimated by the ΛCDM luminosity distance will be fainter by ~1 magnitude at z = 13 and the difference becomes somewhat larger for greater redshifts. Brightness tests are more sensitive to biases than angular diameter measurements. However, a well-established standard candle in JWST data could discern brightness with sufficient precision to distinguish between the competing models.

One such standard candle would be a type Ia supernova. These have a visual absolute magnitude of –19.5 at their peak, and would be easily visible to the JWST even at a redshift of 10. If the Doppler model is correct, then estimates of the absolute magnitude using the ΛCDM model would be around –18.6 at a redshift of 10. In such an event, astronomers committed to ΛCDM might argue that type Ia supernovae are not such good standard candles at high redshifts. Determining the light curve of a high redshift supernova would require multiple JWST observations. But the results would be extremely rewarding. Such an event could also distinguish between the Doppler model and the tired light model because the latter predicts no time dilation in the light curve as a function of redshift. The Doppler model predicts the same time dilation as the standard model (1 + z). Such time dilation has been reported in other studies of supernova light curves (Goldhaber et al. 2001; Leibundgut et al. 1996), but at the high redshifts accessible to the JWST there could be no doubt.

Even the existence of type Ia supernovae at extremely high redshifts could be problematic for the big bang model. Type Ia supernova involves the explosion of a white dwarf that is accreting mass from a nearby star. But white dwarfs are thought to be formed from progenitor stars with a typical mass of about 3.5 solar masses, and possibly up to eight solar masses. Stars with such masses should last 400 million years and 55 million years respectively, representing the minimum time since the first star formation for the first white dwarfs to appear. Thus, there shouldn’t be very many at the highest redshifts accessible to JWST. But if type Ia supernovae are found to be relatively as common (after compensating for time dilation) as in the nearby universe, then this would bolster the evidence that we do not see significant galaxy evolution as a function of redshift and would challenge big bang assumptions.

We further predict that we will not find galaxies full of the long sought after population III stars. Biblically, heavy elements like oxygen preceded the creation of the stars since water existed on Day 1 but stars were made on Day 4 (Genesis 1:1–2, 14–19). Therefore, we predict that the JWST will continue to find metallicity in the highest redshifted galaxies. Furthermore, we expect to find such galaxies at increasing redshifts, up to the limit of the detection threshold of the JWST. These will be mature galaxies, massive and well-structured (many of them spiral galaxies), with luminosities and morphologies comparable to nearby galaxies, and with typical angular diameters of around 0.2 arcseconds.

References

Atek, Hakim, Marko Shuntov, Lukas J. Furtak, Johan Richard, Jean-Paul Kneib, Guillaume Mahler, Adi Zitrin, H. J. McCracken, Stéphane Charlot, Jacopo Chevallard and Iryna Chemerynska. 2023. “Revealing Galaxy Candidates out to z~16 With JWST Observations of the Lensing Cluster SMACS0723.” Monthly Notices of the Royal Astronomical Society 519, no. 1 (February) 1201–1220.

Austin, Duncan, Nathan Adams, Christopher J. Conselice, Thomas Harvey, Katherine Ormerod, James Trussler, Qiong Li, Leonardo Ferreria, Pratika Dayal, and Igans Juodžbalis. 2023. “A Large Population of Faint 8 < z < 16 Galaxies Found in the First JWST NIRCam Observations of the NGDEEP Survey.” The Astrophysical Journal Letters 952, no. 1: L7.

Boylan-Kolchin, Michael, 2023. “Stress Testing ΛCDM With High-Redshift Galaxy Candidates.” Nature Astronomy, 7 (13 April): 731–735.

Choudhury, T. R., and T. Padmanabhan. 2005. “Cosmological Parameters From Supernova Observations: A Critical Comparison of Three Data Sets.” Astronomy and Astrophysics 429 (5 January): 807–818.

Costantin, Luca, Pablo G. Péréz-González, Yuchen Guo, Chiarra Buttitta, Shardha Jogee, Micaela B. Bagley, Guillermo Barro, et al. 2023. “A Milky Way-Like Barred Spiral Galaxy At a Redshift of 3.” Nature 623, no. 7987 (16 November): 499–501.

Dennis, Phillip W. 2022. “Mach’s Principle in General Relativity and Reduced Light Travel Times in Cavitated Cosmologies.” Answers Research Journal 15 (October 26): 339–357. https://answersresearchjournal.org/machs-principle-in-general-relativity-and-reduced-light-travel-times-in-cavitated-cosmologies/.

De Sitter, W., 1917. “On Einstein’s Theory of Gravitation and its Astronomical Consequences. Third Paper.” Monthly Notices of the Royal Astronomical Society 78, no. 1 (November): 3–28.

Ferreira, Leonardo, Nathan Adams, Christopher J. Conselice, Elizaveta Sazonova, Duncan Austin, Joseph Caruana, Fabricio Ferrari, et al. 2022. “Panic! At the Disks: First Rest-Frame Optical Observations of Galaxy Structure at z > 3 With JWST In the SMACS 0723 Field.” The Astrophysical Journal Letters 938, no. 1 (October 10): L2.

Goldhaber, G., D. E. Groom, A. Kim, G. Aldering, P. Astier, A. Conley, S. E. Deustua, et al. 2001. “Timescale Stretch Parameterization of Type Ia Supernova B-Band Light Curves.” The Astrophysical Journal 558, no. 1 (September 1): 359–368.

Gupta, Rajendra. 2023. “JWST Early Universe Observations and ΛCDM Cosmology.” Monthly Notices of the Royal Astronomical Society, 524, no. 3 (September): 3385–3395.

Harikane, Yuichi, Masami Ouchi, Masamune Oguri, Yoshiaki Ono, Kimihiko Nakajima, Yuki Isobe, Hiroya Umeda, Ken Mawatari, and Yechi Zhang. 2023. “A Comprehensive Study of Galaxies at z~9–16 Found in the Early JWST Data: Ultraviolet Luminosity Functions and Cosmic Star Formation History at the Pre-reionization Epoch.” The Astrophysical Journal Supplement Series 265, no. 1 (March): 5.

Hartnett, John C. 2015. “Speculation on Redshift in a Created Universe.” Answers Research Journal 8 (February 11) 77–85. https://answersresearchjournal.org/speculation-redshift-created-universe/.

Hogg, David W. 2000. “Distance Measures in Cosmology.” arXiv e-prints. https://arxiv.org/abs/astro-ph/9905116.

Ito, Kei, Francesco Valentino, Gabriel Brammer, Andreas L. Faisst, Steven Gillman, Carlos Gómez-Guijarro, Katriona M. L. Gould et al. 2023 “Size–Stellar Mass Relation and Morphology of Quiescent Galaxies at z ≥ 3 in Public JWST Fields.” arXiv:2307.06994v1.

Labbé, Ivo, Pieter van Dokkum, Erica Nelson, Rachel Bezanson, Katherine A. Suess, Joel Leja, Gabriel Brammer, Katherine Whitaker, Elijah Mathews, Mauro Stefanon and Bingjie Wang. 2023. “A Population of Red Candidate Massive Galaxies ~600 Myr After the Big Bang.” Nature 616, no. 7956 (13 April): 266–269.

Lee, Jeong Hwan, Changbom Park, Ho Seong Hwang, and Minseong Kwon. 2023. “Morphology of Galaxies In JWST Fields: Initial Distribution and Evolution of Galaxy Morphology.” arXiv:2312.04899v2.

Leibundgut, B., R. Schommer, M. Phillips, A. Riess, B. Schmidt, J. Spyromilio, J. Walsh, et al. 1996. “Time Dilation in the Light Curve of the Distant Type Ia Supernova SN 1995K.” The Astrophysical Journal 466, no. 1 (July 20): L21–L24.

Lisle, Jason. 2016. “New Method to Assess the Luminosity Function of Galaxies.” Answers Research Journal 9 (March 30): 67–80. https://answersresearchjournal.org/method-assess-luminosity-function-galaxies/.

Lisle, Jason, 2018. The Physics of Einstein: Black Holes, Time Travel, Distant Starlight, E = mc². Dallas, Texas: Biblical Science Institute.

Lisle, Jason. 2022. “The James Webb Space Telescope.” January 21. Biblical Science Institute. https://biblicalscienceinstitute.com/astronomy/the-james-webb-space-telescope/.

Lovyagin, Nikita, Alexander Raikov, Vladimir Yershov, and Yuri Lovyagin. 2022. “Cosmological Model Tests with JWST.” Galaxies 10, no. 6 (December): 108.

Lubin, Lori M. and Allan Sandage. 2001. “The Tolman Surface Brightness Test for the Reality of the Expansion. IV. A Measurement of the Tolman Signal and the Luminosity Evolution of Early-Type Galaxies.” The Astronomical Journal 122, no. 3 (September 1): 1084–1103.

Morishita, Takahiro, Massimo Stiavelli, Ranga-Ram Chary, Michele Trenti, Pietro Bergamini, Marco Chiaberge, Nicha Leethochawalit, Guido Roberts-Borsani, Xuenjian Shen, and Tommaso Treu. 2023. “Enhanced Sub-kpc Scale Star-formation: Results From A JWST Size Analysis of 341 Galaxies At 5 < z < 14.” arXiv:2308.05018v2.

Ono, Yoshiaki, Yuichi Harikane, Masami Ouchi, Hidenobu Yajima, Makito Abe, Yuki Isobe, Takatoshi Shibuya, John H. Wise, Yechi Zhang, and Kimihiko Nakajima. 2023. “Morphologies of Galaxies at z ≳ 9 Uncovered by JWST/NIRCam Imaging: Cosmic Size Evolution and an Identification of an Extremely Compact Bright Galaxy at z ~ 12.” The Astrophysical Journal 951, no. 1: 72.

Rhoads, James E., Isak G. B. Wold, Santosh Harish, Keunho J. Kim, John Pharo, Sangeeta Malhotra, Austen Gabrielpillai, Tianxing Jiang, and Huan Yang. 2023. “Finding Peas in the Early Universe with JWST.” The Astrophysical Journal Letters 942 , no. 1: L14.

Rybicki, George B., and Alan P. Lightman. 1979. Radiative Processes in Astrophysics. Hoboken, New Jersey: John Wiley and Sons.

Tacchella, Sandro, Benjamin D. Johnson, Brant E. Robertson, Stefano Carniani, Francesco D’Eugenio, Nimisha Kumari, Roberto Maiolino, et al. 2023. “JWST NIRCam + NIRSpec: Interstellar Medium and Stellar Populations of Young Galaxies With Rising Star Formation and Evolving Gas Reservoirs.” Monthly Notices of the Royal Astronomical Society 522, no. 4 (July): 6236–6249.

Tolman, Richard C. 1930. “On the Estimation of Distances in a Curved Universe with a Non-Static Line Element.” Proceedings of the National Academy of Sciences 16, no. 7 (July 15): 511–520.

Trujillo, Ignacio, Gregory Rudnick, Hans-Walter Rix, Ivo Labbé, Marijn Franx, Emanuele Daddi, Pieter G. van Dokkum, et al. 2004. “The Luminosity-Size and Mass-Size Relations of Galaxies Out to z ~ 3.” The Astrophysical Journal 604, no. 2: 521–533.

Wilson, O. C. 1939. “Possible Applications of Supernovae to the Study of the Nebular Red Shifts.” Astrophysical Journal 90, 634–636.

Yang, L., T. Morishita, N. Leethochawalit, M. Castellano, A. Calabrò, T. Treu, A. Bonchi, et al. 2022. “Early Results from GLASS-JWST. V: The First Rest-frame Optical Size–Luminosity Relation of Galaxies at z > 7.” The Astrophysical Journal Letters 938, no. 2: L17.

Zwicky, F. 1929. “On the Red Shift of Spectral Lines through Interstellar Space.” Proceedings of the National Academy of Sciences 15, no. 10 (October 15): 773–779.