The Philosophy of Science 3: The Transition to Modern Science

Introduction

In Faulkner (2022, hereafter Paper 1), I discussed the philosophy of science and how science is done. In a subsequent paper (Faulkner 2023, hereafter Paper 2), I gave a brief description of the history of science from the ancient Greeks through the Middle Ages. At several points in the discussion of Paper 2, I evaluated which type of science various people in this history employed. In this paper, I continue the discussion of Paper 2 (Faulkner 2023) with the transition from medieval science to modern science. A major scientific revolution occurred in the seventeenth century. As evidence of this, consider the fact that in 1600, most people in Europe believed the geocentric (Ptolemaic) model but that by 1700, nearly everyone in Europe was a heliocentrist.

The time of the transition from the Middle Ages to modern times is not distinct. Truly, things were rapidly changing by 1600, but how much earlier can one make the line of demarcation? Some people may make the time of transition to be the discovery of the New World a century earlier, in 1492. Historians generally call this transition to modern times the Renaissance, typically dating it 1400–1600. While the cultural and perhaps philosophical transition is difficult to delineate, most historians of astronomy (and science in general) consider the 1543 publication of Nicolaus Copernicus’ De Revolutionibus Orbium Coelestium (hereafter shortened to De Revolutionibus, as is the way the book is usually referred to) to be a watershed event in the transition to modern times. Interestingly, that same year Andreas Vesalius (1514–1564), the founder of human anatomy, published the influential De Humani Corporis Fabrica Libri Septem (On the Fabric of the Human Body in Seven Books). Consequently, one may say that regarding science, the Middle Ages ended in 1543.

Throughout the Middle Age, astronomers used the Ptolemaic model to predict the positions of the sun, moon, and five naked-eye planets. There were discrepancies between observations of planetary positions and the predictions of the Ptolemaic model. This mismatch was small at first, but it grew each century. The remedy was to modify the original Ptolemaic model, usually in the form of additional, small epicycles. Thus, by the late Middle Ages there were many variations of the Ptolemaic model. The strength of the Ptolemaic model was that it could be modified to account for any new problem that developed.

This process could be extended indefinitely, so why doesn’t anyone use a version of the Ptolemaic model to predict planetary positions today? Just as the ability to modify the Ptolemaic model to account for any new problem that developed was the model’s strength, it also was its weakness. A theory that explains anything and everything ultimately explains nothing. As pointed out in Paper 1 (Faulkner 2022), Karl Popper advanced the tenet that a scientific theory must be capable of being disproved. But if a theory can be freely modified to account for any difficulty that may arise, then that theory cannot be disproved. Thus, the Ptolemaic model ultimately failed Popper’s falsifiability test.

But there was a second problem with the Ptolemaic model. The original version was a bit complicated, but it worked. However, the additional tweaks required to fit the data made the Ptolemaic model unwieldy. Applying Occam’s razor, one might eliminate the Ptolemaic model from further consideration. The problem was that there was not yet a model to compete with the Ptolemaic model. Application of Occam’s razor requires at least two explanations of phenomena that can be compared, not a single explanation. Until a competing model was forthcoming, one could not apply Occam’s razor. Alternately, in Kuhn’s view, a paradigm shift was possible only when a competing model was presented. Nicolaus Copernicus (1473–1543) was spurred to provide this competing model.

Copernicus

There are several misconceptions about Copernicus. One misconception is that he was a priest. While Copernicus received an initial education that could have prepared him for the priesthood (most educated people of the time received the same education), there is no record that he was ever ordained as a priest or entered an order. Besides canon law, Copernicus studied medicine, and he was well versed in mathematics and astronomy. Copernicus also knew several languages. This latter trait, along with his high level of education, obvious intelligence, and family connections made Copernicus a valuable trusted public servant, and he ended up holding several high government posts.

Another misconception is that Copernicus originated the heliocentric model. As we saw in Paper 2 (Faulkner 2023), this is incorrect—Aristarchus had proposed the heliocentric model in the third century B.C. After Aristarchus, there were some other ancient Greeks who adopted the heliocentric model, though it is uncertain how widespread heliocentrism may have been. However, among the ancient Greeks, geocentrism became the dominant cosmology. As also pointed out in Paper 2 (Faulkner 2023), there were two reasons for this. One reason was the lack of observable trigonometric parallax. The heliocentric model required that parallax exist, while the geocentric model did not. In effect, the presence or absence of parallax amounted to a crucial test between the two models. The only response that heliocentrists had to the lack of parallax was to hypothesize that the stars were too distant compared to the size of the earth’s orbit to produce observable parallax. As it turns out, they were correct for the technology to measure parallax did not exist until the 1830s. The other reason the geocentric model was so widely believed in the ancient Greek world was the immense success of the Ptolemaic model to accurately predict planetary positions. If a geocentric model could do this, why look for an alternate model?

A third misconception is that Copernicus first unveiled his heliocentric ideas in De Revolutionibus in 1543. In 1514, Copernicus had circulated among friends and colleagues his Commentariolus (Little Commentary), a manuscript which outlined the basics of his heliocentric model. At the time, Copernicus’ model was very much a work in progress, and he needed additional time to refine it, which is why the Commentariolus was not published until after his death. Commentariolus turned out to be very popular, and discussion and dissemination of its content rapidly spread across Europe. Commentariolus may have been more influential in promoting heliocentrism than De Revolutionibus, which was published three decades later. Copernicus completed the text of De Revolutionibus about a decade prior to its publication but delayed its publication despite urging by many people across Europe to publish it.

A fourth misconception is that the Roman Catholic Church immediately opposed Copernicus’ heliocentric model. In 1533, Johann Albrecht Widmannstetter, secretary to Pope Clement VII, gave a series of lectures on the Copernican model in Rome. The pope and several Roman Catholic cardinals attended the lectures and were most impressed. In 1536, Cardinal Nikolaus von Schönberg wrote to Copernicus, urging him to publish his model.

Roman Catholics were not the only ones who were enthusiastic about Copernicus’ work and encouraged him to publish it. Martin Luther’s close ally, Phillip Melanchthon, arranged for the young Georg Joachim Rheticus to study with some astronomers. Rheticus ended up studying with Copernicus for two years, giving him the distinction of being Copernicus’ only student. Their differences in theology apparently were not a problem, as Rheticus gained Copernicus’ trust. In 1539, Rheticus wrote and published Narratio Prima (First Report), the first description of the Copernican model to appear in print. Apparently encouraged by the positive response to its publication, Copernicus entrusted Rheticus with editing and arranging for publication of his own manuscript. Without Rheticus’ assistance, it is likely that Copernicus’ De Revolutionibus would never have been published.

Copernicus dedicated De Revolutionibus to Pope Paul III, which apparently met with the pope’s approval. Rheticus was not able to oversee the actual publishing of the book, which he handed over to Lutheran theologian Andreas Osiander. With neither the knowledge nor the consent of either Copernicus or Rheticus, Osiander added a preface. In the preface, Osiander stated that

it is not necessary that these hypotheses should be true, or even probably; but it is enough if they provide a calculus which fits the observations. (Osiander 1995, 3)

Osiander did not sign the preface, so many readers at the time probably assumed this reflected the thinking of Copernicus. It was not until later that it was revealed who penned the preface. It’s not clear that this statement in the preface even reflected the thinking of Osiander. In writing the preface, Osiander may have attempted to blunt the criticism that he feared would result from the publication of De Revolutionibus. He needn’t have worried since reaction to publication of De Revolutionibus was largely positive, and it stimulated further discussion of heliocentrism. On the other hand, perhaps this softening in the preface prevented people who thought heliocentrism contradicted the Bible and the traditions of the church from condemning the work. At any rate, discussion of the heliocentric model remained civil for the next 75 years.

A fifth misconception about Copernicus is that his book merely promoted the heliocentric model and gave arguments for it. De Revolutionibus contained something far more important. Copernicus interpreted observations of the five naked eye planets in terms of the heliocentric model to determine the sizes and periods of their orbits. I have described elsewhere how Copernicus did this (Faulkner 2017, 174–177). Apparently, determining the orbital sizes and periods of the planets within the heliocentric model had not been done before. Copernicus expressed the orbital periods in terms of years and orbital sizes in terms of the earth’s orbital size, what we now call the astronomical unit (AU). Copernicus did not know the length of the AU, but that did not matter—many physics problems can be worked out in terms of scaled relationships of this type. This information was key in helping Johannes Kepler determine his three laws of planetary motion the following century.

A sixth misconception about Copernicus is that his model was a dramatic improvement over the Ptolemaic model. It wasn’t. Living during the transition from the Middle Ages to modern times, Copernicus was not prepared intellectually to abandon uniform circular motion to describe the motion of the planets. Consequently, the Copernican model required the use of epicycles. Heliocentrism removed the need of the major epicycle of each planet to explain its retrograde motion, but it still retained other, smaller epicycles to make the theory fit the observations. The task of refining the Copernican model to a very simple description that beautifully fit the observations of planetary motion would fall to Kepler.

How can we categorize the science of Copernicus? It is difficult to classify. Copernicus is best described as a theoretician, someone who develops and refines a model for others to test. Part of his work could be described as employing abductive reasoning. His derivation of orbital sizes and periods of planets is best described as use of deductive reasoning.

Galileo Galilei

Much has been written about Galileo’s contributions. Galileo (1564–1642) conducted physics experiments. For instance, Galileo discovered that the period of swing of a simple pendulum depends upon the length of the pendulum, not upon the mass of the pendulum or the amplitude of swing. Galileo also discovered that heavier objects do not fall at a faster rate than lighter objects. This squarely contradicted Aristotle’s teaching. It is remarkable that in nearly two millennia no one had tested Aristotle’s claim. Galileo also began to appreciate the role friction played in mechanics. He began to formulate ideas about motion that Newton, more than a half century later, would state very elegantly.

However, Galileo is more remembered for the discoveries he made through his telescope than for his physics experiments. Though Galileo did not invent the telescope, he apparently was among the first to put it to use in astronomy. Galileo saw craters on the moon and spots on the sun. Both these were viewed as imperfections on what were thought to be perfect bodies. This contradicted the Aristotelian worldview that had received official endorsement from the Roman Catholic Church through the influence of Thomas Aquinas, as outlined in Paper 2 (Faulkner 2023). Galileo saw Venus go through complete phases similar to lunar phases. With just a little reflection, it was clear that this could only happen if Venus orbited the sun. Within the Ptolemaic model, this was impossible, so Galileo had the first clear evidence that disproved the Ptolemaic model. Galileo had already read Copernicus’ work, as well as much of the discussion of the Copernican cosmology which had convinced him of heliocentrism, but this discovery about Venus seemingly sealed the deal.

Galileo’s observations of Jupiter provided more evidence for the heliocentric model. Galileo saw four small objects orbiting Jupiter. Galileo is generally credited with the discovery of the four large natural satellites, or moons, of Jupiter, so today we collectively call them the Galilean satellites. The orbital periods of the Galilean satellites range between 1.8 days for Io, the innermost one, to 16.7 days for Callisto, the outermost one. Galileo saw here an analog to the moon’s orbital motion around the earth. The Galilean satellites provided a refutation to the Aristotelian claim that if the earth moved, the moon would be left behind. Everyone, whether geocentric or heliocentric, agreed that Jupiter moved. But as Jupiter moved, its four Galilean satellites had no difficulty moving in step with Jupiter.

But Galileo also saw in Jupiter and its four satellites a microcosm of the solar system. Everyone agreed that the sun was much larger than the earth and any planets. To the heliocentrists, it made more sense that the smaller objects, including the earth, should orbit the sun rather than the other way around. Jupiter clearly was larger than the Galilean satellites, and those satellites orbited Jupiter in a manner similar to the planets orbiting the sun, with those satellites closer to Jupiter orbiting more quickly.

It is unfortunate that the Galileo affair
overshadows all the scientific work that Galileo performed. Since the Galileo affair has been extensively discussed in the creation literature (for example, Schirrmacher 2000), I see no reason to rehash that discussion in detail here, so I will only summarize some of the salient points. For further discussion, please see Lessl (1999).

Galileo wasted no time in announcing to the world his astronomical discoveries. Early in 1610, Galileo published Sidereus Nuncius (Starry Messenger) in which he described the Galilean satellites and mountains on the moons that ran counter to Aristotelian physics. He also discussed seeing through his telescope many stars too faint to be seen with the naked eye. Apparently, some of Galileo’s critics objected to additional stars beyond the 1,022 stars that Ptolemy had catalogued. In Sidereus Nuncius Galileo also made his belief in heliocentrism clear. Shortly after publication of Sidereus Nuncius, Galileo discovered the phases of Venus and spots on the sun, which he quickly shared with the world as well. As news of Galileo’s discoveries spread, opposition began to form almost immediately. Some critics claimed that the things Galileo had seen through the telescope were due to imperfections in his telescope’s optics. That counter claim was successful for a while, as telescopes were relatively rare at first. However, other astronomers soon constructed their own telescopes and confirmed Galileo’s observations.

For three years, Galileo managed to keep his arguments based upon the science. At a loss to counter the scientific arguments, Galileo’s critics increasingly shifted to biblical arguments, as the Roman Catholic Church, through the influence of Thomas Aquinas, had come to embrace geocentrism and interpret some biblical passages as teaching geocentrism. In 1613, philosophy professor Cosimo Boscaglia discussed Galileo’s work with Galileo’s patron, Cosimo II de’ Medici and Cosimo II de’ Medici’s mother, Christina of Lorraine. Boscaglia conceded that Galileo’s observations were accurate but insisted that heliocentrism was false because it contradicted Scripture. Benedetto Castelli, a former student of Galileo’s, a mathematician and abbot, was present at the conversation and defended Galileo. When Castelli wrote to Galileo reporting what happened, Galileo responded with a letter to Castelli in which he outlined the way biblical passages that supposedly taught geocentrism ought to be understood.1

This letter was widely circulated and provided fodder to Galileo’s critics. They interpreted the letter as violating the Council of Trent. A product of the Counter-Reformation, the Council of Trent declared many teachings of the Reformation as heretical. The Council of Trent also asserted for the Roman Catholic Church authority to interpret what the Bible says and means. In his letter to Castelli, Galileo appeared to be interpreting Scripture for himself in a manner that contradicted the pronouncements of the Roman Catholic Church, so this amounted to a serious matter. In 1615, one of Galileo’s critics forwarded a complaint and a copy of the Castelli letter to the Inquisition.

The very well-respected theologian Robert Bellarmine was enlisted to decide the matter. Bellarmine was already handling a similar case prompted by an attempt by Paolo Antonio Foscarini, a priest and scientist, to publish an open letter in which he, like Galileo, disputed the interpretation of biblical passages teaching geocentrism. In his decision, Bellarmine admonished both Galileo and Foscarini to treat heliocentrism as theoretical but not factual. Apparently, the false dichotomy between theory and fact as briefly described in Paper 1 (Faulkner 2022) is not new. Bellarmine made it very clear that it was permissible to discuss heliocentrism with this restriction. Bellarmine also made it clear that the situation would change if heliocentrism could be demonstrated with scientific standards then in practice. This frustrated Galileo because he thought that criterion had already been met.

In addition, in January 1616, Monsignor Francesco Ingoli wrote Galileo a letter in which he provided 22 points of rebuttal to heliocentrism. Only four of those points were biblical or theological; the remaining 18 were physical or scientific rebuttals. That is very revealing. Most of Galileo’s critics were motivated more by concern of the undermining of the Aristotelian and Ptolemaic science then widely accepted than by biblical or theological problems. Yet, the myth persists today that the Galileo affair was entirely a religious matter. Galileo did not immediately respond to Ingoli.

The next month, the Inquisition handed down its decision based upon Bellarmine’s judgement, but also influenced by the Ingoli letter. That decision was that heliocentrism was heretical, but no one who had been advocating heliocentrism was punished. That is an important point because at the time the Roman Catholic Church was dealing with heretics very harshly, up to and including execution. Apparently, heliocentrism was not considered nearly as serious as other forms of heresy. The Foscarini letter, as well as the original text of De Revolutionibus, were banned. However, within two years Ingoli had edited De Revolutionibus into an acceptable form, and the edited version was not banned. It is important to emphasize that Galileo and others were not forbidden to teach heliocentrism, but only that they were not permitted to teach heliocentrism as fact. Furthermore, Galileo remained on good terms with both Bellarmine and Pope Paul V, with the latter assuring Galileo that he was safe from prosecution while Pope Paul V remained in office. Pope Paul V died five years later, in 1621. His successor, Pope Gregory XV, was in office for only two years. In 1623, Pope Urban VIII ascended the papacy, and he remained pope the rest of Galileo’s life. Pope Urban VIII was favorably inclined toward Galileo.

For 15 years after the first trial in 1616, Galileo was not silent, but he was more circumspect in his discussions of heliocentrism and challenges to Aristotelian physics. Even his 1624 response to Ingoli did not arouse opposition as his earlier work had. Perhaps Galileo saw that his critics were fighting a losing battle. The Ptolemaic model was rapidly falling out of favor. However, those abandoning the Ptolemaic model did not necessarily embrace heliocentrism right away. Many chose to believe the Tychonic model, though within a few decades support for even the Tychonic model would largely disappear (I shall describe the Tychonic model shortly).

It was in this changing world that Galileo sought to reenter the fray with publication of his Dialogo Sopra i Due Massimi Sistemi del Mondo (Dialogue Concerning the Two Chief World Systems) in 1632. The Dialogue, as this book is usually called, was very different from such works published at the time. Intended as a popular-level book, Galileo chose to write it in Italian rather than Latin to reach a larger audience. Publication required papal approval, which Galileo readily received. The only stipulation the pope gave him was to include the pope’s personal and official position of geocentrism, to which Galileo readily agreed.

As the title suggests, the Dialogue was a conversation about geocentrism and heliocentrism. The three participants were a Copernican scientist named Salviati, an Aristotelian named Simplicio, and a supposedly neutral scholar named Sagredo. Right away even the casual reader may surmise that the name Simplicio could roughly translate as “simpleton.” The arguments Simplicio put forth were poor, and he ended up looking very foolish. Meanwhile, Salvati was able to easily refute Simplicio’s arguments, with Sagredo joining in. The Dialogue turned out to be very popular with Galileo’s intended audience. Since Galileo had put the pope’s words into the foolish looking Simplicio, the pope was understandably furious, and within months of publication of the Dialogue, the pope banned it. All support that Galileo had in Rome immediately collapsed.

Since Galileo had clearly violated the judgement of the 1616 trial, a second trial for Galileo was ordered in early 1633. The facts were indisputable. Since the earlier trial had concluded teaching heliocentrism was heretical (contrary to the teachings of the Roman Catholic Church), Galileo was found guilty of being “vehemently suspect of heresy” as well as disregarding the earlier judgement. The punishment was imprisonment, which was quickly changed to a form of house arrest, a condition under which Galileo lived the last nine years of his life. Why the relatively light sentence when heretics, such as Giordano Bruno,2 were being executed? As I stated before, the Roman Catholic Church did not place heliocentrism in the same class of heresies that Bruno and others were accused of, as evidenced by the fact that the Roman Catholic Church had encouraged open discussion of heliocentrism, something that it never would have allowed of more serious heresies.

The outcome of the Galileo affair has been badly mischaracterized, which has led to a great misunderstanding by most people. For instance, contrary to popular misconception, Galileo was never in any real danger of execution, since he was found to be “vehemently suspect of heresy” but not heresy outright. At the time of the Galileo affair, the Roman Catholic Church was still executing heretics, but not all heresies carried the same penalties. The Roman Catholic Church did not punish Galileo for simply believing the heliocentric model. The Copernican model had been in wide circulation for 75 years with little controversy, so why did it explode around Galileo? The answer to that question has everything to do with Galileo. Galileo was abrasive and abusive of those he disagreed with. If Galileo had behaved himself, there wouldn’t have been a second trial, and there may not have been a first trial either. The resulting condemnation of heliocentrism was a foregone conclusion, a conclusion that Galileo could have avoided. The irony is that within a few years it didn’t matter. Though the Vatican did not officially reverse its condemnation of Galileo until centuries later, within a few years nearly everyone in the West had adopted heliocentrism, and the Roman Catholic Church didn’t object to heliocentrism any longer. That is, just a few decades after the second trial, the Vatican came to tacitly accept heliocentrism.

The dispute about cosmology had almost nothing to do with theology. Rather, the dispute was between two competing scientific models. Theologians initially were not disturbed by Galileo’s claims. Rather, it was Galileo’s fellow scientists who were upholding Aristotelian and Ptolemaic science who objected. It was only after the loud complaints of scientists that the weight of the Roman Catholic Church entered the discussion in the form of the two trials.

Johannes Kepler

As important as Galileo’s work was, Johannes Kepler (1571–1630) played a more significant role in developing the emerging heliocentric model. A contemporary of Galileo, Kepler too had read Copernicus and had become convinced of the heliocentric model. In 1596, Kepler published Mysterium Cosmographicum (The Cosmographic Mystery), probably the first published defense of the Copernican model since Coperinicus’ original work. But it contained far more. There are five perfect, or Platonic solids. There also were five known planets at the time. Kepler thought this was not coincidental, and he proceeded to develop a model connecting these. Not only did Kepler think he had discovered God’s geometrical plan for the universe, but he also saw a sort of theology play out in this cosmology. Being the center of the universe, the sun had a theological correspondence to God the Father. The celestial sphere corresponded to God the Son, and the medium between the two corresponded to God the Holy Spirit. Kepler’s original manuscript included discussion of biblical passages that had been interpreted in terms of geocentrism that he interpreted heliocentrically, but that portion was removed prior to publication. Published 15 years before Galileo first drew attention to heliocentrism and 35 years prior to publication of Galileo’s book that caused such a stir, why did Kepler’s Mysterium Cosmographicum not provoke controversy? Probably because Kepler’s book was not widely read. It also may be that Kepler’s personality was not nearly as prickly as Galileo’s.

Upon completion of this first book, Kepler soon took employment with Tycho Brahe (1546–1601). Over the two previous decades, Tycho had made precise measurements of the positions of the five naked eye planets [with the best instruments of the day]. Tycho wanted to interpret these observations in term of his model. In the Tychonic model, the five naked eye planets orbit the sun, and the sun in turn orbits the earth each year, dragging the five planets along with it. The Tychonic model amounts to the heliocentric model but with a coordinate transformation from the sun to the earth. Therefore, this is a geocentric model, but one that disposes of the need for the main epicycles to explain retrograde motion of the five naked eye planets. Tycho apparently recognized the problems with the Ptolemaic model, but he could not bring himself to totally break from geocentrism, the primary reason being that, as mentioned, there was no observed parallax, which was first observed by Friedrich Bessel in 1838. The Tychonic model could be termed as a geoheliocentric system, a compromise between heliocentrism and geocentrism. Once Galileo’s telescopic observations eliminated the Ptolemaic model, the Tychonic model offered a refuge for those who wished to hold onto a geocentric model. Consequently, the Tychonic model briefly had some adherents in the first half of the seventeenth century, but support for the Tychonic model soon waned.3 Apparently, Aristotle’s objection that the other planets would be left behind if the sun moved around the earth did not apply to the Ptolemaic model.

Why did Tycho hire Kepler to do this task for him? Tycho realized that he needed help from someone who had the skill in mathematics to fit his observations to his model. Kepler probably was the best mathematician in Europe, and he was available. The problem was that Kepler was committed to a heliocentric model, so his heart was not exactly in the job Tycho had hired him to do. The two men differed on this and many other things, so their brief relationship was strained. However, Tycho’s death shortly after the arrival of Kepler probably freed Kepler to pursue what he really believed.

Like everyone else at the time, Kepler began with Aristotelian assumptions, such as uniform circular motion. This led Kepler up several blind alleys, wasting considerable time. The fact that Kepler eventually tried a different shape from a circle was a consequence of his perseverance and being the best mathematician in Europe at the time. Most problematic was the orbit of Mars. When Kepler attempted to fit Mars’ orbit to an ellipse, he was astonished to find how well it worked. The other planets followed suit. Thus, Kepler stumbled upon is first law of planetary motion:

The planets have elliptical orbits, with the sun at one focus.

While this was a departure from circular motion, it was not as radical as it might appear because the Ptolemaic model had already abandoned strict circular motion. Ptolemy had bent to the reality of elliptical orbits by having the earth displaced slightly from center of the deferent of each planet. An off-center circle is a good approximation to an elliptical orbit with the sun at one focus. Of course, as with any approximation, the match is not perfect, and this approximation accounted for some of the errors between observations and predictions of planetary positions that accumulated over the years.

What about uniform motion, even if on an ellipse rather than a circle? Again, it had been known since ancient times that the planets did not exhibit strict uniform motion. Ptolemy handled this by having the epicycle of each planet move uniformly with respect to its equant, not the earth nor the center of its deferent. As with an off-center circle being a good approximation of elliptical motion, this uniform motion with respect to the equant was a good approximation to the true (non-uniform) motion of each planet. What was the true motion of the planets? After attempting different schemes, Kepler finally found a description of planetary motion that perfectly matched the observations, expressed as his second law of planetary motion:

The radius vector of a planet sweeps out equal areas in equal intervals of time.

The radius vector is the line between a planet and the sun. Over a specified interval of time, the radius vector will sweep out an area defined by lines on two sides and a third side that is part of the ellipse. See fig. 1. Perihelion, point P, is the position of closest approach to the sun. Aphelion, the position of greatest distance from the sun, is at point A. Line SP is the radius vector at perihelion. After some time, the planet will move from perihelion to a new position at point 1, defining the radius vector then as line S1. The area swept out is indicated as “Area 1.” Now consider starting at aphelion, with the radius vector there being line SA. After the same interval of time as before, the planet will move to point 2, with the new radius vector being the line S2. The area swept out is indicated as “Area 2.” Note that if the curved section of the orbit between points A and 2 were the same length as the curved section between points P and 1, then the areas swept out would not be the same. The only way the two areas can be the same is if the planet moves more slowly near aphelion than at perihelion.

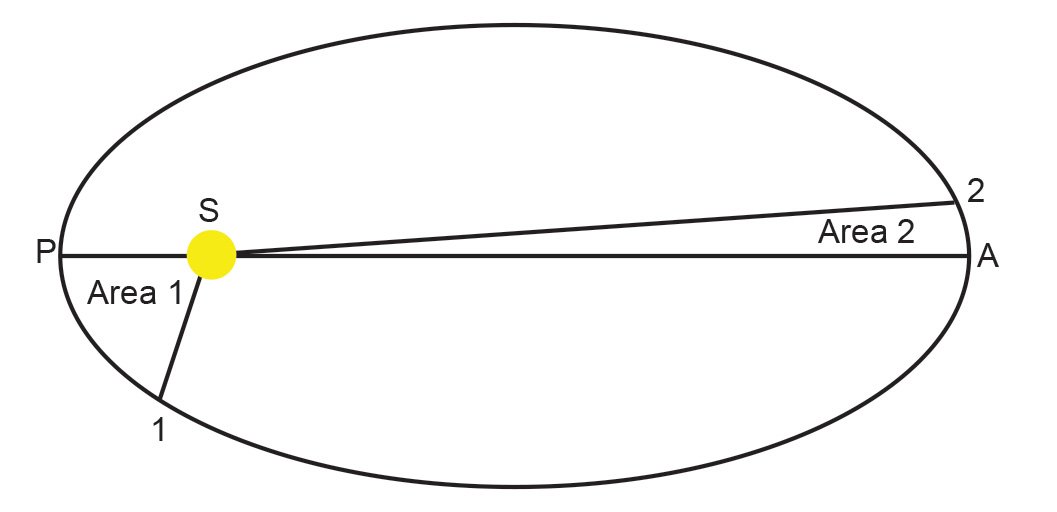
Fig. 1. Illustration of Kepler’s second law of planetary motion. The sun, S, is at one of the two foci of the ellipse. Perihelion, the part of the orbit closest to the sun, is at point P. Point A is aphelion, the part of the orbit farthest from the sun. The planet takes the same time to travel from P to point 1 as it does to travel from A to point 2. Area 1, the area swept out by the radius vector in the first instance, is the same as area 2, the area swept out by the radius vector in the second instance.

Kepler published his first two laws of planetary motion in Astronomia Nova (New Astronomy) in 1609, though the manuscript was finished a few years earlier. Kepler sent a copy to Galileo. The introduction to Astronomia Nova contains arguments for the compatibility of heliocentrism and Scripture, a theme that Galileo would use later in his letter to the Grand Duchess Christina. This work focused on the orbit of Mars, the most difficult planet for Kepler to describe. However, Kepler’s first two laws described the motions of the other four naked eye planets as well. How well did Kepler’s laws describe planetary motion? Better than any other model then available, which for the most part were variations of the Ptolemaic model. Why was Kepler’s model more accurate in its description? Kepler’s laws are an exact and correct description of the motions of the planets. The Ptolemaic model descriptions were approximations to the correct description. This ability of Kepler’s model to correctly describe the world ought to have been the final nail in the coffin of geocentrism. However, there continued to be resistance for a few decades. For instance, some other scientists adopted portions of Kepler’s new cosmology, but rejected other parts, such as adopting elliptical orbits for the planets in a geocentric model.

It took Kepler a bit longer to develop his third law of planetary motion, sometimes called the harmonic law:

The cubes of the semimajor axes of the orbits of the planets are directly proportional to the squares of their orbital periods.

For ease of computation, it is best to express the semimajor axes of the orbits in AUs and the orbital periods in sidereal years. That way, the constant of proportionality is one. Kepler published all three laws of planetary motion for the first time in Epitome Astronomiae Copernicanae (Epitome of Copernican Astronomy) in three volumes between 1618 and 1621. In this work, Kepler explicitly showed how his laws applied to the planets other than Mars for the first time, and he also demonstrated that the motions of the four Galilean satellites discovered a decade earlier also conformed to his three laws. Since Epitome was published shortly after Galileo’s first trial, the Vatican placed this book on its banned list almost immediately. This was not so much in response to Kepler as it was carrying out the edict from Galileo’s first trial.

Kepler did not know why the planets moved in the way described by his three laws. He knew some influence of the sun was responsible for this, and he cast about for a deeper understanding. Kepler proposed that there was some sort of attractive force that the sun exerted, using magnetism as an analogy. A half century later, Newton developed his law of universal gravity. Using Newton’s three laws of motion and his law of gravity, it is a straightforward matter to derive Kepler’s three laws of planetary motion, as often is done in university-level general physics courses. The difference is that Kepler derived his three laws empirically, while Newton derived them from first principles. In this sense, Newton’s laws of motion and gravity are more fundamental, with Kepler’s three laws of planetary motion being consequences of the more fundamental laws. This concordance between an empirical and more theoretical approach is powerful evidence that the science is well established.

How can we best categorize Kepler’s science? Kepler’s approach is clearly abductive, deriving from data the best, most probable explanation of the motion of the planets.

Francis Bacon

Before moving on to the development of physics by Isaac Newton later in the seventeenth century, it is best to discuss the philosophy of science as it existed in the early seventeenth century. A contemporary of Galileo and Kepler, Francis Bacon (1561–1626) published Novum Organum (New Instrument) in 1620. Why did Bacon choose this title? Bacon wrote Novum Organum in response to Organon (Greek for Instrument), the collection of Aristotle’s six works on logic. Aristotelians of Bacon’s time were using deductive reasoning to study the world. To counter this, Bacon argued for a more empirical approach to study of the world. The Aristotelian approach gave rise to the myth that no one did science during the Middle Ages but rather people then reasoned their way to conclusions about the world. While this may have been largely the case, it was not universally true, which is why this is a myth. For instance, as I pointed out in Paper 2 (Faulkner 2023), Roger Bacon had argued an empirical approach three centuries before Francis Bacon. The earlier Bacon was not alone, but he was in a minority in his lifetime. Novum Organum ended up being very influential in the seventeenth century. Why did Francis Bacon succeed in changing attitudes so readily where Roger Bacon was not so successful? It probably was a matter of timing. Science as we know it was starting to blossom. The publication of Novum Organum certainly encouraged the blooming of science, but it also reflected the changing attitude toward the study of the natural world in Europe at the time.

For the next two centuries, scientists busied themselves with doing science rather than spending much time debating what science is and how to do it. Apparently, most scientists of the seventeenth and eighteenth centuries thought that they intuitively knew how to do science, so why spend time writing about how science is conducted? That began to change in the 1830s, as some prominent scientists began to address the philosophy of science more. It was in this period that the term “scientific method” was coined. This scientific method as taught in schools today is often called “Baconian,” reflecting what Bacon laid out in Novum Organum. Except that Bacon did not discuss “the scientific method” that is so often taught
in schools today. Bacon also is credited with introducing inductive reasoning, though that isn’t exactly spelled out in Novum Organum either. Rather, Bacon advocated a more inductive approach to the study of the natural world, in contrast to the deductive approach of the scholastic school of thought at the time. Science is largely inductive and abductive, though that does not mean that scientists do not employ deductive reasoning as well. In Novum Organum, Bacon repeatedly emphasized drawing inferences about the natural world. This is very similar to how science is actually done, not the cookbook approach that many elementary treatments of science teach as described in Paper 1 (Faulkner 2022). Natural science is about drawing reasonable inferences about how the world operates. This is why some historians date the beginning of the modern scientific revolution to the publication of Novum Organum.

Before moving on, I ought to mention that Francis Bacon advocated the dual revelation theory, that God has revealed Himself through two books, the Bible, and the book of nature. The former is special revelation, and the latter is general revelation. The dual revelation theory remains popular among many Christians today. The reasoning is that since God has also revealed Himself through nature (Romans 1:19–20), then these two revelations must agree. This approach is acceptable as far as it goes, but a problem arises when one perceives that general and special revelation disagree. How does one resolve this dilemma? One must recognize that at least one of our understandings of these two revelations must be in error (it is possible that both are wrong too). This calls for reexamination of our interpretation of at least one of our understandings. Unfortunately, today many of those who emphatically believe the dual revelation theory usually end up reinterpreting Scripture to match what they think most scientists have proven about origins and history. This is a dangerous biblical hermeneutic.

The problem is that there is widespread confusion about general revelation, even among outstanding theologians. All the verses that theologians point to about general revelation (for example, Romans 1; Romans 2, Psalm 19; Job 12; Acts 14; Acts 17) teach that general revelation reveals God Himself. Romans 1:19–20 indicates creation does so infallibly so that all people in all times and all places are without excuse for not seeing the evidence of the Creator. However, no verse of the Bible teaches or even hints that the creation reveals how and when God created. Both creation and Scripture agree: God exists, and He has certain attributes, including power, wisdom, righteousness, and eternality. But compromised old-earthers and theistic evolutionists are constantly treating the majority (consensus) view on origins as if it is general revelation. That is completely erroneous thinking.

Isaac Newton

If Novum Organum was the beginning of the modern scientific revolution, then publication of Isaac Newton’s Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) in 1687 amounts to a declaration of victory of that revolution. In the Principia, as this work is normally referred to, Newton (1642–1727) developed mechanics, the area of physics which a class in general physics covers first. The Principia includes calculus, the mathematical framework necessary for doing physics. Foundational to mechanics is Newton’s three laws of motion. The first law of motion states.

An object at rest remains at rest and an object in motion remains in straight-line motion, unless acted upon by an outside force.

The first part of this statement agrees with Aristotle’s opinion about rest—objects at rest will remain at rest unless net forces act upon them. As discussed in Paper 2 (Faulkner 2023), Aristotle thought that rest was the natural state of all objects on earth. To Aristotle, motion was not the natural state, for he observed that unless a force continually acts on a body in motion, the body will come to rest. However, Newton thought that uniform, linear motion was just as natural as rest. What had confused Aristotle was that he failed to realize that friction is a force. A few decades before Newton, Galileo had conducted experiments that suggested if friction could be eliminated, moving objects would continue linear motion indefinitely. Today we take this for granted, but this understanding of friction as a force is of relatively recent origin. This realization removed an impediment to progress in mechanics.

As soon as one recognizes that rest and rectilinear motion are equally natural in the absence of any applied force, this raises the question of what happens when a force acts on a body. In his second law of motion, Newton succinctly described what happens when forces act on bodies:

When a force is applied to a body, the body is accelerated in direct proportion to the force and inversely proportionally to the inertia of the object.

Often this is reduced to equation form, F = ma, where F is the force, a is the acceleration, and m is the inertia, or mass, of the object. The use of boldface indicates that force and acceleration are vectors. Once one adopts units for mass and acceleration, this equation permits a definition of the unit of force. In most problems, several forces may act on a body simultaneously, so the vector sum of all forces is to be applied in the above equation. This equation is a very robust description of how forces act in the world.

Newton’s third law of motion is often misunderstood. The third law of motion states:

For every action there is an equal and opposite reaction.

Most people think of the third law only in terms of dynamic situations, such as recoil from the firing of a gun. However, the third law has many more applications. For instance, when an object rests on a surface, the surface provides an upward force on the body. We often call this a normal force because it is perpendicular, or normal, to a flat, horizontal surface. At the same time, as the surface applies a normal force to the object, the object pushes back on the surface with an equal and opposite force. Since the normal force is upward, the force of the object on the surface is downward. Thus, forces always appear in pairs. These pairs of opposing forces are so common that they often escape our notice.

How did Newton arrive at his three laws of motion? He used good, Baconian empirical science. The three laws of motion are descriptions of how the world works based on careful observations.

The most significant part of the foundation of mechanics is Newton’s law of universal gravity, which states:

Every body in the universe attracts every other body in the universe with a force that is directly proportional to the masses of the two bodies and inversely proportional to the square of the distances between them.

Newton’s law of gravity can be expressed in equation form as

Where m₁ and m₂ are the masses of the two bodies, and r is the distance between the centers of mass of the two bodies. G is a constant of proportionality whose value depends upon the units used to measure the masses and distance.

How did Newton discern that gravity had this functional dependence? First, consider measuring the force of gravity (weight) of objects near the earth’s surface. Let the mass of such a body be m₁. It is a simple matter of experiment to vary the amount of mass and measure the corresponding weight to demonstrate that the force of gravity is directly proportional to m₁. According to Newton’s third law of motion, as the earth pulls down on the mass m₁, m₁ must also pull up on the earth. Since the force of attraction between the two is proportional to the mass of one of the objects, then the force must also be proportional to the mass of the other object, m₂ (in this case, the earth).

What about the inverse square relationship of distance? This came from Newton’s great insight about gravity and physics in general. People had known for thousands of years that the moon moved around the earth each month. Even geocentrists and heliocentrists agreed on this. However, few people had considered why the moon moved this way. Aristotelian thinking asserted that the moon was made of quintessence, which was fundamentally different from the matter of earth and hence followed different rules. Newton rejected this, believing that the moon and other celestial bodies were made of the same sort of matter the earth was made of and hence followed the same sort of rules. According to Newton’s first and second laws of motion, the moon’s motion around the earth each month required a centripetal (center-seeking) force. Since objects on the earth also fell toward the earth’s center, Newton formed the bold hypothesis that the same force that caused objects to fall to the ground on earth was the same force that compelled the moon to fall toward the earth, causing it to orbit the earth each month. Hence, any description of how gravity operates must be capable of describing either situation.

It made sense that the effect of gravity ought to decrease with increasing distance, but what functional relationship did it follow? Was it a simple inverse relationship? Or was it inverse squared? How about inverse cubed? Was it some other power of the distance? Or perhaps it followed some other, more complicated relationship that decreased with increasing distance. Newton developed a simple test to determine this.

Newton showed that when objects interact, the forces involved act through the centers of mass of the objects (this often is demonstrated in general physics classes). Presumably, the earth’s center of mass lies very close to its physical center. We saw in Paper 2 (Faulkner 2023) how in ancient times the distance to the moon was found to be about 60 earth radii. Therefore, the moon’s distance from the earth’s center is about 60 times the distance of objects on the earth’s surface from the earth’s center. By Newton’s time, scientists had measured the acceleration of gravity on the earth’s surface. From his development of mechanics thus far, Newton knew that a centripetal acceleration, a_c, had the form

where v is the velocity and r is the radius of orbit. If T is the time required to complete one orbit, then the average speed of the orbit is

Substituting the second equation into the first results in

Since the orbital distance and period of the moon were already known, Newton easily calculated the centripetal acceleration required to keep the moon in orbit around the earth. He found that the acceleration of gravity on the earth’s surface is 3,600 times the acceleration required to keep the moon in orbit around the earth. The relationship between 60 and 3,600 is squared. Hence, Newton concluded that gravity follows an inverse squared relationship of the distance.

But Newton was not finished. As stated previously, it was a straightforward matter for Newton to derive Kepler’s three laws of planetary motion. Not only did Newton’s law of gravity describe how objects fall on the earth and how the moon orbits the earth each month, but it also described the motion of the planets. Furthermore, since Kepler had already shown the Galilean satellites obeyed his three laws of planetary motion, Newton’s law of gravity also described the motion of Jupiter’s natural satellites. By the time of the publication of the Principia, five natural satellites of Saturn were known. They followed Kepler’s three laws of planetary motion, and hence their motion was described by Newton’s law of gravity. In 1705, Edmund Halley analyzed observations of comets and showed that they too followed Newton’s law of gravity. All this amounts to powerful evidence that Newton’s law of gravity is a correct description of how gravity works.

What kind of science did Newton employ? It clearly was abductive reasoning, observing the world and developing the most likely explanation/description of how the world works. Newton’s work on mechanics did not conform to the cookbook approach to science so often taught in schools that I discussed in Paper 1 (Faulkner 2022). In fact, none of the individuals who led the scientific revolution in the seventeenth century practiced that sort of science. Instead, their work followed the empirical approach to the world that Bacon advocated.

Conclusion

The key issue in the transition of science from the Middle Ages to modern times was the earth’s place in the universe. Was the earth literally at the center of creation, or was the earth one of several planets that orbited a much larger sun? Despite common misconception, the Bible does not teach geocentrism (Faulkner 2001; 2020b), though people have chosen to interpret certain biblical passages that way. That certainly was the position of the Roman Catholic Church once Thomas Aquinas had wedded Aristotelian and Ptolemaic science to Catholic theology. This set up the debacle of the Galileo affair, something that the Roman Catholic Church is still recovering from, and Christians in general are saddled with. I shall have more to say about this in the next paper in this series.

Nor were the early reformers immune to resisting the Copernican model when it came along (Faulkner 2020a). Though he did not mention Copernicus by name, Johannes Mathesius quoted Luther as condemning the heliocentric model prior to publication of De Revolutionibus (Luther 1967). Luther, Melanchthon, Calvin, and other sixteenth century reformers were steeped in Aristotelian and Ptolemaic cosmology as much as nearly everyone else in Europe at the time. Like authorities of the Roman Catholic Church in the next century, the primary arguments the early reformers offered against the Copernican model were scientific, not biblical. And there were Protestants among early heliocentrists. Both Kepler and Rheticus were Protestants. Interestingly, by the time of Galileo’s two trials, Protestant leaders were largely silent on the question of cosmology. Apparently, Protestant leaders acquiesced to heliocentrism long before the Roman Catholic Church did.

As I discussed in Paper 1 (Faulkner 2022), the Protestant worldview tore down the barrier between the heavens above and the world below that was an ancient pagan Greek concept endorsed by the Roman Catholic Church. This had a profound effect on changing the way science would be done. It is no accident that the scientific revolution began to accelerate rapidly in Protestant Europe in the seventeenth century. Many Protestant pastors studied science and pursued scientific investigations as part of their duty to God, a practice that continued through the eighteenth century. That is, science as we know it is a product of Protestant Europe.

Unfortunately, the strong Protestant, biblical influence on science began to wane in the eighteenth century, leading many Christians to retreat from the scientific arena by the end to the nineteenth century. This has led to a secularization of science that persists and continues to grow today. In the next paper, I will trace the history of this, along with the direction that science is taking today.

In this series of papers, I have concentrated on the development of astronomy and to a lesser extent physics. This is partly due to my interests and fields of expertise, but it also a consequence of how much more developed astronomy was as a science in ancient and medieval times. Concurrent with the rise of science out of questions related to astronomy and physics in the seventeenth century, the science of biology as we know it began to develop. Chemistry and geology as we know them developed a bit later. In my next paper I will concentrate more on physics, while recognizing the growth of these other sciences. This is because modern physics that appeared a century ago probably changed the philosophy of science more than any other science.

References

Bacon, Francis. 1620. Novum Organum. London, United Kingdom: John Bill.

Bergman, Jerry. 2014. “Giordano Bruno: The First Martyr of Science or the Last of the Magicians?” Creation Research Society Quarterly 50, no. 4 (Spring): 227–236.

Copernicus, Nicolaus. (1543) 1995. De Revolutionibus Orbium Coelestium. Translated by Charles Glenn Wallis. Amherst, New York: Prometheus Books.

Copernicus, Nicolaus. (1543) 2014. Commentariolus. Scotts Valley, California: Createspace Independent Publishing Platform.

Faulkner, Danny R. 2001. “Geocentrism and Creation.” TJ 15, no. 2 (August): 110–121.

Faulkner, Danny R. 2017. Falling Flat: A Refutation of Flat Earth Claims. Green Forest, Arkansas: Master Books.

Faulkner, Danny R. 2020a. “The Copernican System and the Bible.” February 19. https://answersingenesis.org/science/copernican-system-and-bible/.

Faulkner, Danny R. 2020b. “The Rise of the Modern Geocentric Theory Movement.” September 4. https://answersingenesis.org/astronomy/rise-of-modern-geocentric-theory-movement/.

Faulkner, Danny R. 2022. “The Philosophy of Science. 1: What is Science, and How is Science Done?” Answers Research Journal 15 (November 2): 359–376. https://answersresearchjournal.org/science/philosophy-science/.

Faulkner, Danny R. 2023. “The Philosophy of Science. 2: A Brief History of Science from the Ancient Greeks Through the Middle Ages.” Answers Research Journal 16 (March 29): 155–173. https://answersresearchjournal.org/science/philosophy-science-2/.

Galilei, Galileo. 1610. Sidereus Nuncius. Venice, Italy: Thomas Baglioni.

Galilei, Galileo. 1632. Dialogo Sopra i Due Massimi Sistemi del Mondo. Florence, Italy: Gian Battista Landini.

Kepler, Johannes. 1596. Mysterium Cosmographicum. Tübingen, Germany: Johannes Kepler.

Kepler, Johannes. 1609. Astronomia Nova. Heidelberg, Germany: E. Vögelin.

Kepler, Johannes. 1618. Epitome Astronomiae Copernicanae. Frankfurt, Germany: Gottfried Tambach.

Lessl, Thomas M. 1999. “The Galileo Legend as Scientific Folklore.” Quarterly Journal of Speech 85, no. 2 (5 June): 146–168.

Luther, Martin. 1967. In Luther’s Works, Volume 54 (Table Talk). Translated by Theodore G. Tappert. Edited by Helmut T. Lehmann, 358–359. Philadelphia, Pennsylvania: Fortress Press. Newton, Isaac. 1687. Philosophiæ Naturalis Principia Mathematica. London, United Kingdom: Joseph Streater for the Royal Society.

Osiander, Andrew. (1543) 1995. “Introduction.” In De Revolutionibus Orbium Coelestium by Nicolaus Copernicus. Translated by Charles Glenn Wallis. Amherst, New York: Prometheus Books.

Rheticus, Georg Joachim. 1540. De Libris Revolutionum Copernici Narratio Prima. Danzig, Poland: Franz Rhode.

Schirrmacher, Thomas. 2000. “The Galileo Affair: History or Heroic Hagiography?” Creation Ex Nihilo Technical Journal 14, no. 1 (April), 91–100.

Vesalius, Andreas. 1543. De Humani Corporis Fabrica Libri Septem. Basel, Switzerland: Joannes Oporinus.