Sizes of Galaxies in JWST Data and Cosmology—Reply to Barnes

Keywords: cosmology, JWST, FLRW metric, expanding universe, Tolman test, Doppler model

Introduction

Recent data from the James Webb Space Telescope (JWST) have challenged the standard secular model of origins (the big bang and/or current models of galaxy evolution). First, the JWST detected far more galaxies at higher redshifts than the standard model predicted (Finkelstein et al. 2023; Young 2023). Second, these galaxies are far more massive and well-structured than the standard model predicted (Labbé et al. 2023; Sabti, Muñoz, and Kamionkowski 2024; Stark et al. 2025; Xiao et al. 2024). Such massive, well-structured galaxies were not anticipated at such great redshifts because (in the standard model) such distances correspond to a time very shortly after the big bang. This leaves little time for such massive structures to form. However, these observations are consistent with creation-based predictions which do not require secular formation scenarios (Lisle 2022).

To accommodate these latest observations, most advocates of the big bang have proposed that galaxy formation must have happened at an earlier time. Obviously, if the big bang model is correct, then galaxies must have grown much faster in the early universe than the previous simulations had predicted in order to match the JWST observations. Furthermore, many of these distant galaxies have masses that are comparable to local galaxies (Labbé et al. 2023; Sabti, Muñoz, and Kamionkowski 2024; Stark et al. 2025; Xiao et al. 2024). Given that high redshift galaxies are similar to nearby galaxies in terms of mass, it would be sensible to conclude that they also have a comparable volume. Galaxy merging simulations show that galaxies grow in size by gaining mass. Thus, it was somewhat surprising for secularists to find that high redshift galaxies in JWST data have estimated diameters that are five to ten times smaller than those in the local universe, yet with comparable masses.

But such size estimates depend on a number of assumptions, one of which is that the universe expands in a particular way described mathematically by the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric. The FLRW metric is a solution to Einstein’s field equations when applied to the entire universe under certain simplifying assumptions such as isotropy and homogeneity. The big bang assumes this metric, but the metric itself is compatible with creation models as well.

The FLRW metric predicts a magnification effect that increases with redshift. Namely, an object of a given diameter will appear increasingly small in angular size until reaching a distance corresponding to a redshift of about 1.6, at which point it will appear increasingly large with increasing distance. It is counterintuitive, but objects at redshifts larger than 1.6 look larger and larger as they get farther away. This effect is caused by the expansion of the fabric of space as the light travels through it. The equation describing such magnification is provided in my previous paper (Lisle 2024). Such expansion also causes the light to redshift and naturally explains the Hubble law.

However, this magnification effect is not obvious in any deep field images. Galaxies continue to look smaller with increasing distance, even at redshifts greater than 1.6. Several studies have shown that many high redshift galaxies are about as massive as galaxies in the local universe. So, why do we not see their angular sizes increase systematically with redshift? Two possibilities exist. Either (1) the galaxies in these studies grow over time in linear scale without gaining substantial mass, or (2) the FLRW metric is wrong.

The first possibility would imply that the high redshift galaxies seen in these JWST deep fields are actually five to ten times smaller in diameter than local galaxies while being about the same in mass. This solution would mean that the magnification effect predicted by the FLRW metric does exist, but galaxies grow in such a way so as to cancel it. It would therefore follow that high redshift galaxies are about 1,000 times denser than local galaxies, and that these galaxies decrease in density over cosmic time—expanding without gaining substantial mass. Such an effect is not predicted by computer simulations such as SAGE.

Alternatively, if the FLRW metric is wrong, then perhaps the high redshift galaxies are comparable both in mass and in size to nearby galaxies. This was the conclusion of my previous publication on this topic (Lisle 2024). Namely, if we use a non-expanding metric (such as Minkowski), and assume that redshifts are due entirely to the Doppler effect of a galaxy moving through non-expanding space, then high redshift galaxies are the same both in size and mass to nearby galaxies at all redshifts! Of course, the actual metric of the universe cannot be Minkowski because this metric applies to space with negligible mass. But it is an example of a non-expanding metric in contrast to the FLRW metric.

SAGE

Barnes used the Semi-Analytic Galaxy Evolution (SAGE) model to simulate the evolution of galaxies over time and compute their estimated sizes as a function of redshift (Barnes 2024). I was able to reproduce his results using the same computer simulation with the same parameters. There may be a slight difference in appearance due to the way the data are binned, but the basic result is the same. I then computed the average angular diameter of these galaxies at each redshift assuming the FLRW metric under the standard cosmological parameters. The result is the green curve in fig. 1.

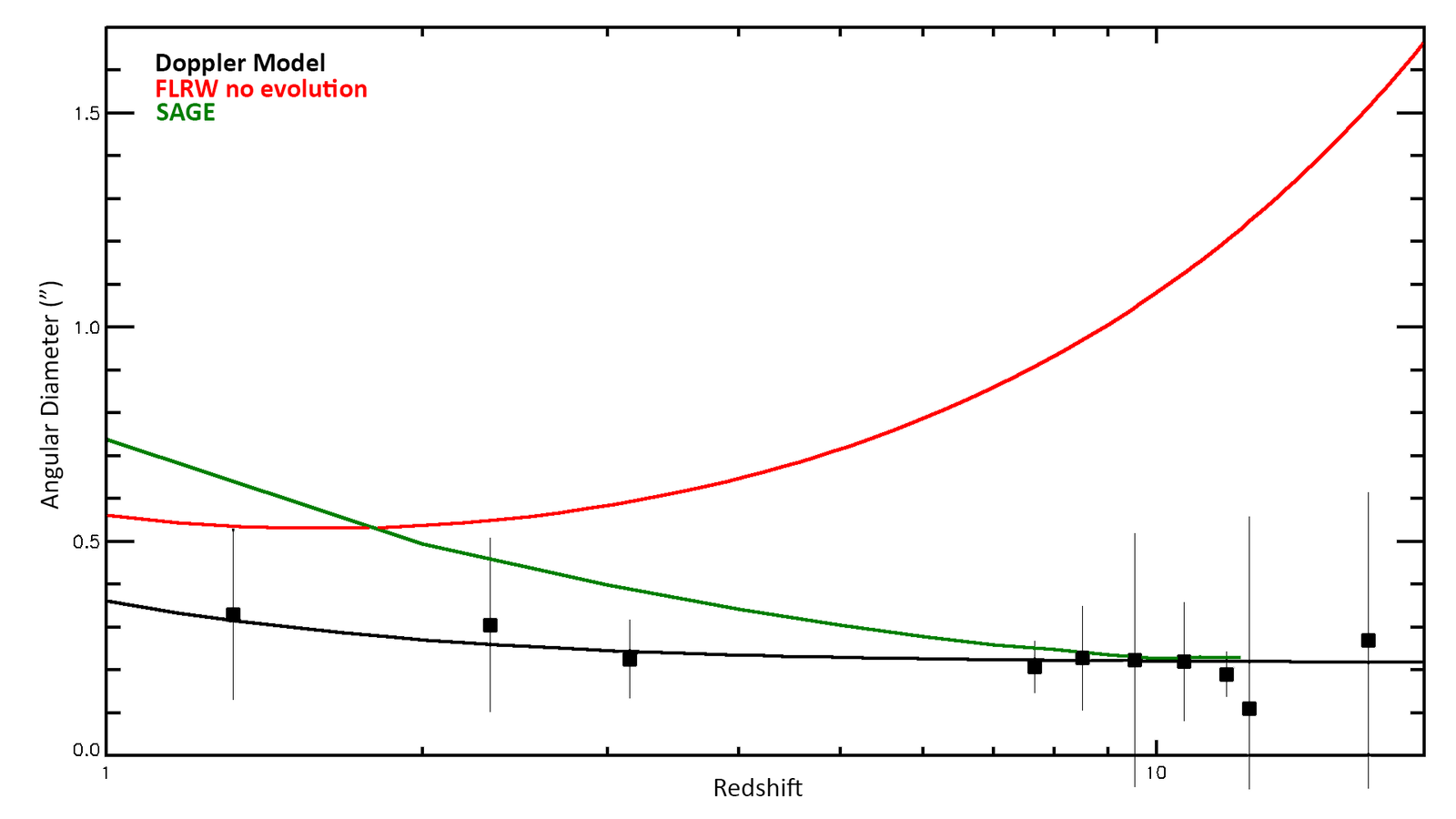
Fig. 1. The average angular diameter of galaxies as a function of redshift for three models is compared with the observational data (squares). The vertical bars indicate the standard deviation.

The boxes are the median observed angular diameters of galaxies from Hubble and JWST deep fields. These are from multiple studies, the details of which are included in my previous paper (Lisle 2024). The black curve is the computed angular size of a 4.5 kpc diameter galaxy as a function of redshift assuming a static metric—namely the Doppler model. The red curve is the angular diameter of a 4.5 kpc diameter galaxy as a function of redshift according to the FLRW metric. The green curve is the average angular diameter of galaxies at each redshift bin according to the SAGE simulation, in which galaxies grow over time.

Barnes states, “By modelling the evolution of this hierarchical structure, the SAGE model shows an adequate consistency with observations.” But does it? The SAGE model does a decent job of fitting the observational data at the high redshifts but is less consistent with observations at lower redshifts. Barnes listed some possible reasons for the inconsistency. Conversely, the Doppler model fits the data at all redshifts and is a much simpler model in that it has virtually no galaxy evolution! I find this absolutely remarkable. In science, a simpler model that fits the data is always preferred to a more complex one.

But the most challenging problem with the SAGE results is the way in which the simulated galaxies gain size. Namely, they do so by gaining mass via mergers. But the high redshift galaxies in the studies we examined already have comparable mass to local galaxies. To my knowledge, no secular simulation predicted this result. Such observations are inconsistent with the SAGE simulation. According to SAGE under the parameters used by Barnes, the average mass of a galaxy at redshift 12 is approximately 80 times less than that of local galaxies! In contrast, JWST observations show that these high redshift galaxies have comparable mass to nearby galaxies. Thus, the SAGE model is eliminated, not on the basis of the size of the galaxies but on the basis of their mass.

In order to accommodate mass estimates of high redshift galaxies from JWST data, astronomers committed to a big bang interpretation would likely assume that galaxy evolution occurred much faster and at an earlier time than previously estimated. Since many studies have shown that many high redshift galaxies are already massive and have similar morphologies to nearby galaxies, it follows that little evolution has occurred between the earlier epochs and the present for those galaxies. Barnes accuses me of a strawman argument here, but in reality, it is simply an accommodation to the observational data. I am aware that secular models did not predict physically large galaxies at high redshifts, but neither did they predict massive galaxies at high redshifts. And the latter are now observationally confirmed.

The Doppler model fits both the angular diameter data and the mass/luminosity data at all redshifts with no substantial galaxy evolution in a non-expanding metric. As I mentioned in my earlier paper (Lisle 2024), there is an alternative way of explaining the data that would allow a FLRW metric. Namely, galaxies must somehow grow larger with time without gaining substantial mass. Furthermore, they must grow in such a way as to match the data at all redshifts. The SAGE simulation suggested by Barnes does not do this. We have already seen that it does not match the angular size data at all redshifts, at least not nearly as well as the Doppler model. And I will now show that it does not match the mass/luminosity data at all.

Galaxy Masses and Luminosities

Galaxies come in a wide range of masses, luminosities, and surface brightnesses. However, statistically, the more mass a galaxy has, the brighter it will be. More mass generally means more stars, which implies higher luminosity. The relationship between mass and luminosity is (statistically) nearly linear (Rojas-Ruiz et al. 2024). That is, a galaxy that is twice as massive as another will be twice as bright on average. In the absence of other data, we can infer, statistically, the masses of galaxies based on their luminosities. The high luminosities of many high redshift galaxies imply that their mass range is comparable to that of the local universe. There is a slight downward trend in estimated luminosity with redshift. But this may be due to an incorrect metric as we show below. In any case, the many high-mass galaxies at high redshifts were not expected by secular models but were predicted by creationists (Lisle 2022).

The SAGE model under the parameters used by Barnes predicts that the average galaxy in the local universe will be 80 times as massive as a galaxy at a redshift of 12. Given that mass is proportional to luminosity, we would therefore expect that galaxies at a redshift of 12 would be about 80 times fainter: a magnitude difference of 4.8. On the other hand, the Doppler model hypothesizes that high redshift galaxies are comparable in both size and luminosity to the local universe. However, the absolute magnitude estimates derived from JWST data assume the FLRW metric. If the true metric is approximately static, then such estimates will be too faint by a factor of 2.5 (1 magnitude) at a redshift of 13. The details of the calculations are included in my previous paper (Lisle 2024). These predictions are compared with the data in fig. 2.

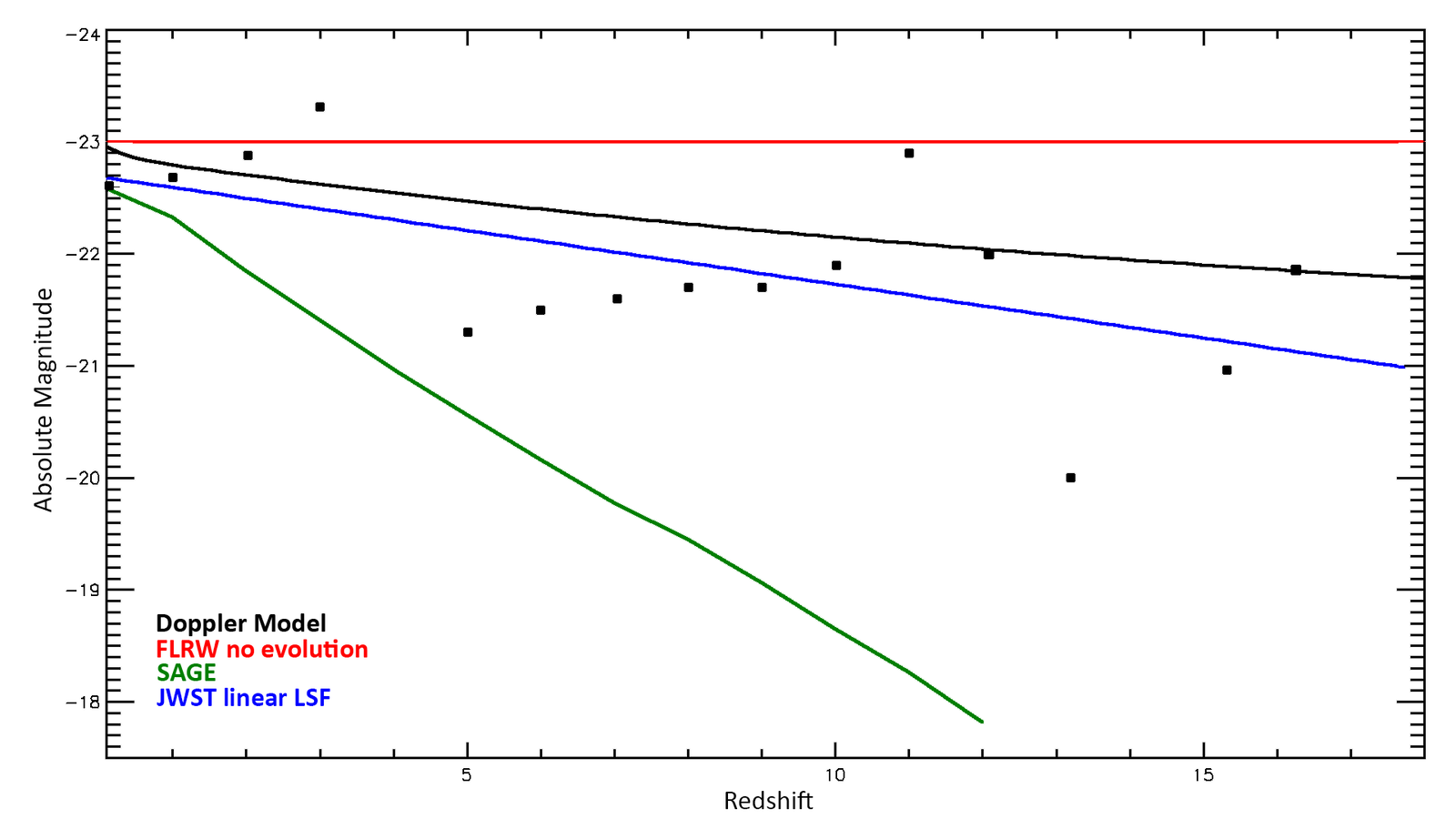
Fig. 2. The relative luminosity of galaxies as a function of redshift for three models is compared with the observed brightest galaxies in each redshift bin (squares). The blue line is the least squares fit of the observational data to a linear function.

The square markers are the estimated magnitude of the brightest galaxy in each redshift bin from JWST observations, assuming the FLRW metric under the standard cosmological parameters. The blue line is a linear least-squares fit to the data to give an indication of the slope. When comparing the models, I have not attempted to estimate the absolute luminosity—only their relative values as a function of redshift. Thus, the model that best matches the slope of the observations is the best fit.

The red line shows the expected absolute magnitudes assuming no evolution with redshift—hence a slope of zero. The black curve is the Doppler model predictions. It seems to match the slope of the observed data very well. The green curve is the predictions of SAGE. Clearly, the SAGE simulation does not remotely match the slope of mass/luminosity estimates of actual galaxies from these JWST deep fields, particularly when projected to higher redshifts. In fact, the FLRW metric with no galaxy evolution actually fits the data better than SAGE. This is why SAGE was not a consideration in my earlier paper; the model had already been eliminated by luminosity observations. The galaxies in the studies under consideration in my previous paper have a luminosity range (and thus mass range) similar to local galaxies as shown in fig. 3 below. To my knowledge, no secular model proposes that galaxies grow in size without gaining substantial mass. Therefore, the conclusion of my original paper stands (Lisle 2024). The secular cosmological models do not fit the observations. The creation-based Doppler model does.

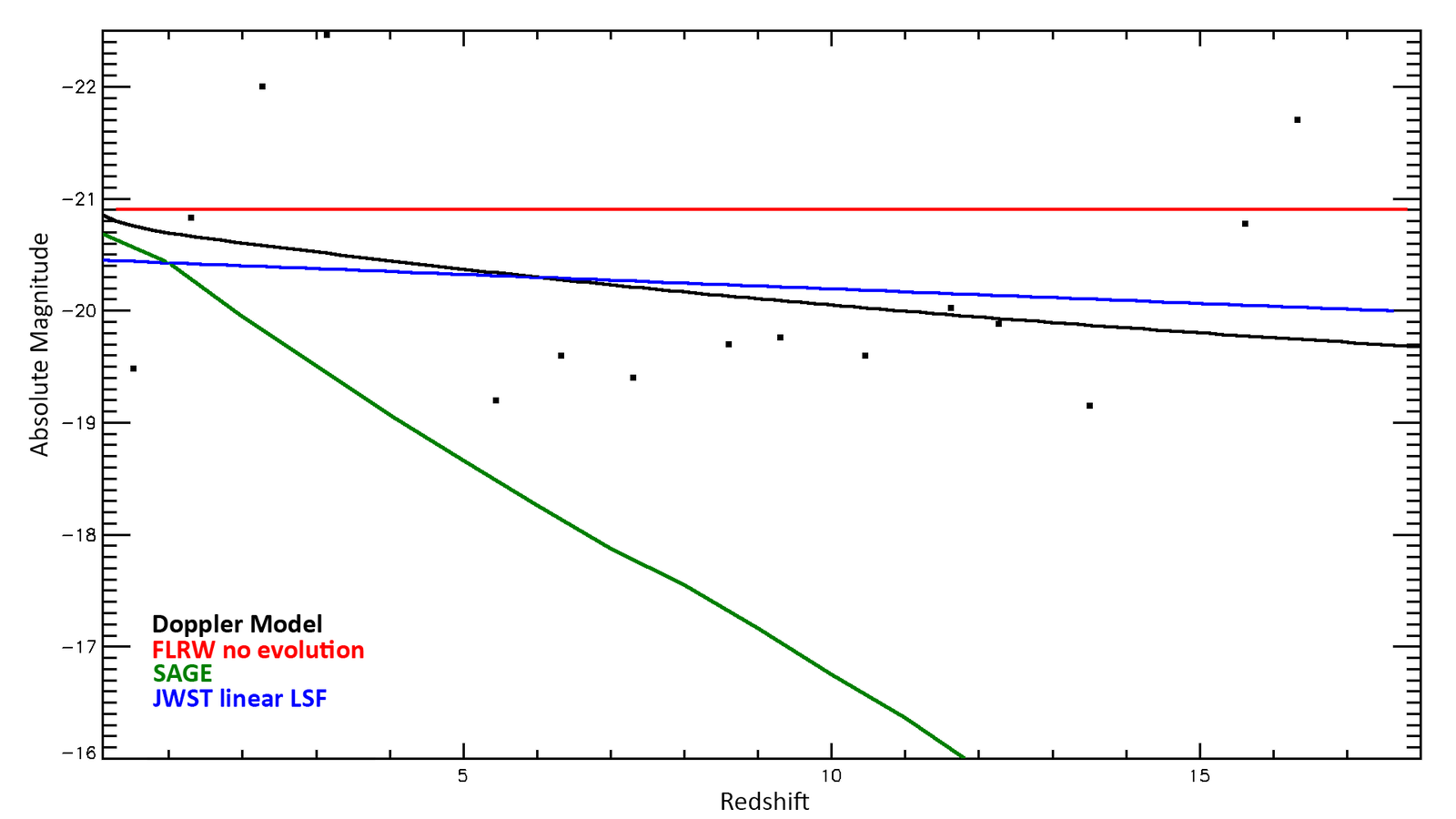
Fig. 3. The relative luminosity of galaxies as a function of redshift for three models is compared with the observed median luminosity in each redshift bin (squares). The blue line is the least squares fit of the observational data to a linear function.

Likewise, if we compare the median luminosity of observed galaxies in each redshift bin of the published studies with that of the Milky Way, we again see that the slope best matches that of the Doppler model, and is not consistent with the predictions of SAGE. See fig. 3. Indeed, the standard model (FLRW) with no galaxy evolution at all (red line) better matches the data than SAGE. We understand that the observational data is likely not capturing many of the lowest luminosity/mass galaxies. Hence, they are underrepresented due to the Malmquist bias. But then again, these would tend to be the smallest galaxies as well and would bias the results of fig. 1 in favor of larger galaxies. Thus, the Malmquist bias does not explain why distant galaxies should appear to have greater density than nearby galaxies. And SAGE does not predict this result. In other words, the Malmquist bias does not explain why SAGE fails to match the observational data.

I will again emphasize that these new observations do not definitively disprove the FLRW metric because new galaxy evolution models could be invoked to explain any discrepancy. However, such models will need to show that galaxies can expand in size in such a way as to match the angular size data at all redshifts. SAGE under the parameters suggested by Barnes does not do this as well as the Doppler model. And they will need to show that such expansion of diameters can occur without a substantial and corresponding increase in mass. SAGE does not. Alternatively, secular astronomers could assume that the mass-luminosity relationship breaks down for high redshift galaxies. That is, they could assume that distant galaxies are anomalously luminous for their mass for whatever reason. If such future models are able to align with the data as well as the Doppler model, then the preferred model will be determined by Occam’s Razor. Namely, which model is simpler?

Other Considerations

I will respond here to a few specific statements by Barnes. He says, “Secondly, the ‘standard model’ prediction of Lisle (2024) bears no resemblance to the actual predictions of the standard model” (Barnes 2024). However, the predictions of the standard model bear no resemblance to the observational data—at least not the mass/luminosity estimates. It is true that I didn’t directly compare the older predictions of the standard model (galaxies slowly growing in both size and mass) because I knew those had already been eliminated by the data. No doubt secular astronomers will develop newer, revised models that are constrained to fit the observational data.

The JWST has shown that many of the highest redshift galaxies are already massive. And to my knowledge, there were no predictions that galaxies grow in size over time without gaining substantial mass. If there were, I would have included them. Certainly, the SAGE model used by Barnes does not. He says, “The increase in masses and physical sizes of haloes and their associated galaxies with time is a firm prediction of analytic, N-body and hydrodynamical simulations of galaxy formation. These models are no secret” (Barnes 2024) [italics added]. But from the observations, we know that many galaxies have not gained substantial mass since a redshift of ~15. These observations are no secret.

Moreover, there was substantial discussion in my paper on galaxy evolution and how galaxies would have to evolve in order to be consistent with observations at all redshifts assuming the FLRW metric under the standard parameters (Lisle 2024). The SAGE model presented by Barnes doesn’t do this because it doesn’t match the size data at all redshifts, and it doesn’t match the mass/luminosity data at all.

Barnes states, “Given the inadequacy of the ‘standard model’ prediction of Lisle (2024), his attempts to perform the Tolman Test should be disregarded” (Barnes 2024). Why? The standard model predictions that JWST would detect only a handful of low-mass galaxies at high redshifts have already failed (Finkelstein et al. 2023; Young 2023). And the newer observations of numerous high mass galaxies at high redshifts, with angular diameters of ~0.2 arcsec, show that the standard model (under any model of stellar evolution so far proposed) does not pass the Tolman test. But it matches the Doppler model extremely well (Lisle 2024). Although this test is not conclusive, there is no reason to dismiss this important result.

He continues, “This is a famously difficult observational test, because galaxies are not ‘standard candles,’ of uniform and predictable luminosity” (Barnes 2024). However, galaxies don’t need to be standard candles to perform the Tolman test. It is a test involving surface brightness (luminosity per unit area) of a large number of galaxies as a function of redshift. The Doppler model proposes that galaxies ranges are approximately comparable at all distances when evaluated using a static metric (as opposed to the FLRW metric). And it works! It gives the correct answer. The standard model does not. Granted, secular astronomers can always invoke galaxy evolution to explain the discrepancy (for example, Lubin and Sandage 2001). The point is that the Doppler model doesn’t need any auxiliary hypotheses to explain the data—as discussed in my original paper (Lisle 2024).

Barnes states, “Lisle (2024) has not even attempted to wrestle with the messy astrophysics required to complete the test—stellar evolution and K-corrections, amongst other things. Thus, no inconsistency can be demonstrated” (Barnes 2024). First, in evaluating the Doppler model, no stellar evolution is required. And while stellar evolution needs to be considered in the standard model, it is not a legitimate reason to dismiss the Tolman test. Furthermore, I discussed the kind of galaxy evolution that would be required to make the standard model compatible with the data. Second, I already showed inconsistency between the mass/luminosity observations and predictions of the standard model. There is indeed inconsistency.

Third, Barnes’s mention of K corrections is perplexing because these only apply to estimating galaxy magnitudes when the light has been redshifted so that much of it no longer falls within the wavelength range of the observing instrument. But the entire point of the JWST was to provide high quality infrared data that would be within the visible range of wavelengths in the rest frame of these galaxies. So, K corrections are not strongly relevant here. Fourth, I used published data regarding luminosity estimates. The astronomers who published such estimates are aware of K corrections. I have written on K corrections and other selection effects in an earlier paper (Lisle 2016). For a more extensive discussion on K corrections, see Hogg et al. (2002).

Barnes states, “It is incorrect for Lisle (2024) to argue that his results ‘suggest that the redshifts of galaxies are entirely the result of a relativistic Doppler effect in non-expanding space’” (Barnes 2024). However, if indeed high redshift galaxies are comparable in linear size to nearby ones, then this is exactly what the data suggest. The expanding metric of FLRW produces a magnification of angular diameter with redshift, whereas a static metric does not. A non-expanding metric with no galaxy evolution matches the observational data at all redshifts.

He continues, “As explained in Peacock (1999, 87), redshifts in all ‘expanding space’ models (FLRW) can be calculated as an accumulation of small Doppler shifts” (Barnes 2024). I agree with Barnes (and Peacock) that this is the case for expanding space models. But the entire point of my paper is that space might not be expanding (Lisle 2024). I am hypothesizing that the FLRW metric is not correct, and that the true metric of the universe may be approximately, and perhaps temporarily, static. At the very least, a non-FLRW metric best accounts for the data.

Therefore, Barnes is mistaken when he says, “In other words, the difference between the ‘expanding space’ picture and the ‘Doppler’ picture is a mere change in perspective, a coordinate transformation. General Relativity is founded on coordinate-independence” (Barnes 2024). However, the metric proposed in the Doppler model is potentially static, and is therefore not merely a coordinate transformation of the (expanding) FLRW metric. They are fundamentally different geometries. A given metric can be expressed using different coordinates, and I have published on the advantages of such (Hamilton and Lisle 2004). Indeed, the difference between ESC and ASC is one of coordinates, leaving the underlying geometry and measurable observations unaffected.

But there is a fundamental difference between an expanding metric like FLRW and a static metric like Minkowski. They are not merely different coordinate systems for expressing the same underlying geometry. Thus, the Doppler model (based on a static metric) makes different observational predictions about the angular size of a given galaxy at a given redshift than the FLRW metric does. That’s the point.

Hence, it is not the case that the Doppler model is “another Big Bang model” or that “the ‘Doppler distance’ is equivalent to the angular diameter distance” (Barnes 2024) when the angular diameter distance has been computed assuming the FLRW metric. Rather, the Doppler model proposes that the visible universe is best represented by an approximately static (non-expanding) metric. As such, it is a radical departure from the FLRW metric that has been assumed for nearly a century. But it accurately predicts the angular sizes and masses/luminosities of galaxies at all redshifts without the need for any galaxy evolution! I find it amazing that such a simple model fits the observational data far better than any of the much more complex secular models.

Barnes is correct when he states, “Lisle proposes to solve this [the distant starlight problem] with the Anisotropic synchrony convention, which implies that we see galaxies as they are now, regardless of how far away they are. This gives the model enough freedom that any observed population of galaxies is consistent with a young universe” (Barnes 2024). Quite right. The Doppler model is not needed to explain distant starlight in a young universe. Rather, it was invoked to explain the angular size and luminosity data in JWST deep fields.

Finally, Barnes concludes with the following statement, “In that case, one might as well attach the [ASC] convention to the Big Bang model and be done with it” (Barnes 2024). Obviously, those of us with a high view of Scripture must reject the big bang since it is not compatible with the details of creation provided in Genesis. Neither the timescale nor the order of events of the big bang match our Creator’s testimony. However, if Barnes means that ASC is compatible with the FLRW metric, then he is correct. The ASC model proposes that the temporal coordinate system used in Scripture is ASC, not ESC. And since the ASC model doesn’t assume any particular metric, it is compatible with either the FLRW metric or the Doppler model.

Why then prefer the Doppler model? It has nothing to do with the issue of distant starlight in a young universe. I stand by the ASC model which answers that question. Rather, I prefer the Doppler model to the FLRW metric because it best fits the observational data from JWST deep fields and does so in a way that is far simpler than the secular models.

Conclusions

The reason that earlier models, like the SAGE model used by Barnes, were not displayed in my earlier paper is because these have already been observationally eliminated by the high luminosities and masses of high redshift galaxies in JWST deep fields (figs. 2 and 3). SAGE under the parameters used by Barnes predicts that the average mass of a galaxy at redshift 12 is 80 times smaller than the average mass of local galaxies. That is not consistent with observations of the cited studies as shown in fig. 3. Presumably, secular astronomers will claim that rapid galaxy evolution happened much earlier in time than previously believed. But then why wouldn’t such massive distant galaxies also be physically large? If the FLRW metric is correct, then many high redshift galaxies are nearly 1,000 times denser than those in the local group. To my knowledge, no secular model had predicted this.

However, such size estimates assume that the fabric of space is expanding according to the FLRW metric. If we instead assume a static metric, then the discrepancy disappears. Under the Doppler model, high redshift galaxies span about the same size and mass range as nearby galaxies. This would imply that no substantial galaxy evolution has taken place. The fit to the data (as shown in figs. 1, 2, and 3) is remarkable.

As I had mentioned in my previous paper, the JWST observations could be interpreted within a FLRW metric if galaxies grow in size over time without gaining substantial mass (Lisle 2024). They would have to do so in such a way as to match the size observations at all redshifts. The SAGE model under the parameters used by Barnes does not do this. It does match the angular size data at high redshifts but not so well at low redshifts. But it does not match the mass/luminosity data at all. So, the Doppler model is currently the only model that fits both size and luminosity data and passes the Tolman test.

Very few advocates of the big bang are willing to read and interact with creation technical literature. And so, I sincerely wish to thank Luke Barnes for his interest and his constructive criticism. I hope that my reply is helpful, clarifying, and advantageous to his own thinking and research.

References

Barnes, Luke A. 2024. “Size of Galaxies in JWST Data and Cosmology—Reply to Lisle.” Answers Research Journal 17 (December 18): 785–789. https://assets.answersresearchjournal.org/doc/v17/galaxies_jwst_data_reply_to_lisle.pdf.

Finkelstein, S, Gene C. K. Leung, Micaela B. Bagley, Mark Dickson, Henry C. Ferguson, Casey Papovich, Hollis B. Akins et al. 2023. “The Complete CEERS Early Universe Galaxy Sample: A Surprisingly Slow Evolution of the Space Density of Bright Galaxies at z ~ 8.5–14.5.” arXiv:2311.04279v1.

Hamilton, Andrew J. S., and Jason P. Lisle. 2004. “The River Model of Black Holes.” arXiv:gr-qc/0411060.

Hogg, David W., Ivan K. Baldry, Michael R. Blanton, and Daniel J. Eisenstein. 2002. “The K Correction.” October 17. http://ned.ipac.caltech.edu/level5/Sept02/Hogg/paper.pdf.

Labbé, Ivo, Pieter van Dokkum, Erica Nelson, Rachel Bezanson, Katherine A. Suess, Joel Leja, Gabriel Brammer, et al. 2023. “A Population of Red Candidate Massive Galaxies ~600 Myr after the Big Bang.” Nature 616, no. 7956 (13 April): 266–269.

Lisle, Jason. 2016. “New Method to Assess the Luminosity Function of Galaxies.” Answers Research Journal 9 (March 30): 67–80. https://answersresearchjournal.org/method-assess-luminosity-function-galaxies/.

Lisle, Jason. 2022. “The James Webb Space Telescope.” January 21. Biblical Science Institute. https://biblicalscienceinstitute.com/astronomy/the-james-webb-space-telescope/.

Lisle, Jason. 2024. “Sizes of Galaxies in JWST Data Suggest New Cosmology.” Answers Research Journal 17 (July 24): 445–457. https://answersresearchjournal.org/cosmology/jwst-data-suggest-new-cosmology/.

Lubin, Lori M. and Allan Sandage. 2001. “The Tolman Surface Brightness Test for the Reality of the Expansion. IV. A Measurement of the Tolman Signal and the Luminosity Evolution of Early-Type Galaxies.” The Astronomical Journal 122, no. 3 (September 1): 1084–1103.

Rojas-Ruiz, Sofia, Micaela B. Bagley, Guido Roberts-Brosani, Tommaso Treu, Steven L. Finkelstein, Takahiro Morishita, Nicha Leethochawalit, et al. 2024. “The BoRG-JWST Survey: Abundance and Mass-to-light Ratio of Luminous z = 7−9 Galaxies from Independent Sight Lines with NIRSpec.” arXiv:2408.00843v1.

Sabti, Nashwan, Julian B. Muñoz, and Marc Kamionkowski. 2024. “Insights from HST into Ultramassive Galaxies and Early-Universe Cosmology.” Physical Review Letters 132, no. 6 (9 February): 061002.

Stark, Daniel P., Michael W. Topping, Ryan Endsley, and Mengtao Tang. 2025. “Observations of the First Galaxies in the Era of JWST.” arXiv:2501.17078v.

Xiao, Mengyuan, Pascal A. Oesch, David Ilbaz, Longji Bing, Erica J. Nelson, Andrea Weibel, Garth D. Illingworth, et al. 2024. “Accelerated Formation of Ultra-Massive Galaxies in the First Billion Years.” Nature 635, no. 8038 (14 November): 311–315.

Young, Monica. 2023. “The James Webb Space Telescope is Finding Too Many Early Galaxies.” Sky & Telescope, January 10.