Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
If extragalactic redshifts are cosmological, then one would expect extragalactic sources to appear fainter with increasing redshift. I show that apparent V magnitude and redshift indeed are correlated in a randomly selected sample of 150 quasars. As a demonstration of the soundness of this test, I applied it to a random sample of 25 “normal” galaxies, showing that their V magnitudes and redshifts are correlated as well. Additionally, if the redshifts of galaxies are cosmological, then one would expect angular diameters of galaxies to decrease with increasing redshift. I demonstrated that this is the case with the sample of 25 galaxies. Therefore, the hypothesis that extragalactic redshifts are cosmological is strongly supported. I encourage fellow recent creationists to abandon their doubts that extragalactic redshifts are cosmological and better focus their work on explaining extragalactic redshifts in terms of a biblical cosmology.
Introduction
I recently reviewed the Hubble relation, cosmological redshifts, and quasars (Faulkner 2018). The major thrust of that paper was to address the widespread doubt among recent creationists that extragalactic redshifts are cosmological, and that the Hubble relation is reliable. Much of that discussion focused on whether quasar redshifts are cosmological and hence are at great distances. That paper also pointed out that recent creationists appear to be unaware that quasars and galaxies are not distinct bins as once thought. Instead, “normal” galaxies and quasars are at opposite ends of a spectrum of characteristics found in extragalactic objects. If one denies that quasars are at great distances, then how does one handle other AGNs1 that often differ from quasars primarily in energy output? Building on that earlier work, I present the results of a simple test of whether quasar redshifts are cosmological.
The Test
If quasar redshifts are cosmological, then one would expect a steady decline in apparent brightness with distance. Begin by making the simplifying assumption that all quasars have the same intrinsic brightness.2 Expressing this assumption in astronomical parlance, we would say that quasars have the same absolute magnitude, M. If distance, d, is expressed in pc then the apparent magnitude, m, is given by
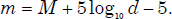
Note that magnitudes are defined in such a way that increasing numerical values correspond to less brightness. Also note that from this equation, apparent magnitude is a function of distance, so that m increases numerically as distance increases. If redshifts are cosmological, then one may in some manner substitute redshift, z, for distance. The exact conversion from distance to redshift is complicated, relying upon what cosmology one assumes, but for low redshifts, z and d are directly proportional. Either way, the fact remains that if redshifts are cosmological, then z or d corresponds with increasing m. Therefore, in a plot of quasar magnitude versus redshift, there ought to be a trend of increasing magnitude with increasing redshift. On the other hand, if quasar redshifts are not cosmological, then there should be no trend in a plot of magnitude versus redshift. Therefore, such a plot amounts to a test of whether redshifts are cosmological or not. Technically, from the above equation, the expected linear relationship is between m and log10 (d) or log10 (z) rather than d or z. However, most observed redshifts are so modest that there is no large difference whether one takes the logarithm or not.
I began with the simple assumption that quasars have the same absolute magnitude, but within the paradigm of cosmological redshifts, quasar luminosities are not all the same. For instance, from a plot in an early paper (Evans and Fala 1974), it appears that the range in absolute magnitudes of quasars is approximately five magnitudes, corresponding to a factor of 100 in brightness. More recently, Sapre and Mishra (1996) considered 21 quasars that, because of their association with nearby bright galaxies with similar redshift, ought not to have much controversy about their redshifts. The derived absolute visual magnitudes of the 21 quasars ranged from −21. 425 to −27.705, a difference of 6.3. In the creation literature, Hartnett (2004) has reproduced a plot of log(z) versus m of more than 7000 quasars from Hewitt and Burbidge (1993). Inspection of that plot shows that the total range in apparent magnitude for a given redshift is slightly larger than the figures above, but that most (> 90%) of quasars fall within a range of five magnitudes.
There are two ways to handle this complication. One way is to select quasars that we have good reason to believe have a narrow range in brightness. The other way is to use a large sample size. If the sample size is sufficiently large, then any trend in magnitude will show up, albeit with a large dispersion in magnitude. I will present the results of both approaches.
In my first method, I used a large sample of quasars taken from the catalogue of Hewitt and Burbidge (1993). Though now 25 years old, this catalogue is still useful, because it was complete up to the end of 1992. More modern quasar catalogues are not so complete. The catalogue contains 7315 objects, nearly all quasars, but also a few BL Lac objects.3 The amount, type, and quality of data that the catalogue drew upon varied widely. In cases of objects with limited data, it is sometimes difficult to distinguish a quasar from a BL Lac object, underscoring the fact that there is a continuum of AGNs. For each quasar, the catalogue listed a name (or names) for each object, its right ascension and declination, V magnitude, B-V color, U-B color,4 z, emission lines present, references, and notes. In a few instances, magnitude, colors, or spectral lines were not listed, because such information was not in the literature at the time. I randomly selected 150 objects from the catalogue. I did this by extracting V and z for the first object listed on the first 156 pages of the catalogue. In the six cases where the first object on a page had no V magnitude, I skipped to the next page. This method spanned from right ascension 00hr 00min to 08hr 43min, encompassing a sample from 38% of the catalogue, covering a little more than a third of the celestial sphere. There is no evidence that quasars have properties that depend upon location in the sky on a large scale, so this sample appears to be random. Furthermore, the sample probably is of sufficient size to overcome the range in absolute magnitudes of quasars.
The plot of the V versus z for this sample is found in Fig. 1. Note that greater magnitude corresponds to lesser brightness, so brightness increases downward. The redshifts range from a little larger than zero to nearly four. As expected, there is much scatter in the vertical direction, because there is a wide range in quasar intrinsic brightness. However, there clearly is a trend of increasing magnitude with increasing redshift, which is expected, if quasar redshifts are cosmological. The line representing a linear regression fit to the data is shown. It has a positive slope, again indicating decreasing brightness with increasing redshift. The magnitudes have greatest spread for low redshift, but there is a tapering in the spread after z = 1.5. Much of this tapering is along the top, where the fainter quasars lie. This almost certainly is a selection effect. Some of the fainter objects at lower redshift may be BL Lac objects, which are intrinsically fainter than quasars, but likely are absent from the data at greater redshift. Furthermore, the plot suggests that there probably is a roughly magnitude 22 cut-off in apparent magnitude in the data. This means that lower luminosity quasars are much more likely to be included at low redshift but are excluded at higher redshift. The lack of lower luminosity quasars at higher redshift reduces the dispersion in magnitude there and causes a flattening of the curve, which is what Fig. 1 shows. This flattening appears to set in a little fainter than magnitude 20. If fainter quasars were included at greater redshift, quasars at magnitude 23 or even 24 would be found at those redshifts. This would make the trend in increasing magnitude with increasing redshift much more obvious.
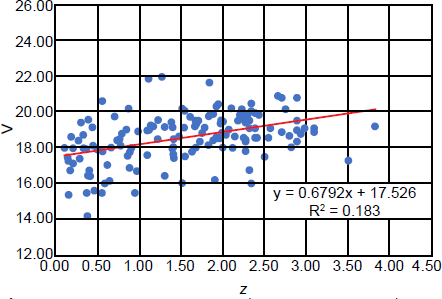
Fig. 1. Plot of apparent V magnitude versus redshift for 150 randomly selected quasars.
To avoid these selection effects to some extent, it would be helpful to use the other method, drawing data from quasars with a more limited range in brightness. The easiest way to do this is to select among the brightest quasars, eliminating the fainter ones, and likely eliminating BL Lac objects as well. Since their discovery more than a half-century ago, the record for the greatest redshift quasar has been set and broken many times. These discoveries often were made using the largest telescopes and most sensitive detectors available at the time, so discoveries of record redshift quasars probably were selecting among the most luminous quasars at any given redshift (the fainter quasars at any given redshift were not detectable, because they were too faint). Therefore, while it is not likely that former redshift record holding quasars have the same intrinsic brightness, the range in their absolute magnitudes ought to have a narrower range than quasars in general catalogues. Table 1 lists 24 quasars that were former record holders for redshift for which I was able to compile both redshifts and V magnitudes. I used SIMBAD (Set of Identifications, Measurements, and Bibliography for Astronomical Data) to select this data. SIMBAD is an interactive website5 hosted by the Centre de Données de Strabourg (Strasbourg Astronomical Data Center, in Strasbourg, France). Astronomers consider SIMBAD to be a very reliable source for astronomical data. The plot of this data is found in Fig. 2. The redshifts are extended from less than four in Fig. 1 to nearly 6.5, an increase of about 70%. The scatter in the magnitudes is slightly less than in Fig. 1, confirming the expectation that this sample set selects from the more luminous quasars. The increase in magnitude with increasing redshift is much more obvious than in Fig. 1. This is further indicated by the greater slope of the linear regression fit to the data.
| Quasar | Redshift | V |
|---|---|---|
| 3C 273 | 0.158 | 12.9 |
| 3C 48 | 0.367 | 16.2 |
| 3C 147 | 0.545 | 17.8 |
| 3C 9 | 2.023 | 18.21 |
| 4C 01.02 | 2.099 | 18.39 |
| 4C 12.39 | 2.12528 | 19.39 |
| PKS 0237-23 | 2.225 | 16.63 |
| 4C 25.05 | 2.384 | 17.5 |
| 5C 02.56 | 2.39237 | 19.71 |
| 4C 05.34 | 2.877 | 18.53 |
| OH471 | 3.408 | 18.49 |
| OQ172 | 3.53 | 17.78 |
| PKS 2000-330 | 3.78 | 18.4 |
| Q1208+1011 | 3.8 | 17.5 |
| Q0046-293 | 4.01 | 19.5 |
| PC 0910+5625 | 4.04 | 20.87 |
| Q000-26 | 4.11 | 17.53 |
| Q0051-279 | 4.43 | 20.5 |
| PC 1158+4635 | 4.73 | 22.42 |
| PC 1247+3406 | 4.897 | 20.4 |
| SDSSp J033829.31+0021563 | 5 | 23.26 |
| SDSS J1030+0524 | 6.309 | 25.44 |
| SDSS J1148.64+525150.3 | 6.419 | 25.04 |
| CFHQS J2329-0301 | 6.43 | 21.7 |
| QSO J1044-0125 | 5.8 | 21.81 |
| J030117.1+002026 | 5.5 | 23.8 |
| QSO J1204-0021 | 5.09201 | 22.94 |
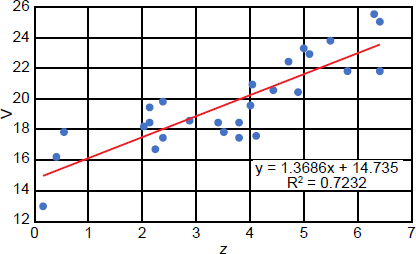
Fig. 2. Plot of apparent V magnitude versus redshift for quasars that are former record holders for largest redshift. All data were taken from SIMBAD.
Finally, I combined both data sets in Fig. 3. The trend in increasing magnitude with increasing redshift is less pronounced than in Fig. 2, but more pronounced than in Fig. 1. The slope of the line representing the linear regression slope is closer to that of Fig. 1 than Fig. 2. This is not surprising, given that the sample size of the data in Fig. 1 is six times larger than the sample size of Fig. 2.
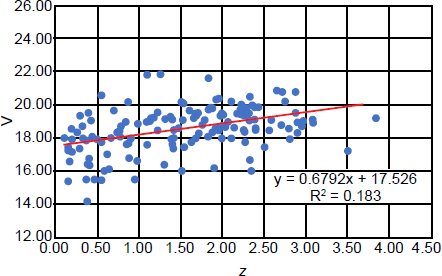
Fig. 3. Combined plot of apparent V magnitude and redshift for 150 randomly selected quasars and former redshift record holders.
Discussion
I anticipate two objections to the methodology employed here. First, within the cosmological redshift paradigm, the relationship between distance and redshift likely is a complex one, so one cannot so simply use redshift as a stand-in for distance. Second, apparent magnitude is not a linear function of distance seemingly implied by fitting a line to the data. These are good points, but they hardly refute the results presented here. First, while redshift and distance are not linearly related, within the cosmological redshift paradigm, a larger redshift always corresponds to greater distance. That is, there are no situations where a greater redshift corresponds to smaller distance. For low redshift, redshift and distance are directly proportional. Within most cosmologies, even at high redshift radical departures from linearity do not exist. Therefore, treating the relationship between redshift and distance as linear ought to work well as a first approximation. Second, by fitting a straight line to the data, I did not intend to imply that apparent magnitude and distance (or redshift) follows a linear relationship. Instead, I merely wanted to emphasize that there was a trend of increasing magnitude with increasing redshift, as predicted by the hypothesis that quasar redshifts are cosmological. The true departure of the data from a linear function probably is a major contributor to the ranges in slopes and y-intercepts of the linear fits to the three sets of data as well as the relatively immodest R-values of the linear fits. Given the non-linear function of the relationship between apparent magnitude and redshift, the slope and y-intercept probably are meaningless physically. For instance, one might think that the slope is related to the Hubble constant, but determining a value for H0 from these slopes would be very difficult to do, if possible at all. And it would depend upon which cosmology one used to make the conversions.
Again, the linear fit to the data ought not to be construed as concluding there is a linear relationship between apparent magnitude and redshift of quasars. Rather, the linear fit merely emphasizes that there clearly is a trend of increasing apparent magnitude with increasing redshift. This trend is predicted by the hypothesis that redshifts of quasars are cosmological. However, the counter-hypothesis, that quasar redshifts are not cosmological, does not make this prediction. If quasar redshifts are independent of distance, then a plot of apparent magnitudes of quasar versus their redshifts ought to be a scatter diagram with no obvious trend. Since this is not the case, this test disproves the hypothesis that quasar redshifts are not cosmological. To the contrary, this test confirms the prediction of the conventional understanding that quasar redshifts are cosmological.
To demonstrate the soundness of this test, I applied it to 25 galaxies, again using data gathered from SIMBAD. To ensure that I had a moderately large range in redshift, I selected one galaxy each from three clusters of galaxies, NGC 4568 from the Virgo Cluster, NGC 4865 from the Coma Cluster, and NGC 1128 from the cluster Abell 400. I randomly selected 22 other galaxies from among NGC galaxies.6 I selected galaxies by searching SIMBAD for NGC objects in bins of 50, starting with NGC 700. I sequentially searched among NGC objects for a suitable galaxy. Upon finding a suitable galaxy, I went to the next bin (the second bin beginning with NGC 750). NGC objects are a mix of galaxies, star clusters, and nebulae, along with a few spurious entries. Of course, I immediately discarded anything other than a galaxy. However, not all galaxies were suitable. All galaxies with NGC designations had redshifts listed, but many did not have V magnitudes.7 I could have used some other magnitude, such as B, which nearly every entry had, but I had used V magnitudes for quasars, and I wanted to keep this test the same for galaxies in every respect. Furthermore, I excluded AGNs, Seyfert galaxies, emission line galaxies, radio galaxies, and galaxies that SIMBAD indicated were large galaxies within groups or clusters, because they are likely to be brighter than normal galaxies. As with the entries in the quasar catalogue I used, NGC numbers increase in terms of right ascension. By the time I got to NGC 1602, the right ascension had increased to include a significant portion of the Milky Way. Obscuration by dust in the galactic plane dims more distant galaxies, and the large density of star clusters and nebulae in the galactic plane resulted in few galaxies among NGC objects in this part of the sky, so I skipped to the bin beginning with NGC 4500 to complete my sample, being careful not to include additional galaxies from the Virgo Cluster found there. The sample included 20 spiral galaxies, four ellipticals, and one irregular. The sample is listed in Table 2.
| Name | Redshift | V magnitude | Angular Diameter arcminutes |
|---|---|---|---|
| NGC 706 | 0.01662 | 12.5 | 1.637 |
| NGC 770 | 0.00882 | 13.49 | 0.643 |
| NGC 821 | 0.00581 | 11.31 | 2.583 |
| NGC 855 | 0.00198 | 12.75 | 2.027 |
| NGC 908 | 0.005 | 10.18 | 5.707 |
| NGC 955 | 0.00506 | 11.97 | 2.057 |
| NGC 1022 | 0.00492 | 11.34 | 2.22 |
| NGC 1055 | 0.00332 | 10.59 | 4.717 |
| NGC 1128 | 0.023 | 13.93 | 0.741 |
| NGC 1184 | 0.0076 | 12.19 | 2.827 |
| NGC 1201 | 0.00567 | 10.64 | 2.76 |
| NGC 1269 | 0.0028 | 8.81 | 5.187 |
| NGC 1300 | 0.00525 | 10.42 | 7.703 |
| NGC 1350 | 0.00637 | 10.52 | 3.843 |
| NGC 1404 | 0.0065 | 10 | 2.4 |
| NGC 1474 | 0.01744 | 13.762 | 1.083 |
| NGC 1510 | 0.00336 | 13.24 | 1.397 |
| NGC 1553 | 0.00403 | 9.4 | 3.573 |
| NGC 1602 | 0.00524 | 13.33 | 0.893 |
| NGC 4568 | 0.00744 | 11.19 | 4.063 |
| NGC 4585 | 0.02433 | 14.6 | 0.95 |
| NGC 4601 | 0.01142 | 14.2 | 1.683 |
| NGC 4706 | 0.01255 | 13.5 | 1.113 |
| NGC 4767 | 0.0099 | 11.53 | 2.077 |
| NGC 4865 | 0.01528 | 13.692 | 0.68 |
Fig. 4 is a plot of magnitude versus redshift for the 25 galaxies. Notice that it has the same general trend as Fig. 1 for quasars, showing an increase in magnitude as redshift increases. This is expected, if galaxy redshifts are cosmological. As before, there is scatter in magnitude at low redshift, though somewhat less scatter than with quasars, probably due to less range in brightness of large galaxies as compared to quasars. Also, as before, there is tapering in the scatter at greater redshift. This tapering again is on the side of greater magnitude, resulting in an apparent flattening in the trend of increasing magnitude with greater redshift. This flattening sets in around z = 0.01 (magnitude 14) in Fig. 4, whereas with quasars, the flattening commenced around z = 1.5. As before, this undoubtedly is due to a selection effect by the limitations of the observations that led to the creation of the New General Catalogue. Indeed, that catalogue was compiled in the late 19th century based entirely upon visual observations using some of the largest telescopes then available. It appears from this data that the cut-off of detection was between magnitude 14 and 15. Much larger modern telescopes and very sensitive detectors today have raised this limit by nearly 20 magnitudes. Again, the trends discussed here are similar to those for quasars in Fig. 1, giving confidence that these trends are real.
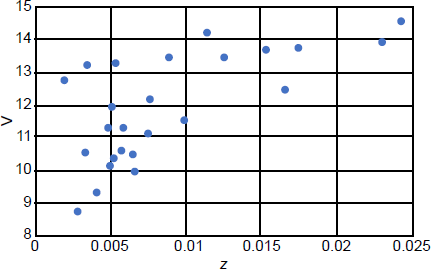
Fig. 4. Plot of apparent V magnitude versus redshift for 25 randomly selected galaxies.
I can quantify the comparison of the flattening trends in the two plots. The ratio of the redshifts where the two plots flatten is 1.5/0.01 = 150. Light decreases with the inverse square of the distance. Therefore, if redshifts are at least approximately proportional to distance, then this ratio corresponds to a factor of 1502 = 22,500 in brightness. Expressing this in magnitudes, Δm = 2.5 log (22,500) = 10.9, which rounds to 11. Within the cosmological redshift paradigm, quasars are about 100 times brighter than galaxies. A factor of 100 in brightness corresponds to a difference of five magnitudes, so the difference between the two curves ought to be about six magnitudes. The flattening trend of Fig. 1 sets in a little fainter than magnitude 20, while the flattening trend of Fig. 4 sets in around magnitude 14. Therefore, the flattening of the two plots conforms to expectation.
There is an additional test that can be applied to galaxies that we cannot apply to quasars. Galaxies are large objects, so they subtend measurable angular diameters on the sky. Assuming that galaxies are the same size, angular diameters of galaxies ought to decrease with increasing distance. Therefore, if galaxy redshifts are cosmological, then there ought to be a linear relationship between galaxy angular diameters and redshift (the redshifts are so small in the galaxy sample here that redshifts and distance ought to be directly proportional, regardless of cosmological models). SIMBAD listed angular sizes, in arcminutes, for all the galaxies in the sample. Each galaxy had two angular sizes, one across the longest diameter, and the other across the shortest diameter. Most galaxies in the sample were spirals, which have round, flat disks. The orientation would affect the shortest diameter, but not the largest, which is what I extracted. These angular diameters are listed in Table 2, and the angular diameters are plotted versus redshift in Fig. 5.
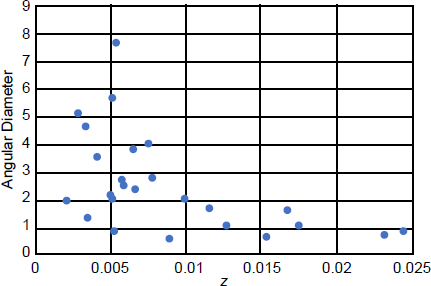
Fig. 5. Plot of angular diameter (in arcminutes) versus redshift for 25 randomly selected galaxies.
Notice that for z < 0.01 there is a general decrease in angular diameter with increasing redshift. This trend flattens out around z = 0.01, the same point where the trend in Fig. 4 flattened out. This flattening probably is due to the same selection effect as in Fig. 4. I had made the simplifying assumption that galaxies in my sample have the same size, but that is only approximately true. Larger galaxies ought to contain more stars, and hence appear brighter. Therefore, the galaxies in the sample at greater redshift (distance) tend to be among the brighter, and hence larger, galaxies, leaving out smaller, fainter galaxies at larger redshift. There is a way to confirm this bias. Notice that in the lower left in Fig. 5 there are three outliers. These three galaxies appear to be smaller than galaxies of similar low redshifts, having angular diameters similar to galaxies with z > 0.1. But notice that in the upper left of Fig. 4 there are three outliers at low redshift. These appear to be galaxies that are under luminous. These are the same three outliers in Fig. 5 (NGC 855, NGC 1510, and NGC 1603). Clearly, these three galaxies are both smaller and less luminous than the other galaxies in the sample. I had assumed (crudely) that galaxies have the same intrinsic brightness, and likely the same size. These three galaxies obviously violate that assumption, so what do these two distributions look like with the three outliers removed? The data for the remaining 22 galaxies are replotted in Figs. 6 and 7. Both trends noted above, increasing magnitude with increasing redshift, and decreasing angular size with increasing redshift, for galaxies with z < 0.01, are much stronger. Therefore, I have presented two lines of evidence that extragalactic redshifts are cosmological.
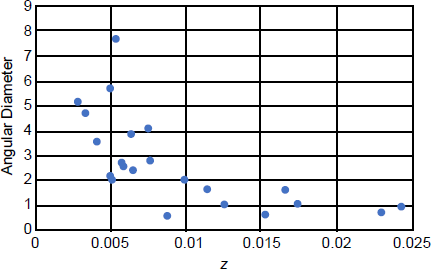
Fig. 6. Replot of Fig. 4 without the three outlier galaxies.
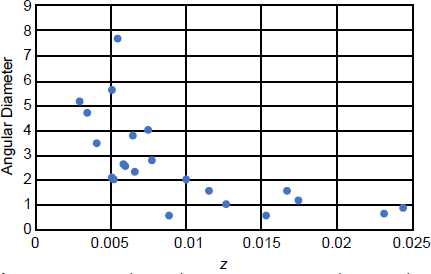
Fig. 7. Replot of Fig. 5 without the three outlier galaxies. Angular diameters are in arcminutes.
Conclusion
As discussed in Faulkner (2018), many recent creationists express doubts that extragalactic redshifts are cosmological. While some recent creationists are doubtful only about quasar redshifts, others are doubtful about galaxy redshifts as well. If extragalactic redshifts are cosmological, then one would expect that apparent magnitude of extragalactic objects would increase with increasing redshift. I have shown here that this relationship is followed for both quasars and “normal” galaxies. Therefore, the hypothesis that extragalactic redshifts are cosmological is confirmed. I also have shown that galaxy angular diameters decrease with increasing redshift, an additional test that confirms that galaxy redshifts are cosmological. Therefore, doubt that extragalactic redshifts are cosmological is unfounded, and recent creationists ought to abandon this doubt. It would be much more productive if extragalactic redshifts were incorporated into developing a recent creation cosmology rather than spending time arguing against cosmological redshifts. For instance, local quasar density is very low, which is easily explained in the evolutionary paradigm as evolving galaxies. However, there is no explanation for this in the creationary paradigm, because so few recent creationists have taken cosmological redshifts seriously.
Note that data presented here do not address the cause of extragalactic redshifts, but they show only that distance and redshift are correlated. Hence, the Hubble relation may be used to find extragalactic distances with some confidence. Expansion of the universe is the simplest, most direct interpretation of the Hubble relation. Furthermore, general relativity predicted universal expansion prior to discovery of the Hubble relation, so the Hubble relation amounts to confirmation of that prediction. Therefore, there is good reason to accept that the universe is expanding. If the universe is expanding, and if extragalactic redshifts are cosmological, then we have little hope of developing a proper biblical cosmology if we deny both.
Could the methodology practiced here be improved upon? Certainly. The sample size could be increased tremendously. However, as one probes to ever more distant and fainter extragalactic objects, the available data lessens. For instance, as I noted earlier, I was surprised with the lack of V magnitudes for many galaxies. It is clear enough that the expected trends are in the data presented here, so the sample sizes were sufficient. I made no correction for extinction due to dust. However, the extragalactic objects selected have relatively high galactic latitude, so extinction probably is no more than a few tenths of a magnitude at most. This is dwarfed by the scatter due to dispersion in absolute magnitudes of galaxies and quasars, so consideration of interstellar extinction hardly would have changed the results. Future studies that extend this work would be most welcome.
References
Evans, A., and D. Falla, 1974. “Absolute Magnitudes for Quasars with Cosmological Redshifts.” The Observatory 94: 45–50.
Faulkner, D. R. 2017. “Are Old Supernova Remnants Really Missing? Re-Evaluating a Well-Known Young-Universe Argument.” Answers Research Journal 10: 245–258.
Faulkner, D. R. 2018. “The Case for Cosmological Redshifts.” Answers Research Journal 11: 31–47.
Hartnett, J. G. 2004. “Quantized Quasar Redshifts in a Creationist Cosmology.” TJ 18 (2): 105–113.
Hewitt, A., and G. Burbidge. 1993. “A Revised and Updated Catalog of Quasi-Stellar Objects.” Astrophysical Journal Supplement Series 87 (2): 451–947.
Sapre, A. K., and V. D. Mishra. 1996. “On the Hubble Diagram of QSOs with Cosmological Redshifts.” Bulletin of the Astronomical Society of India 24: 815–818.
Appendix
Astronomers usually express stellar brightness with magnitudes. This is a very old system (going back at least to Ptolemy in the 2nd century AD) that is based upon the logarithmic response of the eye. The Pogson scale, established in 1856, defines a magnitude difference of five to correspond exactly to a ratio of brightness of 100. Expressed mathematically, this is:
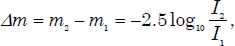
where m is the magnitude and I is the brightness. Note that magnitudes are defined in such a way that higher positive numbers correspond to fainter stars. Also notice that this definition only relates differences in magnitudes without a zero point. However, a zero point has been established by a system of standard stars with magnitudes based upon differences from an agreed upon zero point. Therefore, astronomers making magnitude measurements can calibrate their measurements by referencing their measurements to these standard stars.
Until photography first was employed to measure stellar brightness in the late 19th century, all magnitude measurements were done visually. Astronomers quickly realized that photographically determined magnitudes did not always match those determined visually. This is because of a difference in wavelength response between the eye and the photographic emulsion then in use. The eye’s peak sensitivity is in the yellow-green part of the spectrum, approximately at the center of the range of what the eye can see. However, the original black and white photographic emulsions were most sensitive in blue, with little or no response in the red. Furthermore, the sensitivity of the photographic emulsion extended into the ultraviolet, which the eye cannot see. To distinguish between magnitudes measured these different ways, the symbols mv and mpg were used, with the subscripts meaning “visual” and “photographic,” respectively. Eventually, a photographic emulsion that mimicked what the eye saw was developed, though it did not exactly reproduce what the eye sees. Magnitudes measured this way are termed photovisual, indicated by mpv.
In the 20th century, much more sensitive photoelectric tubes came to be employed to measure stellar brightness. Many of these tubes had broad spectral responses, but since so many visual and photographic magnitude measurements already existed, it was desirable to develop a system so that the new photoelectric measurements would match those made visually and photographically. This was done with a system of filters selected for a particular photoelectric tube’s spectral response. Astronomers decided to call the photoelectric measurements that matched visual measurements V (for visual) magnitude, and the measurements to match photographic magnitudes B (for blue). Additionally, since most photoelectric tubes had significant ultraviolet response, filters were developed to measure U (for ultraviolet) magnitudes. These are considered broad-band filters. Later, a system of intermediate-band filters was developed. To distinguish the two, lower case letters are used for intermediate-band filters. Both systems have been extended into the red and infrared parts of the spectrum. And both systems have been adapted with appropriate filters to match modern CCD (charge coupled device) chips used to measure most stellar magnitudes today.
There are many advantages to having multiwavelength measurements. For instance, because stars have different temperatures, their spectra peak at different wavelengths. Consequently, while the magnitudes of two stars may match in one bandpass, they may not match in another. We can use this to our advantage by taking the difference in magnitude measurements of a star in two different bandpasses. One of the most common of these is B-V. Since these two bandpasses span a part of the spectrum that is highly dependent upon temperature, B-V is a very effective way to express a star’s temperature. Since stellar color is a function of temperature, B-V also expresses the color of a star very well. For instance, a very (hot) blue star has a B-V of −0.10, a red (cool) star has a color of +1.70, and a yellow (medium temperature) star (such as the sun) has a B-V of about +0.60. Astronomers have generalized this to call any difference in magnitude measurements of a star taken at two bandpasses a color.
The magnitudes discussed here are apparent magnitudes, a measure of how bright a star appears. However, how bright a star appears depends upon both the star’s intrinsic brightness and how far the star is. If we know a star’s distance, we can express the star’s intrinsic brightness in terms of its absolute magnitude, defined by the apparent magnitude a star would have if it were at a standard distance of 10 parsecs (pc). To distinguish between apparent magnitude and absolute magnitude, we use m to indicate apparent magnitude and M to indicate absolute magnitude. With knowledge of the inverse square law of the intensity of light with distance, combined with the equation above, the relationship between m and M is,
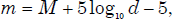
where d is the star’s distance in pc.
It is standard practice consistently to refer to absolute magnitude with M appended by any appropriate subscript, such as MV for absolute V magnitude. However, it is common to express apparent magnitudes with the appropriate bandpass used. For instance, V is used to express apparent V magnitude rather than mV.











